Как найти квантиль хи квадрат - Сайт, где вы сможете решить свои вопросы

Кванти́ли распределе́ния хи-квадра́т — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов, проверка статистических гипотез и непараметрическое оценивание.

Квантиль хи-квадрат — это число (величина хи-квадрат), при котором функция распределения хи-квадрат равна заданной (затребованной) вероятности а.

Равенство функции распределения хи-квадрат вероятности а означает, что с вероятностью а будут наблюдаться значения хи-квадрат, не большие, чем найденный (определенный согласно функции распределения) квантиль хи-квадрат. Таким образом, найти квантиль означает разграничить распределения хи-квадрат согласно заданной вероятности а.

Определение[править | править код]

Пусть $F_{n}$ — функция распределения хи-квадрат $chi ^{2}(n)$ с степенями свободы, и . Тогда alpha -квантилем этого распределения называется число $chi _{alpha ,n}^{2}$ такое, что

$F_{n}left(chi _{{alpha ,n}}^{2}right)=alpha$

Замечания[править | править код]

$F_{n}^{{-1}}(alpha )=chi _{{alpha ,n}}^{2}$

Функция $F_{n}^{{-1}}$ не имеет простого представления. Однако, возможно вычислить её значения численно.

Аппроксимация квантилей[править | править код]

Для получения приближенных значений квантилей распределения хи-квадрат $chi _{{alpha ,n}}^{{2}}$ существуют аппроксимации.

Аппроксимация Корниша-Фишера^[1]

$chi _{{alpha ,n}}^{{2}}=n+A{sqrt {n}}+B+{frac {C}{{sqrt {n}}}}+{frac {D}{n}}+{frac {E}{n{sqrt {n}}}}$ ,

где:

$B={frac {2}{3}}left({{d}^{{2}}}-1right)$

$C=dcdot {frac {{{d}^{{2}}}-7}{9{sqrt {2}}}}$

$D={frac {6{{d}^{{4}}}+14{{d}^{{2}}}-32}{405}}$

$E=dcdot {frac {9{{d}^{{4}}}+256{{d}^{{2}}}-433}{4860{sqrt {2}}}}$

$d=2.0637cdot {{left(ln {frac {1}{1-alpha }}-0.16right)}^{{0.4274}}}-1.5774$ при

$d=-2.0637cdot {{left(ln {frac {1}{alpha }}-0.16right)}^{{0.4274}}}+1.5774$ при

Аппроксимация Голдштейна^[2]

$chi _{{alpha ,n}}^{{2}}=ncdot {{left[sum limits _{{i=0}}^{{6}}{{{n}^{{-{frac {i}{2}}}}}cdot {{d}^{{i}}}cdot left({{a}_{{i}}}+{frac {{{b}_{{i}}}}{n}}+{frac {{{c}_{{i}}}}{{{n}^{{2}}}}}right)}right]}^{{3}}}$ ,

где d определяется аналогично, а коэффициенты a, b,c приведены в таблице

a	b	c
1.0000886	-0.2237368	-0.01513904
0.4713941	0.02607083	-0.008986007
0.0001348028	0.01128186	0.02277679
-0.008553069	-0.01153761	-0.01323293
0.00312558	0.005169654	-0.006950356
-0.0008426812	0.00253001	0.001060438
0.00009780499	-0.001450117	0.001565326

Таблица квантилей[править | править код]

Нижеприведённая таблица получена с помощью функции chi2inv Архивная копия от 4 декабря 2009 на Wayback Machine пакета MATLAB.

Также квантили можно получить с помощью других программных средств:

пакет LibreOffice, электронная таблица Calc, функция CHIINV Архивная копия от 14 ноября 2012 на Wayback Machine.
библиотека scipy для языка python, функция scipy.stats.distributions.chi2.ppf Архивная копия от 7 марта 2016 на Wayback Machine

Чтобы получить значение $chi _{alpha ,n}^{2}$ , необходимо найти строку, соответствующую нужному , и колонку, соответствующую нужному alpha . Искомое число находится в таблице на их пересечении.
Например:

$chi _{{0.025,10}}^{2}=3.2470$

;

$chi _{{0.975,10}}^{2}=20.4832$

Квантили $chi _{alpha ,n}^{2}$

	0,01	0,025	0,05	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95	0,975	0,99
1	0,0002	0,0010	0,0039	0,0158	0,0642	0,1485	0,2750	0,4549	0,7083	1,0742	1,6424	2,7055	3,8415	5,0239	6,6349
2	0,0201	0,0506	0,1026	0,2107	0,4463	0,7133	1,0217	1,3863	1,8326	2,4079	3,2189	4,6052	5,9915	7,3778	9,2103
3	0,1148	0,2158	0,3518	0,5844	1,0052	1,4237	1,8692	2,3660	2,9462	3,6649	4,6416	6,2514	7,8147	9,3484	11,3449
4	0,2971	0,4844	0,7107	1,0636	1,6488	2,1947	2,7528	3,3567	4,0446	4,8784	5,9886	7,7794	9,4877	11,1433	13,2767
5	0,5543	0,8312	1,1455	1,6103	2,3425	2,9999	3,6555	4,3515	5,1319	6,0644	7,2893	9,2364	11,0705	12,8325	15,0863
6	0,8721	1,2373	1,6354	2,2041	3,0701	3,8276	4,5702	5,3481	6,2108	7,2311	8,5581	10,6446	12,5916	14,4494	16,8119
7	1,2390	1,6899	2,1673	2,8331	3,8223	4,6713	5,4932	6,3458	7,2832	8,3834	9,8032	12,0170	14,0671	16,0128	18,4753
8	1,6465	2,1797	2,7326	3,4895	4,5936	5,5274	6,4226	7,3441	8,3505	9,5245	11,0301	13,3616	15,5073	17,5345	20,0902
9	2,0879	2,7004	3,3251	4,1682	5,3801	6,3933	7,3570	8,3428	9,4136	10,6564	12,2421	14,6837	16,9190	19,0228	21,6660
10	2,5582	3,2470	3,9403	4,8652	6,1791	7,2672	8,2955	9,3418	10,4732	11,7807	13,4420	15,9872	18,3070	20,4832	23,2093
11	3,0535	3,8157	4,5748	5,5778	6,9887	8,1479	9,2373	10,3410	11,5298	12,8987	14,6314	17,2750	19,6751	21,9200	24,7250
12	3,5706	4,4038	5,2260	6,3038	7,8073	9,0343	10,1820	11,3403	12,5838	14,0111	15,8120	18,5493	21,0261	23,3367	26,2170
13	4,1069	5,0088	5,8919	7,0415	8,6339	9,9257	11,1291	12,3398	13,6356	15,1187	16,9848	19,8119	22,3620	24,7356	27,6882
14	4,6604	5,6287	6,5706	7,7895	9,4673	10,8215	12,0785	13,3393	14,6853	16,2221	18,1508	21,0641	23,6848	26,1189	29,1412
15	5,2293	6,2621	7,2609	8,5468	10,3070	11,7212	13,0297	14,3389	15,7332	17,3217	19,3107	22,3071	24,9958	27,4884	30,5779
16	5,8122	6,9077	7,9616	9,3122	11,1521	12,6243	13,9827	15,3385	16,7795	18,4179	20,4651	23,5418	26,2962	28,8454	31,9999
17	6,4078	7,5642	8,6718	10,0852	12,0023	13,5307	14,9373	16,3382	17,8244	19,5110	21,6146	24,7690	27,5871	30,1910	33,4087
18	7,0149	8,2307	9,3905	10,8649	12,8570	14,4399	15,8932	17,3379	18,8679	20,6014	22,7595	25,9894	28,8693	31,5264	34,8053
19	7,6327	8,9065	10,1170	11,6509	13,7158	15,3517	16,8504	18,3377	19,9102	21,6891	23,9004	27,2036	30,1435	32,8523	36,1909
20	8,2604	9,5908	10,8508	12,4426	14,5784	16,2659	17,8088	19,3374	20,9514	22,7745	25,0375	28,4120	31,4104	34,1696	37,5662
21	8,8972	10,2829	11,5913	13,2396	15,4446	17,1823	18,7683	20,3372	21,9915	23,8578	26,1711	29,6151	32,6706	35,4789	38,9322
22	9,5425	10,9823	12,3380	14,0415	16,3140	18,1007	19,7288	21,3370	23,0307	24,9390	27,3015	30,8133	33,9244	36,7807	40,2894
23	10,1957	11,6886	13,0905	14,8480	17,1865	19,0211	20,6902	22,3369	24,0689	26,0184	28,4288	32,0069	35,1725	38,0756	41,6384
24	10,8564	12,4012	13,8484	15,6587	18,0618	19,9432	21,6525	23,3367	25,1063	27,0960	29,5533	33,1962	36,4150	39,3641	42,9798
25	11,5240	13,1197	14,6114	16,4734	18,9398	20,8670	22,6156	24,3366	26,1430	28,1719	30,6752	34,3816	37,6525	40,6465	44,3141
26	12,1981	13,8439	15,3792	17,2919	19,8202	21,7924	23,5794	25,3365	27,1789	29,2463	31,7946	35,5632	38,8851	41,9232	45,6417
27	12,8785	14,5734	16,1514	18,1139	20,7030	22,7192	24,5440	26,3363	28,2141	30,3193	32,9117	36,7412	40,1133	43,1945	46,9629
28	13,5647	15,3079	16,9279	18,9392	21,5880	23,6475	25,5093	27,3362	29,2486	31,3909	34,0266	37,9159	41,3371	44,4608	48,2782
29	14,2565	16,0471	17,7084	19,7677	22,4751	24,5770	26,4751	28,3361	30,2825	32,4612	35,1394	39,0875	42,5570	45,7223	49,5879
30	14,9535	16,7908	18,4927	20,5992	23,3641	25,5078	27,4416	29,3360	31,3159	33,5302	36,2502	40,2560	43,7730	46,9792	50,8922
31	15,6555	17,5387	19,2806	21,4336	24,2551	26,4397	28,4087	30,3359	32,3486	34,5981	37,3591	41,4217	44,9853	48,2319	52,1914
32	16,3622	18,2908	20,0719	22,2706	25,1478	27,3728	29,3763	31,3359	33,3809	35,6649	38,4663	42,5847	46,1943	49,4804	53,4858
33	17,0735	19,0467	20,8665	23,1102	26,0422	28,3069	30,3444	32,3358	34,4126	36,7307	39,5718	43,7452	47,3999	50,7251	54,7755
34	17,7891	19,8063	21,6643	23,9523	26,9383	29,2421	31,3130	33,3357	35,4438	37,7954	40,6756	44,9032	48,6024	51,9660	56,0609
35	18,5089	20,5694	22,4650	24,7967	27,8359	30,1782	32,2821	34,3356	36,4746	38,8591	41,7780	46,0588	49,8018	53,2033	57,3421
36	19,2327	21,3359	23,2686	25,6433	28,7350	31,1152	33,2517	35,3356	37,5049	39,9220	42,8788	47,2122	50,9985	54,4373	58,6192
37	19,9602	22,1056	24,0749	26,4921	29,6355	32,0532	34,2216	36,3355	38,5348	40,9839	43,9782	48,3634	52,1923	55,6680	59,8925
38	20,6914	22,8785	24,8839	27,3430	30,5373	32,9919	35,1920	37,3355	39,5643	42,0451	45,0763	49,5126	53,3835	56,8955	61,1621
39	21,4262	23,6543	25,6954	28,1958	31,4405	33,9315	36,1628	38,3354	40,5935	43,1053	46,1730	50,6598	54,5722	58,1201	62,4281
40	22,1643	24,4330	26,5093	29,0505	32,3450	34,8719	37,1340	39,3353	41,6222	44,1649	47,2685	51,8051	55,7585	59,3417	63,6907
41	22,9056	25,2145	27,3256	29,9071	33,2506	35,8131	38,1055	40,3353	42,6506	45,2236	48,3628	52,9485	56,9424	60,5606	64,9501
42	23,6501	25,9987	28,1440	30,7654	34,1574	36,7550	39,0774	41,3352	43,6786	46,2817	49,4560	54,0902	58,1240	61,7768	66,2062
43	24,3976	26,7854	28,9647	31,6255	35,0653	37,6975	40,0496	42,3352	44,7063	47,3390	50,5480	55,2302	59,3035	62,9904	67,4593
44	25,1480	27,5746	29,7875	32,4871	35,9743	38,6408	41,0222	43,3352	45,7336	48,3957	51,6389	56,3685	60,4809	64,2015	68,7095
45	25,9013	28,3662	30,6123	33,3504	36,8844	39,5847	41,9950	44,3351	46,7607	49,4517	52,7288	57,5053	61,6562	65,4102	69,9568
46	26,6572	29,1601	31,4390	34,2152	37,7955	40,5292	42,9682	45,3351	47,7874	50,5071	53,8177	58,6405	62,8296	66,6165	71,2014
47	27,4158	29,9562	32,2676	35,0814	38,7075	41,4744	43,9417	46,3350	48,8139	51,5619	54,9056	59,7743	64,0011	67,8206	72,4433
48	28,1770	30,7545	33,0981	35,9491	39,6205	42,4201	44,9154	47,3350	49,8401	52,6161	55,9926	60,9066	65,1708	69,0226	73,6826
49	28,9406	31,5549	33,9303	36,8182	40,5344	43,3664	45,8895	48,3350	50,8660	53,6697	57,0786	62,0375	66,3386	70,2224	74,9195
50	29,7067	32,3574	34,7643	37,6886	41,4492	44,3133	46,8638	49,3349	51,8916	54,7228	58,1638	63,1671	67,5048	71,4202	76,1539

См. также[править | править код]

Доверительный интервал для дисперсии нормальной выборки.

Примечания[править | править код]

↑ Golberg H., Levine H. Approximate formulas for the percentage points and normalization of t and $chi ^{2}$ // AMS. 1945. V.17. P. 216—225.
↑ Goldstein R.B. Chi-square quantiles, Algorithm 451 // Commun. Assoc. Comp. 1973. V. 16. P. 483—485.

Источник

Кванти́ли (проценти́ли) распределе́ния хи-квадра́т — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов, проверка статистических гипотез и непараметрическое оценивание.

Определение

Пусть ${displaystyle F_{n}}$ — функция распределения хи-квадрат ${displaystyle chi ^{2}(n)}$ с степенями свободы, и . Тогда -квантилью этого распределения называется число ${displaystyle chi _{alpha ,n}^{2}}$ такое, что

${displaystyle F_{n}left(chi _{alpha ,n}^{2}right)=alpha }$

Замечания

${displaystyle F_{n}^{-1}(alpha )=chi _{alpha ,n}^{2}}$

Функция ${displaystyle F_{n}^{-1}}$ не имеет простого представления. Однако, возможно вычислить её значения численно.

Таблица квантилей

Нижеприведённая таблица получена с помощью функции chi2inv пакета MATLAB. Чтобы получить значение ${displaystyle chi _{alpha ,n}^{2}}$ , необходимо найти строку, соответствующую нужному , и колонку, соответствующую нужному . Искомое число находится в таблице на их пересечении.

Пример

${displaystyle chi _{0.025,10}^{2}=3.2470}$

;

${displaystyle chi _{0.975,10}^{2}=20.4832}$

См, также

Распределение хи-квадрат;
Доверительный интервал для дисперсии нормальной выборки,

Квантили ${displaystyle chi _{alpha ,n}^{2}}$

Шаблон:Rq

	0,01	0,025	0,05	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95	0,975	0,99
1	0,0002	0,0010	0,0039	0,0158	0,0642	0,1485	0,2750	0,4549	0,7083	1,0742	1,6424	2,7055	3,8415	5,0239	6,6349
2	0,0201	0,0506	0,1026	0,2107	0,4463	0,7133	1,0217	1,3863	1,8326	2,4079	3,2189	4,6052	5,9915	7,3778	9,2103
3	0,1148	0,2158	0,3518	0,5844	1,0052	1,4237	1,8692	2,3660	2,9462	3,6649	4,6416	6,2514	7,8147	9,3484	11,3449
4	0,2971	0,4844	0,7107	1,0636	1,6488	2,1947	2,7528	3,3567	4,0446	4,8784	5,9886	7,7794	9,4877	11,1433	13,2767
5	0,5543	0,8312	1,1455	1,6103	2,3425	2,9999	3,6555	4,3515	5,1319	6,0644	7,2893	9,2364	11,0705	12,8325	15,0863
6	0,8721	1,2373	1,6354	2,2041	3,0701	3,8276	4,5702	5,3481	6,2108	7,2311	8,5581	10,6446	12,5916	14,4494	16,8119
7	1,2390	1,6899	2,1673	2,8331	3,8223	4,6713	5,4932	6,3458	7,2832	8,3834	9,8032	12,0170	14,0671	16,0128	18,4753
8	1,6465	2,1797	2,7326	3,4895	4,5936	5,5274	6,4226	7,3441	8,3505	9,5245	11,0301	13,3616	15,5073	17,5345	20,0902
9	2,0879	2,7004	3,3251	4,1682	5,3801	6,3933	7,3570	8,3428	9,4136	10,6564	12,2421	14,6837	16,9190	19,0228	21,6660
10	2,5582	3,2470	3,9403	4,8652	6,1791	7,2672	8,2955	9,3418	10,4732	11,7807	13,4420	15,9872	18,3070	20,4832	23,2093
11	3,0535	3,8157	4,5748	5,5778	6,9887	8,1479	9,2373	10,3410	11,5298	12,8987	14,6314	17,2750	19,6751	21,9200	24,7250
12	3,5706	4,4038	5,2260	6,3038	7,8073	9,0343	10,1820	11,3403	12,5838	14,0111	15,8120	18,5493	21,0261	23,3367	26,2170
13	4,1069	5,0088	5,8919	7,0415	8,6339	9,9257	11,1291	12,3398	13,6356	15,1187	16,9848	19,8119	22,3620	24,7356	27,6882
14	4,6604	5,6287	6,5706	7,7895	9,4673	10,8215	12,0785	13,3393	14,6853	16,2221	18,1508	21,0641	23,6848	26,1189	29,1412
15	5,2293	6,2621	7,2609	8,5468	10,3070	11,7212	13,0297	14,3389	15,7332	17,3217	19,3107	22,3071	24,9958	27,4884	30,5779
16	5,8122	6,9077	7,9616	9,3122	11,1521	12,6243	13,9827	15,3385	16,7795	18,4179	20,4651	23,5418	26,2962	28,8454	31,9999
17	6,4078	7,5642	8,6718	10,0852	12,0023	13,5307	14,9373	16,3382	17,8244	19,5110	21,6146	24,7690	27,5871	30,1910	33,4087
18	7,0149	8,2307	9,3905	10,8649	12,8570	14,4399	15,8932	17,3379	18,8679	20,6014	22,7595	25,9894	28,8693	31,5264	34,8053
19	7,6327	8,9065	10,1170	11,6509	13,7158	15,3517	16,8504	18,3377	19,9102	21,6891	23,9004	27,2036	30,1435	32,8523	36,1909
20	8,2604	9,5908	10,8508	12,4426	14,5784	16,2659	17,8088	19,3374	20,9514	22,7745	25,0375	28,4120	31,4104	34,1696	37,5662
21	8,8972	10,2829	11,5913	13,2396	15,4446	17,1823	18,7683	20,3372	21,9915	23,8578	26,1711	29,6151	32,6706	35,4789	38,9322
22	9,5425	10,9823	12,3380	14,0415	16,3140	18,1007	19,7288	21,3370	23,0307	24,9390	27,3015	30,8133	33,9244	36,7807	40,2894
23	10,1957	11,6886	13,0905	14,8480	17,1865	19,0211	20,6902	22,3369	24,0689	26,0184	28,4288	32,0069	35,1725	38,0756	41,6384
24	10,8564	12,4012	13,8484	15,6587	18,0618	19,9432	21,6525	23,3367	25,1063	27,0960	29,5533	33,1962	36,4150	39,3641	42,9798
25	11,5240	13,1197	14,6114	16,4734	18,9398	20,8670	22,6156	24,3366	26,1430	28,1719	30,6752	34,3816	37,6525	40,6465	44,3141
26	12,1981	13,8439	15,3792	17,2919	19,8202	21,7924	23,5794	25,3365	27,1789	29,2463	31,7946	35,5632	38,8851	41,9232	45,6417
27	12,8785	14,5734	16,1514	18,1139	20,7030	22,7192	24,5440	26,3363	28,2141	30,3193	32,9117	36,7412	40,1133	43,1945	46,9629
28	13,5647	15,3079	16,9279	18,9392	21,5880	23,6475	25,5093	27,3362	29,2486	31,3909	34,0266	37,9159	41,3371	44,4608	48,2782
29	14,2565	16,0471	17,7084	19,7677	22,4751	24,5770	26,4751	28,3361	30,2825	32,4612	35,1394	39,0875	42,5570	45,7223	49,5879
30	14,9535	16,7908	18,4927	20,5992	23,3641	25,5078	27,4416	29,3360	31,3159	33,5302	36,2502	40,2560	43,7730	46,9792	50,8922
31	15,6555	17,5387	19,2806	21,4336	24,2551	26,4397	28,4087	30,3359	32,3486	34,5981	37,3591	41,4217	44,9853	48,2319	52,1914
32	16,3622	18,2908	20,0719	22,2706	25,1478	27,3728	29,3763	31,3359	33,3809	35,6649	38,4663	42,5847	46,1943	49,4804	53,4858
33	17,0735	19,0467	20,8665	23,1102	26,0422	28,3069	30,3444	32,3358	34,4126	36,7307	39,5718	43,7452	47,3999	50,7251	54,7755
34	17,7891	19,8063	21,6643	23,9523	26,9383	29,2421	31,3130	33,3357	35,4438	37,7954	40,6756	44,9032	48,6024	51,9660	56,0609
35	18,5089	20,5694	22,4650	24,7967	27,8359	30,1782	32,2821	34,3356	36,4746	38,8591	41,7780	46,0588	49,8018	53,2033	57,3421
36	19,2327	21,3359	23,2686	25,6433	28,7350	31,1152	33,2517	35,3356	37,5049	39,9220	42,8788	47,2122	50,9985	54,4373	58,6192
37	19,9602	22,1056	24,0749	26,4921	29,6355	32,0532	34,2216	36,3355	38,5348	40,9839	43,9782	48,3634	52,1923	55,6680	59,8925
38	20,6914	22,8785	24,8839	27,3430	30,5373	32,9919	35,1920	37,3355	39,5643	42,0451	45,0763	49,5126	53,3835	56,8955	61,1621
39	21,4262	23,6543	25,6954	28,1958	31,4405	33,9315	36,1628	38,3354	40,5935	43,1053	46,1730	50,6598	54,5722	58,1201	62,4281
40	22,1643	24,4330	26,5093	29,0505	32,3450	34,8719	37,1340	39,3353	41,6222	44,1649	47,2685	51,8051	55,7585	59,3417	63,6907
41	22,9056	25,2145	27,3256	29,9071	33,2506	35,8131	38,1055	40,3353	42,6506	45,2236	48,3628	52,9485	56,9424	60,5606	64,9501
42	23,6501	25,9987	28,1440	30,7654	34,1574	36,7550	39,0774	41,3352	43,6786	46,2817	49,4560	54,0902	58,1240	61,7768	66,2062
43	24,3976	26,7854	28,9647	31,6255	35,0653	37,6975	40,0496	42,3352	44,7063	47,3390	50,5480	55,2302	59,3035	62,9904	67,4593
44	25,1480	27,5746	29,7875	32,4871	35,9743	38,6408	41,0222	43,3352	45,7336	48,3957	51,6389	56,3685	60,4809	64,2015	68,7095
45	25,9013	28,3662	30,6123	33,3504	36,8844	39,5847	41,9950	44,3351	46,7607	49,4517	52,7288	57,5053	61,6562	65,4102	69,9568
46	26,6572	29,1601	31,4390	34,2152	37,7955	40,5292	42,9682	45,3351	47,7874	50,5071	53,8177	58,6405	62,8296	66,6165	71,2014
47	27,4158	29,9562	32,2676	35,0814	38,7075	41,4744	43,9417	46,3350	48,8139	51,5619	54,9056	59,7743	64,0011	67,8206	72,4433
48	28,1770	30,7545	33,0981	35,9491	39,6205	42,4201	44,9154	47,3350	49,8401	52,6161	55,9926	60,9066	65,1708	69,0226	73,6826
49	28,9406	31,5549	33,9303	36,8182	40,5344	43,3664	45,8895	48,3350	50,8660	53,6697	57,0786	62,0375	66,3386	70,2224	74,9195
50	29,7067	32,3574	34,7643	37,6886	41,4492	44,3133	46,8638	49,3349	51,8916	54,7228	58,1638	63,1671	67,5048	71,4202	76,1539

Источник

До конца XIX века нормальное распределение считалась всеобщим законом вариации данных. Однако К. Пирсон заметил, что эмпирические частоты могут сильно отличаться от нормального распределения. Встал вопрос, как это доказать. Требовалось не только графическое сопоставление, которое имеет субъективный характер, но и строгое количественное обоснование.

Так был изобретен критерий χ² (хи квадрат), который проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Это произошло в далеком 1900 году, однако критерий и сегодня на ходу. Более того, его приспособили для решения широкого круга задач. Прежде всего, это анализ категориальных данных, т.е. таких, которые выражаются не количеством, а принадлежностью к какой-то категории. Например, класс автомобиля, пол участника эксперимента, вид растения и т.д. К таким данным нельзя применять математические операции вроде сложения и умножения, для них можно только подсчитать частоты.

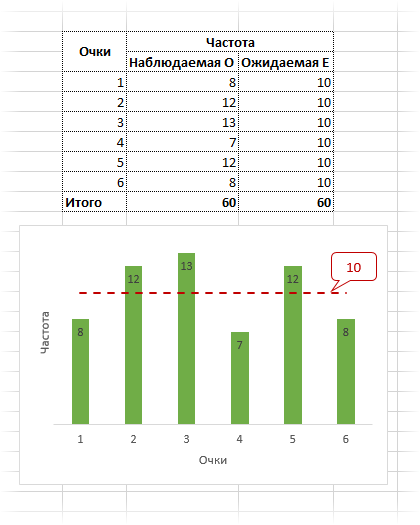
Наблюдаемые частоты обозначим О (Observed), ожидаемые – E (Expected). В качестве примера возьмем результат 60-кратного бросания игральной кости. Если она симметрична и однородна, вероятность выпадения любой стороны равна 1/6 и, следовательно, ожидаемое количество выпадения каждой из сторон равна 10 (1/6∙60). Наблюдаемые и ожидаемые частоты запишем в таблицу и нарисуем гистограмму.

Нулевая гипотеза заключается в том, что частоты согласованы, то есть фактические данные не противоречат ожидаемым. Альтернативная гипотеза – отклонения в частотах выходят за рамки случайных колебаний, расхождения статистически значимы. Чтобы сделать строгий вывод, нам потребуется.

Обобщающая мера расхождения между наблюдаемыми и ожидаемыми частотами.
Распределение этой меры при справедливости гипотезы о том, что различий нет.

Начнем с расстояния между частотами. Если взять просто разницу О — E, то такая мера будет зависеть от масштаба данных (частот). Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.

Обратим внимание на следующие факты. В общем случае количество категорий, по которым измеряются частоты, может быть гораздо больше, поэтому вероятность того, что отдельно взятое наблюдение попадет в ту или иную категорию, довольно мала. Раз так, то, распределение такой случайной величины будет подчинятся закону редких событий, известному под названием закон Пуассона. В законе Пуассона, как известно, значение математического ожидания и дисперсии совпадают (параметр λ). Значит, ожидаемая частота для некоторой категории номинальной переменной E_i будет являться одновременное и ее дисперсией. Далее, закон Пуассона при большом количестве наблюдений стремится к нормальному. Соединяя эти два факта, получаем, что, если гипотеза о согласии наблюдаемых и ожидаемых частот верна, то, при большом количестве наблюдений, выражение

имеет стандартное нормальное распределение.

Важно помнить, что нормальность будет проявляться только при достаточно больших частотах. В статистике принято считать, что общее количество наблюдений (сумма частот) должна быть не менее 50 и ожидаемая частота в каждой группе должна быть не менее 5. Только в этом случае величина, показанная выше, имеет стандартное нормальное распределение. Предположим, что это условие выполнено.

У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной группы. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.

Это и есть статистика для критерия Хи-квадратПирсона. Если частоты действительно соответствуют ожидаемым, то значение статистики Хи-квадрат будет относительно не большим (отклонения находятся близко к нулю). Большое значение статистики свидетельствует в пользу существенных различий между частотами.

«Большой» статистика Хи-квадрат становится тогда, когда появление наблюдаемого или еще большего значения становится маловероятным. И чтобы рассчитать такую вероятность, необходимо знать распределение статистики Хи-квадрат при многократном повторении эксперимента, когда гипотеза о согласии частот верна.

Как нетрудно заметить, величина хи-квадрат также зависит от количества слагаемых. Чем больше слагаемых, тем больше ожидается значение статистики, ведь каждое слагаемое вносит свой вклад в общую сумму. Следовательно, для каждого количества независимых слагаемых, будет собственное распределение. Получается, что χ² – это целое семейство распределений.

И здесь мы подошли к одному щекотливому моменту. Что такое число независимых слагаемых? Вроде как любое слагаемое (т.е. отклонение) независимо. К. Пирсон тоже так думал, но оказался неправ. На самом деле число независимых слагаемых будет на один меньше, чем количество групп номинальной переменной n. Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.

По этому поводу Фишер ввел в статистику новое понятие – степень свободы (degrees of freedom), которое и представляет собой количество независимых слагаемых в сумме. Понятие степеней свободы имеет математическое объяснение и проявляется только в распределениях, связанных с нормальным (Стьюдента, Фишера-Снедекора и сам Хи-квадрат).

Чтобы лучше уловить смысл степеней свободы, обратимся к физическому аналогу. Представим точку, свободно движущуюся в пространстве. Она имеет 3 степени свободы, т.к. может перемещаться в любом направлении трехмерного пространства. Если точка движется по какой-либо поверхности, то у нее уже две степени свободы (вперед-назад, вправо-влево), хотя и продолжает находиться в трехмерном пространстве. Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.

Примерно также распределение статистики может зависеть от меньшего количества элементов, чем нужно слагаемых для его расчета. В общем случае количество степеней свободы меньше наблюдений на число имеющихся зависимостей.

Таким образом, распределение хи квадрат (χ²) – это семейство распределений, каждое из которых зависит от параметра степеней свободы. Формальное определение следующее. Распределение χ² (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.

Далее можно было бы перейти к самой формуле, по которой вычисляется функция распределения хи-квадрат, но, к счастью, все давно подсчитано за нас. Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в Excel.

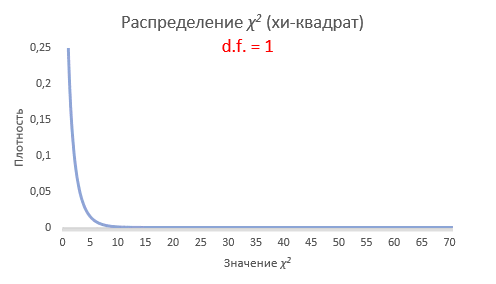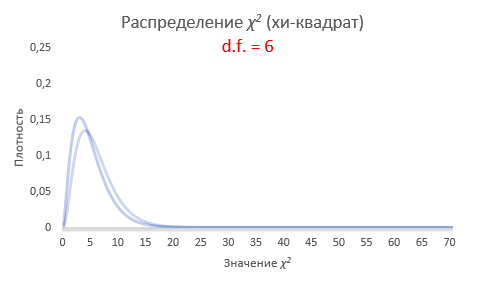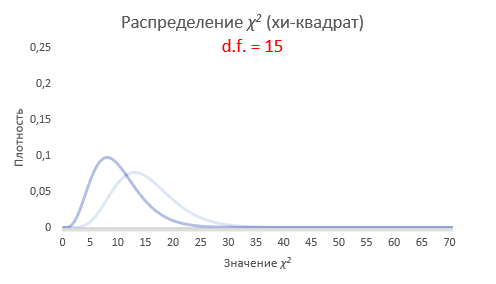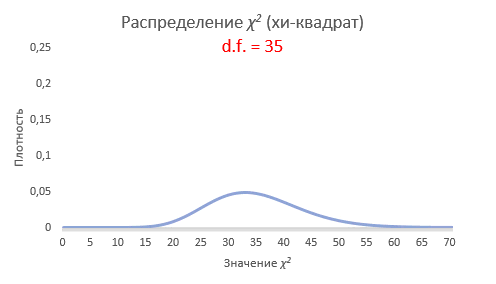
Интересно посмотреть, как меняется форма распределения хи-квадрат в зависимости от количества степеней свободы.

С увеличением степеней свободы распределение хи-квадрат стремится к нормальному. Это объясняется действием центральной предельной теоремы, согласно которой сумма большого количества независимых случайных величин имеет нормальное распределение. Про квадраты там ничего не сказано )).

Проверка гипотезы по критерию Хи квадрат Пирсона

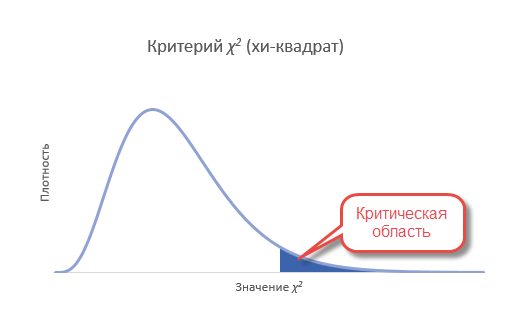
Вот мы и подошли к проверке гипотез по методу хи-квадрат. В целом техника остается прежней. Выдвигается нулевая гипотеза о том, что наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, т.к. они взяты из той же генеральной совокупности). Если этот так, то разброс будет относительно небольшим, в пределах случайных колебаний. Меру разброса определяют по статистике Хи-квадрат. Далее либо полученную статистику сравнивают с критическим значением (для соответствующего уровня значимости и степеней свободы), либо, что более правильно, рассчитывают наблюдаемый p-value, т.е. вероятность получить такое или еще больше значение статистики при справедливости нулевой гипотезы.

Т.к. нас интересует согласие частот, то отклонение гипотезы произойдет, когда статистика окажется больше критического уровня. Т.е. критерий является односторонним. Однако иногда (иногда) требуется проверить левостороннюю гипотезу. Например, когда эмпирические данные уж оооочень сильно похожи на теоретические. Тогда критерий может попасть в маловероятную область, но уже слева. Дело в том, что в естественных условиях, маловероятно получить частоты, практически совпадающие с теоретическими. Всегда есть некоторая случайность, которая дает погрешность. А вот если такой погрешности нет, то, возможно, данные были сфальсифицированы. Но все же обычно проверяют правостороннюю гипотезу.

Вернемся к задаче с игральной костью. Рассчитаем по имеющимся данным значение статистики критерия хи-квадрат.

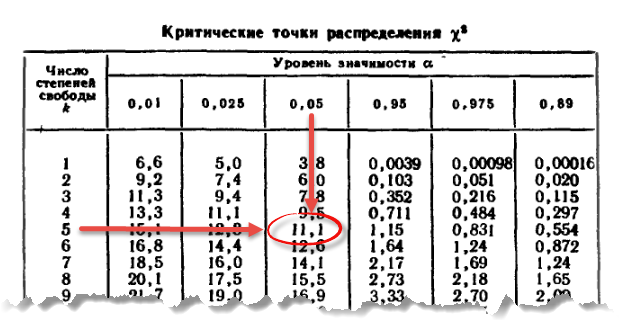
Теперь найдем критическое значение при 5-ти степенях свободы (k) и уровне значимости 0,05 (α) по таблице критических значений распределения хи квадрат.

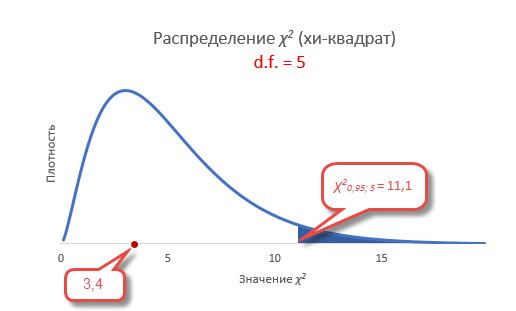
То есть квантиль 0,05 хи квадрат распределения (правый хвост) с 5-ю степенями свободы χ²_{0,05; 5} = 11,1.

Сравним фактическое и табличное значение. 3,4 (χ²) < 11,1 (χ²_{0,05; 5}). Расчетный значение оказалось меньшим, значит гипотеза о равенстве (согласии) частот не отклоняется. На рисунке ситуация выглядит вот так.

Если бы расчетное значение попало в критическую область, то нулевая гипотеза была бы отклонена.

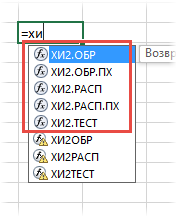
Более правильным будет рассчитать еще и p-value. Для этого нужно в таблице найти ближайшее значение для заданного количества степеней свободы и посмотреть соответствующий ему уровень значимости. Но это прошлый век. Воспользуемся ЭВМ, в частности MS Excel. В эксель есть несколько функций, связанных с хи-квадрат.

Ниже их краткое описание.

ХИ2.ОБР – критическое значение Хи-квадрат при заданной вероятности слева (как в статистических таблицах)

ХИ2.ОБР.ПХ – критическое значение при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.

ХИ2.РАСП – p-value слева (можно рассчитать плотность).

ХИ2.РАСП.ПХ – p-value справа.

ХИ2.ТЕСТ – по двум диапазонам частот сразу проводит тест хи-квадрат. Количество степеней свободы берется на одну меньше, чем количество частот в столбце (так и должно быть), возвращая значение p-value.

Давайте пока рассчитаем для нашего эксперимента критическое (табличное) значение для 5-ти степеней свободы и альфа 0,05. Формула Excel будет выглядеть так:

=ХИ2.ОБР(0,95;5)

Или так

=ХИ2.ОБР.ПХ(0,05;5)

Результат будет одинаковым – 11,0705. Именно это значение мы видим в таблице (округленное до 1 знака после запятой).

Рассчитаем, наконец, p-value для 5-ти степеней свободы критерия χ² = 3,4. Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)

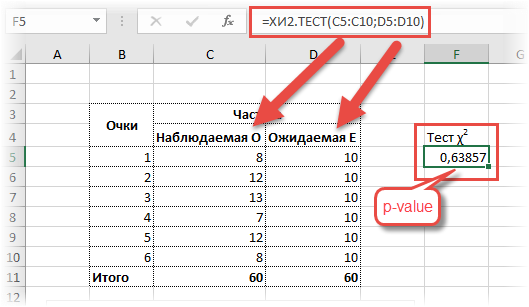
=ХИ2.РАСП.ПХ(3,4;5) = 0,63857

Значит, при 5-ти степенях свободы вероятность получить значение критерия χ² = 3,4 и больше равна почти 64%. Естественно, гипотеза не отклоняется (p-value больше 5%), частоты очень хорошо согласуются.

А теперь проверим гипотезу о согласии частот с помощью теста хи квадрат и функции Excel ХИ2.ТЕСТ.

Никаких таблиц, никаких громоздких расчетов. Указав в качестве аргументов функции столбцы с наблюдаемыми и ожидаемыми частотами, сразу получаем p-value. Красота.

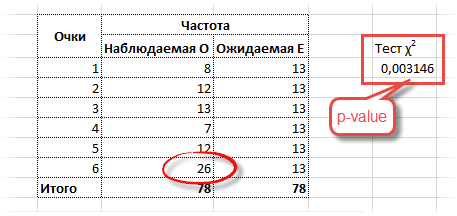
Представим теперь, что вы играете в кости с подозрительным типом. Распределение очков от 1 до 5 остается прежним, но он выкидывает 26 шестерок (количество всех бросков становится 78).

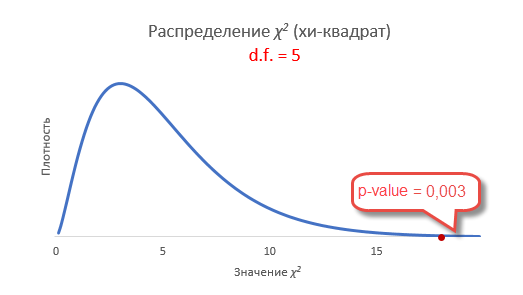
p-value в этом случае оказывается 0,003, что гораздо меньше чем, 0,05. Есть серьезные основания сомневаться в правильности игральной кости. Вот, как выглядит эта вероятность на диаграмме распределения хи-квадрат.

Статистика критерия хи-квадрат здесь получается 17,8, что, естественно, больше табличного (11,1).

Надеюсь, мне удалось объяснить, что такое критерий согласия χ² (хи-квадрат) Пирсона и как с его помощью проверяются статистические гипотезы.

Напоследок еще раз о важном условии! Критерий хи-квадрат исправно работает только в случае, когда количество всех частот превышает 50, а минимальное ожидаемое значение для каждой группы не меньше 5. Если в какой-либо категории ожидаемая частота менее 5, но при этом сумма всех частот превышает 50, то такую категорию объединяют с ближайшей, чтобы их общая частота превысила 5. Если это сделать невозможно, или сумма частот меньше 50, то следует использовать более точные методы проверки гипотез. О них поговорим в другой раз.

Ниже находится видео ролик о том, как в Excel проверить гипотезу с помощью критерия хи-квадрат.

Скачать файл с примером.

Поделиться в социальных сетях:

Источник

Определение

$F_{n}left(chi _{{alpha ,n}}^{2}right)=alpha$

Замечания

$F_{n}^{{-1}}(alpha )=chi _{{alpha ,n}}^{2}$

Функция $F_{n}^{{-1}}$ не имеет простого представления. Однако, возможно вычислить её значения численно.

Аппроксимация квантилей

Аппроксимация Корниша-Фишера^[1]

$chi _{{alpha ,n}}^{{2}}=n+A{sqrt {n}}+B+{frac {C}{{sqrt {n}}}}+{frac {D}{n}}+{frac {E}{n{sqrt {n}}}}$ ,

где:

$B={frac {2}{3}}left({{d}^{{2}}}-1right)$

$C=dcdot {frac {{{d}^{{2}}}-7}{9{sqrt {2}}}}$

$D={frac {6{{d}^{{4}}}+14{{d}^{{2}}}-32}{405}}$

$E=dcdot {frac {9{{d}^{{4}}}+256{{d}^{{2}}}-433}{4860{sqrt {2}}}}$

$d=2.0637cdot {{left(ln {frac {1}{1-alpha }}-0.16right)}^{{0.4274}}}-1.5774$ при

$d=-2.0637cdot {{left(ln {frac {1}{alpha }}-0.16right)}^{{0.4274}}}+1.5774$ при

Аппроксимация Голдштейна^[2]

где d определяется аналогично, а коэффициенты a, b,c приведены в таблице

a	b	c
1.0000886	-0.2237368	-0.01513904
0.4713941	0.02607083	-0.008986007
0.0001348028	0.01128186	0.02277679
-0.008553069	-0.01153761	-0.01323293
0.00312558	0.005169654	-0.006950356
-0.0008426812	0.00253001	0.001060438
0.00009780499	-0.001450117	0.001565326

Таблица квантилей

Нижеприведённая таблица получена с помощью функции chi2inv Архивная копия от 4 декабря 2009 на Wayback Machine пакета MATLAB.

Также квантили можно получить с помощью других программных средств:

пакет LibreOffice, электронная таблица Calc, функция CHIINV Архивная копия от 14 ноября 2012 на Wayback Machine.
библиотека scipy для языка python, функция scipy.stats.distributions.chi2.ppf Архивная копия от 7 марта 2016 на Wayback Machine

$chi _{{0.025,10}}^{2}=3.2470$

;

$chi _{{0.975,10}}^{2}=20.4832$

Квантили $chi _{alpha ,n}^{2}$

	0,01	0,025	0,05	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95	0,975	0,99
1	0,0002	0,0010	0,0039	0,0158	0,0642	0,1485	0,2750	0,4549	0,7083	1,0742	1,6424	2,7055	3,8415	5,0239	6,6349
2	0,0201	0,0506	0,1026	0,2107	0,4463	0,7133	1,0217	1,3863	1,8326	2,4079	3,2189	4,6052	5,9915	7,3778	9,2103
3	0,1148	0,2158	0,3518	0,5844	1,0052	1,4237	1,8692	2,3660	2,9462	3,6649	4,6416	6,2514	7,8147	9,3484	11,3449
4	0,2971	0,4844	0,7107	1,0636	1,6488	2,1947	2,7528	3,3567	4,0446	4,8784	5,9886	7,7794	9,4877	11,1433	13,2767
5	0,5543	0,8312	1,1455	1,6103	2,3425	2,9999	3,6555	4,3515	5,1319	6,0644	7,2893	9,2364	11,0705	12,8325	15,0863
6	0,8721	1,2373	1,6354	2,2041	3,0701	3,8276	4,5702	5,3481	6,2108	7,2311	8,5581	10,6446	12,5916	14,4494	16,8119
7	1,2390	1,6899	2,1673	2,8331	3,8223	4,6713	5,4932	6,3458	7,2832	8,3834	9,8032	12,0170	14,0671	16,0128	18,4753
8	1,6465	2,1797	2,7326	3,4895	4,5936	5,5274	6,4226	7,3441	8,3505	9,5245	11,0301	13,3616	15,5073	17,5345	20,0902
9	2,0879	2,7004	3,3251	4,1682	5,3801	6,3933	7,3570	8,3428	9,4136	10,6564	12,2421	14,6837	16,9190	19,0228	21,6660
10	2,5582	3,2470	3,9403	4,8652	6,1791	7,2672	8,2955	9,3418	10,4732	11,7807	13,4420	15,9872	18,3070	20,4832	23,2093
11	3,0535	3,8157	4,5748	5,5778	6,9887	8,1479	9,2373	10,3410	11,5298	12,8987	14,6314	17,2750	19,6751	21,9200	24,7250
12	3,5706	4,4038	5,2260	6,3038	7,8073	9,0343	10,1820	11,3403	12,5838	14,0111	15,8120	18,5493	21,0261	23,3367	26,2170
13	4,1069	5,0088	5,8919	7,0415	8,6339	9,9257	11,1291	12,3398	13,6356	15,1187	16,9848	19,8119	22,3620	24,7356	27,6882
14	4,6604	5,6287	6,5706	7,7895	9,4673	10,8215	12,0785	13,3393	14,6853	16,2221	18,1508	21,0641	23,6848	26,1189	29,1412
15	5,2293	6,2621	7,2609	8,5468	10,3070	11,7212	13,0297	14,3389	15,7332	17,3217	19,3107	22,3071	24,9958	27,4884	30,5779
16	5,8122	6,9077	7,9616	9,3122	11,1521	12,6243	13,9827	15,3385	16,7795	18,4179	20,4651	23,5418	26,2962	28,8454	31,9999
17	6,4078	7,5642	8,6718	10,0852	12,0023	13,5307	14,9373	16,3382	17,8244	19,5110	21,6146	24,7690	27,5871	30,1910	33,4087
18	7,0149	8,2307	9,3905	10,8649	12,8570	14,4399	15,8932	17,3379	18,8679	20,6014	22,7595	25,9894	28,8693	31,5264	34,8053
19	7,6327	8,9065	10,1170	11,6509	13,7158	15,3517	16,8504	18,3377	19,9102	21,6891	23,9004	27,2036	30,1435	32,8523	36,1909
20	8,2604	9,5908	10,8508	12,4426	14,5784	16,2659	17,8088	19,3374	20,9514	22,7745	25,0375	28,4120	31,4104	34,1696	37,5662
21	8,8972	10,2829	11,5913	13,2396	15,4446	17,1823	18,7683	20,3372	21,9915	23,8578	26,1711	29,6151	32,6706	35,4789	38,9322
22	9,5425	10,9823	12,3380	14,0415	16,3140	18,1007	19,7288	21,3370	23,0307	24,9390	27,3015	30,8133	33,9244	36,7807	40,2894
23	10,1957	11,6886	13,0905	14,8480	17,1865	19,0211	20,6902	22,3369	24,0689	26,0184	28,4288	32,0069	35,1725	38,0756	41,6384
24	10,8564	12,4012	13,8484	15,6587	18,0618	19,9432	21,6525	23,3367	25,1063	27,0960	29,5533	33,1962	36,4150	39,3641	42,9798
25	11,5240	13,1197	14,6114	16,4734	18,9398	20,8670	22,6156	24,3366	26,1430	28,1719	30,6752	34,3816	37,6525	40,6465	44,3141
26	12,1981	13,8439	15,3792	17,2919	19,8202	21,7924	23,5794	25,3365	27,1789	29,2463	31,7946	35,5632	38,8851	41,9232	45,6417
27	12,8785	14,5734	16,1514	18,1139	20,7030	22,7192	24,5440	26,3363	28,2141	30,3193	32,9117	36,7412	40,1133	43,1945	46,9629
28	13,5647	15,3079	16,9279	18,9392	21,5880	23,6475	25,5093	27,3362	29,2486	31,3909	34,0266	37,9159	41,3371	44,4608	48,2782
29	14,2565	16,0471	17,7084	19,7677	22,4751	24,5770	26,4751	28,3361	30,2825	32,4612	35,1394	39,0875	42,5570	45,7223	49,5879
30	14,9535	16,7908	18,4927	20,5992	23,3641	25,5078	27,4416	29,3360	31,3159	33,5302	36,2502	40,2560	43,7730	46,9792	50,8922
31	15,6555	17,5387	19,2806	21,4336	24,2551	26,4397	28,4087	30,3359	32,3486	34,5981	37,3591	41,4217	44,9853	48,2319	52,1914
32	16,3622	18,2908	20,0719	22,2706	25,1478	27,3728	29,3763	31,3359	33,3809	35,6649	38,4663	42,5847	46,1943	49,4804	53,4858
33	17,0735	19,0467	20,8665	23,1102	26,0422	28,3069	30,3444	32,3358	34,4126	36,7307	39,5718	43,7452	47,3999	50,7251	54,7755
34	17,7891	19,8063	21,6643	23,9523	26,9383	29,2421	31,3130	33,3357	35,4438	37,7954	40,6756	44,9032	48,6024	51,9660	56,0609
35	18,5089	20,5694	22,4650	24,7967	27,8359	30,1782	32,2821	34,3356	36,4746	38,8591	41,7780	46,0588	49,8018	53,2033	57,3421
36	19,2327	21,3359	23,2686	25,6433	28,7350	31,1152	33,2517	35,3356	37,5049	39,9220	42,8788	47,2122	50,9985	54,4373	58,6192
37	19,9602	22,1056	24,0749	26,4921	29,6355	32,0532	34,2216	36,3355	38,5348	40,9839	43,9782	48,3634	52,1923	55,6680	59,8925
38	20,6914	22,8785	24,8839	27,3430	30,5373	32,9919	35,1920	37,3355	39,5643	42,0451	45,0763	49,5126	53,3835	56,8955	61,1621
39	21,4262	23,6543	25,6954	28,1958	31,4405	33,9315	36,1628	38,3354	40,5935	43,1053	46,1730	50,6598	54,5722	58,1201	62,4281
40	22,1643	24,4330	26,5093	29,0505	32,3450	34,8719	37,1340	39,3353	41,6222	44,1649	47,2685	51,8051	55,7585	59,3417	63,6907
41	22,9056	25,2145	27,3256	29,9071	33,2506	35,8131	38,1055	40,3353	42,6506	45,2236	48,3628	52,9485	56,9424	60,5606	64,9501
42	23,6501	25,9987	28,1440	30,7654	34,1574	36,7550	39,0774	41,3352	43,6786	46,2817	49,4560	54,0902	58,1240	61,7768	66,2062
43	24,3976	26,7854	28,9647	31,6255	35,0653	37,6975	40,0496	42,3352	44,7063	47,3390	50,5480	55,2302	59,3035	62,9904	67,4593
44	25,1480	27,5746	29,7875	32,4871	35,9743	38,6408	41,0222	43,3352	45,7336	48,3957	51,6389	56,3685	60,4809	64,2015	68,7095
45	25,9013	28,3662	30,6123	33,3504	36,8844	39,5847	41,9950	44,3351	46,7607	49,4517	52,7288	57,5053	61,6562	65,4102	69,9568
46	26,6572	29,1601	31,4390	34,2152	37,7955	40,5292	42,9682	45,3351	47,7874	50,5071	53,8177	58,6405	62,8296	66,6165	71,2014
47	27,4158	29,9562	32,2676	35,0814	38,7075	41,4744	43,9417	46,3350	48,8139	51,5619	54,9056	59,7743	64,0011	67,8206	72,4433
48	28,1770	30,7545	33,0981	35,9491	39,6205	42,4201	44,9154	47,3350	49,8401	52,6161	55,9926	60,9066	65,1708	69,0226	73,6826
49	28,9406	31,5549	33,9303	36,8182	40,5344	43,3664	45,8895	48,3350	50,8660	53,6697	57,0786	62,0375	66,3386	70,2224	74,9195
50	29,7067	32,3574	34,7643	37,6886	41,4492	44,3133	46,8638	49,3349	51,8916	54,7228	58,1638	63,1671	67,5048	71,4202	76,1539

См. также

Доверительный интервал для дисперсии нормальной выборки.

Примечания

↑ Golberg H., Levine H. Approximate formulas for the percentage points and normalization of t and $chi ^{2}$ // AMS. 1945. V.17. P. 216—225.
↑ Goldstein R.B. Chi-square quantiles, Algorithm 451 // Commun. Assoc. Comp. 1973. V. 16. P. 483—485.

Эта страница в последний раз была отредактирована 6 апреля 2022 в 05:55.

Как только страница обновилась в Википедии она обновляется в Вики 2.
Обычно почти сразу, изредка в течении часа.

Источник

Рассмотрим вычисление квантилей для некоторых функций распределений, представленных в

MS

EXCEL

.

Понятие

Квантиля

основано на определении

Функции распределения

. Поэтому, перед изучением

Квантилей

рекомендуем освежить в памяти понятия из статьи

Функция распределения вероятности

Содержание статьи:

Определение
Квантили специальных видов
Квантили стандартного нормального распределения
Квантили распределения Стьюдента
Квантили распределения ХИ-квадрат
Квантили F-распределения
Квантили распределения Вейбулла
Квантили экспоненциального распределения

Сначала дадим формальное определение

квантиля,

затем приведем примеры их вычисления в MS EXCEL.

Определение

Пусть случайная величина

X

, имеет

функцию распределения

F

(

x

).

α-квантилем

(

альфа-

квантиль,

x
_a
,

квантиль

порядка

α, нижний

α-

квантиль

) называют решение уравнения

x
_a
=F
^-1
(α), где

α

– вероятность, что случайная величина х примет значение меньшее или равное x
_a
, т.е. Р(х<= x
_a
)=

α.

Из определения ясно, что нахождение

квантиля

распределения является обратной операцией нахождения вероятности. Т.е. если при вычислении

функции распределения

мы находим вероятность

α,

зная x
_a
, то при нахождении

квантиля

мы, наоборот, ищем

x
_a
зная

α

.

Чтобы пояснить определение, используем график функции

стандартного нормального распределения

(см.

файл примера Лист Определение

):

Примечание

: О построении графиков в MS EXCEL можно прочитать статью

Основные типы диаграмм в MS EXCEL

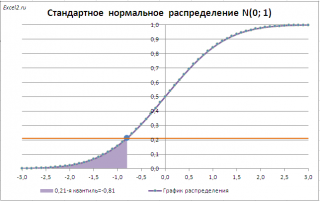
Например, с помощью графика вычислим 0,21-ю

квантиль

, т.е. такое значение случайной величины, что Р(X<=x
_0,21
)=0,21.

Для этого найдем точку пересечения горизонтальной линии на уровне вероятности равной 0,21 с

функцией распределения

. Абсцисса этой точки равна -0,81. Соответственно, 0,21-я

квантиль

равна -0,81. Другими словами, вероятность того, что случайная величина, распределенная

стандартному нормальному закону,

примет значение

меньше

-0,81, равна 0,21 (21%).

Примечание

: При вычислении

квантилей

в MS EXCEL используются

обратные функции распределения

:

НОРМ.СТ.ОБР()

,

ЛОГНОРМ.ОБР()

,

ХИ2.ОБР(),

ГАММА.ОБР()

и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье

Распределения случайной величины в MS EXCEL

Точное значение

квантиля

в нашем случае можно найти с помощью формулы

=НОРМ.СТ.ОБР(0,21)

СОВЕТ

: Процедура вычисления

квантилей

имеет много общего с вычислением

процентилей

выборки

(см. статью

Процентили в MS EXCEL

Квантили специальных видов

Часто используются

Квантили

специальных видов:

процентили

x
_p/100
, p=1, 2, 3, …, 99
квартили

x
_p/4
, p=1, 2, 3
медиана

x
_1/2

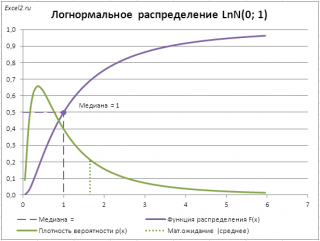
В качестве примера вычислим

медиану (0,5-квантиль)

логнормального распределения

LnN(0;1) (см.

файл примера лист Медиана

).

Это можно сделать с помощью формулы

=ЛОГНОРМ.ОБР(0,5; 0; 1)

Квантили стандартного нормального распределения

Необходимость в вычислении квантилей

стандартного нормального распределения

возникает при

проверке статистических гипотез

и при

построении доверительных интервалов.

Примечание

: Про

проверку статистических гипотез

см. статью

Проверка статистических гипотез в MS EXCEL

. Про

построение доверительных интервалов

см. статью

Доверительные интервалы в MS EXCEL

В данных задачах часто используется специальная терминология:

Нижний квантиль уровня

альфа

(

α

percentage point)

;
Верхний квантиль уровня альфа (upper

α

percentage point)

;
Двусторонние квантили уровня

альфа

.

Нижний квантиль уровня альфа

– это обычный

α-квантиль.

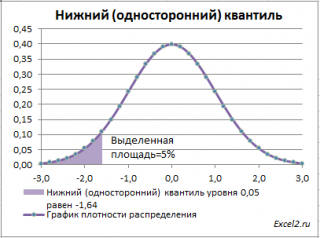
Чтобы пояснить название «

нижний» квантиль

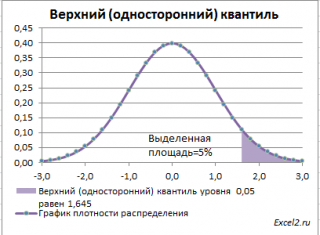
, построим график

плотности вероятности

и

функцию вероятности

стандартного нормального

распределения

(см.

файл примера лист Квантили

).

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше

α-квантиля

. Из определения

квантиля

эта вероятность равна

α

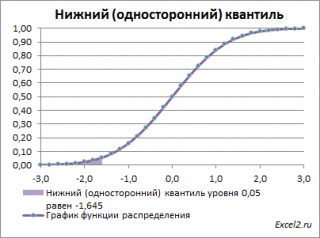
. Из графика

функции распределения

становится понятно, откуда происходит название ”

нижний квантиль” –

выделенная область расположена в нижней части графика.

Для

α=0,05,

нижний 0,05-квантиль

стандартного нормального распределения

равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:

=НОРМ.СТ.ОБР(0,05)

Однако, при

проверке гипотез

и построении

доверительных интервалов

чаще используется “верхний”

α-квантиль.

Покажем почему.

Верхним

α

–

квантилем

называют такое значение x
_α
, для которого вероятность, того что случайная величина X примет значение

больше или равное

x
_α
равна

альфа:

P(X>= x
_α
)=

α

. Из определения понятно, что

верхний альфа

–

квантиль

любого распределения равен

нижнему (1-

α)

–

квантилю.

А для распределений, у которых

функция плотности распределения

является четной функцией,

верхний

α

–

квантиль

равен

нижнему

α

–

квантилю

со знаком минус

.

Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.

Действительно, для

α=0,05,

верхний 0,05-квантиль

стандартного нормального распределения

равен 1,645. Т.к.

функция плотности вероятности

стандартного нормального

распределения

является четной функцией, то вычисления в MS EXCEL

верхнего квантиля

можно сделать по двум формулам:

=НОРМ.СТ.ОБР(1-0,05)

=-НОРМ.СТ.ОБР(0,05)

Почему применяют понятие

верхний

α

–

квантиль?

Только из соображения удобства, т.к. он при

α<0,5

всегда положительный (в случае

стандартного нормального

распределения

). А при проверке гипотез

α

равно

уровню значимости

, который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре

проверки гипотез

пришлось бы записывать условие отклонения

нулевой гипотезы

μ>μ
₀
как Z
₀
>Z
_{1-

α}
, подразумевая, что Z
_{1-

α}
–

обычный

квантиль

порядка

1-

α

(или как Z
₀
>-Z
_α
). C верхнем квантилем эта запись выглядит проще Z
₀
>Z
_α
.

Примечание

: Z
₀
– значение

тестовой статистики

, вычисленное на основе

выборки

. Подробнее см. статью

Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)

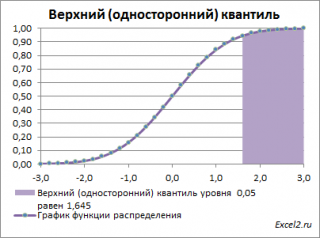
Чтобы пояснить название «

верхний»

квантиль

, построим график

плотности вероятности

и

функцию вероятности

стандартного нормального

распределения

для

α=0,05.

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше

верхнего 0,05-квантиля

, т.е.

больше

значения 1,645. Эта вероятность равна 0,05.

На графике

плотности вероятности

площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика

функции распределения

становится понятно, откуда происходит название “верхний”

квантиль

–

выделенная область расположена в верхней части графика. Если Z
₀
больше

верхнего квантиля

, т.е. попадает в выделенную область, то

нулевая гипотеза

отклоняется.

Также при

проверке двухсторонних гипотез

и построении соответствующих

доверительных интервалов

иногда используется понятие “двусторонний”

α-квантиль.

В этом случае условие отклонения

нулевой гипотезы

звучит как |Z
₀
|>Z
_{α

/2}
, где Z
_{α

/2}
–

верхний

α/2-квантиль

. Чтобы не писать

верхний

α/2-квантиль

, для удобства используют “двусторонний”

α-квантиль.

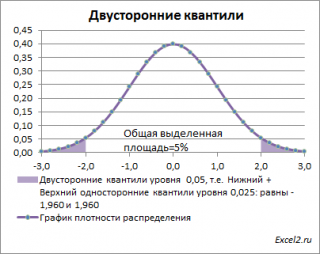
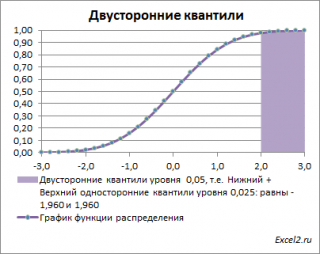
Почему двусторонний? Как и в предыдущих случаях, построим график

плотности вероятности стандартного нормального распределения

и график

функции распределения

.

Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение

между

нижним квантилем уровня α

/2 и

верхним квантилем

уровня α

/2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z
₀
попадает в одну из выделенных областей, то

нулевая гипотеза

отклоняется.

Вычислить

двусторонний

0,05

–

квантиль

это можно с помощью формул MS EXCEL:

=НОРМ.СТ.ОБР(1-0,05/2)

или

=-НОРМ.СТ.ОБР(0,05/2)

Другими словами,

двусторонние α-квантили

задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.

Квантили распределения Стьюдента

Аналогичным образом

квантили

вычисляются и для

распределения Стьюдента

. Например, вычислять

верхний

α/2-

квантиль

распределения Стьюдента с

n

-1 степенью свободы

требуется, если проводится

проверка двухсторонней гипотезы

о

среднем значении

распределения при

неизвестной

дисперсии

(

см. эту статью

Для

верхних квантилей

распределения Стьюдента

часто используется запись t
_α/2,n-1
. Если такая запись встретилась в статье про

проверку гипотез

или про построение

доверительного интервала

, то это именно

верхний квантиль

.

Примечание

:

Функция плотности вероятности распределения Стьюдента

, как и

стандартного нормального распределения

, является четной функцией.

Чтобы вычислить в MS EXCEL

верхний

0,05/2

–

квантиль

для t-распределения с 10 степенями свободы (или тоже самое

двусторонний

0,05-квантиль

), необходимо записать формулу

=СТЬЮДЕНТ.ОБР.2Х(0,05; 10)

или

=СТЬЮДРАСПОБР(0,05; 10)

или

=СТЬЮДЕНТ.ОБР(1-0,05/2; 10)

или

=-СТЬЮДЕНТ.ОБР(0,05/2; 10)

.2X означает 2 хвоста, т.е.

двусторонний квантиль

.

Квантили распределения ХИ-квадрат

Вычислять

квантили

распределения ХИ-квадрат

с

n

-1 степенью свободы

требуется, если проводится

проверка гипотезы

о

дисперсии нормального распределения

(см. статью

Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения

При

проверке таких гипотез

также используются

верхние квантили.

Например, при

двухсторонней гипотезе

требуется вычислить 2

верхних

квантиля

распределения

ХИ
²
: χ
²_α/2,n-1
и

χ
²_1-_α/2,n-1
. Почему требуется вычислить два

квантиля

, не один, как при

проверке гипотез о среднем

, где используется

стандартное нормальное распределение

или

t-распределение

?

Дело в том, что в отличие от

стандартного нормального распределения

и

распределения Стьюдента

, плотность распределения

ХИ
²
не является четной (симметричной относительно оси х). У него все

квантили

больше 0, поэтому

верхний альфа-квантиль

не равен

нижнему (1-альфа)-квантилю

или по-другому:

верхний альфа-квантиль

не равен

нижнему альфа-квантилю

со знаком минус.

Чтобы вычислить

верхний

0,05/2

–

квантиль

для

ХИ
²
-распределения

с

числом степеней свободы

10, т.е.

χ
²_0,05/2,n-1
, необходимо в MS EXCEL записать формулу

=ХИ2.ОБР.ПХ(0,05/2; 10)

или

=ХИ2.ОБР(1-0,05/2; 10)

Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике

функции распределения

.

Чтобы вычислить

верхний

(1-0,05/2)-

квантиль

при том же

числе степеней свободы

, т.е.

χ
²_1-0,05/2,n-1
и необходимо записать формулу

=ХИ2.ОБР.ПХ(1-0,05/2; 10)

или

=ХИ2.ОБР(0,05/2; 10)

Результат равен 3,25.

Квантили F-распределения

Вычислять

квантили

распределения Фишера

с

n
₁
-1 и

n
₂
-1 степенями свободы

требуется, если проводится

проверка гипотезы

о равенстве

дисперсий двух нормальных распределений

(см. статью

Двухвыборочный тест для дисперсии: F-тест в MS EXCEL

При

проверке таких гипотез

используются, как правило,

верхние квантили.

Например, при

двухсторонней гипотезе

требуется вычислить 2

верхних

квантиля

F

-распределения:

F
_{α/2,n1-1,

n

2

-1}
и

F
_{1-α/2,n1-1,

n

2

-1}
. Почему требуется вычислить два

квантиля

, не один, как при

проверке гипотез о среднем

? Причина та же, что и для распределения ХИ
²
– плотность

F-распределения

не является четной

.

Эти

квантили

нельзя выразить один через другой как для

стандартного нормального распределения

.

Верхний альфа-квантиль

F

-распределения

не равен

нижнему альфа-квантилю

со знаком минус.

Чтобы вычислить

верхний

0,05/2-квантиль

для

F

-распределения

с

числом степеней свободы

10 и 12, необходимо записать формулу

=F.ОБР.ПХ(0,05/2;10;12) =FРАСПОБР(0,05/2;10;12) =F.ОБР(1-0,05/2;10;12)

Результат равен 3,37. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике

функции распределения

.

Квантили распределения Вейбулла

Иногда

обратная функция распределения

может быть представлена в явном виде с помощью элементарных функций, например как для

распределения Вейбулла

. Напомним, что функция этого распределения задается следующей формулой:

После логарифмирования обеих частей выражения, выразим x через соответствующее ему значение F(x) равное P:

Примечание

: Вместо обозначения

α-квантиль

может использоваться

p

–

квантиль.

Суть от этого не меняется.

Это и есть обратная функция, которая позволяет вычислить

P

–

квантиль

(

p

–

quantile

). Для его вычисления в формуле нужно подставить известное значение вероятности P и вычислить значение х
_p
(вероятность того, что случайная величина Х примет значение меньше или равное х
_p
равна P).

Квантили экспоненциального распределения

Задача

:

Случайная величина имеет

экспоненциальное распределение

:

Требуется выразить

p

-квантиль

x
_p
через параметр распределения λ и заданную вероятность

p

.

Примечание

: Вместо обозначения

α-квантиль

может использоваться

p-квантиль

. Суть от этого не меняется.

Решение

: Вспоминаем, что

p

-квантиль

– это такое значение x
_p
случайной величины X, для которого P(X<=x
_p
)=

p

. Т.е. вероятность, что случайная величина X примет значение меньше или равное x
_p
равна

p

. Запишем это утверждение с помощью формулы:

По сути, мы записали

функцию вероятности экспоненциального распределения

: F(x
_p
)=

p

.

Из определения

квантиля

следует, что для его нахождения нам потребуется

обратная функция распределения

.

Проинтегрировав вышеуказанное выражение, получим:

Используя это уравнение, выразим x
_p
через λ и вероятность

p

.

Конечно, явно выразить

обратную функцию распределения

можно не для всех

функций распределений

.

Источник

Определение[править | править код]

Замечания[править | править код]

Аппроксимация квантилей[править | править код]

Таблица квантилей[править | править код]

См. также[править | править код]

Примечания[править | править код]

Определение

Замечания

Таблица квантилей

Пример

См, также

Проверка гипотезы по критерию Хи квадрат Пирсона

Определение

Замечания

Аппроксимация квантилей

Таблица квантилей

См. также

Примечания

Определение

Квантили специальных видов

Квантили стандартного нормального распределения

Квантили распределения Стьюдента

Квантили распределения ХИ-квадрат

Квантили F-распределения

Квантили распределения Вейбулла

Квантили экспоненциального распределения

Вам также может понравиться

Как найти гея в ставрополе

Как найти сторону неправильной трапеции

Как найти замыкание в электрической цепи

Добавить комментарий Отменить ответ