Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике – мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
Кванти́ль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Если вероятность задана в процентах, то квантиль называется процентилем или перцентилем (см. ниже).
Например, фраза «90-й процентиль массы тела у новорожденных мальчиков составляет 4 кг»[1] означает, что 90 % мальчиков рождаются с весом, меньшим либо равным 4 кг, а 10 % мальчиков рождаются с весом, большим либо равным 4 кг.
Определение[править | править код]
Рассмотрим вероятностное пространство 







,
В некоторых источниках (например, в англоязычной литературе) 



Замечания[править | править код]
- Если распределение непрерывно, то
-квантиль однозначно задаётся уравнением
где 

- Очевидно, для непрерывных распределений справедливо следующее широко использующееся при построении доверительных интервалов равенство:
- Для эмпирического распределения
-квантиль можно задать следующим способом:
- составляем вариационный ряд значений
(выборка имеет объём
), а также считаем, что
(это необходимо при вычислении 100 % квантили по приводимым ниже формулам);
- находим величину
;
- сравниваем
и
:
-
- a) если
, то полагаем
;
- б) если
, то полагаем
;
- в) если
, то полагаем
.
- a) если
Заданный таким образом 
В некоторых случаях (при большом объёме выборки и эмпирическом распределении, близком к непрерывному) вместо равенства 

Медиана и квартили[править | править код]
Квантили нормального распределения
- 0,25-квантиль называется первым (или нижним) кварти́лем (от лат. quarta — четверть);
- 0,5-квантиль называется медианой (от лат. mediāna — середина) или вторым кварти́лем;
- 0,75-квантиль называется третьим (или верхним) кварти́лем.
Интеркварти́льным размахом (англ. Interquartile range) называется разность между третьим и первым квартилями, то есть 
Дециль[править | править код]
Деци́ль характеризует распределение величин совокупности, при котором девять значений дециля делят её на десять равных частей. Любая из этих десяти частей составляет 1/10 всей совокупности. Так, первый дециль отделяет 10 % наименьших величин, лежащих ниже дециля, от 90 % наибольших величин, лежащих выше дециля.
Так же, как в случае моды и медианы, у интервального вариационного ряда распределения каждый дециль (и квартиль) принадлежит определённому интервалу и имеет вполне определённое значение[2].
Процентиль[править | править код]


В целом, понятия квантиль и процентиль взаимозаменяемы, так же, как и шкалы исчисления вероятностей — абсолютная и процентная.
Процентили также называются перцентилями или центилями.
Квантили стандартного нормального распределения[править | править код]
| Вероятность (уровень квантили), % | 99,99 | 99,90 | 99,00 | 97,72 | 97,50 | 95,00 | 90,00 | 84,13 | 50,00 |
| Квантиль (округлённый до тысячных) | 3,719 | 3,090 | 2,326 | 1,999 | 1,960 | 1,645 | 1,282 | 1,000 | 0,500 |
См. также[править | править код]
- Квантили нормального распределения
- Квантили распределения Стьюдента
- Квантили распределения хи-квадрат
- Нормальное распределение
- Доверительный интервал
- Наукометрия
Примечания[править | править код]
- ↑ Руководство участкового педиатра. — ГЭОТАР-Медиа, 2008. — С. 44. — 354 с.
- ↑ Шмойлова Р. А., Минашкин В. Г., Садовникова Н. А. Практикум по теории статистики. — 3-е изд. — М.: Финансы и статистика, 2011. — С. 130—131. — 416 с. — ISBN 9785279032969..
Ссылки[править | править код]
5.5Непрерывная случайная величина
Пусть некоторая случайная величина имеет бесконечное несчетное множество значений (интервал или объединение интервалов). Дадим определение непрерывной случайной величины.
Определение. Случайная величина X называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, может быть, отдельных точек.
Отметим, что функция распределения непрерывной случайной величины должна обладать характеристическими свойствами.
Рис. 5.4: График функции распределения непрерывной случайной величины
Непрерывные случайные величины обладают следующим свойством: вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю.
На первый взгляд это утверждение может показаться неверным, поскольку вероятность P (α ≤ X ≤ β) складывается из вероятностей попадания случайной величины X в каждую из точек отрезка. Однако теорема сложения вероятностей действует только в случае конечного или счетного множества слагаемых и не работает в случае несчетного множества.
На основании данного утверждения можно сформулировать следующее утверждение: Если X – непрерывная случайная величина, то вероятность попадания случайной величины в интервал (x1, x2) не зависит от того, является ли этот интервал открытым или
закрытым, т.е.
P (x1 < X < x2) = P (x1 ≤ X ≤ x2) = P (x1 < X ≤ x2) = P (x1 ≤ X < x2).
Задание непрерывной случайной величины с помощью функции распределения не является единственным. Введем понятие плотности вероятности непрерывной случайной
36

величины.
Рассмотрим вероятность попадания случайной величины на интервал [x; x + x]. Эта вероятность равна
P (x ≤ X ≤ x + x) = F (x + x) − F (x),
т.е. равна приращению функции распределения F (x) на этом участке. Тогда вероятность, приходящаяся на единицу длины, т.е. средняя плотность вероятности на участке от x до x + x равна
|
P (x ≤ X ≤ x + x) |
= |
F (x + x) − F (x) |
. |
|
x |
x |
Переходя к пределу при x → 0 в последнем равенстве, получим плотность вероятно-
|
сти в точке x: |
||||||
|
lim |
P (x ≤ X ≤ x + |
x) |
= lim |
F (x + |
x) − F (x) |
= F 0(x), |
|
x |
x |
|||||
|
x→0 |
x→0 |
представляющую производную функции F (x).
Определение. Плотностью вероятности непрерывной случайной величины X называется производная ее функции распределения.
Обозначается плотность вероятности f(x) или ϕ(x). По определению
f(x) = F 0(x).
Плотность вероятности, как и функция распределения, является одной из форм закона распределения непрерывной случайной величины, но в отличие от функции распределения, существует только для непрерывных случайных величин.
Свойства плотности вероятности непрерывной случайной величины.
1. Плотность вероятности – неотрицательная функция, на всей области определения
f(x) ≥ 0.
2.Вероятность попадания непрерывной случайной величины в интервал [a, b] равна определенному интегралу от ее плотности вероятности в пределах от a до b, т.е.
|
P (a ≤ X ≤ b) = Za |
b |
|
f(x)dx. |
Геометрически полученная вероятность равна площади фигуры, ограниченной сверху кривой распределения и опирающейся на отрезок [a, b].
3.Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:
x
Z
F (x) = f(t)dt.
−∞
Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения и лежащей левее точки x.
37
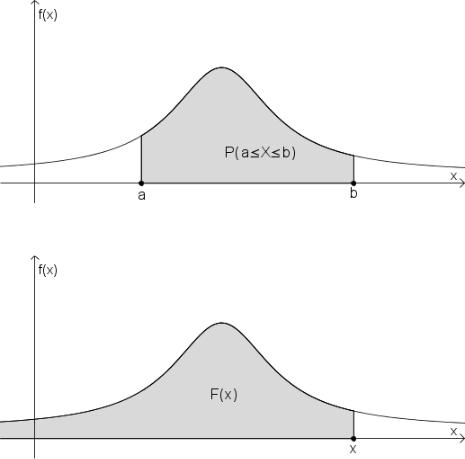
Рис. 5.5: Вероятность попадания в интервал
Рис. 5.6: Геометрическая иллюстрация функции распределения
4.Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице:
+∞
Z
f(x)dx = 1.
−∞
Геометрически это свойство означает, что полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.
5.6Числовые характеристики непрерывной случайной величины
Определение. Математическим ожиданием непрерывной случайной величины X назы-
вается интеграл
+∞
38
Этот интеграл предполагается абсолютно сходящимся. В противном случае, т.е. когда интеграл расходится или сходится условно, считают, что случайная величина X не имеет математического ожидания.
Вероятностный смысл этой формулы такой же, что и для дискретной случайной величины. Это ее среднее значение, точнее – средневзвешенное значение с весовой функцией, равной плотности вероятности.
Математическое ожидание непрерывной случайной величины обладает теми же свойствами, что и математическое ожидание дискретной случайной величины.
Определение дисперсии случайной величины X, данное ранее с помощью формулы
|
2 |
˜ 2 |
), |
|
DX = M[(X − mX ) |
] = M(X |
является общим как для дискретной, так и для непрерывной случайной величины. По
этой формуле имеем
+∞
Z
DX = (x − mX )2f(x)dx.
−∞
Свойства дисперсии, сформулированные для дискретных случайных величин, сохраняются и для случая непрерывных случайных величин.
Определение. Модой непрерывной случайной величины называется точка максимума ее плотности вероятности.
Определение. Медианой (Me X, Me) непрерывной случайной величины называется ее значение, обладающее свойством – вероятности попадания случайной величины X левее и правее медианы равны:
P (X < Me) = P (X > Me).
С помощью функции распределения данное равенство записывается в виде F (Me) = 1 − F (Me) откуда
F (Me) = 1/2.
Если F (x) строго возрастает, то медиана единственна. В случае отсутствия математического ожидания его роль, как среднего, обычно выполняет медиана.
Определение. Коэффициентом асимметрии распределения (скошенности), или просто асимметрией называется число, равное отношению третьего центрального момента случайной величины к кубу ее среднего квадратического отклонения:
aX = µ3/σX3 .
Для непрерывной случайной величины aX > 0, если график одномодальной плотности имеет пологую часть справа, а крутую слева от моды; aX < 0, если наоборот; aX = 0 для симметричного распределения.
Определение. Квантилем порядка p непрерывной случайной величины X называется ее значение xp, удовлетворяющее уравнению
F (xp) = p.
Квантили порядков p = 1/4 и p = 3/4 называются соответственно нижней и верхней квартилями.
Если F (x) строго возрастает, то квантиль xp единственна. Квантиль порядка p = 1/2 есть медиана распределения.
39
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Probability density of a normal distribution, with quartiles shown. The area below the red curve is the same in the intervals (−∞,Q1), (Q1,Q2), (Q2,Q3), and (Q3,+∞).
In statistics and probability, quantiles are cut points dividing the range of a probability distribution into continuous intervals with equal probabilities, or dividing the observations in a sample in the same way. There is one fewer quantile than the number of groups created. Common quantiles have special names, such as quartiles (four groups), deciles (ten groups), and percentiles (100 groups). The groups created are termed halves, thirds, quarters, etc., though sometimes the terms for the quantile are used for the groups created, rather than for the cut points.
q–quantiles are values that partition a finite set of values into q subsets of (nearly) equal sizes. There are q − 1 partitions of the q-quantiles, one for each integer k satisfying 0 < k < q. In some cases the value of a quantile may not be uniquely determined, as can be the case for the median (2-quantile) of a uniform probability distribution on a set of even size. Quantiles can also be applied to continuous distributions, providing a way to generalize rank statistics to continuous variables (see percentile rank). When the cumulative distribution function of a random variable is known, the q-quantiles are the application of the quantile function (the inverse function of the cumulative distribution function) to the values {1/q, 2/q, …, (q − 1)/q}.
Specialized quantiles[edit]
Some q-quantiles have special names:[citation needed]
- The only 2-quantile is called the median
- The 3-quantiles are called tertiles or terciles → T
- The 4-quantiles are called quartiles → Q; the difference between upper and lower quartiles is also called the interquartile range, midspread or middle fifty → IQR = Q3 − Q1.
- The 5-quantiles are called quintiles or pentiles → QU
- The 6-quantiles are called sextiles → S
- The 7-quantiles are called septiles → SP
- The 8-quantiles are called octiles → O
- The 10-quantiles are called deciles → D
- The 12-quantiles are called duo-deciles or dodeciles → DD
- The 16-quantiles are called hexadeciles → H
- The 20-quantiles are called ventiles, vigintiles, or demi-deciles → V
- The 100-quantiles are called percentiles or centiles → P
- The 1000-quantiles have been called permilles or milliles, but these are rare and largely obsolete[1]
Quantiles of a population[edit]
As in the computation of, for example, standard deviation, the estimation of a quantile depends upon whether one is operating with a statistical population or with a sample drawn from it. For a population, of discrete values or for a continuous population density, the k-th q-quantile is the data value where the cumulative distribution function crosses k/q. That is, x is a k-th q-quantile for a variable X if
- Pr[X < x] ≤ k/q or, equivalently, Pr[X ≥ x] ≥ 1 − k/q
and
- Pr[X ≤ x] ≥ k/q.
For a finite population of N equally probable values indexed 1, …, N from lowest to highest, the k-th q-quantile of this population can equivalently be computed via the value of Ip = N k/q. If Ip is not an integer, then round up to the next integer to get the appropriate index; the corresponding data value is the k-th q-quantile. On the other hand, if Ip is an integer then any number from the data value at that index to the data value of the next index can be taken as the quantile, and it is conventional (though arbitrary) to take the average of those two values (see Estimating quantiles from a sample).
If, instead of using integers k and q, the “p-quantile” is based on a real number p with 0 < p < 1 then p replaces k/q in the above formulas. This broader terminology is used when quantiles are used to parameterize continuous probability distributions. Moreover, some software programs (including Microsoft Excel) regard the minimum and maximum as the 0th and 100th percentile, respectively. However, this broader terminology is an extension beyond traditional statistics definitions.
Examples[edit]
The following two examples use the Nearest Rank definition of quantile with rounding. For an explanation of this definition, see percentiles.
Even-sized population[edit]
Consider an ordered population of 10 data values [3, 6, 7, 8, 8, 10, 13, 15, 16, 20]. What are the 4-quantiles (the “quartiles”) of this dataset?
| Quartile | Calculation | Result |
|---|---|---|
| Zeroth quartile | Although not universally accepted, one can also speak of the zeroth quartile. This is the minimum value of the set, so the zeroth quartile in this example would be 3. | 3 |
| First quartile | The rank of the first quartile is 10×(1/4) = 2.5, which rounds up to 3, meaning that 3 is the rank in the population (from least to greatest values) at which approximately 1/4 of the values are less than the value of the first quartile. The third value in the population is 7. | 7 |
| Second quartile | The rank of the second quartile (same as the median) is 10×(2/4) = 5, which is an integer, while the number of values (10) is an even number, so the average of both the fifth and sixth values is taken—that is (8+10)/2 = 9, though any value from 8 through to 10 could be taken to be the median. | 9 |
| Third quartile | The rank of the third quartile is 10×(3/4) = 7.5, which rounds up to 8. The eighth value in the population is 15. | 15 |
| Fourth quartile | Although not universally accepted, one can also speak of the fourth quartile. This is the maximum value of the set, so the fourth quartile in this example would be 20. Under the Nearest Rank definition of quantile, the rank of the fourth quartile is the rank of the biggest number, so the rank of the fourth quartile would be 10. | 20 |
So the first, second and third 4-quantiles (the “quartiles”) of the dataset [3, 6, 7, 8, 8, 10, 13, 15, 16, 20] are [7, 9, 15]. If also required, the zeroth quartile is 3 and the fourth quartile is 20.
Odd-sized population[edit]
Consider an ordered population of 11 data values [3, 6, 7, 8, 8, 9, 10, 13, 15, 16, 20]. What are the 4-quantiles (the “quartiles”) of this dataset?
| Quartile | Calculation | Result |
|---|---|---|
| Zeroth quartile | Although not universally accepted, one can also speak of the zeroth quartile. This is the minimum value of the set, so the zeroth quartile in this example would be 3. | 3 |
| First quartile | The first quartile is determined by 11×(1/4) = 2.75, which rounds up to 3, meaning that 3 is the rank in the population (from least to greatest values) at which approximately 1/4 of the values are less than the value of the first quartile. The third value in the population is 7. | 7 |
| Second quartile | The second quartile value (same as the median) is determined by 11×(2/4) = 5.5, which rounds up to 6. Therefore, 6 is the rank in the population (from least to greatest values) at which approximately 2/4 of the values are less than the value of the second quartile (or median). The sixth value in the population is 9. | 9 |
| Third quartile | The third quartile value for the original example above is determined by 11×(3/4) = 8.25, which rounds up to 9. The ninth value in the population is 15. | 15 |
| Fourth quartile | Although not universally accepted, one can also speak of the fourth quartile. This is the maximum value of the set, so the fourth quartile in this example would be 20. Under the Nearest Rank definition of quantile, the rank of the fourth quartile is the rank of the biggest number, so the rank of the fourth quartile would be 11. | 20 |
So the first, second and third 4-quantiles (the “quartiles”) of the dataset [3, 6, 7, 8, 8, 9, 10, 13, 15, 16, 20] are [7, 9, 15]. If also required, the zeroth quartile is 3 and the fourth quartile is 20.
Relationship to the mean[edit]
For any population probability distribution on finitely many values, and generally for any probability distribution with a mean and variance, it is the case that
where Q(p) is the value of the p-quantile for 0 < p < 1 (or equivalently is the k-th q-quantile for p = k/q), where μ is the distribution’s arithmetic mean, and where σ is the distribution’s standard deviation.[2] In particular, the median (p = k/q = 1/2) is never more than one standard deviation from the mean.
The above formula can be used to bound the value μ + zσ in terms of quantiles.
When z ≥ 0, the value that is z standard deviations above the mean has a lower bound
For example, the value that is z = 1 standard deviation above the mean is always greater than or equal to Q(p = 0.5), the median, and the value that is z = 2 standard deviations above the mean is always greater than or equal to Q(p = 0.8), the fourth quintile.
When z ≤ 0, there is instead an upper bound
For example, the value μ + zσ for z = −3 will never exceed Q(p = 0.1), the first decile.
Estimating quantiles from a sample[edit]
One problem which frequently arises is estimating a quantile of a (very large or infinite) population based on a finite sample of size N.
The asymptotic distribution of the p-th sample quantile is well-known: it is asymptotically normal around the p-th population quantile with variance equal to
where f(xp) is the value of the distribution density at the p-th population quantile (
However, this distribution relies on knowledge of the population distribution; which is equivalent to knowledge of the population quantiles, which we are trying to estimate! Modern statistical packages thus rely on a different technique — or selection of techniques — to estimate the quantiles.
Hyndman and Fan compiled a taxonomy of nine algorithms[4] used by various software packages.
All methods compute Qp, the estimate for the p-quantile (the k-th q-quantile, where p = k/q) from a sample of size N by computing a real valued index h. When h is an integer, the h-th smallest of the N values, xh, is the quantile estimate. Otherwise a rounding or interpolation scheme is used to compute the quantile estimate from h, x⌊h⌋, and x⌈h⌉. (For notation, see floor and ceiling functions).
The first three are piecewise constant, changing abruptly at each data point, while the last six use linear interpolation between data points, and differ only in how the index h used to choose the point along the piecewise linear interpolation curve, is chosen.
Mathematica,[5] Matlab,[6] R[7] and GNU Octave[8] programming languages support all nine sample quantile methods. SAS includes five sample quantile methods, SciPy[9] and Maple[10] both include eight, EViews[11] includes the six piecewise linear functions, Stata[12] includes two, Python[13] includes two, and Microsoft Excel includes two. Mathematica and SciPy support arbitrary parameters for methods which allow for other, non-standard, methods.
The estimate types and interpolation schemes used include:
| Type | h | Qp | Notes |
|---|---|---|---|
| R‑1, SAS‑3, Maple‑1 | Np | x⌈h⌉ | Inverse of empirical distribution function. |
| R‑2, SAS‑5, Maple‑2, Stata | Np + 1/2 | (x⌈h – 1/2⌉ + x⌊h + 1/2⌋) / 2 | The same as R-1, but with averaging at discontinuities. |
| R‑3, SAS‑2 | Np − 1/2 | x⌊h⌉ | The observation numbered closest to Np. Here, ⌊h⌉ indicates rounding to the nearest integer, choosing the even integer in the case of a tie. |
| R‑4, SAS‑1, SciPy‑(0,1), Maple‑3 | Np | x⌊h⌋ + (h − ⌊h⌋) (x⌈h⌉ − x⌊h⌋) | Linear interpolation of the inverse of the empirical distribution function. |
| R‑5, SciPy‑(1/2,1/2), Maple‑4 | Np + 1/2 | Piecewise linear function where the knots are the values midway through the steps of the empirical distribution function. | |
| R‑6, Excel, Python, SAS‑4, SciPy‑(0,0), Maple‑5, Stata‑altdef | (N + 1)p | Linear interpolation of the expectations for the order statistics for the uniform distribution on [0,1]. That is, it is the linear interpolation between points (ph, xh), where ph = h/(N+1) is the probability that the last of (N+1) randomly drawn values will not exceed the h-th smallest of the first N randomly drawn values. | |
| R‑7, Excel, Python, SciPy‑(1,1), Maple‑6, NumPy, Julia | (N − 1)p + 1 | Linear interpolation of the modes for the order statistics for the uniform distribution on [0,1]. | |
| R‑8, SciPy‑(1/3,1/3), Maple‑7 | (N + 1/3)p + 1/3 | Linear interpolation of the approximate medians for order statistics. | |
| R‑9, SciPy‑(3/8,3/8), Maple‑8 | (N + 1/4)p + 3/8 | The resulting quantile estimates are approximately unbiased for the expected order statistics if x is normally distributed. |
Notes:
- R‑1 through R‑3 are piecewise constant, with discontinuities.
- R‑4 and following are piecewise linear, without discontinuities, but differ in how h is computed.
- R‑3 and R‑4 are not symmetric in that they do not give h = (N + 1) / 2 when p = 1/2.
- Excel’s PERCENTILE.EXC and Python’s default “exclusive” method are equivalent to R‑6.
- Excel’s PERCENTILE and PERCENTILE.INC and Python’s optional “inclusive” method are equivalent to R‑7. This is R’s default method.
- Packages differ in how they estimate quantiles beyond the lowest and highest values in the sample, i.e. p < 1/N and p > (N − 1)/N. Choices include returning an error value, computing linear extrapolation, or assuming a constant value.
Of the techniques, Hyndman and Fan recommend R-8, but most statistical software packages have chosen R-6 or R-7 as the default.[14]
The standard error of a quantile estimate can in general be estimated via the bootstrap. The Maritz–Jarrett method can also be used.[15]
Approximate quantiles from a stream[edit]
Computing approximate quantiles from data arriving from a stream can be done efficiently using compressed data structures. The most popular methods are t-digest[16] and KLL.[17] These methods read a stream of values in a continuous fashion and can, at any time, be queried about the approximate value of a specified quantile.
Both algorithms are based on a similar idea: compressing the stream of values by summarizing identical or similar values with a weight. If the stream is made of a repetition of 100 times v1 and 100 times v2, there is no reason to keep a sorted list of 200 elements, it is enough to keep two elements and two counts to be able to recover the quantiles. With more values, these algorithms maintain a trade-off between the number of unique values stored and the precision of the resulting quantiles. Some values may be discarded from the stream and contribute to the weight of a nearby value without changing the quantile results too much. The t-digest maintains a data structure of bounded size using an approach motivated by k-means clustering to group similar values. The KLL algorithm uses a more sophisticated “compactor” method that leads to better control of the error bounds at the cost of requiring an unbounded size if errors must be bounded relative to p.
Both methods belong to the family of data sketches that are subsets of Streaming Algorithms with useful properties: t-digest or KLL sketches can be combined. Computing the sketch for a very large vector of values can be split into trivially parallel processes where sketches are computed for partitions of the vector in parallel and merged later.
Discussion[edit]
Standardized test results are commonly reported as a student scoring “in the 80th percentile”, for example. This uses an alternative meaning of the word percentile as the interval between (in this case) the 80th and the 81st scalar percentile.[18] This separate meaning of percentile is also used in peer-reviewed scientific research articles.[19] The meaning used can be derived from its context.
If a distribution is symmetric, then the median is the mean (so long as the latter exists). But, in general, the median and the mean can differ. For instance, with a random variable that has an exponential distribution, any particular sample of this random variable will have roughly a 63% chance of being less than the mean. This is because the exponential distribution has a long tail for positive values but is zero for negative numbers.
Quantiles are useful measures because they are less susceptible than means to long-tailed distributions and outliers. Empirically, if the data being analyzed are not actually distributed according to an assumed distribution, or if there are other potential sources for outliers that are far removed from the mean, then quantiles may be more useful descriptive statistics than means and other moment-related statistics.
Closely related is the subject of least absolute deviations, a method of regression that is more robust to outliers than is least squares, in which the sum of the absolute value of the observed errors is used in place of the squared error. The connection is that the mean is the single estimate of a distribution that minimizes expected squared error while the median minimizes expected absolute error. Least absolute deviations shares the ability to be relatively insensitive to large deviations in outlying observations, although even better methods of robust regression are available.
The quantiles of a random variable are preserved under increasing transformations, in the sense that, for example, if m is the median of a random variable X, then 2m is the median of 2X, unless an arbitrary choice has been made from a range of values to specify a particular quantile. (See quantile estimation, above, for examples of such interpolation.) Quantiles can also be used in cases where only ordinal data are available.
See also[edit]
- Flashsort – sort by first bucketing by quantile
- Interquartile range
- Descriptive statistics
- Quartile
- Q–Q plot
- Quantile function
- Quantile normalization
- Quantile regression
- Quantization
- Summary statistics
- Tolerance interval (“confidence intervals for the pth quantile”[20])
References[edit]
- ^ Helen Mary Walker, Joseph Lev, Elementary Statistical Methods, 1969, [p. 60 https://books.google.com/books?id=ogYnAQAAIAAJ&dq=permille]
- ^ Bagui, S.; Bhaumik, D. (2004). “Glimpses of inequalities in probability and statistics” (PDF). International Journal of Statistical Sciences. 3: 9–15. ISSN 1683-5603.
- ^ Stuart, Alan; Ord, Keith (1994). Kendall’s Advanced Theory of Statistics. London: Arnold. ISBN 0340614307.
- ^ Hyndman, Rob J.; Fan, Yanan (November 1996). “Sample Quantiles in Statistical Packages”. American Statistician. American Statistical Association. 50 (4): 361–365. doi:10.2307/2684934. JSTOR 2684934.
- ^ Mathematica Documentation See ‘Details’ section
- ^ “Quantile calculation”. uk.mathworks.com.
- ^ Frohne, Ivan; Hyndman, Rob J. (2009). Sample Quantiles. R Project. ISBN 978-3-900051-07-5.
- ^ “Function Reference: quantile – Octave-Forge – SourceForge”. Retrieved 6 September 2013.
- ^ “scipy.stats.mstats.mquantiles — SciPy v1.4.1 Reference Guide”. docs.scipy.org.
- ^ “Statistics – Maple Programming Help”. www.maplesoft.com.
- ^ “EViews 9 Help”. Archived from the original on April 16, 2016. Retrieved April 4, 2016.
- ^ Stata documentation for the pctile and xtile commands See ‘Methods and formulas’ section.
- ^ “statistics — Mathematical statistics functions — Python 3.8.3rc1 documentation”. docs.python.org.
- ^ Hyndman, Rob J. (28 March 2016). “Sample quantiles 20 years later”. Hyndsignt blog. Retrieved 2020-11-30.
- ^ Wilcox, Rand R. (2010). Introduction to Robust Estimation and Hypothesis Testing. ISBN 978-0-12-751542-7.
- ^ Dunning, Ted; Ertl, Otmar (February 2019). “Computing Extremely Accurate Quantiles Using t-Digests”. arXiv:1902.04023 [stat.CO].
- ^ Zohar Karnin, Kevin Lang, Edo Liberty (2016). “Optimal Quantile Approximation in Streams”. arXiv:1603.05346 [cs.DS].
{{cite arxiv}}: CS1 maint: uses authors parameter (link) - ^ “percentile”. Oxford Reference. Retrieved 2020-08-17.
- ^ Kruger, J.; Dunning, D. (December 1999). “Unskilled and unaware of it: how difficulties in recognizing one’s own incompetence lead to inflated self-assessments”. Journal of Personality and Social Psychology. 77 (6): 1121–1134. doi:10.1037/0022-3514.77.6.1121. ISSN 0022-3514. PMID 10626367.
- ^ Stephen B. Vardeman (1992). “What about the Other Intervals?”. The American Statistician. 46 (3): 193–197. doi:10.2307/2685212. JSTOR 2685212.
Further reading[edit]
- Serfling, R. J. (1980). Approximation Theorems of Mathematical Statistics. John Wiley & Sons. ISBN 0-471-02403-1.
External links[edit]
Media related to Quantiles at Wikimedia Commons
Квантиль – что это?
Определение 1. Кванти́ль в математической статистике – число xp такое, что заданная случайная величина X превышает его лишь с фиксированной вероятностью p.
Классное определение, но годится такое определение разве что для википедии, оно не конструктивно, т.е не пригодно для практических целей. Немного терпения, и вам станет понятно данное определение. Более того, вы с легкостью сможете находить квантили любого уровня, а также сможете применять данное понятие для решения задач по статистике.
Как найти квантиль
Попытка №2 – конструктивное определение квантиля:
Определение 1*. Квантилью xp (p-квантилью, квантилью уровня p) случайной величины X, имеющей функцию распределения F (x), называют решение xp уравнения F (x) = p.
Следовательно, для того чтобы найти квантиль xp необходимо найти решение уравнения F (x) = p.
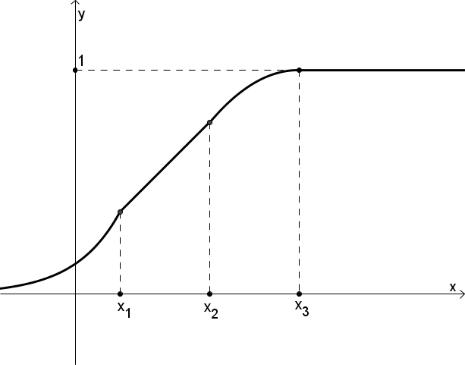
Для наглядности, найдем решение графически:
1. Построим функцию распределения F(x);
2. Построим горизонтальную линию уровня p;
3. Находим точку пересечения данных линий, опускаем перпендикуляр на ось X, получаем квантиль xp (квантиль уровня p) смотри рисунок 1.
Аналогично для дискретной случайной величины X смотри рисунок 2.
Замечание. Для дискретной случайной величины X функция распределения F(x) имеет ступенчатый вид, функция не монотонна. Поэтому решение уравнения F(x) = p в общем случае не однозначно ( в решение попадают интервалы). В таких случаях, для определенности квантилем назначают средину интервала, как показано на рис.2.
Квантили удобны для сравнения различных законов распределения вероятностей. В некоторых случаях пользуются децилями: x0,1 , x0,2 , x0,3 , …, x0,9 . Однако наибольшее распространение получили квартили. Квартилями называют квантили порядков 0,25, 0,5 и 0,75. Будем их обозначать соответственно как k1 , k2 , k3 . Квартили k1 и k3 называют обычно нижней и верхней квартилями. Вторая квартиль k2 совпадает с медианой распределения.
Определение 2. Децилями называют квантили уровня 0,1, 0,2, 0,3, …0,9, обозначают соответственно d1, d2, d3,…d9.
Определение 3. Квартилями называют квантили порядков 0,25, 0,5 и 0,75, обозначают соответственно k1 , k2 , k3 .
Определение 4. Медианой называют квантиль уровня 0,5,
обозначают Me = x0,5.
Ну вот, пришло время, на конкретном примере показать, как находить квантили.
Пример. Пусть имеется выборка дискретной случайной величины X:
| 3 | 0 | 1 | 5 | 1 | 2 | 4 | 5 | 3 | 4 |
| 2 | 4 | 2 | 0 | 2 | 3 | 1 | 3 | 2 | 1 |
| 4 | 3 | 0 | 2 | 1 | 0 | 4 | 2 | 3 | 2 |
Найти квантили уровня 0,2 и 0,3 ( x0,2 и x0,3 )
Решение.
1) Находим функцию распределения дискретной случайной величины:
| Вариант | Частота | Частность | F(X) |
| 0 | 4 | 0,133333 | 0,133333 |
| 1 | 5 | 0,166667 | 0,3 |
| 2 | 8 | 0,266667 | 0,566667 |
| 3 | 6 | 0,2 | 0,766667 |
| 4 | 5 | 0,166667 | 0,933333 |
| 5 | 2 | 0,066667 | 1 |
2) Строим график функции распределения, проводим линии уровня p = 0,2 и p = 0,3,
3) получаем квантили: x0,2 = 1, x0,3 = 1,5, или, можно сказать так, получаем децили d2=1, d3=1,5

























