Как найти квантиль случайной величины пример - Сайт, где вы сможете решить свои вопросы

Мода и медиана случайной величины.
Квантиль уровня случайной величины

Краткая теория

Примеры решения задач

Квантиль – что это?

Как найти квантиль

Параметры дискретного закона распределения

Математическое описание

Построить ряд распределения

Список параметров

Шаблон гистограммы в OpenOffice Calc

Определение[править | править код]

Замечания[править | править код]

Медиана и квартили[править | править код]

Дециль[править | править код]

Процентиль[править | править код]

Квантили стандартного нормального распределения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Мода и медиана случайной величины.Квантиль уровня случайной величины

Краткая теория

Примеры решения задач

Квантиль – что это?

Как найти квантиль

Параметры дискретного закона распределения

Математическое описание

Построить ряд распределения

Список параметров

Шаблон гистограммы в OpenOffice Calc

Определение[править | править код]

Замечания[править | править код]

Медиана и квартили[править | править код]

Дециль[править | править код]

Процентиль[править | править код]

Квантили стандартного нормального распределения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Мода и медиана случайной величины.
Квантиль уровня случайной величины

Мода непрерывной и дискретной случайной величины

Медиана непрерывной и дискретной случайной величины

Квантили и процентные точки случайной величины

Пример 1

Пример 2

Среднее значение

Отклонение от среднего

Квантиль

Построение интервалов

Итого

Бонус

Совет

Мода непрерывной и дискретной случайной величины

Медиана непрерывной и дискретной случайной величины

Квантили и процентные точки случайной величины

Пример 1

Пример 2

Среднее значение

Отклонение от среднего

Квантиль

Построение интервалов

Итого

Бонус

Совет

Вам также может понравиться

Как составить акт ревизии при недостаче

Как найти тайник кости на янтаре

Как найти премию от ставки

Добавить комментарий Отменить ответ

Двусторонний доверительный интервал

Доверительный интервал

Двусторонний доверительный интервал

Доверительный интервал

Краткая теория
Примеры решения задач

Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.

Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность

или плотность вероятности

достигает максимума.

В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.

Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.

Полимодальное распределение

Медианой случайной величины

называют число

, такое, что

То есть вероятность того, что
случайная величина

примет
значение, меньшее медианы

или больше ее,
одна и та же и равна

Для дискретной случайной величины

это число может
не совпадать ни с одним из значений

. Поэтому медиану дискретной случайной величины
определяют как любое число

, лежащее между двумя соседними возможными значениями

такими, что

Для непрерывной случайной величины,
геометрически, вертикальная прямая

, проходящая через точку с абсциссой, равной

, делит площадь фигуры под кривой распределения на две
равные части.

Медиана на графике плотности вероятности непрерывной
случайной величины

Очевидно, что в точке

функция распределения непрерывной случайной
величины равна

, то есть

Медиана на графике функции распределения непрерывной
случайной величины

Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.

Квантилем уровня

(или

– квантилем)
называется такое значение

случайной
величины, при котором функция ее распределения принимает значение, равное

, то есть:

Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть

. Квантили

получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили

) и процентили (квантили

С понятием квантиля тесно связано
понятие процентной точки. Под

точкой
подразумевается квантиль

, то есть такое значение случайной величины

, при котором

Смежные темы решебника:

Структурные средние в статистике – мода, медиана, квантиль, дециль
Дискретная случайная величина
Непрерывная случайная величина

Найти
моду, медиану, квантиль

и 40%-ну точку случайной величины

c плотностью распределения:

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Исследуем
функцию на наибольшее и наименьшее значение на отрезке

Производная:

Производная
не обращается в нуль.

Значения
на концах отрезка:

Следовательно,
мода:

Медиану

найдем из условия:

В нашем
случае получаем:

Значение

принадлежит отрезку

,
следовательно, искомая медиана:

Квантиль

найдем из уравнения:

Значение

принадлежит отрезку

,
следовательно, искомый квантиль:

Найдем
40%-ную точку случайной величины

, или квантиль

из уравнения:

Значение

принадлежит отрезку

,
следовательно, искомая точка:

Ответ:

Найти
моду, медиану, квантиль

случайной величины

, заданной функцией
распределения:

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Найдем
плотность распределения:

Исследуем
функцию на наибольшее и наименьшее значение на отрезке

Производная:

Значения
функции

в стационарных точках и на концах отрезка:

Распределение
полимодальное:

Медиану

найдем из уравнения:

Итак,
медиана:

Квантиль

найдем из уравнения:

Итак:

Ответ:

Краткая теория
Примеры решения задач

Источник

Определение 1. Кванти́ль в математической статистике – число x_p такое, что заданная случайная величина X превышает его лишь с фиксированной вероятностью p.

Классное определение, но годится такое определение разве что для википедии, оно не конструктивно, т.е не пригодно для практических целей. Немного терпения, и вам станет понятно данное определение. Более того, вы с легкостью сможете находить квантили любого уровня, а также сможете применять данное понятие для решения задач по статистике.

Попытка №2 – конструктивное определение квантиля:

Определение 1*. Квантилью x_p (p-квантилью, квантилью уровня p) случайной величины X, имеющей функцию распределения F (x), называют решение x_p уравнения F (x) = p.

Следовательно, для того чтобы найти квантиль x_p необходимо найти решение уравнения F (x) = p.

Для наглядности, найдем решение графически:

1. Построим функцию распределения F(x);

2. Построим горизонтальную линию уровня p;

3. Находим точку пересечения данных линий, опускаем перпендикуляр на ось X, получаем квантиль x_p (квантиль уровня p) смотри рисунок 1.

Аналогично для дискретной случайной величины X смотри рисунок 2.

Замечание. Для дискретной случайной величины X функция распределения F(x) имеет ступенчатый вид, функция не монотонна. Поэтому решение уравнения F(x) = p в общем случае не однозначно ( в решение попадают интервалы). В таких случаях, для определенности квантилем назначают средину интервала, как показано на рис.2.

Квантили удобны для сравнения различных законов распределения вероятностей. В некоторых случаях пользуются децилями: x_0,1 , x_0,2 , x_0,3 , …, x_0,9 . Однако наибольшее распространение получили квартили. Квартилями называют квантили порядков 0,25, 0,5 и 0,75. Будем их обозначать соответственно как k₁ , k₂ , k₃ . Квартили k₁ и k₃ называют обычно нижней и верхней квартилями. Вторая квартиль k₂ совпадает с медианой распределения.

Определение 2. Децилями называют квантили уровня 0,1, 0,2, 0,3, …0,9, обозначают соответственно d₁, d₂, d₃,…d₉.

Определение 3. Квартилями называют квантили порядков 0,25, 0,5 и 0,75, обозначают соответственно k₁ , k₂ , k₃ .

Определение 4. Медианой называют квантиль уровня 0,5,

обозначают Me = x_0,5.

Ну вот, пришло время, на конкретном примере показать, как находить квантили.

Пример. Пусть имеется выборка дискретной случайной величины X:

3	0	1	5	1	2	4	5	3	4
2	4	2	0	2	3	1	3	2	1
4	3	0	2	1	0	4	2	3	2

Найти квантили уровня 0,2 и 0,3 ( x_0,2 и x_0,3 )

Решение.

1) Находим функцию распределения дискретной случайной величины:

Вариант	Частота	Частность	F(X)
0	4	0,133333	0,133333
1	5	0,166667	0,3
2	8	0,266667	0,566667
3	6	0,2	0,766667
4	5	0,166667	0,933333
5	2	0,066667	1

2) Строим график функции распределения, проводим линии уровня p = 0,2 и p = 0,3,

3) получаем квантили: x_0,2 = 1, x_0,3 = 1,5, или, можно сказать так, получаем децили d₂=1, d₃=1,5

Источник

В примерах в данной статье данные генерятся при каждой загрузке страницы. Если Вы хотите посмотреть пример с другими значениями –
обновите страницу .

В статье описано как найти среднее значение и стандартное отклонение. Вы узнаете, что такое квантиль и каких он бывает видов, а также,
как построить доверительный интервал.

Смотря на закон распределения, мы можем понять, какова вероятность того или иного события,
можем сказать, какова вероятность, что произойдёт группа событий, а в этой статье мы рассмотрим, как наши выводы “на глаз” перевести
в математически обоснованное утверждение.

Крайне важное определение: математическое ожидание – это площадь под графиком распределения. Если мы говорим о дискретном распределении –
это сумма событий умноженных на соответсвующие вероятности, также известно как момент:

(2) E(X) = Σ(p_i•X_i) E – от английского слова Expected (ожидание)
Для математического ожидания справедливы равенства:

(3) E(X + Y) = E(X) + E(Y)
(4) E(X•Y) = E(X) • E(Y)

Момент степени k:

(5) ν_k = E(X^k)

Центральный момент степени k:

(6) μ_k = E[X – E(X)]^k

Среднее значение (μ) закона распределения – это математическое ожидание случайной величины
(случайная величина – это событие), например, сколько в среднем посетителей заходит в магазин в час:

Кол-во посетителей	0	1	2	3	4	5	6
Количество наблюдений	95	101	101	35	33	3	32
Таблица 1. Количество посетителей в час

График 1. Количество посетителей в час

Чтобы найти среднее значение всех результатов необходимо сложить всё вместе и разделить на количество результатов:

μ = (95 • 0 + 101 • 1 + 101 • 2 + 35 • 3 + 33 • 4 + 3 • 5 + 32 • 6) / 400 = 747/400 = 1.87

То же самое мы можем проделать используя формулу 2:

μ = M(X) = Σ(X_i•p_i) = 0 • 0.24 + 1 • 0.25 + 2 • 0.25 + 3 • 0.09 + 4 • 0.08 + 5 • 0.01 + 6 • 0.08 = 1.87 Момент первой степени, формула (5)

Собственно, формула 2 представляет собой среднее арифметическое всех значений
Итог: в среднем, 1.87 посетителя в час

Количество посетителей	0	1	2	3	4	5	6
Вероятность (%)	23.8	25.3	25.3	8.8	8.3	0.8	8
Таблица 2. Закон распределения количества посетителей

Посмотрите на это распределение, можно предположить, что в среднем случайная величина равна 100±5, поскольку
кажется, что таких значений несравнимо больше чем тех, что меньше 95 или больше 105:

График 2. График функции вероятности. Распределение ≈ 100±5

Среднее значение по формуле (2): μ = 99.95, но как посчитать, насколько далеко все значения находятся от среднего? Вам должна быть
знакома запись 100±5. Что бы получить это значение ±, нам необходимо определить диапазон значений вокруг среднего. И мы могли бы
использовать в качестве меры удалённости “разность” между средним и случайными величинами:

(7) x_i – μ

но сумма таких расстояний, а следовательно и любое производное от этого числа, будет равно нулю, поэтому в качестве меры выбрали квадрат разниц
между величинами и средним значением:

(8) (x_i – μ)²

Соответственно, среднее значение удалённости – это математическое ожидание квадратов удалённости:

(9) σ² = E[(X – E(X))²]
Поскольку вероятности любой удалённости равносильны – вероятность каждого из них – 1/n, откуда:
(10) σ² = E[(X – E(X))²] = ∑[(X_i – μ)²]/n
Она же формула центрального момента (6) второй степени

σ возведена в квадрат, поскольку вместо расстояний мы взяли квадрат расстояний. σ² называется дисперсией. Корень из дисперсии
называется средним квадратическим отклонением, или среднеквадратическим отклоненим, и его используют в качестве меры разброса:

(11) μ±σ
(12) σ = √(σ²) = √[∑[(X_i – μ)²]/n]

Возвращаясь к примеру, посчитаем среднеквадратическое отклонение для графика 2:

σ = √(∑(x-μ)²/n) = √{[(90 – 99.95)² + (91 – 99.95)² + (92 – 99.95)² + (93 – 99.95)² + (94 – 99.95)² + (95 – 99.95)² + (96 – 99.95)² + (97 – 99.95)² + (98 – 99.95)² + (99 – 99.95)² + (100 – 99.95)² + (101 – 99.95)² + (102 – 99.95)² + (103 – 99.95)² + (104 – 99.95)² + (105 – 99.95)² + (106 – 99.95)² + (107 – 99.95)² + (108 – 99.95)² + (109 – 99.95)² + (110 – 99.95)²]/21} = 6.06

Итак, для графика 2 мы получили:

X = 99.95±6.06 ≈ 100±6 , что немного отличается от полученного “на глаз”

График 3. Функция распределения. Медиана

График 4. Функция распределения. 4-квантиль или квартиль

График 5. Функция распределения. 0.34-квантиль

Для анализа функции распределения ввели понятие квантиль. Квантиль – это случайная величина при заданном уровне вероятности, т.е.:
квантиль для уровня вероятности 50% – это случайная величина на графике плотности вероятности, которая имеет вероятность 50%.
На примере с графиком 3, квантиль уровня 0.5 = 99 (ближайшее значение, поскольку распределение дискретно и события со значением 99.3 просто не существует)

2-квантиль – медиана
4-квантиль – квартиль
10-квантиль – дециль
100-квантиль – перцентиль

То есть, если мы говорим о дециле (10-квантиле), то это означает, что мы разбили график на 10 частей, что соответствует девяти линяям,
и для каждого дециля нашли значение случайной величины.

Также, используется обозначение x-квантиль, где х – дробное число, например, 0.34-квантиль, такая запись означает значение случайной величины при
p = 0.34.

Для дискретного распределения квантиль необходимо выбирать следующим образом: квантиль гарантирует вероятность, поэтому, если рассчитанный
квантиль не совпадает с одним и значений, необходимо выбирать меньшее значение.

Квантили используют для построения доверительных интервалов, которые необходимы для исследования статистики не одного конкретного события (например,
интерес – случайное число = 98), а для группы событий (например, интерес – случайное число между 96 и 99). Доверительный интервал бывает двух видов:
односторонний и двусторонний. Параметр доверительного интервала – уровень доверия. Уровень доверия означает процент событий, которые можно считать успешными.

Двусторонний доверительный интервал строится следующим образом: мы задаёмся уровнем значимости, например, 10%, и выделяем область на графике так, что 90% всех
событий попадут в эту область. Поскольку интервал двусторонний, то мы отсекаем по 5% с каждой стороны, т.е. мы ищем 5й перцентиль, 95й перцентиль и значения
случайной величины между ними будут являться доверительной областью, значения за пределами доверительной области называются “критическая область”

График 6. Плотность вероятности

График 7. Функция распределения с 5 и 95 перцентилями. Цветом выделен доверительный интервал с уровнем доверия 0.9

График 8. Функция вероятности и двусторонний доверительный интервал с уровнем доверия 90%

Левосторонний и правосторонний доверительные интервалы строятся аналогично двустороннему: для левостороннего интервала мы находим перцентиль уровня
[‘один’ минус ‘уровень значимости’]. Таким образом, для построения доверительного левостороннего интервала уровня значимости 4% нам необходимо найти четвёртый перцентиль
и всё, что справа – доверительный интервал, всё что слева – критическая область.

График 9. Левосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал

График 10. Правосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал

Среднее значение – математическое ожидание случайной величины, находится по формуле:

μ = E(X) = Σ(p_i•X_i)

Среднеквадратичное отклонение – математическое ожидание удалённости значений от среднего, находится по формуле:

σ = √(σ²) = √[∑[(X_i – μ)²]/n]

n-квантиль – разделение функции распределения на n равных отрезков, основные типы квантилей:

2-квантиль – медиана
4-квантиль – квартили
10-квантиль – децили
100-квантиль – перцентили

Доверительный интервал уровня α – участок функции вероятности, содержащий α всех возможных значений. Двусторонний доверительный
интервал строится отсечением (1-α)/2 справа и слева. Левосторонний и правосторонний доверительные интервалы строятся отсечением
области (1-α) слева и справа соответственно.

Предположим, мы имеем 100 значений и все разные, например: масса тела Сомалийских пиратов.
Такой набор данных обрабатывать неудобно, мы даже не можем представить их на обычном графике.
Поэтому нам необходимо категоризировать имеющиеся данные и для этого мы делаем следующее:

Запишем наши данные в таблицу:

120	133	70	108	54	86	57	77	61	93
138	64	65	104	121	105	61	103	124	138
126	104	126	87	61	122	110	94	79	115
85	82	77	68	100	84	87	76	106	101
90	128	111	132	61	83	104	138	83	59
72	69	104	120	80	89	136	108	59	100
130	71	59	79	118	102	90	122	124	103
68	75	95	104	90	79	117	76	83	134
138	122	135	110	113	102	67	119	108	89
69	87	108	118	93	90	63	135	59	69
Таблица 3. Вес сомалийских пиратов

Данные разобьём на группы, для начала предлагаю разбить на шесть интервалов:

Узнаём максимальное и минимальное значения, вычитаем их друг из друга и делим на количество
интервалов – получили отрезки:

Максимальное значение: 138
Минимальное значение: 54
Разница: 138 – 54 = 84
Длина интервала: 84 / 6 = 14

Теперь посчитаем количество пиратов (весов, я имею ввиду) в каждом интервале:

#	Интервал	Количество элементов
1.	54 – 68	14
2.	68 – 82	17
3.	82 – 96	20
4.	96 – 110	18
5.	110 – 124	15
6.	124 – 138	12
Таблица 4. Количество элементов в интервалах

Вуа-ля, наше распределение на графике:

График 11. Ряд распределения массы тела сомалийских пиратов

Интервалы лучше брать целыми числами, поэтому, если с выбранным количеством интервалов
размер выходит нецелым, то можно раздвинуть диапазон значений, пример:

Диапазон можно двигать как вверх, так и вниз, но лучше в обе стороны.

Принято делить распределение на 7-8 интервалов, но в каждой конкретной ситуации
Вы можете выбрать отличное количество интервалов, впрочем, как и сделать их
различной длины.

Итак, вот список основных параметров дискретного закона распределения:

Название	Символ	Формула
Математическое ожидание (среднее)	E(X)	Σ(p_i•X_i)
Центральный момент (среднеквадратичное отклонение)	σ_x	σ = √(σ²) = √[∑[(X_i – μ)²]/n]
Длина интервала	R	max(x) – min(x)
Мода	m_o	max P(x = m_o)
1й квантиль	–	F(x) = 0.25
Медиана	m_e	F(x) = 0.5
Дециль	–	F(x) = 0.1
Таблица 5. Основные параметры дискретного закона распределения

Файл histogram_mock.ods содержит шаблон
построения гистограммы.

Вам понравилась статья?
/

Источник

Кванти́ль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Если вероятность задана в процентах, то квантиль называется процентилем или перцентилем (см. ниже).

Например, фраза «90-й процентиль массы тела у новорожденных мальчиков составляет 4 кг»^[1] означает, что 90 % мальчиков рождаются с весом, меньшим либо равным 4 кг, а 10 % мальчиков рождаются с весом, большим либо равным 4 кг.

Рассмотрим вероятностное пространство и $mathbb {P} ^{X}$ — вероятностная мера, задающая распределение некоторой случайной величины . Пусть фиксировано . Тогда alpha -квантилем (или квантилем уровня alpha ) распределения $mathbb {P} ^{X}$ называется число $x_{alpha }in mathbb{R}$ , такое что

${displaystyle mathbb {P} (Xleqslant x_{alpha })leqslant alpha }$

${displaystyle mathbb {P} (Xgeqslant x_{alpha })geqslant 1-alpha .}$

В некоторых источниках (например, в англоязычной литературе) -м -квантилем называется квантиль уровня k/q , то есть (k/q) -квантиль в предыдущих обозначениях.

Если распределение непрерывно, то -квантиль однозначно задаётся уравнением

$F_{X}(x_{alpha })=alpha ,$

где $F_{X}$ — функция распределения $mathbb {P} ^{X}$ .

Очевидно, для непрерывных распределений справедливо следующее широко использующееся при построении доверительных интервалов равенство:

${mathbb {P}}left(x_{{{frac {1-alpha }{2}}}}leqslant Xleqslant x_{{{frac {1+alpha }{2}}}}right)=alpha .$

Для эмпирического распределения -квантиль можно задать следующим способом:

составляем вариационный ряд значений $V_{0}leqslant V_{1}leqslant dots leqslant V_{{N-1}}$ (выборка имеет объём ), а также считаем, что $V_{N}=V_{{N-1}}$ (это необходимо при вычислении 100 % квантили по приводимым ниже формулам);
находим величину ;
сравниваем и :

a) если

, то полагаем $x_{alpha }=V_{{K+1}}$

;

б) если

, то полагаем $x_{{alpha }}=(V_{K}+V_{{K+1}})/2$

;

в) если

, то полагаем $x_{{alpha }}=V_{K}$

Заданный таким образом alpha -квантиль удовлетворяет приведенному выше определению.

В некоторых случаях (при большом объёме выборки и эмпирическом распределении, близком к непрерывному) вместо равенства можно использовать приближённое сравнение (это позволит, например, квантиль уровня 1/3 представлять как 0,33…333 при компьютерной обработке данных).

Квантили нормального распределения

0,25-квантиль называется первым (или нижним) кварти́лем (от лат. quarta — четверть);
0,5-квантиль называется медианой (от лат. mediāna — середина) или вторым кварти́лем;
0,75-квантиль называется третьим (или верхним) кварти́лем.

Интеркварти́льным размахом (англ. Interquartile range) называется разность между третьим и первым квартилями, то есть $x_{{0{,}75}}-x_{{0{,}25}}$ . Интерквартильный размах является характеристикой разброса распределения величины и является робастным аналогом дисперсии. Вместе, медиана и интерквартильный размах могут быть использованы вместо математического ожидания и дисперсии в случае распределений с большими выбросами, либо при невозможности вычисления последних.

Деци́ль характеризует распределение величин совокупности, при котором девять значений дециля делят её на десять равных частей. Любая из этих десяти частей составляет 1/10 всей совокупности. Так, первый дециль отделяет 10 % наименьших величин, лежащих ниже дециля, от 90 % наибольших величин, лежащих выше дециля.

Так же, как в случае моды и медианы, у интервального вариационного ряда распределения каждый дециль (и квартиль) принадлежит определённому интервалу и имеет вполне определённое значение^[2].

-м проценти́лем называют квантиль уровня . Соответственно, медиана является 50-м процентилем, а первый и третий квартиль — 25-м и 75-м процентилями соответственно.

В целом, понятия квантиль и процентиль взаимозаменяемы, так же, как и шкалы исчисления вероятностей — абсолютная и процентная.

Процентили также называются перцентилями или центилями.

Вероятность (уровень квантили), %	99,99	99,90	99,00	97,72	97,50	95,00	90,00	84,13	50,00
Квантиль (округлённый до тысячных)	3,719	3,090	2,326	1,999	1,960	1,645	1,282	1,000	0,500

Квантили нормального распределения
Квантили распределения Стьюдента
Квантили распределения хи-квадрат
Нормальное распределение
Доверительный интервал
Наукометрия

↑ Руководство участкового педиатра. — ГЭОТАР-Медиа, 2008. — С. 44. — 354 с.
↑ Шмойлова Р. А., Минашкин В. Г., Садовникова Н. А. Практикум по теории статистики. — 3-е изд. — М.: Финансы и статистика, 2011. — С. 130—131. — 416 с. — ISBN 9785279032969..

Источник

y = f (x)

y	ES > 0

	ES = 0
	ES < 0
	x
	a

Рис. 2.24

Пример 2.31. Найти коэффициент асимметрии и эксцесс случайной величины, распределенной по так называемому закону Лапласа с плотностью

вероятности	f (x) = 0,5e−	x


	.

Решение. Так как распределение случайной величины X симметрично относительно оси ординат, то все нечетные как начальные, так и центральные моменты равны 0, то есть α1 = 0, α3 = 0, µ3 = 0 и в силу (2.60) ко-

эффициент асимметрии As = 0 . Для нахождения эксцесса необходимо вычис-

лить четные начальные моменты α2 и α4 :

+∞

α2 = ∫ x2 f (x)dx = ∫ x2 (0,5e−

)dx = 2 0,5 ∫ x2e−xdx = 2.

−∞

Следовательно,

DX = µ2 =α2 −α12 = 2 −0 = 2 и σ = DX = 2 .

+∞

α4 = ∫ x4 f (x)dx = ∫ x4

(0,5e−

)dx = 2 0,5 ∫ x4e−xdx = 24.

−∞

Находим эксцесс по формуле (2.61)

µ4

ES =

−3 =

−3 = 3.

σX4

( 2 )4

109

			0,5
				y = f (x)

					x


		0	1
−2	−1		2

Рис. 2.25

Эксцесс распределения положителен, что говорит об островершинности кривой распределения (рис. 2.25).

Кроме рассмотренных выше числовых характеристик случайной величины используются другие, так называемые квантили.

Определение 2.28. Квантилем уровня p случайной величины X на-

зывается решение уравнения
F(xp ) = P( X < xp ) = p,	(2.62)
где p − некоторое число, 0 < p <1.

Квантили x0,25 , x0,5 и x0,75 имеют свои названия: нижняя квантиль, медиана ( Me X = x0,5 ), верхняя квантиль соответственно. Они делят число-

вую прямую на 4 части, вероятности попадания в которые равны 0,25 (рис

2.26).			y
							y = f (x)

						0, 25	0, 25	0, 25	x
						0, 25

				x0,25	x0,5		x0,75
		0
							Рис.	2.26


	С понятием квантиля тесно связано понятие процентной точки. Под
100 p% −ной точкой подразумевается квантиль	x1−p , то есть такое значение

случайной величины X , при котором P{X ≥ x1−p }= p.

Пример 2.32. По данным примера 2.21, найти квантиль x0,3 и 30%-

ную точку случайной величины X .

Решение. Функция распределения

110

x 0 x

F(x) = ∫ f (t)dt = ∫ 0 dt + ∫3t2dt = x3 .

−∞ −∞ 0

Квантиль x0,3 найдем из уравнения (2.62), то есть x0,33 = 0,3 откуда x0,3 ≈ 0,67 . Найдем 30%-ную точку случайной величины X , или квантиль

x0,7 из уравнения x0,73 = 0,7 откуда x0,7 ≈ 0,89 .

Пример 2.33. По данным примера 2.29 найти квантиль x0,7 и 10%-ную

точку случайной величины X .

Решение. Квантиль x0,7

случайной величины X найдем из уравнения

(2.62) с учетом (2.54):

F(x ) =

+Φ

x0,7 −173

= 0,7,

0,7

откуда

−173

0,7

= Φ(t) = 0,2.

Тогда t = 0,524 и x0,7

= 6t +173 ≈176 см.

Это означает, что 70% мужчин данного возраста имеют рост до 176 см.

10%-ная точка – это квантиль x0,9

=181 см (находится аналогично), то

есть 10% мужчин имеют рост не менее 181 см.

Всилу особенностей нормального закона распределения, отмеченных

вначале параграфа, он занимает центральное место в теории и практике ве- роятностно-статистических методов. Большое теоретическое значение нормального закона состоит в том, что с его помощью получен ряд важных распределений, рассматриваемых далее.

2.6.8. Логарифмически-нормальное распределение

111

Определение 2.29. Непрерывная случайная величина X имеет лога-

рифмически-нормальное распределение (сокращенно логнормальное рас-

пределение), если ее логарифм подчинен нормальному закону.

Так как при x > 0 неравенство X < x и ln X < ln x равносильны, то функция распределения логнормального распределения совпадает с функцией нормального распределения для случайной величины ln X , то есть в соответствии с (2.5)

Дифференцируя (2.63) по x , получим выражение плотности для логнормального распределения (рис 2.27)

f (x) =	1	e	−	(ln x−ln a )2
2σ2	.	(2.64)
σ 2π x

Можно доказать, что числовые характеристики случайной величины X , распределенной по логнормальному закону (2.64) имеют вид: математи-

ческое ожидание	σ2	/ 2	2	σ2	(e	σ2	−1) , мода
MX = ae		, дисперсия DX = a e

Mo X = ae−σ2 , медиана Me X = a .
y	y = f (x)

0,8
0,6	a =1, σ = 0,6

Рис 2.27

Очевидно, что чем меньшеσ , тем ближе друг к другу значения моды, медианы и математического ожидания, а кривая распределения – ближе к симметрии. Если в нормальном распределении параметр a выступает в каче-

112

стве среднего значения случайной величины, то в логнормальном – в качест-

ве медианы.

Логнормальное распределение имеет широкое распространение в экономической статистике, статистической физике, биологии, используется для описания распределения доходов, банковских вкладов, цен активов, месячной заработной платы, посевных площадей под разные культуры, долговечность изделий в режиме износа и старения и др.

Пример 2.34. Проведенное исследование показало, что вклады населения в данном банке могут быть описаны случайной величиной X , распре-

деленной по логнормальному закону с параметрами a = 530, σ2 = 0,64 .

Найти: а) средний размер вклада; б)долю вкладчиков, размер вклада которых составляет не менее 1000 ден. ед.; в) моду и медиану случайной величины X и пояснить их смысл.

Решение.

а) Найдем средний размер вклада, т.е.

MX = aeσ2 / 2 = 530e0,64 / 2 = 730 ден. ед.

б) Доля вкладчиков, размер вклада которых составляет не менее 1000 ден. ед, есть

P( X ≥1000) =1− P( X <1000) =1− F(1000).

При определении F(1000) воспользуемся тем, что функция логнор-

мального распределения случайной величины X совпадает с функцией нор-

мального распределения случайной величины ln X . Тогда
			F(x) =	1		ln X −ln a
			2	+ Φ		σ	и

F(1000) =	1	ln1000 −ln530	=	1	+ Φ(0,79)=	1	+ 0,28525	= 0,785.
2	+ Φ	0,64			2	2

Тогда P( X ≥1000) =1−0,785 = 0,215 (см. рис. 2.28).

в) Вычислим моду случайной величины X :

113

Mo X = ae−σ2 = 530e−0,64 ≈ 280 , то есть наиболее часто встречающийся банковский вклад составляет 280 ден. ед. (точнее, наиболее часто встречаю-

щийся элементарный интервал с	центром 280,	то есть интервал
(280 −ε; 280 +ε) ден.yед.).
0,0012
0,0008				a =1, σ = 0,6

0,0004

			Mo X	Me X	MX					x

	0		200	400	600	800	1000	1200	1400

Рис. 2.28

Если исходить из вероятностного смысла параметра a логнормального распределения, то медиана Me X = a = 530 , то есть половина вкладчиков имеют вклады до 530 ден. ед., а другая половина – сверх 530 ден. ед.

2.6.9. Распределение Вейбулла

Определение 2.30. Случайная величина X имеет распределение Вейбулла с параметрами α и λ , где α > 0 и λ > 0 , если плотность имеет вид

(рис. 2.29):

	α−1	−λxα
	e		, x > 0	(2.65)
f (x) = αλx
0,			x ≤ 0

у			у			у
		f (x)		f (x)



	f (x)				λ

		0	<α <1	α =1


		α >1				х	х
			х	114

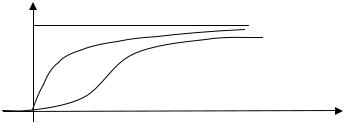
Рис. 2.29

Свойства распределения Вейбулла

1. Непосредственные вычисления показывают, что (рис 2.30)

x			−λxα
F (x) = ∫		−e		, x ≥ 0,
f (t)dt = 1
−∞	0,		x < 0.

2. Математическое ожидание вычисляется по формуле:

MX = λ	−	1	α +1	,

α	Г	α

3. Дисперсия вычисляется по формуле:

	−	2		2		1	1	2

			2
DX = λ		α			Г		−		Г	,	(2.68)
		α	α	2	α
			α

где Г(x)=+∞∫e−tt x−1dt – гамма-функция, значения которой задаются таблично.

y y = F(x)

1
	λ <1

			λ >1

0
	Рис 2.30	x


				в экспоненци-
4. Если α =1, то распределение Вейбулла превращается
альное с показателем λ .

Случайная величина, имеющая распределение Вейбулла, встречается в задачах надежности при оценке времени безотказной работы прибора.

§ 2.7. Предельные теоремы теории вероятностей

Предельные теоремы теории вероятностей устанавливают связь между теоретическими и экспериментальными характеристиками случайных ве-

115

личин при большом числе испытаний над ними. Эти теоремы составляют основу математической статистики.

Предельные теоремы условно делятся на две группы. Первая группа теорем, которая называется законом больших чисел, устанавливает устойчивость средних значений. То есть при большом числе испытаний их средний результат перестает быть случайным и может быть предсказан с достаточной точностью.

Вторая группа теорем, называемая центральной предельной теоремой, устанавливает условия, при которых закон распределения суммы большого числа случайных величин неограниченно приближается к нормальному.

2.7.1. Неравенство Чебышева

Рассмотрим неравенство Чебышева, которое можно использовать, вопервых, для грубой оценки вероятностей событий, связанных со случайными величинами, распределение которых неизвестно, во-вторых для доказатель-

ства ряда теорем закона больших чисел.
Теорема 2.10. Если случайная величина X	имеет математическое
ожидание MX =α и дисперсию DX , то для любого ε > 0 справедливо нера-
венство Чебышева:
P{		X − MX	≥ε}≤ DXε2	(2.69)

Доказательство. Пусть X – непрерывная случайная величина с плот-

ностью f (x) . Вероятность P{X − MX ≥ε} есть вероятность попадания слу-

чайной величины в область, лежащую вне промежутка [a −ε; a +ε]. Можно записать:

a−ε

+∞

X − MX

≥ε}= ∫ f (x)dx + ∫ f (x)dx = ∫ f (x)dx = ∫ 1 f (x)dx ≤

−∞

a+ε

a−ε

≥ε

a−ε

≥ε

116

≤ ∫ (x ε−2a)2

f (x)dx ,

так как область интегрирования

x −a

≥ε можно за-

a−ε

≥ε

(x −a)2

писать в виде (x −a)2 ≥ε2 , откуда 1 ≤

. Имеем

ε2

≥ε}≤

+∞

X − MX

∫

(x −a)2 f (x)dx ≤

∫ (x −a)2 f (x)dx , так как ин-

ε2

a−ε

≥ε

−∞

теграл от неотрицательной функции при расширении области интегрирования может только возрасти. Таки образом

P{				≥ε}≤	1	+∞	2	1
	X − MX		∫	(x −a)	f (x)dx =	DX , то есть
		ε2		ε2

						−∞

P{X − MX ≥ε}≤ DXε2 . Что и требовалось доказать.

Аналогично доказывается неравенство Чебышева и для дискретной случайной величины X принимающей значения x1, x2 ,… с вероятностями

p1, p2 ,… . Для дискретной случайной величины интегралы вида

няются соответствующими суммами ∑

a−ε ≥ε

Неравенство Чебышева можно записать в другой форме:

P{X − MX <ε}≥1− DXε2

В форме (2.69) оно устанавливает верхнюю границу вероятности события, а в форме (2.70) – нижнюю.

Неравенство Чебышева справедливо для любых случайных величин. В частности для случайной величины X = m , имеющей биномиальное распределение с математическим ожиданием MX = a = np и дисперсией

DX = npq оно принимает вид:

P{	m −np	<ε}≥1−	npq	.	(2.71)

	ε2

117

Для частости	m	события в n независимых испытаниях, в каждом из
	n
которых оно может произойти с вероятностью	m	= a , а дисперсия
p = M
			n

m		pq
которых D		=	, неравенство Чебышева имеет вид:
nε	2
	n

		m					pq

P			− p	<ε	≥1	−
	n		nε2

Оценку вероятности попадания случайной величины X в промежуток

[ε; +∞) дает неравенство Маркова.

Теорема 2.11. (Неравенство Маркова). Для любой неотрицательной случайной величины X , имеющей математическое ожидание MX и ε > 0 , справедливо неравенство:

P{X

≥ε}≤

(2.72)

Доказательство.

+∞

f (x)dx = 1

+∞

xf (x)dx ≤ 1

+∞

xf (x)dx = MX

P{X ≥ε}= ∫ f (x)dx

≤ ∫

∫

Что и требовалось доказать. Неравенство (2.72) можно записать в дру-

гой форме:

P{X

<ε}≥1−

(2.73)

Пример 2.35. Оценить с помощью неравенства Чебышева вероятность

того, что отклонение случайной величины

X от своего математического

ожидания будет меньше «трех сигм».

Решение. Полагая ε = 3σ в формуле (2.70), получим

X − MX

< 3σ}≥1−

σ2

=1− 9 =

9 ≈ 0,8889

(3σ)2

2.7.2. Теорема Чебышева

118

Источник

F(x) = P( X < x) = P(ln X < ln x) =