Как найти квартиль в питоне

The main difference of the signatures between numpy.percentile
and pandas.quantile: with pandas the q paramter should be given in a scala between [0-1] instead with numpy between [0-100].

Both of them, by default, use a linear interpolation technique to find such quantities. Instead, DataFrame.describe has a less flexible signature and allow to use only the linear one.

In numpy >= 1.22 the parameter interpolation is deprecated and replaced with method.

Here an example of usage with linear interpolation: (default behavior)

import pandas as pd
import numpy as np


s =[18,45,66,70,76,83,88,90,90,95,95,98, 100]
print(pd.DataFrame(s).quantile(q=[.25, .50, .75]))
print(np.percentile(s, q=[25, 50, 75]))
print(pd.DataFrame(s).describe(percentiles=[.25, .5, .75])) # the parameter is redundant, it's the default behavior

Here using the midpoint interpolation:

s_even = [18,45,66,70,76,83,88,90,90,95,95,98]
print(pd.DataFrame(s_even).quantile(q=[.25, .5, .75], interpolation='midpoint'))
print(np.percentile(s_even, q=[25, 50, 75], interpolation='midpoint')) # verion < 1.22
print(np.percentile(s_even, q=[25, 50, 75], method='midpoint')) # version >= 1.22

s_odd = s_even + [100] # made it odd
print(pd.DataFrame(s_odd).quantile(q=[.25, .50, .75], interpolation='midpoint'))
print(np.percentile(s_odd, q=[25, 50, 75], interpolation='midpoint')) # verion < 1.22
print(np.percentile(s_odd, q=[25, 50, 75], method='midpoint')) # version >= 1.22

Пост №2 для начинающих посвящен описательным статистикам, группированию данных и нормальному распределению. Все эти сведения заложат основу для дальнейшего анализа электоральных данных. Предыдущий пост см. здесь.

Описательные статистики

Описательные статистические величины, или статистики, — это числа, которые используются для обобщения и описания данных. В целях демонстрации того, что мы имеем в виду, посмотрим на столбец с данными об электорате Electorate. Он показывает суммарное число зарегистрированных избирателей в каждом избирательном округе:

def ex_1_6():
    '''Число значений в поле "Электорат"'''
    return load_uk_scrubbed()['Electorate'].count()

650

Мы уже очистили столбец, отфильтровав пустые значения (nan) из набора данных, и поэтому предыдущий пример должен вернуть суммарное число избирательных округов.

Описательные статистики, так называемые сводные статистики, представляют собой разные подходы к измерению свойств последовательностей чисел. Они помогают охарактеризовать последовательность и способны выступать в качестве ориентира для дальнейшего анализа. Начнем с двух самых базовых статистик, которые мы можем вычислить из последовательности чисел — ее среднее значение и дисперсию (варианс).

• Среднее значение

Наиболее распространенный способ усреднить набор данных — взять его среднее значение. Среднее значение на самом деле представляет собой один из нескольких способов измерения центра распределения данных.

Среднее значение числового ряда вычисляется на Python следующим образом:

def mean(xs): 
    '''Среднее значение числового ряда'''
    return sum(xs) / len(xs) 

Мы можем воспользоваться нашей новой функцией mean для вычисления среднего числа избирателей в Великобритании:

def ex_1_7():
    '''Вернуть среднее значение поля "Электорат"'''
    return mean( load_uk_scrubbed()['Electorate'] )

70149.94

На самом деле, библиотека pandas уже содержит функцию mean, которая гораздо эффективнее вычисляет среднее значение последовательности. В нашем случае ее можно применить следующим образом:

load_uk_scrubbed()['Electorate'].mean()

• Медиана

Медиана — это еще одна распространенная описательная статистика для измерения центра распределения последовательности. Если Вы упорядочили все данные от меньшего до наибольшего, то медиана — это значение, которое находится ровно по середине. Если в последовательности число точек данных четное, то медиана определяется, как полусумма двух срединных значений.

def median(xs):
    '''Медиана числового ряда'''
    n = len(xs)
    mid = n // 2
    if n % 2 == 1:
        return sorted(xs)[mid]
    else:
        return mean( sorted(xs)[mid-1:][:2] )

Медианное значение электората Великобритании составляет:

def ex_1_8():
    '''Вернуть медиану поля "Электорат"'''
    return median( load_uk_scrubbed()['Electorate'] )

70813.5

Библиотека pandas тоже располагает встроенной функцией для вычисления медианного значения, которая так и называется median.

• Дисперсия

Среднее арифметическое и медиана являются двумя альтернативными способами описания среднего значения последовательности, но сами по себе они мало что говорят о содержащихся в ней значениях. Например, если известно, что среднее последовательности из девяноста девяти значений равно 50, то мы почти ничего не скажем о том, какого рода значения последовательность содержит.

Она может содержать целые числа от одного до девяноста девяти либо сорок девять нулей и пятьдесят девяносто девяток, а может быть и так, что она девяносто восемь раз содержит отрицательную единицу и одно число 5048, или же вообще все значения могут быть равны 50.

Дисперсия (варианс) последовательности чисел показывает «разброс» данных вокруг среднего значения. К примеру, данные, приведенные выше, имели бы разную дисперсию. На языке математики дисперсия обозначается следующим образом:

где s²  — это математический символ, который часто используют для обозначения дисперсии.

Выражение

def variance(xs):
    '''Дисперсия (варианс) числового ряда,
       несмещенная дисперсия при n <= 30'''
    mu = mean(xs)
    n = len(xs)
    n = n-1 if n in range(1, 30) else n  
    square_deviation = lambda x : (x - mu) ** 2 
    return sum( map(square_deviation, xs) ) / n

Для вычисления квадрата выражения используется оператор языка Python возведения в степень **.

• Стандартное отклонение

Поскольку мы взяли средний квадрат отклонения, т.е. получили квадрат отклонения и затем его среднее, то единицы измерения дисперсии (варианса) тоже будут в квадрате, т.е. дисперсия электората Великобритании будет измеряться «людьми в квадрате». Несколько неестественно рассуждать об избирателях в таком виде. Единицу измерения можно привести к более естественному виду, снова обозначающему «людей», путем извлечения квадратного корня из дисперсии (варианса). В результате получим так называемое стандартное отклонение, или среднеквадратичное отклонение:

def standard_deviation(xs):
    '''Стандартное отклонение числового ряда'''
    return sp.sqrt( variance(xs) )
       
def ex_1_9():
    '''Стандартное отклонение поля "Электорат"'''
    return standard_deviation( load_uk_scrubbed()['Electorate'] )

7672.77

В библиотеке pandas функции для вычисления дисперсии (варианса) и стандартного отклонения имплементированы соответственно, как var и std. При этом последняя по умолчанию вычисляет несмещенное значение, поэтому, чтобы получить тот же самый результат, нужно применить именованный аргумент ddof=0, который сообщает, что требуется вычислить смещенное значение стандартного отклонения:

load_uk_scrubbed()['Electorate'].std( ddof=0 )

• Квантили

Медиана представляет собой один из способов вычислить срединное значение из списка, т.е. находящееся ровно по середине, дисперсия же предоставляет способ измерить разброс данных вокруг среднего значения. Если весь разброс данных представить на шкале от 0 до 1, то значение 0.5 будет медианным.

Для примера рассмотрим следующую ниже последовательность чисел:

[10 11 15 21 22.5 28 30]

Отсортированная последовательность состоит из семи чисел, поэтому медианой является число 21 четвертое в ряду. Его также называют 0.5-квантилем. Мы можем получить более полную картину последовательности чисел, взглянув на 0.0 (нулевой), 0.25, 0.5, 0.75 и 1.0 квантили. Все вместе эти цифры не только показывают медиану, но также обобщают диапазон данных и сообщат о характере распределения чисел внутри него. Они иногда упоминаются в связи с пятичисловой сводкой.

Один из способов составления пятичисловой сводки для данных об электорате Великобритании показан ниже. Квантили можно вычислить непосредственно в pandas при помощи функции quantile. Последовательность требующихся квантилей передается в виде списка.

def ex_1_10():
    '''Вычислить квантили:
       возвращает значение в последовательности xs, 
       соответствующее p-ому проценту'''
    q = [0, 1/4, 1/2, 3/4, 1]
    return load_uk_scrubbed()['Electorate'].quantile(q=q)

0.00     21780.00
0.25     65929.25
0.50     70813.50
0.75     74948.50
1.00    109922.00
Name: Electorate, dtype: float64

Когда квантили делят диапазон на четыре равных диапазона, как показано выше, то они называются квартилями. Разница между нижним (0.25) и верхним (0.75) квартилями называется межквартильным размахом, или иногда сокращенно МКР. Аналогично дисперсии (варианса) вокруг среднего значения, межквартильный размах измеряет разброс данных вокруг медианы.

Группирование данных в корзины

В целях развития интуитивного понимания в отношении того, что именно все эти расчеты разброса значений измеряют, мы можем применить метод под названием группировка в частотные корзины (binning). Когда данные имеют непрерывный характер, использование специального словаря для подсчета частот Counter (подобно тому, как он использовался при подсчете количества пустых значений в наборе данных об электорате) становится нецелесообразным, поскольку никакие два значения не могут быть одинаковыми. Между тем, общее представление о структуре данных можно все-равно получить, сгруппировав для этого данные в частотные корзины (bins).

Процедура образования корзин заключается в разбиении диапазона значений на ряд последовательных, равноразмерных и меньших интервалов. Каждое значение в исходном ряду попадает строго в одну корзину. Подсчитав количества точек, попадающих в каждую корзину, мы можем получить представление о разбросе данных:

На приведенном выше рисунке показано 15 значений x, разбитых на 5 равноразмерных корзин. Подсчитав количество точек, попадающих в каждую корзину, мы можем четко увидеть, что большинство точек попадают в корзину по середине, а меньшинство — в корзины по краям. Следующая ниже функция Python nbin позволяет добиться того же самого результата:

def nbin(n, xs): 
    '''Разбивка данных на частотные корзины'''
    min_x, max_x = min(xs), max(xs)
    range_x = max_x - min_x
    fn = lambda x: min( int((abs(x) - min_x) / range_x * n), n-1 )
    return map(fn, xs)

Например, мы можем разбить диапазон 0-14 на 5 корзин следующим образом:

list( nbin(5, range(15)) )

[0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4]

После того, как мы разбили значения на корзины, мы можем в очередной раз воспользоваться словарем Counter, чтобы подсчитать количество точек в каждой корзине. В следующем ниже примере мы воспользуемся этим словарем для разбиения данных об электорате Великобритании на пять корзин:

def ex_1_11():
    '''Разбиmь электорат Великобритании на 5 корзин'''
    series = load_uk_scrubbed()['Electorate']
    return Counter( nbin(5, series) )

Counter({2: 450, 3: 171, 1: 26, 0: 2, 4: 1})

Количество точек в крайних корзинах (0 и 4) значительно ниже, чем в корзинах в середине — количества, судя по всему, растут по направлению к медиане, а затем снова снижаются. В следующем разделе мы займемся визуализацией формы этих количеств.

Гистограммы

Гистограмма — это один из способов визуализации распределения одной последовательности значений. Гистограммы попросту берут непрерывное распределение, разбивают его на корзины, и изображают частоты точек, попадающих в каждую корзину, в виде столбцов. Высота каждого столбца гистограммы показывает количество точек данных, которые содержатся в этой корзине.

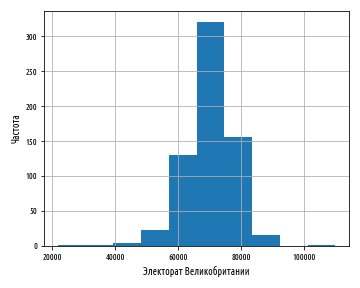
Мы уже увидели, каким образом можно выполнить разбиение данных на корзины самостоятельно, однако в библиотеке pandas уже содержится функция hist, которая разбивает данные и визуализирует их в виде гистограммы.

def ex_1_12():
    '''Построить гистограмму частотных корзин 
       электората Великобритании'''
    load_uk_scrubbed()['Electorate'].hist()
    plt.xlabel('Электорат Великобритании')
    plt.ylabel('Частота')
    plt.show()

Приведенный выше пример сгенерирует следующий ниже график:

Число корзин, на которые данные разбиваются, можно сконфигурировать, передав в функцию при построении гистограммы именованный аргумент bins:

def ex_1_13():
    '''Построить гистограмму частотных корзин 
       электората Великобритании с 200 корзинами'''
    load_uk_scrubbed()['Electorate'].hist(bins=200)
    plt.xlabel('Электорат Великобритании')
    plt.ylabel('Частота')
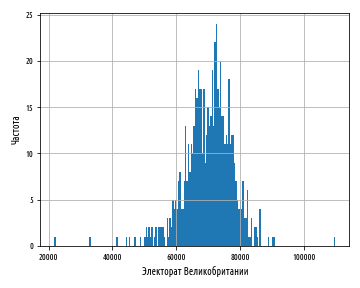
    plt.show()

Приведенный выше график показывает единственный высокий пик, однако он выражает форму данных довольно грубо. Следующий ниже график показывает мелкие детали, но величина столбцов делает неясной форму распределения, в особенности в хвостах:

При выборе количества корзин для представления данных следует найти точку равновесия — с малым количеством корзин форма данных будет представлена лишь приблизительно, а слишком большое их число приведет к тому, что шумовые признаки могут заслонить лежащую в основании структуру.

def ex_1_14():
    '''Построить гистограмму частотных корзин 
       электората Великобритании с 20 корзинами'''
    load_uk_scrubbed()['Electorate'].hist(bins=20)
    plt.xlabel('Электорат Великобритании')
    plt.ylabel('Частота')
    plt.show()

Ниже показана гистограмма теперь уже из 20 корзин:

Окончательный график, состоящий из 20 корзин, судя по всему, пока лучше всего представляет эти данные.

Наряду со средним значением и медианой, есть еще один способ измерить среднюю величину последовательности. Это мода. Мода — это значение, встречающееся в последовательности наиболее часто. Она определена исключительно только для последовательностей, имеющих по меньшей мере одно дублирующее значение; во многих статистических распределениях это не так, и поэтому для них мода не определена. Тем не менее, пик гистограммы часто называют модой, поскольку он соответствует наиболее распространенной корзине.

Из графика ясно видно, что распределение вполне симметрично относительно моды, и его значения резко падают по обе стороны от нее вдоль тонких хвостов. Эти данные приближенно подчиняются нормальному распределению.

Нормальное распределение

Гистограмма дает приблизительное представление о том, каким образом данные распределены по всему диапазону, и является визуальным средством, которое позволяет квалифицировать данные как относящиеся к одному из немногих популярных распределений. В анализе данных многие распределения встречаются часто, но ни одно не встречается также часто, как нормальное распределение, именуемое также гауссовым распределением.

^{Распределение названо нормальным распределением из-за того, что оно очень часто встречается в природе. Галилей заметил, что ошибки в его астрономических измерениях подчинялись распределению, где малые отклонения от среднего значения встречались чаще, чем большие. Вклад великого математика Гаусса в описание математической формы этих ошибок привел к тому, что это распределение стали называть в его честь распределением Гаусса.}

Любое распределение похоже на алгоритм сжатия: оно позволяет очень эффективно резюмировать потенциально большой объем данных. Нормальное распределение требует только два параметра, исходя из которых можно аппроксимировать остальные данные. Это среднее значение и стандартное отклонение.

Центральная предельная теорема

Высокая встречаемость нормального распределения отчасти объясняется центральной предельной теоремой. Дело в том, что значения, полученные из разнообразных статистических распределений, при определенных обстоятельствах имеют тенденцию сходиться к нормальному распределению, и мы это покажем далее.

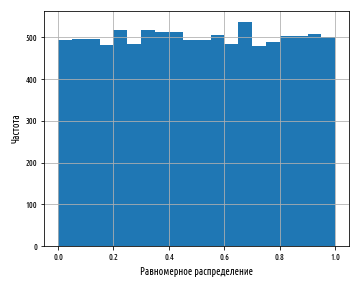
В программировании типичным распределением является равномерное распределение. Оно представлено распределением чисел, генерируемых функцией библиотеки scipy stats.uniform.rvs: в справедливом генераторе случайных чисел все числа имеют равные шансы быть сгенерированными. Мы можем увидеть это на гистограмме, многократно генерируя серию случайных чисел между 0 и 1 и затем построив график с результатами.

def ex_1_15():
    '''Показать гистограмму равномерного распределения 
       синтетического набора данных'''
    xs = stats.uniform.rvs(0, 1, 10000)
    pd.Series(xs).hist(bins=20)
    plt.xlabel('Равномерное распределение')
    plt.ylabel('Частота')
    plt.show()

Обратите внимание, что в этом примере мы впервые использовали тип Series библиотеки pandas для числового ряда данных.

Приведенный выше пример создаст следующую гистограмму:

Каждый столбец гистограммы имеет примерно одинаковую высоту, что соответствует равновероятности генерирования числа, которое попадает в каждую корзину. Столбцы имеют не совсем одинаковую высоту, потому что равномерное распределение описывает теоретический результат, который наша случайная выборка не может отразить в точности. Раздел инференциальной статистики, посвященный проверке статистических гипотез, изучает способы точной количественной оценки расхождения между теорией и практикой, чтобы определить, являются ли расхождения достаточно большими, чтобы обратить на это внимание. В данном случае они таковыми не являются.

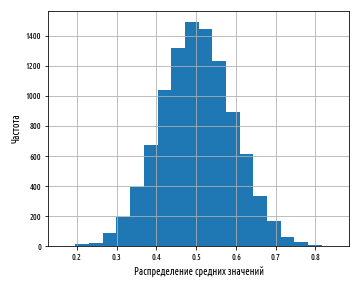
Если напротив сгенерировать гистограмму средних значений последовательностей чисел, то в результате получится распределение, которое выглядит совсем непохоже.

def bootstrap(xs, n, replace=True): 
    '''Вернуть список массивов меньших размеров 
       по n элементов каждый'''
    return np.random.choice(xs, (len(xs), n), replace=replace) 

def ex_1_16():
    '''Построить гистограмму средних значений'''
    xs = stats.uniform.rvs(loc=0, scale=1, size=10000)
    pd.Series( map(sp.mean, bootstrap(xs, 10)) ).hist(bins=20)
    plt.xlabel('Распределение средних значений') 
    plt.ylabel('Частота')
    plt.show()

Приведенный выше пример сгенерирует результат, аналогичный следующей ниже гистограмме:

Хотя величина среднего значения близкая к 0 или 1 не является невозможной, она является чрезвычайно невероятной и становится менее вероятной по мере роста числа усредненных чисел и числа выборочных средних. Фактически, на выходе получается результат очень близкий к нормальному распределению.

Этот результат, когда средний эффект множества мелких случайных колебаний в итоге приводит к нормальному распределению, называется центральной предельной теоремой, иногда сокращенно ЦПТ, и играет важную роль для объяснения, почему нормальное распределение встречается так часто в природных явлениях.

До 20-ого века самого термина еще не существовало, хотя этот эффект был зафиксирован еще в 1733 г. французским математиком Абрахамом де Mуавром, который использовал нормальное распределение, чтобы аппроксимировать число орлов в результате бросания уравновешенной монеты. Исход бросков монеты лучше всего моделировать при помощи биномиального распределения. В отличие от центральной предельной теоремы, которая позволяет получать выборки из приближенно нормального распределения, библиотека scipy содержит функции для эффективного генерирования выборок из самых разнообразных статистических распределений, включая нормальное:

def ex_1_17():
    '''Показать гистограмму нормального распределения 
       синтетического набора данных'''
    xs = stats.norm.rvs(loc=0, scale=1, size=10000)
    pd.Series(xs).hist(bins=20)
    plt.xlabel('Нормальное распределение')
    plt.ylabel('Частота')
    plt.show()

Отметим, что в функции sp.random.normal параметр loc – это среднее значение, scale – дисперсия и size – размер выборки. Приведенный выше пример сгенерирует следующую гистограмму нормального распределения:

По умолчанию среднее значение и стандартное отклонение для получения нормального распределения равны соответственно 0 и 1.

Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.

Следующая часть, часть 3, серии постов «Python, исследование данных и выборы» посвящена генерированию распределений, их свойствам, а также графикам для их сопоставительного анализа