Расчет квартилей для интервального ряда:
Для
расчета квартилей для интервального
ряда
-
Определяем номер квартиля по тем же
формулам, что и для дискретного ряда, -
Определяем квартильный интервал по
накопленной частоте. Это
первый интервал, для которого накопленная
частота будет больше или равна номеру
квартиля. -
Рассчитываем квартиль по формуле:

Где:
J
– номер квартиля,
 –
–
нижняя граница интервала, содержащего
квартиль. Интервал определяется по
накопленной частоте интервалов,
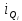 –
–
ширина интервала, содержащего квартиль,
 –
–
накопленная частота интервала,
предшествующего интервалу, содержащему
квартиль,
 –
–
частота интервала, содержащего квартиль.


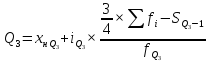
Пример.
Найти первый квартиль для интервального
ряда.
|
Возрастные |
Число |
Накопленная |
|
До |
346 |
346 |
|
20 |
872 |
1218 |
|
25 |
1054 |
2272 |
|
30 |
781 |
3053 |
|
35 |
212 |
3265 |
|
40 |
121 |
3386 |
|
45 |
76 |
3462 |
|
Итого |
3462 |
Решение:
-
Определяем номер первого квартиля по
формуле

-
Первый квартиль находится в возрастной
группе 20-25 лет, так как это первый
интервал, для которого накопленная
частота больше (или равна) номера
квартиля (346<865,75; 1218>865,75). -
Определяем первый квартиль по формуле
-

Это значит, что четверть студентов
младше 22,98 лет.
-
Децили
Децили –
значения признака, делящие ранжированный
ряд на десять равных частей.
Первый
дециль отсекает 1/10 часть совокупности,
а девятый дециль отсекает 9/10 частей.
Таким образом, различают 9 децилей.
Рассчитываются
децили аналогично квартилям.
Расчет децилей для дискретного ряда
-
Определяем номер
дециля по формуле:
 ,
, -
Если номер дециля
– целое число,
то значение дециля будет равно величине
элемента ряда, которое обладает
накопленной частотой равной номеру
дециля. Например, если номер дециля
равен 20, его значение будет равно
значению признака с S =20 (накопленной
частотой равной 20).
Если номер дециля
– нецелое число,
то дециль попадает между двумя
наблюдениями. Значением дециля будет
сумма, состоящая из значения элемента,
для которого накопленная частота равна
целому значению номера дециля, и указанной
части (нецелая часть номера дециля)
разности между значением этого элемента
и значением следующего элемента.
Например, если номер
дециля равна 20,25, дециль попадает между
20-м и 21-м наблюдениями, и его значение
будет равно значению 20-го наблюдения
плюс 1/4 разности между значением 20-го и
21-го наблюдений.
Расчет децилей для интервального ряда
-
Определяем номер
дециля по формуле:
 ,
, -
Определяем децильный
интервал. Это первый интервал, для
которого накопленная частота будет
больше или равна номеру дециля. -
Рассчитываем дециль
по формуле:

где
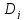 – значение j-го дециля,
– значение j-го дециля,

– нижняя граница децильного интервала;

– ширина децильного интервала;

 –
–
сумма всех частот,

 -накопленная
-накопленная
частота интервала, предшествующего
децильному;

 –
–
частота децильного интервала.
Пример.
Найти 9-ый дециль D9
|
Заработная
|
бригада |
|
|
число |
накопленная частота |
|
|
15 |
20 |
20 |
|
18 |
37 |
57 |
|
20 |
14 |
71 |
|
25 |
4 |
75 |
|
Итого: |
75 |
-
Определяем номер 9-го дециля
для первой бригады
 ;
;
-
Номер дециля – нецелое число. Для
определения дециля нужны значения двух
элементов – х68и х69. Значение
дециля находится между ними.
Определяем
их значение с помощью самой первой
накопленной частоты большей или равной
порядковым номерам элементов (68 и 69).
Х68= 20, х69= 20.
Теперь
определяем значение 9-го дециля:D7=x68+ (х69–
х68)×0,4=20 + (20 – 20)×0,2 =20тыс.руб.
Это значит, что заработная плата90%
рабочих бригады не превышает 18 тыс.руб.
Пример.
Найти седьмой дециль D7
для интервального ряда.
|
Возрастные |
Число |
Накопленная |
|
До |
346 |
346 |
|
20 |
872 |
1218 |
|
25 |
1054 |
2272 |
|
30 |
781 |
3053 |
|
35 |
212 |
3265 |
|
40 |
121 |
3386 |
|
45 |
76 |
3462 |
|
Итого |
3462 |
Решение:
-
Определяем номер седьмого дециля по
формуле
 7×
7×
-
Седьмой дециль находится в возрастной
группе 30-35 лет, так как это первый
интервал, для которого накопленная
частота больше (или равна) номера дециля
(2272<2424,1; 3053>2424,1). -
Определяем седьмой дециль по формуле
-

Это значит, что 70% студентов младше 30,97
лет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

- Определение формулы квартиля

Формула квартиля (оглавление)
- формула
- Примеры
Определение формулы квартиля
Quartile, как звучит его название, представляет собой статистический термин, который делит данные на четверти или четыре определенных интервала. Он в основном делит точки данных на набор данных в 4 кварталах на числовой строке. Мы должны помнить одну вещь: точки данных могут быть случайными, и мы должны сначала разместить эти числа в строке чисел в порядке возрастания, а затем разделить их на квартили. Это в основном расширенная версия медианы. Медиана делит данные на две равные части, а квартили делят их на четыре части. Как только мы разделим данные, четыре квартиля будут:
- 1- й квартиль или нижний квартиль в основном отделяют самые низкие 25% данных от самых высоких 75%.
- 2- й квартиль или средний квартиль, также как и медиана, делит числа на 2 равные части.
- 3- й квартиль или верхний квартиль отделяют самые высокие 25% данных от самых низких 75%.
Формула для квартиля:
Допустим, у нас есть набор данных с N точками данных:
X – (X1, X2, X3 ……… .. XN)
Формула для квартилей имеет вид:
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
В основном это означает, что в наборе данных с N точками данных:
((N + 1) * 1/4) -й член является нижним квартилем
((N + 1) * 2/4) -й член – средний квартиль
((N + 1) * 3/4) -й член – верхний квартиль
Межквартильный диапазон в основном расстояния между нижним квартилем и верхним квартилем.
Примеры формулы Quartile (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет Quartile.
Вы можете скачать этот шаблон Excel Quartile Formula здесь – Шаблон Excel Quartile Formula
Формула квартиля – пример № 1
Допустим, у нас есть наборы данных A, которые содержат 19 точек данных. Рассчитать квартиль для набора данных А.
Набор данных:
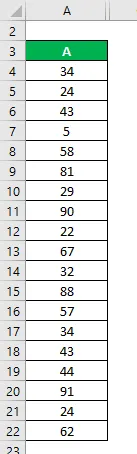
Прежде всего, вы должны расположить этот порядок возрастания, т.е. от низшего к высшему:
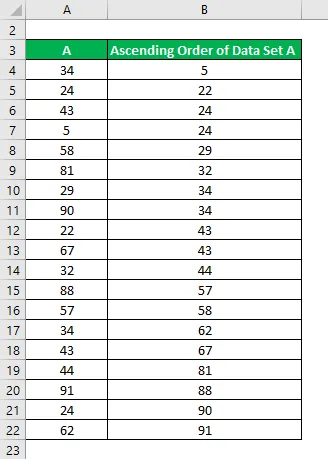
Количество точек данных рассчитывается как:
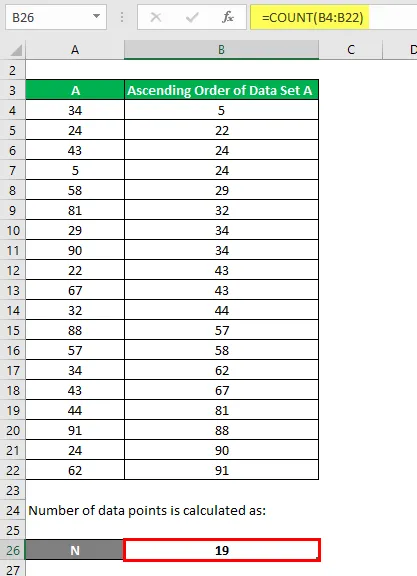
Квартиль рассчитывается по приведенной ниже формуле
Нижний квартиль (Q1) = (N + 1) * 1/4
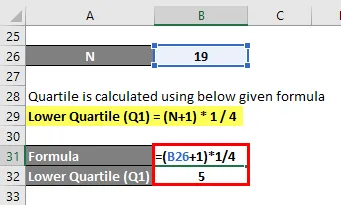
- Нижний квартиль (Q1) = (19 + 1) * 1/4
- Нижний квартиль (Q1) = 20/4 = 5- я точка данных
Итак, нижний квартиль (Q1) = 29
Средний квартал (Q2) = (N + 1) * 2/4

- Средний квартал (Q2) = (19 + 1) * 2/4
- Средний квартал (Q2) = 40/4 = 10- я точка данных
Средний квартал (Q2) = 43
Верхний квартиль (Q3) = (N + 1) * 3/4

- Верхний квартиль (Q3) = (19 + 1) * 3/4
- Верхняя четверть (Q3) = 60/4 = 15- я точка данных
Итак, верхний квартиль (Q3) = 67
Межквартильный диапазон рассчитывается по формуле, приведенной ниже
Межквартильный диапазон = Q3 – Q1
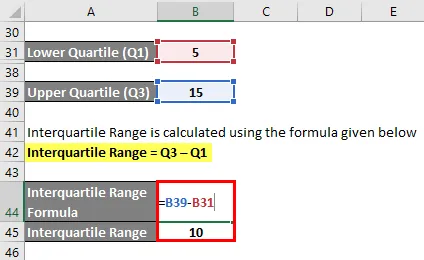
- Межквартильный диапазон = 15–5
- Межквартильный диапазон = 10- я точка данных
Итак, межквартирный диапазон = 43
Если вы видите набор данных, медиана этого набора: (n + 1) / 2 = 20/2 = 10- е значение, т.е. 43, это то же самое, что и Q2.
Умозаключение:
- Значение 29 делит набор данных таким образом, что самые низкие 25% находятся выше него, а самые высокие 75% находятся ниже него
- Значение 43 делит набор данных на две равные части
- Значение 67 делит набор данных таким образом, что самые высокие 25% находятся ниже него, а самые низкие 75% находятся выше него
Формула квартиля – пример № 2
Давайте посмотрим еще один пример того, как компании и предприятия могут использовать этот инструмент для принятия обоснованного решения о том, какой продукт производить.
Предположим, что вы являетесь производителем кроссовок и известным брендом среди спортсменов, которые проводят марафон, занимаются спортом и т.д. удовлетворить спрос.
Вы собрали образец из 15 спортсменов из разных видов спорта. Рассчитать квартиль.
Набор данных приведен ниже:
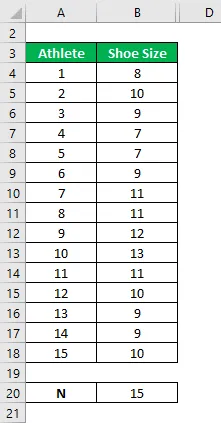
Расположите размер обуви в порядке возрастания.
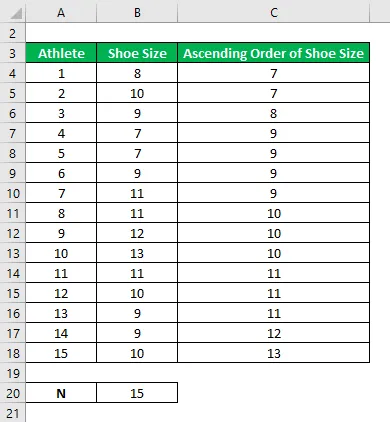
Квартиль рассчитывается по приведенной ниже формуле
Нижний квартиль (Q1) = (N + 1) * 1/4
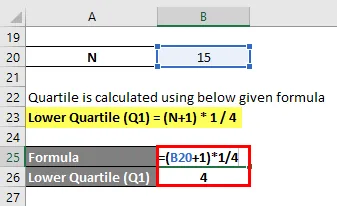
- Нижний квартиль (Q1) = (15 + 1) * 1/4
- Нижний квартиль (Q1) = 16/4 = 4- я точка данных
Итак, нижний квартиль (Q1) = 10
Средний квартал (Q2) = (N + 1) * 2/4
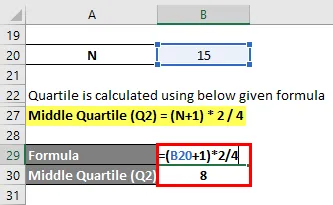
- Средний квартал (Q2) = (15 + 1) * 2/4
- Средний квартал (Q2) = 32/4 = 8- я точка данных
Средний квартал (Q2) = 10
Верхний квартиль (Q3) = (N + 1) * 3/4

- Верхняя четверть (Q3) = (15 + 1) * 3/4
- Верхняя четверть (Q3) = 48/4 = 12- я точка данных
Итак, верхний квартиль (Q3) = 11
Межквартильный диапазон рассчитывается по формуле, приведенной ниже
Межквартильный диапазон = Q3 – Q1
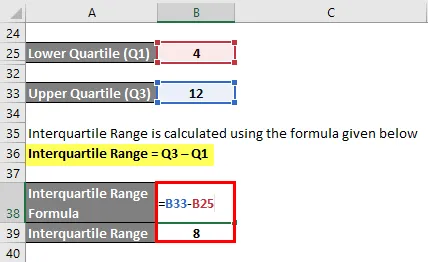
- Межквартильный диапазон = 12 – 4
- Межквартильный диапазон = 8- я точка данных
Итак, межквартирный диапазон = 10
объяснение
Чтобы лучше понять квартили, нам нужно лучше понять медиану. Медиана делит набор данных ровно на две равные половины, но ничего не говорит нам о разбросе данных с обеих сторон. Квартиль является расширенной версией этого и, разделяя набор данных на четыре части, он имеет дело с разбросом значений выше и ниже среднего. Кроме того, существуют другие статистические инструменты, которые сообщают нам о диапазоне набора данных, центре набора данных и т. Д. Но формула квартиля помогает нам понять все эти элементы. Медиана, то есть средний квартиль, говорит нам о центральной точке, а верхний и нижний квартили – о распространении.
Актуальность и использование формулы Quartile
Как обсуждалось выше, формула квартиля помогает нам очень быстро разделить данные на четыре части и, в конечном итоге, облегчает понимание данных в этих частях. Например, учитель класса хочет наградить 25% лучших учеников лакомствами и подарками и хочет дать еще один шанс 25% учеников улучшить свой результат. Он может использовать квартили и может делить данные. Таким образом, если квартили говорят 51, 65, 72, а ученик говорит 78, он получит вкусности. Если у другого ученика будет 48 баллов, у него будет еще один шанс улучшить его, быстро и легко интерпретировать.
Рекомендуемые статьи
Это было руководство к Quartile Formula. Здесь мы обсудим определение и как рассчитать Quartile вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше –
- Примеры формулы выбросов (шаблон Excel)
- Калькулятор для формулы в процентах
- Формула для расчета скорректированного R в квадрате
- Как рассчитать биномиальное распределение?
- Формула квартального отклонения | Примеры | Калькулятор
Структурные средние – мода, медиана, квантиль, дециль
Краткая теория
Наиболее широкое применение в статистике имеют структурные
средние, к числу которых относятся мода и медиана (непараметрические средние).
Мода – величина признака (варианта), которая
встречается в ряду распределения с наибольшей частотой (весом). К моде (Мо)
прибегают для выявления величины признака, имеющей наибольшее распространение
(цена на рынке, по которой было совершено наибольшее число продаж данного
товара, номер обуви, который пользуется наибольшим спросом у покупателей и т.
д.). Мода используется только в совокупностях большой численности. В дискретном
ряду мода находится как варианта, имеющая наибольшую частоту. В интервальном
ряду сначала находится модальный интервал, то есть интервал, обладающий наибольшей частотой, а
затем – приближенное значение модальной величины признака по формуле:
– нижняя граница модального интервала
– величина модального интервала
– частота интервала, предшествующего
модальному
– частота модального интервала
– частота интервала, следующего за модальным
Квантили –
величины, разделяющие совокупность на определенной количество равных по
численности элементов частей. Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили – на 100
частей.
Медиана –
величина признака у единицы, находящейся в середине ранжированного
(упорядоченного) ряда. Если ряд распределения представлен конкретными
значениями признака, то медиана (Me) находится как
серединное значение признака.
Если ряд распределения дискретный, то медиана находится как
серединное значение признака (например, если число значений нечетное – 45, то
соответствует 23 значению признака в ряду
значений, расположенных в порядке возрастания, если число значений четное – 44,
то медиана соответствует полусумме 22 и 23 значений
признака).
Если ряд распределения интервальный, то первоначально
находят медианный интервал, который содержит единицу, находящуюся в середине
ранжированного ряда. Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:
– нижняя граница медианного интервала
– величина медианного интервала
– сумма
частот ряда
– сумма накопленных частот в интервалах,
предшествующих медианному
– частота медианного интервала
Квартили – это значения
признака в ранжированном ряду, выбранные таким образом, что 25% единиц
совокупности будут меньше величины
, 25% единиц будут заключены между
и
; 25% –
между
и
,
остальные 25% превосходят
. Квартили определяются по формулам,
аналогичным формуле для расчета медианы. Для интервального ряда:
Децилем
называется структурная переменная, делящая распределение на 10 равных частей по
числу единиц в совокупности. Децилей 9, а децильных
групп 10. Децили определяются по формулам, аналогичным формуле для расчета
медианы и квартилей.
В целом общая формула для расчета квантилей в интервальном
ряду такова:
– порядковый номер квантиля
– размерность квантиля (на сколько частей эти
квартили делят совокупность)
– нижняя граница квантильного
интервала
– ширина квантильного
интервала
– накопленная частота предквантильного
интервала
Для дискретного ряда номер квантиля можно
найти по формуле:
Примеры решения задач
Задача 1
(дискретный ранжированный ряд)
В
результате исследований установлен среднемесячный доход жильцов одного
подъезда:
|
1.5 |
1.8 |
2 |
2.5 |
2.8 |
2.8 |
2.8 |
3.0 |
3.6 |
3.8 |
|
3.9 |
4 |
5.8 |
5.9 |
6 |
6 |
6 |
6.8 |
7 |
7 |
Определите:
Модальный
и медианный доход, квартили и децили дохода.
Решение
Имеем уже ранжированный ряд – значения дохода жильцов распределены по возрастанию.
Мода
– наиболее часто встречающееся значение. В данном случае имеем ряд с двумя
модами.
и
Медиана
– такое значение признака, которое делит упорядоченное множество данных
пополам.
Квартили
– значения признака в ранжированном ряду, выбранные таким образом, что 25%
единиц совокупности будут меньше величины
; 25% единиц будут
заключены между
и
; 25% – между
и
; остальные 25%
превосходят
.
Дицили делят ряд на 10 равных частей:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
(интервальный ряд)
Для
определения среднего размера вклада в кредитном учреждении были получены
следующие данные:
| Размер вклада, тыс.р. | до 10.0 | 10.0-16.0 | 16.0-22.0 | 22.0-28.0 | 28.0-34.0 | Свыше 34.0 |
|
Удельный вес вкладов, % |
5.0 | 8.0 | 15.0 | 22.0 | 30.0 | 20.0 |
Рассчитайте
структурные средние (моду, медиану,
квартили).
Решение
Вычислим моду размера вклада:
Мода – варианта, которой соответствует наибольшая частота.
Мода вычисляется по формуле:
–
начало модального интервала
–
величина интервала
–
частота модального интервала
–
частота интервала, предшествующего модальному
–
частота интервала, следующего за модальным
Таким образом, наибольшее
количество вкладов имеют размер 30,7 тыс.р.
Медиана – варианта, находящаяся в середине ряда распределения.
Расчет медианы производится по формуле:
-начало
(нижняя граница) медианного интервала
-величина интервала
-сумма всех частот ряда
-частота медианного интервала
-сумма накопленных частот вариантов до
медианного
Таким образом, половина вкладов имеет размер до 28 тыс.р.,
другая половина – более 28 тыс.р.
Вычислим квартили:
Таким
образом 25% вкладов меньше 20,8 тыс.р., 25% вкладов
лежат в интервале от 20,8 тыс.р. до 28 тыс.р., 25% лежат в интервале от 28 тыс.р.
до 33 тыс.р., 25% больше величины в 33 тыс.р.
Задача 3
Постройте
графики для вариационного ряда. На графике покажите моду, медиану, среднюю, квартили.
| Возраст детей (лет) | Число детей (доли) |
| 0-3 | 0.15 |
| 3-6 | 0.2 |
| 6-9 | 0.4 |
| 9-12 | 0.2 |
| 12-15 | 0.05 |
Решение
Вычислим
среднюю
: Для этого просуммируем
произведения середин интервалов и соответствующих частот, и полученную сумму
разделим на сумму частот.
Вычисление моды интервального ряда на графике
Построим
гистограмму.
Мода определяется по
гистограмме распределения. Для этого выбирается самый высокий прямоугольник,
который в данном случае является модальным. Затем правую вершину модального
прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс.
Абсцисса точки пересечения
этих прямых и будет модой распределения
Гистограмма
По
гистограмме получаем, что
Вычисление медианы и квартилей интервального ряда на графике
Построим
кумулятивную кривую частот (график накопленных частот)
Кумулятивная кривая частот
На получившимся графике
накопленных частот из последней получившейся точки (в нашем примере) проведем
линию перпендикулярную к оси
она так же
является максимальной высотой. Поделим ее на 4 части. Через полученные точки
строим параллельную оси
линии которая должна пересекать высоту к оси
и кумуляту. От
места пересечения кумуляты опускаем перпендикуляры. Получившиеся точки есть квартили
и медиана (квартиль при
).
Вывод к задаче
Таким образом
средний возраст детей 6,9 лет. Наибольшее количество детей имеют возраст 7,5
лет. Четверть детей младше 4,5 лет, а самая старшая четверть детей старше 9,1
лет. Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.
You can use the following formulas to find the first (Q1) and third (Q3) quartiles of a normally distributed dataset:
- Q1 = μ – (.675)σ
- Q3 = μ + (.675)σ
Recall that μ represents the population mean and σ represents the population standard deviation.
Also recall that the first quartile represents the 25th percentile of a dataset and the third quartile represents the 75th percentile of a dataset.
The following examples show how to use these formulas in practice.
Example 1: Find Quartiles Using Mean & Standard Deviation
Suppose we have a normally distributed dataset with μ = 300 and σ = 45.
We can use the following formulas to calculate the first and third quartiles of the dataset:
- Q1 = μ – (.675)σ = 300 – (.675)*45 = 269.625
- Q3 = μ + (.675)σ = 300 + (.675)*45 = 330.375
We interpret this to mean that 25% of all values in the dataset fall below 269.625 and 75% of all values in the dataset fall below 330.375.
Using these numbers, we could also calculate the interquartile range to be:
- IQR = Q3 – Q1
- IQR = 330.375 – 269.265
- IQR = 61.11
This represents the spread of the middle 50% of values in the dataset.
Example 2: Find Quartiles Using Mean & Standard Deviation
Suppose we have a normally distributed dataset with μ = 50 and σ = 2.
We can use the following formulas to calculate the first and third quartiles of the dataset:
- Q1 = μ – (.675)σ = 50 – (.675)*2 = 48.65
- Q3 = μ + (.675)σ = 50 + (.675)*2 = 51.35
We interpret this to mean that 25% of all values in the dataset fall below 48.65 and 75% of all values in the dataset fall below 51.35.
Using these numbers, we could also calculate the interquartile range to be:
- IQR = Q3 – Q1
- IQR = 51.35 – 48.65
- IQR = 2.7
This represents the spread of the middle 50% of values in the dataset.
Additional Resources
The following tutorials offer additional information about the normal distribution and quartiles:
An Introduction to the Normal Distribution
Percentile vs. Quartile vs. Quantile: What’s the Difference?
Interquartile Range vs. Standard Deviation: What’s the Difference?
Компании часто организуют статистику в Excel, чтобы лучше понять свои данные. Одна из функций, которую некоторые люди могут использовать в своих электронных таблицах, – это функция квартилей, которая разделяет данные на четыре категории в диапазоне. Узнав больше о квартилях, вы сможете решить, может ли этот расчет дать новое представление о ваших числовых данных.
В этой статье мы обсудим, что такое квартили и как их найти в Excel, а также советы и часто задаваемые вопросы об этой функции.
Что такое квартили?
Квартили – это значения в Excel, которые разделяют числовые значения на четыре части. Люди находят квартили, чтобы понять процентили, например, 25% клиентов с наибольшими расходами. Четыре квартиля включают:
-
Первый квартиль: Первый квартиль включает самые низкие 25% диапазона данных.
-
Второй квартиль: Второй квартиль включает следующую наименьшую группу чисел. В эту группу входят числа через медиану набора данных.
-
Третий квартиль: Третий квартиль – это вторая по величине группа чисел, превышающая медиану.
-
Четвертый квартиль: Четвертый квартиль включает самые высокие 25% чисел в диапазоне данных.
Например, если данные варьируются от одного до восьми, то каждое из них находится в следующих квартилях:
-
Первый квартиль: 1 и 2
-
Второй квартиль: 3 и 4
-
Третий квартиль: 5 и 6
-
Четвертый квартиль: 7 и 8
Как найти квартили в Excel
При нахождении квартилей в Excel можно предпринять несколько шагов:
1. Упорядочьте ваши числа
Чтобы получить квартили, вы можете упорядочить числа в диапазоне данных от наименьшего к наибольшему. В электронной таблице их можно упорядочить в столбце. Например, ваши числа могут быть следующими:
|
A |
B |
|
|
1 |
9 |
1 |
|
2 |
1 |
3 |
|
3 |
3 |
3 |
|
4 |
5 |
5 |
|
5 |
7 |
6 |
|
6 |
6 |
7 |
|
7 |
2 |
9 |
Для формулы квартиля необходимы две основные величины: квартили и массивы. Квартили – это значения, представленные каждым квартилем. Они варьируются от нуля до четырех:
-
0: Это минимальное значение в диапазоне чисел.
-
1: Это первый квартиль или 25-й процентиль.
-
2: Это второй, или медианный, квартиль, или 50-й процентиль.
-
3: Это представляет собой третий квартиль или 75-й процентиль.
-
4: Представляет собой максимальное значение в диапазоне.
3. Выполните функцию
Использование функции квартиля в Excel позволяет получить квартиль для любого набора данных. Для расчета квартилей в Excel используется формула:
=QUARTILE(array, quart)
Где:
-
Массив – это полный диапазон значений, для которых вы хотите найти квартили
-
Кварта – это то, какой квартиль вы хотите найти
Советы по использованию функции квартилей в Excel
Вот несколько советов по использованию функции квартилей в Excel:
Обзор значений
Перед выполнением функции квартиля можно убедиться, что ваши числа расположены в порядке возрастания в одном столбце и являются правильными. Если ячейки пустые или содержат текст или специальные символы, функция выдает сообщение об ошибке. Вы также можете получить сообщение об ошибке, если значение quart в вашей команде меньше нуля или больше четырех.
Рассчитать различные кварты
Каждый квартиль может предоставить вам различную информацию, которую вы можете использовать. Например, вы можете захотеть узнать, какую максимальную сумму тратит клиент в самом низком процентиле покупок, а также в более высоких квартилях. Это может помочь вам определить, как вы можете создать конкретные бизнес-цели для отдельных групп. Для широкого диапазона данных вычисление каждого квартиля может показать больше, чем среднее значение или медиана, так как оно показывает вариации внутри набора данных.
Проверьте точность вручную
Вы можете вручную рассчитать квартили с помощью нескольких формул для проверки информации:
-
Нижний квартиль = (N+1) x 14
-
Средний квартиль = (N+1) x 24
-
Верхний квартиль = (N+1) x 34
N – это количество целых чисел в вашем наборе данных. Результат говорит вам о позиции, которая представляет каждый квартиль. Например, если для формулы нижнего квартиля результат равен шести, шестое число в вашей последовательности будет нижним квартилем. Поскольку четвертый квартиль является максимальным значением в диапазоне, формулы для его расчета не существует.
Часто задаваемые вопросы
Что такое процентиль?
Процентиль – это мера, используемая в статистике, чтобы показать процентное соотношение в наборе данных. Процентили могут указывать процент отклонения от нормы ниже и выше установленного процентиля. Например, оценка в пределах 25-го процентиля ключевого показателя эффективности поставщика показывает, что 25% оценок были ниже. Процентные показатели могут показать предприятиям, как они сравниваются с другими в своей отрасли.
В чем разница между кварталом и квартилем?
Квартал включает все числа в пределах 25% набора данных. Вместо этих отдельных чисел, квартиль – это число, на котором заканчивается один квартал и начинается другой. Вычисление квартилей может помочь вам понять, насколько велика разница между кварталами.
Для чего используются квартили?
Квартили существуют в статистике для измерения величин, таких как процент доходов в определенной демографической группе или развитие ребенка в определенном возрасте. Квартили могут быть полезны компаниям для оценки и установления эталона на основе конкуренции. Например, организация может собирать данные об общем объеме продаж своих ведущих конкурентов. Вычисление квартилей может помочь установить цели, которые помогут удержаться в верхних квартилях.
Что такое аналогичные функции в Excel?
Существует несколько аналогичных функций, которые можно рассчитать в Excel:
-
MIN: Функция MIN вычисляет наименьшее потенциальное значение в наборе данных.
-
MAX: Функция MAX вычисляет наименьшее возможное значение в наборе данных.
-
MEDIAN: Функция MEDIAN вычисляет среднее значение в наборе данных.
-
СРЕДНЕЕ: Функция MEAN вычисляет среднее значение чисел в наборе данных.
Для каждой из них вы можете выбрать пустой квадрат и ввести формулу с массивом данных, которые вы хотите проанализировать. Например, функция MEDIAN может быть такой:
=MEDIAN(A1:A9)
Обратите внимание, что ни одна из компаний, упомянутых в этой статье, не связана с Indeed.

 ,
, ,
,