Расчет квартилей для интервального ряда:
Для
расчета квартилей для интервального
ряда
-
Определяем номер квартиля по тем же
формулам, что и для дискретного ряда, -
Определяем квартильный интервал по
накопленной частоте. Это
первый интервал, для которого накопленная
частота будет больше или равна номеру
квартиля. -
Рассчитываем квартиль по формуле:
Где:
J
– номер квартиля,

нижняя граница интервала, содержащего
квартиль. Интервал определяется по
накопленной частоте интервалов,
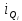
ширина интервала, содержащего квартиль,

накопленная частота интервала,
предшествующего интервалу, содержащему
квартиль,

частота интервала, содержащего квартиль.
Пример.
Найти первый квартиль для интервального
ряда.
|
Возрастные |
Число |
Накопленная |
|
До |
346 |
346 |
|
20 |
872 |
1218 |
|
25 |
1054 |
2272 |
|
30 |
781 |
3053 |
|
35 |
212 |
3265 |
|
40 |
121 |
3386 |
|
45 |
76 |
3462 |
|
Итого |
3462 |
Решение:
-
Определяем номер первого квартиля по
формуле
-
Первый квартиль находится в возрастной
группе 20-25 лет, так как это первый
интервал, для которого накопленная
частота больше (или равна) номера
квартиля (346<865,75; 1218>865,75). -
Определяем первый квартиль по формуле
-
Это значит, что четверть студентов
младше 22,98 лет.
-
Децили
Децили –
значения признака, делящие ранжированный
ряд на десять равных частей.
Первый
дециль отсекает 1/10 часть совокупности,
а девятый дециль отсекает 9/10 частей.
Таким образом, различают 9 децилей.
Рассчитываются
децили аналогично квартилям.
Расчет децилей для дискретного ряда
-
Определяем номер
дециля по формуле:
,
-
Если номер дециля
– целое число,
то значение дециля будет равно величине
элемента ряда, которое обладает
накопленной частотой равной номеру
дециля. Например, если номер дециля
равен 20, его значение будет равно
значению признака с S =20 (накопленной
частотой равной 20).
Если номер дециля
– нецелое число,
то дециль попадает между двумя
наблюдениями. Значением дециля будет
сумма, состоящая из значения элемента,
для которого накопленная частота равна
целому значению номера дециля, и указанной
части (нецелая часть номера дециля)
разности между значением этого элемента
и значением следующего элемента.
Например, если номер
дециля равна 20,25, дециль попадает между
20-м и 21-м наблюдениями, и его значение
будет равно значению 20-го наблюдения
плюс 1/4 разности между значением 20-го и
21-го наблюдений.
Расчет децилей для интервального ряда
-
Определяем номер
дециля по формуле:
,
-
Определяем децильный
интервал. Это первый интервал, для
которого накопленная частота будет
больше или равна номеру дециля. -
Рассчитываем дециль
по формуле:
где
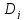
– нижняя граница децильного интервала;
– ширина децильного интервала;

сумма всех частот,

частота интервала, предшествующего
децильному;

частота децильного интервала.
Пример.
Найти 9-ый дециль D9
|
Заработная |
бригада |
|
|
число |
накопленная частота |
|
|
15 |
20 |
20 |
|
18 |
37 |
57 |
|
20 |
14 |
71 |
|
25 |
4 |
75 |
|
Итого: |
75 |
-
Определяем номер 9-го дециля
для первой бригады

-
Номер дециля – нецелое число. Для
определения дециля нужны значения двух
элементов – х68и х69. Значение
дециля находится между ними.
Определяем
их значение с помощью самой первой
накопленной частоты большей или равной
порядковым номерам элементов (68 и 69).
Х68= 20, х69= 20.
Теперь
определяем значение 9-го дециля:D7=x68+ (х69–
х68)×0,4=20 + (20 – 20)×0,2 =20тыс.руб.
Это значит, что заработная плата90%
рабочих бригады не превышает 18 тыс.руб.
Пример.
Найти седьмой дециль D7
для интервального ряда.
|
Возрастные |
Число |
Накопленная |
|
До |
346 |
346 |
|
20 |
872 |
1218 |
|
25 |
1054 |
2272 |
|
30 |
781 |
3053 |
|
35 |
212 |
3265 |
|
40 |
121 |
3386 |
|
45 |
76 |
3462 |
|
Итого |
3462 |
Решение:
-
Определяем номер седьмого дециля по
формуле
7×
-
Седьмой дециль находится в возрастной
группе 30-35 лет, так как это первый
интервал, для которого накопленная
частота больше (или равна) номера дециля
(2272<2424,1; 3053>2424,1). -
Определяем седьмой дециль по формуле
-
Это значит, что 70% студентов младше 30,97
лет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In statistics, a quartile is a type of quantile which divides the number of data points into four parts, or quarters, of more-or-less equal size. The data must be ordered from smallest to largest to compute quartiles; as such, quartiles are a form of order statistic. The three main quartiles are as follows:
- The first quartile (Q1) is defined as the middle number between the smallest number (minimum) and the median of the data set. It is also known as the lower or 25th empirical quartile, as 25% of the data is below this point.
- The second quartile (Q2) is the median of a data set; thus 50% of the data lies below this point.
- The third quartile (Q3) is the middle value between the median and the highest value (maximum) of the data set. It is known as the upper or 75th empirical quartile, as 75% of the data lies below this point.[1]
Along with the minimum and maximum of the data (which are also quartiles), the three quartiles described above provide a five-number summary of the data. This summary is important in statistics because it provides information about both the center and the spread of the data. Knowing the lower and upper quartile provides information on how big the spread is and if the dataset is skewed toward one side. Since quartiles divide the number of data points evenly, the range is not the same between quartiles (i.e., Q3–Q2 ≠ Q2–Q1) and is instead known as the interquartile range (IQR). While the maximum and minimum also show the spread of the data, the upper and lower quartiles can provide more detailed information on the location of specific data points, the presence of outliers in the data, and the difference in spread between the middle 50% of the data and the outer data points.[2]
Definitions[edit]
| Symbol | Names | Definition |
|---|---|---|
| Q1 |
|
splits off the lowest 25% of data from the highest 75% |
| Q2 |
|
cuts data set in half |
| Q3 |
|
splits off the highest 25% of data from the lowest 75% |
Computing methods[edit]
Discrete distributions[edit]
For discrete distributions, there is no universal agreement on selecting the quartile values.[3]
Method 1[edit]
- Use the median to divide the ordered data set into two-halves.
- If there is an odd number of data points in the original ordered data set, do not include the median (the central value in the ordered list) in either half.
- If there is an even number of data points in the original ordered data set, split this data set exactly in half.
- The lower quartile value is the median of the lower half of the data. The upper quartile value is the median of the upper half of the data.
This rule is employed by the TI-83 calculator boxplot and “1-Var Stats” functions.
Method 2[edit]
- Use the median to divide the ordered data set into two-halves.
- If there are an odd number of data points in the original ordered data set, include the median (the central value in the ordered list) in both halves.
- If there are an even number of data points in the original ordered data set, split this data set exactly in half.
- The lower quartile value is the median of the lower half of the data. The upper quartile value is the median of the upper half of the data.
The values found by this method are also known as “Tukey’s hinges”;[4] see also midhinge.
Method 3[edit]
- If there are even numbers of data points, then Method 3 starts off the same as Method 1 or Method 2 above and you can choose to include or not include the median as a datapoint. If you choose to include the median as a new datapoint, proceed to step 2 or 3 of Method 3 because you now have an odd number of datapoints.
- If there are (4n+1) data points, then the lower quartile is 25% of the nth data value plus 75% of the (n+1)th data value; the upper quartile is 75% of the (3n+1)th data point plus 25% of the (3n+2)th data point.
- If there are (4n+3) data points, then the lower quartile is 75% of the (n+1)th data value plus 25% of the (n+2)th data value; the upper quartile is 25% of the (3n+2)th data point plus 75% of the (3n+3)th data point.
Method 4[edit]
If we have an ordered dataset 






where 

To find the first, second, and third quartiles of the dataset we would evaluate 


Example 1[edit]
Ordered Data Set: 6, 7, 15, 36, 39, 40, 41, 42, 43, 47, 49
| Method 1 | Method 2 | Method 3 | Method 4 | |
|---|---|---|---|---|
| Q1 | 15 | 25.5 | 20.25 | 15 |
| Q2 | 40 | 40 | 40 | 40 |
| Q3 | 43 | 42.5 | 42.75 | 43 |
Example 2[edit]
Ordered Data Set: 7, 15, 36, 39, 40, 41
As there are an even number of data points, the first three methods all give the same results.
| Method 1 | Method 2 | Method 3 | Method 4 | |
|---|---|---|---|---|
| Q1 | 15 | 15 | 15 | 13 |
| Q2 | 37.5 | 37.5 | 37.5 | 37.5 |
| Q3 | 40 | 40 | 40 | 40.25 |
Continuous probability distributions[edit]
Quartiles on a cumulative distribution function of a normal distribution
If we define a continuous probability distributions as 


The CDF gives the probability that the random variable 












Outliers[edit]
There are methods by which to check for outliers in the discipline of statistics and statistical analysis. Outliers could be a result from a shift in the location (mean) or in the scale (variability) of the process of interest.[6] Outliers could also be evidence of a sample population that has a non-normal distribution or of a contaminated population data set. Consequently, as is the basic idea of descriptive statistics, when encountering an outlier, we have to explain this value by further analysis of the cause or origin of the outlier. In cases of extreme observations, which are not an infrequent occurrence, the typical values must be analyzed. In the case of quartiles, the Interquartile Range (IQR) may be used to characterize the data when there may be extremities that skew the data; the interquartile range is a relatively robust statistic (also sometimes called “resistance”) compared to the range and standard deviation. There is also a mathematical method to check for outliers and determining “fences”, upper and lower limits from which to check for outliers.
After determining the first and third quartiles and the interquartile range as outlined above, then fences are calculated using the following formula:
Boxplot Diagram with Outliers
where Q1 and Q3 are the first and third quartiles, respectively. The lower fence is the “lower limit” and the upper fence is the “upper limit” of data, and any data lying outside these defined bounds can be considered an outlier. Anything below the Lower fence or above the Upper fence can be considered such a case. The fences provide a guideline by which to define an outlier, which may be defined in other ways. The fences define a “range” outside which an outlier exists; a way to picture this is a boundary of a fence, outside which are “outsiders” as opposed to outliers. It is common for the lower and upper fences along with the outliers to be represented by a boxplot. For a boxplot, only the vertical heights correspond to the visualized data set while horizontal width of the box is irrelevant. Outliers located outside the fences in a boxplot can be marked as any choice of symbol, such as an “x” or “o”. The fences are sometimes also referred to as “whiskers” while the entire plot visual is called a “box-and-whisker” plot.
When spotting an outlier in the data set by calculating the interquartile ranges and boxplot features, it might be simple to mistakenly view it as evidence that the population is non-normal or that the sample is contaminated. However, this method should not take place of a hypothesis test for determining normality of the population. The significance of the outliers vary depending on the sample size. If the sample is small, then it is more probable to get interquartile ranges that are unrepresentatively small, leading to narrower fences. Therefore, it would be more likely to find data that are marked as outliers.[7]
Computer software for quartiles[edit]
| Environment | Function | Quartile Method |
|---|---|---|
| Microsoft Excel | QUARTILE.EXC | Method 4 |
| Microsoft Excel | QUARTILE.INC | Method 3 |
| TI-8X series calculators | 1-Var Stats | Method 1 |
| R | fivenum | Method 2 |
| Python | numpy.percentile | Method 3 |
| Python | pandas.DataFrame.describe | Method 3 |
Excel:
The Excel function QUARTILE(array, quart) provides the desired quartile value for a given array of data, using Method 3 from above. In the Quartile function, array is the dataset of numbers that is being analyzed and quart is any of the following 5 values depending on which quartile is being calculated. [8]
| Quart | Output QUARTILE Value |
|---|---|
| 0 | Minimum value |
| 1 | Lower Quartile (25th percentile) |
| 2 | Median |
| 3 | Upper Quartile (75th percentile) |
| 4 | Maximum value |
MATLAB:
In order to calculate quartiles in Matlab, the function quantile(A,p) can be used. Where A is the vector of data being analyzed and p is the percentage that relates to the quartiles as stated below. [9]
| p | Output QUARTILE Value |
|---|---|
| 0 | Minimum value |
| 0.25 | Lower Quartile (25th percentile) |
| 0.5 | Median |
| 0.75 | Upper Quartile (75th percentile) |
| 1 | Maximum value |
See also[edit]
- Five-number summary
- Range
- Box plot
- Interquartile range
- Summary statistics
- Quantile
References[edit]
- ^ a b c A modern introduction to probability and statistics: understanding why and how. Dekking, Michel, 1946–. London: Springer. 2005. pp. 236-238. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Knoch, Jessica (February 23, 2018). “How are Quartiles Used in Statistics?”. Magoosh. Archived from the original on December 10, 2019. Retrieved February 24, 2023.
- ^ Hyndman, Rob J; Fan, Yanan (November 1996). “Sample quantiles in statistical packages”. American Statistician. 50 (4): 361–365. doi:10.2307/2684934. JSTOR 2684934.
- ^ Tukey, John Wilder (1977). Exploratory Data Analysis. ISBN 978-0-201-07616-5.
- ^ “6. Distribution and Quantile Functions” (PDF). math.bme.hu.
- ^ Walfish, Steven (November 2006). “A Review of Statistical Outlier Method”. Pharmaceutical Technology.
- ^ Dawson, Robert (July 1, 2011). “How Significant is a Boxplot Outlier?”. Journal of Statistics Education. 19 (2). doi:10.1080/10691898.2011.11889610.
- ^ “How to use the Excel QUARTILE function | Exceljet”. exceljet.net. Retrieved December 11, 2019.
- ^ “Quantiles of a data set – MATLAB quantile”. www.mathworks.com. Retrieved December 11, 2019.
External links[edit]
- Quartile – from MathWorld Includes references and compares various methods to compute quartiles
- Quartiles – From MathForum.org
- Quartiles calculator – simple quartiles calculator
- Quartiles – An example how to calculate it
Квартили в статистике
|
Интервалы |
Диапазон по продолжительности жизни |
Число стран (частота), f |
Накопленная частота, f |
|
1 |
60,8 — 63,53 |
6 |
6 |
|
2 |
63,53 – 66,25 |
13 |
19 |
|
3 |
66,25 – 68,98 |
12 |
31 |
|
4 |
68,98 – 71,70 |
18 |
49 |
|
5 |
71,70 — 74,43 |
37 |
86 |
|
6 |
74,43 — 77,15 |
22 |
108 |
|
7 |
77,15 — 79,88 |
27 |
135 |
|
8 |
79,88 — 82,60 |
15 |
150 |
Аналогично определению медианы вычисляются значения признака, делящие совокупность на 4 равные по численности части – квартили, которые обозначаются заглавной латинской буквой Q с подписным значком номера квартиля. Для первого и третьего квартилей приводим формулы и расчет:
Первый квартиль
Значение квартиля Q1 находится в интервале 68,98 – 71,70, соответствующего частоте fQ1 = 150:4 = 37,5
Третий квартиль
Значение квартиля находится в интервале 68,98 – 71,70, соответствующего частоте fQ3 = (3*150):4 = 112,5
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
Структурные средние – мода, медиана, квантиль, дециль
Краткая теория
Наиболее широкое применение в статистике имеют структурные
средние, к числу которых относятся мода и медиана (непараметрические средние).
Мода – величина признака (варианта), которая
встречается в ряду распределения с наибольшей частотой (весом). К моде (Мо)
прибегают для выявления величины признака, имеющей наибольшее распространение
(цена на рынке, по которой было совершено наибольшее число продаж данного
товара, номер обуви, который пользуется наибольшим спросом у покупателей и т.
д.). Мода используется только в совокупностях большой численности. В дискретном
ряду мода находится как варианта, имеющая наибольшую частоту. В интервальном
ряду сначала находится модальный интервал, то есть интервал, обладающий наибольшей частотой, а
затем – приближенное значение модальной величины признака по формуле:
– нижняя граница модального интервала
– величина модального интервала
– частота интервала, предшествующего
модальному
– частота модального интервала
– частота интервала, следующего за модальным
Квантили –
величины, разделяющие совокупность на определенной количество равных по
численности элементов частей. Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили – на 100
частей.
Медиана –
величина признака у единицы, находящейся в середине ранжированного
(упорядоченного) ряда. Если ряд распределения представлен конкретными
значениями признака, то медиана (Me) находится как
серединное значение признака.
Если ряд распределения дискретный, то медиана находится как
серединное значение признака (например, если число значений нечетное – 45, то
соответствует 23 значению признака в ряду
значений, расположенных в порядке возрастания, если число значений четное – 44,
то медиана соответствует полусумме 22 и 23 значений
признака).
Если ряд распределения интервальный, то первоначально
находят медианный интервал, который содержит единицу, находящуюся в середине
ранжированного ряда. Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:
– нижняя граница медианного интервала
– величина медианного интервала
– сумма
частот ряда
– сумма накопленных частот в интервалах,
предшествующих медианному
– частота медианного интервала
Квартили – это значения
признака в ранжированном ряду, выбранные таким образом, что 25% единиц
совокупности будут меньше величины
, 25% единиц будут заключены между
и
; 25% –
между
и
,
остальные 25% превосходят
. Квартили определяются по формулам,
аналогичным формуле для расчета медианы. Для интервального ряда:
Децилем
называется структурная переменная, делящая распределение на 10 равных частей по
числу единиц в совокупности. Децилей 9, а децильных
групп 10. Децили определяются по формулам, аналогичным формуле для расчета
медианы и квартилей.
В целом общая формула для расчета квантилей в интервальном
ряду такова:
– порядковый номер квантиля
– размерность квантиля (на сколько частей эти
квартили делят совокупность)
– нижняя граница квантильного
интервала
– ширина квантильного
интервала
– накопленная частота предквантильного
интервала
Для дискретного ряда номер квантиля можно
найти по формуле:
Примеры решения задач
Задача 1
(дискретный ранжированный ряд)
В
результате исследований установлен среднемесячный доход жильцов одного
подъезда:
|
1.5 |
1.8 |
2 |
2.5 |
2.8 |
2.8 |
2.8 |
3.0 |
3.6 |
3.8 |
|
3.9 |
4 |
5.8 |
5.9 |
6 |
6 |
6 |
6.8 |
7 |
7 |
Определите:
Модальный
и медианный доход, квартили и децили дохода.
Решение
Имеем уже ранжированный ряд – значения дохода жильцов распределены по возрастанию.
Мода
– наиболее часто встречающееся значение. В данном случае имеем ряд с двумя
модами.
и
Медиана
– такое значение признака, которое делит упорядоченное множество данных
пополам.
Квартили
– значения признака в ранжированном ряду, выбранные таким образом, что 25%
единиц совокупности будут меньше величины
; 25% единиц будут
заключены между
и
; 25% – между
и
; остальные 25%
превосходят
.
Дицили делят ряд на 10 равных частей:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
(интервальный ряд)
Для
определения среднего размера вклада в кредитном учреждении были получены
следующие данные:
| Размер вклада, тыс.р. | до 10.0 | 10.0-16.0 | 16.0-22.0 | 22.0-28.0 | 28.0-34.0 | Свыше 34.0 |
|
Удельный вес вкладов, % |
5.0 | 8.0 | 15.0 | 22.0 | 30.0 | 20.0 |
Рассчитайте
структурные средние (моду, медиану,
квартили).
Решение
Вычислим моду размера вклада:
Мода – варианта, которой соответствует наибольшая частота.
Мода вычисляется по формуле:
–
начало модального интервала
–
величина интервала
–
частота модального интервала
–
частота интервала, предшествующего модальному
–
частота интервала, следующего за модальным
Таким образом, наибольшее
количество вкладов имеют размер 30,7 тыс.р.
Медиана – варианта, находящаяся в середине ряда распределения.
Расчет медианы производится по формуле:
-начало
(нижняя граница) медианного интервала
-величина интервала
-сумма всех частот ряда
-частота медианного интервала
-сумма накопленных частот вариантов до
медианного
Таким образом, половина вкладов имеет размер до 28 тыс.р.,
другая половина – более 28 тыс.р.
Вычислим квартили:
Таким
образом 25% вкладов меньше 20,8 тыс.р., 25% вкладов
лежат в интервале от 20,8 тыс.р. до 28 тыс.р., 25% лежат в интервале от 28 тыс.р.
до 33 тыс.р., 25% больше величины в 33 тыс.р.
Задача 3
Постройте
графики для вариационного ряда. На графике покажите моду, медиану, среднюю, квартили.
| Возраст детей (лет) | Число детей (доли) |
| 0-3 | 0.15 |
| 3-6 | 0.2 |
| 6-9 | 0.4 |
| 9-12 | 0.2 |
| 12-15 | 0.05 |
Решение
Вычислим
среднюю
: Для этого просуммируем
произведения середин интервалов и соответствующих частот, и полученную сумму
разделим на сумму частот.
Вычисление моды интервального ряда на графике
Построим
гистограмму.
Мода определяется по
гистограмме распределения. Для этого выбирается самый высокий прямоугольник,
который в данном случае является модальным. Затем правую вершину модального
прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс.
Абсцисса точки пересечения
этих прямых и будет модой распределения
Гистограмма
По
гистограмме получаем, что
Вычисление медианы и квартилей интервального ряда на графике
Построим
кумулятивную кривую частот (график накопленных частот)
Кумулятивная кривая частот
На получившимся графике
накопленных частот из последней получившейся точки (в нашем примере) проведем
линию перпендикулярную к оси
она так же
является максимальной высотой. Поделим ее на 4 части. Через полученные точки
строим параллельную оси
линии которая должна пересекать высоту к оси
и кумуляту. От
места пересечения кумуляты опускаем перпендикуляры. Получившиеся точки есть квартили
и медиана (квартиль при
).
Вывод к задаче
Таким образом
средний возраст детей 6,9 лет. Наибольшее количество детей имеют возраст 7,5
лет. Четверть детей младше 4,5 лет, а самая старшая четверть детей старше 9,1
лет. Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.
Содержание
Спрятать
- Что такое квартиль?
- Как работают квартили
- Какова цель квартилей?
- Как найти квартили в Excel
- №1. Сортируйте свои числа
- № 2. Выполнить задание
- Советы по использованию функции квартиля в Excel
- №1. Ценности следует пересмотреть.
- № 2. Определить различные кварты
- №3. Вручную проверьте точность.
- Что такое квартильный пример?
- #Шаг 1: подсчитайте количество наблюдений в наборе данных
- #Шаг 2: Отсортируйте наблюдения по возрастанию
- #Шаг 3: Найдите первый квартиль
- #Шаг 4: Найдите второй квартиль
- #Шаг 5: Найдите третий квартиль
- Как интерпретировать квартили
- №1. Сравнение наблюдений
- № 2. медиана
- №3. Межквартильный размах (IQR)
- Формулы квартилей
- №1. Для первого квартиля, сокращенно Q1.
- № 2. Для второго квартиля, сокращенно Q2.
- №3. Для третьего квартиля, сокращенно Q3.
- № 4. Для межквартильного диапазона.
- Как рассчитывается квартиль?
- №1. Пример Квартиль 1
- № 2. Пример 2 квартили
- Почему он называется квартилем?
- Как разделить данные на 4 квартили?
- Что такое 25-процентный квартиль?
- Что такое 5 квартилей?
- Каковы шаги, чтобы найти первый квартиль?
- Для чего используется формула квартилей?
- Как мы используем квартиль?
- Заключение
- Статьи по теме
- Рекомендации
Компании часто используют Excel для организации статистики, чтобы лучше понимать свои данные. Функция квартилей, которая делит данные на четыре категории в диапазоне, — это одна из функций, которую некоторые люди могут использовать в своих электронных таблицах. Понимание квартилей может помочь вам решить, может ли этот расчет дать новое понимание ваших числовых данных. В этой статье мы объясним, что такое квартиль, на упрощенном примере, как он рассчитывается и его цель среди других основных фактов, которые вам необходимо знать. Давайте продолжим!
Что такое квартиль?
Квартиль — это статистический термин, который относится к разделению наблюдений на четыре определенных интервала на основе значений данных и того, как они соотносятся со всем набором наблюдений.
Квартили — это значения Excel, которые делят числовые значения на четыре части. Люди предпочитают квартили процентилям, например 25% самых высокооплачиваемых клиентов. Четыре квартили следующие:
- Первый квартиль: Первый квартиль включает самые низкие 25% диапазона данных.
- Второй квартиль: Второй квартиль включает следующую низшую группу чисел. В эту группу входят числа через медиану набора данных.
- Третий квартиль: Третий квартиль – это вторая по величине группа чисел выше медианы.
- Четвертый квартиль: четвертый квартиль включает 25% самых высоких чисел в диапазоне данных.
Например, если данные колеблются от одного до восьми, каждый попадает в один из следующих квартилей:
- Первый квартиль: 1 и 2
- Второй квартиль: 3 и 4
- Третий квартиль: 5 и 6
- Четвертая квартиль: 7 и 8
Как работают квартили
Quartiles делит данные на четверти, так что 25% измерений меньше нижнего квартиля, 50% меньше медианы и 75% меньше верхнего квартиля, точно так же, как медиана делит данные пополам, так что 50% измерений ниже медианы и 50% выше ее.
Набор данных разделен на четыре диапазона, каждый из которых содержит 25% точек данных, с использованием трех квартильных значений: нижнего, медианного и верхнего. Нижний квартиль, или первый квартиль, обозначается как Q1 и представляет собой среднее число между наименьшим и медианным значениями набора данных. Медиана также находится во втором квартиле, Q2. Верхний или третий квартиль, обозначаемый как Q3, является центральной точкой распределения, лежащей между медианой и наибольшим числом.
Теперь мы можем наметить четыре группы, образованные квартилями. Первый набор значений включает наименьшее число до Q1; второй набор включает Q1 в медиану; третий набор включает медиану для Q3; и четвертая категория включает Q3 до самой высокой точки данных во всем наборе.
Какова цель квартилей?
Квартили удивительно полезны и могут служить цели в различных контекстах. Одна из хороших целей квартилей заключается в том, что они могут помочь вам понять основную тенденцию и изменчивость вашего набора данных и даже помочь вам найти выбросы. Отображение их в виде диаграммы может помочь вам понять распределение ваших данных.
Q2 — это медиана, и она делит набор данных пополам. Для асимметричных распределений это полезная мера центральной тенденции. Межквартильный размах (IQR) является мерой изменчивости. Интервал между первым и третьим квартилями.
IQR = Q3 – Q1
Большие IQR указывают на более широкий диапазон значений. Независимо от формы распределения половина наблюдений попадает в межквартильный диапазон.
Медиана и межквартильный размах являются более надежными показателями, чем более привычные среднее значение и стандартное отклонение. Выбросы мало влияют на любую статистику, потому что они не зависят от каждого значения. Кроме того, межквартильный диапазон идеально подходит для асимметричных распределений, таких как медиана.
Еще одно полезное назначение квартилей заключается в том, что они также могут помочь вам найти выбросы.
Как найти квартили в Excel
При поиске квартилей в Excel у вас есть несколько вариантов:
№1. Сортируйте свои числа
Вы можете получить свои квартили, упорядочив числа в диапазоне данных от самого низкого до самого высокого. В электронной таблице вы можете отсортировать их по столбцу. Например, ваши числа могут быть:
| A | B | |
| 1 | 9 | 1 |
| 2 | 1 | 3 |
| 3 | 3 | 3 |
| 4 | 5 | 5 |
| 5 | 7 | 6 |
| 6 | 6 | 7 |
| 7 | 2 | 9 |
Формула квартилей требует двух основных значений: квартили и массивы. Каждый квартиль представляет собой отдельный набор значений. Они пронумерованы от 0 до 4:
- 0: наименьшее значение в диапазоне чисел.
- 1: Это первый квартиль или 25-й процентиль.
- 2: Это второй или медианный квартиль или 50-й процентиль.
- 3: Это 75-й процентиль или третий квартиль.
- 4: это самое высокое значение в диапазоне.
№ 2. Выполнить задание
В Excel функция квартиля возвращает квартиль для любого набора данных. В Excel для расчета квартилей используется следующая формула:
= КВАРТИЛЬ (массив; кварта)
Где:
- Наблюдения и советы этой статьи мы подготовили на основании опыта команды массив представляет весь диапазон значений, для которых вы хотите найти квартили.
- кварта какой квартиль вы хотите найти.
Советы по использованию функции квартиля в Excel
Вот несколько советов по использованию функции квартилей Excel:
№1. Ценности следует пересмотреть.
Перед запуском функции квартиля дважды проверьте, чтобы ваши числа были в порядке возрастания в одном столбце и были правильными. Функция генерирует сообщение об ошибке, если какая-либо из ячеек пуста или содержит текст или специальные символы. Если значение кварты в вашей команде меньше нуля или больше четырех, вы можете получить сообщение об ошибке.
№ 2. Определить различные кварты
Каждая кварта может предоставить вам уникальные данные, которые вы можете использовать. Например, вам может быть интересно узнать, сколько покупатель тратит в самом низком процентиле покупок, а также в верхних квартилях. Это может помочь вам определить, как создавать конкретные бизнес-цели для определенных групп. Вычисление каждого квартиля для широкого диапазона данных может показать вам больше, чем среднее значение или медиану, поскольку оно показывает изменение в наборе данных.
№3. Вручную проверьте точность.
Чтобы проверить ваши данные, вы можете вручную рассчитать квартили, используя следующие формулы:
- Нижний квартиль = (N+1) x 1/4
- Средний квартиль = (N+1) x 2/4
- Верхний квартиль = (N+1) x 3/4
Число N обозначает количество целых чисел в вашем наборе данных. Результат указывает, какой квартиль представляет каждая позиция. Например, если формула нижнего квартиля дает результат шесть, шестое число в вашей последовательности является нижним квартилем. Формулы для расчета четвертого квартиля не существует, поскольку это максимальное значение в диапазоне.
Что такое квартильный пример?
Рассмотрите возможность проведения небольшого исследования развития речи у детей в возрасте 1–6 лет. Вы пишете статью об исследовании и хотите включить возрастные квартили детей.
| Age (years) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| частота | 2 | 3 | 4 | 1 | 2 | 2 |
#Шаг 1: Подсчитайте количество наблюдений в наборе данных.
n = 2 + 3 + 4 + 1 + 2 + 2 = 14
#Шаг 2: Сортировка наблюдений в порядке возрастания
1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 5, 5, 6, 6
#Шаг 3: найти первый квартиль
n * (1/4) = 14 * (1/4) = 3.5
3.5 не является целым числом, поэтому Q1 — это число в позиции 4.
1, 1, 2, 22, 3, 3, 3, 3, 4, 5, 5, 6, 6
Q1 = 2 года
#Шаг 4: найти второй квартиль
n * (2/4) = 14 * (2/4) = 7
7 — целое число, поэтому Q2 — это среднее чисел в позициях 7 и 8.
1, 1, 2, 2, 2, 3, 3, 33, 4, 5, 5, 6, 6
Q2 = (3 + 3) / 2
Q2 = 3 года
#Шаг 5: найти третий квартиль
n * (3/4) = 14 * (3/4) = 10.5
10.5 не является целым числом, поэтому Q3 — это число в позиции 11.
1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 55, 6, 6
Q3 = 5 года
Как интерпретировать квартили
Квартили могут предоставить полезную информацию о конкретном наблюдении или наборе данных.
№1. Сравнение наблюдений
Квартили могут помочь вам понять наблюдение по отношению к остальной части выборки или генеральной совокупности. Вы можете определить, находится ли наблюдение в нижних 25 %, средних 50 % или верхних 25 %, сравнив его с квартилями.
№ 2. медиана
Медиана, или второй квартиль, является мерой центральной тенденции. Это среднее число является хорошим индикатором среднего или наиболее центрального значения данных, особенно для асимметричных распределений или распределений с выбросами.
№3. Межквартильный размах (IQR)
Межквартильный размах (IQR) является мерой изменчивости. Это расстояние между первой и третьей квартилями. Он представляет собой распределение средних 50% данных.
IQR = Q3 – Q1
IQR является превосходной мерой изменчивости для асимметричных или заполненных выбросами распределений. Поскольку IQR включает только средние 50% данных, на него не влияют экстремальные значения, в отличие от диапазона.
- Асимметрия: Расстояние между квартилями может указывать на то, является ли распределение асимметричным или симметричным.
- Выявление выбросов: Выбросы можно определить с помощью межквартильного диапазона (IQR). Выбросы — это наблюдения, которые либо чрезвычайно высоки, либо чрезвычайно низки. Выброс определяется как любое наблюдение, которое более чем на 1.5 IQR отличается от первого или третьего квартиля.
Формулы квартилей
Существуют четыре основные формулы квартилей, используемые для определения первого, второго, третьего и интерквартилей.
№1. Для первого квартиля, сокращенно Q1.
Первый квартиль = Q1 = ((n + 1) / 4)-й член
№ 2. Для второго квартиля, сокращенно Q2.
Второй квартиль = Q2 = ((n + 1) / 2)-й член
№3. Для третьего квартиля, сокращенно Q3.
Третий квартиль = Q3 = (3(n + 1)/4)-й член
№ 4. Для межквартильного диапазона.
Межквартильный = Q3 – Q1 = (3(n + 1)/4) й член – ((n + 1)/4) й термин
Мы можем написать общую формулу для расчета квартиля, используя три приведенные выше формулы для первого, второго и третьего квартилей.
Как рассчитывается квартиль?
Квартили можно легко рассчитать с помощью формул.
№1. Пример Квартиль 1
Оценить все квартильные части данного набора данных, 2, 9, 7, 29, 34, 61, 25, 19, 16?
Решения
- Шаг 1: Начните с заданного набора чисел.
2, 9, 7, 29, 34, 61, 25, 19, 16
- Шаг 2: Отсортируйте заданный набор чисел в порядке возрастания.
2, 7, 9, 16, 19, 25, 29, 34, 61
- Шаг 3: Подсчитайте данный набор чисел и умножьте на n.
N = 9
- Шаг 4: Используя общую формулу квартилей, определите первый, второй и третий квартиль.
Qk = k (n + 1) / 4)-й член
- Шаг 5: Подставьте k = 1, 2, 3 вместо первого, второго и третьего квартилей.
Для к = 1
Q1 = 1 (9 + 1) / 4)-й член
Q1 = 1 (10) / 4)-й член
Q1 = (10) / 4)-й член
Q1 = (5) / 2)-й член
Q1 = 2.5-й срок
Для к = 2
Q2 = 2 (9 + 1) / 4)-й член
Q2 = 2 (10) / 4)-й член
Q2 = (10/2)-й член
Q2 = 5-й срок
Для к = 3
Q3 = 3 (9 + 1) / 4)-й член
Q3 = 3 (10) / 4)-й член
Q3 = (30/4)-й член
Q3 = (15/2)-й член
Q3 = 7.5-й срок
- Шаг 6: Возьмите рассчитанные значения из организованного набора данных квартилей.
Для Q1
Q1 = 2.5-й срок
Q1 = 2-й срок + 3-й срок / 2
Q1 = 7 + 9/2
Q1 = 16/2
Q1 = 8
Для Q2
Q2 = 5-й срок
Q2 = 19
Для Q3
Q3 = 7.5-й срок
Q3 = 7-й + 8-й / 2
Q3 = 29 + 34 / 2
Q3 = 63/2
Q3 = 31.5
- Шаг 7: Примените общую формулу для расчета межквартильного диапазона и введите значения.
межквартильный = Q3 – Q1
межквартильный = 31.5 – 8
межквартильный = 23.5
В результате квартили данного множества равны Q1 = 8. Q2 = 19, Q3 = 31.5 и интерквартиль = 23.5.
№ 2. Пример 2 квартили
Найдите интерквартиль следующего набора данных: 23, 19, 3, 12, 22, 18, 11?
Решения
- Шаг 1: Начните с заданного набора чисел.
23, 19, 3, 12, 22, 18, 11
- Шаг 2: Отсортируйте заданный набор чисел в порядке возрастания.
3, 11, 12, 18, 19, 22, 23
- Шаг 3: Подсчитайте данный набор чисел и умножьте на n.
N = 7
- Шаг 4: Теперь применим общую интерквартильную формулу.
Межквартильный диапазон = Q3 – Q1
- Шаг 5: Определите первый и третий квартили.
Для Q1
Q1 = (n + 1) / 4)-й член
Q1 = (7 + 1) / 4)-й член
Q1 = (8) / 4)-й член
Q1 = 2-й срок
Для Q3
Q3 = 3(n + 1) / 4)-й член
Q3 = 3(7 + 1) / 4)-й член
Q3 = 3(8) / 4)-й срок
Q3 = (24/4)-й член
Q3 = 6-й срок
- Шаг 6: введите результаты третьего и первого квартилей в формулу межквартили.
межквартильный = 6-й срок – 2-й срок
межквартильный = 22 – 11
межквартильный = 11
Почему он называется квартилем?
Квартиль — это тип квантиля в статистике, который делит количество точек данных на четыре части или четверти примерно одинакового размера. Для вычисления квартилей данные должны быть упорядочены от наименьшего к наибольшему; таким образом, квартили являются разновидностью порядковой статистики.
Как разделить данные на 4 квартили?
Щелкните пустую ячейку где-нибудь на листе в Excel. Например, выберите ячейку B1. Введите «= КВАРТИЛЬ (A1: A10,1)» после ввода.
Что такое 25-процентный квартиль?
25-й процентиль также называют первым или нижним квартилем. 25-й процентиль — это значение, при котором 25% ответов находятся ниже него, а 75% ответов — выше него.
Что такое 5 квартилей?
Сводка состоит из пяти значений: самых экстремальных значений набора данных (максимальное и минимальное значения), нижнего и верхнего квартилей и медианы. Эти значения представлены в следующем порядке: минимальное значение, нижний квартиль (Q1), медианное значение (Q2), верхний квартиль (Q3) и максимальное значение.
Каковы шаги, чтобы найти первый квартиль?
Мы используем следующие шаги для определения первого квартиля:
- Не забудьте расположить точки данных в порядке от наименьшей до наибольшей важности.
- Найдите медиану всего набора данных и разделите его на две равные части.
- Возьмите медиану нижней половины набора данных.
Для чего используется формула квартилей?
Набор наблюдений делится на четыре равные части по формуле квартилей. Первый квартиль расположен между первым членом и медианой. Медиана представляет второй квартиль. Третий квартиль — это значение, которое находится между медианой и последним членом.
Как мы используем квартиль?
Квартили часто используются в данных о продажах и опросах для классификации населения. Например, КВАРТИЛЬ можно использовать для определения 25% самых высоких доходов населения.
Заключение
Теперь вы можете понять все основные понятия, связанные с квартилем, просто прочитав эту статью. В этом руководстве подробно и последовательно объясняется цель и все, что вам нужно знать о квартиле, включая пример и способ его расчета. Пожалуйста, оставьте вопрос в разделе комментариев, если вам нужна дополнительная помощь.
Статьи по теме
- СРЕДНЯЯ СТОИМОСТЬ СТРАХОВАНИЯ ДОМА: лучшие практики и тарифы Великобритании на 2023 год (обновлено)
- Список компаний на триллион долларов 2019/2020
- 5 кредитных историй: почему они важны? (+ Подробное руководство для начинающих)
- YOY: годовой анализ, расчеты роста и инвестиций, формулы и примеры
- СКОЛЬКО СТОИТ ДОМ В США В 2023 ГОДУ.
- САМООЦЕНКА: Подробное объяснение и все, что вы должны знать
Рекомендации
- scribbr
- Финансовая
- р-блогеры
- В самом деле



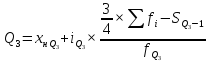


 ,
, ,
,






 ,
, ,
, 7×
7×








