Как найти легкие примеры

Не все обладают хорошими знаниями по математике, но всем нужно сдать экзамен. Поэтому нужно тренироваться на лёгких вариантах.

И так, чтобы получить 3 нужно набрать 8 баллов. 2 по геометрии и 6 по алгебре.

Алгебра

1. 1 задание. Оно самое лёгкое из первых пяти

2. 6 задание. Решить пример уровня 7-го класса.

3.8 задание. Пример со степенями. Задание 8-го класса.

4. 9 задание. Уравнение 8-го класса.

5.10 задание. Вероятность

6.12 задание. Прогрессия. Формулы для вычислений даны в справочных материалах.

7. 13 задание. Сократить и подсчитать, можно без сокращения, для тех, кто не помнит ни одной формулы сокращённого умножения.

8. 14 задание. Подставить числа, вместо букв и подсчитать

Геометрия

1. 16 задание. 8 класс

2. 19 задание. На клеточном поле.

3. 20 задание. Какое из утверждений верное. Его можно решить методом исключения

Удачи вам. Возможно, в скором времени выпущу такое про русский язык.

Примеры на сложение и вычитание — простейшие операции, с которых начинается знакомство детей с математикой. Чтобы щелкать арифметические задачи как орешки, нужно практиковаться как можно чаще. Предлагаем вашему вниманию примеры, которые помогут ребенку «набить руку» — от совсем легких к более сложным.

Примеры на сложение и вычитание для дошкольников

Данные примеры в одно и два действия могут осилить дошкольники. Важно, чтобы ребенок запомнил правило: от перемены мест слагаемых сумма не меняется.

Сложение и вычитание до 5

Сложение и вычитание до 10

Вставь пропущенные знаки

От ребенка требуется понять, какой знак («+» или «–») должен стоять на месте пустой клетки, чтобы получилось верное равенство. Если ответ не кажется очевидным сразу, малыш решает в уме два примера, подставив как плюс, так и минус.

Эти задания подойдут для дошкольников, освоивших устный счет в пределах 10.

Что нужно сделать с цифрами 3 и 4, чтобы получить 7? Очевидно, сложить (если вычесть 4 из 3, получится отрицательное число, а это понятие ребенку-дошкольнику и ученику первых классов пока не известно).

А что нужно сделать с 9 и 4, чтобы вышло 5? Не сложить: 9 + 4 = 13. Зато 9 — 4 = 5.

По тому же принципу решаются остальные примеры.

Если складывать и вычитать числа до 10 умеет большинство дошколят, то примеры на сложение и вычитание в пределах 20, с переходом через разряд, предлагают уже ученикам первого класса. Переход через разряд происходит, когда в одном равенстве смешиваются однозначные и двузначные числа: например, при сложении двух цифр мы получаем двузначное число (5 + 7 = 12), при вычитании из двузначного числа — однозначное.

Вот несколько упражнений:

Сложение и вычитание в пределах 20

Подставь пропущенное число

Это, по сути, завуалированные уравнения в одно действие. Для их решения ребенок должен уметь оперировать двузначными числами, знать такие понятия, как слагаемые, уменьшаемое, вычитаемое, разность и сумма, и понимать принципы решения уравнений со сложением и вычитанием.

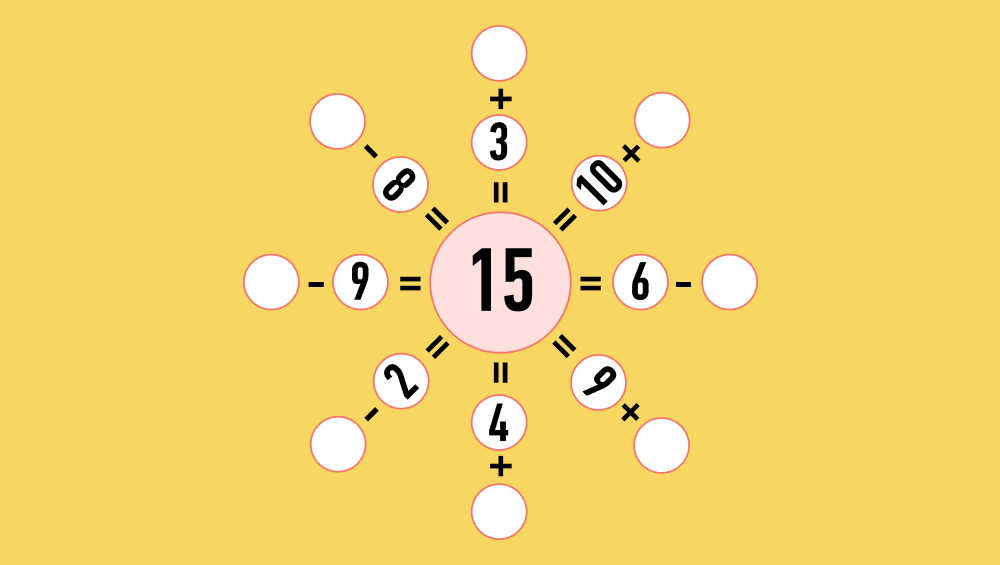
В центре — число 15, которое должно получиться в результате всех предложенных равенств. Число, от которого нужно отнять 8, чтобы получить 15, получаем, прибавив 8 к 15. Уменьшаемое равно 23.

3 + х (пропущенное число в равенстве) = 15. Отнимаем от суммы одно слагаемое, чтобы получить второе: 15 — 3 = 12.

Подставьте числа, чтобы получились верные равенства

Здесь от ребенка также требуется уметь складывать и вычитать в пределах 20. Придется последовательно решить в уме несколько примеров, чтобы найти верную комбинацию чисел.

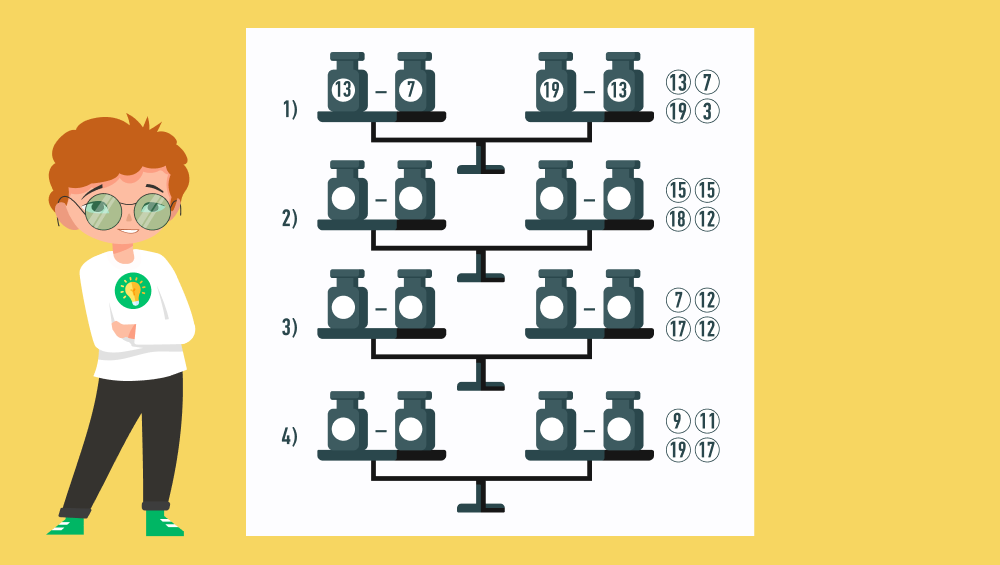
Итак, нам даны четыре числа: 12, 18 и 15 (дважды). С их помощью, выполняя вычитание, нужно получить два одинаковых числа — слева и справа. Наблюдательный ученик быстро заметит, что 18 — 15 = 15 — 12 (= 3). В данном случае уменьшаемые и вычитаемые располагаются друг от друга крест-накрест.

Что нужно сделать с числами 7, 17 и 12 (дважды), чтобы получить верное неравенство? Опять же путем нехитрой подстановки вычисляем: 17 — 12 = 12 — 7 = 5.

По той же схеме решаем последний пример: 19 — 11 = 17 — 9 = 8.

Задачи на сложение и вычитание до 20

Чтобы ребенок не заскучал за примерами, можно «упаковать» их в занимательные математические игры или задачи с интересными условиями. Представляем три примера заданий на сложение и вычитание в пределах 20:

1. Мама приготовила 16 пирожков с мясом на всю семью и накрыла на стол. Невоспитанный, но ловкий котенок Степа сумел утащить два пирожка. Сколько пирожков осталось на столе?
2. У Маши было 16 книг. В день ее рождения родственники преподнесли ей еще 2. Так совпало, что еще 1 книгу подарили ей одноклассники. Сколько книг оказалось у Маши?
3. В январе было 10 праздничных дней и еще 6 выходных, когда Коля не ходил в школу. Из всех своих свободных январских дней мальчик провел 5 у бабушки, 1 — в большом семейном кругу и еще 1 — в гостях у друга, в остальные был с родителями. Сколько свободных дней за месяц мальчик провел с мамой и папой?

Примеры на сложение и вычитание для 2 класса

Эти задания — уже для второклассников, которые полностью освоили сложение и вычитание двузначных чисел, умеют выполнять арифметические операции как в уме, так и в столбик.

Сложение двузначных чисел

Вычитание двузначных чисел

Задачи на сложение и вычитание в пределах 100

1. Оля весит 30 килограммов, а ее маленькая сестра — всего 12. На сколько килограммов старшая сестра тяжелее младшей?
2. Между третьим и вторым этажом Мишиного дома — 11 ступенек, столько же — между вторым и первым. А на первом этаже всего 4 ступеньки до выхода из подъезда. Сколько ступенек приходится преодолеть Мише по пути на улицу, если он живет на третьем этаже?
3. У Анны Сергеевны 28 дней оплачиваемого отпуска в год. Весной она уже брала отпуск на 10 дней. Летом семья предложила ей уехать на две недели на море. Хватит ли Анне Сергеевне отпуска, чтобы отправиться на морской курорт? Останется ли у нее еще несколько дней отпуска?

Примеры на сложение и вычитание для 3 класса

С такими примерами легко справятся ученики третьего класса. Многие из примеров на трехзначные числа уже сложно решить в уме — у ребенка должен сформироваться навык арифметического подсчета в столбик. Впрочем, если он способен справляться со сложением и вычитанием длинных чисел в уме, это большой плюс.

Сложение трехзначных чисел

Вычитание трехзначных чисел

Задачи на сложение и вычитание в пределах 1000

1. Ира пришла в продуктовый магазин. Она решила купить плавленый сыр за 200 рублей, масло за 120 рублей и хлеб за 53 рубля. Сколько денег потратит Ира?
2. За три предновогодних дня в супермаркете раскупили 745 килограммов мандаринов. В первый день купили 143 килограмма, во второй — еще 211. Сколько килограммов мандаринов купили в последний предновогодний день?
3. В юности Денис любил покупать журналы. Его любимый журнал об автомобилях стоил 187 рублей, однако с тех пор он подорожал на 83 рубля. А журнал о звездах стоил 94 рубля, теперь же — на 43 рубля дороже. Сколько денег придется заплатить Денису сейчас, если он решит по старой памяти купить оба журнала?

Примеры на сложение и вычитание для 4 класса

Ученику четвертого класса уже вполне по силам примеры и задачи, требующие сложения и вычитания чисел в пределах 10 000. Упражнения для практики:

Сложение до 10 000

Вычитание до 10 000

Задачи на сложение и вычитание в пределах 10 000

1. Платье в бутике стоило 2000 рублей, но в честь праздника на него сделали скидку. Теперь оно подешевело на 238 рублей. Сколько теперь стоит платье?
2. Прабабушка Светы — долгожительница. Она родилась в далеком 1916 году. Сколько ей лет, если сейчас 2020-й?
3. Семья из двух человек съездила в тур выходного дня за 5800 рублей. В эту сумму входили транспортные расходы, расходы на питание и экскурсии. Транспортные расходы семьи составили 2200 рублей, на питание ушло еще 1700. Сколько денег ушло на экскурсии?

Математика — это не только решение примеров и уравнений, но и развитие логического мышления, умения работать с информацией, анализировать, отделять главное от второстепенного, выстраивать причинно-следственные связи и принимать верные решения. Умназия предлагает большое количество математических задач на логику и смекалку в сюжетном игровом формате с приятной озвучкой и красочными иллюстрациями:

• Задачи по математике для 1 класса
• Задачи по математике для 2 класса
• Задачи по математике для 3 класса
• Задачи по математике для 4 класса
• Задачи по математике для 5 класса

Шаг за шагом: как решить легкие примеры алгебры восьмого класса

Алгебра является одним из важнейших разделов математики, который изучается на протяжении всего среднего образования. Однако, для многих учеников решение примеров в алгебре может быть сложным и запутанным делом. Чтобы решить примеры алгебры восьмого класса без проблем, необходимо следовать нескольким простым шагам.

Шаг 1: Понимание основных понятий

Перед тем как решать примеры в алгебре, нужно понимать основные понятия, такие как переменные, уравнения, коэффициенты, степени и т.д. Если вы забыли какое-то понятие, обратитесь к учебнику или задайте вопрос вашему учителю.

Шаг 2: Преобразование выражений

Часто в алгебре нужно переставлять части уравнения или выражения, чтобы подойти к правильному ответу. Нужно уметь раскрывать скобки, сокращать и раскрывать дроби, выносить общие множители и т.д.

Шаг 3: Решение уравнений

Чтобы решить уравнение, нужно выразить переменную и узнать её значение. Для этого находят общий знаменатель и объединяют слагаемые. Далее переменная переносится в одну сторону уравнения, а все остальные слагаемые в другую.

Шаг 4: Проверка решения

После того, как вы нашли ответ на пример, не забудьте проверить его. Для этого нужно подставить найденное значение переменной в исходное уравнение и убедиться, что его правая часть совпадает с левой.

Шаг 5: Практика

Как и любой другой навык, решение примеров алгебры требует практики. Старайтесь решать как можно больше примеров, чтобы закрепить знания и умения.

Вывод

Как видно, решение примеров в алгебре не является сложным процессом, если следовать нескольким простым шагам. Главное – регулярная практика и понимание основных понятий.

Сложные примеры – легкие решения

• Авторы
• Руководители
• Файлы работы
• Презентация
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

ВВЕДЕНИЕ

Тема моей научно-практической работы – «Сложные примеры – легкие решения». Я выбрала эту тему для своей работы, так как для меня очень интересна и увлекательна математика. Чем дольше я учусь в школе и чем больше изучаю математику, тем чаще задаюсь вопросом: «Как можно решать такие сложные задачи и примеры быстро и, не прибегая к помощи калькулятора или компьютера». Интерес к этим вопросам побудил меня искать информацию в интернете, читать статьи и книги с этим связанные, спрашивать своих одноклассников и друзей, что они используют, чтобы облегчить себе изучение математики. Оказалось, что существует масса приемов устного счета, зная которые можно очень быстро считать в уме. Владение такими приемами не только облегчает изучение математики, но и значительно помогает в простой жизни. Мне захотелось поделиться со всеми найденной информацией, но для того, чтоб все легко запомнилось, появилась идея изложить в стихах алгоритмы решения примеров.

Цель моей работы – разработать свое пособие-напоминание, в котором изложены основные алгоритмы решения примеров на умножение и деление двузначных и трехзначных чисел. Это пособие выполнить в виде брошюры с примерами, объяснениями решений в стихах, которые я сочинила сама и иллюстрациями.

Моя гипотеза – с помощью моего пособия дети проявят большой интерес к математике, научатся быстро решать в уме сложные примеры, в том числе благодаря стихотворной форме изложения алгоритма.

Задачи моей работы:

Ознакомиться с алгоритмами решений сложных математических решений в уме.

Выяснить, что знают мои одноклассники о таких приемах.

Сочинить стих – объяснение про каждый пример, используемый в моем пособии.

Составить пособие и распечатать его в виде брошюры.

2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Каждый день каждый человек десятки, а то и сотни раз сталкивается с математикой. Начиная с момента пробуждения, мы весь день применяем в жизни наши математические навыки, иногда не замечая этого (как для приготовления завтрака и измерения пропорций), а иногда (как в магазине, например) вполне осознанно.

Чтобы что-то посчитать, человек применяет свои вычислительные навыки. И навыки эти нужно развивать. А развить их может каждый человек, независимо от его феноменальных математических способностей, хотя бы для того, чтобы не стать жертвой обмана в магазине или на рынке.

Развивать их можно, в том числе и с помощью применения различных техник и приемов устного счета. С давних времен люди изобретали или находили все новые такие приемы.

Когда я начала изучать этот вопрос, поняла, что мало знать о таких методах, их надо разобрать, запомнить, и тогда ты сможешь их активно применять в жизни. Разбираться с приемами устного счета оказалось не так уж сложно. Но вот запомнить столько различных задач сразу не удалось.

Так мне пришло в голову, что наиболее понравившиеся мне методы нужно зарифмовать. Ведь стихи запоминаются всегда лучше прозы. Пока я сочиняла стихи, все, используемые мной для работы математические примеры запомнились сами собой. Тогда и возникла идея поделиться своими стихами со своими друзьями, чтобы они тоже смогли легко запомнить алгоритмы решения сложных примеров.

Вас может удивит, но такая смесь математики и литературы дала очень хорошие результаты.

В ходе работы над своим проектом я ознакомилась со множеством подобных работ других учеников и пришла к выводу, что во всех случаях, когда ученики целенаправленно в счете использовали общеизвестные алгоритмы устного счета, скорость вычислений значительно увеличивалась, иногда даже в два раза. В просмотренных мною работах приводились таблицы с результатами таких экспериментов. Поэтому, я не стала доказывать в своей работе результативность применения различных методов устного счета. Это факт общепризнанный.

Моей задачей стало облегчить сам способ запоминания этих методов. Поскольку я очень люблю стихи и в повседневной жизни часто что-нибудь рифмую, выбор способа запоминания стал очевиден.

Вот что у меня получилось.

ПРАКТИЧЕСКАЯ ЧАСТЬ

3.1 Умножение на 11 числа, сумма цифр которого не превышает 10.

Надо мысленно раздвинуть цифры этого числа и поставить между ними сумму этих цифр.

63 х 11 = 693

26 х 11 = 286

Сложи числа две половинки

Помести их в серединку

3.2 Умножение на 11 числа, сумма цифр которого больше или равна 10.

Надо мысленно раздвинуть цифры этого числа и поставить между ними сумму этих цифр. Единицы числа записываем в середину, а десяток прибавляем к первой цифре.

78 х 11 = 858

64 х 11 = 704

Сложи числа две половинки

Помести их в серединку.

Про десяток не забудь,

Прибавь к началу, Умным будь!

3.3 Умножение на 111 (если сумма чисел множимого меньше 10).

Также мысленно раздвигаем цифры этого числа, находим сумму цифр данного двузначного числа и ставим ее в середину дважды.

36 х 111 = 3996

3 + 6 = 9

42 х 111 = 4662

4 + 2 = 6

Опять сложи две половинки

Помести их в серединку.

Только дважды повтори,

Так как единицы три.

3.4 Умножение на 111 (если сумма чисел множимого больше 10).

Опять мысленно раздвигаем это число, складываем цифры и вставляем их в середину числа. Но поскольку сумма цифр составляет двузначное число, прибавляем его к первым цифрам.

76 х 111 = 8436

(7+6=13)

7136

13

8436

И вновь сложи две половинки

Снова вставь их в серединку

Ну, а так как число двузначное

нужно вставить в ответ два раза

Мы прибавим его однозначно

К первым цифрам. И без отказа!

3.5 Умножение на 25.

Чтобы умножить число на 25 , надо данное число (36) умножить на 100 и произведение разделить на 4:

37 х 25 = 900

(37 х 100) : 4 = 925

Если множимое делится на 4, то сначала можно разделить множимое на 4 и полученное частное умножить на а 100.

48 х 25 = 1200

(48 : 4) х 100 = 1200

При умножении на двадцать пять

Число на сто нам надо умножать,

Потом разделим на четыре,

Вот и ответ мы получили

3.6 Деление на 25.

Чтобы разделить число на 25, надо разделить его на 100 (если делится на 100) и полученное частное умножить на 4, или сначала делимое умножить на 4, а потом полученное произведение разделить на 100:

800 : 25 = (800 : 100) х 4 = 32

225 : 25 = (225 х 4) : 100 = 9

Сделаем наоборот от предыдущего примера

При делении на двадцать пять

Число на сто нам нужно разделять

Потом уже умножим на четыре

Вот снова и ответ мы получили

А если разделить на сто нельзя

То мы пойдем другим путем, друзья

Сначала на четыре мы умножим

Потом на сто поделим и отложим.

3.7 Умножение чисел от 11 до 19.

Умножать такие числа можно используя следующую формулу, которую стоит запомнить.

100 + 10 х (а + в) + а х в

Где а и в это единицы множителей

Формула только на первый взгляд кажется сложной

Любое число из диапазона от 11 до 19 представляем как десятки и единицы.

Получаем формулу: (10+a)×(10+b).

Раскрываем скобки: 100+10×b+10×a+a×b.

Выносим за скобки общий множитель и получаем окончательную формулу, по которой можно считать и которую есть смысл запомнить: 100+10×(a+b)+a×b.

14 х 18 = 252

100 + 10 х (4 + 8) + 4 х 8 =

= 100 + 120 + 32 = 252

Чтобы перемножить два числа

Между десятью и двадцатью

Единицы перемножь сперва

И запомни как свою семью.

А еще сложи их и умножь

На десятку. Это тоже впрок.

Вот теперь сложи все результаты

И еще плюс сто. И весь урок.

3.8 Старинный русский способ умножения.

Умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа.

32 х 13

16 х 26

8 х 52

4 х 104

2 х 208

1 х 416

32 х 13 = 416

Произведение не изменяется, если один множитель вдвое увеличить, а другой вдвое уменьшить.

Первое число дели на два,

Второе же, напротив, умножай.

Дели до единицы и тогда

Записывай ответ и отдыхай!

Произведение не изменяется, если один множитель вдвое увеличить, а другой вдвое уменьшить.

Немного усложняется, если делимое нечётное число, то нужно откинуть единицу и делить остаток пополам, но в результате прибавить все те числа, которые стоят напротив нечётных чисел левого столбца.

19 х 17

((19-1):2) = 9 х 34

((9-1):2) = 4 х 68

2 х 136

1 х 272

19 х 17 = 272 + 17 + 34 = 323

А если разделить на 2 нельзя,

То просто единицу убирай

Все делать точно так же продолжай

А то, что не делил – к ответу прибавляй

3.9 Умножение двузначных чисел на 9, 99, 999.

К первому множителю приписать столько нулей, сколько девяток во втором множителе, и из результата вычесть первый множитель.

28 х 9 = 280 – 28 = 152.

18 х 99 = 1800 – 18 = 1782.

23 х 999 = 23000 – 23=22977.

Так как 10а-а=9а, то для умножения числа а на 9 достаточно от увеличенного в 10 раз числа а отнять само число. Аналогично умножение на 99 и на 999. Число а умножают на 100 и на 1000 и отнимают само число.

Сколько девяток – столько нулей

Пусть даже три, ты не робей

Смело нули к числу припиши,

Ну, а потом, число отними.

3.10 Умножение трёхзначного числа на 999.

Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа. Тогда получается шестизначное произведение: первые три цифры есть умножаемое число, только на уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9.

385 х 999 = 384615

Но в принципе, здесь работает тот же принцип, что и в предыдущем примере.

385 х 999 = 385000 – 385 = 384615

Даже, если множитель трехзначный

Три нуля к нему прибавить можно

И само число из цифры этой

Вычесть для тебя совсем не сложно.

3.11 Умножение чисел от 91 до 99 друг на друга.

Первый множитель вычесть из 100, второй множитель вычесть из 100, результаты сложить. Сумму вычесть из 100 и записать ответ первыми цифрами ответа. Далее перемножить ответы и записать следующими цифрами ответа.

97 х 96 = 9312

100 – 97 = 3, 100 – 94 = 4.

4 + 3 = 7, 100 – 7 = 93, 4 х 3 = 12.

Из ста вычесть и второй и первый

Все сложить, поверьте, это верно.

Результат опять от ста отнимем

И началом для ответа примем.

А в конец ответа – очень просто,

Перемножим отнятое от ста.

3.12 Умножение трёхзначных чисел от 101 до 109.

Если к одному из чисел прибавить единицы второго числа, то это

будут первые цифры ответа, затем перемножить единицы – это будут

последние цифры ответа.

105 х 107=11235.

105 + 7 = 112, 5 х 7 = 35.

Целое число плюс единицы

И отправим их за знак «равно»

Только единицы перемножим

И поставим рядом заодно.

3.13 Умножение двузначного числа на 101.

Самое простое правило: припишите число к самому себе.

57 х 101 = 5757

На сто один умножить просто

Число ставь рядом как по росту.

3.14 Применение моего пособия.

Стихи получились не сложными и легкими в запоминании. Я раздала своим одноклассникам брошюры, в которых объясняются сами методы устного счета и рядом располагаются стихи для запоминания метода.

Спустя месяц, я провела исследование способом анкетирования и получила такие результаты. Из 29 опрошенных 20 человек сказали, что мои стихи им очень помогли в запоминании способов быстрого счета.

ЗАКЛЮЧЕНИЕ

В заключение я бы хотела сказать, что выбранная мной тема мне очень понравилась, мне было очень интересно искать разные возможности облегчения устного счета. Оказалось очень интересно и захватывающе самой разбираться в примерах, проверять и перепроверять работает ли алгоритм, сочинять стихи и разрабатывать свое пособие, а потом раздать его друзьям.

В ходе работы над проектом мне удалось кратко познакомиться с историей появления различных приемов устного счета и узнать, как человечество развивалось в этом направлении.

Цель моей работы было создание своего пособия по запоминанию некоторых методов устного счета. Указанное пособие основано на стихах про математические примеры, которые я сочинила сама. Цель моей работы достигнута.

После знакомства с моей брошюрой, ребята стали интересоваться математикой и, в частности, исследованием алгоритмов устного счета. А это, в свою очередь, развивает память, мышление, другие умственные способности, приучает к поиску решений в любых жизненных ситуациях. Таким образом, казалось бы простая тема получила большой отклик у моих одноклассников и все получили новые знания.

СПИСОК ЛИТЕРАТУРЫ

Арутюнян Е., Левитас Г. “Занимательная математика” -М.:АСТ-пресс,1999г.

Владимиров, А. И. Интересные способы быстрого счета / А. И. Владимиров, В. В. Михайлова, С. П. Шмелева. — Текст : непосредственный // Юный ученый. — 2016. — № 6.1 (9.1). — С. 15-17. — URL: https://moluch.ru/young/archive/9/633/ (дата обращения: 27.10.2020).

Гарднер М.  “Математические чудеса и тайны.”  М. 1978.

ГлейзерГ.И.” История математики в школе.” – М,1981.

“Библиотечка Первого сентября»,серия «Математика».Вып.3(15).  http//portfolio 1 September ru/subjest

ПРИЛОЖЕНИЕ

Просмотров работы: 2326

1000 примеров на сложение и вычитание в пределах 10

Математика для 1 класса. Распечатать карточки сложение и вычитание в пределах 10.

Как распечатать карточки.

наводим курсор на картинку, нажимаем левую кнопку мышки, картинка откроется в новом окне, нажимаем правую кнопку мышки, далее Вы можете выбрать:

• «Сохранить как…»
• «Копировать»
• либо сразу «Печать».

Рекомендуем сохранять изображение, так с ним легче работать при печати.

Не забудьте добавить в закладки

Таблица сложения до 10 распечатать

Примеры на сложение и вычитание в пределах 10 распечатать

Что бы поощрить ребенка, предложите ему математические раскраски:

Источник

Быстрое обучение детей счету примеров в пределах 10 и 20

Обучение будущего школьника счету в пределах 10 – это первый шаг к устному счету. Важно, чтобы ребенок запомнил процессы всех вычислений, как делают это старшие. Второй этап состоит из осваивания основных методов вычисления. Преимуществом здесь уже становится не произвольное получение из воспоминаний готовых ответов, а осознание и заучивание способов сложения и вычитания в цифрах. Как научить ребенка считать примеры в пределах 10, какие игровые приемы можно использовать для лучшего усвоения?

Учимся решать примеры до 10

Для того чтобы выучиться верно и мгновенно считать, нужно постоянно решать примеры. Для высчитывания и запоминания на начальных этапах следует сделать акцент на мышлении ребенка на основе наглядных образов. Здесь возникает проблема: дети часто не воспринимают математические понятия. Решением станут практические действия с жизненными примерами.

Учителя используют три основных метода для обучения счету:

1. На принципе знания числового состава
2. Запоминать наизусть таблицы действий, включая деление и умножение.
3. Использовать спец.приемы для получения результата.

Рассмотрим все методики по порядку.

Примеры на вычитание с картинками

Принцип знания состава

Подготовка должна начинаться с изучения азов математики. Рассказывая ребенку, нужно объяснять, что каждое число это группа с заданным количеством элементов.

Состав числа для запоминания

Важно! Мало сосчитать до пяти. Убедитесь, что вы предлагаете показать пять пальцев, положить на стол пять конфет или изобразить на листке пять кругов.

Необходимо связать число и сказочных героев или другие знакомые для ученика предметы:

1. Одна репка.
2. Две стороны у монетки.
3. Три медведя.
4. Четыре стороны света.
5. Пять пальцев на ручке малыша.

Ребенка важно приучать к картинке, соединенной со всеми элементами. Необходимо играть в математическое домино. Для этого нужно взять десять кубиков с размером ребра 1,5-2 см, стоящих в коробке. Подойдут и детали конструктора Лего. Если нет подходящих предметов, то можно распечатать другие пособия.

Исходя из знания состава, ребенок может решить, складывать ему или вычитать. Например, чтобы ответить, сколько будет «шесть плюс три», он должен знать, что 6 и 3 равняются 9. А «семь минус два» получится пять, потому что 7 это 2 и 5.

Пособие для изучения состава

Запоминания таблиц наизусть

Есть большое количество приемов приучить ребенка сразу запомнить таблицы. Почти половина примеров на сложение и вычитание бессознательно заучиваются детьми по окончании ознакомления с законом перемещения.

Можно брать стихи, подпевки. Самым популярным образцом служит строка песни «Дважды два четыре, это всем известно в целом мире». Отличную информацию находят, познакомившись с методикой Николая Зайцева, программой «Песнезнайка».

Для закрепления знания табличных данных, можно предложить детям работать с:

• раскрасками;
• компьютерными играми по математике;
• мультимедийными презентациями.

Умение прибавлять в тестах со звездочкой поможет потом учить сложный материал.

Использование вычислительных приемов

Наивысший уровень результата устного счета – это способность нахождения самого быстрого и удобного метода для подсчета итога. Так, например, одним из легких способов обучить школьника считать на занятиях является техника присчитывания и «перепрыгивания». Дети быстро усваивают, что при добавлении 1 получается последующее значение, а при уменьшении на 1 получается предыдущее. После этого можно узнать о лучшем напарнике числа 2 – кузнечике, который умеет перескочить цифру и вызвать результат сложения или вычитания 2.

Как объяснить связь сложения и вычитания

Для лучшего восприятия следует научить малыша составу. Методика заключается в трех шагах:

1. На привычных предметах усвоить, что одно из слагаемых может меняться в сторону уменьшения, другое возрасти при одинаковой сумме. Удачным пособием станут упаковки для яиц (по 10); боксы для печенья (по 6,8 или 12), календарные дни (по 7).
2. Следует проследить, чтобы ребенок сделал записи в тетради по возможным комбинациям числительных.
3. Вместе с учеником подготовить карточки с надписями: 6 + 3 = 9; 4 + 5 = 9; 2 + 7 = 9; 1 + 8 = 9. Лучше распределить каждый пример на отдельную карточку.

Теперь нужно приложить усилия к запоминанию. Ребенок должен наизусть, не считая, запомнить все возможные комбинации слагаемых, дающих одну сумму. Не нужны длинные занятия. Успех придет быстрее, когда урок на запоминание будет быстрым, как перерыв между лепкой или рисованием.

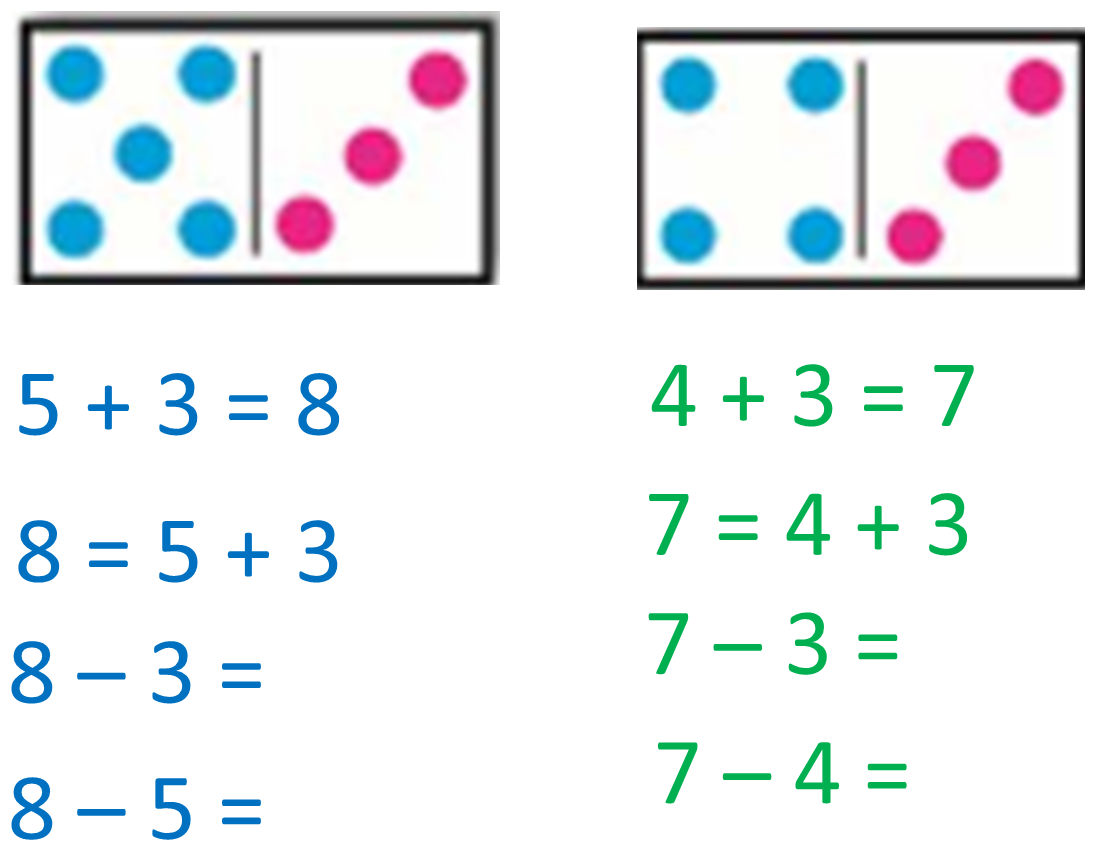
Связь между сложением и вычитанием

Если ребенок все запомнил и не пытается «посчитать», можно приступать к следующему шагу. При замене знакомых карточек новыми, малыш должен писать сразу ответы. Приступаем к самому сложному – вычитать, используя знание составляющих. Вначале необходимо повторить карточки с действиями. Потом нужно спросить у ребенка, что будет с результатом, если убрать одно из слагаемых.

Данная цепочка поможет оценить связь сложения с вычитанием методом запоминания. Ученик должен понять, что вспомнить знакомое сочетание легче, чем считать в уме. В дальнейшем принцип поможет легче освоить решение линейных уравнений.

Когда можно решать примеры в пределах 20

При полном усвоении навыков счета до 10 рекомендуют приступить к действиям на втором десятке. Здесь необходимо только понимание, без подсказки и списывания у соседа. Как научить считать и разъяснять примеры ребенку в пределах 20? Следует придерживаться пошаговой методики:

1. Выучить порядковый счет второго десятка, очередность каждого элемента числового ряда. Для облегчения запоминания используют одинаковые предметы – карточки, кубики. Нанести числа только на первые десять единиц. Разложить их рядами, первый десяток с подписями, под ним второй, «слепой».
2. Запоминать по схеме 14 – к слову четыре добавляется «– надцать», и так с каждым новым термином. Ребенок должен усвоить смысл названия порядковых чисел от 11 до двадцати.
3. Приступить к понятию первый десяток, потом добавлять элементы второго ряда и проговаривать действия. «Десять плюс четыре получится четырнадцать». Должны прозвучать так все данные в интервале второго десятка.
4. Отработать действия со сложением без перехода. По типу 10 + 6 = 16; 16 – 6 = 10. Когда этот этап освоен, выполняют действия повышенной сложности.

Пазлы для счета до 20

Примеры с переходом через десяток требуют развивать навыки устного счета. Знание состава числа при равной сумме облегчают запоминание алгоритма расчета по действиям на сложение и вычитание в пределах 100.

Как научить решать примеры в уме?

Для облегчения устного счета эффективны упражнения для ежедневной тренировки. К шести годам детвора может самостоятельно сосчитать количество конфет, кубиков или мячиков. Им не нужно использовать свои пальчики. Родителям необходимо вовремя подсказать, направить малыша для формирования навыков решения примеров в уме. Ребенок должен освоить:

• простейший счет;
• сумму и разность;
• различие между «большим» или «меньшим» значением.

Визуальное восприятие счета – решение в столбик поможет быстрее научиться считать устно. Педагоги начального обучения рекомендуют начинать с простого. Сосчитать количество фруктов, от ребенка нужно услышать итоговый ответ, без проговаривания последовательных цифр числового ряда.

Несколько уроков, и малыш поймет, что можно сразу называть сумму. Для усложнения спрашивают, а если добавить еще три груши, сколько всего будет фруктов. «Добавки» не должно быть перед глазами. Юному счетоводу придется представить в уме и дать правильный ответ.

Прибавляем в уме

Следует устно повторять примеры на состав, учитывая все возможные двузначные пары. Для облегчения задачи можно применить карточки, затем полностью отказаться от них, перейдя целиком на устный счет. Все задания легче выполнять в течение дня, чтобы освоить быстрее счет:

• Во время прогулки повторить с ребенком список планируемых покупок. После расчета у кассы малыш должен перечислить все товары. Если список не полный, малыш должен правильно назвать продукты или предметы для дальнейшего шопинга.
• Номерные знаки на машинах послужат разминкой для сложения или вычитания на улице. Различные сочетания цифр помогают быстрее научиться считать. Если впереди машина с трехзначным номером, можно сложить все составляющие. Затем отнимать из самого большого значения наименьшее.
• В учебных материалах опубликованы задачки для дошкольников. Они сопровождаются рисунками, четверостишьями, чтобы добавить игровую изюминку к «сухой» математике.

Важно! Каждый ребенок имеет особенности развития, одному будет легче усвоить материал, другой может схватывать на лету. Нужно грамотно направлять и помогать изучать азы математики.

Дети тренируются в устном счете

Интересные способы научить прибавлять и отнимать

Ребенок должен запомнить многие числовые комбинации. Чтобы помочь лучше понять этот материал, рекомендуется предложить ему следующие задачи:

• Рассортировать данное количество объектов в три тарелки, создав разные комбинации (варианты разные: повесить игрушки на две елки, расставить цветы в двух вазах, разместить гномов в двух домах);
• дополнить число до желаемого;
• заполнить ячейки, в которых записан состав с присвоенным номером;
• дорисовать домино.

Поможет усвоить устный счет игра в интервал между значениями. Мама говорит, что загадала определенное число в промежутке от 5 до 18. Ребенок должен угадать, если он ошибается, взрослый определяет место в ряду, регулируя поиски словами «больше», «меньше», «добавь один», «отними два».

Ребенку будет сложно понять на уроках математику в первом классе, если он не усвоил технику счета. Терпение, игровые методы, непринужденность и регулярность упражнений это необходимые условия для успешного обучения. Даже одна десятая материала, усвоенного ребенком самостоятельно, поможет освоить школьную программу.

Источник