Определение правой и левой тройки векторов
Вы будете перенаправлены на Автор24
Понятие тройки векторов
Из курса физики известно, что скалярные величины или скаляры – это величины, вполне определяемые одним численным значением (например, масса, температура, объём, расстояние и пр.). То есть любое вещественное число является скаляром.
Векторные величины или векторы – это величины, которые определяют и численным значением, и направлением. Например, скорость.
Линейно зависимыми называются такие векторы $a,b,c. $, что если подобрать такие числа $x,y,z. $, из которых по крайней мере одно не равно $0$, то будет иметь место тождество $xa+yb+zc+. =0$. Если три вектора $a,b,c$ не равны $0$ и линейно зависимы, то они компланарны.
Связка трёх векторов – это приведённая к общему началу тройка некомпланарных векторов $a,b,c$.
Определение правой и левой тройки векторов
Приведём чертёж правой связки.
Рисунок 1. Чертёж правой связки. Автор24 — интернет-биржа студенческих работ
Рассмотрим кратчайшее вращение $vec=a$ к $vec=b$ на плоскости $OAB$ со стороны направления $vec=c$. Мы увидим, что вращение идёт против часовой стрелки.
Если большой палец и указательный пальцы левой руки вытянуть, а средний согнуть под углом ладони, то три пальца в порядке большой-указательный-средний составят правую связку. Те же пальцы на левой руке составят левую связку.
На чертеже левой связки то же вращение идёт по часовой стрелке.
Рисунок 2. Чертеж левой связки. Автор24 — интернет-биржа студенческих работ
Готовые работы на аналогичную тему
Способы преобразования правой связки в левую и обратно:
- перестановка местами двух любых векторов;
- изменение знака при одном из векторов;
- замена какого-нибудь вектора его зеркальным отображением относительно плоскости двух других векторов.
Правая и левая системы координат
Напомним, что координатная ось – это ось, на которой выбрано начало и единица масштаба.
Ортогональная или прямоугольная система координат в пространстве – это система из трёх взаимно перпендикулярных координатных осей $Ox, Oy$ и $Oz$ с общим началом $O$. Ортами в ортогональной системе координат называют единичные векторы (то есть векторы равные $1$).
Рассмотрим чертёж ортогональной системы координат в пространстве. Отметим на ней орты $i, j, k$.
Рисунок 3. Чертёж ортогональной системы координат в пространстве. Автор24 — интернет-биржа студенческих работ
$i, j, k$ образуют правую связку. Система координат в данном случае называется правой.
Система координат называется левой, когда орты образуют левую связку. То есть:
Рисунок 4. Левая система координат. Автор24 — интернет-биржа студенческих работ
Подведём итог. В статье мы дали определение связки тройки векторов, описали правую и левую тройку векторов, а также правую и левую систему координат, как вытекающую тему из определения правой и левой тройки векторов. Стоит сказать, что на практике определение правой и левой тройки векторов со временем происходит интуитивно или “на автомате”. Самое важное, это один раз понять, как это делается. Также стоит заметить, что чаще в задачах используется всё-таки правая тройка векторов и соответственно правая система координат.
Правая и левая тройки векторов
Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.
Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
любую работу
Все еще сложно?
Наши эксперты помогут разобраться
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
Векторное произведение векторов
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
Сочетательное свойство
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/formules_4_4.php
http://skysmart.ru/articles/mathematic/vektornoe-proizvedenie-vektorov
[/spoiler]
Векторное произведение в трёхмерном евклидовом пространстве
Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого численно равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой[⇨]. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.
Таким образом, для определения векторного произведения двух векторов необходимо задать ориентацию пространства, то есть сказать, какая тройка векторов является правой, а какая — левой. При этом не является обязательным задание в рассматриваемом пространстве какой-либо системы координат. В частности, при заданной ориентации пространства результат векторного произведения не зависит от того, является ли рассматриваемая система координат правой или левой. При этом формулы выражения координат векторного произведения через координаты исходных векторов в правой и левой ортонормированной прямоугольной системе координат отличаются знаком.
Векторное произведение не обладает свойствами коммутативности и ассоциативности. Оно является антикоммутативным и, в отличие от скалярного произведения векторов, результат является опять вектором.
Полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы коллинеарны.
Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения.
История[править | править код]
Векторное произведение было введено У. Гамильтоном в 1846 году[1] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю[2].
Определение[править | править код]
Векторным произведением вектора 


Обозначения:
Замечания[править | править код]
В качестве определения можно использовать описанное далее выражение векторного произведения в координатах в правой (или левой) прямоугольной системе координат.
Также в качестве исходного определения может быть взят набор алгебраических свойств векторного произведения.
Правые и левые тройки векторов в трёхмерном евклидовом пространстве[править | править код]
Рассмотрим упорядоченную тройку некомпланарных (линейно независимых) векторов 
Геометрическое определение[править | править код]
Совместим начала векторов в одной точке. Упорядоченная тройка некомпланарных векторов 



Определение с помощью руки[править | править код]
Другое определение связано с правой рукой человека, откуда и берётся название. На рисунке тройка векторов 


Алгебраическое определение[править | править код]
Существует также аналитический способ определения правой и левой тройки векторов, который требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора 


- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Замечания[править | править код]
Определения «правой» и «левой» тройки векторов зависят от ориентации пространства, но не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого определение самого векторного произведения. При этом формулы выражения координат векторного произведения через координаты исходных векторов будут отличаться знаком в правой и левой прямоугольной системе координат.
Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.
При заданной ориентации пространства система координат называется правой (левой), если тройка из векторов с координатами 


Геометрическое определение и определение с помощью руки сами задают ориентацию пространства. Алгебраическое определение задаёт способ разбить тройки некомпланарных векторов на два класса одинаково ориентированных векторов, но оно не задаёт ориентацию пространства, а использует уже заданную — ту, на основании которой данная система координат считается правой или левой. При этом, если ориентация системы координат неизвестна, можно сравнивать знак определителя со знаком определителя другой тройки некомпланарных векторов, ориентация которой известна — если знаки совпадают, то тройки одинаково ориентированы, если знаки противоположны — тройки ориентированы противоположно.
Свойства[править | править код]
Геометрические свойства векторного произведения[править | править код]
Рисунок 1: Площадь параллелограмма равна модулю векторного произведения
Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на
a × b и вектора
b × c на
a, первым шагом является нахождение векторного произведения (модуль которого равен площади одной из сторон), а вторым — нахождение скалярного произведения (которое равно объёму параллелепипеда)
- При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов так же, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Алгебраические свойства векторного произведения[править | править код]
Далее ![{displaystyle [{vec {a}},;{vec {b}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fcceaa8d6f8c20cebf7ca9374dc08a23130ba6a)



| Представление | Описание |
|---|---|
![{displaystyle [{vec {a}},;{vec {b}}]=-[{vec {b}},{vec {a}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c267366cadb584259b3c50b0e4e36382c5f9e9bd)
|
Антикоммутативность. |
![{displaystyle [alpha cdot {vec {a}},;{vec {b}}]=[{vec {a}},;alpha cdot {vec {b}}]=alpha cdot [{vec {a}},;{vec {b}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b268a3e418241b2c2fc88d8472c2a2e1566f356)
|
Ассоциативность умножения на скаляр. |
![{displaystyle [{vec {a}}+{vec {b}},;{vec {c}}]=[{vec {a}},;{vec {c}}]+[{vec {b}},;{vec {c}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3161075b7aad486d9877967a12eb2d725bca5d3)
|
Дистрибутивность по сложению. |
![{displaystyle [[{vec {a}},;{vec {b}}],;{vec {c}}]+[[{vec {b}},;{vec {c}}],;{vec {a}}]+[[{vec {c}},{vec {a}}],;{vec {b}}]={vec {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00f9fa2cabab740204011537035a86bb96df0a3b)
|
Тождество Якоби. |
![{displaystyle [{vec {a}},;{vec {a}}]={vec {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2b6acb122bbc38e8a68353a2a7230885ff4d8c5)
|
|
![{displaystyle [{vec {a}},;[{vec {b}},;{vec {c}}]]={vec {b}}cdot langle {vec {a}},;{vec {c}}rangle -{vec {c}}cdot langle {vec {a}},;{vec {b}}rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7b7dbf2d84c0db27feb86c85c41b7d122646f07)
|
Формула «БАЦ минус ЦАБ», тождество Лагранжа. |
![{displaystyle |[{vec {a}},,{vec {b}}]|^{2}+langle {vec {a}},,{vec {b}}rangle ^{2}=|{vec {a}}|^{2}cdot |{vec {b}}|^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff5696724e36f03030ef3350e333494d1d774ec)
|
Частный случай мультипликативности нормы кватернионов. |
![{displaystyle langle [{vec {a}},,{vec {b}}],,{vec {c}}rangle =langle {vec {a}},,[{vec {b}},,{vec {c}}]rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5b749162f3b3230fc7193d64f2f3910b791bcc9)
|
Значение этого выражения называют смешанным произведением векторов  , ,  , ,  . .
|
Выражение в координатах[править | править код]
В правом ортонормированном базисе[править | править код]
Если два вектора 

то их векторное произведение имеет координаты
Для запоминания этой формулы удобно использовать мнемонический определитель:
где 


где 
В левом ортонормированном базисе[править | править код]
Если базис левый ортонормированный, то векторное произведение в координатах имеет вид
Для запоминания, аналогично:
или
Формулы для левой системы координат можно получить из формул правой системы координат, записав те же векторы 


В произвольной аффинной системе координат[править | править код]
Векторное произведение в произвольной аффинной системе координат 
![{displaystyle [{vec {a}},;{vec {b}}]={begin{vmatrix}[{vec {e}}_{2},;{vec {e}}_{3}]&[{vec {e}}_{3},;{vec {e}}_{1}]&[{vec {e}}_{1},;{vec {e}}_{2}]\a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb7e80caef757b2bce0dd092ebd459a32081f489)
Вариации и обобщения[править | править код]
Кватернионы[править | править код]
Координаты векторного произведения в правом ортонормированном базисе можно также записать в кватернионной форме, поэтому буквы 



Заметим, что соотношения через векторное произведение между 







Преобразование к матричной форме[править | править код]
Векторное произведение двух векторов в координатах в правом ортонормированном базисе можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть 
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь 

С такой формой записи также зачастую проще работать (например, в эпиполярной геометрии[en]).
Из общих свойств векторного произведения следует, что
и
а так как ![{displaystyle [{vec {a}}]_{times }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ce3ad0fa3e8a55fb73d95f8fda29459fdd7b2b2)
В такой форме записи легко доказывается тождество Лагранжа (правило «БАЦ минус ЦАБ»).
Распространение на матрицы[править | править код]
В трёхмерном случае можно определить в координатах в произвольном базисе векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу 
Умножение матрицы на вектор слева определяется аналогично, если представить 
Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например (


После этого можно изменить форму записи для векторного произведения:


где ротор матрицы 

Размерности, не равные трём[править | править код]
Пусть 
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение 
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора 






Такое обобщение дает гиперплощадь размерности 
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при 
.
Эта конструкция называется внешним произведением.
Для двумерного случая операция
.
называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению.)
Алгебра Ли векторов[править | править код]
Векторное произведение вводит на 



См. также[править | править код]
Произведения векторов
Другое
- Ротор
- Дивергенция
Примечания[править | править код]
- ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101.
- ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
Литература[править | править код]
-
- Кочин Н.Е. Векторное исчисление и начала тензорного исчисления. АН СССР: Изд-во «НАУКА», М. 1965.
Ссылки[править | править код]
- Многомерное векторное произведение Архивная копия от 5 сентября 2015 на Wayback Machine
- Векторное произведение и его свойства. Примеры решения задач Архивная копия от 23 февраля 2011 на Wayback Machine
- В. И. Гервидс. Правое и левое вращение. НИЯУ МИФИ (10 марта 2011). — Физические демонстрации. Дата обращения: 3 мая 2011. Архивировано 23 декабря 2015 года.
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Понятие тройки векторов
Из курса физики известно, что скалярные величины или скаляры – это величины, вполне определяемые одним численным значением (например, масса, температура, объём, расстояние и пр.). То есть любое вещественное число является скаляром.
Векторные величины или векторы – это величины, которые определяют и численным значением, и направлением. Например, скорость.
Линейно зависимыми называются такие векторы $a,b,c,…$, что если подобрать такие числа $x,y,z,…$, из которых по крайней мере одно не равно $0$, то будет иметь место тождество $xa+yb+zc+…=0$. Если три вектора $a,b,c$ не равны $0$ и линейно зависимы, то они компланарны.
Определение 1
Связка трёх векторов – это приведённая к общему началу тройка некомпланарных векторов $a,b,c$.
Определение правой и левой тройки векторов
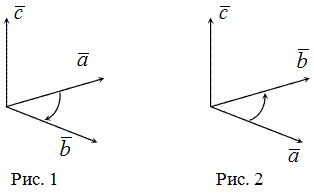
Приведём чертёж правой связки.
Рисунок 1. Чертёж правой связки. Автор24 — интернет-биржа студенческих работ
Рассмотрим кратчайшее вращение $vec{OA}=a$ к $vec{OB}=b$ на плоскости $OAB$ со стороны направления $vec{OC}=c$. Мы увидим, что вращение идёт против часовой стрелки.
Если большой палец и указательный пальцы левой руки вытянуть, а средний согнуть под углом ладони, то три пальца в порядке большой-указательный-средний составят правую связку. Те же пальцы на левой руке составят левую связку.
На чертеже левой связки то же вращение идёт по часовой стрелке.
Рисунок 2. Чертеж левой связки. Автор24 — интернет-биржа студенческих работ
«Определение правой и левой тройки векторов» 👇
Способы преобразования правой связки в левую и обратно:
- перестановка местами двух любых векторов;
- изменение знака при одном из векторов;
- замена какого-нибудь вектора его зеркальным отображением относительно плоскости двух других векторов.
Правая и левая системы координат
Напомним, что координатная ось – это ось, на которой выбрано начало и единица масштаба.
Ортогональная или прямоугольная система координат в пространстве – это система из трёх взаимно перпендикулярных координатных осей $Ox, Oy$ и $Oz$ с общим началом $O$. Ортами в ортогональной системе координат называют единичные векторы (то есть векторы равные $1$).
Рассмотрим чертёж ортогональной системы координат в пространстве. Отметим на ней орты $i, j, k$.
Рисунок 3. Чертёж ортогональной системы координат в пространстве. Автор24 — интернет-биржа студенческих работ
$i, j, k$ образуют правую связку. Система координат в данном случае называется правой.
Система координат называется левой, когда орты образуют левую связку. То есть:
Рисунок 4. Левая система координат. Автор24 — интернет-биржа студенческих работ
Подведём итог. В статье мы дали определение связки тройки векторов, описали правую и левую тройку векторов, а также правую и левую систему координат, как вытекающую тему из определения правой и левой тройки векторов. Стоит сказать, что на практике определение правой и левой тройки векторов со временем происходит интуитивно или “на автомате”. Самое важное, это один раз понять, как это делается. Также стоит заметить, что чаще в задачах используется всё-таки правая тройка векторов и соответственно правая система координат.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Три некомпланарных вектора $overline{a}$,
$overline{b}$ и $overline{c}$, приведенных к общему началу, образуют так
называемую связку трех векторов (или тройку векторов).
Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.
Тройка векторов $overline{a}$, $overline{b}$ и $overline{c}$ называется левой, если
поворот от вектора $overline{a}$ к вектору $overline{b}$, видимый с конца третьего вектора $overline{c}$,
осуществляется по ходу часовой стрелки (рис. 1).
Тройка векторов $overline{a}$, $overline{b}$ и $overline{c}$ называется правой, если
поворот от вектора $overline{a}$ к вектору $overline{b}$, видимый с конца третьего вектора $overline{c}$,
осуществляется против хода часовой стрелки (рис. 2).
Как определить правая или левая тройка (векторы)?
В учебнике приводятся примеры параллелепипедов, построенных как написано на левой и правой тройке.
Но не могу понять почему тройки разные, если в обоих случаях направление против часовой стрелки.
Подскажите пожалуйста, почему на втором рисунке левая тройка?
-
Вопрос заданболее трёх лет назад
-
2526 просмотров
Пригласить эксперта
На левом рисунке a->b->c по часовой, на правом a->b->c – против часовой
Вопрос старый, но если у кого больше развито пространственно-образное мышление, то есть одна мнемоника. Нам в институте рассказывали, что можно определять по руке. Делаешь “базис” из пальцев: ладонь на себя, первый вектор – большой палец вверх, второй вектор – указательный палец в сторону, третий вектор – средний палец на себя. Дальше смотрим, какая рука больше подходит. Если получится “подставить” правую руку, не меняя продолжения пальцев (это важно), то тройка правая. Правило “против часовой” тоже подходит.
-
Показать ещё
Загружается…
19 мая 2023, в 16:10
8000 руб./за проект
19 мая 2023, в 16:10
500 руб./за проект
19 мая 2023, в 16:08
500 руб./за проект




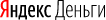






![{displaystyle {vec {c}}=[{vec {a}}{vec {b}}]=[{vec {a}},;{vec {b}}]={vec {a}}times {vec {b}}={vec {a}}wedge {vec {b}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5a3d46d305869c011f8a753ce0d97ef8e4a1d6b)



![{displaystyle [{vec {a}},;{vec {b}}]=Scdot {vec {e}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/659fe55fa7f1bfab81949bac7f9b6f460757c681)
![{displaystyle [{vec {a}},;{vec {c}}]=mathrm {Pr} _{vec {e}}{vec {a}}cdot |{vec {c}}|cdot {vec {g}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26453e25f5aa1dc2dad2f1ed1f24b394eded9bb5)
![{displaystyle V=|langle {vec {a}},;[{vec {b}},;{vec {c}}]rangle |.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/972d8b2c2701aa4ae5182148ac7c6cb92a0d3413)
![{displaystyle V=langle [{vec {a}},;{vec {b}}],;{vec {c}}rangle =langle {vec {a}},;[{vec {b}},;{vec {c}}]rangle .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4ba1da1621205def6e3ddee53ed9da404935595)


![{displaystyle [{vec {a}},;{vec {b}}]=(a_{y}b_{z}-a_{z}b_{y},;a_{z}b_{x}-a_{x}b_{z},;a_{x}b_{y}-a_{y}b_{x}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8fa16c4870edfe489e439614c671ec685b64f9d)
![{displaystyle [{vec {a}},;{vec {b}}]={begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/818e785f93fc9cd53f4f882597537ad8476659bf)
![{displaystyle [{vec {a}},;{vec {b}}]_{i}=sum _{j,k=1}^{3}varepsilon _{ijk}a_{j}b_{k},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/884a02d2b2631870d926e02e05aa096567f1e905)
![{displaystyle [{vec {a}},;{vec {b}}]=(a_{z}b_{y}-a_{y}b_{z},;a_{x}b_{z}-a_{z}b_{x},;a_{y}b_{x}-a_{x}b_{y}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4d1b7b0d23f2ccb4af924ee87204176da7fc0a8)
![{displaystyle [{vec {a}},;{vec {b}}]=-{begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f56fb817c1e28c69a08c1a46c6f1be6437fdf1c)
![{displaystyle [{vec {a}},;{vec {b}}]_{i}=-sum _{j,k=1}^{3}varepsilon _{ijk}cdot a_{j}cdot b_{k}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/705f278074d43d4cb83db2fd851bddd932582f0f)
![{displaystyle [{vec {a}},;{vec {b}}]={begin{vmatrix}mathbf {i} '&mathbf {j} '&mathbf {k} '\a'_{x}&a'_{y}&a'_{z}\b'_{x}&b'_{y}&b'_{z}end{vmatrix}}={begin{vmatrix}mathbf {i} &mathbf {j} &-mathbf {k} \a_{x}&a_{y}&-a_{z}\b_{x}&b_{y}&-b_{z}end{vmatrix}}=-{begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}end{vmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d05a08e910950583fa4c3f9e7b363fe82382c8a7)
![{displaystyle [{vec {a}},;{vec {b}}]=[{vec {a}}]_{times }{vec {b}}={begin{bmatrix},0&!-a_{3}&,,a_{2}\,,a_{3}&0&!-a_{1}\-a_{2}&,,a_{1}&,0end{bmatrix}}{begin{bmatrix}b_{1}\b_{2}\b_{3}end{bmatrix}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d1268e590490db993a3574e13841d9955073618)
![{displaystyle [{vec {b}},;{vec {a}}]={vec {b}}^{T}[{vec {a}}]_{times }={begin{bmatrix}b_{1}&b_{2}&b_{3}end{bmatrix}}{begin{bmatrix},0&!-a_{3}&,,,a_{2}\,,,a_{3}&,0&!-a_{1}\-a_{2}&,,a_{1}&,0end{bmatrix}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d163f8714882cb75d0fe91fd0fe0a93ac9c8195)
![{displaystyle [{vec {a}}]_{times }{stackrel {rm {def}}{=}}{begin{bmatrix},,0&!-a_{3}&,,,a_{2}\,,,a_{3}&0&!-a_{1}\!-a_{2}&,,a_{1}&,,0end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6701f98adf14d2921adea5a5d3cbbe6d9f9c2606)
![{displaystyle {vec {a}}=[{vec {c}},;{vec {d}}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a4bce0e24a417993522bf6133db91745b4ce931)
![{displaystyle [{vec {a}}]_{times }=({vec {c}}{vec {d}}^{T})^{T}-{vec {c}}{vec {d}}^{T}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a53070c790d8540b97a2f17fa238bf7ff9cc6379)
![{displaystyle [{vec {a}}]_{times },{vec {a}}={vec {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2d08aa98b8ce0ef3e88dd25b53fa1ea518ab097)
![{displaystyle {vec {a}}^{T},[{vec {a}}]_{times }={vec {0}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6c6723cdec70d60f8c5831cdeeac63502f97898)
![{displaystyle {vec {b}}^{T},[{vec {a}}]_{times },{vec {b}}=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab0dc1827a8eeb2a15e00388fa40ca9e69786a8d)







![int limits _{{Sigma }}left[{mathbf {dSigma }};left[nabla ;{mathbf a}right]right]=int limits _{{partial Sigma }}{mathbf a}times d{mathbf {r}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ddc1050c16cf5e8d86331cd846329deba025ea5)








