Как найти левый фокус эллипса - Сайт, где вы сможете решить свои вопросы

Эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки до двух точек равняется постоянной величине.

Что такое эллипс и фокусное расстояние

Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .

Обозначим фокусы эллипса $F_{1}$ и $F_{2}$ . Допустим, что расстояние $F_{1}{F_{2}}$ = – фокусное расстояние.

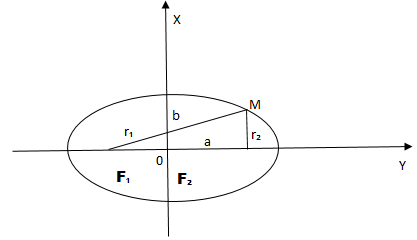
Рис. 1

$F_{1}, F_{2}$ – фокусы .

$F_{1} = (c, 0)$ ; $F_{2} = (- c ; 0)$ ,

– половина расстояния между фокусами;

– большая полуось;

– малая полуось.

Теорема:

Фокусное расстояние и полуоси связаны соотношением:

Если точка находится на пересечении эллипса с вертикальной осью, $r_{1} + r_{2} = 2 * sqrt{b^2 + c^2}$ (теорема Пифагора). Если же точка находится на пересечении его с горизонтальной осью, $r_1} + r_{2} = a - c + a + c$ . Так как по определению сумма $r_{1} + r_2}$ – постоянная величина, то приравнивая получается:

$a^2 = b^2 + c^2to{r_{1} + r_{2} = 2a$ .

Уравнение эллипса

Уравнение элиппса бывает двух видов:

Каноническое уравнение эллипса.
Параметрическое уравнение эллипса.

Сначала рассмотрим каноническое уравнение эллипса:

Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:

$1 = {x^2over{a^2}} + {y^2over{b^2}}$

Если центр эллипсa смещен в точку с координатами $(x_{0}, y_{0})$ тогда уравнение:

$1 = {(x - x_{0})^2over{a^2}} + {(y - y_{0})^2over{b^2}}$

Чтобы получить каноническое уравнение эллипса, разместим $F_{1}$ и $F_{2}$ на оси симметричной к началу координат. Тогда у фокусов будут такие координаты $F_{2}(-c, 0)$ и $F_{2}(c, 0)$ (см. рис. 2).

Пусть – произвольная точка эллипса. Обозначим через $r_{2}$ и $r_{1}$ – расстояние от точки к фокусам. Согласно с определением эллипса:

$r_{1} + r_{2} = 2a$

(1)

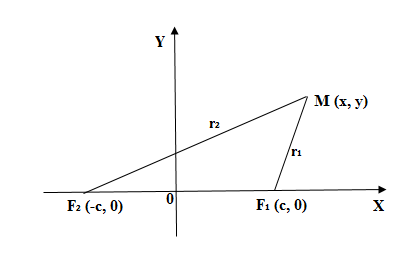
Рис. 2

Подставим в (1) $r_{1} = F_{1}M = sqrt{(x - c)^2 + (y - 0)^2}$ , $r_{2} = sqrt{(x + c)^2 + y^2}$ и освободимся от иррациональности, подняв обе части к квадрату, получим:

$r_{2} = 2a - r_{1}tosqrt{(x + c)^2 + y^2} = 2a - sqrt{(x - c)^2 + y^2}}to{x^2 + 2cx + c^2 + y^2} = 4a^2 - 4asqrt{(x - c)^2) + y^2} + x^2 - 2cx + c^2 + y^2to{4a}sqrt{(x - c^2 + y^2} = 4a^2 - 4cxarrowvert:4$

$asqrt{(x - c)^2 + y^2} =a^2 - cx$

(подносим к квадрату обе части): $to{a^2x^2 - 2ca^2x + a^2c^2 + a^2y^2} = {a^4 - 2ca^2x + c^2x^2to{(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)arrowvert:a^2(a^2 - c^2)$ ,

${x^2over{a^2}} + {y^2over{a^2 - c^2}} = 1$

Обозначим: , получаем каноническое уравнение эллипса:

${x^2over{a^2}} + {y^2over{b^2}} = {1}$

(2)

Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из $Delta{F_{1}}MF_{2}$ у нас получается $F_{2}M + F_{1}M > F_{1}F_{2}to{r_{1} + r_{2}} > 2c$ . Так как $r_{1} + r_{2} = 2a$ , тогда , и поэтому .

Для построения эллипса обратим внимание, что если точка $M_{1}(x, y)$ принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки $M_{2}(-x, y), M_{3}(-x, -y), M_{4}(x, -y)$ тоже удовлетворяют это уравнение: из

${x^2over{a^2}} + {y^2over{b^2}} = 1to{(pm{x})^2over{a^2}} + {(pm{y})^2over{b^2}} = {1}$ .

Точки $M_{1}, M_{2}, M_{3}, M_{4}$ – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.

Из уравнения (2) находим $y = pm{{b}over{a}}sqrt{a^2 - x^2$ , для первой четверти ${y} = {bover{a}}sqrt{a^2 - x^2}$ .

Если , тогда . Если же , тогда . Точки $A_{1}(a, 0)$ и $B_{1}(0, b)$ , а также симметричные с ними $A_{2}(-a, 0)$ , $B_{2}(0, -b)$ – вершины эллипса, точка – центр эллипса, $A_{1}A_{2}$ = большая ось, $B_{1}B_{2} = 2b$ – малая ось эллипса.

Если первой четверти, тогда из $y = {bover{a}}sqrt{a^2 - x^2$ получается, что при возрастании от к значение падает от к . (рис. 3)

Параметрическое уравнение выглядит так:

$left{ begin{aligned} x = a{cos}alpha\ y = b{sin}alpha end{aligned}quad {0leqalpha < 2pi right$

Основные свойства эллипса

Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.

1. Угол между касательной к эллипсу и фокальным радиусом $r_{1}$ равен углу между касательной и фокальным радиусом $r_{2}$ .

2. Уравнение касательной к эллипсу в точке с координатами $(x_{M}, y_{M})$ :

$1 = {x x_{M}over{a^{2}}} + {y y_{M}over{b^{2}}}$ .

3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).

4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.

5. Если вписать эллипс с фокусами $F_{1}$ и $F_{2}$ у треугольника , тогда выполняется соотношение:

= ${{overline{F_{1}A} * overline{F_{2}A}}over{overline{CA} * overline{AB}}} + {{overline{F_{1}B} * overline{F_{2}B}}over{overline{AB} * overline{BC}}} + {{overline{F_{1}C} * overline{F_{2}C}}over{overline{BC} * overline{CA}}}$

Эксцентриситет эллипса

Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается

Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда $c = {sqrt{a^2 + b^2}} = 0to{varepsilon = 0}$ – получается круг. Если же , тогда – эллипс превращается в отрезок. В некоторых случаях . Для фокальных радиусов приведём без доказательства такие формулы:

$left{ begin{aligned} r_{1} = a - varepsilon{x},\ r_{2} = a + varepsilon, end{aligned} quad{xin[-a, a]. right$

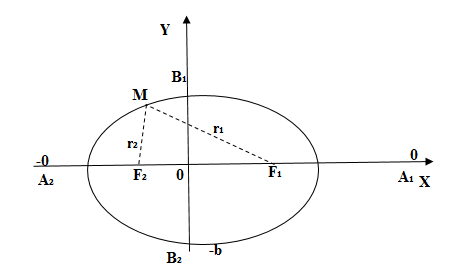
Рис. 3

Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и , тогда вычислим $c = {sqrt{a^2 + b^2}}$ – полуфокусное расстояние.

Строим фокусы $F_{1}$ и $F_{2}$ на расстоянии один от другого Концы не растянутой нити длиной закрепляем в точках $F_{1}$ и $F_{2}$ . Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.

Примеры решения задач

Задача

Задан эллипс уравнением ${x^2over{25}} + {y^2over{9}} = 1$ и точки $M_{0}(4; 1,8), M_{1}(3; 2,4)$ . Необходимо:

убедиться, что точки $M_{0}$ и $M_{1}$ лежат на эллипсе;
найти полуоси эллипса и координаты его фокусов;
найти расстояние от точки $M_{0}$ к фокусам;
убедиться, что сумма этих расстояний равна длине большой оси;
найти эксентриситет эллипса.

Решение

1. Подставим координаты точки $M_{0}$ в левую часть уравнения эллипса:

${x^2over{25}} + {y^2over{9}} = {4^2over25}} + {1,8 * 1,8over{9}} = {16over25}} + {36over{100}} = {16over{25}} + {9over25}} = 1$ – точка $M_{0}$ лежит на эллипсе. Аналогично для $M_{1}(3; 2,4)$ :

точка $M_{1}$ лежит на эллипсе.

2. С канонического ${x^2over{a^2}} + {y^2over{b^2}} = {1}$ и данного уравнения ${x^2over{25}} + {y^2over{9}} = 1$ эллипса выходит: $a^2 = {25},quad{b^2 = 9}to{a = 5, b = 3}.$ Из равенства получается:

$b^2 = a^2 - c^2to {c^2 = a^2 - b^2 = 25 - 9} = {16}to{c = 4}$ – полуфокусное расстояние. Координаты фокусов $F_{1}(4; 0)$ и $F_{2}(-4; 0)$ .

3. Найдём фокальные радиусы точки $M_{0}$ :

$r_{2} = F_{2}M_{0} = sqrt{(4 - (-4))^2 + 1,8^2} = sqrt{64 + 3,24} = sqrt{67,24} = 8,2$

$r_{1} = F_{1}M_{0} = sqrt{(4 - 4)^2 + 1,8^2} = 1,8.$

4. Найдём сумму $r_{1} + r_{2} = 1, 8 + 8.2 = 10 = 2 * 5 = 2a$ , что отвечает определению эллипса.

5. Эксцентриситет находится по формуле .

Задача

Найти оси, вершины и фокусы эллипса

Решение

Сведём обычное уравнение к каноническому:

$169x^2 + 25y^2 - 4225 = 0to{x^2over{25}} + {y^2over{169}} = 1$

, $b^2 = 169to{a = 5, b = 13}$ . Вершины эллипса в точках $A_{1}(5, 0)$ , $B_{1}(0, 13)$ , $A_{2}(-5, 0)$ , $B_{2}(0, -13)$ . Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае больше, чем , то эллипс, который вытянут вдоль оси , находим полуфокусное расстояние $c = sqrt{b^2 - a^2} = sqrt{169 - 25} = sqrt{144} = 12$ .

Фокусы в точках $F_{1}(0, 12)$ и $F_{2}(0, -12)$ . (см. рис. 3)

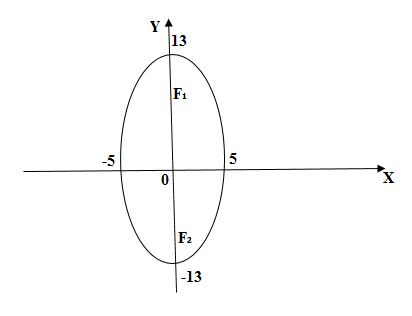
Рис. 4

Найти оси, вершины и фокусы эллипса $25x^2 + 144y^2 = 3600quad{:}arrowvertto{25x^2over{3600}} + {144y^2over{3600}} = {1}to{x^2over{144}} + {y^2over{25}} = {1}$ или ${X^2over{12^2}} + {y^2over{5^2}} = {1}$ . Построить эллипс.

Сравнивая последнее уравнение с уравнением (2), у нас получается:

, $b^2 = 5^2to{a = 12, b = 5}$ . Откуда находим оси эллипса: , и координаты вершин: $A_{1}(12, 0)$ , $A_{2} (-12, 0)$ , $B_{1}(0, 5)$ , $B_{2}(0, -5)$ . Дальше из формулы:

$b^2 = a^2 - c^2to{c^2 = a^2 - b^2 = 144 - 25 = 119}to{c = sqrt{119}}approx{10,91}$ . Значит, фокусами эллипса есть точки: $F_{1}(sqrt{119}, 0)$ и $F_{2}(-sqrt{119}, 0)$ . Для построения эллипса отложим на осях и вершины $A_{1}, B_{1}, A_{2}, B_{2}$ соответственно соединим их плавной линией, (см. задачу 1).

Замечание! Если в каноническом уравнении ${x^2over{a^2}} + {y^2over{b^2}} = {1}$ большей полуосью будет , тогда фокусы эллипса будут расположены на оси и тогда $c = sqrt{b^2 - a^2}$ .

Источник

Эллипсом называется множество точек
плоскости, сумма расстояний от которых
до двух данных точек

и

этой плоскости, называемых фокусами,
есть величина постоянная, равная
,
,
большая, чем расстояние между фокусами
.

Е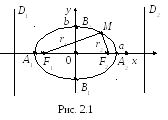сли
оси координат расположены по отношению
к эллипсу так, как на рис. 2.1, а фокусы
эллипса находятся на оси

на равных расстояниях от начала координат
в точках

и
,
то получится простейшее (каноническое)
уравнение эллипса:

(2.2)

где

– большая,

– малая полуось эллипса, причем
,

и

(
– половина расстояния между фокусами)
связаны соотношением
.

Точки
,
.
,

называются вершинами эллипса, оси
симметрии

и

– главными осями, а центр симметрии 0 –
центром эллипса.

Векторы

и

называются фокальными радиус–векторами,
а числа

и

– фокальными радиусами точки
,
принадлежащей эллипсу (в силу определения
эллипса для любой его точки
).
В частном случае

фокусы

и

совпадают с центром, а каноническое
уравнение имеет вид
,
или
,
т. е. описывает окружность радиуса

с центром в начале координат.

Форма эллипса (мера его сжатия)
характеризуется его эксцентриситетом

(;
при

эллипс является окружностью, а т. к.
,
то
).

Прямые

и
,
перпендикулярные главной оси и проходящие
на расстоянии

от центра, называются директрисами
эллипса.

Фокальные радиусы-векторы выражаются
через абсциссу точки эллипса по формулам

и
.

Если центр эллипса с полуосями

и

смещен в точку
,
то его каноническое уравнение имеет
вид

.
(2.3)

Примеры

1. Какую линию определяет уравнение
?

Разделим данное уравнение почленно на
12:
.
Сравнивая полученное уравнение с
уравнением (2.2), заключаем, что оно
определяет эллипс с полуосями
,
.
Найдем фокусы этого эллипса. Так как
,
то
,
.
Следовательно, фокусы эллипса находятся
в точках
,
.

2. Даны координаты точек
,

и радиус окружности
,
центр которой находится в начале
координат. Требуется:

а) составить каноническое уравнение
эллипса, проходящего через данные точки

и
;

б) найти полуоси, фокусы и эксцентриситет
этого эллипса;

в) найти все точки пересечения эллипса
с данной окружностью;

г) построить эллипс и окружность.

Решение.

а) Пусть

– искомое уравнения эллипса. Этому
уравнению должны удовлетворять координаты
данных точек. Следовательно, подставляя
координаты точек, получим

Отсюда находим
,
.
Итак, уравнение эллипса имеет вид
.

б)
,

– соответственно большая и малая полуоси
эллипса. Для эллипса
,
значит
,
откуда
.
Следовательно,
,

– соответственно левый и правый фокусы
эллипса. Эксцентриситет эллипса
.

в) Найдем точки пересечения эллипса с
данной окружностью. Уравнение окружности
.
Решая систему уравнений

получим

,
,
.
Но
,
значит
,
откуда
.
Итак, существуют две точки пересечения
эллипса и окружности

и
.

г) Построить эллипс и окружность.

3. Большая ось эллипса равна 12, а
директрисами его служат прямые
.
Найти уравнение эллипса и его
эксцентриситет.

Решение. По условию
.
Из уравнений директрис

и формулы

находим
.
Тогда
.
Следовательно, искомое уравнение эллипса
есть
,
а эксцентриситет его
.

4. Эллипс касается оси

в точке

и пересекает ось

в точках

и
.
Зная, что оси эллипса параллельны осям
координат, составить его уравнение.

Решение. Будем искать уравнение
эллипса в виде (2.3). Так как эллипс касается
оси
,
то
.
Далее,
,
т. к. прямая

параллельна оси

и отсекает на оси

отрезок
.
Следовательно, уравнение эллипса имеет
вид
.
Полуось
.
В таком случае получим

– уравнение эллипса. Найдем
.
Так как

лежит на эллипсе, то ее координаты
удовлетворяют его уравнению, т. е.
.
Итак, искомое уравнение эллипса
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Эллипс: определение, свойства, построение

Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух заданных точек F_1 , и F_2 есть величина постоянная (2a) , бо́льшая расстояния (2c) между этими заданными точками (рис.3.36,а). Это геометрическое определение выражает фокальное свойство эллипса.

Фокальное свойство эллипса

Точки F_1 , и F_2 называются фокусами эллипса, расстояние между ними 2c=F_1F_2 — фокусным расстоянием, середина отрезка F_1F_2 — центром эллипса, число — длиной большой оси эллипса (соответственно, число — большой полуосью эллипса). Отрезки F_1M и F_2M , соединяющие произвольную точку эллипса с его фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки эллипса, называется хордой эллипса.

Отношение $e=frac{c}{a}$ называется эксцентриситетом эллипса. Из определения (2a>2c) следует, что 0leqslant e<1 . При e=0 , т.е. при c=0 , фокусы F_1 и F_2 , а также центр совпадают, и эллипс является окружностью радиуса (рис.3.36,6).

Геометрическое определение эллипса, выражающее его фокальное свойство, эквивалентно его аналитическому определению — линии, задаваемой каноническим уравнением эллипса:

$frac{x^2}{a^2}+frac{y^2}{b^2}=1.$

(3.49)

Действительно, введем прямоугольную систему координат (рис.3.36,в). Центр эллипса примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось или первую ось эллипса), примем за ось абсцисс (положительное направление на ней от точки F_1 к точке F_2 ); прямую, перпендикулярную фокальной оси и проходящую через центр эллипса (вторую ось эллипса), примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).

Эллипс и его фокальные свойства, эксцентриситет эллипса

Составим уравнение эллипса, пользуясь его геометрическим определением, выражающим фокальное свойство. В выбранной системе координат определяем координаты фокусов F_1(-c,0),~F_2(c,0) . Для произвольной точки M(x,y) , принадлежащей эллипсу, имеем:

$vline,overrightarrow{F_1M},vline,+vline,overrightarrow{F_2M},vline,=2a.$

Записывая это равенство в координатной форме, получаем:

$sqrt{(x+c)^2+y^2}+sqrt{(x-c)^2+y^2}=2a.$

Переносим второй радикал в правую часть, возводим обе части уравнения в квадрат и приводим подобные члены:

$(x+c)^2+y^2=4a^2-4asqrt{(x-c)^2+y^2}+(x-c)^2+y^2~Leftrightarrow ~4asqrt{(x-c)^2+y^2}=4a^2-4cx.$

Разделив на 4, возводим обе части уравнения в квадрат:

a^2(x-c)^2+a^2y^2=a^4-2a^2cx+c^2x^2~Leftrightarrow~ (a^2-c^2)^2x^2+a^2y^2=a^2(a^2-c^2).

Обозначив $b=sqrt{a^2-c^2}>0$ , получаем b^2x^2+a^2y^2=a^2b^2 . Разделив обе части на a^2b^2ne0 , приходим к каноническому уравнению эллипса:

$frac{x^2}{a^2}+frac{y^2}{b^2}=1.$

Следовательно, выбранная система координат является канонической.

Если фокусы эллипса совпадают, то эллипс представляет собой окружность (рис.3.36,6), поскольку a=b . В этом случае канонической будет любая прямоугольная система координат с началом в точке Oequiv F_1equiv F_2 , a уравнение x^2+y^2=a^2 является уравнением окружности с центром в точке и радиусом, равным .

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.49), и только они, принадлежат геометрическому месту точек, называемому эллипсом. Другими словами, аналитическое определение эллипса эквивалентно его геометрическому определению, выражающему фокальное свойство эллипса.

Директориальное свойство эллипса

Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии $frac{a^2}{c}$ от нее. При c=0 , когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).

Эллипс с эксцентриситетом 0<e<1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство эллипса). Здесь и — один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е. F_1,d_1 или F_2,d_2 .

В самом деле, например, для фокуса F_2 и директрисы d_2 (рис.3.37,6) условие $frac{r_2}{rho_2}=e$ можно записать в координатной форме:

$sqrt{(x-c)^2+y^2}=ecdot!left(frac{a^2}{c}-xright)$

Избавляясь от иррациональности и заменяя $e=frac{c}{a},~a^2-c^2=b^2$ , приходим к каноническому уравнению эллипса (3.49). Аналогичные рассуждения можно провести для фокуса F_1 и директрисы $d_1colonfrac{r_1}{rho_1}=e$ .

Эллипс и его директориальное свойство, эксцентриситет эллипса

Уравнение эллипса в полярной системе координат

Построение кривой эллипса по точкам в полярной системе координат

Уравнение эллипса в полярной системе координат F_1rvarphi (рис.3.37,в и 3.37(2)) имеет вид

$r=frac{p}{1-ecdotcosvarphi}$

где $p=frac{b^2}{a}$ фокальный параметр эллипса.

В самом деле, выберем в качестве полюса полярной системы координат левый фокус F_1 эллипса, а в качестве полярной оси — луч F_1F_2 (рис.3.37,в). Тогда для произвольной точки M(r,varphi) , согласно геометрическому определению (фокальному свойству) эллипса, имеем r+MF_2=2a . Выражаем расстояние между точками и F_2(2c,0) (см. пункт 2 замечаний 2.8):

$begin{aligned}F_2M&=sqrt{(2c)^2+r^2-2cdot(2c)cdot rcos(varphi-0)}=\[3pt] &=sqrt{r^2-4cdot ccdot rcdotcosvarphi+4cdot c^2}.end{aligned}$

Следовательно, в координатной форме уравнение эллипса F_1M+F_2M=2a имеет вид

$r+sqrt{r^2-4cdot ccdot rcdotcosvarphi+4cdot c^2}=2cdot a.$

Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:

$r^2-4cdot ccdot rcdotcosvarphi+4cdot c^2~Leftrightarrow~acdot!left(1-frac{c}{a}cdotcosvarphiright)!cdot r=a^2-c^2.$

Выражаем полярный радиус и делаем замену $e=frac{c}{a},~b^2=a^2-c^2,~p=frac{b^2}{a}$ :

$r=frac{a^2-c^2}{acdot(1-ecdotcosvarphi)} quad Leftrightarrow quad r=frac{b^2}{acdot(1-ecdotcosvarphi)} quad Leftrightarrow quad r=frac{p}{1-ecdotcosvarphi},$

что и требовалось доказать.

Геометрический смысл коэффициентов в уравнении эллипса

Найдем точки пересечения эллипса (см. рис.3.37,а) с координатными осями (вершины зллипса). Подставляя в уравнение y=0 , находим точки пересечения эллипса с осью абсцисс (с фокальной осью): x=pm a . Следовательно, длина отрезка фокальной оси, заключенного внутри эллипса, равна . Этот отрезок, как отмечено выше, называется большой осью эллипса, а число — большой полуосью эллипса. Подставляя x=0 , получаем y=pm b . Следовательно, длина отрезка второй оси эллипса, заключенного внутри эллипса, равна . Этот отрезок называется малой осью эллипса, а число — малой полуосью эллипса.

Действительно, $b=sqrt{a^2-c^2}leqslantsqrt{a^2}=a$ , причем равенство b=a получается только в случае c=0 , когда эллипс является окружностью. Отношение $k=frac{b}{a}leqslant1$ называется коэффициентом сжатия эллипса.

Замечания 3.9

1. Прямые x=pm a,~y=pm b ограничивают на координатной плоскости основной прямоугольник, внутри которого находится эллипс (см. рис.3.37,а).

2. Эллипс можно определить, как геометрическое место точек, получаемое в результате сжатия окружности к ее диаметру.

Действительно, пусть в прямоугольной системе координат Oxy уравнение окружности имеет вид x^2+y^2=a^2 . При сжатии к оси абсцисс с коэффициентом 0<kleqslant1 координаты произвольной точки M(x,y) , принадлежащей окружности, изменяются по закону

$begin{cases}x'=x,\y'=kcdot y.end{cases}$

Подставляя в уравнение окружности x=x' и $y=frac{1}{k}y'$ , получаем уравнение для координат образа M'(x',y') точки M(x,y) :

$(x')^2+{left(frac{1}{k}cdot y'right)!}^2=a^2 quad Leftrightarrow quad frac{(x')^2}{a^2}+frac{(y')^2}{k^2cdot a^2}=1 quad Leftrightarrow quad frac{(x')^2}{a^2}+frac{(y')^2}{b^2}=1,$

поскольку b=kcdot a . Это каноническое уравнение эллипса.

3. Координатные оси (канонической системы координат) являются осями симметрии эллипса (называются главными осями эллипса), а его центр — центром симметрии.

Действительно, если точка M(x,y) принадлежит эллипсу $frac{x^2}{a^2}+frac{y^2}{b^2}=1$ . то и точки M'(x,-y) и M''(-x,y) , симметричные точке относительно координатных осей, также принадлежат тому же эллипсу.

4. Из уравнения эллипса в полярной системе координат $r=frac{p}{1-ecosvarphi}$ (см. рис.3.37,в), выясняется геометрический смысл фокального параметра — это половина длины хорды эллипса, проходящей через его фокус перпендикулярно фокальной оси ( r=p при $varphi=frac{pi}{2}$ ).

Эксцентриситет, коэффициент сжатия и фокусы эллипса

5. Эксцентриситет характеризует форму эллипса, а именно отличие эллипса от окружности. Чем больше , тем эллипс более вытянут, а чем ближе к нулю, тем ближе эллипс к окружности (рис.3.38,а). Действительно, учитывая, что $e=frac{c}{a}$ и c^2=a^2-b^2 , получаем

$e^2=frac{c^2}{a^2}=frac{a^2-b^2}{a^2}=1-{left(frac{a}{b}right)!}^2=1-k^2,$

где — коэффициент сжатия эллипса, 0<kleqslant1 . Следовательно, $e=sqrt{1-k^2}$ . Чем больше сжат эллипс по сравнению с окружностью, тем меньше коэффициент сжатия и больше эксцентриситет. Для окружности k=1 и e=0 .

6. Уравнение $frac{x^2}{a^2}+frac{y^2}{b^2}=1$ при a<b определяет эллипс, фокусы которого расположены на оси (рис.3.38,6). Это уравнение сводится к каноническому при помощи переименования координатных осей (3.38).

7. Уравнение $frac{(x-x_0)^2}{a^2}+frac{(y-y_0)^2}{b^2}=1,~ageqslant b$ определяет эллипс с центром в точке O'(x_0,y_0) , оси которого параллельны координатным осям (рис.3.38,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36).

При a=b=R уравнение (x-x_0)^2+(y-y_0)^2=R^2 описывает окружность радиуса с центром в точке O'(x_0,y_0) .

Параметрическое уравнение эллипса

Параметрическое уравнение эллипса в канонической системе координат имеет вид

$begin{cases}x=acdotcos{t},\ y=bcdotsin{t},end{cases}0leqslant t<2pi.$

Действительно, подставляя эти выражения в уравнение (3.49), приходим к основному тригонометрическому тождеству cos^2t+sin^2t=1 .

Пример построения эллипса в канонической системе координат

Пример 3.20. Изобразить эллипс $frac{x^2}{2^2}+frac{y^2}{1^2}=1$ в канонической системе координат Oxy . Найти полуоси, фокусное расстояние, эксцентриситет, коэффициент сжатия, фокальный параметр, уравнения директрис.

Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: a=2 — большая полуось, b=1 — малая полуось эллипса. Строим основной прямоугольник со сторонами 2a=4,~2b=2 с центром в начале координат (рис.3.39). Учитывая симметричность эллипса, вписываем его в основной прямоугольник. При необходимости определяем координаты некоторых точек эллипса. Например, подставляя x=1 в уравнение эллипса, получаем

$frac{1^2}{2^2}+frac{y^2}{1^2}=1 quad Leftrightarrow quad y^2=frac{3}{4} quad Leftrightarrow quad y=pmfrac{sqrt{3}}{2}.$

Следовательно, точки с координатами $left(1;,frac{sqrt{3}}{2}right)!,~left(1;,-frac{sqrt{3}}{2}right)$ — принадлежат эллипсу.

Вычисляем коэффициент сжатия $k=frac{b}{a}=frac{1}{2}$ ; фокусное расстояние $2c=2sqrt{a^2-b^2}=2sqrt{2^2-1^2}=2sqrt{3}$ ; эксцентриситет $e=frac{c}{a}=frac{sqrt{3}}{2}$ ; фокальный параметр $p=frac{b^2}{a}=frac{1^2}{2}=frac{1}{2}$ . Составляем уравнения директрис: $x=pmfrac{a^2}{c}~Leftrightarrow~x=pmfrac{4}{sqrt{3}}$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Как найти координаты фокусов эллипса?

Pawok
[16.9K]

9 лет назад

Как, зная уравнение эллипса, найти координаты его фокусов?

Далия Slave
[21.9K]

9 лет назад

Предположим, для эллипса, заданного формулой х*х/(49) + у*у/(25) = 1

координаты фокусов имеют следующий вид

(а*с , 0) и (-а*с, 0), где с = корень(а*а-б*б)/а

в нашем случае а = 7, б = 5

значит с = корень(49-25)/5 = корень(24)/5 = 2*корень(6) / 5

И таким образом, координаты фокусов

(2*корень(6) , 0) и (-2*корень(6) , 0)

автор вопроса выбрал этот ответ лучшим

комментировать

в избранное

ссылка

отблагодарить

Lalique
[53.5K]

6 лет назад

Координаты фокусов эллипса вычислить достаточно просто.

Например, дано уравнение эллипса: х^2/13^2 + у^2/12^2 = 1.

13- длина большой полуоси; 12 – длина малой полуоси.

Теперь нам нужно найти вспомогательный параметр С:

С=корень квадратный из (13^2-12^2)=корень квадратный из 25=5

Решением задачи будут такие координаты:

F1=(5;0); F2=(-5;0).

Фокусы эллипса – это особые его точки, из которых строятся прямые к дуге эллипса. И сумма этих прямых (в любой точке эллипса) – есть величина одинаковая.

комментировать

в избранное

ссылка

отблагодарить

Mefody66
[35.1K]

9 лет назад

Кажется, Далия дала правильный ответ, только на а делить не надо.

Общее уравнение эллипса

(x-x0)^2/a^2 + (y-y0)^2/b^2 = 1

Здесь A(x0, y0) – центр эллипса, a, b – полуоси.

Расстояние |F1F2| = 2c, где с можно найти из условия

c^2 = |a^2 – b^2|

Если координатные оси параллельны осям эллипса, то координаты фокусов F1(x0 – c, y0), F2(x0 + c, y0).

комментировать

в избранное

ссылка

отблагодарить

Знаете ответ?

Источник

Построить такой график можно здесь: https://www.desmos.com/

Что мы знаем со школы про эллипс? К сожалению, исходя из своей практики работы с учениками, многие вплоть до 11 класса не сталкиваются с такой замечательной плоской фигурой, впрочем как и с её частным случаем – окружностью. Некоторые знают только примерный вид уравнения…

Кстати, какое оно? Каноническим уравнением эллипса считается следующее уравнение:

Каноническое уравнение эллипса

Почему оно именно такое? Что ж, это можно вывести из определения. Поэтому давайте его напишем.

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.

Давайте сделаем рисунок и попробуем вывести каноническое уравнение из определения эллипса.

Математика эллипса: всё, что нужно знать

Обозначим фокусы через F₁ и F₂, расстояние между ними через 2c, а сумму расстояний от произвольной точки эллипса M(x; y) до фокусов – через 2a. По определению 2а > 2c, т.е. а > c.

Для вывода уравнения эллипса выберем систему координат OXY так, чтобы фокусы F₁ и F₂ лежали а оси OX, а начало координат совпадало с серединой отрезка F₁F₂. Тогда фокусы будут иметь следующие координаты: F₁(-c; 0) и F₂(+c; 0).

Тогда, согласно определению эллипса, MF₁ + MF₂ = 2a, то есть:

Мы вывели каноническое уравнение эллипса и доказали, что оно эквивалентно начальному уравнению из определения.

Эллипс – кривая второго порядка.

Исследование формы эллипса по его уравнению

Установим форму эллипса, используя его каноническое уравнение.

1. Каноническое уравнение содержит x и y только в четных степенях, поэтому если точка (x; y) принадлежит эллипсу, то ему также принадлежат точки (x; -y), (-x; y), (-x; -y). Отсюда следует, что эллипс симметричен относительно осей координат Ox и Oy, а также точки O(0; 0), которая является центром эллипса.

2. Точки пересечения эллипса с осями координат. Положив y = 0, находим две точки A₁(a; 0) и A₂(-a;0), в которых ось Ox пересекает эллипс. Положив в уравнении x = 0, находим точки пересечения эллипса с осью Oy: B₁(0; b) и B₂(0; -b). Все эти 4 точки называются вершинами эллипса.

Отрезки A₁A₂ и B₁B₂, а также их длины 2a и 2b называются соответственно большой и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.

3. Также из канонического уравнения следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства

Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми x = ±a и y = ±b.

4. В каноническом уравнении сумма неотрицательных слагаемых (x/a)² и (y/b)² равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т.е. если |x| возрастает, то |y| уменьшается и наоборот.

Дополнительные сведения об эллипсе

Форма эллипса зависит от отношения b/a. При a = b = R эллипс превращается в окружность, уравнение эллипса принимает вид x² + y² = R². Однако, в качестве характеристики формы эллипса чаще используется отношение c/a.

Отношение c/a половины расстояния между фокусами к большей полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой «эпсилон» ε:

Из последней строки видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным, то есть больше походить на окружность, быть ближе к ней по форме. Если положить ε = 0, то эллипс превращается в окружность.

Пусть M(x; y) – произвольная точка эллипса с фокусами F₁ и F₂. Длины отрезков F₁M = r₁ и F₂M = r₂ называются фокальными радиусами точки M.
Очевидно, что r₁ + r₂ = 2a.

Тогда имеют место быть формулы: r₁ = a + εx и r₂ = a + εx

Выведем эти формулы

Прямые x = ±a/ε называются директрисами эллипса. Значение директрисы эллипса выявляется следующим утверждением.

Теорема

Если r – расстояние от произвольной точки эллипса до какого-нибудь фокуса, d – расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение r/d есть величина постоянная, равная эксцентриситету эллипса: r/d = ε.

Из равенства a² – c² = b² следует, что a > b. Если же a < b, то каноническое уравнение (x/a)² + (y/b)² = 1 определяет эллипс, большая ось которого 2b лежит на оси OY, а малая ось 2a – лежит на оси Ox. Фокусы такого эллипса находятся в точках F₁(0; +c) и F₂(0; -c), где c = √(b² – a²).

Площадь фигуры, ограниченной эллипсом

Допустим, что перед нами стоит следующая задача:
Вычислить площадь фигуры, ограниченной эллипсом.

Решение:

Зададим эллипс параметрическими уравнениями:
x = a⋅cos(t) и y = b ⋅ sin(t). Кстати, выразив косинус и синус из каждого, а потом возведя в квадрат оба уравнения, сложив их, можно прийти к каноническому уравнению эллипса.

В силу симметричности эллипса относительно начала координат, нам достаточно найти площадь 1/4 части эллипса, а затем умножить результат на 4. Сделаем подходящий рисунок.

Здесь x изменяется от 0 до a, следовательно параметр t изменяется от π/2 до 0. Площадь четверти эллипса будем искать с помощью интегрирования функции, задающей эллипс в первой четверти координат.

Вывод формулы для площади эллипса

Длина дуги эллипса (периметр эллипса)

Вывод длины дуги эллипса через эллиптический интеграл

Ознакомиться с эллиптическими интегралами

Стоит заметить, что для окружности всё получается гораздо проще, и мы легко выводим формулу, знакомую нам со школы C = 2πR.

Вывод длины дуги окружности

Приближённые формулы для периметра

Точные формулы для периметра

Джеймс Айвори и Фридрих Бессель независимо друг от друга получили формулу для периметра эллипса:

Площадь сегмента эллипса

Площадь сегмента между дугой, выпуклой влево, и вертикальной хордой , проходящей через точки (x; y) и (x; -y) можно определить по формуле:

Если эллипс задан уравнением Ax² + Bxy + Cy² = 1, то площадь можно определить по формуле

Физический смысл фокусов

1. Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.

2. Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.

3. Если F₁ и F₂ — фокусы эллипса, то для любой точки M, принадлежащей эллипсу, угол между касательной в этой точке и прямой F₁M равен углу между касательно и прямой F₂M.

4. Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.

5. Эволютой эллипса является астроида , вытянутая вдоль вертикальной оси. Эволюта плоской кривой — геометрическое место точек , являющихся центрами кривизны кривой. По отношению к своей эволюте любая кривая является эвольвентой .

6. Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипсы и только они имеет максимальную аффинную длину .
Аффинная длина — параметр плоской кривой , который сохраняется при эквиаффинных преобразованиях (то есть аффинных преобразованиях , сохраняющих площадь ).

7. Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (всё время касаясь её) а второй конец лестницы будет скользить по полу (всё время касаясь его), тогда любая фиксированная точка лестницы (не на её концах), будет двигаться по дуге некоторого эллипса. Это свойство остаётся верным, если мы возьмём точку не внутри лестницы-отрезка, а на её мыслимом продолжении. Последнее свойство используется в описанном выше эллипсографе.

Построение эллипса с помощью иголок, нитки и карандаша.

Построение эллипса с помощью иголок, нитки и карандаша.

Эллипсы в астрономии. Все планеты и другие небесные тела Солнечной системы движутся вокруг Солнца по эллиптическим орбитам, в одном из фокусов – Солнце. Этот закон был открыт ещё Кеплером. Ближайшую точку к Солнцу Земля проходит 4 января, таким образом, для северного полушария зима чуть теплее, чем для южного. К тому же, из-за такой формы орбиты, зима для северного полушария чуть короче, то есть период между осенним и весенним равноденствием не ровно 1/2 года, а меньше. Действительно, на южном полюсе температуры бывают ниже, чем на северном полюсе.

Физическое свойство фокусировки. Лучи, испущенные из одного фокуса, после отражения соберутся во втором фокусе. Название «фокус» как раз и связано со словом «фокусировка» лучей. Если на орбите Земли расположить зеркала, так чтобы они были повёрнуты ровно по касательной к орбите, то все лучи соберутся во 2 фокусе, то есть из той точки будет видно, что вся орбита светится.

Последнее свойство используется в физике для построение оптических резонаторов в лазерной технике. Лампа накачки размещается вдоль одной из фокальных осей зеркально отражающего эллиптического цилиндра, а лазерный стержень располагается вдоль другой фокальной оси. На второй фокальной оси помещают активную среду. А свойства эллиптической поверхности помогают быть уверенными в том, что вся энергия лампы накачки соберется в области активной среды.

Почитать подробнее здесь

Поместим в одном из фокусов зеркального эллипса лампочку
и проследим за выпущенными из неё лучами света. Отразившись от эллипса, они соберутся в другом фокусе. Причём окажутся там одновременно:

Зрительно напомним геометрическое определение эллипса: эллипс есть множество точек M плоскости, сумма расстояний от которых до данных точек A и B постоянна:

Решим вспомогательную задачу. Даны две точки по одну сторону от прямой. Мы хотим пройти из A в B, набрав по пути воды из реки l.

Мы хотим пройти из A в B, набрав по пути воды из реки l. В какой точке M надо набирать воду, чтобы общий путь имел минимальную длину?

Рассмотрим точку B’, симметричную точке B. Тогда XB = XB’. Длина AX+XB = AX+XB’ минимальна, когда ломаная AXB’ превращается в прямую.

Мы хотим пройти из A в B, набрав по пути воды из реки l. В какой точке набирать воду? Ответ: в точке пересечения l с AB’ (где B’ симметрична B относительно l). Заодно мы доказали равенство углов. Мы хотим пройти из A в B, набрав по пути воды из реки l. Где набирать воду?
Ответ 1: в точке пересечения l с AB’.
Ответ 2: там, где «угол падения равен углу отражения».

Принцип Ферма: свет выбирает кратчайший путь между двумя точками.

Вернемся к доказательству оптического свойства эллипса. На эллипсе сумма AM+MB постоянна. А для точек вне эллипса эта сумма больше, AX+XB > AM+MB.

В частности, если провести в точке M касательную к эллипсу, то для любой другой точки X на этой касательной AX+XB > AM+MB. Значит, по предыдущей задаче «угол падения равен углу отражения».

…по предыдущей задаче «угол падения равен углу отражения». Оптическое свойство эллипса доказано.

Многофокусные эллипсы

N-эллипс — обобщение эллипса , имеющее более двух фокусов. N-эллипсы называют также мультифокальными эллипсами , полиэллипсами, k -эллипсами, эллипсами Чирнхауса . Впервые такие фигуры исследовал Джеймс Максвелл в 1846 году.

Пусть на плоскости задано n точек (ui , vi ) (фокусы ), тогда n -эллипс является геометрическим местом точек плоскости, для которых сумма расстояний до n фокусов является постоянной величиной d . В виде формулы данное утверждение записывается как

1-эллипс представляет собой окружность , 2-эллипс — обычный эллипс. Обе данные кривые являются алгебраическими кривыми степени 2.

Для любого числа n фокусов n -эллипс представляет собой замкнутую выпуклую кривую. Кривая является гладкой вне окрестностей фокуса.

Эллипс с 4-мя фокусами и фокусным расстоянием d = 7

Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram

Источник

Что такое эллипс и фокусное расстояние

Уравнение эллипса

Основные свойства эллипса

Эксцентриситет эллипса

Примеры решения задач

Примеры

Эллипс: определение, свойства, построение

Фокальное свойство эллипса

Директориальное свойство эллипса

Уравнение эллипса в полярной системе координат

Геометрический смысл коэффициентов в уравнении эллипса

Параметрическое уравнение эллипса

Как найти координаты фокусов эллипса?

Исследование формы эллипса по его уравнению

Дополнительные сведения об эллипсе

Площадь фигуры, ограниченной эллипсом

Длина дуги эллипса (периметр эллипса)

Площадь сегмента эллипса

Физический смысл фокусов

Многофокусные эллипсы

Вам также может понравиться

Как исправить если пересолила майонез домашний

Где найти как нарисовать таблицу

Как исправить провисшие двери на ваз 2107

Добавить комментарий Отменить ответ