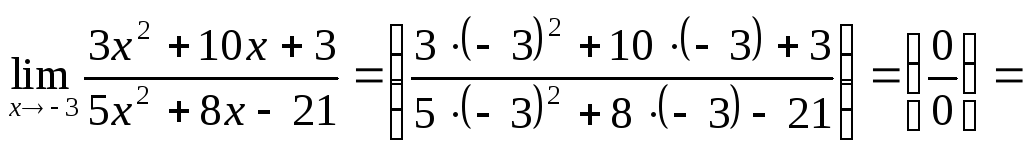Как найти лимит дроби

Правило Лопиталя

Примеры нахождения пределов функций по правилу Лопиталя

Пределы дробно-рациональных функций с квадратичными выражениями

В случае
неопределённости
следует разложить квадратичное выражение
на множители. Для этого можно

а)
воспользоваться тождеством
,
гдеи– корни уравнения,
найденные по формуле;

б)
учесть, что, когда
,
то– один из корней, и другой кореньможно найти по теореме Виета, например,
из равенства,
где;

в)
применить равенство
,
где
.

Пример 7.

(решили уравнения
ии применили 1-й способ).

Пример 8.

.

В уравнении
свободный коэффициент –10 разделили на
коэффициент, стоящий перед(число 4). Результат разделили на известный
корень 2. Получили 2-й корень.

Затем в уравнении
нашли 2-й корень из условия,
где 2 – известный корень, а 6 – свободный
коэффициент (Теорема Виета).

Пример 9.

.

Скобка
получена как,
а остальные найдены 3-м способом.

ПР6. Раскройте
неопределённость
,
разложив дробь на множители:

1) а)
; б); в);
г);

2) а)
; б); в);
г);

3) а)
; б); в);
г);

4) а)
; б); в);
г).

Пример 10.

.

Предел дробно-рациональной функции в бесконечности

Пусть дана функция
(см. стр. 16) и надо найти.
Оказывается, прився дробь ведёт себя так, как отношение
старших степеней:

.

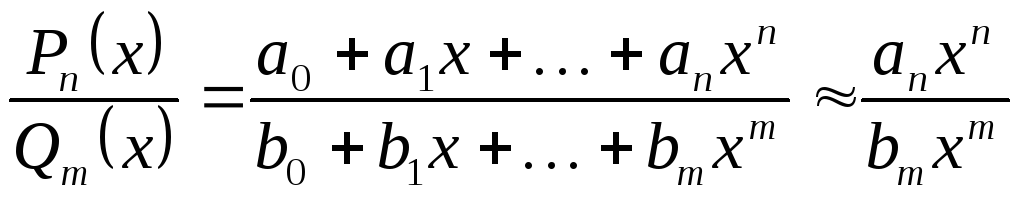
Тогда
.
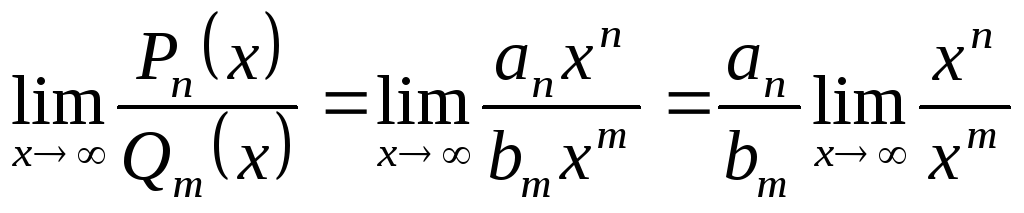
Обозначим.
Возможны 3 случая:

1)
,
тогда,
где

();

2)
,
тогда,
где

();

3)
,
тогда.

Таким образом,
предел равен

а) бесконечности,
если степень числителя больше, чем
степень знаменателя;

б) 0 в противоположном
случае;

в) отношению
старших коэффициентов, если степени
равны.

ПР7.
Найдите пределы

1) а)
; б); в); г); д);

2) а)
; б); в); г);
д);

3) а)
; б); в); г);
д);

ПР8.
Найдите пределы

1) а)
; б); в);

2) а)
; б); в);

3) а)
; б); в).

Пример 11. Оставив
в числителе и в знаменателе старшие
степени, находим

а)
;

б)
;

в)
.

Пример 12.
Оставив старшие степени, видим, что

а)
;

б)
;

в)
.

Обратите внимание,
что знак бесконечности (если таковая
получается) в ответе не указывается.
Тем не менее, если обе старшие степени
– чётные (или если обе нечётные), очевидно,
их отношение всегда положительно, что
можно учесть.

ПР9. Найдите
пределы функций
в точках,,,,,
а также при.

.

Пределы иррациональных функций

Если функция
содержит корень, подставляем, как обычно,
предельную точку. Сложности связаны с
неопределённостью
,
когда приходится умножать числитель и
знаменатель насопряжённое
выражение.

Выражения сопряжены
относительно
разности квадратов,
если их произведение превращается в
разность квадратов по формуле
.

Примеры сопряжённых выражений

а)
сопряжено с,
при этом;

б)
сопряжено с,
и тогда;

в)
сопряжено с,
поскольку

,

причём под корнем
всё остаётся без изменений;

г)
сопряжено с:

.

ПР10. Найдите
пределы иррациональных функций простой
подстановкой:

1) а)
; б); в); г);

2) а)
; б); в); г);

3) а)
; б); в); г);

4) а)
; б); в); г).

Пример 13.
Подставив указанные точки, находим
значения

а)
;

б)

.

ПР11. Раскройте
неопределённость
,
умножив числитель и знаменатель дроби
на подходящее сопряжённое выражение и
сократив одинаковые скобки:

1) а)
; б); в); г);

2) а)
; б); в); г);

3) а)
; б); в); г);

4) а)
; б); в);

г)
; д); е).

Пример 14.

.

Пример 15.

.

Пример 16.

.

ПР12. Умножьте
числитель и знаменатель на выражение,
сопряжённое к числителю, а затем – на
выражение, сопряжённое к знаменателю.
Сократив скобки, раскройте неопределённость
:

1) а)
; б); в); г);

2) а)
; б); в); г);

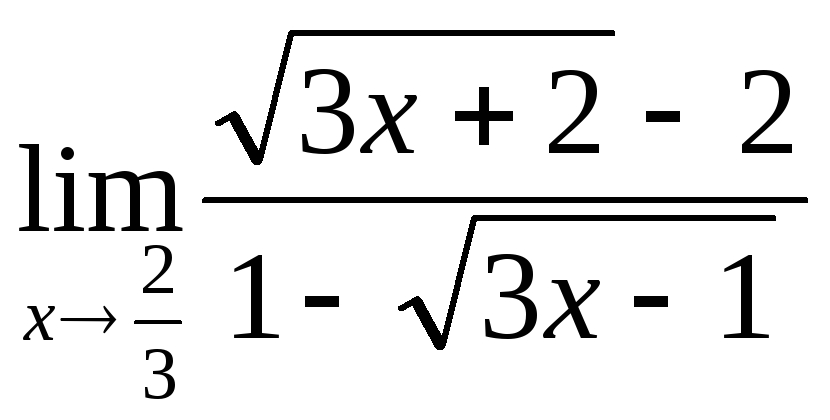
3) а)
; б); в);

4) а)
; б); в).

Пример 17.
Умножим, чтобы получить разность
квадратов:

.

Пример 18.
Так же, как в примере 17,

.

Иррациональные
пределы при
в случае неопределённостинаходят подобно рациональным, при помощи
старших степеней, а в случае неопределённостисводят её кпри помощи сопряжённого выражения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.

Примеры решений нахождения предела функции

Пример 1

Найдите предел функции $limlimits_{xto 1} frac{3x^2+1}{4x-1} $

Решение

Нахождение всегда следует начинать с подстановки значения $x$, расположенного под значком предела в функцию. В данном задании подставляем $x=1$ в дробь. $$ limlimits_{xto 1} frac{3x^2+1}{4x-1} = frac{3cdot 1^2 + 1}{4cdot 1-1} = frac{4}{3} $$

Ответ

$$limlimits_{xto 1} frac{3x^2+1}{4x-1} =frac{4}{3}$$

Пример 2

Найти значение предела $limlimits_{xto 3} frac{sqrt{4x-3}-3}{x^2-9}$

Решение

Подставляем $x=3$ в предел и получаем неопределенность ноль делить на ноль. $$limlimits_{xto 3} frac{sqrt{4x-3}-3}{x^2-9} = frac{0}{0}$$ Это означает, что прямо так сразу как в предыдущем примере получить ответ не удастся. Сначала нужно избавиться от неопределенности путем уничтожения корня. Для этого умножим и разделим одновременно дробь на сопряженное число к числителю, отличающееся от него только знаком. $$limlimits_{xto 3} frac{sqrt{4x-3}-3}{x^2-9} = limlimits_{xto 3} frac{(sqrt{4x-3}-3)(sqrt{4x-3}+3)}{(x^2-9)(sqrt{4x-3}+3)} = $$ Воспользуемся формулой разности квадратов $(a-b)(a+b)=a^2-b^2$ для упрощения выражения в числителе дроби. $$ = limlimits_{xto 3} frac{4x-3-9}{(x^2-9)(sqrt{4x-3}+3)} = limlimits_{xto 3} frac{4(x-3)}{(x^2-9)(sqrt{4x-3}+3)} = $$ Распишем в знаменателе разность квадратов и затем сократим на $x-3$ числитель и знаменатель. $$ = limlimits_{xto 3} frac{4(x-3)}{(x-3)(x+3)(sqrt{4x-3}+3)} = limlimits_{xto 3} frac{4}{(x+3)(sqrt{4x-3}+3)} = $$ Снова пробуем подставить $x=3$ в предел и получаем ответ. $$ = frac{4}{(3+3)(sqrt{4cdot 3-3}+3)} = frac{4}{6 cdot 6} = frac{1}{9} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$limlimits_{xto 3} frac{sqrt{4x-3}-3}{x^2-9} = frac{1}{9}$$

Пример 3

Найти указанный предел функции $limlimits_{xto infty} frac{2x^5+3x^4+x^3+1}{x^5+10x^4+5}$

Решение

Подставляя в предел точку $x=infty$ имеем неопределенность бесконечность делить на бесконечность. $$limlimits_{xto infty} frac{2x^5+3x^4+x^3+1}{x^5+10x^4+5} = frac{infty}{infty} $$ Вынесем за скобки в числителе и знаменателе старшие степени $x$. $$limlimits_{xto infty} frac{2x^5+3x^4+x^3+1}{x^5+10x^4+5} = limlimits_{xto infty} frac{x^5(2+frac{3}{x} + frac{1}{x^2}+frac{1}{x^5})}{x^5(1+frac{10}{x}+frac{5}{x^5})} = $$ Выполняем сокращение дроби на $x^5$. Затем, зная что по определению $limlimits_{xto infty} frac{1}{x} = 0$ проводим вычисление до самого ответа. $$ = limlimits_{xto infty} frac{2+frac{3}{x} + frac{1}{x^2}+frac{1}{x^5}}{1+frac{10}{x}+frac{5}{x^5}} = frac{2+3 cdot 0 + 0 + 0}{1+10 cdot 0 + 5 cdot 0} = frac{2}{1} = 2 $$

Ответ

$$limlimits_{xto infty} frac{2x^5+3x^4+x^3+1}{x^5+10x^4+5} = 2$$

Пример 4

Найти предел $limlimits_{xto 0} frac{4xsin 3x}{x^2}$

Решение

При подстановке $x=0$ в функцию получаем неопределенность ноль делить на ноль. Избавимся от нее с помощью первого замечательного предела $limlimits_{xto 0} frac{sin x}{x} = 1$. Преобразуем выражение в числителе под эту формулу. $$sin 3x = frac{sin 3x}{3x} cdot 3x $$ Тогда выполнив замену в числителе на полученное преобразование получаем новый предел. $$limlimits_{xto 0} frac{4xsin 3x}{x^2} = limlimits_{xto 0} frac{4x cdot frac{sin 3x}{3x}cdot 3x}{x^2} = $$ Итак, замечаем, что $limlimits_{xto 0} frac{sin 3x}{3x} = 1$ и упрощаем предел. $$ = limlimits_{xto 0} frac{4x cdot 3x}{x^2} = limlimits_{xto 0} frac{12x^2}{x^2} = 12$$

Ответ

$$limlimits_{xto 0} frac{4xsin 3x}{x^2} = 12 $$

Пример 5

Найти указанный предел $limlimits_{xto infty} frac{x^2}{e^x} $

Решение

При подстановке $x=infty$ в дробь получаем неопределенность бесконечность делить на бесконечность. $$limlimits_{xto infty} frac{x^2}{e^x} = frac{infty}{infty} $$ Этот предел очень удобно и быстро вычислить по правилу Лопиталя $limlimits_{xto a} frac{f(x)}{g(x)} = limlimits_{xto a} frac{f'(x)}{g'(x)}$. Словами оно означает, что предел отношения двух функций равен пределу отношения производных от этих функций. То есть производная нужно для того, чтобы избавиться от неопределенностей $frac{0}{0}$ или $frac{infty}{infty}$. $$limlimits_{xto infty} frac{x^2}{e^x} = limlimits_{xto infty} frac{(x^2)’}{(e^x)’} = limlimits_{xto infty} frac{2x}{e^x} = $$ Если снова подставить $x=infty$ в последний предел, то окажется, что неопределенность никуда не пропала. Но можно повторить действия ещё раз для последнего предела и тем самым получить числовой ответ. $$ = limlimits_{xto infty} frac{(2x)’}{(e^x)’} = limlimits_{xto infty} frac{2}{e^x} = (frac{2}{infty}) = 0 $$

Ответ

$$limlimits_{xto infty} frac{x^2}{e^x} = 0$$

Если в процессе трансформации, некоторая величина неограниченно приближается к числу a, то это число является пределом (lim) данной величины. Число а всегда находится в интервале определения функции.

Предел функции:
lim⁡x→af(x)=Alim limits _{x rightarrow a} {f(x)} = A

При бесконечном росте к функции 1/x1/x предел стремится к нулю:

lim⁡x→∞1x=0lim limits _{xrightarrow infty}{frac{1}{x}=0}

Правила решения пределов

• предел суммы двух функций равен сумме пределов этих функций;
• предел произведения двух функций равен произведению пределов этих функций;
• предел частного двух функций равен частному пределов этих функций;
• предел числа в степени (корня из числа) равен степени (корню) предела этого числа;
• постоянный множитель (число) выносится за знак предела;
• предел числа равен этому числу

Примеры задач в практическом применении пределов функции

Пример 1

Предел приближения к числу

lim⁡x→15×3+123x−8×4+x2=lim⁡x→15⋅13+123⋅1−814+12=5+123−84+1=15lim limits _{x rightarrow 1} {frac{5x^3+frac{12}{3x}-8^x}{4+x^2}}=lim limits _{x rightarrow 1} {frac{5{cdot1}^3+frac{12}{3cdot1}-8^1}{4+1^2}}=frac{5+ frac{12}{3}-8}{4+1}=frac{1}{5}

Однако не всегда предел приближения к числу разрешается. В некоторых случаях возможна неопределенность.

lim⁡x→1×2−2x+1x−1=lim⁡x→112−2⋅1+11−1=<00>lim limits _{x rightarrow 1}{frac{x^2-2x+1}{x-1}}=lim limits _{x rightarrow 1}{frac{1^2-2cdot1+1}{1-1}}= <frac{0}{0}>

Неопределенность вида <00><frac{0}{0}> возможно разрешить путем разложения числителя или знаменателя на множители.

lim⁡x→1×2−2x+1x−1=lim⁡x→1(x−1)(x−1)x−1=lim⁡x→1(x−1)=1−1=0lim limits _{x rightarrow 1}{frac{x^2-2x+1}{x-1}}=lim limits _{x rightarrow 1}{frac{left(x-1right)left(x-1right)}{x-1}}=lim limits _{x rightarrow 1}{left(x-1right)=1-1=0}

Другой способ раскрытия неопределенности – правило Лопиталя (производная от числителя и знаменателя пока неопределенность не спадет)

lim⁡x→1×2−2x+1x−1=lim⁡x→1(x2−2x+1)‘(x−1)‘=lim⁡x→12x−21=lim⁡x→12x−2=lim⁡x→12⋅1−2=0lim limits _{x rightarrow 1}{frac{x^2-2x+1}{x-1}}=lim limits _{x rightarrow 1}{frac{left(x^2-2x+1right)^`}{left(x-1right)^`}}=lim limits _{x rightarrow 1}{frac{2x-2}{1}}=lim limits _{x rightarrow 1}{2x-2}=lim limits _{x rightarrow 1}{2cdot1-2=0}

Пример 2

Предел приближения к бесконечности

lim⁡x→∞x2−4x+21+x2=lim⁡x→∞∞2−4⋅∞+21+∞2=<∞∞>lim limits _{x rightarrow infty}{frac{x^2-4x+2}{1+x^2}}=lim limits _{x rightarrow infty}{frac{infty^2-4cdot infty+2}{1+ infty^2}}= <frac{infty} {infty}>

Неопределенность вида, <∞∞><frac{infty} {infty}> возможно разрешить только путем деления каждого члена функции на xx в большей степени (в данном примере максимальная степень x2x^2).

lim⁡x→∞x2x2−4xx2+2x21x2+x2x2=lim⁡x→∞1−4x+2x21x2+1lim limits _{x rightarrow infty}{frac{frac{x^2}{x^2}-frac{4x}{x^2}+frac{2}{x^2}}{frac{1}{x^2}+frac{x^2}{x^2}}}=lim limits _{x rightarrow infty}{frac{1-frac{4}{x}+frac{2}{x^2}}{frac{1}{x^2}+1}}

Зная, что lim⁡x→∞1x=0lim limits _{x rightarrow infty}{frac{1}{x}=0},

причем в числителе дроби может быть любое число, а в знаменателе х любой степени, имеем

lim⁡x→∞1−4x+2x21x2+1=lim⁡x→∞1−4∞+2∞21∞2+1=lim⁡x→∞1−0+00+1=11=1lim limits _{x rightarrow infty}{frac{1-frac{4}{x}+frac{2}{x^2}}{frac{1}{x^2}+1}}=lim limits _{x rightarrow infty}{frac{1-frac{4}{infty}+frac{2}{infty^2}}{frac{1}{infty^2}+1}}=lim limits _{x rightarrow infty}{frac{1-0+0}{0+1}=frac{1}{1}}=1

Другие неопределенности

• 1∞1^infty – раскрытие через второй замечательный предел;
• 000^0, ∞0infty^0 – необходимо найти логарифм предела;
• 0⋅∞0cdotinfty, ∞−∞infty-infty – преобразование функции, правило Лопиталя.

Замечательные пределы (математические тождества)

lim⁡x→0sinxx=1lim limits _{x rightarrow 0}{frac{sinx}{x}=1}

lim⁡x→∞(1+1x)x=elim limits _{x rightarrow infty}{left(1+frac{1}{x}right)^x=e}

Примеры применения замечательных пределов

Пример 1

Вычислить предел функции lim⁡x→0sin3x9xlim limits _{x rightarrow 0}{frac{sin3x}{9x}}

lim⁡x→0sin⁡3x9x=<00>lim limits _{x rightarrow 0} frac{sin3x}{9x}=<frac{0}{0}>

Выполним преобразования

lim⁡x→0sin3x9x=lim⁡x→0sin⁡3×3⋅3x=13lim⁡x→0sin3x3x=13⋅1=13lim limits _{x rightarrow 0}{frac{sin3x}{9x}}=lim limits _{x rightarrow 0}{frac{sin3x}{3cdot3x}}=frac{1}{3}lim limits _{x rightarrow 0}{frac{sin3x}{3x}}=frac{1}{3}cdot1=frac{1}{3}

Пример 2

Вычислить предел функции

lim⁡x→∞(x+5x+4)(x+4)lim limits _{x rightarrow infty} (frac {x+5}{x+4})^{(x+4)}

lim⁡x→∞(x+5x+4)(x+4)=<∞∞>∞lim limits _{x rightarrow infty} (frac {x+5}{x+4})^{(x+4)}= <frac {infty} {infty}>^ {infty}

Выполним преобразования (прибавление и отнимание единицы)

lim⁡x→∞(x+5x+4)(x+4)=lim⁡x→∞(1−1+x+5x+4)(x+4)=lim⁡x→∞(1−x+4x+4+x+5x+4)(x+4)=lim limits _{x rightarrow infty} (frac {x+5}{x+4})^{(x+4)}=lim limits _{x rightarrow infty} (1-1+frac {x+5}{x+4})^{(x+4)}= lim limits _{x rightarrow infty} (1-frac {x+4}{x+4} + frac {x+5}{x+4})^{(x+4)}=

lim⁡x→∞(1+x+5−x−4x+4)(x+4)=lim⁡x→∞(1+1x+4)(x+4)=elim limits _{x rightarrow infty} (1+frac {x+5-x-4}{x+4})^{(x+4)}= lim limits _{x rightarrow infty} (1+frac {1}{x+4})^{(x+4)}=e

Пределы находят практическое применение в различных областях математики, геометрии, экономики и финансов, поэтому умение разрешать такие задачи и быстро раскрывать неопределенности крайне необходимо для достижения иной главной цели.

Тест по теме «Примеры решения пределов»