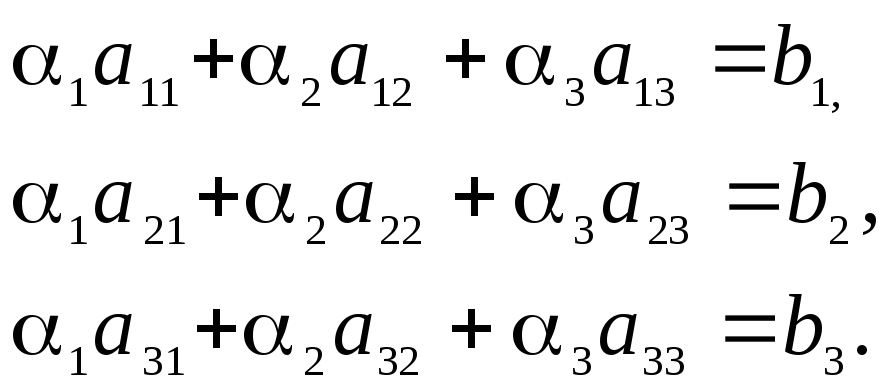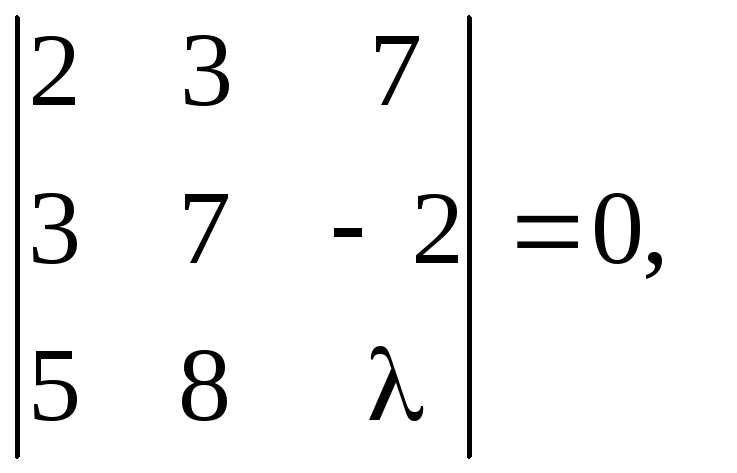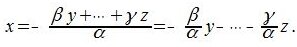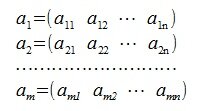Как найти линейно независимые векторы матрицы

Линейно зависимые и линейно независимые вектора.

Навигация по странице:

• Определение линейной комбинации векторов
• Определение линейно независимой комбинации векторов
• Определение линейно зависимой комбинации векторов
• Свойства линейно зависимых векторов
• Примеры задач на линейную зависимость и линейную независимость векторов

Определение. Линейной комбинацией векторов a₁, …, a_n с коэффициентами x₁, …, x_n называется вектор

x₁a₁ + … + x_na_n.

Определение. Линейная комбинация x₁a₁ + … + x_na_n называется тривиальной, если все коэффициенты x₁, …, x_n равны нулю.

Определение. Линейная комбинация x₁a₁ + … + x_na_n называется нетривиальной, если хотя быбы один из коэффициентов x₁, …, x_n не равен нулю.

Определение. Вектора a₁, …, a_n называются линейно независимыми, если не существует нетривиальной комбинации этих векторов равной нулевому вектору.

То есть вектора a₁, …, a_n линейно независимы если x₁a₁ + … + x_na_n = 0 тогда и только тогда, когда x₁ = 0, …, x_n = 0.

Определение. Вектора a₁, …, a_n называются линейно зависимыми, если существует нетривиальная комбинация этих векторов равная нулевому вектору.

Свойства линейно зависимых векторов:

• Для 2-х и 3-х мерных векторов.

  Два линейно зависимые вектора – коллинеарные. (Коллинеарные вектора – линейно зависимы.)
  .

• Для 3-х мерных векторов.

  Три линейно зависимые вектора – компланарные. (Три компланарные вектора – линейно зависимы.)

• Для n -мерных векторов.

  n + 1 вектор всегда линейно зависимы.

Примеры задач на линейную зависимость и линейную независимость векторов:

Пример 1. Проверить будут ли вектора a = {3; 4; 5}, b = {-3; 0; 5}, c = {4; 4; 4}, d = {3; 4; 0} линейно независимыми.

Решение:

Вектора будут линейно зависимыми, так как размерность векторов меньше количества векторов.

Пример 2. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1} линейно независимыми.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

x₁a + x₂b + x₃c₁ = 0

Это векторное уравнение можно записать в виде системы линейных уравнений

	x1 + x2 = 0
x1 + 2x2 – x3 = 0
x1 + x3 = 0

Решим эту систему используя метод Гаусса

1100
12-10
1010

~

из второй строки вычтем первую; из третей строки вычтем первую:

1100
1 – 12 – 1-1 – 00 – 0
1 – 10 – 11 – 00 – 0

~

1100
01-10
0-110

~

из первой строки вычтем вторую; к третей строке добавим вторую:

1 – 01 – 10 – (-1)0 – 0
01-10
0 + 0-1 + 11 + (-1)0 + 0

~

1010
01-10
0000

Данное решение показывает, что система имеет множество решений, то есть существует не нулевая комбинация значений чисел x₁, x₂, x₃ таких, что линейная комбинация векторов a, b, c равна нулевому вектору, например:

–a + b + c = 0

а это значит вектора a, b, c линейно зависимы.

Ответ: вектора a, b, c линейно зависимы.

Пример 3. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 2} линейно независимыми.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

x₁a + x₂b + x₃c₁ = 0

Это векторное уравнение можно записать в виде системы линейных уравнений

	x1 + x2 = 0
x1 + 2x2 – x3 = 0
x1 + 2x3 = 0

Решим эту систему используя метод Гаусса

1100
12-10
1020

~

из второй строки вычтем первую; из третей строки вычтем первую:

1100
1 – 12 – 1-1 – 00 – 0
1 – 10 – 12 – 00 – 0

~

1100
01-10
0-120

~

из первой строки вычтем вторую; к третей строке добавим вторую:

1 – 01 – 10 – (-1)0 – 0
01-10
0 + 0-1 + 12 + (-1)0 + 0

~

1010
01-10
0010

~

из первой строки вычтем третью; к второй строке добавим третью:

1 – 00 – 01 – 10 – 0
0 + 01 + 0-1 + 10 + 0
0010

~

1010
0100
0010

Данное решение показывает, что система имеет единственное решение x₁ = 0, x₂ = 0, x₃ = 0, а это значит вектора a, b, c линейно независимые.

Ответ: вектора a, b, c линейно независимые.

1.
Линейно зависимые и независимые системы
векторов. Пусть
– произвольное вещественное векторное
пространство,,.Линейной
комбинацией векторов
с коэффициентаминазывается вектор,
получаемый по правилу

.

Линейная
комбинация
называетсянетривиальной,
если в ней хотя бы один из коэффициентов
отличен от нуля. Линейная комбинация
виданазываетсятривиальной;
она, очевидно, равна нулевому вектору
.

Система
векторов
называетсялинейно
зависимой,
если существует хотя бы одна нетривиальная
линейная комбинация этих векторов,
равная нулевому вектору. В противном
случае, т.е. если только тривиальная
линейная комбинация данных векторов
равна нулевому вектору, векторы называются
линейно
независимыми.

ТЕОРЕМА
(критерий линейной зависимости). Для
того чтобы система векторов
линейного пространства была линейно
зависимой, необходимо и достаточно,
чтобы, по крайней мере, один из этих
векторов являлся линейной комбинацией
остальных.

1)
Если среди векторов
имеется хотя бы один нулевой вектор, то
вся система векторов линейно зависима.

2)
Если среди векторов
некоторые образуют линейно зависимую
систему, то и вся системалинейно зависима.

Типовые
примеры.

1.
Являются ли линейно зависимыми
(независимыми) векторы

►По
определению линейная зависимость или
независимость векторов устанавливается
исходя из условия равенства нулю линейной
комбинации этих векторов

или
в развёрнутом виде

Если
эти равенства выполняются при условии,
что хотя бы один из коэффициентов
отличен от нуля, то векторы линейно
зависимы. Записанные равенства
представляют собой однородную систему
линейных уравнений относительно
коэффициентов.
Эта система имеет нетривиальное решение
(т.е. решение, в котором не всеодновременно равны нулю) только при
условии равенства нулю определителя
системы. В рассматриваемом случае
определитель системы равен

Таким
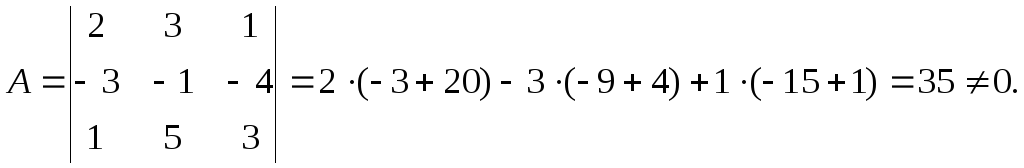
образом система имеет лишь тривиальное
решение и исходная совокупность векторов
линейно независима.◄

2.
При каких
векторлинейно выражается через векторы

►По
условию задачи надо найти такие
,
при которых выполняется равенство

или
в развёрнутом виде

Записанные
соотношения представляют собой систему
неоднородных линейных уравнений
относительно
– коэффициентов линейной комбинации. В
соответствии с теоремой Кронекера-Капелли
эта система совместна, если ранг основной
матрицы системы равен рангу расширенной
матрицы. Выпишем расширенную матрицу
для заданных условий:

Сначала
определим ранг основной матрицы. Видно,
что отличные от нуля миноры второго
порядка в матрице имеются, наТиповой
пример, минор, стоящий в левом верхнем
углу. Вычислим теперь минор третьего
порядка (определитель) основной матрицы

.

Следовательно,
ранг основной матрицы равен двум. Таким
образом рассматриваемая система будет
совместна, если ранг расширенной матрицы
также будет равен двум. Для этого
необходимо, чтобы второй минор третьего
порядка расширенной матрицы был равен
нулю, т.е.

откуда
следует

◄

2.
Базис и размерность
линейного пространства.
Фундаментальным
вопросом теории линейных пространств
является вопрос о том, можно ли, а если
можно, то как, произвольный вектор
пространства представить в виде линейной
комбинации фиксированного набора
векторов из этого пространства. Далее
мы получим ответ на этот вопрос.

Система
линейно независимых векторов
векторного пространстваназываетсябазисом
этого пространства, если любой вектор
из
может быть представлен в виде линейной
комбинации векторов этой системы, т.е.
для каждого векторасуществуют вещественные числатакие, что имеет место равенство

.

Это
равенство называется разложением
вектора

по базису
,
а числаназываютсякоординатами
вектора
относительно базиса
(или в базисе)
.

Утверждение.Базисом линейного пространства решений
одно­родной системы является ее
фундаментальная система реше­ний.

ТЕОРЕМА
(о единственности разложения по базису).
Каждый вектор
пространстваможет быть разложен по базису
единственным
образом, т.е. координаты каждого вектора
в базисе

определяются однозначно.

Главное
значение базиса заключается в том, что
операции сложения векторов и умножения
их на числа при задании базиса превращаются
в соответствующие операции над числами
– координатами этих векторов. А именно,
справедлива следующая

ТЕОРЕМА.
При сложении
двух любых векторов линейного пространства
их координаты (относительно любого
базиса пространства) складываются; при
умножении
произвольного вектора на любое число
все координаты этого вектора умножаются
на.

Типовой
пример. Исследуем вопрос о базисе
пространства,
введенного ранее при рассмотрении
Типовой примеров векторных пространств.
Покажем, чтоэлементовуказанного пространства образуют базис.

►Во-первых, эти векторы
линейно независимы. Проверка линейной
независимости набора
состоит в определении значений,
при которых возможно равенство

.

Но в силу только что
доказанной теоремы

,

а последний вектор
является нулевым лишь при условии
.
Во-вторых, всякий векторзаведомо представим в виде линейной
комбинации векторов:и, значит, наборобразует базис. ◄

Векторное
пространство
называется
-мерным,
если в нем существуютлинейно независимых векторов, а любыевекторов уже являются линейно зависимыми.
При этом числоназываетсяразмерностьюпространства.

Размерность
векторного пространства, состоящего
из одного нулевого вектора, принимается
равной нулю.

Размерность
пространства
обычно обозначают символом.

Векторное
пространство
называетсябесконечномерным, если
в нем существует любое число линейно
независимых векторов. В этом случае
пишут.

Выясним
связь между понятиями базиса и размерности
пространства.

ТЕОРЕМА.Если
– векторное пространство размерности,
то любыелинейно независимых векторов этого
пространства образуют его базис.

ТЕОРЕМА.Если векторное пространство
имеет базис, состоящий извекторов, то.

Утверждение.
Rⁿ=n.

Линейная зависимость и линейная независимость векторов

Векторы x, y, …, z называются  линейно зависимыми векторами, если существуют числа α, β, …, γ, из которых хотя бы одно отлично от нуля, такие что справедливо равенство:

Другими словами линейная зависимость группы векторов означает, что существует среди них вектор, который можно представить линейной комбинацией других векторов этой группы.

Допустим 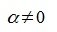. Тогда

Следовательно вектор x линейно зависим из векторов этой группы.

Векторы x, y, …, z называются линейно  независимыми векторами, если из равенства (0) следует, что

α=β= …= γ=0.

То есть группы векторов линейно независимы, если ни один вектор не может быть представлен линейной комбинацией других векторов этой группы.

Определение линейной зависимости векторов

Пусть заданы m векторов строк порядка n:

(1)

Составим матрицу из этих векторов и добавим с правой стороны столбец, в котором запишем индексы соответствующих строк:

(2)

Сделав Гауссово исключение, приведем матрицу (2) к верхнему треугольному виду. Элементы последнего столбца изменяются только тогда, когда строки переставляются. После m шагов исключения получим:

где i₁, i₂, …, i_m – индексы строк, полученные при возможной перестановки строк. Рассматривая полученные строки из индексов строк исключаем те, которые соответствуют нулевым вектором строк. Оставшиеся строки образуют линейно независимые векторы. Отметим, что при составлении матрицы (2) изменяя последовательность векторов строк, можно получить другую группу линейно независимых векторов. Но подпространство, которую оба эти группы векторов образуют совпадают.

В линейной алгебре линейная зависимость — это свойство, которое может иметь подмножество линейного пространства. При линейной зависимости существует нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу. При отсутствии такой комбинации, то есть, когда коэффициенты единственной такой линейной комбинации равны нулю, множество называется линейно независимым.

Пример[править | править код]

В векторы , и линейно независимы, так как уравнение

имеет только одно — тривиальное — решение.

Векторы и являются линейно зависимыми, так как

а, значит,

Определение[править | править код]

Пусть будет линейное пространство над полем и . называется линейно независимым множеством, если любое его конечное подмножество является линейно независимым.

Конечное множество называется линейно независимым, если единственная линейная комбинация, равная нулю, тривиальна, то есть все её коэффициенты равны нулю:

Если существует такая линейная комбинация с минимум одним , называется линейно зависимым. Обратите внимание, что в первом равенстве подразумевается , а во втором .

Свойства[править | править код]

Применение[править | править код]

Линейные системы уравнений

Линейная система уравнений, где  — количество переменных, имеет однозначное решение тогда и только тогда, когда столбцы её основной матрицы являются линейно независимыми.

Ранг матриц

Ранг матрицы равен максимальному числу её линейно независимых строк или столбцов.

Геометрический смысл

Базис

Базис линейного пространства является максимальным множеством линейно независимых векторов (максимальность понимается в том смысле, что при добавлении к этому множеству любого вектора этого пространства новое множество уже не будет линейно независимым).

См. также[править | править код]

• Базис
• Ранг матрицы
• Система линейных уравнений
• Аффинная независимость