Все курсы > Оптимизация > Занятие 4 (часть 1)
Прежде чем обратиться к теме множественной линейной регрессии, давайте вспомним, что было сделано до сих пор. Возможно, будет полезно посмотреть эти уроки, чтобы освежить знания.
- В рамках вводного курса мы узнали про моделирование взаимосвязи переменных и минимизацию ошибки при обучении алгоритма, а также научились строить несложные модели линейной регрессии с помощью библиотеки sklearn.
- При изучении объектно-ориентированного программирования мы создали класс простой линейной регрессии. Сегодня эти знания пригодятся при создании классов более сложных моделей.
- Также рекомендую вспомнить умножение векторов и матриц.
- Кроме того, в рамках текущего курса по оптимизации мы познакомились с понятием производной и методом градиентного спуска, а также построили модель простой линейной регрессии (использовав метод наименьших квадратов и градиент).
- Наконец, на прошлом занятии мы вновь поговорили про взаимосвязь переменных.
В рамках сегодняшнего занятия мы с нуля построим несколько алгоритмов множественной линейной регрессии.
Регрессионный анализ
Прежде чем обратиться к практике, обсудим некоторые теоретические вопросы регрессионного анализа.
Генеральная совокупность и выборка
Как мы уже знаем, множество всех имеющихся наблюдений принято считать генеральной совокупностью (population). И эти наблюдения, если в них есть взаимосвязи, можно теоретически аппроксимировать, например, линией регрессии. При этом важно понимать, что это некоторая идеальная модель, которую мы никогда не сможем построить.
Единственное, что мы можем сделать, взять выборку (sample) и на ней построить нашу модель, предполагая, что если выборка достаточно велика, она сможет достоверно описать генсовокупность.
Отклонение прогнозного значения от фактического для «идеальной» линии принято называть ошибкой (error или true error).
$$ varepsilon = y-hat{y} $$
Отклонение прогноза от факта для выборочной модели (которую мы и строим) называют остатками (residuals или residual error).
$$ varepsilon = y-f(x) $$
В этом смысле среднеквадратическую ошибку (mean squared error, MSE) корректнее называть средними квадратичными остатками (mean squared residuals).
На практике ошибку и остатки нередко используют как взаимозаменяемые термины.
Уравнение множественной линейной регрессии
Посмотрим на уравнение множественной линейной регрессии.
$$ y = theta_0 + theta_1x_1 + theta_2x_2 + … + theta_jx_j + varepsilon $$
В отличие от простой линейной регрессии в данном случае у нас несколько признаков x (независимых переменных) и несколько коэффициентов $ theta $ («тета»).
Интерпретация результатов модели
Коэффициент $ theta_0 $ задает некоторый базовый уровень (baseline) при условии, что остальные коэффициенты равны нулю и зачастую не имеет смысла с точки зрения интерпретации модели (нужен лишь для того, что поднять линию на нужный уровень).
Параметры $ theta_1, theta_2, …, theta_n $ показывают изменение зависимой переменной при условии «неподвижности» остальных коэффициентов. Например, каждая дополнительная комната может увеличивать цену дома в 1.3 раза.
Переменная $ varepsilon $ (ошибка) представляет собой отклонение фактических данных от прогнозных. В этой переменной могут быть заложены две составляющие. Во-первых, она может включать вариативность целевой переменной, описанную другими (не включенными в нашу модель) признаками. Во-вторых, «улавливать» случайный шум, случайные колебания.
Категориальные признаки
Модель линейной регрессии может включать категориальные признаки. Продолжая пример с квартирой, предположим, что мы строим модель, в которой цена зависит от того, находится ли квартира в центре города или в спальном районе.
Перед этим переменную необходимо закодировать, создав, например, через Label Encoder признак «центр», который примет значение 1, если квартира в центре, и 0, если она находится в спальном районе.
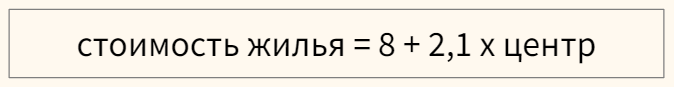
В модели, представленной выше, если квартира находится в центре (переменная «центр» равна единице), ее стоимость составит 10,1 миллиона рублей, если на окраине (переменная «центр» равна нулю) — лишь восемь.
Для категориального признака с множеством классов можно использовать one-hot encoding, если между классами признака отсутствует иерархия,
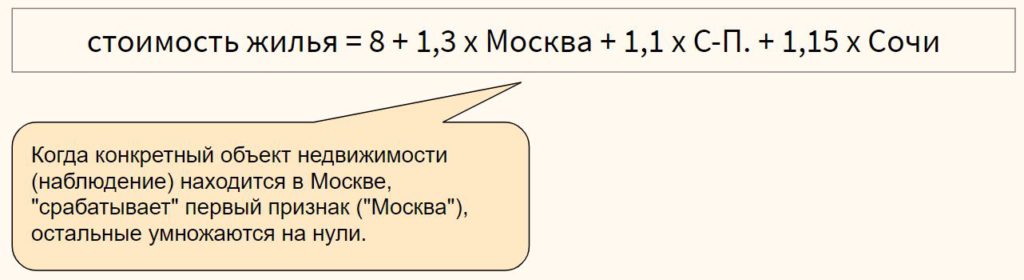
или, например, ordinal encoding в случае наличия иерархии классов в признаке

Выбросы в линейной регрессии
Как и коэффициент корреляции Пирсона, модель линейной регрессии чувствительна к выбросам (outliers), то есть наблюдениям, серьезно выпадающим из общей совокупности. Сравните рисунки ниже.
При наличии выброса (слева), линия регрессии имеет наклон и может использоваться для построения прогноза. Удалив это наблюдение (справа), линия регрессии становится горизонтальной и построение прогноза теряет смысл.
При этом различают два типа выбросов:
- горизонтальные выбросы или влиятельные точки (leverage points) — они сильно отклоняются от среднего по оси x; и
- вертикальные выбросы или просто выбросы (influential points) — отклоняются от среднего по оси y
Ключевое отличие заключается в том, что вертикальные выбросы влияют на наклон модели (изменяют ее коэффициенты), а горизонтальные — нет.
Сравним два графика.
На левом графике черная точка (leverage point) сильно отличается от остальных наблюдений, но наклон прямой линии регрессии с ее появлением не изменился. На правом графике, напротив, появление выброса (influential point) существенно изменяет наклон прямой.
На практике нас конечно больше интересуют influential points, потому что именно они существенно влияют на качество модели.
Если в простой линейной регрессии мы можем оценить leverage и influence наблюдения графически⧉, в многомерной модели это сделать сложнее. Можно использовать график остатков (об этом ниже) или применить один из уже известных нам методов выявления выбросов.
Про выявление leverage и infuential points можно почитать здесь⧉.
Допущения модели регрессии
Применение алгоритма линейной регрессии предполагает несколько допущений (assumptions) или условий, при выполнении которых мы можем говорить о качественно построенной модели.
1. Правильный выбор модели
Вначале важно убедиться, что данные можно аппроксимировать с помощью линейной модели (correct model specification).
Оценить распределение данных можно через график остатков (residuals plot), где по оси x отложен прогноз модели, а на оси y — сами остатки.
В отличие от простой линейной регрессии мы не используем точечную диаграмму X vs. y, потому что хотим оценить зависимость целевой переменной от всех признаков сразу.
Остатки модели относительно ее прогнозных значений должны быть распределены случайным образом без систематической составляющей (residuals do not follow a pattern).
- Если вы попробовали применить линейную модель с коэффициентами первой степени ($x_n^1$) и выявили некоторый паттерн в данных, можно попробовать полиномиальную или какую-либо еще функцию (об этом ниже).
- Кроме того, количественные признаки можно попробовать преобразовать таким образом, чтобы их можно было аппроксимировать прямой линией.
- Если ни то, ни другое не помогло, вероятно данные не стоит моделировать линейной регрессией.
Также замечу, что график остатков показывает выбросы в данных.
2. Нормальность распределения остатков
Среднее значение остатков должно быть равно нулю. Если это не так, и среднее значение меньше нуля (скажем –5), то это значит, что модель регулярно недооценивает (underestimates) фактические значения. В противном случае, если среднее больше нуля, переоценивает (overestimated).
Кроме того, предполагается, что остатки следуют нормальному распределению.
$$ varepsilon sim N(0, sigma) $$
Проверить нормальность остатков можно визуально с помощью гистограммы или рассмотренных ранее критериев нормальности распределения.
Если остатки не распределены нормально, мы не сможем провести статистические тесты на значимость коэффициентов или построить доверительные интервалы. Иначе говоря, мы не сможем сделать статистически значимый вывод о надежности нашей модели.
Причинами могут быть (1) выбросы в данных или (2) неверный выбор модели. Решением может быть, соответственно, исследование выбросов, выбор новой модели и преобразование как признаков, так и целевой переменной.
3. Гомоскедастичность остатков
Гомоскедастичность (homoscedasticity) или одинаковая изменчивость остатков предполагают, что дисперсия остатков не изменяется для различных наблюдений. Противоположное и нежелательное явление называется гетероскедастичностью (heteroscedasticity) или разной изменчивостью.
Гетероскедастичность остатков показывает, что модель ошибается сильнее при более высоких или более низких значениях признаков. Как следствие, если для разных прогнозов у нас разная погрешность, модель нельзя назвать надежной (robust).
Как правило, гетероскедастичность бывает изначально заложена в данные. Ее можно попробовать исправить через преобразование целевой переменной (например, логарифмирование)
4. Отсутствие мультиколлинеарности
Еще одним важным допущением является отсутствие мультиколлинеарности. Мультиколлинеарность (multicollinearity) — это корреляция между зависимыми переменными. Например, если мы предсказываем стоимость жилья по квадратным метрам и количеству комнат, то метры и комнаты логичным образом также будут коррелировать между собой.
Почему плохо, если такая корреляция существует? Базовое предположение линейной регрессии — каждый коэффициент $theta$ оказывает влияние на конечный результат при условии, что остальные коэффициенты постоянны. При мультиколлинеарности на целевую переменную оказывают эффект сразу несколько признаков, и мы не можем с точностью интерпретировать каждый из них.
Также говорят о том, что нужно стремиться к экономной (parsimonious) модели то есть такой модели, которая при наименьшем количестве признаков в наибольшей степени объясняет поведение целевой переменной.
Variance inflation factor
Расчет коэффициента
Variance inflation factor (VIF) или коэффициент увеличения дисперсии позволяет выявить корреляцию между признаками модели.
Принцип расчета VIF заключается в том, чтобы поочередно делать каждый из признаков целевой переменной и строить модель линейной регрессии на основе оставшихся независимых переменных. Например, если у нас есть три признака $x_1, x_2, x_3$, мы поочередно построим три модели линейной регрессии: $x_1 sim x_2 + x_3, x_2 sim x_1 + x_3$ и $x_3 sim x_1 + x_3$.
Обратите внимание на новый для нас формат записи целевой и зависимых переменных модели через символ $sim$.
Затем для каждой модели (то есть для каждого признака $x_1, x_2, x_3$) мы рассчитаем коэффициент детерминации $R^2$. Если он велик, значит данный признак можно объяснить с помощью других независимых переменных и имеется мультиколлинеарность. Если $R^2$ мал, то нельзя и мультиколлинеарность отсутствует.
Теперь рассчитаем VIF на основе $R^2$:
$$ VIF = frac{1}{1-R^2} $$
При таком способе расчета большой (близкий к единице) $R^2$ уменьшит знаменатель и существенно увеличит VIF, при небольшом коэффициенте детерминации коэффициент увеличения дисперсии наоборот уменьшится.
Замечу, что $1-R^2$ принято называть tolerance.
Другие способы выявления мультиколлинеарности
Для выявления корреляции между независимыми переменными можно использовать точечные диаграммы или корреляционные матрицы. При этом важно понимать, что в данном случае мы выявляем зависимость лишь между двумя признаками. Корреляцию множества признаков выявляет только коэффициент увеличения дисперсии.
Интерпретация VIF
VIF находится в диапазон от единицы до плюс бесконечности. Как правило, при интерпретации показателей variance inflation factor придерживаются следующих принципов:
- VIF = 1, между признаками отсутствует корреляция
- 1 < VIF $leq$ 5 — умеренная корреляция
- 5 < VIF $leq$ 10 — высокая корреляция
- Более 10 — очень высокая
После расчета VIF можно по одному удалять признаки с наибольшей корреляцией и смотреть как изменится этот показатель для оставшихся независимых переменных.
5. Отсутствие автокорреляции остатков
На занятии по временным рядам (time series), мы сказали, что автокорреляция (autocorrelation) — это корреляция между значениями одной и той же переменной в разные моменты времени.
Применительно к модели линейной регрессии автокорреляция целевой переменной (для простой линейной регрессии) и автокорреляция остатков, residuals autocorrelation (для модели множественной регрессии) означает, что результат или прогноз зависят не от признаков, а от самой этой целевой переменной. В такой ситуации признаки теряют свою значимость и применение модели регрессии становится нецелесообразным.
Причины автокорреляции остатков
Существует несколько возможных причин:
- Прогнозирование целевой переменной с высокой автокорреляцией (например, если мы моделируем цену акций с помощью других переменных, то можем ожидать высокую автокорреляцию остатков, поскольку цена акций как правило сильно зависит от времени)
- Удаление значимых признаков
- Другие причины
Автокорреляция первого порядка
Дадим формальное определение автокорреляции первого порядка (first order correlation), то есть автокорреляции с лагом 1.
$$ varepsilon_t = pvarepsilon_{t-1} + u_t $$
где $u_t$ — некоррелированная при различных t одинаково распределенная случайная величина (independent and identically distributed (i.i.d.) random variable), а $p$ — коэффициент автокорреляции, который находится в диапазоне $-1 < p < 1$. Чем он ближе к нулю, тем меньше зависимость остатка $varepsilon_t$ от остатка предыдущего периода $varepsilon_{t-1}$.
Такое уравнение также называется схемой Маркова первого порядка (Markov first-order scheme).
Обратите внимание, что для модели автокорреляции первого порядка коэффициент автокорреляции $p$ совпадает с коэффициентом авторегрессии AR(1) $varphi$.
$$ y_t = c + varphi cdot y_{t-1} $$
Разумеется, мы можем построить модель автокорреляции, например, третьего порядка.
$$ varepsilon_t = p_1varepsilon_{t-1} + p_2varepsilon_{t-2} + p_3varepsilon_{t-3} + u_t $$
Выявление автокорреляции остатков
Для выявления автокорреляции остатков можно использовать график последовательности и график остатков с лагом 1, график автокорреляционной функции или критерий Дарбина-Уотсона.
График последовательности и график остатков с лагом 1
На графике последовательности (sequence plot) по оси x откладывается время (или порядковый номер наблюдения), а по оси y — остатки модели. Кроме того, на графике остатков с лагом 1 (lag-1 plot) остатки (ось y) можно сравнить с этими же значениями, взятыми с лагом 1 (ось x).
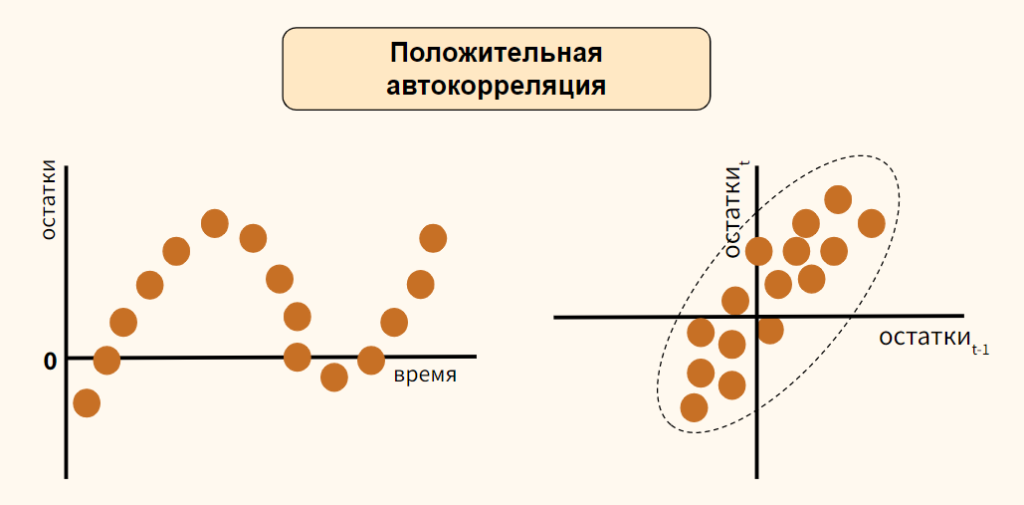
Рассмотрим вариант положительной автокорреляции (positive autocorrelation) на графиках остатков типа (а) и (б).
Как вы видите, при положительной автокорреляции в большинстве случаев, если одно наблюдение демонстрирует рост по отношению к предыдущему значению, то и последующее будет демонстрировать рост, и наоборот.
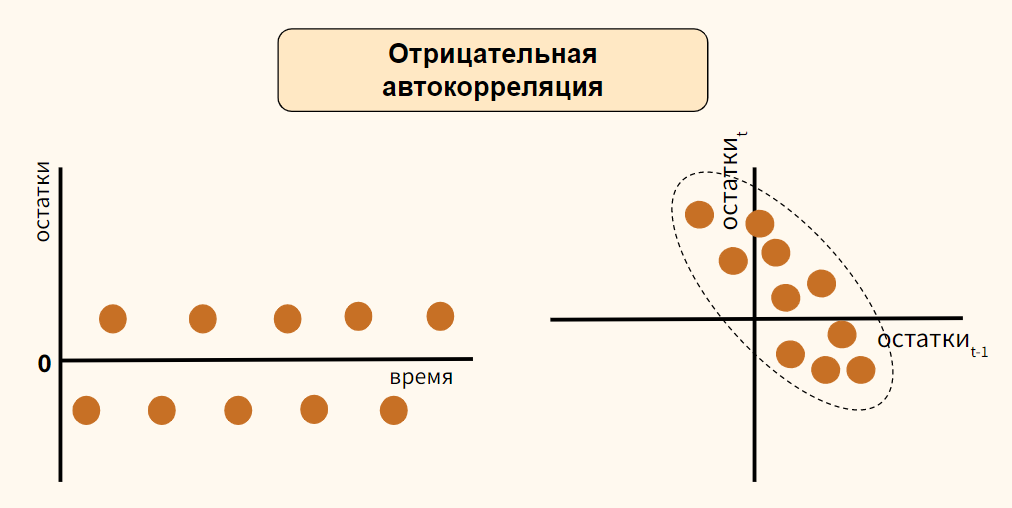
Теперь обратимся к отрицательной автокорреляции (negative autocorrelation).
Здесь наоборот, если одно наблюдение демонстрирует рост показателя по отношению к предыдущему значению, то последующее наблюдение будет наоборот снижением. Опять же справедливо и обратное утверждение.
В случае отсутствия автокорреляции мы не должны увидеть на графиках какого-либо паттерна.
График автокорреляционной функции
Еще один способ выявить автокорреляцию — построить график автокорреляционной функции (autocorrelation function, ACF).
Напомню, такой график показывает автокорреляцию данных с этими же данными, взятыми с первым, вторым и последующими лагами.
Критерий Дарбина-Уотсона
Количественным выражением автокорреляции является критерий Дарбина-Уотсона (Durbin-Watson test). Этот критерий выявляет только автокорреляцию первого порядка.
- Нулевая гипотеза утверждает, что такая автокорреляция отсутствует ($p=0$),
- Альтернативная гипотеза соответственно утверждает, что присутствует
- Положительная ($p approx -1$) или
- Отрицательная ($p approx 1$) автокорреляция
Значение теста находится в диапазоне от 0 до 4.
- При показателе близком к двум можно говорить об отсутствии автокорреляции
- Приближение к четырем говорит о положительной автокорреляции
- К нулю, об отрицательной
Как избавиться от автокорреляции
Автокорреляцию можно преодолеть, добавив значимый признак в модель, выбрав иной тип модели (например, полиномиальную регрессию) или в целом перейдя к моделированию и прогнозированию временного ряда.
Рассмотрение этих методов находится за рамками сегодняшнего занятия. Перейдем к практике.
Определение множественной линейной регрессии
Модели множественной линейной регрессии — это тип модели регрессии, который имеет дело с одной зависимой переменной и несколькими независимыми переменными. Регрессионный анализ — это статистический метод или техника, используемая для определения взаимосвязей между переменными, имеющими причинно-следственную связь. Регрессии также могут показать, насколько близко и точно можно определить взаимосвязь.
Регрессии полезны для количественной оценки связи или взаимосвязи между одной переменной и другими переменными, ответственными за нее. Результаты позже используются для прогнозирования вовлеченных компонентов. Большинство эмпирических экономических исследований включают регрессию. Они также широко используются в социологии, статистике и психологии.
Оглавление
- Определение множественной линейной регрессии
- Объяснение множественной линейной регрессии
- Формула
- Пример
- Предположения
- Линейность:
- Постоянная дисперсия:
- Особые случаи:
- Нормальность:
- Мультиколинеарность:
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
- Множественный линейный регрессионный анализ — это статистический метод или инструмент для обнаружения причинно-следственных корреляций между переменными. Регрессии отражают, насколько сильны и стабильны отношения.
- Модель множественной линейной регрессии — это простая модель линейной регрессии, но с расширениями. В линейной регрессии есть только одна объясняющая переменная. Здесь имеются различные объясняющие переменные.
- Это помогает делать прогнозы для необходимой информации от задействованных компонентов.
- Его применение включает определение процентного содержания жира в организме у взрослых. Выявление факторов, которые могут повлиять на образование, чтобы помочь правительству разработать политику и т. д.
Объяснение множественной линейной регрессии
Множественные модели линейной регрессии помогают установить взаимосвязь между двумя или более независимыми переменными. Независимые переменные. Независимая переменная — это объект, период времени или входное значение, изменения которого используются для оценки влияния на измеряемое выходное значение (т. е. конечную цель). в математическом, статистическом или финансовом моделировании. Подробнее и одной зависимой переменной. Эта модель является расширением простой модели линейной регрессии. В базовой линейной регрессии есть только одна объясняющая переменная. Однако в множественных линейных регрессиях есть несколько объясняющих переменных. Поэтому, когда в соединении есть две или более контролируемых переменных, применяется Множественная линейная регрессия. Особенно это актуально в следующих случаях:
- Чтобы найти степень или степень, в которой две или более независимых переменных и одна зависимая переменная связаны (например, как осадки, температура, рН почвы и количество добавленных удобрений влияют на рост плодов).
- Значение зависимой переменной при заданном значении независимых переменных (например, ожидаемая урожайность фруктов при определенных уровнях осадков, температуре, рН почвы и добавлении удобрений)
Интерпретация множественной линейной регрессии помогает делать прогнозы и служит руководством для принятия ключевых решений. Например, правительства могут использовать эти исходные данные для разработки политики социального обеспечения. Кроме того, различные веб-сайты предоставляют свои калькуляторы для проверки значений. Кроме того, для этого можно использовать программные инструменты, такие как SPSS.
Формула
Множественные модели линейной регрессии часто используются в качестве эмпирических моделей или для аппроксимационных функций. Например, хотя точная функциональная взаимосвязь между значениями Y и X (X1 X2…… Xn) неизвестна, модель линейной регрессии обеспечивает адекватное приближение к истинной неизвестной функции для определенных диапазонов переменных регрессора. Хотя пользоваться онлайн-калькуляторами и программным обеспечением SPSS несложно, очень важно знать, как рассчитываются значения.
Можно использовать следующую формулу для расчета множественной линейной регрессии:
YI= β0+β1X1 β2X2 +…..+…+βkXk+ e.
Приведенное выше уравнение является просто расширением простой линейной регрессии. Здесь выходная переменная — Y, а связанные входные переменные — в терминах X, причем каждый предиктор имеет свой коэффициент наклона или регрессии (β). Кроме того, первый член (β0) является константой пересечения, которая является значением Y. В этом случае любое значение всех предикторов отсутствует (т. е. когда все члены X равны 0). Оба их значения одинаковы. K — регрессор или переменная-предиктор. ε должен дать место для стандартных ошибок. Другими словами, это мера дисперсии среднего значения выборки, связанная со средним значением генеральной совокупности, а не стандартное отклонение. Подробнее.
Пример
Рассмотрим пример, чтобы лучше понять множественную линейную регрессию.
Возьмем значения X1 как 0, 11, 11, значения X2 как 1, 5, 4 и значения Y как 11, 15 и 13.
Здесь,
- Сумма X1 = 22
- Сумма Х2 = 10
- Сумма Y = 39
- Х1 = 7,3333
- Х2 = 3,3333
- Среднее Y = 13
Сумма квадратов:
- (SSX1) = 80,6667
- И, (SSX2) = 8,6667
Сумма продуктов:
- (SPX1Y) = 22
- (SPX2Y) = 8
- И, (SPX1X2) = 25,6667
Уравнение регрессии = ŷ = b1X1 + b2X2 + a
β 1 = ((SPX1Y)*(SSX2)-(SPX1X2)*(SPX2Y)) / ((SSX1)*(SSX2)-(SPX1X2)*(SPX1X2)) = -14,67/40,33 = -0,36364
β 2 = ((SPX2Y)*(SSX1)-(SPX1X2)*(SPX1Y)) / ((SSX1)*(SSX2)-(SPX1X2)*(SPX1X2)) = 80,67/40,33 = 2
a = MY – β 1MX1 – β 2MX2 = 13 – (-0,36*7,33) – (2*3,33) = 9
Следовательно, ŷ = -0,36364X1 + 2X2 + 9
Предположения
Расчет множественной линейной регрессии требует нескольких допущений, и некоторые из них заключаются в следующем:
Линейность
Можно смоделировать линейную (прямолинейную) связь между Y и X, используя множественную регрессию. Любые криволинейные отношения не учитываются. Это можно проанализировать с помощью точечных диаграмм на первичных стадиях. В то же время на остаточных графиках можно обнаружить нелинейные закономерности.
Постоянная дисперсия
Для всех значений X дисперсия ε постоянна. Чтобы обнаружить это, можно использовать остаточные графики X. Также легко принять постоянную дисперсию, если остаточные графики имеют прямоугольную форму. Кроме того, существует непостоянная дисперсия, и ее необходимо учитывать, если на остаточном графике обнаруживается изменяющаяся форма клина.
Особые случаи
Предполагается, что данные исключаются из всех специальных пунктов, возникающих в результате разовых событий. Соответственно, регрессионная модель может иметь непостоянную дисперсию, ненормальность или другие проблемы, если они этого не делают.
Нормальность
Когда кто-то использует проверки гипотез и доверительные интервалы, предполагается, что существует нормальное распределение ε.
Мульти коллинеарность
Наличие почти линейных связей среди множества независимых переменных называется колинеарностью или мультиколинеарностью. Здесь, поскольку мультиколинеарность вызывает множество трудностей при регрессионном анализе, предполагается, что данные не являются мультиколинеарными.
Часто задаваемые вопросы (FAQ)
Что такое множественная линейная регрессия?
Множественная линейная регрессия рассматривается как расширение простой линейной регрессии, в котором участвуют одна или несколько независимых переменных, кроме одной зависимой переменной.
В чем разница между линейной и множественной регрессией?
Множественная линейная регрессия имеет одну или несколько переменных x и y, одну зависимую переменную и более одной независимой переменной. В линейной регрессии есть только одна переменная x и y.
Каковы преимущества множественной регрессии?
Аналитики имеют в виду теоретическую взаимосвязь, и регрессионный анализ подтверждает их. Он направлен на поиск уравнения, которое обобщает взаимосвязь между набором данных. Анализ также помогает делать меньше предположений о наборе значений.
Почему важна множественная линейная регрессия?
Основная цель интерпретации множественной линейной регрессии состоит в том, чтобы предвидеть переменную отклика. Например, это могут быть продажи, время доставки, эффективность, анализ вождения автомобиля, заполняемость больниц, процент массы тела одного пола и т. д. Эти прогнозы могут быть чрезвычайно полезны для планирования, мониторинга или анализа процесса или системы.
Рекомендуемые статьи
Это было Руководство по множественной линейной регрессии и ее определению. Здесь мы объясним формулу, предположение и их объяснения вместе с примерами. Вы можете узнать больше из следующих статей –
- Нелинейная регрессияНелинейная регрессияНелинейная регрессия относится к регрессионному анализу, в котором модель регрессии отображает нелинейную связь между зависимой переменной и независимыми переменными.Подробнее
- НелинейностьНелинейностьНелинейность — это косвенная корреляция между независимыми и зависимыми переменными, которая не может инкапсулировать прямые линии. Поскольку независимая переменная изменяется в нелинейной зависимости, зависимая переменная не изменяется с той же величиной.Подробнее
- Линейная регрессия в ExcelЛинейная регрессия В ExcelЛинейная регрессия — это статистический инструмент Excel, который используется в качестве модели прогнозного анализа для изучения взаимосвязи между двумя наборами данных. Используя этот анализ, мы можем оценить взаимосвязь между зависимыми и независимыми переменными.Подробнее
Множественная линейная регрессия вручную (шаг за шагом)
17 авг. 2022 г.
читать 2 мин
Множественная линейная регрессия — это метод, который мы можем использовать для количественной оценки взаимосвязи между двумя или более переменными-предикторами и переменной- откликом .
В этом руководстве объясняется, как выполнить множественную линейную регрессию вручную.
Пример. Множественная линейная регрессия вручную
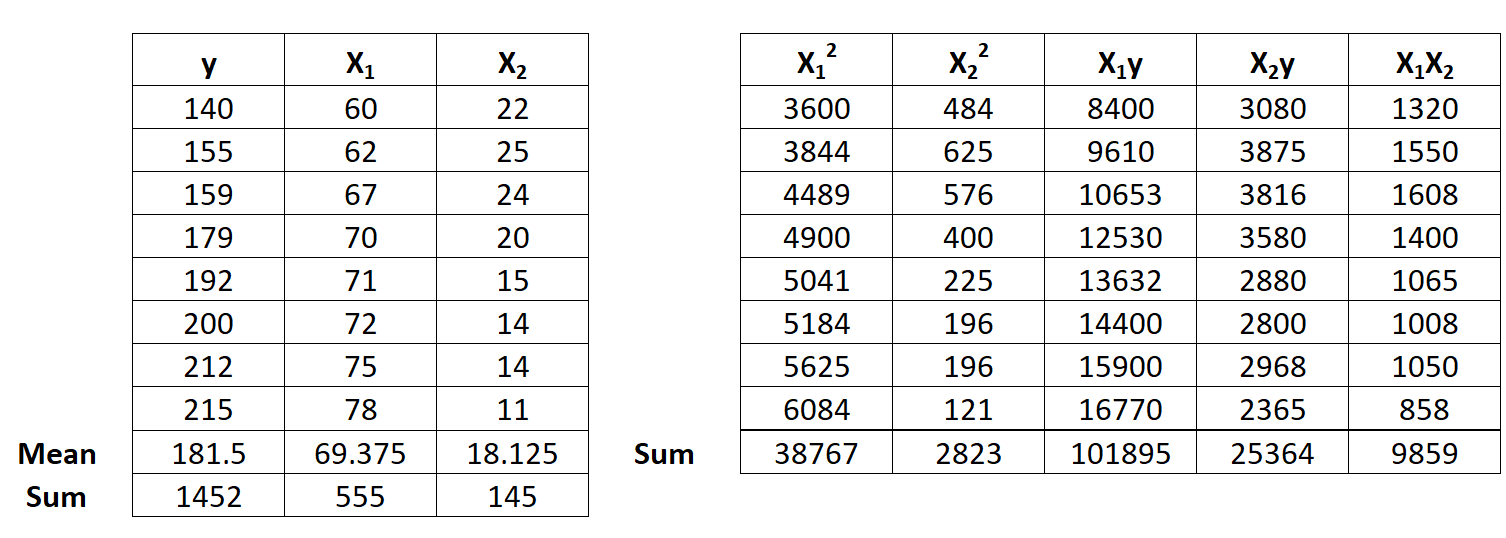
Предположим, у нас есть следующий набор данных с одной переменной ответа y и двумя переменными-предикторами X 1 и X 2 :
Используйте следующие шаги, чтобы подогнать модель множественной линейной регрессии к этому набору данных.
Шаг 1: Рассчитайте X 1 2 , X 2 2 , X 1 y, X 2 y и X 1 X 2 .
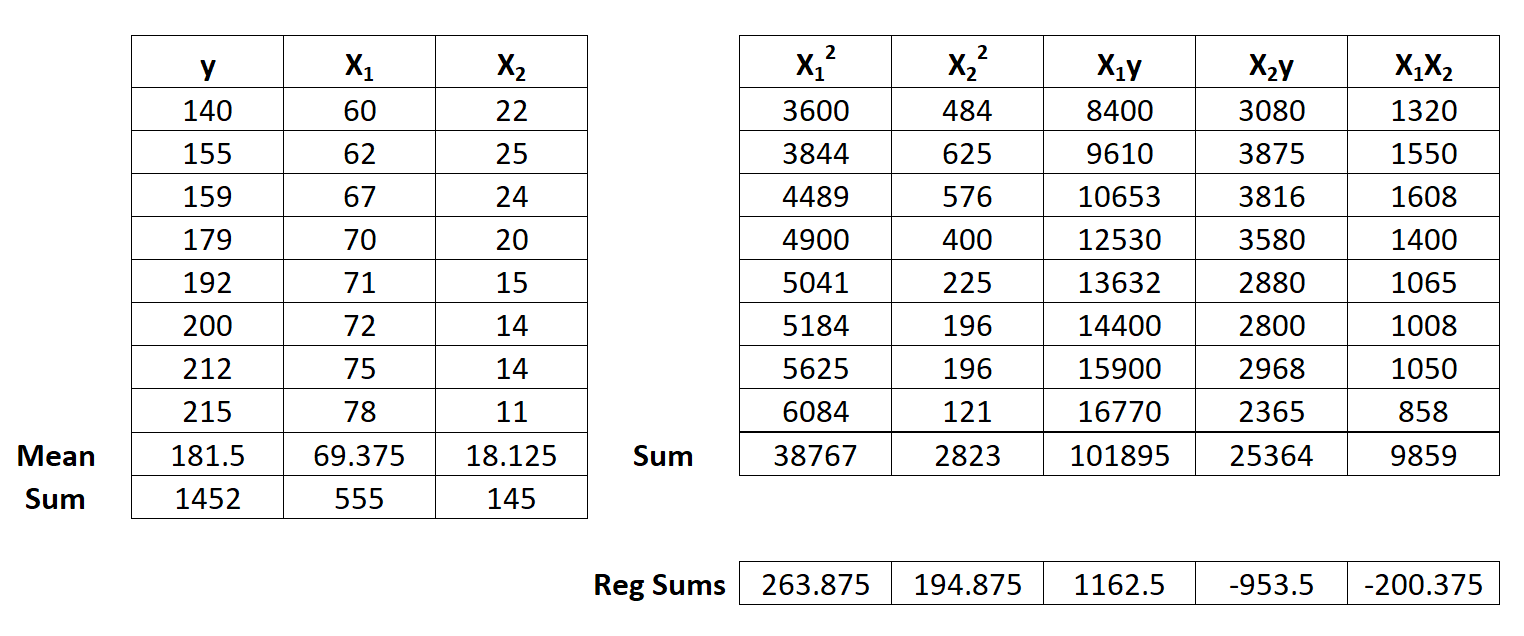
Шаг 2: Рассчитайте суммы регрессии.
Затем выполните следующие расчеты суммы регрессии:
- Σ x 1 2 = Σ X 1 2 – (ΣX 1 ) 2 / n = 38 767 – (555) 2 / 8 = 263,875
- Σ x 2 2 = Σ X 2 2 – (ΣX 2 ) 2 / n = 2,823 – (145) 2 / 8 = 194,875
- Σ x 1 y = Σ X 1 y – (ΣX 1 Σy) / n = 101 895 – (555 * 1 452) / 8 = 1 162,5
- Σ x 2 y = Σ X 2 y – (ΣX 2 Σy) / n = 25 364 – (145 * 1 452) / 8 = -953,5
- Σ x 1 x 2 = Σ X 1 X 2 – (ΣX 1 ΣX 2 ) / n = 9 859 – (555 * 145) / 8 = -200,375
Шаг 3: Рассчитайте b 0 , b 1 и b 2 .
Формула для расчета b 1 : [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 ) (Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Таким образом, b 1 = [(194,875)(1162,5) – (-200,375)(-953,5)] / [(263,875) (194,875) – (-200,375) 2 ] = 3,148
Формула для расчета b 2 : [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 ) (Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Таким образом, b 2 = [(263,875)(-953,5) – (-200,375)(1152,5)] / [(263,875) (194,875) – (-200,375) 2 ] = -1,656
Формула для расчета b 0 : y – b 1 X 1 – b 2 X 2
Таким образом, b 0 = 181,5 – 3,148(69,375) – (-1,656)(18,125) = -6,867.
Шаг 5: Поместите b 0 , b 1 и b 2 в оценочное уравнение линейной регрессии.
Расчетное уравнение линейной регрессии: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
В нашем примере это ŷ = -6,867 + 3,148x 1 – 1,656x 2 .
Как интерпретировать уравнение множественной линейной регрессии
Вот как интерпретировать это оценочное уравнение линейной регрессии: ŷ = -6,867 + 3,148x 1 – 1,656x 2
б 0 = -6,867.Когда обе переменные-предикторы равны нулю, среднее значение y равно -6,867.
б 1 = 3,148.Увеличение x 1 на одну единицу связано с увеличением y на 3,148 единиц в среднем, если предположить, что x 2 поддерживается постоянным.
б 2 = -1,656.Увеличение x 2 на одну единицу связано с уменьшением y на 1,656 единицы в среднем, если предположить, что x 1 поддерживается постоянным.
Дополнительные ресурсы
Введение в множественную линейную регрессию
Как выполнить простую линейную регрессию вручную
В
рассмотренных ранее задачах на фактор
Y
влиял только один фактор X,
а влияние всех остальных было мало и
приводило к случайному разбросу значений
Y.
Однако часто на результирующий фактор
Y
достаточно сильно может влиять сразу
несколько других факторов. Если на
переменную Y
в равной степени влияют несколько
независимых переменных, то такая
зависимость описывается множественной
регрессией.
Переменная Y
при этом называется результирующим
признаком
или результатом,
а остальные, влияющие на него показатели,
— независимыми
факторами.
Множественная
линейная регрессия.
Рассмотрим
случай, когда независимые переменные
входят в уравнение регрессии линейно.
Такая множественная регрессия называется
линейной.
Рассмотрим простейший случай линейной
множественной регрессии — двухфакторную
регрессию. В этом случае на результат
Y
влияют два фактора: Х1
и Х2.
Ее уравнение имеет вид
.
Например,
предположим,
что зависимость расходов на продукты
питания по совокупности семей
характеризуется следующим уравнением:
,
где
y
— расходы семьи за месяц на продукты
питания, тыс. р.;
x1
— месячный доход на одного члена семьи,
тыс. р.;
x2
— размер семьи, человек.
Анализ
данного уравнения позволяет сделать
выводы — с ростом дохода на одного члена
семьи на 1 тыс. р. расходы на питание
возрастут в среднем на 350 р. при том же
среднем размере семьи. Иными словами,
35 % дополнительных семейных расходов
тратится на питание. Увеличение размера
семьи при тех же ее доходах предполагает
дополнительный рост расходов на питание
на 730 р. Третий параметр не подлежит
экономической интерпретации.
Для
оценки качества уравнения регрессии
используются парные коэффициенты
корреляции, которые вычисляются по
формулам:


Коэффициенты
характеризуют влияние каждого фактора
Х1
и Х2
на
результат Y.
Коэффициент
характеризует влияние факторов друг
на друга. Если это влияние высоко, то
это негативный признак, т. к. факторы Х1
и Х2
должны быть независимыми.
Для
оценки совокупного влияния факторов
Х1
и Х2
на результат рассчитывается множественный
коэффициент корреляции, который для
двухфакторной модели равен
.
В
общем виде уравнение линейной множественной
регрессии имеет вид:
.
Для
нахождения неизвестных параметров
этого уравнения нужно решить систему
уравнений, которая имеет вид

Для
определения степени влияния факторов
на результат и для оценки степени их
влияния друг на друга вычисляют величины
и
,
которые называются парными
коэффициентами корреляции.
ПРИМЕР
3.5.1.
Некоторая организация занимается
торговлей компьютерами. Она определила,
что на количество продаж Y
основное влияние оказывают следующие
факторы: цена товара
,
затраты на рекламу
и число конкурирующих организаций в
регионе
.
Результаты
наблюдений приведены в табл. 3.5.1.
Таблица
3.5.1
|
Х1 |
20 |
20 |
18 |
17 |
17 |
19 |
18 |
16 |
16 |
16 |
15 |
15 |
14 |
14 |
|
Х2 |
37 |
38 |
36 |
42 |
47 |
55 |
53 |
54 |
49 |
50 |
52 |
52 |
51 |
54 |
|
Х3 |
3 |
4 |
3 |
5 |
4 |
3 |
2 |
3 |
2 |
2 |
1 |
2 |
1 |
3 |
|
Y |
112 |
132 |
129 |
134 |
132 |
137 |
139 |
139 |
138 |
143 |
141 |
146 |
148 |
150 |
Построим
линейное уравнение множественной
регрессии.
РЕШЕНИЕ.
Для этого предварительно исследуем
матрицу парных коэффициентов корреляции.
Вводим исходные данные вместе с подписями
в ячейки А1–О4. Для построения матрицы
парной корреляции вызываем меню
«Сервис/Анализ данных» (если пункт меню
отсутствует, то вызываем «Сервис/Надстройки»
и ставим галочку напротив строки «Пакет
анализа»). Выбираем пункт «Корреляция».
В появившемся окне в поле «Входной
интервал» задаем ссылку на таблицу —
А1–О4. Указываем группирование «По
строкам». Ставим флажок в «Метки в первом
столбце» (так как в ссылках на таблицу
указаны подписи строк). В области
«Параметры вывода» ставим флажок
напротив «Выходной интервал» и напротив
в поле даем ссылку на какую-либо ячейку,
откуда будет осуществляться вывод
данных, например А7. Нажимая «ОК», получаем
нижнюю половину матрицы парной корреляции.
Для общей оценки мультиколлинеарности
факторов и адекватности регрессионной
модели рассчитаем определители матриц
.
Сформируем полную матрицу парных
коэффициентов корреляции. В С8 задаем
формулу «=В9»,
в D8
— ссылку «=B10»,
в D9
— «=С10»,
в Е8 — «=В11»,
в Е9 — «=С11»,
в Е10 — «D11».
Далее, для вычисления определителей в
ячейку А13 вводим заголовок «
=»
и в В13 ставим курсор и задаем функцию
«МОПРЕД» (категория «Математические»),
в которой аргумент «Массив» является
ссылкой на ячейки B8:E11. В ячейку А14 вводим
заголовок «
=»
и в В14 ставим курсор и задаем функцию
«МОПРЕД» с аргументом «Массив» — ссылкой
на B8:D10. Результат — 0,427104
(ближе к 0, чем к 1), что говорит о достаточно
высокой общей мультиколлинеарности.
Найдем теперь коэффициент множественной
корреляции. В А15 вводим «Rх=»,
а в В15 —
формулу «=КОРЕНЬ(1–В13/В14)».
Результат 0,883788 говорит о достаточно
высокой связи между фактором и функцией
отклика.
Проведем
теперь отбор факторов. Рассмотрим
матрицу коэффициентов парной корреляции.
Видно, что
.
Факторы
можно считать коллинеарными
(интеркоррелированными), если их парный
коэффициент по модулю больше 0,7. В нашем
случае таких пар факторов нет. Все
факторы можно считать независимыми
друг от друга и использовать в регрессионном
уравнении. Определим теперь влияние
каждого фактора
на функцию отклика Y.
Для этого рассмотрим коэффициенты
парной корреляции
.
Видно, что третий коэффициент –0,45
намного меньше по модулю, чем примерная
граница 0,7, поэтому влияние третьего
фактора Х3
на результат мало и его можно отбросить
из рассмотрения.
Копируем
теперь на А18–О20 функцию отклика и
значимые факторы (1, 2 и 4 строки
соответственно А1–О2 копируем в А18–О19,
а А4–О4 — в А20–О20). В ячейку А22 вводим
заголовок «Линейная» и в соседнюю В22
вводим функцию, определяющую параметры
линейной регрессии «=ЛИНЕЙН» (категория
«Статистические»). Аргументы функции:
«Изв_знач_у» — B20:O20 (значения функции),
«Изв_знач_х» — B18:O19 (значения двух
значимых аргументов), «Константа» — 1
(расчет свободного члена), «Стат» — 1
(вывод дополнительных характеристик
регрессии). Результат вычислений функции
ЛИНЕЙН в случае функции нескольких
переменных
имеет вид (табл. 3.5.2).
Таблица
3.5.2
|
Коэффициент |
Коэффициент |
Коэффициент |
Коэффици-ент |
|
|
Стандартная |
Стандартная |
… |
Стандартная |
Стандартная |
|
Коэффициент |
Среднеквадратическое |
… |
нет |
нет |
|
F-статистика |
Степень |
… |
нет |
нет |
|
Регрессионная |
Остаточная |
… |
нет |
нет |
В
нашем случае имеем два фактора
,
поэтому обводим пять строк и три столбца
В22–D26
и нажимаем F2
и Ctrl+Shift+Enter.
Первая
строка результата — значения параметров
регрессионного уравнения
— числа
.
Следовательно, уравнение регрессии
есть
.
Вторая строка — стандартные ошибки
коэффициентов. Все они меньше самих
коэффициентов, это значит, что коэффициенты
значимы. В ячейках D24–D26
стоят значения «#Н/Д»
(нет данных), как и должно быть в
соответствии с табл.3.5.2.
Коэффициент
детерминации равен 0,7783. Видно, что
F-критерий
регрессионной модели равен 19,3097. Проверим
модель на адекватность. Вычислим
критическое значение статистики. Вводим
в ячейку Н22 подпись «F-критическое»
а в I22
вводим функцию FРАСПОБР,
имеющую аргументы: «Вероятность» —
уровень значимости, если он не задан в
условии (как в нашем случае), то обычно
его принимаем 0,05. Аргумент «Степени_свободы_1»
— число независимых переменных (у нас
их две —
).
Аргументом «Степени_свободы_2» служит
число, показанное в ячейке С25 (в данном
примере 11). Видно, что F-статистика
больше ее критического значения, поэтому
модель адекватна.
Что
дают полученное уравнение и коэффициенты
корреляции? Во-первых, парные коэффициенты
показывают, какие факторы сильнее влияют
на результат, а какие слабее, что позволяет
эффективно управлять политикой
организации. В примере самый сильный
фактор — цена товара, его коэффициент
максимален
по величине и отрицателен, что говорит
о том, что с ростом цены прибыль растет.
Во-вторых, уравнение позволяет делать
прогнозы. Так, если цена товара х1
=
21, затраты на рекламу х2
=
48, а число конкурентов х3
=
3, то количество продаж Y можно ожидать
порядка
Множественная
нелинейная регрессия.
Множественная
нелинейная регрессия отличается от
линейной только тем, что в ней нужно
делать замену переменных.
ПРИМЕР
3.5.2.Предприятие
выпускает продукцию, количество которой
за месяц Y
(тыс. шт.) зависит от затрат материальных
ресурсов
(т.), трудозатрат
(тыс. ч.) и энергозатрат
(млн кВт). При расширении производства
наблюдалась следующая эмпирическая
зависимость между выпуском Y
и затратами ресурсов
(табл. 3.5.3).
Таблица
3.5.3
|
Х1 |
16 |
20 |
18 |
22 |
21 |
24 |
27 |
26 |
28 |
31 |
35 |
34 |
33 |
34 |
|
Х2 |
50 |
55 |
58 |
50 |
57 |
59 |
62 |
64 |
59 |
64 |
59 |
62 |
65 |
70 |
|
Х3 |
7 |
6 |
7 |
8 |
10 |
8 |
9 |
7 |
11 |
10 |
12 |
11 |
9 |
13 |
|
Y |
45 |
50,3 |
54,1 |
55,1 |
60,8 |
65,6 |
68,8 |
66,6 |
73,2 |
81,9 |
91,8 |
86,1 |
83,1 |
93,1 |
Из
теории производственных функций
известно, что зависимость результирующего
признака (функции откликов) от факторов
имеет вид
.
Вводим исходные данные вместе с подписями
в ячейки А1–О4. Построить регрессионную
модель.
РЕШЕНИЕ.
Чтобы привести уравнение к линейному
виду, нужно прологарифмировать уравнение
.
Вводим вместо исходных данных их
логарифмы. Для этого в ячейки А5–А8
вводим подписи «Ln
X1»,
«Ln
X2»,
«LnX3»,
«LnY».
Ставим курсор в ячейку В5 и вводим функцию
LN
(категория «Математические») с аргументом
«Число» В1, которое отобразится в строке
формул в виде «=LN(В1)»,
затем переносим формулу на все данные,
автозаполняя ячейки В5–О8. После этого
исследуем матрицу парных коэффициентов
корреляции. Для построения матрицы
вызываем меню «Сервис/Анализ данных»
и выбираем пункт «Корреляция». В
появившемся окне в поле «Входной
интервал» задаем ссылку на преобразованные
данные — А5–О8. Указываем группирование
«По строкам». Ставим флажок в «Метки в
первом столбце» (так как в ссылках на
таблицу указаны подписи строк). В области
«Параметры вывода» ставим флажок
напротив «Выходной интервал» и напротив
в поле даем ссылку на какую-либо ячейку,
откуда будет осуществляться вывод
данных, например А10, и нажимаем «ОК».
Для общей оценки мультиколлинеарности
факторов и адекватности регрессионной
модели рассчитаем определители матриц
.
Сформируем полную матрицу парных
коэффициентов корреляции. В С11 задаем
формулу «=В12»,
в D11
— ссылку «=B13»,
в D12
— «=С13»,
в Е11 — «=В14»,
в Е12 — «=С14»,
в Е13 — «=D14».
Далее для вычисления определителей в
ячейку А16 вводим заголовок «
=«
и в В16 ставим курсор и задаем функцию
«МОПРЕД» (категория «Математические»),
в которой аргумент «Массив» является
ссылкой на ячейки B11:E114. В ячейку А17
вводим заголовок «
=«
и в В17 ставим курсор и задаем функцию
«МОПРЕД» с аргументом «Массив» — ссылкой
на B11:D13. Результат — 0,163303,
он близок к нулю, что говорит о достаточно
сильной общей мультикорреляции факторов
между собой. Найдем теперь коэффициент
множественной корреляции. В А18 вводим
«Rх=»,
а в В18 формулу «=КОРЕНЬ(1–В16/В17)».
Результат 0,993187 говорит о достаточно
высокой связи между фактором и функцией
отклика.
Проведем
теперь отбор факторов. Видно, что первый
фактор сильно связан и со вторым и с
третьим, поэтому его выводим из
регрессионной модели. Одновременно
видно, что влияние второго и третьего
фактора на функцию Y
достаточно сильно, поэтому принимаем
к рассмотрению регрессионную модель
.
В строках с номерами 20—22 копируем
значимые факторы. Для этого в А20–А22
вводим подписи «Ln
X2,
LnX3,
LnY»,
а в В20 вводим функцию «=LN(B2)»
и автозаполняем ее В20–О22. В ячейку А24
вводим заголовок «Линейная» и в соседнюю
В24 вводим функцию, определяющую параметры
линейной регрессии «=ЛИНЕЙН». Аргументы
функции: «Изв_знач_у» — B22:O22, «Изв_знач_х»
— B20:O21, «Константа» = 1, «Стат» = 1. Далее
обводим 5 строк и три столбца В24–D28
(т. к. находим параметры функции Y
и двух факторов
),
и нажимаем F2
и Ctrl+Shift+Enter.
Первая строка результата — значения
параметров преобразованного регрессионного
уравнения. Чтобы получить данные
исходного уравнения, вводим в G10,
G11
и G12
подписи «
«,
а в соседние ячейки Н10, Н11 и Н12 формулы
«=C24»,
«=B24»
и «=EXP(D24)».
В результате уравнение регрессии есть
.
Вторая строка — стандартные ошибки
коэффициентов. Все они меньше самих
коэффициентов, это значит, что коэффициенты
значимы. Коэффициент
детерминации равен 0,892. Видно, что
F-критерий
регрессионной модели равен 45,359. Проверим
модель на адекватность. Вычислим
критическое значение статистики. Вводим
в ячейку Н24 подпись «F-критическое»
а в I24
вводим функцию FРАСПОБР,
имеющую аргументы: «Вероятность» —
0,05 (т. к.
),
«Степени_свободы_1» — 2 (число независимых
переменных равно двум —
).
Аргументом «Степени_свободы_2» служит
число, показанное в ячейке С27 (в данном
примере: 11). Видно, что F-статистика
больше ее критического значения, поэтому
модель адекватна, следовательно, по ней
можно делать те же выводы, что и в
предыдущем примере.
Множественная
регрессия с фиктивными переменными.
Рассмотрим
еще один пример множественной регрессии
и корреляции — с введением фиктивных
переменных.
Фиктивные
переменные вводятся в случае, если
показатель, влияющий на функцию отклика,
нельзя измерить количественно. Рассмотрим
их применение на следующем примере.
ПРИМЕР
3.5.3. Строительная
организация продает облицовочную плитку
в трех городах: Воронеже, Липецке и
Курске. Маркетинговая служба хочет
определить влияние отчислений на рекламу
Y
(тыс. р.) на количество проданной продукции
Х (млн шт.). При этом предполагается, что
зависимость фактора Х на функцию Y
линейная и степень влияния факторов
друг на друга (коэффициент а
уравнения регрессии) во всех городах
примерно одинаков, но различный спрос
на продукцию (свободный член уравнения).
Организация желает включить в регрессионную
модель такой фактор, как «город». Имеются
следующие статистические данные (табл.
3.5.4-3.5.6).
г.
Воронеж
Таблица
3.5.4
|
X |
25 |
14 |
19 |
27 |
33 |
31 |
12 |
16 |
28 |
|
Y |
37 |
24 |
25 |
39 |
42 |
43 |
22 |
27 |
27 |
г.
Липецк
Таблица
3.5.5
|
X |
13 |
18 |
19 |
24 |
21 |
17 |
31 |
29 |
16 |
27 |
22 |
21 |
|
Y |
30 |
33 |
33 |
41 |
35 |
31 |
45 |
45 |
30 |
40 |
33 |
32 |
г.
Курск
Таблица
3.5.6
|
X |
16 |
15 |
11 |
19 |
27 |
31 |
29 |
22 |
19 |
26 |
|
Y |
22 |
20 |
18 |
25 |
28 |
35 |
32 |
27 |
26 |
31 |
РЕШЕНИЕ.
Введем фиктивные переменные
В
результате получаем регрессионную
функцию трех переменных
,
а результаты наблюдений можно записать
в виде табл. 3.5.7.
Таблица
3.5.7
|
Y |
37 |
24 |
25 |
39 |
42 |
43 |
22 |
27 |
27 |
30 |
33 |
33 |
41 |
35 |
31 |
45 |
|
X |
25 |
14 |
19 |
27 |
33 |
31 |
12 |
16 |
28 |
13 |
18 |
19 |
24 |
21 |
17 |
31 |
|
Z1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Z2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Y |
45 |
30 |
40 |
33 |
32 |
22 |
20 |
18 |
25 |
28 |
35 |
32 |
27 |
26 |
31 |
Y |
|
X |
29 |
16 |
27 |
22 |
21 |
16 |
15 |
11 |
19 |
27 |
31 |
29 |
22 |
19 |
26 |
X |
|
Z1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Z1 |
|
Z2 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Z2 |
Вводим
эти данные в электронную таблицу. В
А1–А4 вводим подписи “Y”,
“X”,
“Z1”,
“Z2”.
В ячейки В1–AF4
вводим данные из табл. 3.5.7. Данные вводятся
в 4 строки и 31 столбец, не считая заголовки.
Посмотрим, имеются ли мультиколлинеарные
факторы. Для этого находим матрицу
коэффициентов интеркорреляции. Вызываем
меню «Сервис (Данные)/Анализ данных» и
выбираем пункт «Корреляция». В появившемся
окне в поле «Входной интервал» задаем
ссылку на данные — факторы: А2–AF4.
Указываем группирование «По строкам».
Ставим флажок в «Метки в первом столбце»
(так как в ссылках на таблицу указаны
подписи строк). В области «Параметры
вывода» ставим флажок напротив «Выходной
интервал» и напротив в поле даем ссылку
на какую-либо ячейку, откуда будет
осуществляться вывод данных, например
А7 и нажимаем «ОК». Ставим курсор в С8 и
делаем ссылку «=В9»,
в D8
— ссылку «=В10»,
в D9
— ссылку «=С10».
Ставим курсор в ячейку G7,
вводим заголовок «
=«
и в H7 ставим курсор и задаем функцию
«МОПРЕД» с аргументом «Массив» — ссылкой
на B8:D10. Результат — 0,7352005,
близок к единице, что говорит о достаточно
слабой зависимости факторов между
собой. Все факторы оставляем в регрессионной
модели, вычисляем параметры регрессии.
Ставим курсор в А12 и даем заголовок
«Параметры регрессии», а затем переводим
курсор в А13 и вызываем функцию «ЛИНЕЙН»,
аргументы которой:
«Изв_знач_у» — B1:AF1,
«Изв_знач_х» — B2:AF4,
«Константа» = 1, «Стат» = 1. Далее обводим
5 строк и 4 столбца А13–D17
и нажимаем F2
и Ctrl+Shift+Enter.
В первой строке — коэффициенты
регрессионного уравнения, следовательно,
уравнение регрессии есть
.
Вторая строка — стандартные ошибки
коэффициентов. Все они меньше самих
коэффициентов, это значит, что коэффициенты
значимы.
Проверим
модель на адекватность. Видно, что
F-критерий
регрессионной модели равен 63,703. Вычислим
критическое значение статистики. Вводим
в ячейку G13 подпись «F-критическое»,
а в Н13 вводим функцию FРАСПОБР,
имеющую аргументы: «Вероятность» —
0,05 (произвольно примем по умолчанию),
«Степени_свободы_1» — 3 (число независимых
переменных равно трем —
).
Аргументом «Степени_свободы_2» служит
число, показанное в ячейке В16 (в данном
примере — 27). Видно, что F-статистика
больше ее критического значения, поэтому
модель адекватна. Построим уравнение
регрессии для каждого города в отдельности.
Вводим в G15
подпись «Воронеж», в Н15 — подпись «а=«,
в I15
— формулу «=C13»
, в Н16 — «b=«,
в I16
— «=D13+B13».
Уравнение для Воронежа есть
Аналогично рассчитываем для Липецка.
Вводим в G17
подпись «Липецк», в Н17 подпись «а=«,
в I17
— формулу «=C13»
, в Н18 — «b=«,
в I18
— «=D13+А13».
Результат
.
Для Курска вводим в G19
подпись «Курск», в Н19 — подпись «а=«,
в I19
— формулу «=C13»
, в Н20 — «b=«,
в I20
— «=D13».
Результат
.
Теперь при прогнозировании и анализе
можно учитывать, в каком городе мы
продаем плитку.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример решения задачи. Эконометрические модели
Условие задачи
По 20
предприятиям региона изучается зависимость выработки продукции на одного
работника
(тыс.руб.) от ввода в действие новых основных
фондов
(% от стоимости фондов на
конец года) и от удельного
веса рабочих высокой квалификации в общей численности рабочих
(смотри таблицу своего варианта).
Требуется:
| № |
|
|
|
№ |
|
|
|
| 1 | 7 | 3.7 | 9 | 11 | 10 | 6.8 | 21 |
| 2 | 7 | 3.7 | 11 | 12 | 11 | 7.4 | 23 |
| 3 | 7 | 3.9 | 11 | 13 | 11 | 7.8 | 24 |
| 4 | 7 | 4.1 | 15 | 14 | 12 | 7.5 | 26 |
| 5 | 8 | 4.2 | 17 | 15 | 12 | 7.9 | 28 |
| 6 | 8 | 4.9 | 19 | 16 | 12 | 8.1 | 30 |
| 7 | 8 | 5.3 | 19 | 17 | 13 | 8.4 | 31 |
| 8 | 9 | 5.1 | 20 | 18 | 13 | 8.7 | 32 |
| 9 | 10 | 5.6 | 20 | 19 | 13 | 9.5 | 33 |
| 10 | 10 | 6.1 | 21 | 20 | 14 | 9.7 | 35 |
Решение задачи
Для
удобства проведения расчетов поместим результаты промежуточных расчетов в
таблицу:
| № |
|
|
|
|
|
|
|
|
|
| 1 | 7 | 3.7 | 9 | 25.9 | 63 | 33.3 | 13.69 | 81 | 49 |
| 2 | 7 | 3.7 | 11 | 25.9 | 77 | 40.7 | 13.69 | 121 | 49 |
| 3 | 7 | 3.9 | 11 | 27.3 | 77 | 42.9 | 15.21 | 121 | 49 |
| 4 | 7 | 4.1 | 15 | 28.7 | 105 | 61.5 | 16.81 | 225 | 49 |
| 5 | 8 | 4.2 | 17 | 33.6 | 136 | 71.4 | 17.64 | 289 | 64 |
| 6 | 8 | 4.9 | 19 | 39.2 | 152 | 93.1 | 24.01 | 361 | 64 |
| 7 | 8 | 5.3 | 19 | 42.4 | 152 | 100.7 | 28.09 | 361 | 64 |
| 8 | 9 | 5.1 | 20 | 45.9 | 180 | 102 | 26.01 | 400 | 81 |
| 9 | 10 | 5.6 | 20 | 56 | 200 | 112 | 31.36 | 400 | 100 |
| 10 | 10 | 6.1 | 21 | 61 | 210 | 128.1 | 37.21 | 441 | 100 |
| 11 | 10 | 6.8 | 21 | 68 | 210 | 142.8 | 46.24 | 441 | 100 |
| 12 | 11 | 7.4 | 23 | 81.4 | 253 | 170.2 | 54.76 | 529 | 121 |
| 13 | 11 | 7.8 | 24 | 85.8 | 264 | 187.2 | 60.84 | 576 | 121 |
| 14 | 12 | 7.5 | 26 | 90 | 312 | 195 | 56.25 | 676 | 144 |
| 15 | 12 | 7.9 | 28 | 94.8 | 336 | 221.2 | 62.41 | 784 | 144 |
| 16 | 12 | 8.1 | 30 | 97.2 | 360 | 243 | 65.61 | 900 | 144 |
| 17 | 13 | 8.4 | 31 | 109.2 | 403 | 260.4 | 70.56 | 961 | 169 |
| 18 | 13 | 8.7 | 32 | 113.1 | 416 | 278.4 | 75.69 | 1024 | 169 |
| 19 | 13 | 9.5 | 33 | 123.5 | 429 | 313.5 | 90.25 | 1089 | 169 |
| 20 | 14 | 9.7 | 35 | 135.8 | 490 | 339.5 | 94.09 | 1225 | 196 |
| Сумма | 202 | 128.4 | 445 | 1384.7 | 4825 | 3136.9 | 900.42 | 11005 | 2146 |
| Ср.знач. | 10.100 | 6.420 | 22.250 | 69.235 | 241.250 | 156.845 | 45.021 | 550.250 | 107.300 |
Найдем
средние квадратические отклонения признаков:
Линейное уравнение множественной регрессии
Для
нахождения параметров линейного уравнения множественной регрессии:
необходимо
решить следующую систему линейных уравнений относительно неизвестных параметров
:
либо
воспользоваться готовыми формулами:
Рассчитаем
сначала парные коэффициенты корреляции:
Таким
образом, получили следующее уравнение множественной регрессии:
Стандартизированное уравнение множественной регрессии
Коэффициенты
и
стандартизированного уравнения регрессии
находятся по формулам:
То есть
уравнение будет выглядеть следующим образом:
Так как
стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно
сказать, что ввод в действие новых основных фондов оказывает большее влияние на
выработку продукции, чем удельный вес рабочих высокой квалификации.
Коэффициенты эластичности
Сравнивать
влияние факторов на результат можно также при помощи средних коэффициентов
эластичности:
Вычисляем:
Т.е.
увеличение только основных фондов (от своего среднего значения) или только
удельного веса рабочих высокой квалификации на 1% увеличивает в среднем
выработку продукции на 0,503% или 0,214% соответственно. Таким образом,
подтверждается большее влияние на результат
фактора
, чем фактора
.
Коэффициенты парной корреляции
Коэффициенты парной корреляции мы уже нашли:
Они
указывают на весьма сильную связь каждого фактора с результатом, а также
высокую межфакторную зависимость (факторы
и
явно коллинеарны, так как
). При такой сильной
межфакторной зависимости рекомендуется один из факторов исключить из
рассмотрения.
Частные коэффициенты корреляции
Частные
коэффициенты корреляции характеризуют тесноту связи между результатом и
соответствующим факторов при элиминировании (устранении влияния) других
факторов, включенных в уравнение регрессии.
При двух
факторах частные коэффициенты корреляции рассчитываются следующим образом:
Если
сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за
высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные
оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной
коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у
которого теснота парной зависимости меньше, чем теснота межфакторной связи.
Коэффициент множественной корреляции
Коэффициент
множественной корреляции определить по формуле:
Коэффициент
множественной корреляции показывает на весьма сильную связь всего набора
факторов с результатом.
Нескорректированный коэффициент множественной детерминации
оценивает долю вариации результата за счет
представленных в уравнении факторов в общей вариации результата. Здесь эта доля
составляет 98.4% и указывает на высокую степень обусловленности вариации
результата вариацией факторов, иными словами – на весьма тесную связь факторов
с результатом.
Скорректированный
коэффициент множественной корреляции:
определяет
тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает
такую оценку тесноты связи, которая не зависит от числа факторов и поэтому
может сравниваться по разным моделям с разным числом факторов. Оба коэффициента
указывают на высокую (более 95%) детерминированность результата
в модели факторами
и
.
Критерий Фишера
Оценку
надежности уравнения регрессии в целом и показателя тесноты связи
дает
–критерий Фишера:
В нашем
случае фактическое значение
–критерия Фишера:
Получили,
что
(при
), то есть вероятность
случайно получить такое значение
– критерия не превышает допустимый уровень
значимости 5%. Следовательно, полученное значение не случайно, оно
сформировалось под влиянием существенных факторов, то есть подтверждается
статистическая значимость всего уравнения и показателя тесноты связи
.
С
помощью частных
–критериев Фишера оценим целесообразность
включения в уравнение множественной регрессии фактора
после
и фактора
после
при помощи формул:
Найдем
и
.
Получили,
что
. Следовательно, включение
в модель фактора
после того, как в модель включен фактор
статистически нецелесообразно: прирост
факторной дисперсии за счет дополнительного признака
оказывается незначительным, несущественным;
фактор
включать в уравнение после фактора
не следует.
Если
поменять первоначальный порядок включения факторов в модель и рассмотреть
вариант включения
после
, то результат расчета
частного
–критерия для
будет иным.
, то есть вероятность его
случайного формирования меньше принятого стандарта
. Следовательно, значение
частного
– критерия для дополнительно включенного
фактора
не случайно, является статистически значимым,
надежным, достоверным: прирост факторной дисперсии за счет дополнительного
фактора
является существенным.
Фактор
должен присутствовать в уравнении, в том числе в варианте, когда он
дополнительно включается после фактора
.