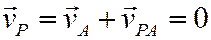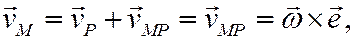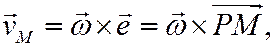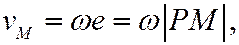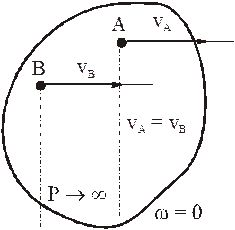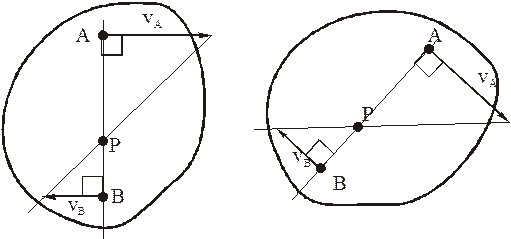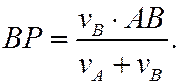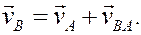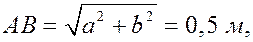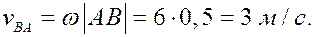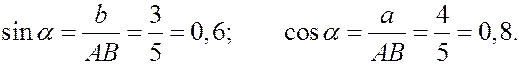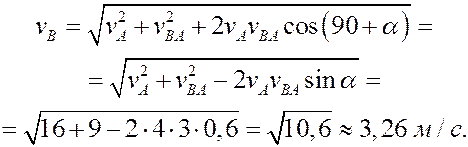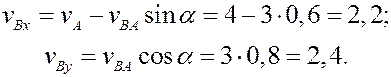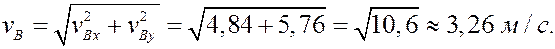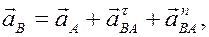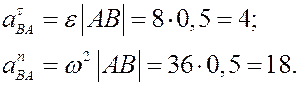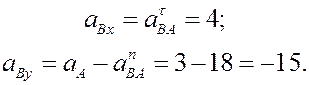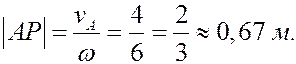Как найти линейное ускорение центра колеса

Решение.
Для решения задачи используем закон сохранения энергии. Потенциальная энергия переходит в кинетическую энергию. Кинетическая энергия состоит из энергии поступательного движения и энергии вращательного движения.

[ mcdot gcdot h=frac{mcdot {{upsilon }^{2}}}{2}+frac{Jcdot {{omega }^{2}}}{2} (1). ]

m – масса тела которое скатывается, h – высота с которой скатывается тело (см. рис.), υ – линейная скорость тела, J – момент инерции тела, ω – угловая скорость вращения тела.
Запишем формулу нахождения высоты наклонной плоскости с которой скатывается тело

h = l∙sinα    (2).

Длина наклонной плоскости определится по формуле

[ l=frac{{{upsilon }^{2}}}{2cdot a} (3).
 ]

Подставим (2) в (3) выразим ускорение

[ a=frac{{{upsilon }^{2}}cdot sin alpha }{2cdot h} (4).
 ]

Угловая скорость связана с линейной скоростью

[ omega =frac{upsilon }{R} (5). ]

Момент инерции диска определяется по формуле

[ J=frac{mcdot {{R}^{2}}}{2} (6). ]

Подставим (6) и (5) в (1):

[ mcdot gcdot h=frac{mcdot {{upsilon }^{2}}}{2}+frac{mcdot {{R}^{2}}cdot {{upsilon }^{2}}}{2cdot 2cdot {{R}^{2}}},gcdot h=frac{3cdot {{upsilon }^{2}}}{4}, {{upsilon }^{2}}=frac{4cdot gcdot h}{3} (7). ]

Подставим (7) в (4) выразим ускорение диска:

[ a=frac{4cdot gcdot hcdot sin alpha }{3cdot 2cdot h},a=frac{2cdot gcdot sin alpha }{3}. ]

• 

Ускорение центра масс

Теорема о движении центра масс является общей теоремой динамики, она утверждает, что ускорение центра масс не зависит от действия внутренних сил.

Ускорение центра масс согласно теореме движения центра масс, определяется как сумма внешних сил (по отношению к системе), при этом принято считать, что силы приложены к некой материальной точке, расположенной в центре масс.

При поступательном движении любого твердого тела, ускорение всех его точек независимо от момента времени одинаково и, таким образом, эквивалентно ускорению центра масс. Исходя из этого, теорему движения центра масс можно использовать для исследования и решения задач поступательного движения твердых тел.

Ускорение центра масс формула

Общий вид:

а =∑F

Скатывание шара по наклонной поверхности:

Пример возможных задач

Найти линейное ускорение центра масс некого шара, который скатывается без скольжения по наклонной плоскости. Угол наклона 20 град., начальная скорость шара 0.

Ответ

В виду того, что шар находится в неподвижном состоянии, сила трения принимается равной 0. Таким образом, решение задачи сводится к уравнению:

а = g*sin(α) = 9.81*sin(20) = 9.81*0.34 = 3,3354 м/с²

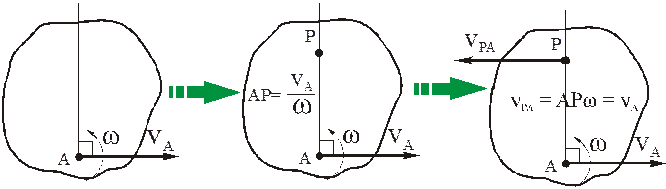
Иногда удобно рассмотреть скорость движения тела по окружности через угловую скорость. Она показывает, на какой угол успевает повернуться тело за единицу времени. На Рис.1. мотоциклист, переместившись из точки (A) в точку ({A}^{’}), повернулся на угол (Delta varphi) за время (t).
$$omega=frac{Deltavarphi}{t} , (рад/сек);$$
В международной системе единиц измерения угловую скорость принято измерять в радианах в секунду. Кроме обычных градусов углы можно измерять в радианах, с ними вы должны были столкнуться в школьном курсе тригонометрии.

И так, при движении по окружности можно двумя способами измерять скорость – при помощи линейной скорости (какое расстояние проходит тело за единицу времени) и при помощи угловой скорости (на какой угол поворачивается тело за единицу времени). Эти скорости, очевидно, должны быть связаны между собой.

Но прежде чем, вывести это соотношение, представьте, что отрезок (AO) вращается по окружности (см.Рис.1.) и за время (t) переходит в отрезок ({A}^{’}O) – точка (A) переходит в точку ({A}^{’}), а точка (B) – в точку ({B}^{’}).

При этом точка (A) проходит за время (t) расстояние равное длине дуги окружности ({AA}^{’}), а точка (B) за тоже самое время (ведь обе точки лежат все время на одной прямой) расстояние ({BB}^{’}).

Выпишем формулы для линейных скоростей точек (A) и (B):
$$V_{A}=frac{{AA}^{’}}{t};$$
$$V_{B}=frac{{BB}^{’}}{t};$$
Из рисунка 1 видно, что ({AA}^{‘}>{BB}^{‘}), а значит линейная скорость точки (A) больше скорости точки (B):
$$V_{A}>V_{B};$$
Можно сделать важный вывод, что чем дальше точка находится от центра, тем больше ее скорость относительно точек, находящихся на этой же прямой.

А на какой угол успевают повернуться точки (A) и (B) за одно и тоже время (t)?

Из рисунка 1 видно, что они обе поворачиваются на один и тот же угол (Deltavarphi). А так как угловая скорость по определению, это отношение угла ко времени, то угловые скорости точек (A) и (B) одинаковые.

И так, что мы имеем – оказывается, что при удалении линейная скорость растет, а угловая скорость при этом не меняется. Тогда логичной выглядит следующая формула, связывающая угловую и линейную скорости:

$$V=omega*R; ,,(1)$$

где (V) – линейная скорость,

(omega) – угловая скорость,

(R) – радиус вращения.

Тангенциальное ускорение

Теперь представим, что мотоциклист едет по круглому мототреку не с постоянной скоростью, а равноускорено/равнозамедлено. В этом случае говорят, говорят, что мотоциклист движется с тангенциальным ускорением.

Тангенциальное ускорение – это обычное ускорение, к которому мы привыкли в курсе кинематики. Оно показывает на сколько успевает измениться скорость за единицу времени, например, за секунду.

Тангенциальное ускорение всегда направлено по касательной к траектории. Если тело ускоряется, то оно сонаправлено с линейной скоростью, а если замедляется, то направлено в противоположную сторону. (см.Рис.3, показано синей стрелкой (vec{a_{/tau}}))

При равноускоренномравнозамедленном движении тангенциальное ускорение можно посчитать по формуле:
$$a_{tau}=frac{V_к-V_н}{t};$$
где (V_к) – конечная скорость;

(V_н) – начальная скорость;

(t) – время, за которое скорость изменилась с (V_н) до (V_к).

При любом неравномерном движение по криволинейной траектории (окружности), у тела обязательно есть два вида ускорений – нормальное, направленное к центру, перпендикулярно скорости, и тангенциальное, направленное по касательной к траектории. Нормальное ускорение отвечает за изменение направления вектора линейной скорости, а тангенциальное за изменение величины линейной скорости.

Если тело движется с постоянной скоростью, то тангенциальное ускорение равно (0).

Если тело движется по прямой, то нормальное ускорение равно (0).

Векторно сложим эти два ускорения по правилу параллелограмма, и получим вектор общего ускорения, которым обладает тело при движении по окружности. (см. Рис.3., фиолетовая стрелка (vec{a})).

Пример 2

Колесо радиуса R вращается с постоянной скоростью. Во сколько раз отличаются центростремительные ускорения двух точек расположенный на расстояниях (R/2) и (R/3) от центра колеса

Решение:
Так как любая точка колеса вращается с одинаковой угловой скоростью (omega), то воспользуемся формулой для центростремительного ускорения через угловую скорость:
$$a_n=omega^2*r;$$
Пусть точка А вращается по окружности радиусом (R/2), а точка В – (R/3).
$$a_{nA}=omega^2*frac{R}{2};$$
$$a_{nB}=omega^2*frac{R}{3};$$
$$frac{a_{nA}}{a_{nB}}=frac{omega^2*frac{R}{2}}{omega^2*frac{R}{3}}=frac{R}{2}*frac{3}{R}=1,5$$
Ответ:(frac{a_{nA}}{a_{nB}}=1.5.)

Кинематика колеса.

Движение
колеса имеет сложную структуру. Колесо
перекатывается по поверхности дороги
теоретически без проскальзывания, в то
время как в действительности проскальзывание
существует, но составляет сравнительно
небольшую величину.

Введём
три системы координат: xy – неподвижную
относительно поверхности дороги; x1y1
– подвижную относительно поверхности
дороги; x1y1
– подвижную и связанную с рамой велосипеда
или осью колеса, x2y2
– подвижную и связанную непосредственно
с колесом, которая, таким образом,
совершает сложное движение. Система
координат x1y1
совершает переносное поступательное
движение, в котором все точки имеют
одинаковую скорость V.
Система координат x2y2
совершает относительное вращательное
движение, в котором каждая точка колеса
движется с окружной скоростью Vp
= wp,
где w
– угловая скорость относительного
движения; p
– расстояние от начала координат O1
до рассматриваемой точки. Векторная
сумма переносной и относительной
скоростей любой точки колеса равна
абсолютной скорости Va=V+Vp

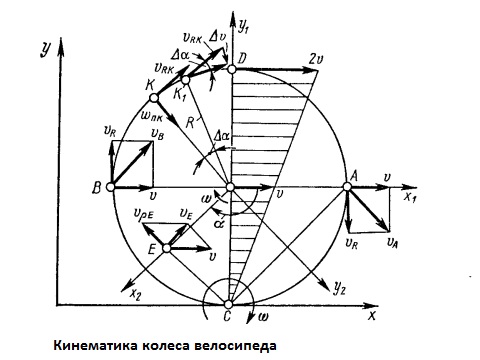
Точка
C
является точкой касания колеса с
поверхностью дороги и является неподвижной
при принятом выше условии – отсутствии
проскальзывания колеса относительно
дороги и деформации однотрубки. Скорость
точки С, принадлежащей колесу (p=R),
равна

Для
произвольной точки E
колеса, находящейся на расстоянии p=O1E
от оси колеса, скорость определится как
векторная сумма Ve=V+VpE.
Численное значение скорости точки E
может быть определено с помощью выражения

С
другой стороны, плоскопараллельное
движение колеса в каждый момент времени
можно представить как вращение около
мгновенного центра вращения. В данном
случае мгновенным центром вращения
является мгновенный центр скоростей в
точке C,
в котором скорость равна нулю. Положение
мгновенного центра скоростей можно
определить также как точку пересечения
перпендикуляров к направлениям векторов
абсолютных скоростей двух произвольных
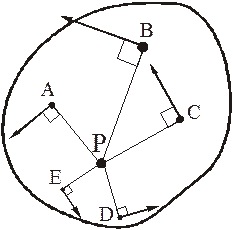
точек колеса, например А и Е.

Тогда
скорость любой точки колеса определяется
выражением V=wp,
где W
– угловая скорость вращения колеса
вокруг мгновенного центра скоростей,
равная угловой скорости вращения колеса
вокруг своей оси O1;
p
– расстояние от рассматриваемой точки
до мгновенного центра вращения. Так,
для точки D
это расстояние составляет Pd=2R,
для точек A
и B
будет Pв=Pа=Rsqrt2;
для произвольной точки Е

Направлен
вектор абсолютной скорости в сторону
вращения перпендикулярно к соответствующему
отрезку P,
соединяющему мгновенный центр скоростей
с рассматриваемой точкой.

Окружная
скорость любой i-й
точки Vri
направлена по касательной к траектории
её движения относительно оси вращения
колеса O1.
По мере увеличения угла “a”
точка A
последовательно занимает положения C,
B
и D,
а вектор Vri,
оставаясь постоянным по величине, меняет
своё направление. Это объясняется
наличием нормального ускорения движения
даже при равномерном вращении колеса,
т.е. при тангенциальном ускорении, равном
нулю. При бесконечно малом угле поворота
delta(a),
на который колесо поворачивается за
бесконечно малый промежуток времени
delta(t),
скорости в точках K
и K1
представляют собой равные по величине
векторы Vrk
и Vrk1,
касательные к окружности в этих точках.
Перенеся вектор скорости Vrk
в точку K1
получим вектор delta(V),
представляющий собой изменение скорости
точки K
при переходе в положение K1
за время delta(t).
Из подобия треугольников и с учётом
того, что delta(t)->0,
можно записать

Отсюда
следует, что нормальное ускорение точки
K

Это
ускорение направлено к центру колеса
и называется центростремительным. В
случае неравномерного движения полное
ускорение складывается из нормального
и тангенциального, которые взаимно
перпендикулярны:

Кинетостатика
системы

При
движении велогонщик и велосипед образуют
единую движущуюся систему, в которой
силы взаимодействия являются внутренними
и сами по себе не могут обеспечить
движения общего центра масс системы.
Для движения необходимы внешние силы,
которые в данном случае сводятся к силам
тяжести, силам трения колёс о дорожное
покрытие и силам аэродинамического
сопротивления.

Для
начала рассмотрим отдельно взятые
ведущее и ведомое колёса велосипеда, а
затем систему гонщик-велосипед в целом.

Ведущее
колесо.

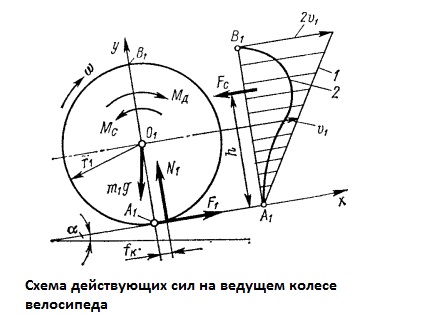
К
ведущему колесу массой m1
с моментом инерции J1
приложен движущий момент Mд,
под действием которого со стороны дороги
возникает сила трения скольжения F1=fN1,
где N1
– сила нормального давления; f
– коэффициент трения скольжения. Точка
A1
является мгновенным центром вращения
и её скорость равна нулю. Поэтому f
есть коэффициент трения покоя, величина
которого неопределенна и может принимать
значения от 0 до fmax.
Эпюра скоростей 1 в диаметральном сечении
колеса A1B1
является фактически эпюрой скоростей
набегающего воздушного потока, сила
сопротивления которого Fe,
приложенная в центре масс эпюры 2
суммарного лобового и вихревого
сопротивлений, создаёт момент полного
аэродинамического сопротивления Мe.

Колесо,
имеющее пневматическую шину в виде
однотрубки, деформируется в зоне контакта
с поверхностью дороги, что приводит к
смещению реакции N1
на некоторую величину fк,
называемую коэффициентом трения качения
Mк1=fкN1.
Учитывая малось величины fк,
в дальнейшем будем считать реакцию N1
приложенной в точке A1.

Уравнения
движения колеса запишутся в виде системы:

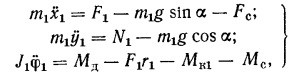
Где
x1,
y1
– координаты положения оси колеса O1;
Ф1 – угол поворота ведущего (заднего)
колеса; “a”
– угол наклона поверхности дороги к
горизонтали.

Если
колесо катится без проскальзывания, то
x1=r1Ф1;
y1=0;
N1=m1g*cos”a”.
Сила трения F1
без учёта
сил аэродинамического сопротивления

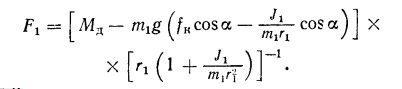
Движущий
момент Mд
в правой части уравнения может принимать
различные значения, но если правая часть
уравнения станет больше, чем fmax
N1,
то появится проскальзывание колеса
относительно дороги и увеличение Mд
оказывается нецелесообразным. Максимальное
ускорение составляет величину

Характерно,
что под уклон (“a”<0)
можно обеспечить движение без
проскальзывания с большими ускорениями.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Все задачи на определение положения мгновенного центра ускорений плоской фигуры можно свести к трем указанным ниже основным случаям, каждому из которых, очевидно, соответствует ряд частных случаев, зависящих от характера движения плоской фигуры.

2.2.1. Случай А. По условию задачи известна точка плоской фигуры, ускорение которой в данный момент времени равно нулю. Эта точка и является мгновенным центром ускорений.

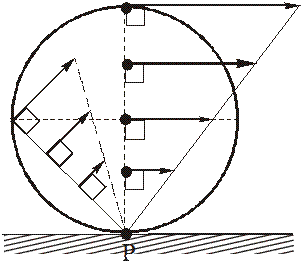
Рассмотрим, например, качение без скольжения колеса по прямолинейному рельсу с постоянной скоростью центра (рис. 8).

Мгновенный центр скоростей Р находится в точке соприкосновения колеса с рельсом. Поэтому:

где R – радиус колеса.

Угловая скорость вращения колеса:

.

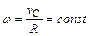
Центр колеса движется равномерно по прямой, следовательно, его ускорение:

т. е. центр колеса является мгновенным центром ускорений.

Так как колесо вращается равномерно, то ускорения всех точек колеса равны центростремительным ускорениям этих точек в их вращательном движении вокруг мгновенного центра ускорений. Например, ускорения точек обода определяются:

.

Ускорение каждой точки колеса направлено к мгновенному центру ускорений. В рассмотренном примере наглядно видно, что мгновенный центр скоростей Р и мгновенный центр ускорений Q является различными точками плоской фигуры. Мгновенный центр скоростей, не имея в данный момент скорости, имеет ускорение , мгновенный центр ускорений, не имея в данный момент ускорения, имеет постоянную скорость .

2.2.2. Случай В. Известны модуль и направление ускорения какой-либо точки А плоской фигуры , а также угловая скорость и угловое ускорение фигуры.

Определим положение мгновенного центра ускорений.

а) Неравномерное вращение: ω ≠ 0; ε ≠ 0. В этом случае мгновенный центр ускорений находится на отрезке, составляющем с направлением ускорения , угол

, (9)

который отложен от ускорения точки в сторону , на расстоянии от точки А, равном:

(10)

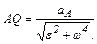
На рис. 9 показан случай ускоренного вращения плоской фигуры, а на рис. 10 – случай замедленного вращения.

Рис. 9	Рис. 10

Как видно, направление вращения на построение угла не влияет и угол всегда откладывается от направления ускорения в сторону .

б)Равномерное вращение: ω ≠ 0, ε = 0 (также момент, когда ε = 0 при неравномерном вращении) (рис. 11).

Рис. 11	Рис. 12

и = 0,

т. е. ускорения всех точек направлены к мгновенному центру ускорений. Расстояние от точки до мгновенного центра ускорений определяется по

.

в) Момент, когда угловая скорость становится равной нулю: ω = 0,

ε ≠ 0. В этом случае:

, = 90°,

т. е. ускорения всех точек направлены перпендикулярно к отрезкам, соединяющим эти точки с мгновенным центром ускорений (рис. 12).

Расстояние от точки до мгновенного центра ускорений определяется по формуле:

. (11)

Угловая скорость фигуры обычно обращается в нуль при изменении направления вращения фигуры.

г) Момент, когда угловая скорость и угловое ускорение становится равными нулю при непоступательном движении ω = 0, ε = 0.

В этом случае ускорения всех точек плоской фигуры в данный момент геометрически равны, так как ускорение любой точки равно ускорению полюса (рис. 13).

.

Рис.13.	Рис. 14.

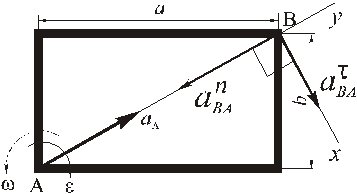
2.2.3. Случай С. Известны модули и направления ускорений двух точек плоской фигуры. Допустим, что известны ускорения точек А и В плоской фигуры и (рис. 14).

Примем точку А за полюс, тогда на основании (4) можно получить:

.

Построим при точке В параллелограмм ускорений по заданной диагонали и одной из сторон . Другая сторона параллелограмма опре-

делит ускорение во вращении точки В фигуры вокруг полюса А. Ускорение составляет угол с отрезком АВ, соединяющим точку В с полюсом А.

Отсчитывая полученный угол от ускорения к отрезку АВ, получаем направление , в данном случае противоположное направлению вращения часовой стрелки. Определив угол и направление , отложим этот угол от ускорений точек А и В по направлению . Две полученные полупрямые продолжим до пересечения в точке Q, которая и будет мгновенным центром ускорений.

Этот способ определения положения мгновенного центра ускорений не требует определения угла путем вычислений. Если положение мгновенного центра ускорений по этому способу определяется графически, то ускорения точек должны быть отложены в масштабе по их истинным направлениям.

Рис.15	Рис. 16

Рассмотрим случаи, когда ускорения точек плоской фигуры параллельны. Положение мгновенного центра ускорений в этом случае определяется на основании того, что:

• модули ускорений точек пропорциональны длинам отрезков, соединяющих точки с мгновенным центром ускорений:

• ускорения точек составляют с отрезками, соединяющими точки с мгновенным центром ускорений, один и тот же угол

.

На рис. 15 и 16 выполнено построение для случая:

, ω = 0, ε ≠ 0.

Рис.17.	Рис. 18.

На рис. 19 и рис. 20 построен мгновенный центр ускорений для случая:

=0, , ε = 0, ω ≠ 0.

В случае (рис. 21) мгновенный центр ускорений находится в бесконечности, а ускорения всех точек плоской фигуры геометрически равны.

Дата добавления: 2015-10-06 ; просмотров: 1286 | Нарушение авторских прав

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

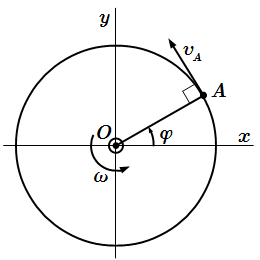
Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

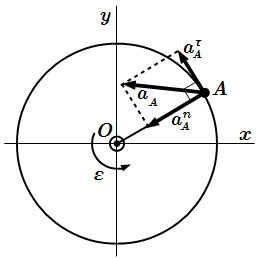
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

Пример решения задачи

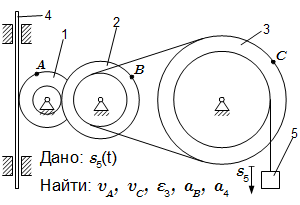
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r₁ = 2 см, R₁ = 4 см, у колеса 2 – r₂ = 6 см, R₂ = 8 см, у колеса 3 – r₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s₅ = t 3 – 6t (см). Положительное направление для s₅ – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Определение скоростей точек A и C

Точка A лежит на окружности радиуса R₁ с центром в точке O₁, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Точка B лежит на окружности радиуса R₂ с центром O₂, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Определение ускорения рейки 4

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019

Мгновенным центром скоростей (МЦС) называется такая точка плоской фигуры, скорость которой в данный момент времени равна нулю.

При любом непоступательном движении плоской фигуры такая точка всегда существует. Действительно,

Пусть в данный момент времени известно положение МЦС фигуры. Тогда, принимая его за полюс и учитывая, что 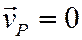, получим по формуле (4) для произвольной точки фигуры

т.е. знание МЦС упрощает определение скоростей точек плоской фигуры, т.к. сразу позволяет определить модуль скорости по формуле (5) и направление: .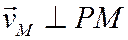

Таким образом, при известном МЦС вектор скорости любой точки плоской фигуры равен

модуль определяется по формуле

направлен вектор к отрезку РМ, соединяющему МЦС с данной точкой М, в сторону вращения фигуры вокруг МЦС.

В силу вышесказанного, возникает важная задача об определении положения МЦС плоской фигуры.

Положение мгновенного центра скоростей плоской фигуры может быть найдено, если:

1) задан закон движения (1) плоской фигуры (МЦС определяется с помощью дифференциальных равенств);

2) известны направления скоростей двух точек плоской фигуры, или их траектории.

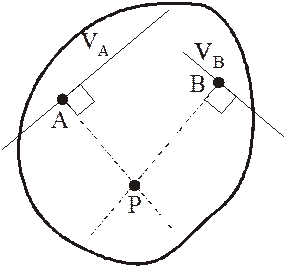
Рассмотрим только случай 2). Пусть известны направления скоростей двух точек А и В фигуры. Тогда для нахождения МЦС надо из этих точек опустить перпендикуляры к направлениям скоростей. В точке пересечения этих перпендикуляров и будет МЦС.

Частные случаи определения МЦС.

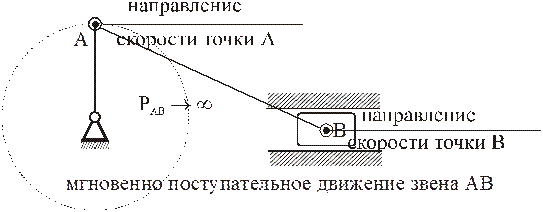
а) скорости точек параллельны, но точки не лежат на общем перпендикуляре к скоростям

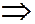
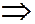
Ясно, что в этом случае перпендикуляры к скоростям параллельны, пересекаются в ¥, угловая скорость фигуры = 0 и скорости всех её точек в данный момент равны между собой. Такое движение фигуры называют мгновенно поступательным.

Замечание. Не путать мгновенно поступательное движение с поступательным: при поступательном движении скорости и ускорения всех точек равны между собой в любой момент времени, а при мгновенно поступательном равны только скорости всех точек (но не ускорения – они не равны друг другу!) и только в данный момент.

б) скорости двух точек фигуры параллельны, направлены в одну сторону и их модули не равны друг другу, а точки лежат на одном перпендикуляре к скоростям

В этом случае одних направлений скоростей не достаточно: должны быть известны и их модули.

Для нахождения МЦС надо концы векторов скоростей соединить прямой линией: в точке её пересечения с продолжением отрезка АВ и будет МЦС.

Если известно расстояние АВ, то легко получить

в) то же, что и в предыдущем случае, но векторы скоростей направлены в разные стороны; в этом случае модули скоростей могут быть и равны между собой, но должны быть известны.

Нахождение МЦС также аналогично предыдущему: концы векторов скоростей соединяем прямой линией – в точке её пересечения с отрезком АВ будет МЦС.

Если задано расстояние АВ, то аналогично пункту б) можно найти

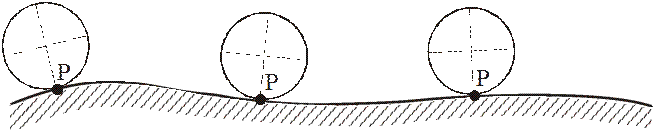
г) качение колеса без скольжения по любой гладкой неподвижной поверхности.

Если колесо всё время остаётся в вертикальной плоскости, и отсутствуют повороты вокруг вертикальной оси, то оно совершает плоскопараллельное движение. В этом случае положение МЦС сразу известно: в точке контакта колеса с поверхностью. Действительно, если нет скольжения, то скорость точки контакта равна скорости соответствующей точки поверхности, т.е. нулю (поверхность неподвижна). По определению МЦС – здесь он и находится.

В связи с этим, интересно посмотреть распределение скоростей точек катящегося без скольжения колеса:

скорость верхней точки колеса в два раза больше скорости его центра!

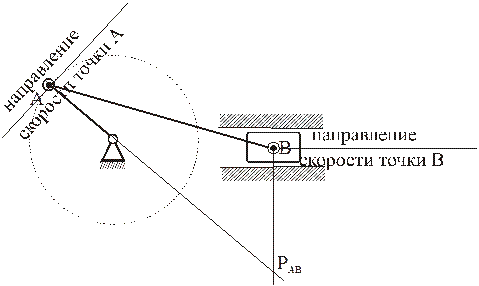
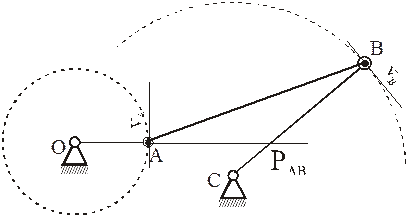
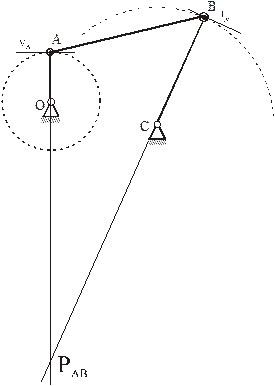
Примеры определения МЦС для шатуна АВ кривошипно-ползунного механизма.

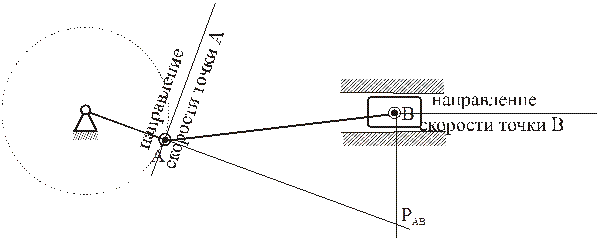
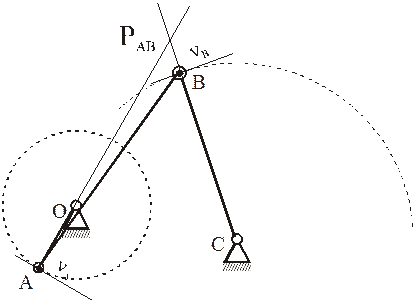
Определение МЦС для шатуна АВ кривошипно-коромыслового механизма:

Рассмотрим пример определения скорости и ускорения точки плоской фигуры.

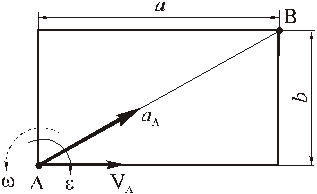
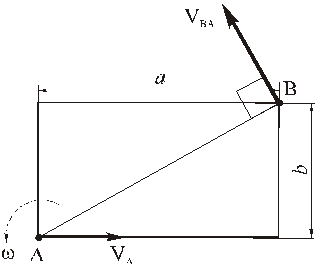
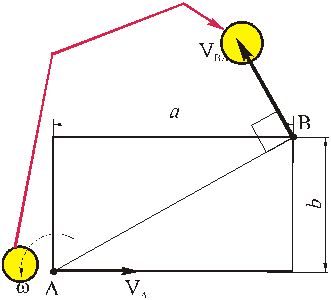
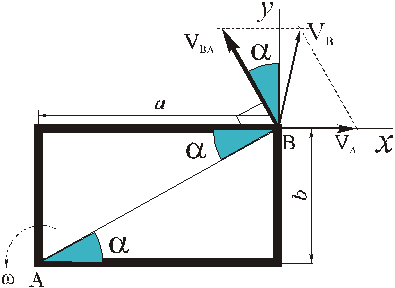
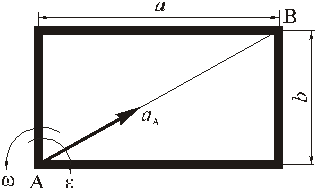
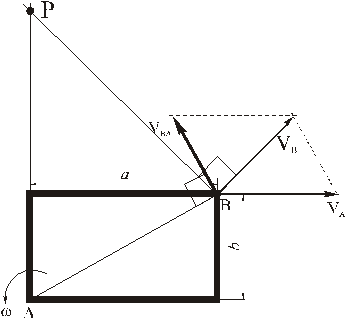
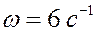
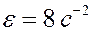
Прямоугольная пластина со сторонами a = 0,4 м и b = 0,3 м движется в своей плоскости. В данный момент времени скорость точки А пластины равна по модулю v_A = 4 м/с, модуль ускорения этой точки равен a_A = 3 м/с 2 , модули угловой скорости и углового ускорения фигуры равны соответственно , . Направления показаны на рисунке.

Определить скорость и ускорение точки B плоской фигуры в этот момент времени.

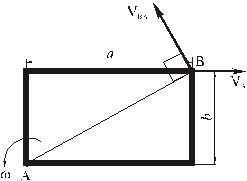
РЕШЕНИЕ. Принимая за полюс точку А, для определения скорости точки B используем формулу (4):

Вычислив расстояние АВ

по формуле (5) найдём модуль скорости точки В при её вращении вокруг полюса А

Изображаем вектор ():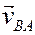

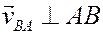
(стрелка вектора 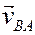должна быть направлена в сторону вращения фигуры!).

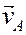
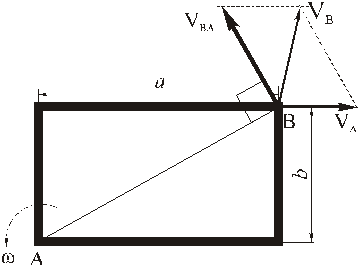
Вектор скорости полюса переносим параллельно в точку В,

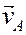
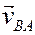
согласно равенству (4) складываем векторы и .

Для определения модуля скорости находим :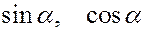

Теперь модуль скорости можно найти двумя способами:

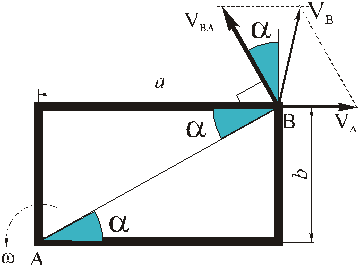
по теореме косинусов (формула (6))

При определении скорости вторым способом выбираем оси координат

и проектируем (4) на эти оси:

Ускорение точки В определяем по формуле (8)

принимая за полюс точку А с известным ускорением.

По формулам (10) и (12) находим модули ускорений

Изображаем векторы этих ускорений:

.

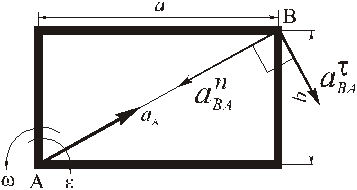
Так как согласно (8) для определения вектора ускорения точки В надо складывать три вектора, то выбираем оси координат

и проектируем (8) на эти оси:

Модуль ускорения будет

Геометрически (на рисунке) вектор ускорения строится при помощи «векторного многоугольника»: от заданной точки в выбранном масштабе последовательно откладываются векторы так, что конец предыдущего вектора является началом следующего; сумма векторов – вектор, идущий из заданной точки в конец последнего вектора.

Зная скорость точки А и угловую скорость фигуры можно найти положение мгновенного центра скоростей. Из равенства (15) следует

Используя доказательство существования МЦС, получаем.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10825 — | 7386 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно