Ещё одним параметром, характеризующий систему из линз и сферических зеркал, является линейное увеличение.
Линейным увеличением называется отношение высоты получившегося изображения к высоте предмета:
Г (1)
- где
Вопрос о поиске данного параметра может возникнуть и в задачах на построение, и в задачах на формулы тонкой линзы и сферического зеркала.
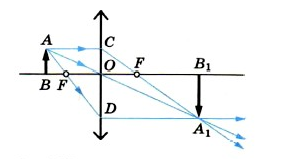
Пусть даны предмет, линза и изображение предмета в линзе (рис. 1).
Рис. 1. Линейное увеличение
При построении мы использовали луч от предмета (), который проходит через главный оптический центр линзы (при этом не преломляясь). При этом у нас получились два подобных треугольника (подобие по трём углам). Тогда, используя подобие, можем записать:
Г (2)
Вывод: вопросы, связанные с линейным увеличением, решаются или через логику построения в системах (рис.1), или через соотношение (2) при наличии численных значений параметров линз.
Формула тонкой линзы — формула, связывающая три величины: расстояние от предмета до линзы, расстояние от изображения до линзы и фокусное расстояние линзы.
Условные обозначения:
- расстояние от предмета до линзы — d (м);
- расстояние от изображения до линзы— f (м);
- фокусное расстояние линзы — F (м).
Вывод формулы
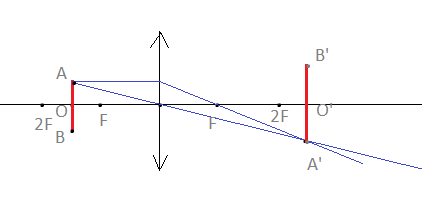
Обратимся к рисунку, который мы использовали для объяснения правила построения изображений в собирающих линзах:
Видно, что треугольники АОВ и А1В1О подобные (по двум углам). Следовательно:
BOOB1=ABA1B1
По двум углам также являются подобными треугольники COF и FA1B1. Отсюда делаем вывод, что:
COA1B1=OFFB1
Линия предмета образует с частью главной оптической оси, перпендикуляром, проведенным из верхней точки к линзе, и частью самой линзы прямоугольник. Следовательно, его противоположные стороны равны:
AB=CO
Следовательно:
ABA1B1=COA1B1
Отсюда следует, что:
BOOB1=OFFB1
BO является расстоянием от предмета до линзы. Обозначим его за d. OB1 является расстоянием от линзы до изображения. Обозначим его за f. OF является фокусным расстоянием линзы. Обозначим его за F. FB1 является разностью расстояния от линзы до изображения и фокусного расстояния линзы. Поэтому это выражение мы можем записать так:
df=Ff−F
Избавимся от знаменателей и получим:
fd−Fd=fF
Или можно записать так:
fF+Fd=fd
Теперь все члены равенства поделим на произведение Ffd. В результате вычислений получим формулу тонкой линзы:
Формула тонкой линзы
1d+1f=1F
Поскольку величиной, равной обратной фокусному расстоянию, является оптическая сила, формулу тонкой линзы можно записать следующим образом:
1d+1f=D
Величины d, ƒ и F могут быть как положительными, так и отрицательными. Отметим (без доказательства), что при применении формулы тонкой линзы знаки нужно ставить перед членами уравнения согласно следующим правилам.
Правила расстановки знаков перед членами уравнения в формуле линзы
- Если линза собирающая, то ее фокус действительный, и перед членом 1F ставят знак «плюс» (1F).
- Если линза рассеивающая, то ее фокус мнимый, и перед членом 1F ставят знак «минус» (−1F).
- Если изображение действительное, то перед величиной 1d ставят знак «плюс» (1d).
- Если изображение мнимое, то перед величиной 1d ставят знак «минус» (−1d).
- Величина 1f всегда имеет знак «плюс», поскольку расстояние от предмета до линзы всегда положительное.
Иногда случается, что перед величинами F, f и d знаки неизвестны. Тогда при вычислениях перед ними ставят знаки «плюс». Но если в результате вычислений фокусного расстояния или расстояния от линзы до изображения либо до источника получается отрицательная величина, то это означает, что фокус, изображение или источник мнимые.
Пример №1. Фокусное расстояние линзы равно 10 см. Найти расстояние от предмета до линзы, если расстояние от нее до изображения составляет 15 см.
Переводить в СИ единицы измерения не будем, поскольку они однородны. Так как все величины выражены в см, то и ответ будет выражен в см.
Применим формулу тонкой линзы:
1d+1f=1F
1d+115=110
Умножим выражение на 150d:
150+10d=15d
5d=150
d=30 (см)
Увеличение линзы
Раньше мы уже упоминали, что изображение, полученное в линзе, может быть увеличенным или уменьшенным. Различие размеров предмета и изображения характеризуется увеличением.
Определение
Линейное увеличение — отношение линейного размера изображения к линейному размеру предмета. Линейное увеличение обозначают буквой Γ.
Чтобы найти линейное увеличение изображения предмета в линзе, снова обратимся к первому рисунку этого параграфа. Если высота предмета АВ равна h, а высота изображения А1В1 равна Н, то:
Γ=Hh
Мы уже выяснили, что треугольники АОВ и ОА1В1 подобны. Поэтому:
Hh=|f||d|
Где H — высота изображения предмета, h — высота самого предмета.
Отсюда вытекает, что увеличение линзы равно:
Γ=|f||d|
Пример №2. Предмет имеет высоту h = 2 см. Какое фокусное расстояние F должна иметь линза, расположенная от экрана на расстоянии f = 4 м, чтобы изображение указанного предмета имело высоту H = 1 м?
2 см = 0,02 м
Сначала применим формулы тонкой линзы:
1d+1f=1F
Она необходима, чтобы выразить фокусное расстояние линзы:
F=dfd+f
Расстояние от предмета до линзы неизвестно. Но его можно выразить из формулы увеличения линзы:
Γ=fd=Hh
Отсюда это расстояние равно:
d=fhH
Подставим полученное выражение в формулу фокусного расстояния линзы:
F=fhHffhH+f=f2hH·
Hfh+fH=fhH+h
F=fhH+h=4·0,021+0,02≈0,08 (м)=8 (см)
Задание EF17760

Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Сделать рисунок — построить изображение в линзе.
3.Записать формулу для нахождения площади полученной фигуры.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Оптическая сила линзы: D = 2,5 дптр.
• Сторона треугольника AC = 4 см.
4 см = 0,04 м
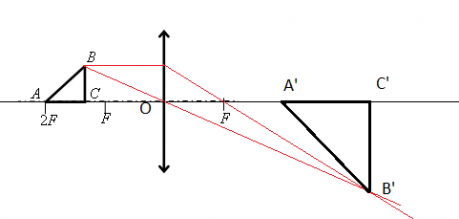
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d+1f=1F
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F+1f=1F
1f=1F−12F=2−12F=12F
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D=12,5=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76+1f=1F
1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4
fC=0,76·0,40,76−0,4=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´=ACA´C´
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´=ACA´C´
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17685
Линза с фокусным расстоянием F=1м даёт на экране изображение предмета, увеличенное в 4 раза. Каково расстояние от предмета до линзы?
Ответ:
а) 0,50 м
б) 0,75 м
в) 1,25 м
г) 1,50 м
Линза с фокусным расстоянием F=1м даёт на экране изображение предмета, увеличенное в 4 раза. Каково расстояние от предмета до линзы?
Алгоритм решения
1.Записать известные данные.
2.Записать формулу увеличения линзы и формулу тонкой линзы.
3.Выразить из обеих формул расстояние от линзы до изображения предмета.
4.Приравнять правые части выражений.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем известные данные:
• Фокусное расстояние линзы: F = 1 м.
• Увеличение линзы: Γ = 4.
Запишем формулу увеличения линзы и выразим из нее расстояние от линзы до изображения предмета:
Γ=fd
f=Γd
Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Приравняем правые части последних выражений:
Γd=dFd−F
Поделим на d и выразим расстояние от предмета до линзы:
Γ=Fd−F
d=FΓ+F=14+1=1,25 (м)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18124
Предмет высотой 6 см расположен на горизонтальной главной оптической оси тонкой собирающей линзы на расстоянии 30 см от её оптического центра. Высота изображения предмета 12 см. Найдите фокусное расстояние линзы.
Ответ:
а) 5 см
б) 10 см
в) 20 см
г) 36 см
Алгоритм решения
1.Записать известные данные.
2.Записать формулу увеличения линзы в двух вариантах и выразить из нее расстояние от изображения до линзы.
3.Записать формулу тонкой линзы и тоже выразить из нее расстояние от изображения до линзы.
4.Приравнять правые части выражений.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем известные данные:
• Расстояние от оптического центра линзы до предмета: d = 30 cм.
• Высота предмета: h = 6 см.
• Высота изображения: H = 12 см.
Так как все данные измеряются в сантиметрах, переводить единицы измерения величин в СИ нет необходимости. Просто ответ будет получен тоже в сантиметрах.
Запишем формулу увеличения линзы:
Γ=Hh=fd
Отсюда расстояние от изображения до линзы равно:
f=Hdh
Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Приравняем правые части последних выражений:
Hdh=dFd−F
Поделим на d, у множим на h(d –F) и выразим фокусное расстояние:
Hh=Fd−F
H(d−F)=hF
Hd−HF=hF
hF+HF=Hd
F(h+H)=Hd
F=Hdh+H=12·3012+6=20 (см)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF19112
В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со скоростью v = 5 м/с движется точечный источник света. Расстояние между плоскостями d = 15 см. Центр окружности находится на главной оптической оси линзы. Фокусное расстояние линзы F = 10 см. Найдите скорость движения изображения точечного источника света. Сделайте пояснительный чертёж, указав ход лучей в линзе. Ответ запишите в м/с.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
3.Записать формулу тонкой линзы и определить из нее расстояние от изображения до линзы.
4.Записать формулу линейного увеличения линзы двумя способами для вычисления радиусов окружностей, по которым движутся точка и ее изображение.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Фокусное расстояние линзы: F = 10 см.
• Расстояние от линзы до плоскости, в которой вращается точка: d = 15 см.
• Скорость вращения точки: v = 5 м/с.
10 см = 0,1 м
15 см = 0,15 м
Выполним рисунок. Для его построения достаточно найти изображение точки А. Затем в противоположную сторону отложим перпендикуляр и на таком же расстоянии от главной оптической оси будет находиться изображение точки B.
Глядя со стороны, мы будем видеть вместо окружности, которую описывает точка, линию AB. Она равн диаметру окружности, по которой движется точка. Обозначим ее радиус OA за r. Изображением окружности будет окружность. Вместо нее мы со стороны также увидим отрезок — A´B´. Обозначим радиус O´A´ за R.
Запишем формулу тонкой линзы и выразим из нее расстояние от изображения до линзы:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Формулу линейного увеличения линзы можно определить как отношение радиуса окружности, по которой движется точка-изображение, к радиусу окружности, по которой движется сама точка:
Γ=Rr
Линейное увеличение также определяется формулой:
Γ=fd
Следовательно:
Rr=fd
Подставим сюда выражение, найденное для расстояния от изображения до линзы из формулы тонкой линзы:
Rr=dFd(d−F)=Fd−F
Так как изображение будет двигаться вслед за точкой, то угловые скорости этой точки и изображения будут равны. Поэтому:
ω=vr=VR
Отсюда линейная скорость движения изображения равна:
V=Rvr=Fvd−F=0,1·50,15−0,1=10 (мс)
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.9k
Увеличение микроскопа
Увеличением
микроскопа
называется отношение линейных размеров
изображения предмета, видимого в
микроскоп, к линейным размерам того же
предмета, видимого невооруженным глазом
на расстоянии наилучшего видения (для
нормального глаза оно равняется 25см).
Известно,
что увеличение микроскопа можно найти,
пользуясь формулой:
|
|
(1) |
где
l
– расстояние между верхним фокусом
объектива и нижним фокусом окуляра; L
– расстояние наилучшего видения; равное
25 см; F1
и F2
– фокусные расстояния объектива и
окуляра.
Зная
фокусные расстояния F1,
F2
и расстояние между ними l
можно найти увеличение микроскопа.
На
практике не используются микроскопы с
увеличением свыше 1500–2000, т.к. возможность
различения мелких деталей объекта в
микроскопе ограничена. Это ограничение
обусловливается влиянием дифракции
света, в проходящей структуре данного
объекта. В связи с этим пользуются
понятиями предела разрешения и разрешающей
способности микроскопа.
Определение предела разрешения микроскопа
Пределом
разрешения микроскопа
называется то наименьшее расстояние
между двумя точками предмета, при котором
они видимы в микроскопе раздельно. Это
расстояние определяется по формуле:
|
|
(2) |
где
λ – длина волны света; n
– показатель преломления среды между
объективом и объектом; u
– апертурный угол объектива, равный
углу между крайними лучами конического
светового пучка, входящего в объектив
микроскопа.
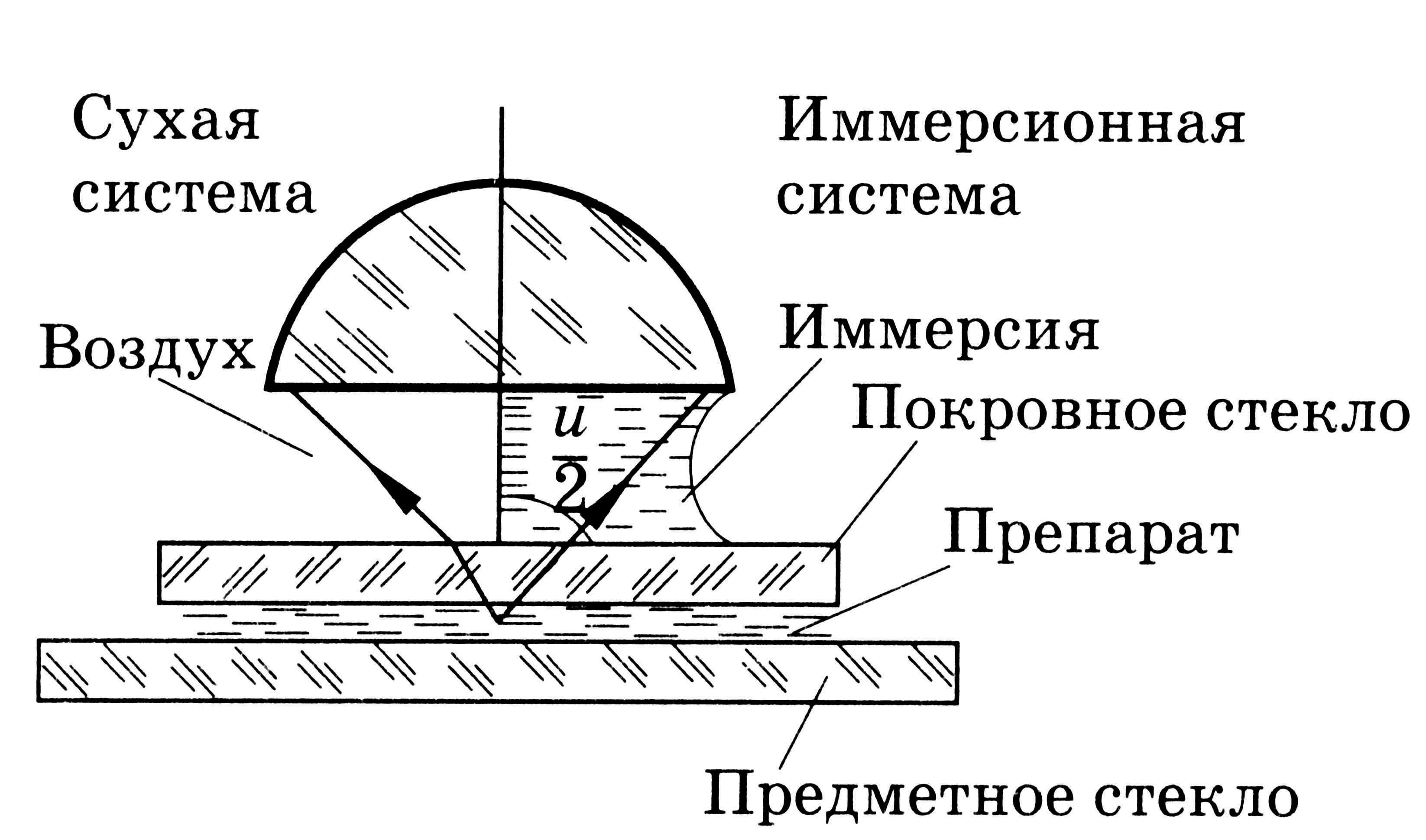
Реально
свет от предмета распространяется к
объективу микроскопа в некотором конусе
(рис. 2 а), который характеризуется угловой
апертурой – углом u
между крайними лучами конического
светового пучка, входящего в оптическую
систему. В предельном случае, согласно
Аббе, крайними лучами конического
светового пучка будут лучи, соответствующие
центральному (нулевому) и 1-му главному
максимумам (рис. 2 б).
Величина
2nsin
U
называется числовой апертурой микроскопа.
Числовая апертура может быть увеличена
с помощью специальной жидкой среды –
иммерсии
–
в пространстве между объективом и
покровным стеклом микроскопа.
|
|
|
|
а) |
б) |
|
Рис. |
В
иммерсионных системах по сравнению с
тождественными “сухими” системами
получают больший апертурный угол (рис.
3).
Рис.3.
Схема иммерсионной системы
В
качестве иммерсии используют воду (n
=
1,33),
кедровое масло (n
=
1,514) и др. Для каждой иммерсии специально
рассчитывают объектив, и его можно
применять только с данной иммерсией.
Из
формулы видно, что предел разрешения
микроскопа зависит от длины волны света
и числовой апертуры микроскопа. Чем
меньше длина волны света и чем больше
величина апертуры, тем меньше Z, а,
следовательно, больше предел разрешения
микроскопа. Для белого (дневного) света
можно принять среднее значение длины
волны λ
= 0,55мкм. Показатель преломления для
воздуха равен n
= 1.
Микроскоп мбс-1
МБС-1
– cтереоскопический
микроскоп, дающий прямое объемное
изображение рассматриваемого предмета
как в проходящем, так и в отраженном
свете.
Микроскоп
состоит из 4 основных частей:
– cтолик;
– штатив;
– оптическая
головка с механизмом грубой подачи;
– окулярная
насадка.
Столик
микроскопа состоит из круглого корпуса,
внутри которого вмонтирован поворотный
отражатель с зеркальной и матовой
поверхностями. Для работы с дневным
освещением в корпусе предусмотрен
вырез, через который свободно проходит
свет. С задней стороны корпуса столика
имеется резьбовое отверстие для работы
с электрическим осветителем. На штативе
микроскопа крепится оптическая головка
– основная часть прибора, в которую
вмонтированы наиболее ответственные
оптические узлы.
В
корпусе оптической головки помещен
барабан с с установленными в нем
галилеевыми системами. Вращением оси
барабана с помощью рукояток с нанесенными
цифрами 0,6; 1; 2; 4; 7 добиваются различного
увеличения объективов. Каждое положение
барабана четко фиксируется специальным
пружинным фиксатором. С помощью рукоятки
на штативе микроскопа, перемещающей
оптическую головку, добиваются наиболее
резкого изображения рассматриваемого
объекта.
Вся
оптическая головка может перемещаться
по стержню штатива и закрепляться в
любом положении с помощью винта. Окулярная
насадка состоит из направляющей,
представляющей прямоугольную деталь
с двумя отверстиями для оправ объективов.
Наблюдая
в окуляры нужно разворотом окулярных
трубок найти такое положение, при котором
два изображения сводятся в одно. Далее
произвести фокусировку микроскопа на
исследуемый предмет, а вращением
отражателя добиться равномерного
освещения поля. При настройке освещенности
патрон с лампой перемещается в сторону
коллектора до получения наилучшей
освещенности наблюдаемого объекта.
В
основном МБС-1 предназначен для
препарировальных работ, для наблюдения
объектов, а также для проведения линейных
измерений или измерений площадей
участков препарата. Оптическая схема
микроскопа представлена на рис. 4.
Оптическая
схема микроскопа МБС-1 представлена на
рис. 4.
При
работе в проходящем свете источник
света (1) с помощью отражателя (2) и
коллектора (3) освещает прозрачный
препарат, установленный на предметный
столик (4).
В
качестве объектива применена специальная
система, состоящая из 4-х линз (5) с фокусным
расстоянием = 80 мм и 2-х пар галилеевых
систем (6) и (7), за которыми находятся
объективы (8) с фокусным расстоянием 160
мм, которые образуют изображение объекта
в фокальных плоскостях окуляров.
Общее
линейное увеличение оптической системы,
состоящей из объектива (5), галилеевых
систем (6) и (7) и объективов (8) составляет:
0,6;
1;
2;
4;
7.
За объективами (8) установлены 2 призмы
Шмидта (9), которые позволяют разворачивать
окулярные трубки по глазу наблюдателя
без разворота изображения объектива.
|
5
4
6
2
6
3
1 10
9
8
7 7 |
1
2
3
4
5
6,
8
9
10 |
|
Рис. |
К
микроскопу МБС-1 прилагаются 3 пары
окуляров (10) с увеличением 6;
8;
12,5
и один окулярный микрометр 8-кратного
увеличения с сеткой. Они позволяют
варьировать общее увеличение микроскопа
от 3,6 до 88 (табл. 1). Общее увеличение
микроскопа – произведение увеличения
окуляра на увеличение объектива.
Таблица
1.
Оптическая
характеристика микроскопа МБС-1
|
Увеличение окуляра |
Увеличение |
||||
|
0,6 |
1 |
2 |
4 |
7 |
|
|
6 |
3,6 |
6 |
12 |
24 |
42 |
|
8 |
4,5 |
8 |
16 |
32 |
56 |
|
12,5 |
7 |
12,5 |
25 |
50 |
88 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
22.02.2015177.66 Кб137.doc
- #
- #
- #
- #
22.02.2015335.87 Кб238.doc
- #
22.02.2015954.88 Кб808.doc
- #
22.02.2015374.78 Кб178.doc
- #
- #
- #
- #
Увеличение – это процесс появления объекта с целью визуального осмотра и анализа. Микроскопы, бинокли и телескопы все увеличивают, используя специальные приемы, встроенные в светопропускающие линзы различных форм.
Линейное увеличение относится к одному из свойств выпуклых линз или тех, которые показывают внешнюю кривизну, как сфера, которая была сильно уплощена. Их аналогами в оптическом мире являются вогнутые линзы, или те, которые изогнуты внутрь и излучают световые лучи не так, как выпуклые линзы.
Принципы увеличения изображения
Когда световые лучи, проходящие параллельно, изгибаются, когда они проходят через выпуклую линзу, они изгибаются и, таким образом, фокусируются на общей точке на противоположной стороне линзы. Эта точка, F, называется фокусной точкой , а расстояние до F от центра объектива, обозначаемое f , называется фокусным расстоянием .
Сила увеличительной линзы является обратной величиной ее фокусного расстояния: P = 1 / f . Это означает, что объективы с коротким фокусным расстоянием имеют сильные возможности увеличения, в то время как более высокое значение f означает меньшую мощность увеличения.
Определено линейное увеличение
Линейное увеличение, также называемое боковым увеличением или поперечным увеличением, представляет собой просто отношение размера изображения объекта, создаваемого линзой, к истинному размеру объекта. Если изображение и объект находятся в одном и том же физическом носителе (например, в воде, воздухе или в космическом пространстве), то формула бокового увеличения – это размер изображения, деленный на размер объекта:
M = frac {-i} {o}
Здесь M – увеличение, i – высота изображения, а o – высота объекта. Знак минус (иногда опускается) является напоминанием о том, что изображения объектов, образованных выпуклыми зеркалами, выглядят перевернутыми или перевернутыми.
Формула объектива
Физическая формула линзы соотносит фокусное расстояние изображения, образованного тонкой линзой, расстояние изображения от центра линзы и расстояние от объекта до центра линзы. Уравнение
Гидроразрыва {1} {d_o} + гидроразрыва {1} {d_i} = гидроразрыва {1} {F}
Допустим, вы положили тюбик губной помады на 10 см от выпуклой линзы с фокусным расстоянием 6 см. Как далеко изображение появится на другой стороне объектива?
Для d o = 10 и f = 4 имеем:
begin {align} & frac {1} {10} + frac {1} {d_i} = frac {1} {4} & frac {1} {d_i} = 0.15 \ & d_i = 6.7 {конец выровнен}
Здесь вы можете поэкспериментировать с разными числами, чтобы понять, как изменение физической настройки влияет на оптические результаты в этом типе проблемы.
Обратите внимание, что это еще один способ выразить концепцию линейного увеличения. Отношение d i к d o такое же, как отношение i к o . То есть отношение высоты объекта к высоте его изображения совпадает с отношением длины объекта к длине его изображения.
Титбиты увеличения
Отрицательный знак применительно к изображению, которое появляется на противоположной стороне линзы от объекта, указывает на то, что изображение является «реальным», т. Е. Что оно может быть спроецировано на экран или какой-либо другой носитель. Виртуальное изображение, с другой стороны, появляется на той же стороне линзы, что и объект, и не связано с отрицательным знаком в соответствующих уравнениях.
Хотя такие темы выходят за рамки настоящего обсуждения, различные уравнения объективов, относящиеся к множеству реальных ситуаций, многие из которых связаны с изменениями в средах (например, из воздуха в воду), могут быть легко обнаружены на интернет.
Микроскоп
Микроскопом называют оптический прибор, служащий для рассматривания очень мелких предметов (в том числе невидимых невооруженным глазом).
Микроскоп состоит из двух собирающих короткофокусных линз — объектива и окуляра, расстояние между которыми может изменяться.
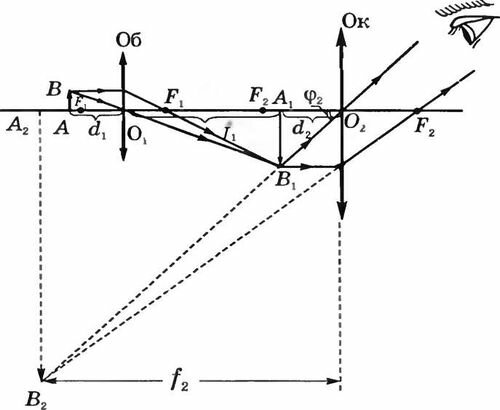
Ход лучей в микроскопе показан на рисунке 16.56. Объектив создает действительное, перевернутое, увеличенное промежуточное изображение A1B1 предмета АВ.
С помощью микрометрического винта окуляр помещают относительно объектива таким образом, чтобы это промежуточное изображение A1B1 оказалось между передним фокусом F2 и оптическим центром O2 окуляра. Тогда окуляр становится лупой и создает мнимое, прямое (относительно промежуточного) и увеличенное изображение А2В2 предмета АВ. Использование микроскопа приводит к значительному увеличению угла зрения, под которым глаз рассматривает предмет ((varphi_2 gg varphi_1)) что позволяет видеть детали, не видимые невооруженным глазом. Линейное увеличение микроскопа.
(Gamma = frac{A_2B_2}{AB} = frac{A_2B_2}{A_1B_1} cdot frac{A_1B_1}{AB}.)
Так как (frac{A_2B_2}{A_1B_1} = Gamma_{ok}) — линейное увеличение окуляра и (frac{A_1B_1}{AB} = Gamma_{ob}) линейное увеличение объектива, то линейное увеличение микроскопа (Gamma = Gamma_{ok} cdot Gamma_{ob}.)
Из рисунка 16.56 видно, что (Gamma_{ob} = frac{A_1B_1}{AB} = frac{O_1A_1}{O_1A}.) где (~O_1A_1 = O_1F_1 + F_1F_2 + F_2A_1.)
Обозначим (~delta) расстояние между задним фокусом объектива и передним фокусом окуляра, т.е. (~delta = F_1F_2 .) Так как (~delta gg O_1F_1) и (~delta gg F_2A_1 ,) то (~O_1A_1 approx delta.) Поскольку (O_1A approx F_{ob}) где Fob — фокусное расстояние объектива, получаем
(Gamma_{ob} = frac{delta}{F_{ob}} .)
Линейное увеличение окуляра определяют по той же формуле, что и увеличение лупы, т.е. (Gamma_{ok} = frac{d_0}{F_{ok}} ,) где d0 — расстояние наилучшего зрения, Fok — фокусное расстояние окуляра.
Тогда получим (Gamma = frac{delta cdot d_0}{F_{ob} cdot F_{ok}}) — линейное увеличение микроскопа.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 487-489.