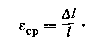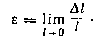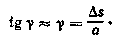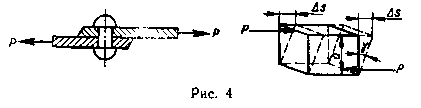Деформация
– изменение формы и размеров тела,
возникающие при приложении к
рассматриваемому телу внешних сил.
Деформации разделяются
на упругие и остаточные. Упругими
деформациями называются такие изменения
формы и размеров тела, которые исчезают
после удаления вызвавших их сил, и тело
полностью возвращается в первоначальную
форму. Те деформации, которые остаются
в теле после удаления внешних сил,
называются остаточными.
Перемещение
–
изменение положения точки тела в
пространстве вследствие
изменения его формы и размеров под
действием нагрузки.
Линейная
деформация
– характеризует изменение размеров
тела. Различают абсолютную
деформацию ΔL
и относительную
деформацию ε
= ΔL/L.
Угловая
деформация – характеризует
изменение формы тела и чаще всего
называется углом
сдвига.
Угол
сдвига —
это изменение первоначально прямого
угла. γ
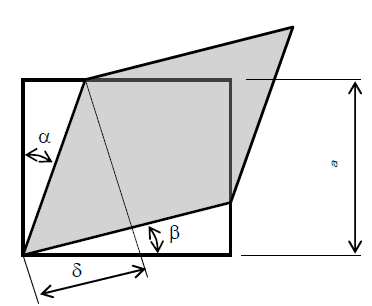
= α + β .
Полная
деформация —
это сумма линейной и угловой деформации.
7.Принцип независимости действия сил.
Для
рассчитываемых реальных объектов
(линейно деформируемых систем) справедливо
утверждение, которое называется принципом
независимости действия сил(принципом
суперпозиции или наложения). Этот принцип
применяется тогда, когда упругие
деформации конструкции достаточно малы
и они не вызывают изменения в расположении
нагрузок, считается справедливым закон
Гука. В этом случае результат воздействия
на конструкцию системы нагрузок равен
сумме результатов воздействия каждой
нагрузки в отдельности.
2. Растяжение и сжатие прямого бруса
1. Принцип Сен-Венана,
гипотеза Бернулли
Принцип Сен-Венана –
напряжение в местах достаточно удалённых
от мест приложения нагрузки распределяется
равномерно.
Гипотеза Бернулли –
поперечные сечения, плоские до деформации,
остаются плоскими и после деформации
(гипотеза Плоских сечений).
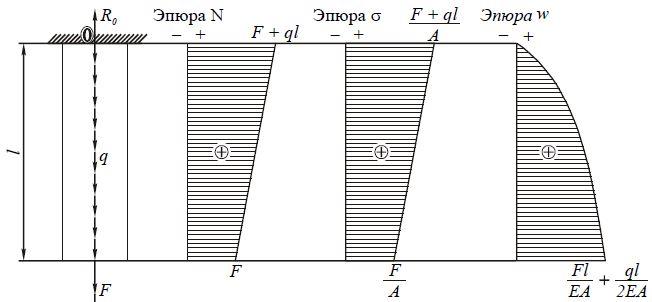
2. Определение
внутренних усилий. Эпюры продольных
сил.
Внутреннее усилие
численно равно алгебраической сумме
всех сил, расположенных по одну сторону
от рассматриваемого сечения (метод
сечений).По двум точкам строим эпюру N.
3. Определение
напряжений, эпюра напряжений.
Напряжения численно
равны усилию на участке, деленному на
площадь этого участка
4. Напряжения в
наклонных сечениях к оси бруса.
;
;
5. Закон Гука при
растяжении сжатии. Модуль упругости Е
и коэффициент Пуассона μ. Жёсткость при
растяжении и сжатии.
Закон Гука – абсолютное
удлинение (укорочение) стержня прямо
пропорционально действующей силе, длине
стержня и обратно пропорционально
произведению ЕА, называемому ЖЁСТКОСТЬЮ
стержня при растяжении и сжатии.
;
;
;
E-модуль
Юнга – коэффициент пропорциональности.
Коэффициент Пуассона
– Отношение относительной поперечной
деформации к относительной продольной
деформации взятое по абсолютной величине.
μ=|εпоп/εпрод|
6. Перемещение
поперечных сечений бруса. Эпюры
перемещений.
Полное перемещение
бруса вычисляется как сумма перемещений
на предыдущих участках
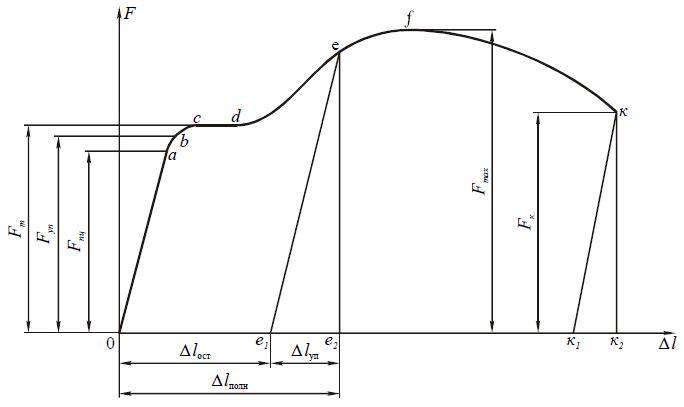
7. Диаграммы растяжения
и сжатия пластичных и хрупких материалов.
Основные характеристики прочности и
пластичности материалов. Наклёп.
σпц=Fпц/A0
– предел
пропорциональности;
σуп=Fуп/A0
– предел упругости;
σт=Fт/А0
– предел текучести;
σпр=Fmax/A0
– предел
прочности при растяжении
А0–
первоначальная площадь поперечного
сечения. Начиная с точки d
диаграммы деформация идет при дальнейшем
увеличении нагрузки, происходит
упрочнение металла. Упрочнение металла
в результате прохождения пластической
деформации называется наклёпом.
8. Методы расчёта по
допускаемым напряжениям, разрушающим
нагрузкам и предельным состояниям.
Технико-экономические факторы влияющие
на величину коэффициента запаса
прочности.
По допускаемым
напряжениям:
;
;
;
;
[σ]=σ0/n;
[σ]=σт/nт(текучести);
[σ]в=σв/nв(прочность
при разрушении хруп.ких мат)
По предельным
состояниям:
;
;
;
По разрушающим
нагрузкам:
;
σ0
– напряжение
соответствующее наступлению опасного
состояния; n-коэф.
запаса проч.
nт=1,4-1,6(пластичные
материалы) nв=2,5-3,0(хрупкие
материалы)
9. Основные виды задач
в сопромате: определение напряжений,
подбор сечений, определение допускаемой
нагрузки по разным методам.(см. предыдущие
вопросы)
По допускаемым
напряжениям:
;
;
;
;
По предельным
состояниям:
;
;
;
По разрушающим
нагрузкам:
;
10. Статически
неопределимые задачи при растяжении и
сжатии. Учёт температуры и неточности
изготовления. Определение предельных
нагрузок.
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ
СИСТЕМЫ
Задачи на стержни
1) Статическая
сторона
Составить уравнения
равновесия
2) Геометрическая
сторона
Схема деформированного
состояния
3) Физическая сторона
Выражаем деформации
через внутренние усилия
4) Математическая
сторона
Совместно решаем
уравнения
5) Подбор сечения
Проверка по допускаемым
напряжениям
Задачи на изменение
температуры
9. Основные виды задач
в сопромате: определение напряжений,
подбор сечений, определение допускаемой
нагрузки по разным методам.(см. предыдущие
вопросы)
3.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
1. Статические моменты.
Определение центра тяжести плоской
фигуры.
Статическим моментом
сечения относительно данной оси
называется сумма произведений элементарных
площадей dA
на их расстояния до данной оси (например,
x
или y),
которая распространяется на всю площадь
сечения A.
Статические моменты
инерции плоской фигуры:
Оси, проходящие через
центр тяжести, называются центральными
осями инерции.
Центр тяжести – это
точка, обладающая свойством, что
относительно любой оси проведённой
через эту точку, статический момент
равен 0.
Определение положения
центра тяжести:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Виды деформаций.
Понятие о деформированном состоянии материала.
Реальные тела могут деформироваться, т. е. изменять свою форму и размеры. Деформации тел происходят вследствие нагружения их внешними силами или изменения температуры. При деформации тела его точки, а также мысленно проведенные линии или сечения перемещаются в плоскости или в пространстве относительно своего исходного положения.
При нагружении твердого тела в нем возникают внутренние силы взаимодействия частиц, оказывающие противодействие внешним силам и стремящиеся вернуть частицы тела в положение, которое они занимали до деформации.
При решении задач сопромата различают упругие деформации, исчезающие после прекращения действия вызвавших их сил, и пластические, или остаточные, деформации, не исчезающие после снятия нагрузок. В большинстве случаев для величин деформаций элементов конструкций устанавливают определенные ограничения.
В сопротивлении материалов изучаются следующие основные виды деформирования стержней или виды их деформаций: растяжение и сжатие, сдвиг (или срез), кручение, изгиб. Рассматриваются также более сложные деформации, получающиеся в результате сочетания нескольких основных видов деформаций.
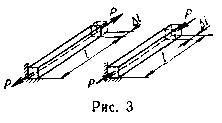
Растяжение или сжатие возникает, например, в случае, когда к стержню вдоль его оси приложены противоположно направленные силы (рис. 3). При этом происходит поступательное перемещение сечений вдоль оси стержня, который при растяжении удлиняется, а при сжатии укорачивается. Изменение первоначальной длины стержня L называется абсолютным удлинением (при растяжении) или абсолютным укорочением (при сжатии).
Отношение абсолютного удлинения (укорочения) к первоначальной длине L стержня или его участка называется средним относительным удлинением (укорочением) на длине L или средней линейной относительной деформацией стержня или его участка:
Истинное линейное относительное удлинение, или относительная линейная деформация в точке, определяется как относительная деформация участка при L→0:
На растяжение или сжатие работают многие элементы конструкций: стержни ферм, колонны, штоки поршневых машин, стяжные болты и др.
Сдвиг, или срез, возникает, когда внешние силы смешают два параллельных плоских сечения стержня одно относительно другого при неизменном расстоянии между ними (рис. 4). Величина смещения dS называется абсолютным сдвигом. Отношение абсолютного сдвига к расстоянию между смещающимися плоскостями (тангенс угла у) называется относительным сдвигом. Вследствие малости угла у можно принять
Относительный сдвиг является угловой деформацией, характеризующей перекос элемента.
На сдвиг, или срез, работают, например, заклепки и болты, скрепляющие элементы, которые внешние силы стремятся сдвинуть друг относительно друга.
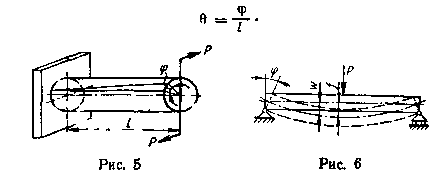
Кручение возникает при действии на стержень внешних сил, образующих момент относительно его оси (рис. 5). Деформация кручения сопровождается поворотом поперечных сечений стержня друг относительно друга вокруг его оси. Угол поворота одного сечения стержня относительно другого, находящегося на расстоянии L, называется углом закручивания на длине L. Отношение угла закручивания ф к длине L называется относительным углом закручивания.
На кручение работают валы, шпиндели токарных и сверлильных станков и другие детали.
Изгиб (рис. 6) заключается в искривлении оси прямого стержня или в изменении кривизны кривого стержня. Происходящее при изгибе перемещение какой-либо точки оси стержня выражается вектором, начало которого совмещено с первоначальным положением точки, а конец — с положением той же точки в деформированном стержне, В прямых стержнях перемещения точек, направленные перпендикулярно к начальному положению оси, называются прогибами. Обозначим прогибы буквой w, а наибольший из них — буквой f. При изгибе также происходит поворот сечений стержня вокруг осей, лежащих в плоскостях сечений. Углы поворота сечений относительно своих начальных положений обозначим буквой ф.
На изгиб работают балки междуэтажных перекрытий, мостов, оси железнодорожных вагонов, листовые рессоры, валы, зубья шестерен, спицы колес, рычаги и многие другие детали.
Описанные выше простейшие деформации стержня дают представление об изменении его формы и размеров в целом, но ничего не говорят о степени и характере деформированного состояния материала. Исследования показывают, что деформированное состояние тела является неравномерным и изменяется от точки к точке. При этом деформированное состояние в точке тела полностью определяется шестью компонентами деформации: тремя относительными линейными деформациями и тремя относительными угловыми деформациями.
Основные гипотезы о свойствах материала, используемые в механике деформируемого тела. Внешние и внутренние силы. Схематизация геометрии реального объекта.
Гипотеза сплошности и однородности: материал представляет собой однородную сплошную среду; свойства материала во всех точках тела одинаковы и не зависят от размеров тела. Об изотропности: физико-механические свойства материала одинаковы по всем направлениям. Об идеальной упругости материала: тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию.
Нагрузки: внешн( распред. и сосредоточ.) Принцип Сен-Венанна: в делениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.Внутр(доп. силы взаимод. между частицами тела, возник. в последствии его деформации. Принцип независимости действия сил (принцип суперпозиции): результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения. Схематизация геометрии объекта сводится к рассмотрению бруса, оболочки, пластины и объемного тела. Брусом называется тело, два измерения которого малы по сравнению с третьим. Пластина(частный случай оболочки)- элемент конструкции, у которого одно измерение (толщина) мало по сравнению с двумя другими. Массивное тело – элемент конструкции, у которого все размеры имеют один порядок.
Нормальные и касательные напряжения. Понятие о напряженном состоянии в точке тела.
Напряжение – интенсивность внутренних сил, т.е. величина внутр. силы, приход на 1S в данной точке данного сечения. Полным напряжением p, а его нормальной σ и касательными τ составляющими. Нормальное напряжение (σx) – интенсивность осевого внутреннего усилия, или осевое усилие. Касательное напряжение (τy, τz) – интенсивность внутренних поперечных сил, или поперечная сила. Совокупность напряж. на всех элементарных площадках, проходящих через точку тела, назыв. напряженным состоянием в точке тела. τxy = τyx; τ yz= τzy; τ zx= τxz. В зависимости от того, сколько главных напряжений действует в окрестности данной точки, различают три вида напряженного состояния: 1) линейное (одноосное) – если одно главное напряжение отлично от нуля, а два других равны нулю 2) плоское (двухосное) – если два главных напряжения отличны от нуля, а одно равно нулю; 3) объемное (трехосное) – если все три главных напряжения отличны от нуля.
Линейные и угловые деформации. Понятие о деформированном состоянии в точке тела.
Деформированное состояние в точке – это совокупность относительных линейных деформаций и углов сдвига для всевозможных направлений осей, проведенных через данную точку. Угловая деформация( xy
yz
zx ) характеризует изменение формы тела и чаще всего называется углом сдвига. Линейная деформация(εx,εy, εz ) характеризует изменение размеров тела. Различают абсолютную деформацию ΔL и относительную деформацию ε = ΔL/L.
Основные принципы в сопротивлении материалов: принцип начальных размеров, принцип независимости действия сил, принцип Сен-Венана.
Принцип начальных размеров утверждает, что при составлении уравнений равновесия деформированного тела можно пренебречь его деформацией и рассматривать тело как жесткое, недеформированное, имеющее те же размеры, какие оно имело до нагружения. Принцип независимости действия сил (принцип суперпозиции): результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения. Принцип Сен-Венанна: в делениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.
Метод сечений. Внутренние силовые факторы в поперечных сечениях стержня. Виды нагружения стержня.
Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.1)В интересующем месте рассекаем.2)одну часть отбрасываем.3)действие отброш. части на оставш. заменяем оставш. внутр. Силами.4) при известных внешн силах все внутр силовые факторы опред из ур-я статики из отсеч части тела. В процессе деформации бруса, под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего в нем возникают внутренние силы. Под действием внешних нагрузок в поперечном сечении бруса возникают следующие внутренние силовые факторы: Nz = N – продольная растягивающая (сжимающая) сила, Mк = Mz – крутящий (скручивающий) момент, Qx (Qy) – поперечные силы , Mx (My) – изгибающие моменты. В зависимости от вида и количества силовых факторов в сечении выделяют следующие простейшие виды нагружения: растяжение сжатие (присутствует только N≠0); кручение (Mк≠0); изгиб (Mx≠0 или My≠0 и/или Qy или Qx≠0); сложное нагружение.
Растяжение (сжатие) прямого стержня. Определение нормальных напряжений, продольных деформаций и перемещений. Закон Гука при растяжении (сжатии).
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю. Растягивающие продольные силы принято считать положительными, а сжимающие – отрицательными. Для определения продольной силы используется метод сечений. Nz равномерно распределяется по площади поперечного сечения стержня, вызывая нормальные напряжения. Ϭ=N/A. В наклонном сечении возникают нормальные σα =σ и касательные τα=1/2σsin2α напряжения. При растяжении (сжатии) наблюдаются абсолютные и относительные деформации :l1 – l = Δl – абсолютная продольная деформация(удлинение);h1 – h =-Δh -абсолютная поперечная деформация(сужение); Относит прод деформ
,относительная поперечная деформация:
.Коэф.Пуассона
.В результате деформации бруса его поперечные сечения получают линейные перемещения U(z). Так, перемещение сечения В, находящегося на расстоянии z от закрепленного конца, равно удлинению Δlz части бруса длиной z, заключенной между неподвижным и рассматриваемым сечением. Закон Гука: Ϭ=Eε(для одноосного); Δl=Nl/EA(удлинение).
Определение напряжений в наклонных площадках стержня при растяжении (вывод формул).
Напряжения в наклонных площадках наблюдаются, если мысленно «разрезать» стержень, растягиваемый силами P, наклонной плоскостью под углом к поперечному сечению, проходящей через точку K, и отбросить правую часть.
,
-полное напряжение;
,тогда, если разложить
.При увеличении угла
нормальное напряжение в точке К будет постепенно уменьшаться от своего максимального значения (
) до нуля. Касательное напряжение при этом будет сначала возрастать от нулевого до максимального значения (
) при
, а затем убывать и при угле
снова станет равным нулю.
Следовательно, наибольшее нормальное напряжение действительно возникает в точках поперечного сечения стержня. В продольном сечении оно равно нулю. Следовательно, продольные волокна не давят друг на друга. Наибольшие касательные напряжения возникают в наклонных сечениях, расположенных под углом к оси стержня. В поперечном и продольном сечениях они равны нулю.
Работа внешних сил при растяжении (сжатии) стержня и потенциальная энергия деформации растянутого стержня. Удельная потенциальная энергия деформации при растяжении.
Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу W на соответствующих перемещениях. Одновременно с этим в упругом теле накапливается потенциальная энергия его деформирования U. При действии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. W = U + K. W=1/2 =U. Удельн пот энергия
Связь между продольной и поперечной деформациями при одноосном растяжении. Коэффициент Пуассона. Объемная деформация при одноосном растяжении. Предельное значение коэффициента Пуассона для изотропного материала.
Пусть в результате деформации первоначальная длина стержня l станет равной. Δl. Изменение длины называется абсолютным удлинением стержня.
Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением или продольной деформацией. .Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:
. Установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона
. Для различных материалов коэффициент Пуассона изменяется в пределах
. Для пробки
для каучука
- ГЛАВНАЯ >
- ПРЕДМЕТЫ >
- СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ >
- ПОНЯТИЕ О ДЕФОРМАЦИЯХ (ЛИНЕЙНЫХ, УГЛОВЫХ, АБСОЛЮТНЫХ И ОТНОСИТЕЛЬНЫХ). ОБОЗНАЧЕНИЯ, РАЗМЕРНОСТИ И ПРЕДЕЛЫ ИЗМЕНЕНИЯ
Понятие о деформациях (линейных, угловых, абсолютных и относительных). Обозначения, размерности и пределы изменения
Без воды — краткий вариант ответа,
легко понять и
запомнить
Изменение формы или размеров тела, вызванное нагрузкой, изменением температуры или другими воздействиями называется деформацией.
Деформация делится на два вида – линейные и угловые.
Изменение линейных размеров тела называется линейной деформацией.
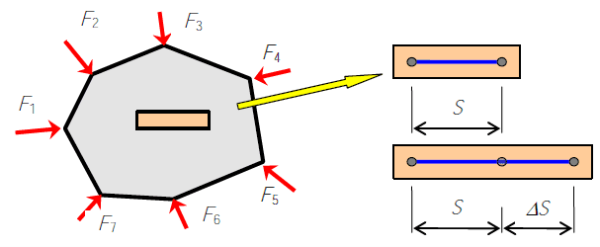
Линейную деформация тела разделяют на абсолютную △S и относительную линейную ε деформации.
Относительная линейная деформация в точке тела равна пределу отношения абсолютной деформации отрезка волокна к длине отрезка, если длина отрезка стремится к нулю.
где
-
S — длина отрезка волокна;
-
△S — деформация (удлинение или укорочение) отрезка волокна.
Линейная деформация волокна тела
Изменение угловых размеров тела называется угловой деформацией.
Угловая деформация элемента
где
-
δ – абсолютная угловая деформация (обычно не употребляется в расчетах);
-
γ – относительная угловая деформация (угол сдвига), величина безразмерная.
Теперь на ZNZN можно делать свои конспекты
Легко создавать, делиться и просматривать с устройств
Доступно в ПК-версии сайта