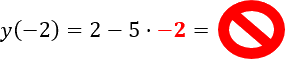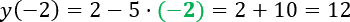Как найти линейную функцию без графика

На этой странице находится вопрос Как определить точку пересечения функций без построения графика?. Здесь же – ответы на него,
и похожие вопросы в категории Алгебра, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 5 – 9 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.

Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».

После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.

В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.

Как получить значение функции

Рассмотрим задание.
Функция задана формулой «y = 2x − 1»

1. Вычислить «y» при «x = 15»
2. Найти значение «x», при котором
   значение «y» равно «−19».

---

Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.

Запись решения выглядит следующим образом.

y(15) = 2 · 15 − 1 = 30 − 1 = 29

Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.

То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .

−19 = 2x − 1

Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.

−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18

Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.

−2x = 18       | · (−1)
2x = −18                

Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .

2x = −18     | (: 2)
x = −9                

Как проверить верно ли равенство для функции

Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».

Верно ли равенство
«f(−2) = −18»?

---

Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.

Неправильно

Правильно

С помощью расчетов мы получили
«f(−2) = 12».

Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.

Как проверить, что точка принадлежит графику функции

Рассмотрим функцию «y = x² −5x + 6»

Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).

---

Для этой задачи нет необходимости, строить график заданной функции.

Вернемся к нашему заданию. Подставим в функцию «y = x² − 5x + 6»
координаты точки (1; 2).

Вместо «x» подставим «1».
Вместо «y» подставим «2».

2 = 1² − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)

У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.

Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x² − 5x + 6»?

Вместо «x» подставим «0».
Вместо «y» подставим «1».

1 = 0² − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)

В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x² − 5x + 6»

Как получить координаты точки функции

С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.

Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.

Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.

Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».

Полученное значение «−3» на оси «Oy» и будет искомым значением «y».

Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».

Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.

y(2) = −2 · 2 + 1 = −4 + 1 = −3

При расчетах мы также получили y = −3.

Значит, мы правильно получили координаты с графика функции.

При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».

Только подстановка значений в формулу функции дает точные результаты.

---

Ваши комментарии

Оставить комментарий:

---

По теореме Виета.

Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).

Однако не всегда можно быстро решить квадратное уравнение при помощи первых двух методов. Еще один вариант — нахождение корней через дискриминант (Д), т. е. дополнительный параметр, позволяющий сразу находить решения. Он находится по следующей формуле: Д=(-S)^2 -4PU.

Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д

Учитель физики, информатики и вычислительной техники. Победитель конкурса лучших учителей Российской Федерации в рамках Приоритетного Национального Проекта “Образование”.

Как найти координаты точек пересечения графика функции: примеры решения

Вы будете перенаправлены на Автор24

В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.

Первый способ

Первый и самый простой – это воспользоваться тем, что в этой точке координаты будут равны и приравнять графики, а из того что получится можно найти $x$. Затем найденный $x$ подставить в любое из двух уравнений и найти координату игрек.

Найдём точку пересечения двух прямых $y=5x + 3$ и $y=x-2$, приравняв функции:

Теперь подставим полученный нами икс в любой график, например, выберем тот, что попроще — $y=x-2$:

$y=-frac<1> <2>– 2 = – 2frac12$.

Точка пересечения будет $(-frac<1><2>;- 2frac12)$.

Второй способ

Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.

Узнайте, в каких точках пересекаются графики параболы $y=2x^2-2x-1$ и пересекающей её прямой $y=x+1$.

Решение:

Второе уравнение проще первого, поэтому подставим его вместо $y$:

Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:

Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:

$y_1= 2 + 1 = 3; y_2=1 – frac<1> <2>= frac<1><2>$.

Точки пересечения будут $(2;3)$ и $(-frac<1><2>; frac<1><2>)$.

Третий способ

Готовые работы на аналогичную тему

Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.

Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.

Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.

Найдите точку пересечения графиков на общем рисунке.

Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ

Решение:

Тут всё просто: ищем точки пересечения пунктиров, опущенных с графиков с осями абсцисс и ординат и записываем по порядку. Здесь точка пересечения равна $(2;3)$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 07.05.2021

Координаты точки пересечения двух прямых – примеры нахождения

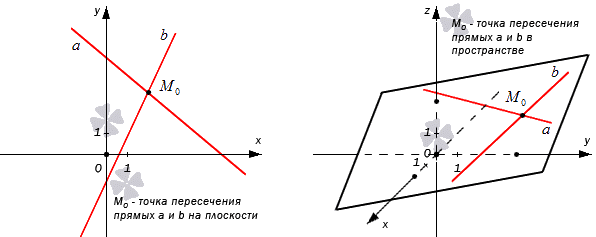
Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.

Точка пересечения двух прямых – определение

Необходимо дать определение точкам пересечения двух прямых.

Раздел взаимного расположения прямых на плоскости показывает, что они могут совпадать , быть параллельными, пересекаться в одной общей точке или скрещивающимися. Две прямые, находящиеся в пространстве, называют пересекающимися, если они имеют одну общую точку.

Определение точки пересечения прямых звучит так:

Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.

Рассмотрим на рисунке, приведенном ниже.

Нахождение координат точки пересечения двух прямых на плоскости

Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.

Если на плоскости имеется система координат О х у , то задаются две прямые a и b . Прямой a соответствует общее уравнение вида A 1 x + B 1 y + C 1 = 0 , для прямой b – A 2 x + B 2 y + C 2 = 0 . Тогда M 0 ( x 0 , y 0 ) является некоторой точкой плоскости необходимо выявить , будет ли точка М 0 являться точкой пересечения этих прямых.

Чтобы решить поставленную задачу, необходимо придерживаться определения. Тогда прямые должны пересекаться в точке, координаты которой являются решением заданных уравнений A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M 0 ( x 0 , y 0 ) считается их точкой пересечения.

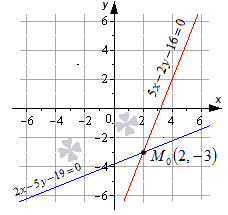
Даны две пересекающиеся прямые 5 x – 2 y – 16 = 0 и 2 x – 5 y – 19 = 0 . Будет ли точка М 0 с координатами ( 2 , – 3 ) являться точкой пересечения.

Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М 0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что

5 · 2 – 2 · ( – 3 ) – 16 = 0 ⇔ 0 = 0 2 · 2 – 5 · ( – 3 ) – 19 = 0 ⇔ 0 = 0

Оба равенства верные, значит М 0 ( 2 , – 3 ) является точкой пересечения заданных прямых.

Изобразим данное решение на координатной прямой рисунка, приведенного ниже.

Ответ: заданная точка с координатами ( 2 , – 3 ) будет являться точкой пересечения заданных прямых.

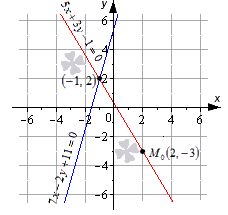
Пересекутся ли прямые 5 x + 3 y – 1 = 0 и 7 x – 2 y + 11 = 0 в точке M 0 ( 2 , – 3 ) ?

Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что

5 · 2 + 3 · ( – 3 ) – 1 = 0 ⇔ 0 = 0 7 · 2 – 2 · ( – 3 ) + 11 = 0 ⇔ 31 = 0

Второе равенство не является верным, значит, что заданная точка не принадлежит прямой 7 x – 2 y + 11 = 0 . Отсюда имеем, что точка М 0 не точка пересечения прямых.

Чертеж наглядно показывает, что М 0 – это не точка пересечения прямых. Они имеют общую точку с координатами ( – 1 , 2 ) .

Ответ: точка с координатами ( 2 , – 3 ) не является точкой пересечения заданных прямых.

Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.

Задаются две пересекающиеся прямые a и b уравнениями вида A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 , расположенных в О х у . При обозначении точки пересечения М 0 получим, что следует продолжить поиск координат по уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .

Из определения очевидно, что М 0 является общей точкой пересечения прямых. В этом случае ее координаты должны удовлетворять уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Иными словами это и есть решение полученной системы A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 .

Значит, для нахождения координат точки пересечения , необходимо все уравнения добавить в систему и решить ее.

Заданы две прямые x – 9 y + 14 = 0 и 5 x – 2 y – 16 = 0 на плоскости. необходимо найти их пересечение.

Данные по условию уравнения необходимо собрать в систему, после чего получим x – 9 y + 14 = 0 5 x – 2 y – 16 = 0 . Чтобы решить его, разрешается первое уравнение относительно x , подставляется выражение во второе:

x – 9 y + 14 = 0 5 x – 2 y – 16 = 0 ⇔ x = 9 y – 14 5 x – 2 y – 16 = 0 ⇔ ⇔ x = 9 y – 14 5 · 9 y – 14 – 2 y – 16 = 0 ⇔ x = 9 y – 14 43 y – 86 = 0 ⇔ ⇔ x = 9 y – 14 y = 2 ⇔ x = 9 · 2 – 14 y = 2 ⇔ x = 4 y = 2

Получившиеся числа являются координатами, которые необходимо было найти.

Ответ: M 0 ( 4 , 2 ) является точкой пересечения прямых x – 9 y + 14 = 0 и 5 x – 2 y – 16 = 0 .

Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.

Определить координаты точек пересечения прямых x – 5 = y – 4 – 3 и x = 4 + 9 · λ y = 2 + λ , λ ∈ R .

Для начала необходимо привести уравнения к общему виду. Тогда получаем, что x = 4 + 9 · λ y = 2 + λ , λ ∈ R преобразуется таким образом:

x = 4 + 9 · λ y = 2 + λ ⇔ λ = x – 4 9 λ = y – 2 1 ⇔ x – 4 9 = y – 2 1 ⇔ ⇔ 1 · ( x – 4 ) = 9 · ( y – 2 ) ⇔ x – 9 y + 14 = 0

После чего беремся за уравнение канонического вида x – 5 = y – 4 – 3 и преобразуем. Получаем, что

x – 5 = y – 4 – 3 ⇔ – 3 · x = – 5 · y – 4 ⇔ 3 x – 5 y + 20 = 0

Отсюда имеем, что координаты – это точка пересечения

x – 9 y + 14 = 0 3 x – 5 y + 20 = 0 ⇔ x – 9 y = – 14 3 x – 5 y = – 20

Применим метод Крамера для нахождения координат:

∆ = 1 – 9 3 – 5 = 1 · ( – 5 ) – ( – 9 ) · 3 = 22 ∆ x = – 14 – 9 – 20 – 5 = – 14 · ( – 5 ) – ( – 9 ) · ( – 20 ) = – 110 ⇒ x = ∆ x ∆ = – 110 22 = – 5 ∆ y = 1 – 14 3 – 20 = 1 · ( – 20 ) – ( – 14 ) · 3 = 22 ⇒ y = ∆ y ∆ = 22 22 = 1

Ответ: M 0 ( – 5 , 1 ) .

Имеется еще способ для нахождения координат точки пересечения прямых, находящихся на плоскости. Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x = x 1 + a x · λ y = y 1 + a y · λ , λ ∈ R . Тогда вместо значения x подставляется x = x 1 + a x · λ и y = y 1 + a y · λ , где получим λ = λ 0 , соответствующее точке пересечения, имеющей координаты x 1 + a x · λ 0 , y 1 + a y · λ 0 .

Определить координаты точки пересечения прямой x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x – 5 = y – 4 – 3 .

Необходимо выполнить подстановку в x – 5 = y – 4 – 3 выражением x = 4 + 9 · λ , y = 2 + λ , тогда получим:

4 + 9 · λ – 5 = 2 + λ – 4 – 3

При решении получаем, что λ = – 1 . Отсюда следует, что имеется точка пересечения между прямыми x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x – 5 = y – 4 – 3 . Для вычисления координат необходимо подставить выражение λ = – 1 в параметрическое уравнение. Тогда получаем, что x = 4 + 9 · ( – 1 ) y = 2 + ( – 1 ) ⇔ x = – 5 y = 1 .

Ответ: M 0 ( – 5 , 1 ) .

Для полного понимания темы, необходимо знать некоторые нюансы.

Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 + C 2 = 0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.

Даны прямые x 3 + y – 4 = 1 и y = 4 3 x – 4 . Определить, имеют ли они общую точку.

Упрощая заданные уравнения, получаем 1 3 x – 1 4 y – 1 = 0 и 4 3 x – y – 4 = 0 .

Следует собрать уравнения в систему для последующего решения:

1 3 x – 1 4 y – 1 = 0 1 3 x – y – 4 = 0 ⇔ 1 3 x – 1 4 y = 1 4 3 x – y = 4

Отсюда видно, что уравнения выражаются друг через друга, тогда получим бесконечное множество решений. Тогда уравнения x 3 + y – 4 = 1 и y = 4 3 x – 4 определяют одну и ту же прямую. Поэтому нет точек пересечения.

Ответ: заданные уравнения определяют одну и ту же прямую.

Найти координаты точки пересекающихся прямых 2 x + ( 2 – 3 ) y + 7 = 0 и 2 3 + 2 x – 7 y – 1 = 0 .

По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:

2 x + ( 2 – 3 ) y + 7 = 0 2 ( 3 + 2 ) x – 7 y – 1 = 0 ⇔ 2 x + ( 2 – 3 ) y = – 7 2 ( 3 + 2 ) x – 7 y = 1 ⇔ ⇔ 2 x + 2 – 3 y = – 7 2 ( 3 + 2 ) x – 7 y + ( 2 x + ( 2 – 3 ) y ) · ( – ( 3 + 2 ) ) = 1 + – 7 · ( – ( 3 + 2 ) ) ⇔ ⇔ 2 x + ( 2 – 3 ) y = – 7 0 = 22 – 7 2

Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.

Второй способ решения.

Для начала нужно определить наличие пересечения прямых.

n 1 → = ( 2 , 2 – 3 ) является нормальным вектором прямой 2 x + ( 2 – 3 ) y + 7 = 0 , тогда вектор n 2 → = ( 2 ( 3 + 2 ) , – 7 – нормальный вектор для прямой 2 3 + 2 x – 7 y – 1 = 0 .

Необходимо выполнить проверку коллинеарности векторов n 1 → = ( 2 , 2 – 3 ) и n 2 → = ( 2 ( 3 + 2 ) , – 7 ) . Получим равенство вида 2 2 ( 3 + 2 ) = 2 – 3 – 7 . Оно верное, потому как 2 2 3 + 2 – 2 – 3 – 7 = 7 + 2 – 3 ( 3 + 2 ) 7 ( 3 + 2 ) = 7 – 7 7 ( 3 + 2 ) = 0 . Отсюда следует, что векторы коллинеарны. Значит, прямые являются параллельными и не имеют точек пересечения.

Ответ: точек пересечения нет, прямые параллельны.

Найти координаты пересечения заданных прямых 2 x – 1 = 0 и y = 5 4 x – 2 .

Для решения составляем систему уравнений. Получаем

2 x – 1 = 0 5 4 x – y – 2 = 0 ⇔ 2 x = 1 5 4 x – y = 2

Найдем определитель основной матрицы. Для этого 2 0 5 4 – 1 = 2 · ( – 1 ) – 0 · 5 4 = – 2 . Так как он не равен нулю, система имеет 1 решение. Отсюда следует, что прямые пересекаются. Решим систему для нахождения координат точек пересечения:

2 x = 1 5 4 x – y = 2 ⇔ x = 1 2 4 5 x – y = 2 ⇔ x = 1 2 5 4 · 1 2 – y = 2 ⇔ x = 1 2 y = – 11 8

Получили, что точка пересечения заданных прямых имеет координаты M 0 ( 1 2 , – 11 8 ) .

Ответ: M 0 ( 1 2 , – 11 8 ) .

Нахождения координат точки пересечения двух прямых в пространстве

Таким же образом находятся точки пересечения прямых пространства.

Когда заданы прямые a и b в координатной плоскости О х у z уравнениями пересекающихся плоскостей, то имеется прямая a , которая может быть определена при помощи заданной системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 1 = 0 а прямая b – A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 .

Когда точка М 0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0

Рассмотрим подобные задания на примерах.

Найти координаты точки пересечения заданных прямых x – 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0

Составляем систему x – 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0 и решим ее. Чтобы найти координаты, необходимо решать через матрицу. Тогда получим основную матрицу вида A = 1 0 0 0 1 2 3 2 0 4 0 – 2 и расширенную T = 1 0 0 1 0 1 2 – 3 4 0 – 2 4 . Определяем ранг матрицы по Гауссу.

1 = 1 ≠ 0 , 1 0 0 1 = 1 ≠ 0 , 1 0 0 0 1 2 3 2 0 = – 4 ≠ 0 , 1 0 0 1 0 1 2 – 3 3 2 0 – 3 4 0 – 2 4 = 0

Отсюда следует, что ранг расширенной матрицы имеет значение 3 . Тогда система уравнений x – 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x – 27 – 4 = 0 в результате дает только одно решение.

Базисный минор имеет определитель 1 0 0 0 1 2 3 2 0 = – 4 ≠ 0 , тогда последнее уравнение не подходит. Получим, что x – 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0 ⇔ x = 1 y + 2 z = – 3 3 x + 2 y – 3 . Решение системы x = 1 y + 2 z = – 3 3 x + 2 y = – 3 ⇔ x = 1 y + 2 z = – 3 3 · 1 + 2 y = – 3 ⇔ x = 1 y + 2 z = – 3 y = – 3 ⇔ ⇔ x = 1 – 3 + 2 z = – 3 y = – 3 ⇔ x = 1 z = 0 y = – 3 .

Значит, имеем, что точка пересечения x – 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0 имеет координаты ( 1 , – 3 , 0 ) .

Ответ: ( 1 , – 3 , 0 ) .

Система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 имеет только одно решение. Значит, прямые a и b пересекаются.

В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.

Поэтому система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.

Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.

Заданы уравнения прямых x + 2 y – 3 z – 4 = 0 2 x – y + 5 = 0 и x – 3 z = 0 3 x – 2 y + 2 z – 1 = 0 . Найти точку пересечения.

Для начала составим систему уравнений. Получим, что x + 2 y – 3 z – 4 = 0 2 x – y + 5 = 0 x – 3 z = 0 3 x – 2 y + 2 z – 1 = 0 . решаем ее методом Гаусса:

1 2 – 3 4 2 – 1 0 – 5 1 0 – 3 0 3 – 2 2 1

1 2 – 3 4 0 – 5 6 – 13 0 – 2 0 – 4 0 – 8 11 – 11

1 2 – 3 4 0 – 5 6 – 13 0 0 – 12 5 6 5 0 0 7 5 – 159 5

1 2 – 3 4 0 – 5 6 – 13 0 0 – 12 5 6 5 0 0 0 311 10

Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.

Ответ: нет точки пересечения.

Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.

Заданы две прямые x = – 3 – λ y = – 3 · λ z = – 2 + 3 · λ , λ ∈ R и x 2 = y – 3 0 = z 5 в О х у z . Найти точку пересечения.

Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что

x = – 3 – λ y = – 3 · λ z = – 2 + 3 · λ ⇔ λ = x + 3 – 1 λ = y – 3 λ = z + 2 3 ⇔ x + 3 – 1 = y – 3 = z + 2 3 ⇔ ⇔ x + 3 – 1 = y – 3 x + 3 – 1 = z + 2 3 ⇔ 3 x – y + 9 = 0 3 x + z + 11 = 0 x 2 = y – 3 0 = z 5 ⇔ y – 3 = 0 x 2 = z 5 ⇔ y – 3 = 0 5 x – 2 z = 0

Находим координаты 3 x – y + 9 = 0 3 x + z + 11 = 0 y – 3 = 0 5 x – 2 z = 0 , для этого посчитаем ранги матрицы. Ранг матрицы равен 3 , а базисный минор 3 – 1 0 3 0 1 0 1 0 = – 3 ≠ 0 , значит, что из системы необходимо исключить последнее уравнение. Получаем, что

3 x – y + 9 = 0 3 x + z + 11 = 0 y – 3 = 0 5 x – 2 z = 0 ⇔ 3 x – y + 9 = 0 3 x + z + 11 = 0 y – 3 = 0

Решим систему методом Крамер. Получаем, что x = – 2 y = 3 z = – 5 . Отсюда получаем, что пересечение заданных прямых дает точку с координатами ( – 2 , 3 , – 5 ) .

[spoiler title=”источники:”]

http://spravochnick.ru/matematika/kak_nayti_koordinaty_tochek_peresecheniya_grafika_funkcii_primery_resheniya/

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/koordinaty-tochki-peresechenija-dvuh-prjamyh-prime/

[/spoiler]

Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.

Координаты точки пересечения графиков функций

Как найти?

1. Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие $ x $, а в правую остальные и найти корни, полученного уравнения.
2. Второй способ заключается в том, что нужно составить систему уравнений и решить её путём подстановки одной функции в другую
3. Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.

Случай двух линейных функций

Рассмотрим две линейные функции $ f(x) = k_1 x+m_1 $ и $ g(x) = k_2 x + m_2 $. Эти функции называются прямыми. Построить их достаточно легко, нужно взять любые два значения $ x_1 $ и $ x_2 $ и найти $ f(x_1) $ и $ (x_2) $. Затем повторить тоже самое и с функцией $ g(x) $. Далее визуально найти координату точки пересечения графиков функций.

Следует знать, что линейные функции имеют только одну точку пересечения и только тогда, когда $ k_1 neq k_2 $. Иначе, в случае $ k_1=k_2 $ функции параллельны друг другу, так как $ k $ – это коэффициент угла наклона. Если $ k_1 neq k_2 $, но $ m_1=m_2 $, тогда точкой пересечения будет $ M(0;m) $. Это правило желательно запомнить для ускоренного решения задач.

Пример 1

Пусть даны $ f(x) = 2x-5 $ и $ g(x)=x+3 $. Найти координаты точки пересечения графиков функций.

Решение

Как это сделать? Так как представлены две линейные функции, то первым делом смотрим на коэффициент угла наклона обеих функций $ k_1 = 2 $ и $ k_2 = 1 $. Замечаем, что $ k_1 neq k_2 $, поэтому существует одна точка пересечения. Найдём её с помощью уравнения $ f(x)=g(x) $: $$ 2x-5 = x+3 $$ Переносим слагаемые с $ x $ в левую часть, а остальные в правую: $$ 2x – x = 3+5 $$ $$ x = 8 $$ Получили $ x=8 $ абциссу точки пересечения графиков, а теперь найдём ординату. Для этого подставим $ x = 8 $ в любое из уравнений хоть в $ f(x) $, либо в $ g(x) $: $$ f(8) = 2cdot 8 – 5 = 16 – 5 = 11 $$ Итак, $ M (8;11) $ – является точкой пересечения графиков двух линейных функций. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ M (8;11) $$

Пример 2

Дано $ f(x)=2x-1 $ и $ g(x) = 2x-4 $. Найти точки пересечения графиков функций.

Решение

Как найти? Опять же обращаем внимание на то, что угловые коэффициенты равны $ k_1 = k_2 = 2 $. Это означает, что линейные функции параллельны между собой, поэтому у них нет точек пересечения!

Ответы

Графики функций параллельны, нет точек пересечения.

 Случай двух нелинейных функций 

Пример 3

Найти координаты точки пересечения графиков функций: $ f(x)=x^2-2x+1 $ и $ g(x)=x^2+1 $

Решение

Как быть с двумя нелинейными функциями? Алгоритм простой: приравниваем уравнения друг к другу и находим корни: $$ x^2-2x+1=x^2+1 $$ Разносим по разным сторонам уравнения члены с $ x $ и без него: $$ x^2-2x-x^2=1-1 $$ $$ -2x=0 $$ $$ x=0 $$ Найдена абцисса искомой точки, но её недостаточно. Ещё нехватает ординаты $ y $. Подставляем $ x = 0 $ в любое из двух уравнений условия задачи. Например: $$ f(0)=0^2-2cdot 0 + 1 = 1 $$ $ M (0;1) $ – точка пересечения графиков функций

Ответ

$$ M (0;1) $$

Принадлежит ли графику функции точка

Как определить, принадлежит ли графику функции точка? Это можно сделать, не выполняя построения графика.

График функции проходит через точку, если координаты этой точки обращают формулу функции в верное числовое равенство.

Таким образом, чтобы выяснить, принадлежит ли графику функции точка, надо подставить координаты точки в формулу функции. Если получится верное числовое равенство, точка лежит на графике.

1) Принадлежат ли графику функции y=10x-3 точки A(-2; 17) и B(1; 7)?

График функции проходит через точки A и B, если их координаты обращают формулу y=10x-3 в верное числовое равенство.

Подставляем в формулу функции вместо y ординату точки A (y=17), а вместо x — абсциссу (x=-2). Имеем:

Значит, точка A графику функции y=10x-3 не принадлежит.

Ординату 7 точки B подставляем в формулу функции y=10x-3 вместо y, абсциссу 1 — вместо x. Имеем:

Следовательно, точка B принадлежит графику функции y=10x-3.

Ответ: точка B принадлежит графику функции, точка A — не принадлежит.

2) Какие из точек A(2;15), B(-1;-15), C(-10; 243) принадлежат графику функции y=3x²+5x-7?

В формулу функции y=3x²+5x-7 вместо y подставляем ординату точки, вместо каждого x — абсциссу.

Верные равенства получили для точек A и C. Значит, эти точки принадлежат графику функции y=3x²+5x-7, а точка B — не принадлежит.

Как решать задачи на функцию

Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок «Что такое функция в математике».

После того, как вы действительно поймете, что такое функция (возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.

В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.

Как получить значение функции

Рассмотрим задание. Функция задана формулой « y = 2x − 1 »

1. Вычислить « y » при « x = 15 »
2. Найти значение « x », при котором значение « y » равно « −19 ».

Для того, чтобы вычислить « y » при « x = 15 » достаточно подставить в функцию вместо « x » необходимое числовое значение.

Запись решения выглядит следующим образом.

Для того, чтобы найти « x » по известному « y », необходимо подставить вместо « y » в формулу функции числовое значение.

То есть теперь наоборот, для поиска « x » мы подставляем в функцию « y = 2x − 1 » вместо « y » число « −19 » .

Мы получили линейное уравнение с неизвестным « x », которое решается по правилам решения линейных уравнений.

Запомните!

Не забывайте про правило переноса в уравнениях.

При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на противоположный .

Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас требуется умножить и левую, и правую часть на « −1 » для смены знака.

Теперь разделим и левую, и правую часть на « 2 », чтобы найти « x » .

Как проверить верно ли равенство для функции

Рассмотрим задание. Функция задана формулой « f(x) = 2 − 5x ».

Верно ли равенство « f(−2) = −18 »?

Чтобы проверить верно ли равенство, нужно подставить в функцию « f(x) = 2 − 5x » числовое значение « x = −2 » и сопоставить с тем, что получится при расчетах.

Важно!

Когда подставляете отрицательное число вместо « x », обязательно заключайте его в скобки.

Не забывайте использовать правило знаков.

Неправильно

Правильно

С помощью расчетов мы получили « f(−2) = 12 ».

Это означает, что « f(−2) = −18 » для функции « f(x) = 2 − 5x » не является верным равенством.

Как проверить, что точка принадлежит графику функции

Рассмотрим функцию « y = x 2 −5x + 6 »

Требуется выяснить, принадлежит ли графику этой функции точка с координатами (1; 2) .

Для этой задачи нет необходимости, строить график заданной функции.

Запомните!

Чтобы определить, принадлежит ли точка функции, достаточно подставить её координаты в функцию (координату по оси « Ox » вместо « x » и координату по оси « Oy » вместо « y »).

Если получится верное равенство , значит, точка принадлежит функции.

Вернемся к нашему заданию. Подставим в функцию « y = x 2 − 5x + 6 » координаты точки (1; 2) .

Вместо « x » подставим « 1 ». Вместо « y » подставим « 2 ».

У нас получилось верное равенство, значит, точка с координатами (1; 2) принадлежит заданной функции.

Теперь проверим точку с координатами (0; 1) . Принадлежит ли она
функции « y = x 2 − 5x + 6 »?

Вместо « x » подставим « 0 ». Вместо « y » подставим « 1 ».

В этом случае мы не получили верное равенство. Это означает, что точка с координатами (0; 1) не принадлежит функции « y = x 2 − 5x + 6 »

Как получить координаты точки функции

С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат в формулу функции получается верное равенство.

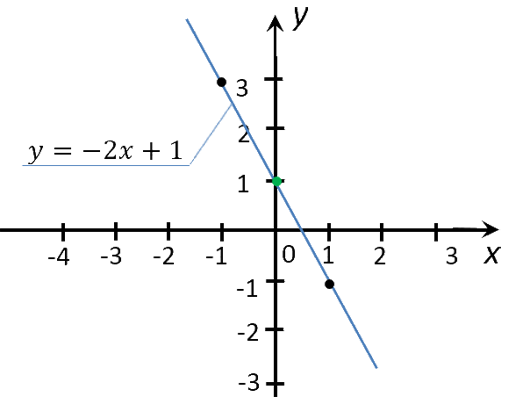
Рассмотрим функцию « y(x) = −2x + 1 ». Её график мы уже строили в предыдущем уроке.

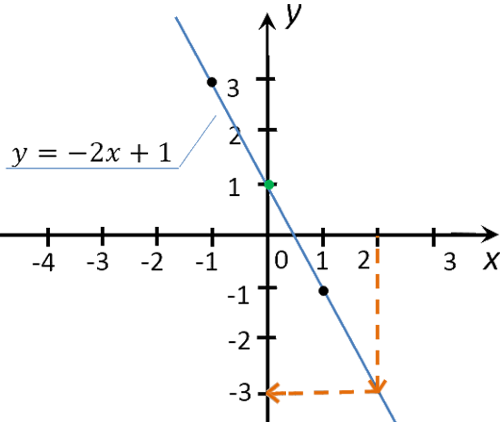
Найдем на графике функции « y(x) = −2x + 1 », чему равен « y » при x = 2 .

Для этого из значения « 2 » на оси « Ox » проведем перпендикуляр к графику функции. Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси « Oy ».

Полученное значение « −3 » на оси « Oy » и будет искомым значением « y ».

Убедимся, что мы правильно сняли координаты точки для x = 2
в функции « y(x) = −2x + 1 ».

Для этого мы подставим x = 2 в формулу функции « y(x) = −2x + 1 ». Если мы правильно провели перпендикуляр, мы также должны получить в итоге y = −3 .

При расчетах мы также получили y = −3 .

Значит, мы правильно получили координаты с графика функции.

Важно!

Все полученные координаты точки с графика функции обязательно проверяйте подстановкой значений « x » в функцию.

При подстановке числового значения « x » в функцию в результате должно получиться то же значение « y », которое вы получили на графике.

При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».

Исследование графика функции

На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:

• область определения функции
• область значений функции
• нули функции
• промежутки возрастания и убывания
• точки максимума и минимума
• наибольшее и наименьшее значение функции на отрезке.

Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .

Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .

Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .

На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.

Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .

Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .

Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .

Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.

Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.

Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.

На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .

Определим, что такое точки максимума и минимума функции.

Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.

На нашем рисунке — точка максимума.

Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».

На нашем рисунке — точка минимума.

Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.

Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .

А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.

Аналогично, максимум нашей функции равен . Он достигается в точке .

Можно сказать, что экстремумы функции равны и .

Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.

В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.

В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.