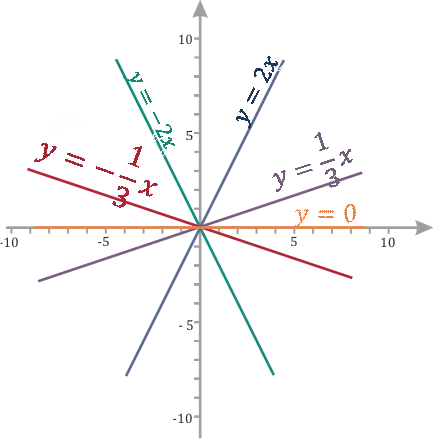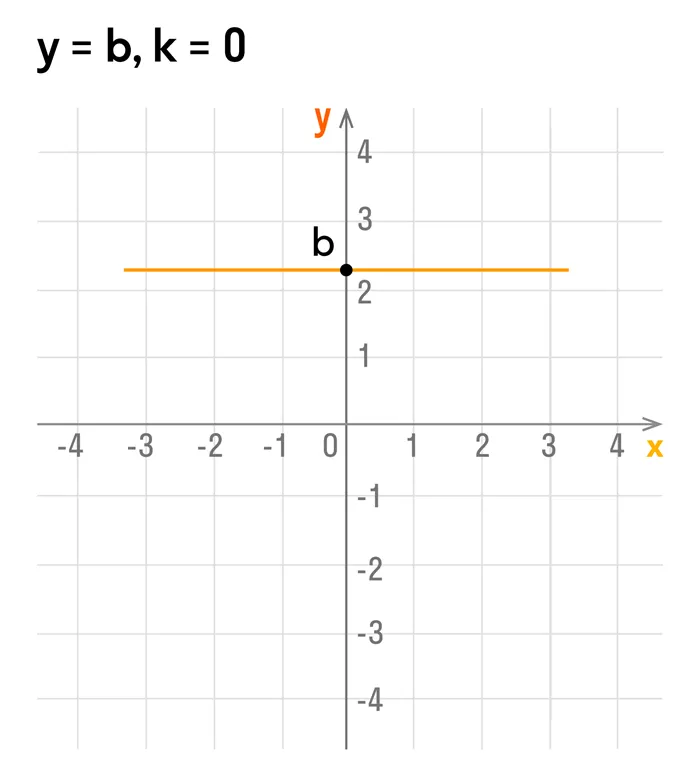Как найти линейную функцию по графику ответы

График линейной функции, его свойства и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Понятие линейной функции

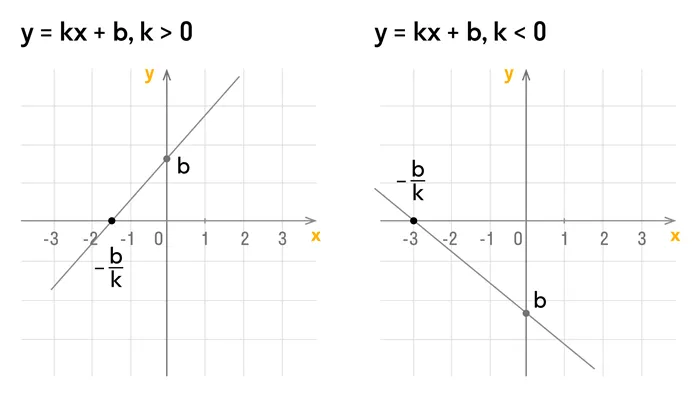
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х – 2. Значит:

• если х = 0, то у = -2;
• если х = 2, то у = -1;
• если х = 4, то у = 0;
• и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».

Функция	Коэффициент «k»	Коэффициент «b»
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».

Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!

Свойства линейной функции

1. Область определения функции — множество всех действительных чисел.
2. Множеством значений функции является множество всех действительных чисел.
3. График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
4. Функция не имеет ни наибольшего, ни наименьшего значений.
5. Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
   b ≠ 0, k = 0, значит y = b — четная;
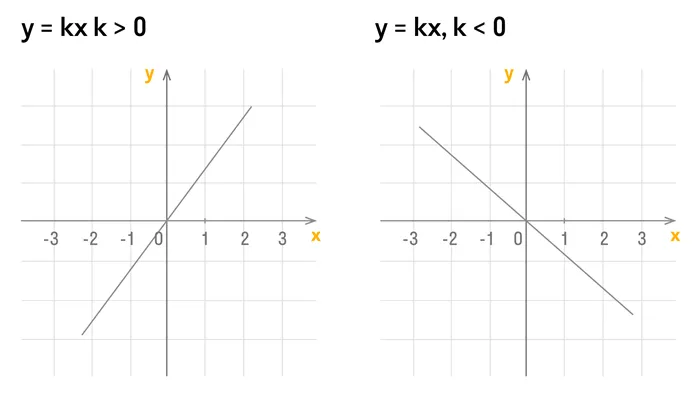
   b = 0, k ≠ 0, значит y = kx — нечетная;
   b ≠ 0, k ≠ 0, значит y = kx + b — функция общего вида;
   b = 0, k = 0, значит y = 0 — как четная, так и нечетная функция.
6. Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
7. График функции пересекает оси координат:
   ось абсцисс ОХ — в точке (-b/k, 0);
   ось ординат OY — в точке (0; b).
8. x=-b/k — является нулем функции.
9. Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
   Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
10. Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0: функция принимает отрицательные значения на промежутке (-∞, – b /_k) и положительные значения на промежутке (- b /_k, +∞)
    При k b /_k, +∞) и положительные значения на промежутке (-∞, – b /_k).
11. Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом.
    Если k > 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

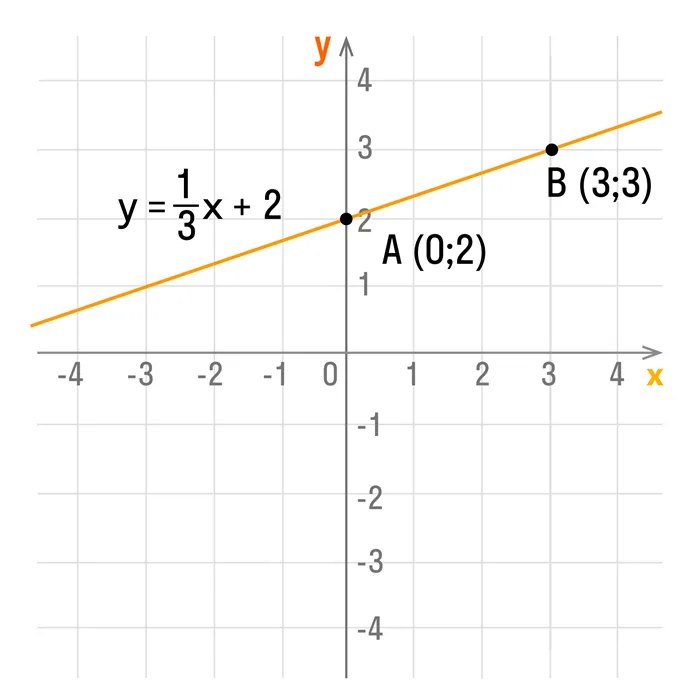
Например, чтобы построить график функции y = 1 /₃x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

• если k > 0, то график наклонен вправо;
• если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
• если b 1 /₂x + 3, y = x + 3.

Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.

В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).

Теперь рассмотрим графики функций y = -2x + 3, y = – 1 /₂x + 3, y = -x + 3.

В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.

Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).

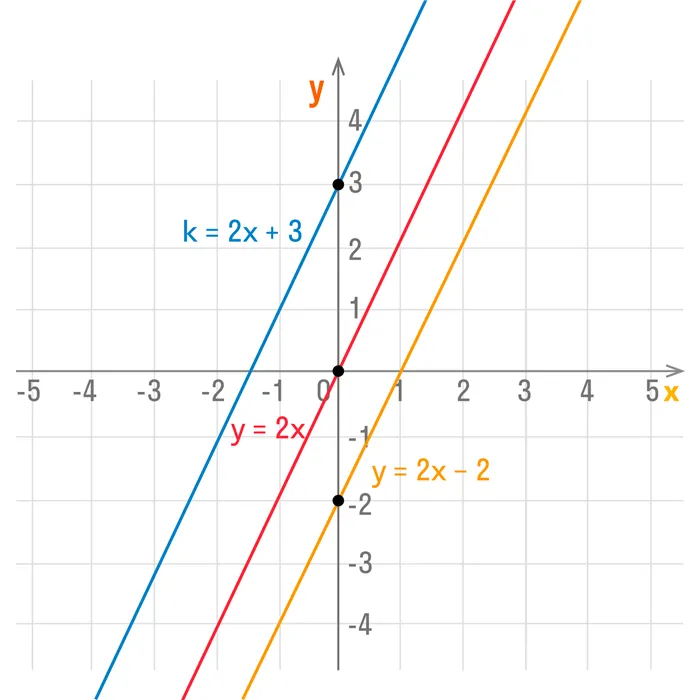
Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x – 2.

Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.

При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

• график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
• график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
• график функции y = 2x – 2 (b = -2) пересекает ось OY в точке (0; -2).

Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.

Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.

Если k 0, то график функции y = kx + b выглядит так:

0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>

Точки пересечения графика функции y = kx + b с осями координат:

• С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
  Координаты точки пересечения с осью OY: (0; b).
• С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = – b /_k.
  Координаты точки пересечения с осью OX: (- b /_k; 0)

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

• В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
  Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
  Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
  2 = -4(-3) + b
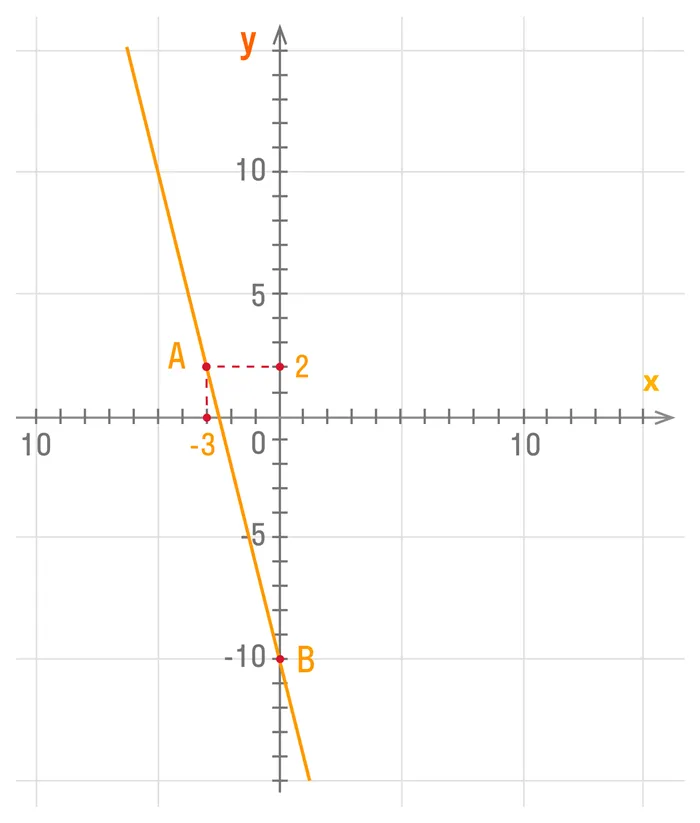
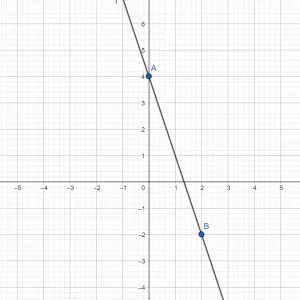
  b = -10
• Таким образом, нам надо построить график функции y = -4x – 10
  Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
  Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

1. Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
   Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
2. Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
3. Вычтем из второго уравнения системы первое, и получим k = 3.
   Подставим значение k в первое уравнение системы, и получим b = -2.

Алгоритм определения формулы линейной функции по графику

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Выполнила учительница математики МБОУ Башкирский лицей № 1 муниципального района Учалинский район Республики Башкортостан Хидиятова Залифа Даутовна

Алгоритм определения формулы линейной функции по графику”

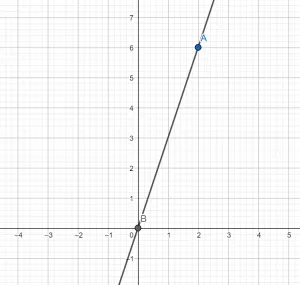
На рисунке представлен график функции у = kx +b.
Записать формулу линейной функции, соответствующей данному графику.

1) Так как ордината точки пересечения графика функции с осью Оy равна 1, следовательно, b=1.
Значит, у = kx+ 1

2) Выбираем на графике произвольную точку, например, А (2;2) и определяем её координаты: если x = 2, то у = 2. Подставим в нашу формулу вместо Х и У и получим уравнение относительно k.
2 = 2k+1
2k=1
k = 0.5 Записываем формулу линейной функции: у = 0,5х + 1.

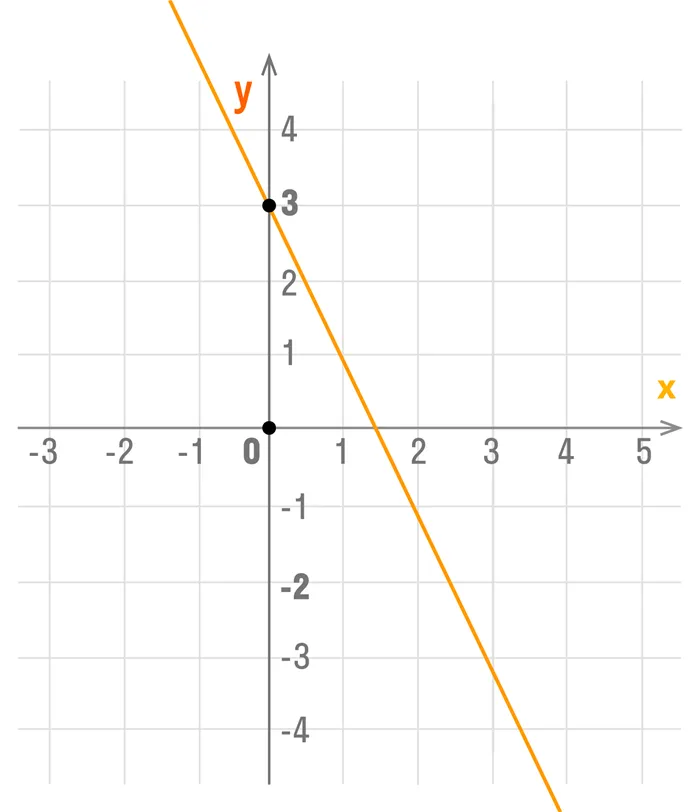
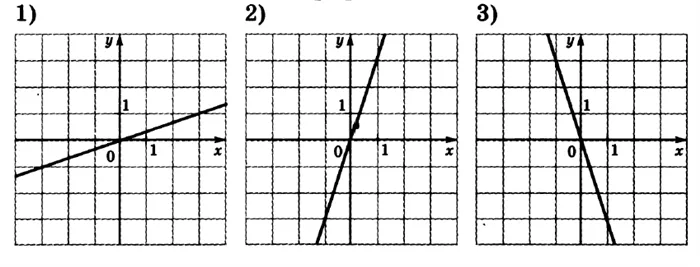
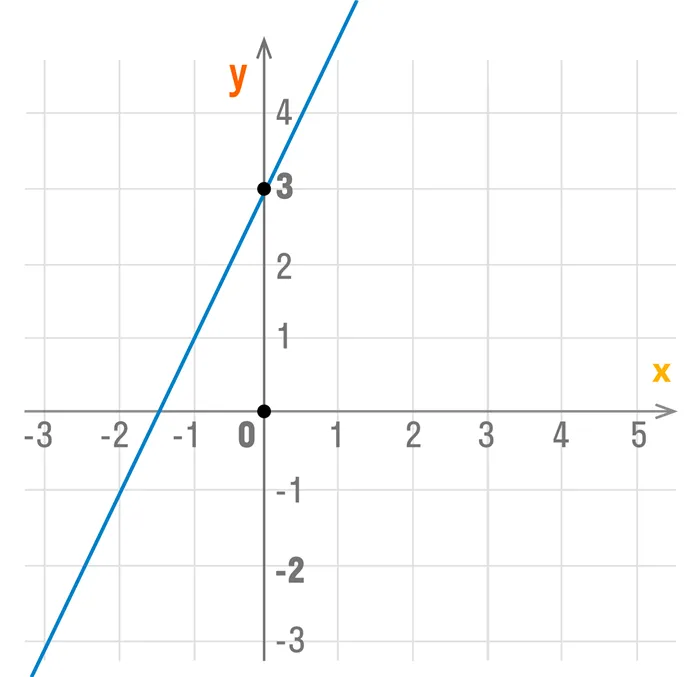
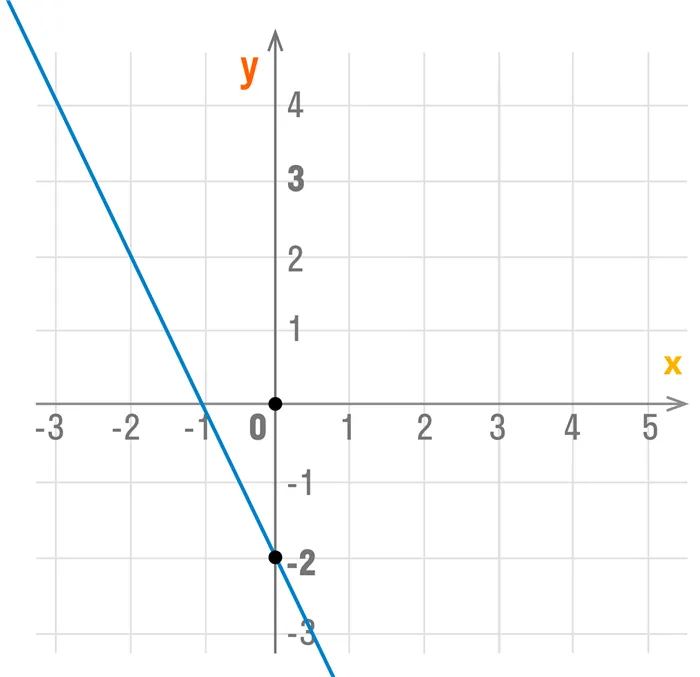
Написать ФОРМУЛУ линейной функции У= КХ+В, график которой изображен на рисунке :

Это ВПР задание 8) это ответ:

ВНИМАНИЕ : задание на сегодня 16 апреля

Внимание : вот эти следующие задания пока НЕ РЕШАТЬ.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 956 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 685 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 569 280 материалов в базе

Материал подходит для УМК

«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.

16. Линейная функция и её график

Другие материалы

• 16.09.2020
• 199
• 11

• 31.03.2020
• 1166
• 30

• 16.03.2020
• 225
• 1

• 16.03.2020
• 191
• 1

• 08.03.2020
• 281
• 6

• 20.02.2020
• 1243
• 70

• 21.01.2020
• 180
• 0

• 09.12.2019
• 418
• 13

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 30.09.2020 15903
• DOCX 549.2 кбайт
• 155 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Хидиятова Залифа Даутовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 38483
• Всего материалов: 37

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Онлайн-конференция о создании школьных служб примирения

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Как найти k и b по графику линейной функции?

В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции , т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):

В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.

Способ 1

Первый способ основывается на трех фактах:

Линейная функция пересекает ось (y) в точке (b).
Примеры:

Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.

Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).

Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.

(b=3) – это сразу видно. Функция идет вниз, значит (k 0). (k=+frac=frac<4><4>=1,b=1). (f(x)=x+1).

Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:

Вычтем второе уравнение из первого, чтоб убрать (b):

(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).

Картинку в хорошем качестве, можно скачать нажав на кнопку “скачать статью”.

[spoiler title=”источники:”]

http://infourok.ru/algoritm-opredeleniya-formuly-linejnoj-funkcii-po-grafiku-4463697.html

http://cos-cos.ru/ege/zadacha203/376/

[/spoiler]

Инфоурок

›

Алгебра

›Конспекты›Алгоритм определения формулы линейной функции по графику

Алгоритм определения формулы линейной функции по графику

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Функция	Коэффициент k	Коэффициент b
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

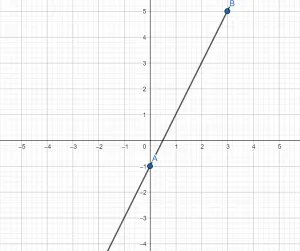
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Если k > 0 и b

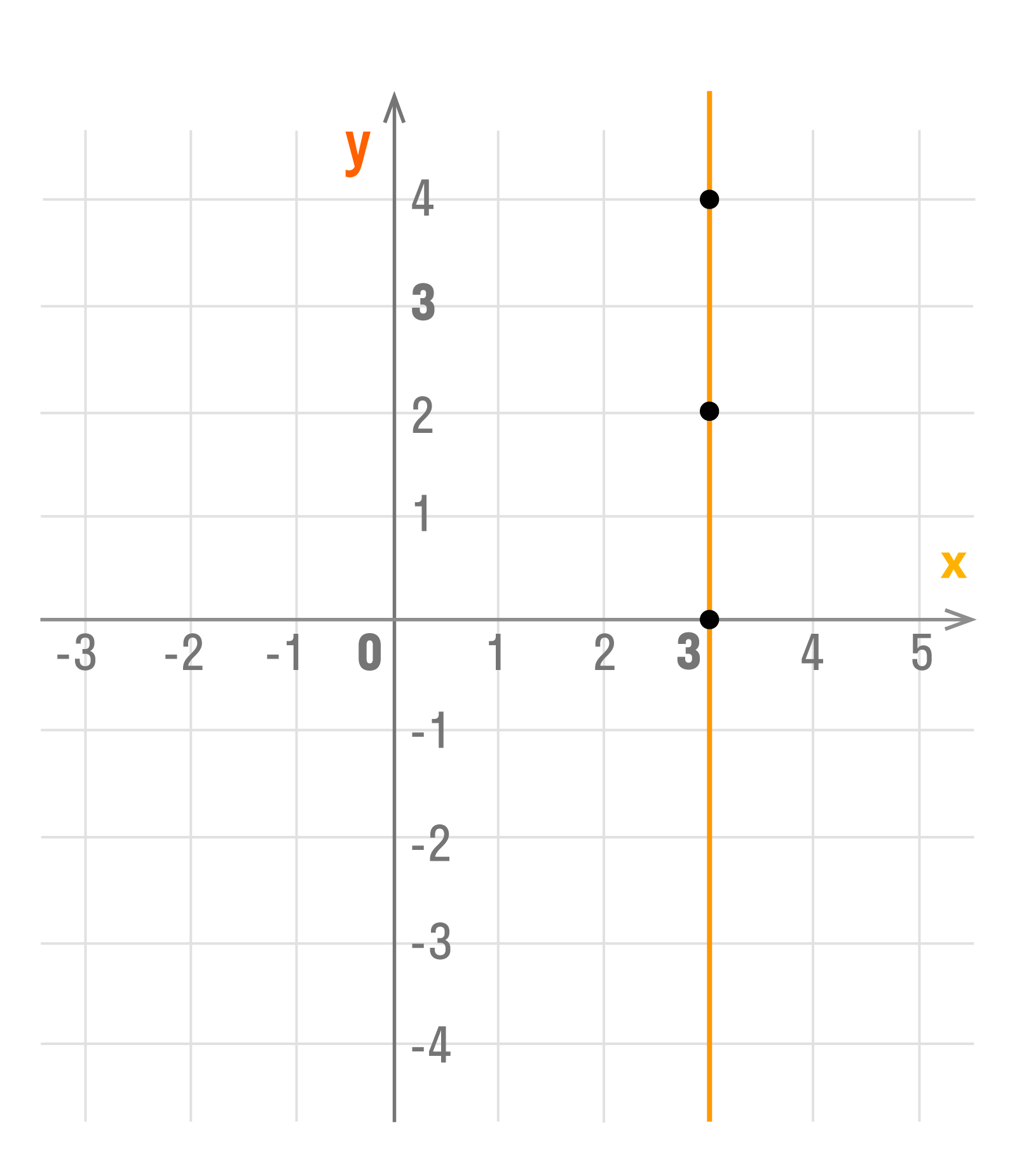
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ перпендикулярен графику функции y = k₂x + b₂, если k₁k₂ = −1 или k₁ = −1/k₂.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x — 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x — 2.

Алгоритм определения формулы линейной функции по графику

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выполнила учительница математики МБОУ Башкирский лицей № 1 муниципального района Учалинский район Республики Башкортостан Хидиятова Залифа Даутовна

Алгоритм определения формулы линейной функции по графику»

На рисунке представлен график функции у = kx +b.
Записать формулу линейной функции, соответствующей данному графику.

1) Так как ордината точки пересечения графика функции с осью Оy равна 1, следовательно, b=1.
Значит, у = kx+ 1

2) Выбираем на графике произвольную точку, например, А (2;2) и определяем её координаты: если x = 2, то у = 2. Подставим в нашу формулу вместо Х и У и получим уравнение относительно k.
2 = 2k+1
2k=1
k = 0.5 Записываем формулу линейной функции: у = 0,5х + 1.

Написать ФОРМУЛУ линейной функции У= КХ+В, график которой изображен на рисунке :

Это ВПР задание 8) это ответ:

ВНИМАНИЕ : задание на сегодня 16 апреля

Внимание : вот эти следующие задания пока НЕ РЕШАТЬ.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 925 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 684 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 578 832 материала в базе

Материал подходит для УМК

«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.

16. Линейная функция и её график

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 16.09.2020
• 199
• 11

• 31.03.2020
• 1166
• 30

• 16.03.2020
• 227
• 1

• 16.03.2020
• 191
• 1

• 08.03.2020
• 282
• 6

• 20.02.2020
• 1246
• 71

• 21.01.2020
• 180
• 0

• 09.12.2019
• 418
• 13

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 30.09.2020 16027
• DOCX 549.2 кбайт
• 155 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Хидиятова Залифа Даутовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 38658
• Всего материалов: 37

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

В России действуют более 3,5 тысячи студенческих отрядов

Время чтения: 2 минуты

Профессия педагога на третьем месте по популярности среди абитуриентов

Время чтения: 1 минута

В Забайкалье в 2022 году обеспечат интернетом 83 школы

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Как найти k и b по графику линейной функции?

В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции , т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):

В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.

Способ 1

Первый способ основывается на трех фактах:

Линейная функция пересекает ось (y) в точке (b).
Примеры:

Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.

Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).

Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.

(b=3) – это сразу видно. Функция идет вниз, значит (k 0). (k=+frac=frac<4><4>=1,b=1). (f(x)=x+1).

Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:

Вычтем второе уравнение из первого, чтоб убрать (b):

(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).

Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».

K и B — числовые коэффициенты функции. Это может быть любое число, например, положительное, отрицательное или дробное.

Линейная функция, ее свойства и график

Функция, заданная видом y = kx+b, где x — переменная, а k и b — некоторые числа, называется линейной функцией. Переменная x называется независимой переменной, а переменная y — зависимой переменной.

Графиком линейной функции является линия. Чтобы провести прямую линию, достаточно получить два значения x и получить два значения y, в результате чего получатся две точки, через которые проходит одна прямая.

Число K называется угловым коэффициентом линии.

Свойства линейной функции

1. Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
2. Областью значений также является множество всех действительных чисел.
3. Функция не имеет ни наибольших, ни наименьших значений.
4. При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
5. При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
6. При k=0 прямая параллельна оси х.
7. Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.

Рассмотрим пример линии до уровня координат в соответствии со значениями K и B

Пример №1

Постройте график функции y = 2x -1. Для облегчения расчетов, структурирования и т.д. создайте таблицу значений x и y.

Чтобы построить график, выберите два значения x. Желательно, чтобы одно из них было равно нулю, а второе значение (выберите три).

Затем замените значение x в уравнении и вычислите соответствующее значение y.

Запишите значение y в таблицу:.

Постройте систему координат, запишите в ней координаты A (0; -1) и B (3; 5) и проведите прямую линию к этим двум точкам.

Таким образом, из печати видно, что угловой коэффициент положительный. Это означает, что график растет, что видно на графике.

Каждое из этих уравнений является уравнением прямой линии. Решение системы заключается в нахождении цен, которые удовлетворяют как первому, так и второму уравнению. Однако, поскольку они определяют точки, для решения системы необходимо найти точки на первой и второй прямых, то есть пересечения прямых.

Как меняется график при разных (k)?

Определите, как влияет на графикКоэффициент. (k ) рисует различные функции с различными (k ): (⢙), (-⢙), (2 ), (-2 ), (0 ). В этом случае ⌘ (b ) равен (равен нулю) для всех функций, что устраняет его влияние. Другими словами, нарисуйте графики функций: (y = fracx ), (y = — fracx), (y = 2x ), (y = -2x ), (y = 0 ).

В случае (k = 2 ) и ʉ (ʉ frac ) функция возрастает, а в случае ʉ (k = -2 ) и ʉ (- frac) — убывает. На практике:.

При любом (k>0) функция возрастает и при любом (k

Также можно заметить, что болеефактор в случае В случае (k ) график более «острый».

Как по графику определить коэффициент k?

1. Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента (k) плюс, если убывает – минус.
2. Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:

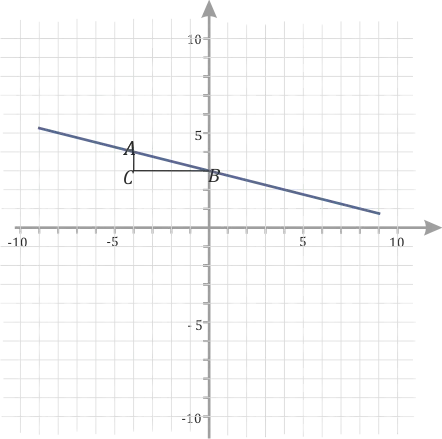
Чтобы найти значение (k ) по модулю (т.е. без учета знаков), нужно разделить вертикальную сторону треугольника на горизонтальные плоскости. Можно воспользоваться эмпирическим правилом. Стояние ошеломляет». В этих случаях (| k | = frac ). Следовательно, в первом графе ⌘ (k = 2 ), а во втором ⌘ (k = — frac ).

Как меняется график при разных значениях (b)?

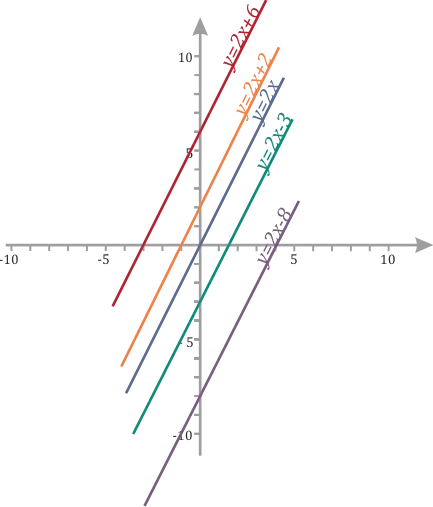
Чтобы определить, как (b ) влияет на графики, нарисуйте различные функции с разными Ј (b ): Ј (6 ), Ј (2 ), Ј (0 ), Ј (-3 ), Ј (-3 ), Ј (-3 ). (-8 ). Для всех функций установите ⌘(k ) равным ⌘(2 ).

Вы можете легко увидеть, поднимается ли линия на ⌘(b ) (если (b>0 )) или опускается относительно ⌘(| b | ).<0)).

For (ː displaystyle k ). Функция ⌘ (⌘ displaystyle left (b = 0 right)). () Измените функцию displaystyle k ) и посмотрите, что произойдет на графике.

Свойства линейной функции

Определяющей областью функции является сумма всех действительных чисел.

Сумма функции — это сумма всех действительных чисел.

Графиком линейной функции является линия. Чтобы провести прямую, достаточно знать две точки. Положение линии на уровне координат зависит от значений коэффициентов K и B.

Функция не имеет наибольшего или наименьшего значения.

Превосходство и нерелевантность линейной функции зависит от значений коэффициентов k и b.

b ≠ 0, k = 0, поэтому y = b является хорошим, и

b = 0, k ≠ 0, поэтому y = kx не требуется.

b ≠ 0, k ≠ 0, где y = kx + b — общая функция и

b = 0, k = 0, поэтому y = 0 является как четной, так и нечетной функцией.

Линейные функции не обладают свойством периодичности, так как их спектр непрерывен.

График функции пересекает координатные оси.

ось OX — в точке (-b / k; 0), ось

Ось OY — в точке (0; b).

x = -b/k является точкой нуля функции.

Для b=0 и k=0 функция y=0 равна нулю при любом значении переменной x.

Если b≠0 и k=0, то функция y=b обращается в нуль при любом значении переменной x.

Функция монотонно возрастает в области определения до k>0 и монотонно убывает до k.< 0 .

Для k> 0 функция принимает отрицательные значения в интервале (-∞; -b / k) и положительные значения в интервале (-b / k; +∞).

Коэффициент k представляет собой угол, образованный линией в положительном направлении OX. Следовательно, k называется угловым коэффициентом.

Для линейных функций есть два особых случая.

Когда b = 0, уравнение принимает вид y=kx. Такая функция называется прямо пропорциональной. График представляет собой линию, проходящую через начало координат.

• Если k = 0, то уравнение примет вид y = b. График — прямая, которая параллельна оси OX и проходит через точку (0; b) .

Построение линейной функции

В геометрии есть аксиомы. Любые две точки могут пересекаться по прямой и только по одной. Из этой аксиомы следует, что для построения графика функции y = kx + b достаточно найти только две точки. Для этого нужно задать два значения x, заменить их уравнением функции и вычислить соответствующее значение y.

Например, чтобы построить график функции y = 1 / 3x + 2, можно взять x = 0 и x = 3, а нормали этих точек будут y = 2 и y = 3. Возьмем точки A (0; 2) и B (3; 3). Соедините их, чтобы получить график:.

В уравнении функции y=kx + b коэффициент k участвует в наклоне графика функции.

Если k>0, то график наклонен вправо.

Коэффициент b отвечает за смещение графика вдоль OY.

Если b> 0, то график функции y = kx + b строится из y = kx путем сдвига вверх на b единиц вдоль оси OY.

Постройте три графика функции.

Проанализируйте формы. Поскольку коэффициент k больше нуля для всех функций, все графики наклонены вправо. Чем выше значение k, тем круче линия.

Поскольку b = 3 для каждой функции, все графики пересекают ось OY в точке (0; 3).

Давайте посмотрим на графики функций.

На этот раз коэффициент k меньше нуля для всех функций, а графики функций перекошены влево. Чем больше k, тем круче становится линия.

Коэффициент b равен 3, и график также пересекает ось OY в точке (0; 3).

Исследуйте график функции.

Коэффициенты k теперь равны во всех уравнениях функции. Получаются три параллельные линии.

Коэффициенты b различны, и эти графики пересекают ось OY в разных точках.

График функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3).

График функции y=2x (b = 0) пересекает ось OY в начальной точке (0; 0).

График функции y=2x —2 (b = -2) пересекает ось OY в точке (0; -2).

Линии с одинаковым угловым коэффициентом параллельны.

Резюме. Если известны знаки коэффициентов k и b, то можно увидеть график функции y = kx+b.

Если k< 0 и b > 0, график функции y = kx+b имеет вид

Если k > 0 и b > 0, график функции y = kx+b имеет вид

Решение задач на линейную функцию

Чтобы решить задачу и построить график линейной функции, необходимо вспомнить и использовать вышеуказанные свойства и правила. Практикуйтесь!

Пример 1. Постройте график функции y = kx + b, если известно, что она проходит через точку A (-3; 2) и параллельна прямой y = -4x.

Уравнение функции y = kx + b имеет два неизвестных параметра, k и b. Поэтому в рассматриваемом тексте нам нужно найти два условия, характеризующие график функции.

График функции y=kx+b параллелен прямой y=-4x, поэтому k = -4. Это означает, что уравнением функции является y = -4x+b.

Осталось найти Б. Мы видим, что график функции y = -4x + b проходит через точку A (-3; 2). Подставьте координаты точки в уравнение функции, чтобы получить правильное уравнение.

Поэтому необходимо построить график функции y = -4x-10.

Мы уже знаем точку A (-3; 2), поэтому давайте найдем точку B (0; -10).

Расположим эти точки в координатной плоскости и соединим их прямыми линиями.

Пример 2. Напишите уравнение прямой, проходящей через точку A (1; 1). B (2; 4).

Если прямая проходит через точку с заданными координатами, то координаты точки удовлетворяют уравнению y = kx+b.

Поэтому замена координат точки в уравнении прямой дает верное равенство.

Подставьте координаты каждой точки в уравнение y = kx + b, чтобы получить одновременное линейное уравнение.

Вычтите первое уравнение из второго уравнения системы, чтобы получить k = 3.

Подставьте значение k в первое уравнение системы, чтобы получить b=-2.

Предположим, что нам даны две линейные функции (назовем эту линию) и (назовем эту линию). При различных комбинациях коэффициентов этих функций эти линии либо пересекаются в некоторой точке (перпендикулярно или произвольно), либо не пересекаются. Другими словами, они параллельны. Давайте рассмотрим эти варианты.

Свойства зависимости

Перед решением задачи следует обратить внимание на свойства линейных функций. Есть две позиции, которые зависят от коэффициента k. Для k> 0 функция обладает следующим свойством: если k > 0, то функция линейна.

1. Графиком является прямая линия.
2. D(y) = (-∞;∞).
3. При отрицательных значениях аргумента значение функции эквивалентно отрицательной величине. Если независимая переменная — положительная величина, то и зависимая принимает только положительные значения. В этом моменте ключевую роль играет величина сдвига влево или вправо b.
4. Возрастает на E(у).
5. Отсутствие экстремумов.
6. Непрерывная и нечетная.
7. Период отсутствует.

Таким образом, график линейной функции — это прямая линия, и ее свойства необходимо исследовать по определенному алгоритму. Необходимо соблюдать основные свойства.

С осью OY. Представление всех точек, принадлежащих оси OY, равно нулю. Поэтому, чтобы найти пересечение с OY, x в уравнении функции заменяется на ноль. Тогда y = b.

График линейной функции

Как упоминалось выше, график этой функции — прямая линия.

Как известно из геометрии, прямую можно провести через две точки (т.е. если известны две точки, принадлежащие прямой, то этого достаточно).

Предположим, у нас есть линейная функция ⌘ (y = 2x + 1 ). Чтобы построить его, необходимо вычислить координаты любых двух точек.

Другими словами, вам нужно взять два значения члена ⌘(x ) и вычислить соответствующие два значения функции.

Затем для каждой пары ⌘(⌘ слева (x; y справа)⌘) найдите точку в системе координат и проведите прямую через эти две точки.

Проще всего найти функцию с аргументом (x = 0: y слева (0 справа) = 2 cdot 0 + 1 = 1 ).

Поэтому координаты первой точки ⌘(⌘ слева (0; 1 справа)．

Предположим, что остальные числа ⌘(x ). Например, ǫ (x = 1: y слева (1 справа) = 2 cdot 1 + 1 = 3 ).

Координаты второй точки ⌘ (⌘ слева (1; 3 справа)).

Поместите следующие две точки в координатную плоскость.

Затем с помощью линейки проведите линию через следующие две точки.

И вот график создан!

Теперь на том же графике нарисуем еще два графика: ⌘ (y = -1 ) и ǫ (y = -x + 2 ).

Создайте свою собственную аналогичным образом: вычислите значения y для любых двух значений ǫ(x ), отметьте эти точки на графике и проведите через них линию.

Открыть ответы…

Мы постоянно совершенствуем это руководство, и вы можете помочь в этом. Неограниченный доступ и использование руководства Юклава (более 100 статей по всем темам использования и применения, более 2000 решенных задач, более 20 онлайн семинаров и семинаров).

Видно, что все три линии имеют разные уклоны и пересекают оси координат в разных точках. Это вкладчики( displaystyle k ) и displaystyle b ).

Давайте узнаем, чем они занимаются.

Коэффициенты линейной функции

Сначала посмотрим, что делают факторы (⌘ displaystyle b ). Рассмотрим функцию ⌘ (⌘ displaystyle y = x+b ), т.е. ⌘ (⌘ displaystyle k = 1 ).

Посмотрите, что происходит на графике, изменив (⌘ displaystyle b ).

(⌘ displaystyle b: b = -2, давайте построим график с различными значениями ⌘ text< ->1, {text< >0, {text< >1, {text< >2 ):.

Что вы можете сказать о них? Чем отличаются графики?

Скоро вы в этом убедитесь. Чем больше (Lo_ displaystyle b ), тем больше линий размещается.

Далее, обратите внимание на следующее. График пересекает ось ⌘ (⌘ displaystyle mathbf ) в точке с координатами, равными ⌘ (⌘ displaystyle mathbf )!

И это правда. Как найти пересечение графика с помощью оси ⌘ (⌘ displaystyle y )? Что такое ⌘ (⌘ displaystyle x ) в такой момент времени?

В любой точке вертикальной оси (так называется ось ⌘ (⌘ displaystyle y ), если вы забыли) ⌘ (⌘ displaystyle x = 0 ).

Поэтому просто замените функцию ⌘ (⌘ displaystyle x = 0 ) и вы получите расположение графика на оси ⌘ (⌘ displaystyle y ).

For (ː displaystyle k ). Функция ⌘ (⌘ displaystyle left (b = 0 right)). () Измените функцию displaystyle k ) и посмотрите, что произойдет на графике.

⌘ displaystyle k = -3, давайте построим график ⌘ text< ->1, {text< >0, {text< >1, {text< >2: ס)

Ну, теперь мы это поняли: displaystyle k ) влияет на тенденцию графика.

Чем больше модуль (то есть, несмотря на синус), тем более «острой» (бездной — с большим углом к оси ɛ — ɛ displaystyle ox ɛ) является линия.

Анализ. Постройте новый график (⌘ displaystyle y = kx+b ):.

Выберите на графике две точки ɑ (ɑ displaystyle a ) и ɑ (ɑ displaystyle b ). Для простоты мы выбрали точку на пересечении графика с линией. Точка ⌘ (⌘ displaystyle b ) может находиться в любой точке прямой.

Рассмотрим прямоугольный треугольник 섹 (섹 displaystyle ab ), построенный в сечении 섹 (섹 displaystyle ab ), подчиненном прямоугольнику 섹 (섹 displaystyle ab ).

На диаграмме показано, что හ (⌘ displaystyle ac = x ) и හ (⌘ displaystyle bc = y-b ).

Замените (⌘ displaystyle y = kx+b ) на ߋ (⌘ displaystyle bc: bc = y-b = kx+b-b = kx ).

bc = k cdot ac> rightrrow> k = frac >> =<mathop<rm tg> nolimits> alpha ).

Поэтому коэффициент ⌘ (⌘ displaystyle k ) равен тангенсу угла наклона графика, то есть углу между графиком и осью расстояния.

Поэтому (коэффициент ⌘ (⌘ displaystyle k )) обычно называют угловым коэффициентом.

Если (⌘ displaystyle k = 0 ), то ⌘ (⌘ также ⌘)<mathop<rm tg> nolimits> alpha = 0, ⌘), поэтому ⌘ (⌘ displaystyle alpha = 0 ), т.е. линия параллельна оси глубины на.

Понимание геометрического значения коэффициентов очень важно, так как они часто используются в различных задачах на линейные функции.

Разбор еще трех задач на линейную функцию

1. найдите коэффициенты ዄ (ዄ displaystyle k ) и ዄ (ዄ displaystyle b ) линейной функции, график которой изображен на рисунке. Напишите уравнение функции.

Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике

Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)

Параметры США часто включают исследование функции или, по крайней мере, знание ее свойств.

Чтобы научиться исследовать функцию, лучше всего научиться визуализировать ее графически.

В этом уроке вы рассмотрите основные элементарные функции, научитесь представлять их графически и узнаете, как на них влияют различные параметры (коэффициенты функции).

Преобразования графиков функций. ЕГЭ 18. Задачи с параметром.

Научились ли вы строить графики функций? Что произойдет, если вы измените один из тарифов сейчас? Или «инкапсулировать» часть функции в раздел?

Можно ли просто переместить/расширить старую диаграмму вместо того, чтобы создавать новую для этой цели?

Вы можете! И в этом уроке вы узнаете, как выполнять такие преобразования.

Благодаря этим преобразованиям вы поймете, как выглядит график функции для всех значений параметра, и научитесь решать задачи США, связанные с этим вопросом.