§ 9 ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЁ ГРАФИК
1. Преобразование уравнения ах + by + с = 0 к виду у = kx + m
Алгоритм построения графика уравнения ах + by + с = 0, который мы сформулировали в § 8, при всей его чёткости и определённости математикам не очень нравится. Обычно они выдвигают претензии к первым двум шагам алгоритма. Зачем, говорят они, дважды решать уравнение относительно переменной у: сначала ах1 + by + с = 0, затем ах2 + by + с = 0? Не лучше ли сразу выразить у из уравнения ах + by + с = 0, тогда легче будет проводить вычисления (и, главное, быстрее)? Давайте проверим.
Рассмотрим сначала уравнение Зх — 2у + 6 = 0 (см. пример 2 из § 8), т. е. 2у = Зх + 6.
Умножив обе части уравнения на ½ получим …
Впрочем, тот же результат мы получили бы, если обе части исходного уравнения почленно разделили на 2. Обычно предпочитают в подобных случаях говорить не об умножении, а о почленном делении обеих частей уравнения на одно и то же число.
Придавая х конкретные значения, легко вычислить соответствующие значения у. Например, при х = 0 получаем у = 3; при х = -2 имеем у = 0; при х = 2 имеем у = 6; при х = 4 получаем у = 9. Видите, как легко и быстро найдены точки (0; 3), (-2; 0), (2; 6) и (4; 9), которые были выделены в примере 2 из § 8.
Точно так же уравнение 5х — 2у = 0 (см. пример 4 из § 8) можно было преобразовать к виду 2у = 5х и, далее, у = 2,5х; нетрудно найти точки (0; 0) и (2; 5), удовлетворяющие этому уравнению. Наконец, уравнение Зх + 2у — 16 = 0 из того же примера можно было преобразовать к виду 2у = 16 — Зх и, далее, у — 8 — -х.
Из этого уравнения можно найти решения (0; 8) и (2; 5), которые ему удовлетворяют.
Рассмотрим теперь указанные преобразования в общем виде.
Случаи, когда в уравнении ах + by + с = 0 коэффициенты а и b равны нулю, мы рассмотрели в § 8. Там же мы отметили, что в случае, когда а Ф О, b = 0, графиком уравнения является прямая, параллельная оси у.
Рассмотрим случай, когда b ≠ 0. Имеем ах + by + с = 0; (1) bу = -ах – с;
Введя обозначения … получаем у = kx + m.
Таким образом, линейное уравнение (1) с двумя переменными х и у в случае, когда b ≠ 0, можно преобразовать к виду у = kx + m (2) где k, m — числа (коэффициенты).
Это частный вид линейного уравнения. Зная, чему равен х, по правилу у = kx + m всегда можно найти, чему равен у. Будем называть уравнение (2) линейной функцией.
С помощью уравнения (2) легко, указав конкретное значение х, вычислить соответствующее значение у. Пусть, например, у = 2х + 3. Тогда:
если х = 0, то у = 3;
если х = 1, то у = 5;
если х = -1, то у = 1;
если х = 3, то у = 9 и т. д.
Обычно эти результаты оформляют в виде таблицы:
Значения у из второй строки таблицы называют значениями линейной функции у = 2х + 3 соответственно в точках х = 0, х = 1, х = -1, х = 3.
В уравнении (1) переменные хну равноправны, а в уравнении (2) — нет: конкретные значения мы придаём одной из них — переменной х, тогда как значение переменной у зависит от выбранного значения переменной х. Поэтому обычно говорят, что х — независимая переменная (или аргумент), у — зависимая переменная.
Частным случаем теоремы 1 из § 8 является следующая теорема.
ТЕОРЕМА 2. Графиком линейной функции у = kx + m является прямая.
ПРИМЕР 1. Построить график линейной функции у = 2х + 3.
Решение: Составим таблицу:
х I 0 I 1
У I 3 I 5
Построим на координатной плоскости хОу точки (0; 3) и (1; 5) и проведём через них прямую. Это и есть график линейной функции у = 2х + 3 (рис. 34).
Замечание. В русском языке часто один и тот же объект называют по-разному, например: «дом», «здание», «сооружение», «коттедж», «особняк», «барак», «хибара», «избушка». В математическом языке ситуация примерно та же. Скажем, равенство с двумя переменными у = kx + m, где k, m — конкретные числа, можно назвать линейной функцией, можно назвать линейным уравнением с двумя переменными х и у (или с двумя неизвестными x и у), можно назвать формулой, можно назвать соотношением, связывающим х и у, можно, наконец, назвать зависимостью между хну. Это неважно, главное — понимать, что во всех случаях речь идёт о математической модели у = kx + m.
2. Линейные функции как математические модели реальных ситуаций
Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции. Приведём примеры.
Первая ситуация. На складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Если пройдёт х дней, то количество у угля на складе (в тоннах) выразится формулой у = 500 + ЗОх. Таким образом, линейная функция у = ЗОх + 500 есть математическая модель ситуации.
Теперь нетрудно установить, что:
- при х = 2 имеем у = 560 (в уравнение у = ЗОх + 500 подставили х = 2 и получили у = 560);
- при х = 4 имеем у = 620;
- при х = 10 имеем у = 800.
Вторая ситуация. На складе было 500 т угля. Ежедневно стали увозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Здесь математической моделью ситуации является линейная функция у = 500 — ЗОх. С помощью этой модели нетрудно ответить на вопрос задачи:
- если х = 2, то у = 440 (в уравнение у = 500 — ЗОх подставили х = 2 и получили у = 440);
- если х = 4, то у = 380;
- если х = 10, то у = 200.
Третья ситуация. Турист проехал на автобусе 15 км от пункта А до пункта В, а затем продолжил движение в том же направлении, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от пункта А будет турист через 2 ч, через 4 ч, через 5 ч ходьбы?
Математической моделью ситуации является линейная функция у = 15 + 4х, где х — время ходьбы (в часах), у — расстояние от А (в километрах). С помощью этой модели отвечаем на вопрос задачи:
- если х = 2, то у = 23 (в уравнение у = 15 + 4х подставили х = 2 и получили у = 23);
- если х = 4, то у = 31;
- если х = 6, то у = 39.
Итак, в каждой из рассмотренных ситуаций математической моделью служит линейная функция. Но (внимание!), строго говоря, все три составленные модели не совсем точны, они не учитывают тех ограничений на переменную, которые вытекают из смысла задачи. Ведь ясно, что в первой ситуации независимая переменная х может принимать только значения 1, 2, 3, …, поскольку х — число дней. Следовательно, уточнённая математическая модель первой ситуации выглядит так:
у = 500 + ЗОх, где х — натуральное число.
Вторую ситуацию необходимо уточнить условием у > 0. Это значит, что независимая переменная х, обозначающая, как и в первой ситуации, число дней, может принимать только значения 1, 2, 3, …, 16. Действительно, если х = 16, то по формуле у = 500 — ЗОх находим у = 500 — 30 • 16 = 20. Значит, уже на 17-й день вывезти со склада 30 т угля не удастся, поскольку на складе к этому дню останется всего 20 т и процесс вывоза угля придётся прекратить. Следовательно, уточнённая математическая модель второй ситуации выглядит так:
у = 500 — ЗОх, у > 0 или у = 500 — ЗОх, где х = 1, 2, 3, …, 16.
В третьей ситуации независимая переменная х теоретически может принять любое неотрицательное значение (х = 0, х = 2, х = 3,5 и т. д.), но практически турист не может шагать с постоянной скоростью без сна и отдыха сколько угодно времени. Значит, нам нужно было принять разумные ограничения для х, скажем, 0 < х < 6 (т.е. турист идёт не более 6 ч).
Напомним, что геометрической моделью нестрогого двойного неравенства 0 < х < 6 служит отрезок [0; 6] координатной прямой (рис. 35). Значит, уточнённая модель третьей ситуации выглядит так: у = 15 + 4х, где х принадлежит отрезку [0; 6].
Условимся вместо фразы «х принадлежит множеству X» писать х е X (читают: «элемент х принадлежит множеству X», е — знак принадлежности). Как видите, наше знакомство с математическим языком постоянно продолжается. Множество натуральных чисел обычно обозначают буквой N. Значит, вместо фразы «х — натуральное число» мы можем использовать соотношение х е N.
Если линейную функцию у = kx + m надо рассматривать не при всех значениях х, а лишь для значений х из некоторого числового множества X, то пишут у = kx + m, х ∈ Х.
А теперь запишем более точные математические модели для рассмотренных выше трёх ситуаций.
- Первая ситуация: у = 500 + ЗОх, х е N.
- Вторая ситуация: у = 500 — ЗОх, х е {1, 2, 3, …, 16}.
- Третья ситуация: у = 15 + 4х, х е [0; 6].
3. Построение графика линейной функции на заданном промежутке
Построить график линейной функции:
Решение: а) Составим таблицу для линейной функции у = -2х + 1:
х | -3 | 2
y I 7 I -3
Построим на координатной плоскости хОу точки (-3; 7) и (2; -3) и проведём через них прямую линию. Это график уравнения у = -2х + 1. Далее выделим отрезок, соединяющий построенные точки (рис. 36). Этот отрезок и есть график линейной функции у = -2х + 1, где х е [-3; 2].
Обычно говорят, что мы построили график линейной функции у = -2х + 1 на отрезке [-3; 2].
б) Чем отличается этот пример от предыдущего? Линейная функция та же (у = -2х + 1), значит, и графиком её служит та же прямая. Но — будьте внимательны! — на этот раз х е (-3; 2), т. е. значения х = -3 и х = 2 не рассматриваются, они не принадлежат интервалу (-3; 2). Как мы отмечали концы интервала на координатной прямой? Светлыми кружочками (рис. 39), об этом мы говорили в § 5. Точно так же и точки (-3; 7) и (2; -3) придётся отметить на чертеже светлыми кружочками. Это будет напоминать нам о том, что берутся лишь те точки прямой у = -2х + 1, которые лежат между точками, отмеченными кружочками (рис. 37). Впрочем, иногда в таких случаях используют не светлые кружочки, а стрелки (рис. 38). Это непринципиально: главное — понимать, о чём идёт речь.
ПРИМЕР 3. На координатной прямой отмечены точки А(-4), В(-3). Найти наибольшее и наименьшее значения линейной функции у = х/2 + 4 на отрезке [0; 6].
Решение: Составим таблицу для линейной функции. Построим на координатной плоскости хОу точки (0; 4) и (6; 7) и проведём через них прямую — график линейной функции
Нам нужно рассмотреть эту линейную функцию не целиком, а на отрезке [0; 6], т. е. для х е [0; 6]. Соответствующий отрезок графика выделен на чертеже. Обратим внимание, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 — это и есть наибольшее значение линейной функции у = х/2 + 4 на отрезке [0; 6]. Обычно используют такую запись:
Замечаем, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке 40 части прямой, равна 4 — это и есть наименьшее значение линейной функции у — iх + 4 на отрезке [0; 6]. Обычно используют такую запись:
Ответ: унаиб = 7, унаим = 4.
ПРИМЕР 4. Найти унаиб и унаим для линейной функции у = -1,5х + 3,5:
- а) на отрезке [1; 5];
- б) на интервале (1; 5);
- в) на полуинтервале [1; 5);
- г) на луче [0; +оо);
- д) на луче (~°°; 3].
Решение
Составим таблицу для линейной функции. Построим на координатной плоскости хОу точки (1; 2) и (5; -4) и проведём через них прямую (рис. 41—45). Выделим на построенной прямой часть, соответствующую значениям х из отрезка [1; 5] (рис. 41), из интервала (1; 5) (рис. 42), из полуинтервала [1; 5) (рис. 43), из луча [0; +°°) (рис. 44), из луча (~°°; 3] (рис. 45).
а) С помощью рисунка 41 нетрудно сделать вывод, что унаиб = 2 (этого значения линейная функция достигает при х = 1), а унаим = -4 (этого значения линейная функция достигает при х = 5).
б) В отличие от предыдущего случая, оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, из рассмотрения исключены (рис. 42). Среди остальных точек графика нет ни точки с наименьшей ординатой, ни точки с наибольшей ординатой. Значит, ни наибольшего, ни наименьшего значений на заданном интервале у данной линейной функции нет.
в) С помощью рисунка 43 заключаем, что унаиб 2 (как и в первом случае), а наименьшего значения у линейной функции нет (как и во втором случае).
г) унаиб = 3,5 (этого значения линейная функция достигает при х = 0), а унаим не существует (рис. 44).
д) унаим = -1 (этого значения линейная функция достигает при х — 3), а унаиб не существует (рис. 45).
4. Свойства линейной функции
ПРИМЕР 5. Построить график линейной функции у = 2х — 6. С помощью графика ответить на следующие вопросы:
а) при каком значении х будет у = 0;
б) при каких значениях х будет у > 0;
в) при каких значениях х будет у < 0?
Решение: Составим таблицу для линейной функции у = 2х — 6:
Через точки (0; -6) и (3; 0) проведём прямую — график линейной функции у = 2х — 6 (рис. 46).
- а) у = 0 при х = 3. График пересекает ось х в точке х = 3, это и есть точка с ординатой у — 0.
- б) у > 0 при х > 3. В самом деле, если х > 3, то соответствующая часть прямой расположена выше оси х, значит, ординаты соответствующих точек прямой положительны.
- в) у < 0 при х < 3. В самом деле, если х < 3, то соответствующая часть прямой расположена ниже оси х, значит, ординаты соответствующих точек прямой отрицательны.
Обратите внимание, что в этом примере мы с помощью графика решили:
- а) уравнение 2х — 6 = 0 (получили х = 3);
- б) неравенство 2х — 6 > 0 (получили х > 3);
- в) неравенство 2х — 6 < 0 (получили х < 3).
Рассмотрим график линейной функции, изображённый на рисунке 47, а. Если двигаться по этому графику слева направо, то ординаты точек графика всё время увеличиваются, мы как бы «поднимаемся в горку». В таких случаях математики употребляют термин возрастание и говорят так: если к > 0, то линейная функция у = kx + m возрастает.
Рассмотрим график линейной функции, изображённый на рисунке 47, б. Если двигаться по этому графику слева направо, то ординаты точек графика всё время уменьшаются, мы как бы «спускаемся с горки». В таких случаях математики употребляют термин убывание и говорят так: если k < 0, то линейная функция у = kx + m убывает.
ПРИМЕР 6. На рисунке 48 изображён график движения автомобиля между пунктами 1 и 2. По оси t отмечено время (в часах), по оси S — расстояние до пункта 1. Требуется охарактеризовать весь процесс движения словами.
Решение: Точка А соответствует началу движения. До пункта 2 автомобиль доехал за 1 1/3 ч — об этом можно судить по абсциссе точки D. Пройденное расстояние равно 50 км — об этом можно судить по ординате точки D. Значит, можно вычислить скорость движения автомобиля: v = 50 : 4/3 = 37,5 км/ч.
На участке графика DE ордината постоянна, т. е. расстояние от пункта 1 не менялось. Это значит, что автомобиль не двигался (стоял в пункте 2). Причём он стоял в промежутке от 1^ ч до 2-| ч (это абсциссы точек D и Е). Остановка длилась, таким образом, 1 ч 20 мин.
На обратный путь после остановки автомобиль потратил столько же времени, сколько на путь от 1 до 2, значит обратно он ехал с той же скоростью.
Вопросы для самопроверки
- Что такое линейная функция?
- Что является графиком линейной функции?
- Сколько точек достаточно взять для построения графика линейной функции?
- Опишите процесс построения графика линейной функции у = 2х + 3, где х е [0; 2]. Что изменится, если х е (0; 2)?
- Дана линейная функция у = kx + m, х е X, где X — некоторый числовой промежуток. Что такое унаим, унаиб?
- Дано: у = 2х + 3, х е [0; +оо). Найдите, если возможно, унаим, унаиб. Что изменится, если х е (0; +оо)? если х е (—оо; 0]? если X € (-оо; 0)?
- Как с помощью графика линейной функции у = kx + m, где k Ф 0, решить: а) уравнение kx + m = 0; б) неравенство kx + m > 0; в) неравенство kx + m < 0?
- В каком случае линейная функция возрастает, а в каком — убывает? Как об этом можно судить по графику линейной функции?
Линейная функция — функция вида y=kx+b (для функций одной переменной).

Определение и геометрический смысл
Рассмотрим уравнение с двумя неизвестными х и у:

где  и b — заданные числа. Этому уравнению удовлетворяет бесконечное множество пар чисел х и у.
и b — заданные числа. Этому уравнению удовлетворяет бесконечное множество пар чисел х и у.
Например, уравнению

удовлетворяют следующие пары:

и т. д.
Для того чтобы найти пару чисел, удовлетворяющих уравнению ( * ), нужно придать х произвольное числовое значение и подставить в уравнение ( * ), тогда у получит определенное числовое значение. Например, если х = 27, то у = 2 x 27 — 6 = 48. Очевидно, что пара чисел х =27 и у =48 удовлетворяет уравнению (*). Так же и в случае уравнения (1) можно придать х произвольное числовое значение и получить для у соответствующее числовое значение.
Так как в данном уравнении х может принимать любое числовое значение, то его называют переменной величиной. Поскольку выбор этого числового значения ничем не ограничен, то х называют независимой переменной величиной или аргументом.
Для у получаются также различные значения, но уже в зависимости от выбранного значения х; поэтому у называют зависимым переменным или функцией.
Функцию у, определяемую уравнением (1), называют линейной функцией.
Пример:
Вычислить значения линейной функции, определяемой уравнением у = 0,5х + 3,7, при следующих значениях независимого переменного: х1 = 0, х2 = —0,5, х3 = —7,6.
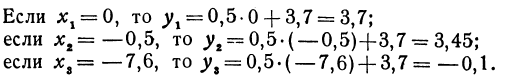
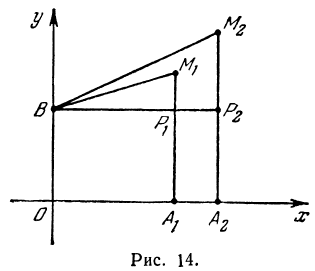
Покажем, что если принять пару чисел х и у, удовлетворяющих уравнению (1), за абсциссу и ординату точки, то геометрическим местом этих точек будет прямая линия (рис. 14).
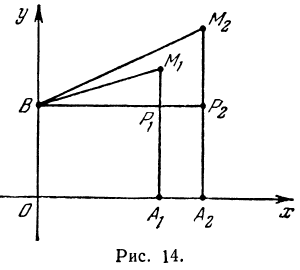
В самом деле, рассмотрим точку В(0, b) и точки М1(х1, у1) и М2(х2, у2), координаты которых удовлетворяют уравнению (1), т. е.
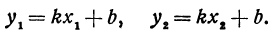
Обозначим проекции точек М1 и М2 на ось Ох через А1 и A2, тогда ОА1 = х1, ОА2 = х2, А1М1= у1, А2М2 = у2. Проведем из точки В прямую, параллельную оси Ох. При этом получим b = ОВ = А1Р1 = А2Р2.
Предположим, что точки BМ1 и М2 не лежат народной прямой. Соединяя точку В с точками М1 и М2, получим два прямоугольных треугольника ВР1М1 и ВР2М2, из которых имеем:
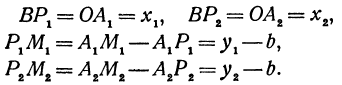
Но так как х1, у1 и х2, у2 удовлетворяют уравнению (1), то
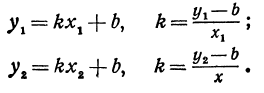
Иначе говоря,
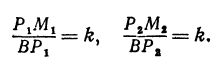
Выражения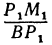 и
и 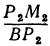 являются отношениями противоположных катетов к прилежащим для уг лов
являются отношениями противоположных катетов к прилежащим для уг лов  Р1ВМ1 и
Р1ВМ1 и  Р2ВМ2. Следовательно, tg
Р2ВМ2. Следовательно, tg  Р1ВМ1 =
Р1ВМ1 =  и tg
и tg Р2ВМ2 =
Р2ВМ2 =  , а поэтому и
, а поэтому и  Р1ВМ1 =
Р1ВМ1 =  P2BM2 так как углы острые. Это значит, что точки М2 и В лежат на одной прямой. Но мы предположили, что эти точки не лежат на одной прямой. Таким образом, мы пришли к противоречию, а это и доказывает, что точки M1, М2 и В лежат на одной прямой. Обозначим угол Р1ВМ1 через а. Этот угол образован прямой ВМ1 с положительным направлением оси Ох.
P2BM2 так как углы острые. Это значит, что точки М2 и В лежат на одной прямой. Но мы предположили, что эти точки не лежат на одной прямой. Таким образом, мы пришли к противоречию, а это и доказывает, что точки M1, М2 и В лежат на одной прямой. Обозначим угол Р1ВМ1 через а. Этот угол образован прямой ВМ1 с положительным направлением оси Ох.
Так как М1 и М2 — произвольные точки, координаты которых удовлетворяют уравнению (1), то можно сделать следующее заключение: любая точка, координаты которой удовлетворяют уравнению (1), лежит на прямой, отсекающей на оси Оу отрезок ОВ = b и образующей с положительным направлением оси Ох угол а такой, что tg a =  .
.
Число b называется начальной ординатой, число  — угловым коэффициентом прямой.
— угловым коэффициентом прямой.
Предыдущие рассуждения позволяют сделать вывод: линейная функция y =  x + b определяет на плоскости прямую, у которой начальная ордината равна Ъ, а угловой коэффициент
x + b определяет на плоскости прямую, у которой начальная ордината равна Ъ, а угловой коэффициент  .
.
Например, линейная функция 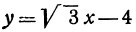 определяет на координатной плоскости прямую, отсекающую на оси Оу отрезок —4 и наклоненную к оси Ох под углом в 60°, так как tg60° =
определяет на координатной плоскости прямую, отсекающую на оси Оу отрезок —4 и наклоненную к оси Ох под углом в 60°, так как tg60° = 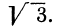 .
.
Если имеем определенную прямую, отсекающую на оси Оу отрезок b и наклоненную к оси Ох под углом 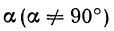 , тангенс которого равен то, взяв произвольную абсциссу, найдем на указанной прямой только одну точку, имеющую эту абсциссу, т. е. по заданному х найдется только одна точка, а следовательно, и одно значение у.
, тангенс которого равен то, взяв произвольную абсциссу, найдем на указанной прямой только одну точку, имеющую эту абсциссу, т. е. по заданному х найдется только одна точка, а следовательно, и одно значение у.
Очевидно, имеет место и такое предложение:
Всякой прямой, отсекающей на оси Оу отрезок b и наклоненной к оси Ох под углом, тангенс которого равен числу  соответствует линейная функция y =
соответствует линейная функция y =  x + b.
x + b.
Координаты любой тонки, лежащей на указанной прямой, удовлетворяют уравнению (1), поэтому уравнение у =  х + b называют уравнением прямой. Таким образом, всякая линейная функция является уравнением некоторой прямой.
х + b называют уравнением прямой. Таким образом, всякая линейная функция является уравнением некоторой прямой.
Отметим частные случаи.
1.Пусть b = 0, т. е. линейная функция определяется уравнением

Прямая, определяемая этим уравнением, проходит через начало координат. Здесь у пропорционален х, т. е. если х увеличить (уменьшить) в несколько раз, то и у увеличится (уменьшится) во столько же раз.
2.Пусть  = 0, т. е. tgа = 0, откуда а = 0. Линейная функция определяется уравнением
= 0, т. е. tgа = 0, откуда а = 0. Линейная функция определяется уравнением

Этому уравнению соответствует прямая, параллельная оси Ох и отстоящая от нее на расстояние b.
На основании всего сказанного в этом параграфе легко решаются следующие задачи.
Задача:
Даны точки А (3, 5) и В(— 1, 4). Нужно узнать, лежат ли эти точки на прямой, уравнение которой имеет вид

Решение:
Если точка лежит на прямой, то ее координаты должны удовлетворять уравнению прямой. Поэтому для решения задачи подставим координаты точки А в уравнение (*), получим 5 = 2 x 3 — 1. Это тождество, следовательно, точка А лежит на прямой. Подставляя координаты точки В, получаем 4 = 2(— 1)—1 = —3. Отсюда видно, что точка В не лежит на прямой.
Задача:
Построить прямую, уравнение которой

Решение:
Чтобы построить прямую, надо знать, например, две ее точки. Поэтому дадим х произвольное значение, например х = 2, и найдем из уравнения (**) значение
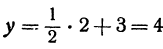
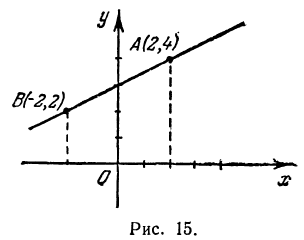
Значит, точка A (2, 4) лежит на прямой.
Это первая точка. Теперь дадим х какое-нибудь другое значение, например х = —2, и вычислим у из уравнения (**).
Получим
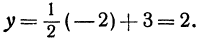
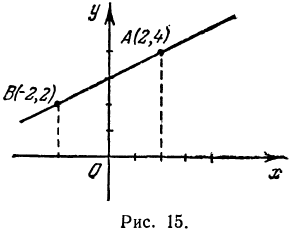
Точка B ( — 2, 2) лежит на прямой. Это вторая точка. Строим точки A и B (рис. 15) и проводим через них прямую, это и есть искомая прямая.
Основное свойство линейной функции
Рассмотрим линейную функцию у =  х + b. Найдем значение этой функции при
х + b. Найдем значение этой функции при
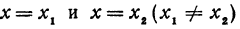
Здесь первое и второе значения х различны, они отличаются друг от друга на величину х2 — х1. Величину разности х2 — х1, на которую изменяется x при переходе от x1 к х2, назовем приращением независимого переменного х. Эту величину часто будем обозначать через h, так что h = x2 — x1. Найдем, насколько изменилось значение у при изменении х1 на h . Для этого вычтем из у2 значение у1
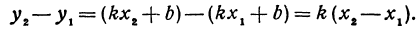
Таким образом,
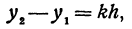
т. е. приращение линейной функции пропорционально приращению независимого переменного.
Это и есть основное свойство линейной функции. Заметим, что х2 может быть больше, а может быть и меньше, чем х1. Поэтому h = x2 — x1 может быть как положительным, так и отрицательным числом, иначе говоря, приращение h независимого переменного может быть любого знака. То же самое относится и к приращению функции, т. е. к величине у2—у1.
Пример:
Найдем приращение функции y = 0,6x—3, если приращение независимого переменного h = 0,1.
По основному свойству у2—у1 = 0,6 x 0,1 = 0,06.
Приращение этой же функции y = 0,6x—3 , если h = —3, будет равно у2—у1 = 0,6 x (— 3) = —1,8. В этом случае приращения независимого переменного и функции отрицательны, т. е. в этом случае и независимое переменное и функция не увеличиваются, а уменьшаются.
Пример:
Найдем приращение функции у = —2x+10 при изменении х на h = —0,5. Будем иметь
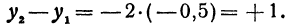
Задачи на прямую
Задача:
Найти угол y между двумя прямыми, заданными уравнениями
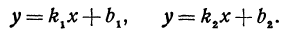
Решение:
При пересечении прямых образуются четыре попарно равных угла. Найдя один из них, легко найти и другие. На рис. 16 прямые обозначены соответственно (1) и (2).
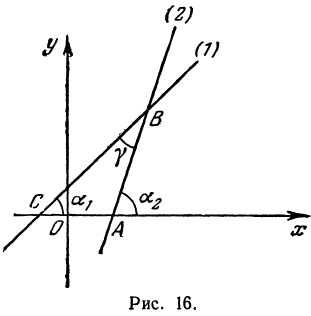
Угол хАВ является внешним по отношению к треугольнику ABC, поэтому он равен сумме двух внутренних углов треугольника, с ним не смежных, т. е.
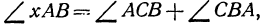
откуда
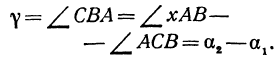
Но углы а1 и а2 непосредственно неизвестны, а известны их тангенсы
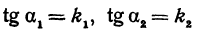
Поэтому напишем
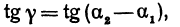
или
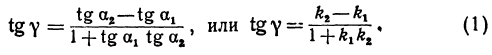
Пример:
Найти угол между прямыми, заданными уравнениями
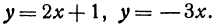
Здесь
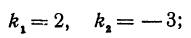
применяя формулу (1), получим;
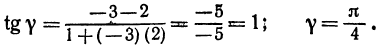
Если же будем считать, что
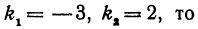
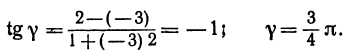
Получены два ответа: сначала найден острый угол между заданными прямыми, а затем — тупой.
Если заданы две параллельные прямые, то углы а1 и а2 равны, как соответственные, следовательно, тангенсы их тоже равны
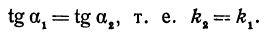
Таким образом, мы приходим к выводу: если прямые параллельны, то их угловые коэффициенты равны.
Если прямые перпендикулярны, то угол между ними равен 90°, т. е. 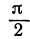 . Но тангенс прямого угла не существует, поэтому формула (1) не должна давать ответа, а это может быть только в том случае, когда знаменатель равен нулю (на нуль делить нельзя):
. Но тангенс прямого угла не существует, поэтому формула (1) не должна давать ответа, а это может быть только в том случае, когда знаменатель равен нулю (на нуль делить нельзя):
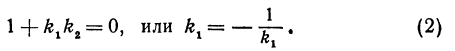
Это и есть условие перпендикулярности двух прямых. Это условие удобно запомнить в следующей формулировке: если две прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.
Пример:
Найдем угол между прямыми, заданными уравнениями
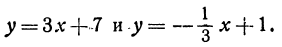
Здесь угловые коэффициенты (первый равен 3, а второй 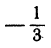 обратны по величине и противоположны по знаку, следовательно, рассматриваемые прямые перпендикулярны.
обратны по величине и противоположны по знаку, следовательно, рассматриваемые прямые перпендикулярны.
Задача:
Даны две точки: M1(x1, у1) и М2(х2, у2), где 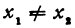 (т. е. эти точки не лежат на одной прямой, параллельной оси Оу). Написать уравнение прямой, проходящей через точки M1 и М2.
(т. е. эти точки не лежат на одной прямой, параллельной оси Оу). Написать уравнение прямой, проходящей через точки M1 и М2.
Решение:
Искомая прямая не параллельна оси Оу, поэтому ее уравнение можно написать в виде 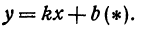 Значит, для решения задачи надо определить числа
Значит, для решения задачи надо определить числа  и b.
и b.
Так как прямая проходит через точки М1 и М2, то координаты этих точек должны удовлетворять уравнению ( * ), т. е.

В уравнениях ( ** ) и (*** ) все числа, кроме  и b, известны, поэтому эти уравнения можно рассматривать как систему уравнений относительно
и b, известны, поэтому эти уравнения можно рассматривать как систему уравнений относительно  и b. Решая систему, находим:
и b. Решая систему, находим:
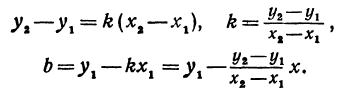
Подставляя найденные выражения в уравнение (*), получим
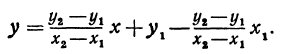
Это и есть уравнение прямой, проходящей через две точки, не расположенные на прямой, параллельной оси Оу.
Полученному уравнению можно придать форму, удобную для запоминания, а именно:
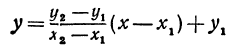
или

Задача:
Написать уравнение прямой, проходящей через данную точку М(х1,у1) и образующей с осью Ох угол а.
Решение:
Прежде всего найдем угловой коэффициент искомой прямой: он равен тангенсу угла а. Обозначим 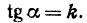 Значит, уравнение прямой можно написать в виде
Значит, уравнение прямой можно написать в виде 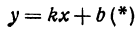 где пока число b неизвестно. Так как прямая должна проходить через точку M, то координаты точки М удовлетворяют этому уравнению, т. е.
где пока число b неизвестно. Так как прямая должна проходить через точку M, то координаты точки М удовлетворяют этому уравнению, т. е.
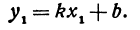
Находим отсюда неизвестное b, получим 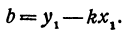 . Подставляя найденное в уравнение (*), будем иметь
. Подставляя найденное в уравнение (*), будем иметь
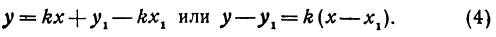
Это и есть уравнение прямой, проходящей через точку М в заданном направлении.
Если в уравнении (4) менять направление, не меняя точку M, то получим уравнение всех прямых, проходящих через заданную точку. Уравнение 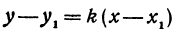 , в котором
, в котором  переменное, а х1 и у1 не меняются, называется уравнением пучка прямых, проходящих через точку М(х1, у1).
переменное, а х1 и у1 не меняются, называется уравнением пучка прямых, проходящих через точку М(х1, у1).
Пример:
Напишем уравнение прямой, проходящей через точку М( — 2, 3) и образующей с осью Ох угол 45°.
Так как tg 45° = 1, то угловой коэффициент равен 1; х1 = —2; у1 = 3. Уравнение прямой запишется в виде
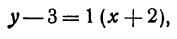
или
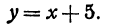
Общее уравнение прямой. Неявная линейная функция
Рассмотрим уравнение первой степени с двумя неизвестными

Решим его относительно у:

т. е. мы получили линейную функцию, где 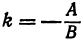 ,
,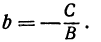 Уравнения (1) и (2) равносильны, поэтому пара чисел х и у, удовлетворяющих уравнению (2), будет удовлетворять и уравнению (1). Так как уравнению (2) соответствует некоторая прямая, то эта же прямая будет соответствовать и уравнению (1).
Уравнения (1) и (2) равносильны, поэтому пара чисел х и у, удовлетворяющих уравнению (2), будет удовлетворять и уравнению (1). Так как уравнению (2) соответствует некоторая прямая, то эта же прямая будет соответствовать и уравнению (1).
Координаты любой точки, лежащей на этой прямой, удовлетворяют уравнению (1), поэтому будем называть его также уравнением прямой.
Рассмотрим особо случай, когда B = 0, так как на нуль делить нельзя.
Уравнение (1) примет вид
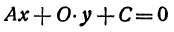
или
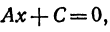
откуда
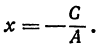
Поэтому, каков бы ни был у, х всегда равен 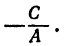 Это имеет место для прямой, параллельной оси Оу; в самом деле, на ней можно найти точку с любой ординатой, но все точки этой прямой имеют одну и ту же абсциссу.
Это имеет место для прямой, параллельной оси Оу; в самом деле, на ней можно найти точку с любой ординатой, но все точки этой прямой имеют одну и ту же абсциссу.
Таким образом, любому уравнению первой степени соответствует некоторая прямая. Придавая в уравнении (1) коэффициентам А, В и С различные значения, можно получить любое уравнение первой степени. Поэтому уравнение (1) называют общим уравнением прямой.
Из уравнения (1) (если 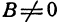 ) можно определить у, т. е. получить линейную функцию; поэтому говорят, что уравнение (1) определяет неявно линейную функцию или что уравнение (1) есть неявная линейная функция.
) можно определить у, т. е. получить линейную функцию; поэтому говорят, что уравнение (1) определяет неявно линейную функцию или что уравнение (1) есть неявная линейная функция.
Система двух уравнений первой степени
Напомним, что две прямые, расположенные на плоскости, могут или пересекаться, или быть параллельными (т. е. не пересекаться), или сливаться (в этом случае можно сказать, что они пересекаются в каждой своей точке).
Рассмотрим систему двух уравнений
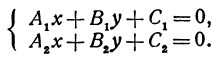
Каждое из этих уравнений является уравнением прямой. Решить систему — это значит найти значения х и у, которые удовлетворяют и первому и второму уравнениям. Но так как х и у определяют точку, то следовательно, решить систему—это значит найти точку, лежащую и на первой и на второй прямых, т. е. найти точку пересечения прямых.
Пример:
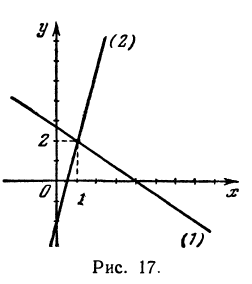
Найдем точку пересечения двух прямых:
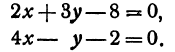
Решая эту систему, получим: х = 1, у = 2, т. е. прямые пересекаются в точке (1,2) (рис. 17).
Пример:
Найдем точку пересечения двух прямых:
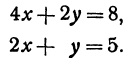
Решая эту систему, получим:
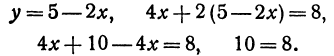
Последнее равенство нелепо, значит, прямые не пересекаются, Рис. 17. т. е. они параллельны.
Пример:
Найдем точку пересечения данных прямых
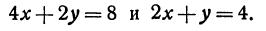
Решая эту систему, получим:
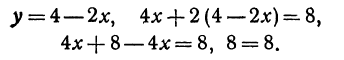
Полученное равенство всегда справедливо, т. е. справедливо при любом значении x. Это значит, что две прямые пересекаются в каждой своей точке, что может быть только тогда, когда они сливаются.
Заметим, что два уравнения, рассматриваемые в этом примере, являются равносильными, поэтому они и представляют одну и ту же прямую.
Примеры решения линейной функции
Линейная функция встречается в формулировках многих физических законов и технических задач. Приведем примеры.
Пример:
Если точка движется равномерно по прямой, то ее расстояние от выбранной точки (от начала координат) выражается при помощи уравнения 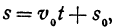
где — начальное расстояние, v0 — скорость, t — время; это, как мы уже знаем, есть линейная функция.
Пример:
Закон Ома записывается в виде 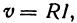
где v — напряжение, R — сопротивление и I — ток. Если не изменяется, то v является линейной функцией тока I .
Пример:
Если стоимость провоза единицы товара по железной дороге равна а руб. за километр, то стоимость v провоза N единиц товара на l км равна 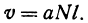
Если же стоимость товара на месте равна М руб., то после перевозки за него надо заплатить
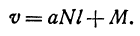
Здесь v—линейная функция l.
Линейная функция встречается в различных областях, но, где бы она ни встречалась, ее всегда можно рассматривать как уравнение прямой. Этим обстоятельством часто пользуются при решении задач.
Задача:
Два города А и В, расстояние между которыми равно 300 км, находятся на одной железнодорожной магистрали. На этой же магистрали между городами А и В надо выбрать пункт С, в котором предполагается устроить склад нефти для снабжения указанных городов. Надо выбрать пункт С так, чтобы общая стоимость перевозок нефти для снабжения города А и города В была наименьшей. Известно, что город А потребляет 400 т нефти, а город В—200 т. Перевозка одной тонны нефти на один километр обходится в а руб.
Решение:
Обозначим расстояние от А до предполагаемого пункта С через х. Тогда расстояние от города В до С равно 300 — х. Стоимость перевозки одной тонны нефти из С в A равна ах руб., а перевозки 400 т—400аx руб. Аналогично перевозка нефти из С в В будет стоить 200а (300 — х) руб. Стоимость всех перевозок, которую обозначим через у, будет выражаться так:
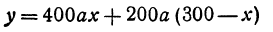
или
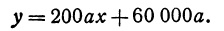
Это линейная функция. Если примем х за абсциссу, а у за ординату точки, то полученная линейная функция определяет уравнение некоторой прямой. Угловой коэффициент ее равен 200а, т. е. положителен, следовательно, эта прямая образует с осью Ох острый угол и поэтому с увеличением независимого переменного поднимается вверх. По смыслу задачи величина х заключена между 0 и 300, т. е.  При х = 0 величина у принимает значение 60 000а, а при x = 300— значение 120 000а. Ясно, что 60 000а есть наименьшее из возможных значений, 120 000а— наибольшее.
При х = 0 величина у принимает значение 60 000а, а при x = 300— значение 120 000а. Ясно, что 60 000а есть наименьшее из возможных значений, 120 000а— наибольшее.
Так как пункт С надо выбрать так, чтобы стоимость была наименьшей, то его следует расположить в городе A, если же этого сделать нельзя по каким-либо соображениям, то, чем ближе расположить его к A, тем выгодней.
Примеры применения линейной функции





Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Выпуклые множества точек
- Система координат

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>
0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x – 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x – 2.
Линейная функция в математике с примерами решения и образцами выполнения
Линейная функция — функция вида y=kx+b (для функций одной переменной).

Определение и геометрический смысл
Рассмотрим уравнение с двумя неизвестными х и у:

где  и b — заданные числа. Этому уравнению удовлетворяет бесконечное множество пар чисел х и у.
и b — заданные числа. Этому уравнению удовлетворяет бесконечное множество пар чисел х и у.

удовлетворяют следующие пары:

Для того чтобы найти пару чисел, удовлетворяющих уравнению ( * ), нужно придать х произвольное числовое значение и подставить в уравнение ( * ), тогда у получит определенное числовое значение. Например, если х = 27, то у = 2 x 27 — 6 = 48. Очевидно, что пара чисел х =27 и у =48 удовлетворяет уравнению (*). Так же и в случае уравнения (1) можно придать х произвольное числовое значение и получить для у соответствующее числовое значение.
Так как в данном уравнении х может принимать любое числовое значение, то его называют переменной величиной. Поскольку выбор этого числового значения ничем не ограничен, то х называют независимой переменной величиной или аргументом.
Для у получаются также различные значения, но уже в зависимости от выбранного значения х; поэтому у называют зависимым переменным или функцией.
Функцию у, определяемую уравнением (1), называют линейной функцией.
Пример:
Вычислить значения линейной функции, определяемой уравнением у = 0,5х + 3,7, при следующих значениях независимого переменного: х1 = 0, х2 = —0,5, х3 = —7,6.
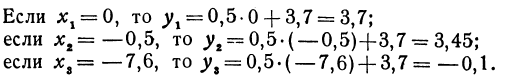
Покажем, что если принять пару чисел х и у, удовлетворяющих уравнению (1), за абсциссу и ординату точки, то геометрическим местом этих точек будет прямая линия (рис. 14).

В самом деле, рассмотрим точку В(0, b) и точки М1(х1, у1) и М2(х2, у2), координаты которых удовлетворяют уравнению (1), т. е.
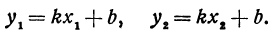
Обозначим проекции точек М1 и М2 на ось Ох через А1 и A2, тогда ОА1 = х1, ОА2 = х2, А1М1= у1, А2М2 = у2. Проведем из точки В прямую, параллельную оси Ох. При этом получим b = ОВ = А1Р1 = А2Р2.
Предположим, что точки BМ1 и М2 не лежат народной прямой. Соединяя точку В с точками М1 и М2, получим два прямоугольных треугольника ВР1М1 и ВР2М2, из которых имеем:
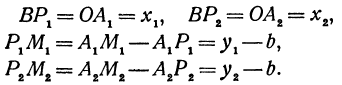
Но так как х1, у1 и х2, у2 удовлетворяют уравнению (1), то
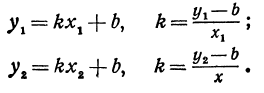
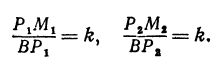
Выражения 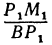 и
и 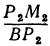 являются отношениями противоположных катетов к прилежащим для уг лов
являются отношениями противоположных катетов к прилежащим для уг лов  Р1ВМ1 и
Р1ВМ1 и  Р2ВМ2. Следовательно, tg
Р2ВМ2. Следовательно, tg  Р1ВМ1 =
Р1ВМ1 =  и tg
и tg  Р2ВМ2 =
Р2ВМ2 =  , а поэтому и
, а поэтому и  Р1ВМ1 =
Р1ВМ1 =  P2BM2 так как углы острые. Это значит, что точки М2 и В лежат на одной прямой. Но мы предположили, что эти точки не лежат на одной прямой. Таким образом, мы пришли к противоречию, а это и доказывает, что точки M1, М2 и В лежат на одной прямой. Обозначим угол Р1ВМ1 через а. Этот угол образован прямой ВМ1 с положительным направлением оси Ох.
P2BM2 так как углы острые. Это значит, что точки М2 и В лежат на одной прямой. Но мы предположили, что эти точки не лежат на одной прямой. Таким образом, мы пришли к противоречию, а это и доказывает, что точки M1, М2 и В лежат на одной прямой. Обозначим угол Р1ВМ1 через а. Этот угол образован прямой ВМ1 с положительным направлением оси Ох.
Так как М1 и М2 — произвольные точки, координаты которых удовлетворяют уравнению (1), то можно сделать следующее заключение: любая точка, координаты которой удовлетворяют уравнению (1), лежит на прямой, отсекающей на оси Оу отрезок ОВ = b и образующей с положительным направлением оси Ох угол а такой, что tg a =  .
.
Число b называется начальной ординатой, число  — угловым коэффициентом прямой.
— угловым коэффициентом прямой.
Предыдущие рассуждения позволяют сделать вывод: линейная функция y =  x + b определяет на плоскости прямую, у которой начальная ордината равна Ъ, а угловой коэффициент
x + b определяет на плоскости прямую, у которой начальная ордината равна Ъ, а угловой коэффициент  .
.
Например, линейная функция 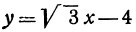 определяет на координатной плоскости прямую, отсекающую на оси Оу отрезок —4 и наклоненную к оси Ох под углом в 60°, так как tg60° =
определяет на координатной плоскости прямую, отсекающую на оси Оу отрезок —4 и наклоненную к оси Ох под углом в 60°, так как tg60° = 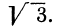 .
.
Если имеем определенную прямую, отсекающую на оси Оу отрезок b и наклоненную к оси Ох под углом 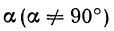 , тангенс которого равен то, взяв произвольную абсциссу, найдем на указанной прямой только одну точку, имеющую эту абсциссу, т. е. по заданному х найдется только одна точка, а следовательно, и одно значение у.
, тангенс которого равен то, взяв произвольную абсциссу, найдем на указанной прямой только одну точку, имеющую эту абсциссу, т. е. по заданному х найдется только одна точка, а следовательно, и одно значение у.
Очевидно, имеет место и такое предложение:
Всякой прямой, отсекающей на оси Оу отрезок b и наклоненной к оси Ох под углом, тангенс которого равен числу  соответствует линейная функция y =
соответствует линейная функция y =  x + b.
x + b.
Координаты любой тонки, лежащей на указанной прямой, удовлетворяют уравнению (1), поэтому уравнение у =  х + b называют уравнением прямой. Таким образом, всякая линейная функция является уравнением некоторой прямой.
х + b называют уравнением прямой. Таким образом, всякая линейная функция является уравнением некоторой прямой.
Отметим частные случаи.
1.Пусть b = 0, т. е. линейная функция определяется уравнением

Прямая, определяемая этим уравнением, проходит через начало координат. Здесь у пропорционален х, т. е. если х увеличить (уменьшить) в несколько раз, то и у увеличится (уменьшится) во столько же раз.
2.Пусть  = 0, т. е. tgа = 0, откуда а = 0. Линейная функция определяется уравнением
= 0, т. е. tgа = 0, откуда а = 0. Линейная функция определяется уравнением

Этому уравнению соответствует прямая, параллельная оси Ох и отстоящая от нее на расстояние b.
На основании всего сказанного в этом параграфе легко решаются следующие задачи.
Задача:
Даны точки А (3, 5) и В(— 1, 4). Нужно узнать, лежат ли эти точки на прямой, уравнение которой имеет вид

Решение:
Если точка лежит на прямой, то ее координаты должны удовлетворять уравнению прямой. Поэтому для решения задачи подставим координаты точки А в уравнение (*), получим 5 = 2 x 3 — 1. Это тождество, следовательно, точка А лежит на прямой. Подставляя координаты точки В, получаем 4 = 2(— 1)—1 = —3. Отсюда видно, что точка В не лежит на прямой.
Задача:
Построить прямую, уравнение которой

Решение:
Чтобы построить прямую, надо знать, например, две ее точки. Поэтому дадим х произвольное значение, например х = 2, и найдем из уравнения (**) значение
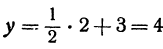
Значит, точка A (2, 4) лежит на прямой.
Это первая точка. Теперь дадим х какое-нибудь другое значение, например х = —2, и вычислим у из уравнения (**).
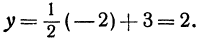
Точка B ( — 2, 2) лежит на прямой. Это вторая точка. Строим точки A и B (рис. 15) и проводим через них прямую, это и есть искомая прямая.

Основное свойство линейной функции
Рассмотрим линейную функцию у =  х + b. Найдем значение этой функции при
х + b. Найдем значение этой функции при
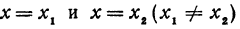
Здесь первое и второе значения х различны, они отличаются друг от друга на величину х2 — х1. Величину разности х2 — х1, на которую изменяется x при переходе от x1 к х2, назовем приращением независимого переменного х. Эту величину часто будем обозначать через h, так что h = x2 — x1. Найдем, насколько изменилось значение у при изменении х1 на h . Для этого вычтем из у2 значение у1
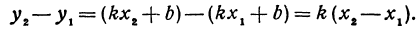
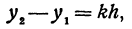
т. е. приращение линейной функции пропорционально приращению независимого переменного.
Это и есть основное свойство линейной функции. Заметим, что х2 может быть больше, а может быть и меньше, чем х1. Поэтому h = x2 — x1 может быть как положительным, так и отрицательным числом, иначе говоря, приращение h независимого переменного может быть любого знака. То же самое относится и к приращению функции, т. е. к величине у2—у1.
Пример:
Найдем приращение функции y = 0,6x—3, если приращение независимого переменного h = 0,1.
По основному свойству у2—у1 = 0,6 x 0,1 = 0,06.
Приращение этой же функции y = 0,6x—3 , если h = —3, будет равно у2—у1 = 0,6 x (— 3) = —1,8. В этом случае приращения независимого переменного и функции отрицательны, т. е. в этом случае и независимое переменное и функция не увеличиваются, а уменьшаются.
Пример:
Найдем приращение функции у = —2x+10 при изменении х на h = —0,5. Будем иметь
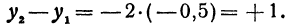
Задачи на прямую
Задача:
Найти угол y между двумя прямыми, заданными уравнениями
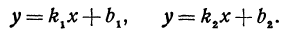
Решение:
При пересечении прямых образуются четыре попарно равных угла. Найдя один из них, легко найти и другие. На рис. 16 прямые обозначены соответственно (1) и (2).

Угол хАВ является внешним по отношению к треугольнику ABC, поэтому он равен сумме двух внутренних углов треугольника, с ним не смежных, т. е.
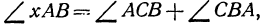
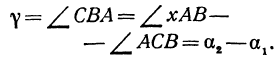
Но углы а1 и а2 непосредственно неизвестны, а известны их тангенсы
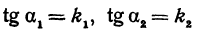
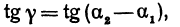
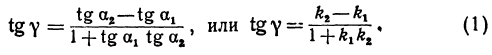
Пример:
Найти угол между прямыми, заданными уравнениями
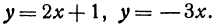
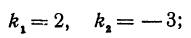
применяя формулу (1), получим;
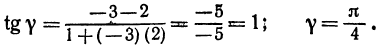
Если же будем считать, что
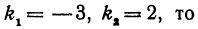
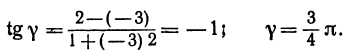
Получены два ответа: сначала найден острый угол между заданными прямыми, а затем — тупой.
Если заданы две параллельные прямые, то углы а1 и а2 равны, как соответственные, следовательно, тангенсы их тоже равны
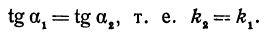
Таким образом, мы приходим к выводу: если прямые параллельны, то их угловые коэффициенты равны.
Если прямые перпендикулярны, то угол между ними равен 90°, т. е. 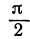 . Но тангенс прямого угла не существует, поэтому формула (1) не должна давать ответа, а это может быть только в том случае, когда знаменатель равен нулю (на нуль делить нельзя):
. Но тангенс прямого угла не существует, поэтому формула (1) не должна давать ответа, а это может быть только в том случае, когда знаменатель равен нулю (на нуль делить нельзя):
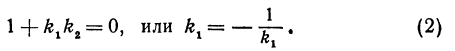
Это и есть условие перпендикулярности двух прямых. Это условие удобно запомнить в следующей формулировке: если две прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.
Пример:
Найдем угол между прямыми, заданными уравнениями
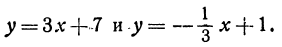
Здесь угловые коэффициенты (первый равен 3, а второй 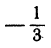 обратны по величине и противоположны по знаку, следовательно, рассматриваемые прямые перпендикулярны.
обратны по величине и противоположны по знаку, следовательно, рассматриваемые прямые перпендикулярны.
Задача:
Даны две точки: M1(x1, у1) и М2(х2, у2), где 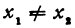 (т. е. эти точки не лежат на одной прямой, параллельной оси Оу). Написать уравнение прямой, проходящей через точки M1 и М2.
(т. е. эти точки не лежат на одной прямой, параллельной оси Оу). Написать уравнение прямой, проходящей через точки M1 и М2.
Решение:
Искомая прямая не параллельна оси Оу, поэтому ее уравнение можно написать в виде 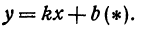 Значит, для решения задачи надо определить числа
Значит, для решения задачи надо определить числа  и b.
и b.
Так как прямая проходит через точки М1 и М2, то координаты этих точек должны удовлетворять уравнению ( * ), т. е.

В уравнениях ( ** ) и (*** ) все числа, кроме  и b, известны, поэтому эти уравнения можно рассматривать как систему уравнений относительно
и b, известны, поэтому эти уравнения можно рассматривать как систему уравнений относительно  и b. Решая систему, находим:
и b. Решая систему, находим:
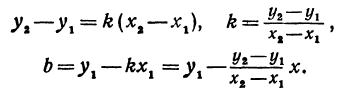
Подставляя найденные выражения в уравнение (*), получим
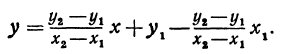
Это и есть уравнение прямой, проходящей через две точки, не расположенные на прямой, параллельной оси Оу.
Полученному уравнению можно придать форму, удобную для запоминания, а именно:
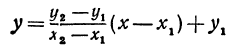

Задача:
Написать уравнение прямой, проходящей через данную точку М(х1,у1) и образующей с осью Ох угол а.
Решение:
Прежде всего найдем угловой коэффициент искомой прямой: он равен тангенсу угла а. Обозначим 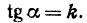 Значит, уравнение прямой можно написать в виде
Значит, уравнение прямой можно написать в виде 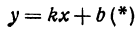 где пока число b неизвестно. Так как прямая должна проходить через точку M, то координаты точки М удовлетворяют этому уравнению, т. е.
где пока число b неизвестно. Так как прямая должна проходить через точку M, то координаты точки М удовлетворяют этому уравнению, т. е.
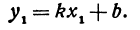
Находим отсюда неизвестное b, получим 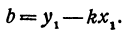 . Подставляя найденное в уравнение (*), будем иметь
. Подставляя найденное в уравнение (*), будем иметь
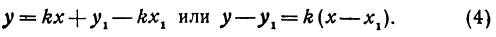
Это и есть уравнение прямой, проходящей через точку М в заданном направлении.
Если в уравнении (4) менять направление, не меняя точку M, то получим уравнение всех прямых, проходящих через заданную точку. Уравнение 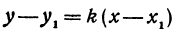 , в котором
, в котором  переменное, а х1 и у1 не меняются, называется уравнением пучка прямых, проходящих через точку М(х1, у1).
переменное, а х1 и у1 не меняются, называется уравнением пучка прямых, проходящих через точку М(х1, у1).
Пример:
Напишем уравнение прямой, проходящей через точку М( — 2, 3) и образующей с осью Ох угол 45°.
Так как tg 45° = 1, то угловой коэффициент равен 1; х1 = —2; у1 = 3. Уравнение прямой запишется в виде
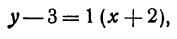
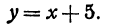
Общее уравнение прямой. Неявная линейная функция
Рассмотрим уравнение первой степени с двумя неизвестными

Решим его относительно у:

т. е. мы получили линейную функцию, где 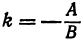 ,
,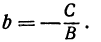 Уравнения (1) и (2) равносильны, поэтому пара чисел х и у, удовлетворяющих уравнению (2), будет удовлетворять и уравнению (1). Так как уравнению (2) соответствует некоторая прямая, то эта же прямая будет соответствовать и уравнению (1).
Уравнения (1) и (2) равносильны, поэтому пара чисел х и у, удовлетворяющих уравнению (2), будет удовлетворять и уравнению (1). Так как уравнению (2) соответствует некоторая прямая, то эта же прямая будет соответствовать и уравнению (1).
Координаты любой точки, лежащей на этой прямой, удовлетворяют уравнению (1), поэтому будем называть его также уравнением прямой.
Рассмотрим особо случай, когда B = 0, так как на нуль делить нельзя.
Уравнение (1) примет вид
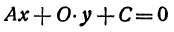
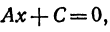
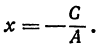
Поэтому, каков бы ни был у, х всегда равен 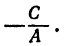 Это имеет место для прямой, параллельной оси Оу; в самом деле, на ней можно найти точку с любой ординатой, но все точки этой прямой имеют одну и ту же абсциссу.
Это имеет место для прямой, параллельной оси Оу; в самом деле, на ней можно найти точку с любой ординатой, но все точки этой прямой имеют одну и ту же абсциссу.
Таким образом, любому уравнению первой степени соответствует некоторая прямая. Придавая в уравнении (1) коэффициентам А, В и С различные значения, можно получить любое уравнение первой степени. Поэтому уравнение (1) называют общим уравнением прямой.
Из уравнения (1) (если 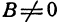 ) можно определить у, т. е. получить линейную функцию; поэтому говорят, что уравнение (1) определяет неявно линейную функцию или что уравнение (1) есть неявная линейная функция.
) можно определить у, т. е. получить линейную функцию; поэтому говорят, что уравнение (1) определяет неявно линейную функцию или что уравнение (1) есть неявная линейная функция.
Система двух уравнений первой степени
Напомним, что две прямые, расположенные на плоскости, могут или пересекаться, или быть параллельными (т. е. не пересекаться), или сливаться (в этом случае можно сказать, что они пересекаются в каждой своей точке).
Рассмотрим систему двух уравнений
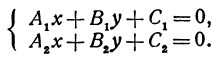
Каждое из этих уравнений является уравнением прямой. Решить систему — это значит найти значения х и у, которые удовлетворяют и первому и второму уравнениям. Но так как х и у определяют точку, то следовательно, решить систему—это значит найти точку, лежащую и на первой и на второй прямых, т. е. найти точку пересечения прямых.
Пример:
Найдем точку пересечения двух прямых:
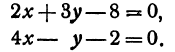
Решая эту систему, получим: х = 1, у = 2, т. е. прямые пересекаются в точке (1,2) (рис. 17).

Пример:
Найдем точку пересечения двух прямых:
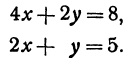
Решая эту систему, получим:
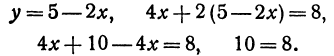
Последнее равенство нелепо, значит, прямые не пересекаются, Рис. 17. т. е. они параллельны.
Пример:
Найдем точку пересечения данных прямых
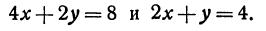
Решая эту систему, получим:
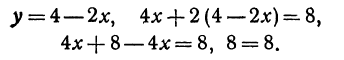
Полученное равенство всегда справедливо, т. е. справедливо при любом значении x. Это значит, что две прямые пересекаются в каждой своей точке, что может быть только тогда, когда они сливаются.
Заметим, что два уравнения, рассматриваемые в этом примере, являются равносильными, поэтому они и представляют одну и ту же прямую.
Примеры решения линейной функции
Линейная функция встречается в формулировках многих физических законов и технических задач. Приведем примеры.
Пример:
Если точка движется равномерно по прямой, то ее расстояние от выбранной точки (от начала координат) выражается при помощи уравнения 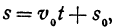
где — начальное расстояние, v0 — скорость, t — время; это, как мы уже знаем, есть линейная функция.
Пример:
Закон Ома записывается в виде 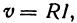
где v — напряжение, R — сопротивление и I — ток. Если не изменяется, то v является линейной функцией тока I .
Пример:
Если стоимость провоза единицы товара по железной дороге равна а руб. за километр, то стоимость v провоза N единиц товара на l км равна 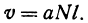
Если же стоимость товара на месте равна М руб., то после перевозки за него надо заплатить
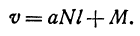
Здесь v—линейная функция l.
Линейная функция встречается в различных областях, но, где бы она ни встречалась, ее всегда можно рассматривать как уравнение прямой. Этим обстоятельством часто пользуются при решении задач.
Задача:
Два города А и В, расстояние между которыми равно 300 км, находятся на одной железнодорожной магистрали. На этой же магистрали между городами А и В надо выбрать пункт С, в котором предполагается устроить склад нефти для снабжения указанных городов. Надо выбрать пункт С так, чтобы общая стоимость перевозок нефти для снабжения города А и города В была наименьшей. Известно, что город А потребляет 400 т нефти, а город В—200 т. Перевозка одной тонны нефти на один километр обходится в а руб.
Решение:
Обозначим расстояние от А до предполагаемого пункта С через х. Тогда расстояние от города В до С равно 300 — х. Стоимость перевозки одной тонны нефти из С в A равна ах руб., а перевозки 400 т—400аx руб. Аналогично перевозка нефти из С в В будет стоить 200а (300 — х) руб. Стоимость всех перевозок, которую обозначим через у, будет выражаться так:
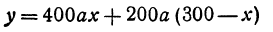
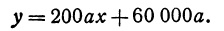
Это линейная функция. Если примем х за абсциссу, а у за ординату точки, то полученная линейная функция определяет уравнение некоторой прямой. Угловой коэффициент ее равен 200а, т. е. положителен, следовательно, эта прямая образует с осью Ох острый угол и поэтому с увеличением независимого переменного поднимается вверх. По смыслу задачи величина х заключена между 0 и 300, т. е.  При х = 0 величина у принимает значение 60 000а, а при x = 300— значение 120 000а. Ясно, что 60 000а есть наименьшее из возможных значений, 120 000а— наибольшее.
При х = 0 величина у принимает значение 60 000а, а при x = 300— значение 120 000а. Ясно, что 60 000а есть наименьшее из возможных значений, 120 000а— наибольшее.
Так как пункт С надо выбрать так, чтобы стоимость была наименьшей, то его следует расположить в городе A, если же этого сделать нельзя по каким-либо соображениям, то, чем ближе расположить его к A, тем выгодней.
Примеры применения линейной функции





Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:






















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Алгоритм определения формулы линейной функции по графику
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Выполнила учительница математики МБОУ Башкирский лицей № 1 муниципального района Учалинский район Республики Башкортостан Хидиятова Залифа Даутовна
Алгоритм определения формулы линейной функции по графику”
На рисунке представлен график функции у = kx +b.
Записать формулу линейной функции, соответствующей данному графику.

1) Так как ордината точки пересечения графика функции с осью Оy равна 1, следовательно, b=1.
Значит, у = kx+ 1
2) Выбираем на графике произвольную точку, например, А (2;2) и определяем её координаты: если x = 2, то у = 2. Подставим в нашу формулу вместо Х и У и получим уравнение относительно k.
2 = 2k+1
2k=1
k = 0.5 Записываем формулу линейной функции: у = 0,5х + 1.
Написать ФОРМУЛУ линейной функции У= КХ+В, график которой изображен на рисунке :
Это ВПР задание 8) это ответ:




ВНИМАНИЕ : задание на сегодня 16 апреля



Внимание : вот эти следующие задания пока НЕ РЕШАТЬ.


Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 932 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 682 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 308 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 573 923 материала в базе
Материал подходит для УМК
«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
16. Линейная функция и её график
Другие материалы
- 16.09.2020
- 199
- 11
- 31.03.2020
- 1166
- 30
- 16.03.2020
- 227
- 1
- 16.03.2020
- 191
- 1
- 08.03.2020
- 281
- 6
- 20.02.2020
- 1245
- 71
- 21.01.2020
- 180
- 0
- 09.12.2019
- 418
- 13
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 30.09.2020 15967
- DOCX 549.2 кбайт
- 155 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Хидиятова Залифа Даутовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 38577
- Всего материалов: 37
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
Объявлен конкурс дизайн-проектов для школьных пространств
Время чтения: 2 минуты
ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек
Время чтения: 2 минуты
В России могут объявить Десятилетие науки и технологий
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
[spoiler title=”источники:”]
http://lfirmal.com/primery-primeneniya-linejnoj-funkcii/
http://infourok.ru/algoritm-opredeleniya-formuly-linejnoj-funkcii-po-grafiku-4463697.html
[/spoiler]
Содержание:
Рассмотрим уравнение с двумя неизвестными 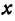

где 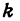 и
и 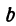 —заданные числа. Этому уравнению удовлетворяет бесконечное множество пар чисел
—заданные числа. Этому уравнению удовлетворяет бесконечное множество пар чисел 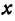 и
и 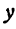 .
.
Например, уравнению

удовлетворяют следующие пары:

и т. д.
Для того чтобы найти пару чисел, удовлетворяющих уравнению 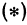 , нужно придать
, нужно придать  произвольное числовое значение и подставить в уравнение
произвольное числовое значение и подставить в уравнение 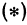 , тогда
, тогда  получит определенное числовое значение. Например, если
получит определенное числовое значение. Например, если 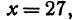
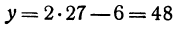 . Очевидно, что пара чисел
. Очевидно, что пара чисел 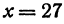 и
и 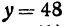 удовлетворяет уравнению
удовлетворяет уравнению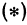 . Так же и в случае уравнения (1) можно придать
. Так же и в случае уравнения (1) можно придать  произвольное числовое значение и получить для
произвольное числовое значение и получить для  соответствующее числовое значение.
соответствующее числовое значение.
Так как в данном уравнении  может принимать любое числовое значение, то его называют переменной величиной. Поскольку выбор этого числового значения ничем не ограничен, то
может принимать любое числовое значение, то его называют переменной величиной. Поскольку выбор этого числового значения ничем не ограничен, то  называют независимой переменной величиной или аргументом.
называют независимой переменной величиной или аргументом.
Для  получаются также различные значения, но уже в зависимости от выбранного значения
получаются также различные значения, но уже в зависимости от выбранного значения  ; поэтому
; поэтому  называют зависимым переменным или функцией.
называют зависимым переменным или функцией.
Функцию  , определяемую уравнением (1), называют линейной функцией.
, определяемую уравнением (1), называют линейной функцией.
Пример:
Вычислить значения линейной функции, определяемой уравнением 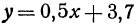 , при следующих значениях независимого переменного:
, при следующих значениях независимого переменного: 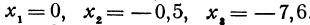 .
.
Решение:
Если 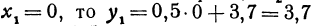 ; если
; если 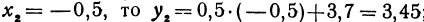 ; если
; если 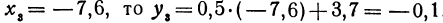 .
.
Покажем, что если принять пару чисел 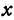 и
и 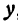 , удовлетворяющих уравнению (1), за абсциссу и ординату точки, то геометрическим местом этих точек будет прямая линия (рис. 14).
, удовлетворяющих уравнению (1), за абсциссу и ординату точки, то геометрическим местом этих точек будет прямая линия (рис. 14).
В самом деле, рассмотрим точку 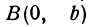 и точки
и точки 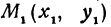 и
и 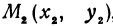 , координаты которых удовлетворяют уравнению (1), т. е.
, координаты которых удовлетворяют уравнению (1), т. е. 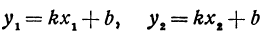 . Обозначим проекции точек
. Обозначим проекции точек 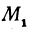 , и
, и 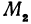 на ось
на ось 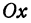 через
через 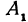 , и
, и 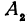 , тогда
, тогда 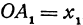 ,
,  Проведем из точки
Проведем из точки 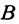 прямую, параллельную оси
прямую, параллельную оси 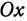 . При этом получим
. При этом получим 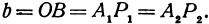
Предположим, что точки 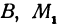 и
и 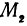 , не лежат на родной прямой. Соединяя точку
, не лежат на родной прямой. Соединяя точку 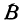 с точками
с точками 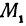 , и
, и 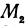 , получим два прямоугольных треугольника
, получим два прямоугольных треугольника 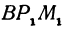 и
и 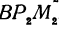 , из которых имеем:
, из которых имеем:
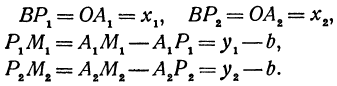
Но так как 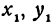 и
и 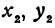 удовлетворяют уравнению (1), то
удовлетворяют уравнению (1), то
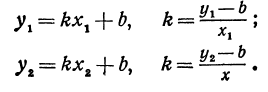
Иначе говоря,
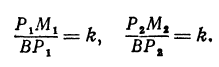
Выражения 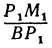 и
и 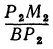 являются отношениями противоположных катетов к прилежащим для углов
являются отношениями противоположных катетов к прилежащим для углов 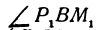 и
и 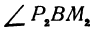 . Следовательно,
. Следовательно, 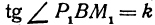 и
и 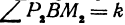 — а поэтому и
— а поэтому и  так как углы острые. Это значит, что точки
так как углы острые. Это значит, что точки 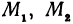 и
и 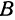 лежат на одной прямой. Но мы предположили, что эти точки не лежат на одной прямой. Таким образом, мы пришли к противоречию, а это и доказывает, что точки
лежат на одной прямой. Но мы предположили, что эти точки не лежат на одной прямой. Таким образом, мы пришли к противоречию, а это и доказывает, что точки 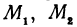 и
и 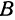 лежат на одной прямой. Обозначим угол
лежат на одной прямой. Обозначим угол 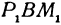 через
через 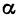 . Этот угол образован прямой
. Этот угол образован прямой 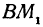 с положительным направлением оси
с положительным направлением оси 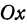 .
.
Так как 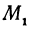 и
и 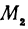 — произвольные точки, координаты которых удовлетворяют уравнению (1), то можно сделать следующее заключение: любая точка, координаты которой удовлетворяют уравнению (1), лежит на прямой, отсекающей на оси
— произвольные точки, координаты которых удовлетворяют уравнению (1), то можно сделать следующее заключение: любая точка, координаты которой удовлетворяют уравнению (1), лежит на прямой, отсекающей на оси 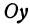 отрезок
отрезок 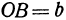 и образующей с положительным направлением оси
и образующей с положительным направлением оси 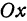 угол
угол 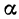 такой, что
такой, что 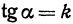 .
.
Число 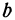 называется начальной ординатой, число
называется начальной ординатой, число 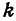 — угловым коэффициентом прямой.
— угловым коэффициентом прямой.
Предыдущие рассуждения позволяют сделать вывод: линейная функция 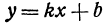 определяет на плоскости прямую, у которой начальная ордината равна
определяет на плоскости прямую, у которой начальная ордината равна 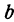 , а угловой коэффициент
, а угловой коэффициент 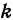 .
.
Например, линейная функция 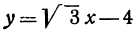 определяет на координатной плоскости прямую, отсекающую на оси
определяет на координатной плоскости прямую, отсекающую на оси 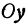 отрезок —4 и наклоненную к оси
отрезок —4 и наклоненную к оси 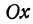 под углом в 60°, так как
под углом в 60°, так как 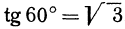 .
.
Если имеем определенную прямую, отсекающую на оси 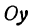 отрезок
отрезок 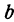 и наклоненную к оси
и наклоненную к оси 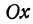 под углом
под углом 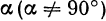 тангенс которого равен
тангенс которого равен 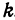 , то, взяв произвольную абсциссу, найдем на указанной прямой только одну точку, имеющую эту абсциссу, т. е. по заданному
, то, взяв произвольную абсциссу, найдем на указанной прямой только одну точку, имеющую эту абсциссу, т. е. по заданному 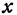 найдется только одна точка, а следовательно, и одно значение
найдется только одна точка, а следовательно, и одно значение 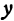 .
.
Очевидно, имеет место и такое предложение: Всякой прямой, отсекающей на оси 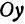 отрезок
отрезок 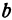 и наклоненной к оси
и наклоненной к оси 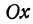 под углом, тангенс которого равен числу
под углом, тангенс которого равен числу 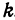 , соответствует линейная функция
, соответствует линейная функция 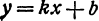 .
.
Координаты любой, точки, лежащей на указанной прямой, удовлетворяют уравнению (1), поэтому уравнение 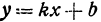 называют уравнением прямой.
называют уравнением прямой.
Таким образом, всякая линейная функция является уравнением некоторой прямой.
Отметим частные случаи.
1. Пусть 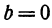 , т. е. линейная функция определяется уравнением
, т. е. линейная функция определяется уравнением

Прямая, определяемая этим уравнением, проходит через начало координат. Здесь 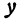 пропорционален
пропорционален 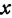 , т. е. если
, т. е. если 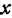 увеличить (уменьшить) в несколько раз, то и
увеличить (уменьшить) в несколько раз, то и 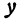 увеличится (уменьшится) во столько же раз.
увеличится (уменьшится) во столько же раз.
2. Пусть 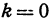 , т. е.
, т. е. 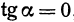 , откуда
, откуда 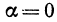 . Линейная функция определяется уравнением
. Линейная функция определяется уравнением

Этому уравнению соответствует прямая, параллельная оси 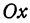 и отстоящая от нее на расстояние
и отстоящая от нее на расстояние 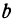 .
.
На основании всего сказанного в этом параграфе легко решаются следующие задачи.
Пример:
Даны точки 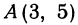 и
и 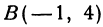 . Нужно узнать, лежат ли эти точки на прямой, уравнение которой имеет вид
. Нужно узнать, лежат ли эти точки на прямой, уравнение которой имеет вид

Решение:
Если точка лежит на прямой, то ее координаты должны удовлетворять уравнению прямой. Поэтому для решения задачи подставим координаты точки 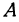 в уравнение
в уравнение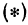 , получим
, получим 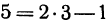 . Это тождество, следовательно, точка
. Это тождество, следовательно, точка 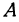 лежит на прямой. Подставляя координаты точки
лежит на прямой. Подставляя координаты точки 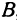 , получаем
, получаем 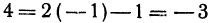 . Отсюда видно, что точка
. Отсюда видно, что точка 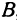 не лежит на прямой.
не лежит на прямой.
Пример:
Построить прямую, уравнение которой

Решение:
Чтобы построить прямую, надо знать, например, две ее точки. Поэтому дадим 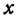 произвольное значение, например
произвольное значение, например 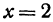 , и найдем из уравнения
, и найдем из уравнения 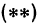 значение
значение 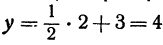 . Значит, точка
. Значит, точка 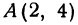 лежит на прямой. Это первая точка. Теперь дадим
лежит на прямой. Это первая точка. Теперь дадим 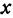 какое-нибудь другое значение, например
какое-нибудь другое значение, например 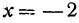 , и вычислим у из уравнения
, и вычислим у из уравнения 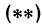 . Получим
. Получим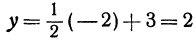 . Точка
. Точка 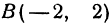 лежит на прямой. Это вторая точка. Строим точки
лежит на прямой. Это вторая точка. Строим точки 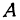 и
и 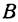 (рис. 15) и проводим через них прямую, это и есть искомая прямая.
(рис. 15) и проводим через них прямую, это и есть искомая прямая.
Основное свойство линейной функции
Рассмотрим линейную функцию 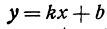 . Найдем значение этой функции при
. Найдем значение этой функции при 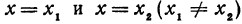 :
:

Здесь первое и второе значения 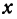 различны, они отличаются друг от друга на величину
различны, они отличаются друг от друга на величину 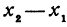 Величину разности
Величину разности  , на которую изменяется
, на которую изменяется 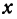 при переходе от
при переходе от 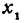 к
к 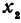 , назовем приращением независимого переменного
, назовем приращением независимого переменного 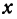 . Эту величину часто будем обозначать через
. Эту величину часто будем обозначать через 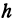 , так что
, так что 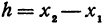 . Найдем, насколько изменилось значение
. Найдем, насколько изменилось значение 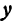 при изменении
при изменении 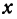 , на
, на 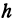 . Для этого вычтем из
. Для этого вычтем из 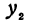 значение
значение 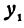 :
:
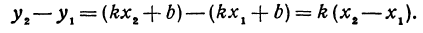
Таким образом,
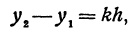
т. е. приращение линейной функции пропорционально приращению независимого переменного.
Это и есть основное свойство линейной функции.
Заметим, что 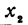 , может быть больше, а может быть и меньше, чем
, может быть больше, а может быть и меньше, чем 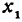 . Поэтому
. Поэтому 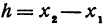 может быть как положительным, так и отрицательным числом, иначе говоря, приращение
может быть как положительным, так и отрицательным числом, иначе говоря, приращение 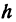 независимого переменного может быть любого знака. То же самое относится и к приращению функции, т. е. к величине
независимого переменного может быть любого знака. То же самое относится и к приращению функции, т. е. к величине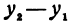 .
.
Пример:
Найдем приращение функции 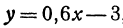 , если приращение независимого переменного
, если приращение независимого переменного 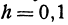 .
.
Решение:
По основному свойству 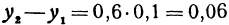 . Приращение этой же функции
. Приращение этой же функции 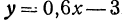 , если
, если 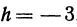 , будет равно
, будет равно 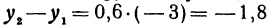 . В этом случае приращения независимого переменного и функции отрицательны, т. е. в этом случае и независимое переменное и функция не увеличиваются, а уменьшаются.
. В этом случае приращения независимого переменного и функции отрицательны, т. е. в этом случае и независимое переменное и функция не увеличиваются, а уменьшаются.
Пример:
Найдем приращение функции 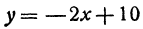 при изменении
при изменении 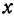 на
на  . Решение:
. Решение:
Будем иметь

Задачи на прямую
Пример:
Найти угол 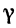 между двумя прямыми, заданными уравнениями
между двумя прямыми, заданными уравнениями
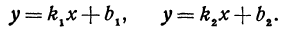
Решение:
При пересечении прямых образуются четыре попарно равных угла. Найдя один из них, легко найти и другие. На рис. 16 прямые обозначены соответственно (1) и (2).
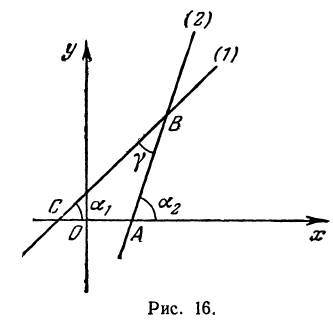
Угол 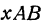 является внешним по отношению к треугольнику
является внешним по отношению к треугольнику 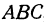 , поэтому он равен сумме двух внутренних углов треугольника, с ним не смежных, т. е.
, поэтому он равен сумме двух внутренних углов треугольника, с ним не смежных, т. е. 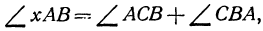 откуда
откуда 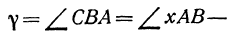
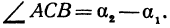 Но углы
Но углы 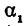 и
и 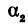 , непосредственно неизвестны, а известны их тангенсы
, непосредственно неизвестны, а известны их тангенсы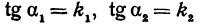 . Поэтому напишем
. Поэтому напишем
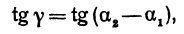
или
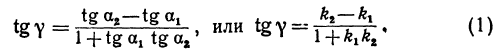
- Заказать решение задач по высшей математике
Пример:
Найти угол между прямыми, заданными уравнениями 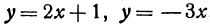 . Здесь
. Здесь 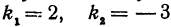 ;
;
Решение:
Применяя формулу (1), получим:
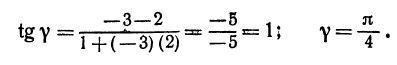
Если же будем считать, что 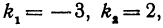 то
то
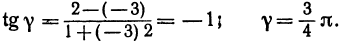
Получены два ответа: сначала найден острый угол между заданными прямыми, а затем — тупой.
Если заданы две параллельные прямые, то углы 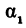 и
и 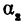 , равны, как соответственные, следовательно, тангенсы их тоже равны
, равны, как соответственные, следовательно, тангенсы их тоже равны
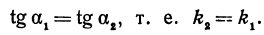
Таким образом, мы приходим к выводу: если прямые параллельны, то их угловые коэффициенты равны.
Если прямые перпендикулярны, то угол между ними равен 90°, т. е. 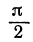 . Но тангенс прямого угла не существует, поэтому формула (1) не должна давать ответа, а это может быть только в том случае, когда знаменатель равен нулю (на нуль делить нельзя):
. Но тангенс прямого угла не существует, поэтому формула (1) не должна давать ответа, а это может быть только в том случае, когда знаменатель равен нулю (на нуль делить нельзя):
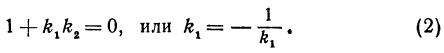
Это и есть условие перпендикулярности двух прямых. Это условие удобно запомнить в следующей формулировке: если две прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.
Пример:
Найдем угол между прямыми, заданными уравнениями 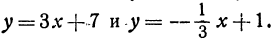 Здесь угловые коэффициенты (первый равен 3, а второй
Здесь угловые коэффициенты (первый равен 3, а второй 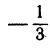 ) обратны по величине и противоположны по знаку.
) обратны по величине и противоположны по знаку.
Решение:
Следовательно, рассматриваемые прямые перпендикулярны.
Пример:
Даны две точки: 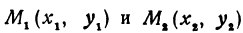 , где
, где 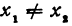 , (т. е. эти точки не лежат на одной прямой, параллельной оси
, (т. е. эти точки не лежат на одной прямой, параллельной оси 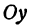 ). Написать уравнение прямой, проходящей через точки
). Написать уравнение прямой, проходящей через точки 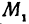 и
и 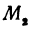 .
.
Решение:
Искомая прямая не параллельна оси 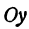 , поэтому ее уравнение можно написать в виде
, поэтому ее уравнение можно написать в виде 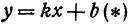 . Значит, для решения задачи надо определить числа
. Значит, для решения задачи надо определить числа 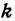 и
и 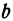 . Так как прямая проходит через точки
. Так как прямая проходит через точки 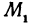 , и
, и 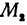 , то координаты этих точек должны удовлетворять уравнению
, то координаты этих точек должны удовлетворять уравнению 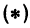 , т. е.
, т. е.

В уравнениях 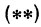 и
и 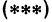 все числа, кроме
все числа, кроме 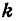 и
и 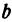 , известны, поэтому эти уравнения можно рассматривать как систему уравнений относительно
, известны, поэтому эти уравнения можно рассматривать как систему уравнений относительно 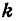 и
и 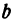 .
.
Решая систему, находим:
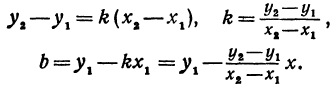
Подставляя найденные выражения в уравнение 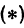 , получим
, получим
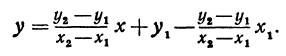
Это и есть уравнение прямой, проходящей через две точки, не расположенные на прямой, параллельной оси 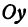 . Полученному уравнению можно придать форму, удобную для запоминания, а именно:
. Полученному уравнению можно придать форму, удобную для запоминания, а именно:
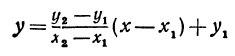
или
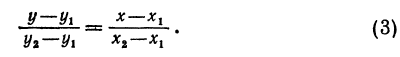
Пример:
Написать уравнение прямой, проходящей через данную точку 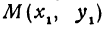 и образующей с осью
и образующей с осью 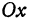 угол
угол 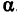 .
.
Решение:
Прежде всего найдем угловой коэффициент искомой прямой: он равен тангенсу угла 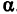 . Обозначим
. Обозначим 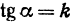 . Значит, уравнение прямой можно написать в виде
. Значит, уравнение прямой можно написать в виде 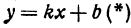 , где пока число
, где пока число 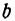 неизвестно.
неизвестно.
Так как прямая должна проходить через точку 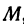 , то координаты точки
, то координаты точки 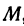 удовлетворяют этому уравнению, т. е.
удовлетворяют этому уравнению, т. е.
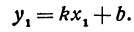
Находим отсюда неизвестное 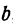 , получим
, получим 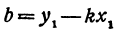 . Подставляя найденное в уравнение
. Подставляя найденное в уравнение 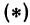 , будем иметь
, будем иметь
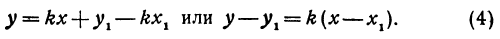
Это и есть уравнение прямой, проходящей через точку 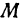 в заданном направлении.
в заданном направлении.
Если в уравнении (4) менять направление, не меняя точку 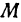 , то получим уравнение всех прямых, проходящих через заданную точку. Уравнение
, то получим уравнение всех прямых, проходящих через заданную точку. Уравнение 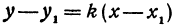 , в котором
, в котором 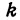 переменное, а
переменное, а 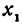 и
и 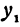 не меняются, называется уравнением пучка прямых, проходящих через точку
не меняются, называется уравнением пучка прямых, проходящих через точку 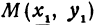 .
.
Пример:
Напишем уравнение прямой, проходящей через точку 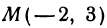 и образующей с осью
и образующей с осью 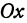 угол 45°.
угол 45°.
Решение:
Так как 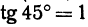 , то угловой коэффициент равен 1;
, то угловой коэффициент равен 1; 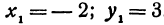 . Уравнение прямой запишется в виде
. Уравнение прямой запишется в виде
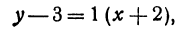
или
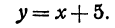
Общее уравнение прямой. Неявная линейная функция
Рассмотрим уравнение первой степени с двумя неизвестными

Решим его относительно 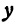 :
:

т. е. мы получили линейную функцию, где 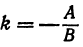 ,
, 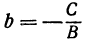
Уравнения (1) и (2) равносильны, поэтому пара чисел 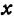 и
и 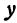 , удовлетворяющих уравнению (2), будет удовлетворять и уравнению (1). Так как уравнению (2) соответствует некоторая прямая, то эта же прямая будет соответствовать и уравнению (1).
, удовлетворяющих уравнению (2), будет удовлетворять и уравнению (1). Так как уравнению (2) соответствует некоторая прямая, то эта же прямая будет соответствовать и уравнению (1).
Координаты любой точки, лежащей на этой прямой, удовлетворяют уравнению (1), поэтому будем называть его также уравнением прямой. Рассмотрим особо случай, когда 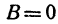 , так как на нуль делить нельзя. Уравнение (1) примет вид
, так как на нуль делить нельзя. Уравнение (1) примет вид 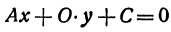 или
или 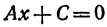 , откуда
, откуда 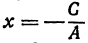 . Поэтому, каков бы ни был
. Поэтому, каков бы ни был 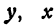 всегда равен
всегда равен 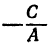 . Это имеет место для прямой, параллельной оси
. Это имеет место для прямой, параллельной оси  ; в самом деле, на ней можно найти точку с любой ординатой, но все точки этой прямой имеют одну и ту же абсциссу. Таким образом, любому уравнению первой степени соответствует некоторая прямая. Придавая в уравнении (1) коэффициентам А, В и С различные значения, можно получить любое уравнение первой степени. Поэтому уравнение (1) называют общим уравнением прямой.
; в самом деле, на ней можно найти точку с любой ординатой, но все точки этой прямой имеют одну и ту же абсциссу. Таким образом, любому уравнению первой степени соответствует некоторая прямая. Придавая в уравнении (1) коэффициентам А, В и С различные значения, можно получить любое уравнение первой степени. Поэтому уравнение (1) называют общим уравнением прямой.
Из уравнения (1) (если 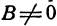 ) можно определить
) можно определить  , т. е. получить линейную функцию; поэтому говорят, что уравнение (1) определяет неявно линейную функцию или что уравнение (1) есть неявная линейная функция.
, т. е. получить линейную функцию; поэтому говорят, что уравнение (1) определяет неявно линейную функцию или что уравнение (1) есть неявная линейная функция.
Система двух уравнений первой степени
Напомним, что две прямые, расположенные на плоскости, могут или пересекаться, или быть параллельными (т. е. не пересекаться), или сливаться (в этом случае можно сказать, что они пересекаются в каждой своей точке). Рассмотрим систему двух уравнений
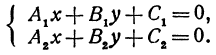
Каждое из этих уравнений является уравнением прямой. Решить систему — это значит найти значения 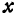 и
и 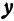 , которые удовлетворяют и первому и второму уравнениям. Но так как
, которые удовлетворяют и первому и второму уравнениям. Но так как 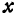 и
и 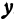 определяют точку, то следовательно, решить систему—это значит найти точку, лежащую и на первой и на второй прямых, т. е. найти точку пересечения прямых.
определяют точку, то следовательно, решить систему—это значит найти точку, лежащую и на первой и на второй прямых, т. е. найти точку пересечения прямых.
Пример:
Найдем точку пересечения двух прямых:
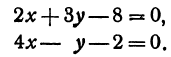
Решение:
Решая эту систему, получим: 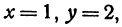 т. е. прямые пересекаются в точке (1, 2) (рис. 17).
т. е. прямые пересекаются в точке (1, 2) (рис. 17).
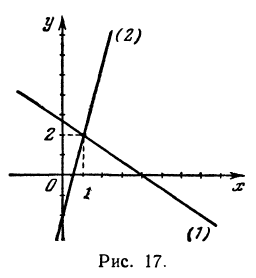
Пример:
Найдем точку пересечения двух прямых:
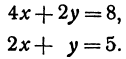
Решение:
Решая эту систему, получим: 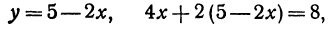
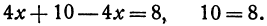 Последнее равенство нелепо, значит, прямые не пересекаются, т. е. они параллельны.
Последнее равенство нелепо, значит, прямые не пересекаются, т. е. они параллельны.
Пример:
Найдем точку пересечения данных прямых
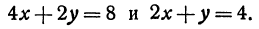
Решение:
Решая эту систему, получим:
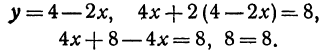
Полученное равенство всегда справедливо, т. е. справедливо при любом значении 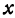 . Это значит, что две прямые пересекаются в каждой своей точке, что может быть только тогда, когда они сливаются.
. Это значит, что две прямые пересекаются в каждой своей точке, что может быть только тогда, когда они сливаются.
Заметим, что два уравнения, рассматриваемые в этом примере, являются равносильными, поэтому они и представляют одну и ту же прямую.
Примеры применения линейной функции
Линейная функция встречается в формулировках многих физических законов и технических задач. Приведем примеры.
Пример:
Если точка движется равномерно по прямой, то ее расстояние от выбранной точки (от начала координат) выражается при помощи уравнения 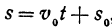 , где
, где 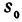 — начальное расстояние,
— начальное расстояние,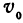 —скорость,
—скорость,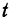 — время; это, как мы уже знаем, есть линейная функция.
— время; это, как мы уже знаем, есть линейная функция.
Пример:
Закон Ома записывается в виде 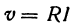 , где
, где 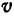 — напряжение,
— напряжение, 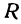 — сопротивление и
— сопротивление и 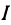 —ток. Если
—ток. Если 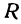 не изменяется, то
не изменяется, то 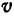 является линейной функцией тока
является линейной функцией тока 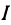 .
.
Пример:
Если стоимость провоза единицы товара по железной дороге равна 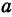 руб. за километр, то стоимость
руб. за километр, то стоимость 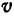 провоза
провоза 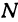 единиц товара на
единиц товара на 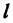 км равна
км равна 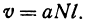
Если же стоимость товара на месте равна 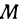 руб., то после перевозки за него надо заплатить
руб., то после перевозки за него надо заплатить
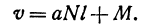
Здесь 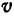 — линейная функция
— линейная функция 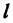 .
.
Линейная функция встречается в различных областях, но, где бы она ни встречалась, ее всегда можно рассматривать как уравнение прямой. Этим обстоятельством часто пользуются при решении задач.
Пример:
Два города А и В, расстояние между которыми равно 300 км, находятся на одной железнодорожной магистрали. На этой же магистрали между городами А к В надо выбрать пункт С, в котором предполагается устроить склад нефти для снабжения указанных городов. Надо выбрать пункт С так, чтобы общая стоимость перевозок нефти для снабжения города А и города В была наименьшей. Известно, что город А потребляет 400 т нефти, а город В —200 т. Перевозка одной тонны нефти на один километр обходится в 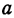 руб.
руб.
Решение:
Обозначим расстояние от А до предполагаемого пункта С через 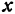 . Тогда расстояние от города В до С равно 300 —
. Тогда расстояние от города В до С равно 300 — 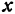 . Стоимость перевозки одной тонны нефти из С в А равна
. Стоимость перевозки одной тонны нефти из С в А равна 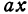 руб., а перевозки 400 т—400
руб., а перевозки 400 т—400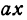 руб. Аналогично перевозка нефти из С в В будет стоить
руб. Аналогично перевозка нефти из С в В будет стоить 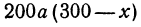 руб. Стоимость всех перевозок, которую обозначим через
руб. Стоимость всех перевозок, которую обозначим через 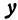 , будет выражаться так:
, будет выражаться так:
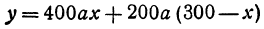
или
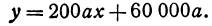
Это линейная функция. Если примем 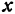 за абсциссу, а
за абсциссу, а 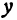 за ординату точки, то полученная линейная функция опредеяет уравнение некоторой прямой. Угловой коэффициент ее равен
за ординату точки, то полученная линейная функция опредеяет уравнение некоторой прямой. Угловой коэффициент ее равен 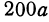 , т. е. положителен, следовательно, эта прямая образует с осью
, т. е. положителен, следовательно, эта прямая образует с осью 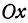 острый угол и поэтому с увеличением независимого переменного поднимается вверх. По смыслу задачи величина
острый угол и поэтому с увеличением независимого переменного поднимается вверх. По смыслу задачи величина 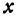 заключена между 0 и 300, т. е.
заключена между 0 и 300, т. е. 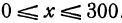 . При
. При 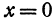 величина у принимает значение 60000а, а при
величина у принимает значение 60000а, а при 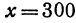 — значение 120000а. Ясно, что 60 000а есть наименьшее из возможных значений, 120 000а— наибольшее.
— значение 120000а. Ясно, что 60 000а есть наименьшее из возможных значений, 120 000а— наибольшее.
Так как пункт С надо выбрать так, чтобы стоимость была наименьшей, то его следует расположить в городе А; если же этого сделать нельзя по каким-либо соображениям, то, чем ближе расположить его к А, тем выгодней.
- Квадратичная функция
- Тригонометрические функции
- Производные тригонометрических функции
- Производная сложной функции
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
- Координаты на плоскости
K и B — числовые коэффициенты функции. Это может быть любое число, например, положительное, отрицательное или дробное.
Линейная функция, ее свойства и график
Функция, заданная видом y = kx+b, где x — переменная, а k и b — некоторые числа, называется линейной функцией. Переменная x называется независимой переменной, а переменная y — зависимой переменной.
Графиком линейной функции является линия. Чтобы провести прямую линию, достаточно получить два значения x и получить два значения y, в результате чего получатся две точки, через которые проходит одна прямая.
Число K называется угловым коэффициентом линии.
Свойства линейной функции
- Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
- Областью значений также является множество всех действительных чисел.
- Функция не имеет ни наибольших, ни наименьших значений.
- При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
- При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
- При k=0 прямая параллельна оси х.
- Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.
Рассмотрим пример линии до уровня координат в соответствии со значениями K и B
Пример №1
Постройте график функции y = 2x -1. Для облегчения расчетов, структурирования и т.д. создайте таблицу значений x и y.
Чтобы построить график, выберите два значения x. Желательно, чтобы одно из них было равно нулю, а второе значение (выберите три).
Затем замените значение x в уравнении и вычислите соответствующее значение y.
Запишите значение y в таблицу:.
Постройте систему координат, запишите в ней координаты A (0; -1) и B (3; 5) и проведите прямую линию к этим двум точкам.
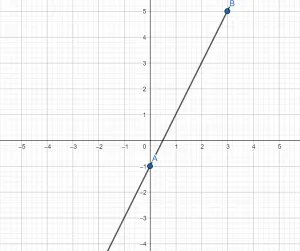
Таким образом, из печати видно, что угловой коэффициент положительный. Это означает, что график растет, что видно на графике.
Каждое из этих уравнений является уравнением прямой линии. Решение системы заключается в нахождении цен, которые удовлетворяют как первому, так и второму уравнению. Однако, поскольку они определяют точки, для решения системы необходимо найти точки на первой и второй прямых, то есть пересечения прямых.
Как меняется график при разных (k)?
Определите, как влияет на графикКоэффициент. (k ) рисует различные функции с различными (k ): (⢙), (-⢙), (2 ), (-2 ), (0 ). В этом случае ⌘ (b ) равен (равен нулю) для всех функций, что устраняет его влияние. Другими словами, нарисуйте графики функций: (y = fracx ), (y = — fracx), (y = 2x ), (y = -2x ), (y = 0 ).
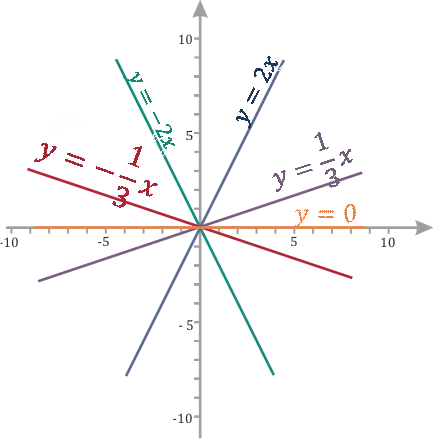
В случае (k = 2 ) и ʉ (ʉ frac ) функция возрастает, а в случае ʉ (k = -2 ) и ʉ (- frac) — убывает. На практике:.
При любом (k>0) функция возрастает и при любом (k
Также можно заметить, что болеефактор в случае В случае (k ) график более «острый».
Как по графику определить коэффициент k?
- Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента (k) плюс, если убывает – минус.
- Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:

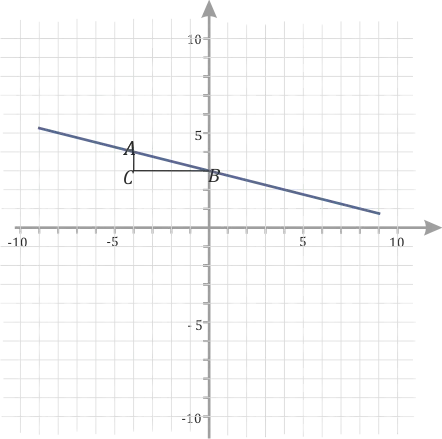
Чтобы найти значение (k ) по модулю (т.е. без учета знаков), нужно разделить вертикальную сторону треугольника на горизонтальные плоскости. Можно воспользоваться эмпирическим правилом. Стояние ошеломляет». В этих случаях (| k | = frac ). Следовательно, в первом графе ⌘ (k = 2 ), а во втором ⌘ (k = — frac ).
Как меняется график при разных значениях (b)?
Чтобы определить, как (b ) влияет на графики, нарисуйте различные функции с разными Ј (b ): Ј (6 ), Ј (2 ), Ј (0 ), Ј (-3 ), Ј (-3 ), Ј (-3 ). (-8 ). Для всех функций установите ⌘(k ) равным ⌘(2 ).
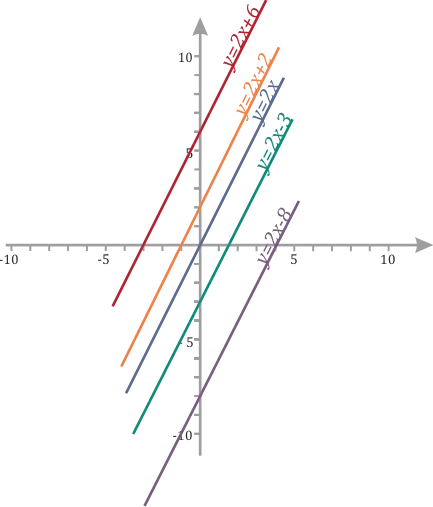
Вы можете легко увидеть, поднимается ли линия на ⌘(b ) (если (b>0 )) или опускается относительно ⌘(| b | ).<0)).
For (ː displaystyle k ). Функция ⌘ (⌘ displaystyle left (b = 0 right)). () Измените функцию displaystyle k ) и посмотрите, что произойдет на графике.
Свойства линейной функции
Определяющей областью функции является сумма всех действительных чисел.
Сумма функции — это сумма всех действительных чисел.
Графиком линейной функции является линия. Чтобы провести прямую, достаточно знать две точки. Положение линии на уровне координат зависит от значений коэффициентов K и B.
Функция не имеет наибольшего или наименьшего значения.
Превосходство и нерелевантность линейной функции зависит от значений коэффициентов k и b.
b ≠ 0, k = 0, поэтому y = b является хорошим, и
b = 0, k ≠ 0, поэтому y = kx не требуется.
b ≠ 0, k ≠ 0, где y = kx + b — общая функция и
b = 0, k = 0, поэтому y = 0 является как четной, так и нечетной функцией.
Линейные функции не обладают свойством периодичности, так как их спектр непрерывен.
График функции пересекает координатные оси.
ось OX — в точке (-b / k; 0), ось
Ось OY — в точке (0; b).
x = -b/k является точкой нуля функции.
Для b=0 и k=0 функция y=0 равна нулю при любом значении переменной x.
Если b≠0 и k=0, то функция y=b обращается в нуль при любом значении переменной x.
Функция монотонно возрастает в области определения до k>0 и монотонно убывает до k.< 0 .
Для k> 0 функция принимает отрицательные значения в интервале (-∞; -b / k) и положительные значения в интервале (-b / k; +∞).
Коэффициент k представляет собой угол, образованный линией в положительном направлении OX. Следовательно, k называется угловым коэффициентом.
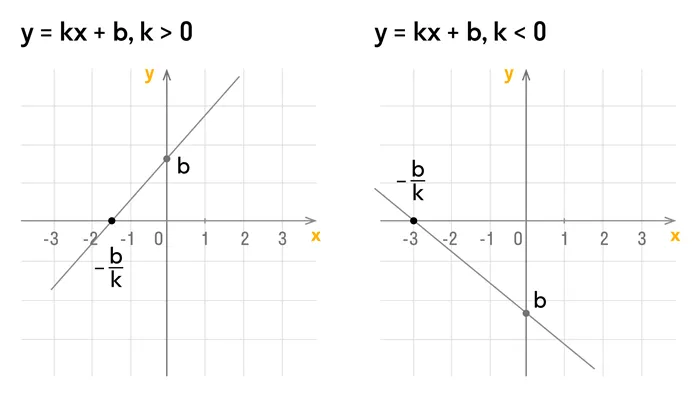
Для линейных функций есть два особых случая.
Когда b = 0, уравнение принимает вид y=kx. Такая функция называется прямо пропорциональной. График представляет собой линию, проходящую через начало координат.
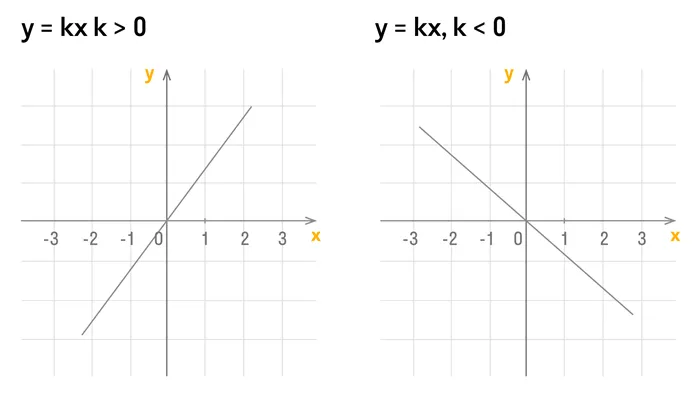
- Если k = 0, то уравнение примет вид y = b. График — прямая, которая параллельна оси OX и проходит через точку (0; b) .
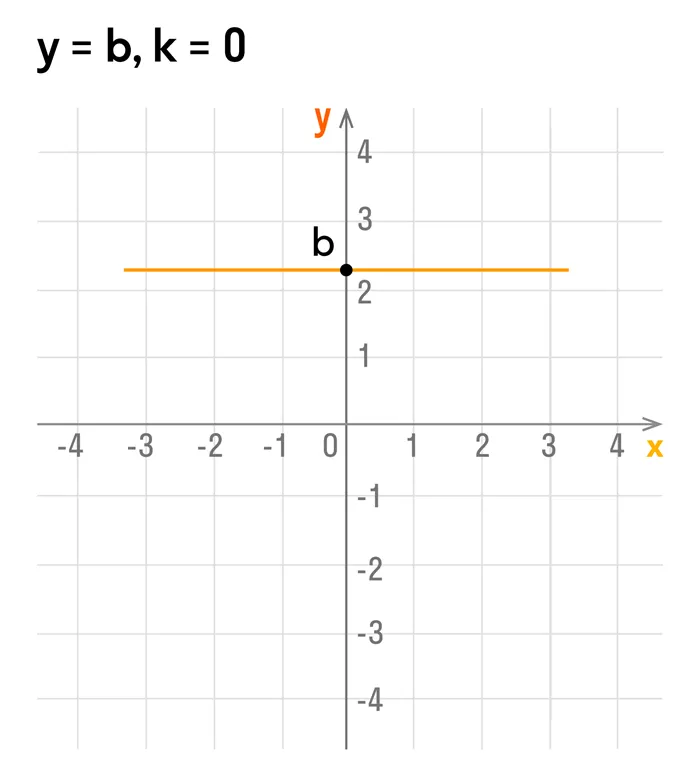
Построение линейной функции
В геометрии есть аксиомы. Любые две точки могут пересекаться по прямой и только по одной. Из этой аксиомы следует, что для построения графика функции y = kx + b достаточно найти только две точки. Для этого нужно задать два значения x, заменить их уравнением функции и вычислить соответствующее значение y.
Например, чтобы построить график функции y = 1 / 3x + 2, можно взять x = 0 и x = 3, а нормали этих точек будут y = 2 и y = 3. Возьмем точки A (0; 2) и B (3; 3). Соедините их, чтобы получить график:.
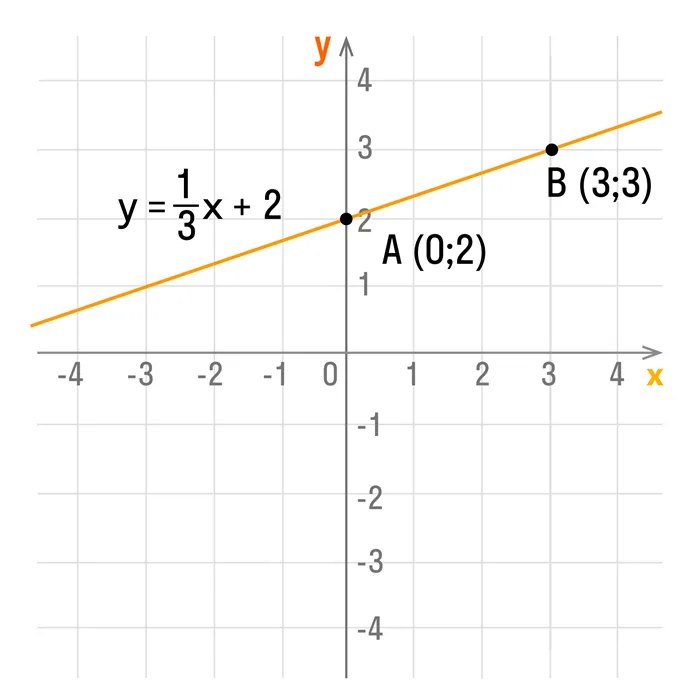
В уравнении функции y=kx + b коэффициент k участвует в наклоне графика функции.
Если k>0, то график наклонен вправо.
Коэффициент b отвечает за смещение графика вдоль OY.
Если b> 0, то график функции y = kx + b строится из y = kx путем сдвига вверх на b единиц вдоль оси OY.
Постройте три графика функции.
Проанализируйте формы. Поскольку коэффициент k больше нуля для всех функций, все графики наклонены вправо. Чем выше значение k, тем круче линия.
Поскольку b = 3 для каждой функции, все графики пересекают ось OY в точке (0; 3).
Давайте посмотрим на графики функций.
На этот раз коэффициент k меньше нуля для всех функций, а графики функций перекошены влево. Чем больше k, тем круче становится линия.
Коэффициент b равен 3, и график также пересекает ось OY в точке (0; 3).
Исследуйте график функции.
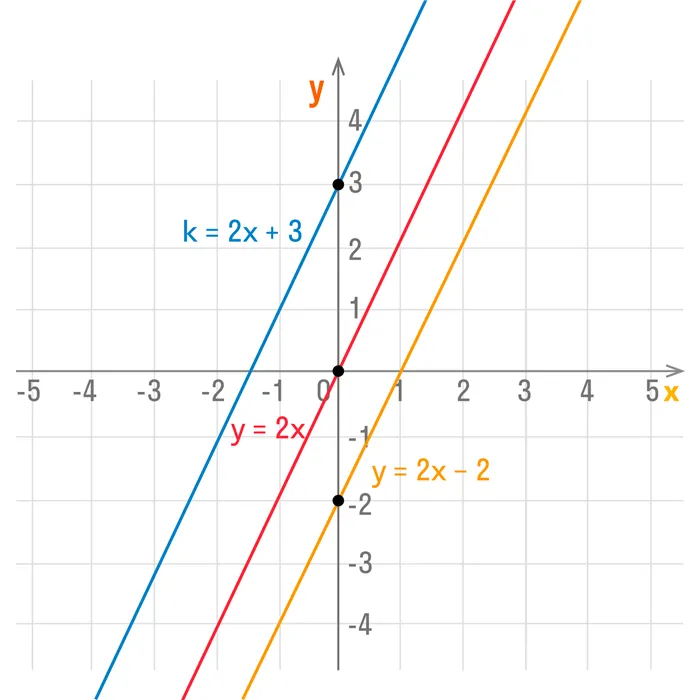
Коэффициенты k теперь равны во всех уравнениях функции. Получаются три параллельные линии.
Коэффициенты b различны, и эти графики пересекают ось OY в разных точках.
График функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3).
График функции y=2x (b = 0) пересекает ось OY в начальной точке (0; 0).
График функции y=2x —2 (b = -2) пересекает ось OY в точке (0; -2).
Линии с одинаковым угловым коэффициентом параллельны.
Резюме. Если известны знаки коэффициентов k и b, то можно увидеть график функции y = kx+b.
Если k< 0 и b > 0, график функции y = kx+b имеет вид
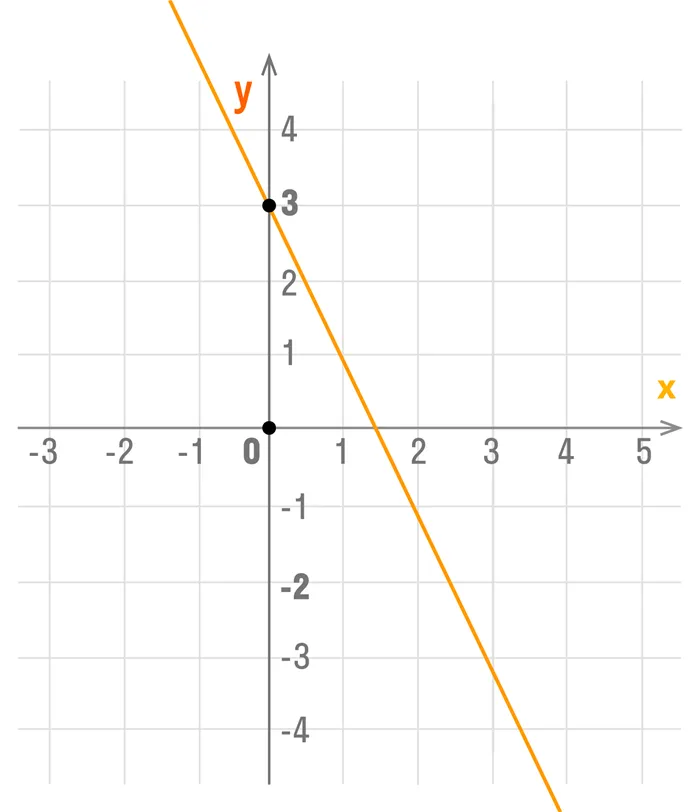
Если k > 0 и b > 0, график функции y = kx+b имеет вид
Решение задач на линейную функцию
Чтобы решить задачу и построить график линейной функции, необходимо вспомнить и использовать вышеуказанные свойства и правила. Практикуйтесь!
Пример 1. Постройте график функции y = kx + b, если известно, что она проходит через точку A (-3; 2) и параллельна прямой y = -4x.
Уравнение функции y = kx + b имеет два неизвестных параметра, k и b. Поэтому в рассматриваемом тексте нам нужно найти два условия, характеризующие график функции.
График функции y=kx+b параллелен прямой y=-4x, поэтому k = -4. Это означает, что уравнением функции является y = -4x+b.
Осталось найти Б. Мы видим, что график функции y = -4x + b проходит через точку A (-3; 2). Подставьте координаты точки в уравнение функции, чтобы получить правильное уравнение.
Поэтому необходимо построить график функции y = -4x-10.
Мы уже знаем точку A (-3; 2), поэтому давайте найдем точку B (0; -10).
Расположим эти точки в координатной плоскости и соединим их прямыми линиями.
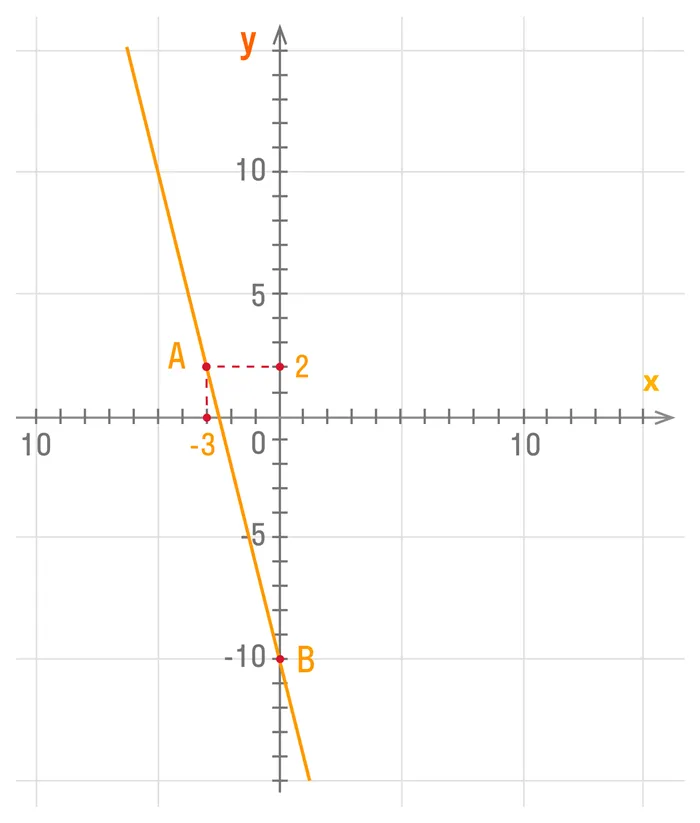
Пример 2. Напишите уравнение прямой, проходящей через точку A (1; 1). B (2; 4).
Если прямая проходит через точку с заданными координатами, то координаты точки удовлетворяют уравнению y = kx+b.
Поэтому замена координат точки в уравнении прямой дает верное равенство.
Подставьте координаты каждой точки в уравнение y = kx + b, чтобы получить одновременное линейное уравнение.
Вычтите первое уравнение из второго уравнения системы, чтобы получить k = 3.
Подставьте значение k в первое уравнение системы, чтобы получить b=-2.
Предположим, что нам даны две линейные функции (назовем эту линию) и (назовем эту линию). При различных комбинациях коэффициентов этих функций эти линии либо пересекаются в некоторой точке (перпендикулярно или произвольно), либо не пересекаются. Другими словами, они параллельны. Давайте рассмотрим эти варианты.
Свойства зависимости
Перед решением задачи следует обратить внимание на свойства линейных функций. Есть две позиции, которые зависят от коэффициента k. Для k> 0 функция обладает следующим свойством: если k > 0, то функция линейна.

- Графиком является прямая линия.
- D(y) = (-∞;∞).
- При отрицательных значениях аргумента значение функции эквивалентно отрицательной величине. Если независимая переменная — положительная величина, то и зависимая принимает только положительные значения. В этом моменте ключевую роль играет величина сдвига влево или вправо b.
- Возрастает на E(у).
- Отсутствие экстремумов.
- Непрерывная и нечетная.
- Период отсутствует.
Таким образом, график линейной функции — это прямая линия, и ее свойства необходимо исследовать по определенному алгоритму. Необходимо соблюдать основные свойства.
С осью OY. Представление всех точек, принадлежащих оси OY, равно нулю. Поэтому, чтобы найти пересечение с OY, x в уравнении функции заменяется на ноль. Тогда y = b.
График линейной функции
Как упоминалось выше, график этой функции — прямая линия.
Как известно из геометрии, прямую можно провести через две точки (т.е. если известны две точки, принадлежащие прямой, то этого достаточно).
Предположим, у нас есть линейная функция ⌘ (y = 2x + 1 ). Чтобы построить его, необходимо вычислить координаты любых двух точек.
Другими словами, вам нужно взять два значения члена ⌘(x ) и вычислить соответствующие два значения функции.
Затем для каждой пары ⌘(⌘ слева (x; y справа)⌘) найдите точку в системе координат и проведите прямую через эти две точки.
Проще всего найти функцию с аргументом (x = 0: y слева (0 справа) = 2 cdot 0 + 1 = 1 ).
Поэтому координаты первой точки ⌘(⌘ слева (0; 1 справа).
Предположим, что остальные числа ⌘(x ). Например, ǫ (x = 1: y слева (1 справа) = 2 cdot 1 + 1 = 3 ).
Координаты второй точки ⌘ (⌘ слева (1; 3 справа)).
Поместите следующие две точки в координатную плоскость.
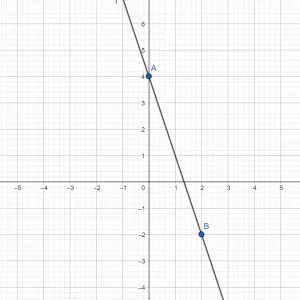
Затем с помощью линейки проведите линию через следующие две точки.
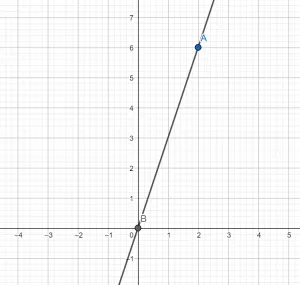
И вот график создан!
Теперь на том же графике нарисуем еще два графика: ⌘ (y = -1 ) и ǫ (y = -x + 2 ).
Создайте свою собственную аналогичным образом: вычислите значения y для любых двух значений ǫ(x ), отметьте эти точки на графике и проведите через них линию.
Открыть ответы…
Мы постоянно совершенствуем это руководство, и вы можете помочь в этом. Неограниченный доступ и использование руководства Юклава (более 100 статей по всем темам использования и применения, более 2000 решенных задач, более 20 онлайн семинаров и семинаров).
Видно, что все три линии имеют разные уклоны и пересекают оси координат в разных точках. Это вкладчики( displaystyle k ) и displaystyle b ).
Давайте узнаем, чем они занимаются.
Коэффициенты линейной функции
Сначала посмотрим, что делают факторы (⌘ displaystyle b ). Рассмотрим функцию ⌘ (⌘ displaystyle y = x+b ), т.е. ⌘ (⌘ displaystyle k = 1 ).
Посмотрите, что происходит на графике, изменив (⌘ displaystyle b ).
(⌘ displaystyle b: b = -2, давайте построим график с различными значениями ⌘ text< ->1, {text< >0, {text< >1, {text< >2 ):.
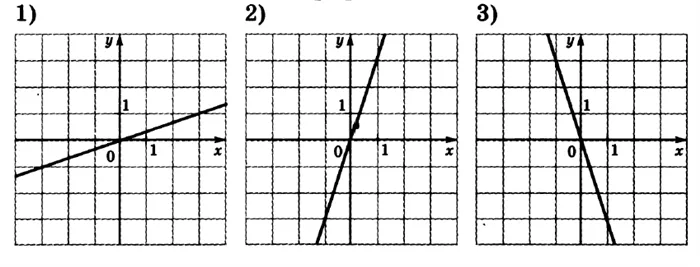
Что вы можете сказать о них? Чем отличаются графики?
Скоро вы в этом убедитесь. Чем больше (Lo_ displaystyle b ), тем больше линий размещается.
Далее, обратите внимание на следующее. График пересекает ось ⌘ (⌘ displaystyle mathbf ) в точке с координатами, равными ⌘ (⌘ displaystyle mathbf )!
И это правда. Как найти пересечение графика с помощью оси ⌘ (⌘ displaystyle y )? Что такое ⌘ (⌘ displaystyle x ) в такой момент времени?
В любой точке вертикальной оси (так называется ось ⌘ (⌘ displaystyle y ), если вы забыли) ⌘ (⌘ displaystyle x = 0 ).
Поэтому просто замените функцию ⌘ (⌘ displaystyle x = 0 ) и вы получите расположение графика на оси ⌘ (⌘ displaystyle y ).
For (ː displaystyle k ). Функция ⌘ (⌘ displaystyle left (b = 0 right)). () Измените функцию displaystyle k ) и посмотрите, что произойдет на графике.
⌘ displaystyle k = -3, давайте построим график ⌘ text< ->1, {text< >0, {text< >1, {text< >2: ס)

Ну, теперь мы это поняли: displaystyle k ) влияет на тенденцию графика.
Чем больше модуль (то есть, несмотря на синус), тем более «острой» (бездной — с большим углом к оси ɛ — ɛ displaystyle ox ɛ) является линия.
Анализ. Постройте новый график (⌘ displaystyle y = kx+b ):.
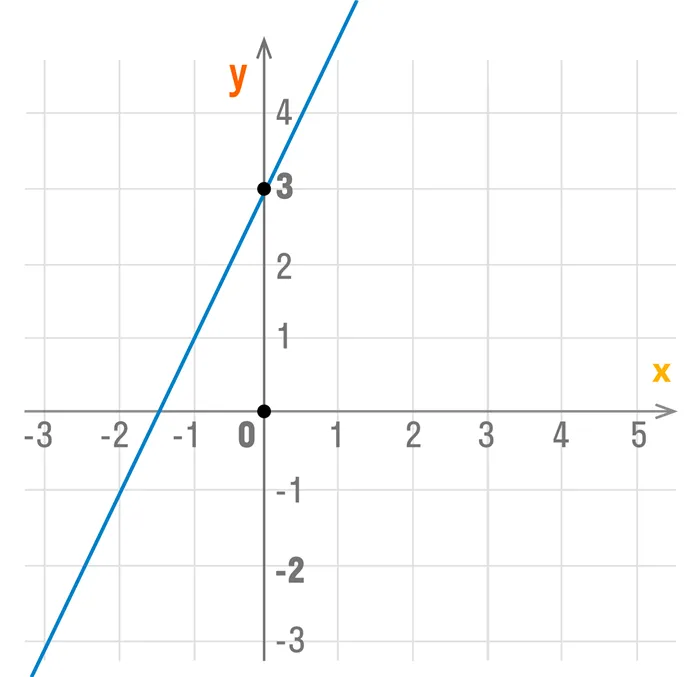
Выберите на графике две точки ɑ (ɑ displaystyle a ) и ɑ (ɑ displaystyle b ). Для простоты мы выбрали точку на пересечении графика с линией. Точка ⌘ (⌘ displaystyle b ) может находиться в любой точке прямой.
Рассмотрим прямоугольный треугольник 섹 (섹 displaystyle ab ), построенный в сечении 섹 (섹 displaystyle ab ), подчиненном прямоугольнику 섹 (섹 displaystyle ab ).
На диаграмме показано, что හ (⌘ displaystyle ac = x ) и හ (⌘ displaystyle bc = y-b ).
Замените (⌘ displaystyle y = kx+b ) на ߋ (⌘ displaystyle bc: bc = y-b = kx+b-b = kx ).
bc = k cdot ac> rightrrow> k = frac >> =<mathop<rm tg> nolimits> alpha ).
Поэтому коэффициент ⌘ (⌘ displaystyle k ) равен тангенсу угла наклона графика, то есть углу между графиком и осью расстояния.
Поэтому (коэффициент ⌘ (⌘ displaystyle k )) обычно называют угловым коэффициентом.
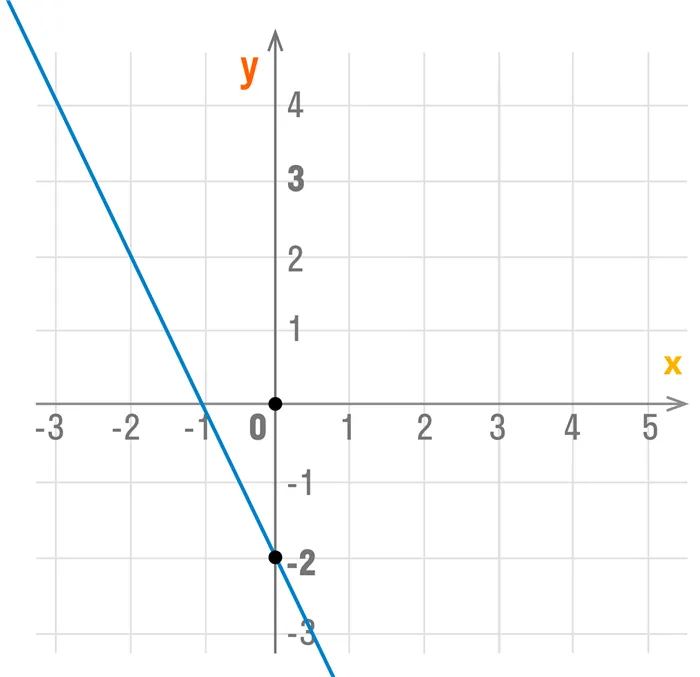
Если (⌘ displaystyle k = 0 ), то ⌘ (⌘ также ⌘)<mathop<rm tg> nolimits> alpha = 0, ⌘), поэтому ⌘ (⌘ displaystyle alpha = 0 ), т.е. линия параллельна оси глубины на.
Понимание геометрического значения коэффициентов очень важно, так как они часто используются в различных задачах на линейные функции.
Разбор еще трех задач на линейную функцию
1. найдите коэффициенты ዄ (ዄ displaystyle k ) и ዄ (ዄ displaystyle b ) линейной функции, график которой изображен на рисунке. Напишите уравнение функции.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
Параметры США часто включают исследование функции или, по крайней мере, знание ее свойств.
Чтобы научиться исследовать функцию, лучше всего научиться визуализировать ее графически.
В этом уроке вы рассмотрите основные элементарные функции, научитесь представлять их графически и узнаете, как на них влияют различные параметры (коэффициенты функции).
Преобразования графиков функций. ЕГЭ 18. Задачи с параметром.
Научились ли вы строить графики функций? Что произойдет, если вы измените один из тарифов сейчас? Или «инкапсулировать» часть функции в раздел?
Можно ли просто переместить/расширить старую диаграмму вместо того, чтобы создавать новую для этой цели?
Вы можете! И в этом уроке вы узнаете, как выполнять такие преобразования.
Благодаря этим преобразованиям вы поймете, как выглядит график функции для всех значений параметра, и научитесь решать задачи США, связанные с этим вопросом.
