Пример 1.
Матрицы 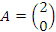 и
и 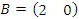 составлены из одних и тех же элементов, но имеют различные размеры.
составлены из одних и тех же элементов, но имеют различные размеры.
Следовательно, A ≠ B.
***
Пример 2.
Матрицы 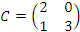 и
и 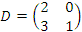 составлены из одних и тех же элементов и имеют одинаковые размеры. Однако не все соответствующие матричные элементы попарно равны.
составлены из одних и тех же элементов и имеют одинаковые размеры. Однако не все соответствующие матричные элементы попарно равны.
Следовательно, C ≠ D.
***
Пример 3.
Если 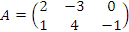 , то
, то 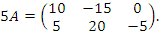 .
.
***
Пусть
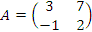 и
и 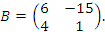
Тогда
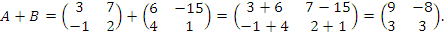
***
Вычислим линейную комбинацию 2A – 3B матриц A и B в условиях предыдущего примера:
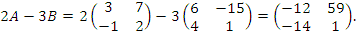
***
Матричное уравнение
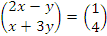
равносильно системе двух линейных уравнений:
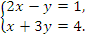
Примеры решения задач
1.
Найти линейную комбинацию матриц
![]() ,
,
где![]() ,
,![]() .
.
Решение:
![]()
![]() .
.
2.
Пусть
![]() – матрица размерности 2x
– матрица размерности 2x
3,
 – матрица размерности 3 х 3. Найти
– матрица размерности 3 х 3. Найти
произведения![]() и
и![]() (если это возможно).
(если это возможно).
Решение:
Используем
формулу (2.1):

Произведение
![]() не существует, так как число столбцов
не существует, так как число столбцов
матрицыB
не совпадает с числом строк матрицы A:
![]() .
.
3.
Найти![]() ,
,
если![]() .
.
Решение:
![]() .
.
![]() .
.
4.
Найти значение матричного многочлена
![]() ,
,
если
![]() ,
,
![]() .
.
Решение:
![]() .
.

![]() .
.
5.
Транспонировать матрицу
![]() .
.
Решение:
Так как у матрицы A
две строки и три столбца, то у матрицы
![]() будет три строки и два столбца:
будет три строки и два столбца: .
.
6.
Дана матрица
 .
.
Найти обратную матрицу.
Решение:
Воспользуемся первым способом нахождения
обратной матрицы, т.е. формулой (2.2).
Вычисляем определитель матрицы A:
 .
.
Так
как
![]() ,
,
то матрица![]() существует. Найдем алгебраические
существует. Найдем алгебраические
дополнения ко всем элементам матрицыA:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Составим
присоединенную матрицу:
 .
.
Находим обратную матрицу, поделив каждый
элемент присоединенной матрицы на
определитель матрицы A.
Получаем ответ:
 .
.
7.
Решить матричное уравнение:
![]() .
.
Решение:
Запишем данное матричное уравнение в
виде
![]() .
.
Его решением является матрица
![]() (если существует матрица
(если существует матрица![]() ).
).
Найдем определитель матрицыA:
![]() .
.
Значит,
обратная матрица
существует, и исходное уравнение имеет
(единственное) решение. Найдем обратную
матрицу:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Найдем
решение матричного уравнения:
![]() .
.
8.
Найти обратную к матрице
![]() ,
,
используя метод элементарных
преобразований.
Решение:
Припишем справа единичную матрицу
![]() .
.
Разделив первую
строку на три и обнулив элемент в первом
столбце ниже тройки, получим
 .
.
Умножив
вторую строку на три и обнулив элемент
во втором столбце выше
![]() ,
,
получим
![]() .
.
Таким
образом,
![]() .
.
Задачи для самостоятельного решения
1.
Найти линейную комбинацию матриц
![]() ,
,
где
 .
.
2.
Найти произведения матриц
![]() и
и![]()
(если они существуют), где
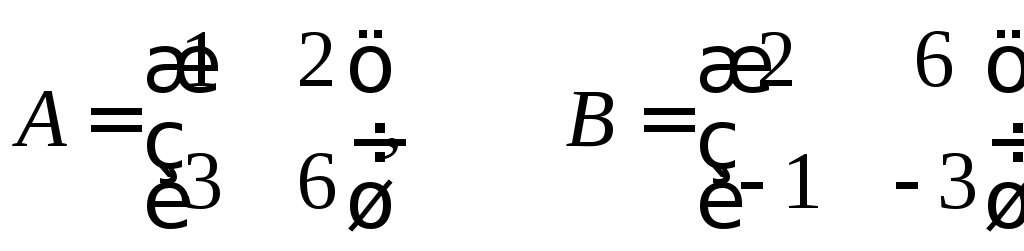 .
.
3.
Проверить коммутируют ли матрицы
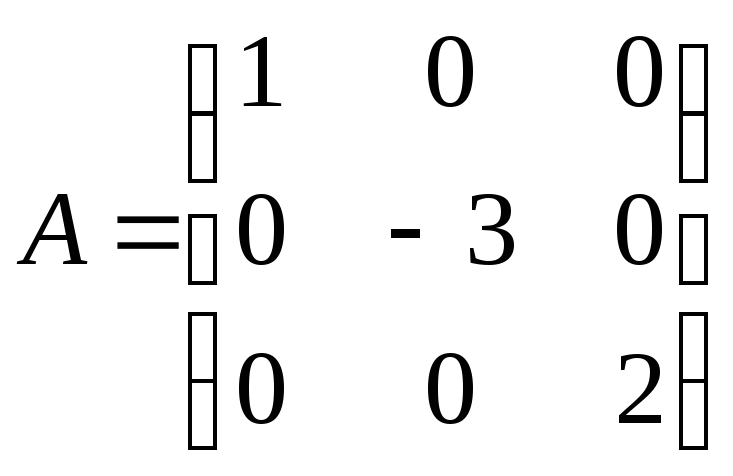
и
 .
.
4.
Найти значение матричного многочлена
![]() ,
,
если![]() и
и![]() .
.
5.
Вычислить произведение
![]() при заданной матрице
при заданной матрице
 .
.
6.
Привести к ступенчатому виду матрицу
 .
.
7.
Найти произведения матриц
![]() и
и![]() ,
,
где
![]() .
.
8.
Найти обратную матрицу к матрице
 .
.
Решить
матричные уравнения:
9.
![]() ;
;
10.
 .
.
11.
Найти линейную комбинацию матриц
![]() ,
,
где
 .
.
12.
Найти произведения матриц
![]() и
и![]()
(если они существуют), где
 .
.
13.
Проверить, коммутируют ли матрицы
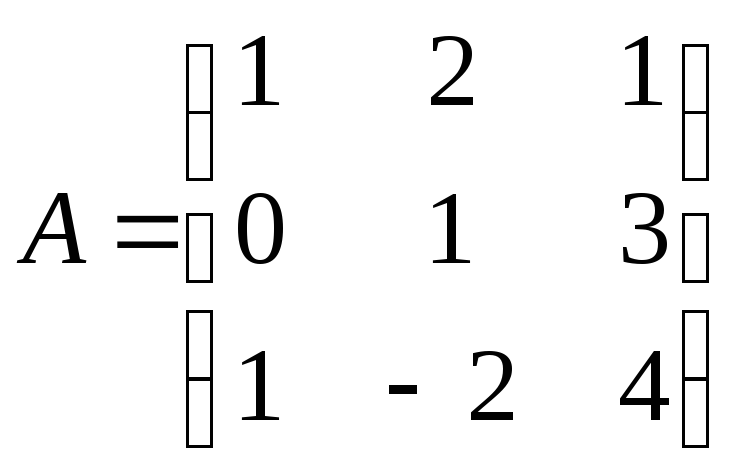
и
 .
.
14.
Найти значение матричного многочлена
![]() ,
,
если
![]() .
.
15.
Вычислить произведение
![]() при заданной матрице
при заданной матрице![]() .
.
16.
Привести к ступенчатому виду матрицу
 .
.
17.
Найти произведения матриц
![]() и
и![]() ,
,
если
![]() .
.
18.
Найти обратную матрицу к матрице
 .
.
Решить
матричные уравнения:
19.
![]() ;
;
20.
 .
.
Ответы:
1)
 ;
;
2)
 ;3)
;3)
Да;
4) ![]() ;5)
;5)
 ;
;
6)
 ;7)
;7)
![]() ;8)
;8)  ;9)
;9)
![]() ;10)
;10)
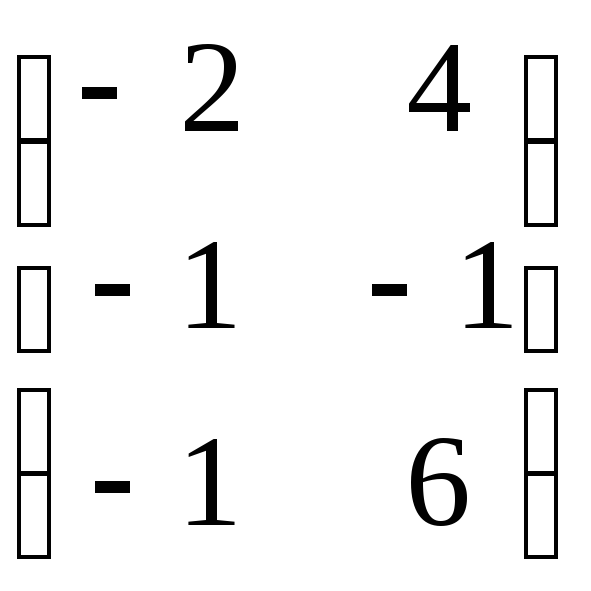 ;11)
;11)
 ;
;
12)
![]() ;13)
;13)
Нет; 14)
![]() ;15)
;15) ![]() ;
;
16)  ;17)
;17)
![]() ;18)
;18)
 ;19)
;19) ![]() ;20)
;20)  .
.
ПРАКТИЧЕСКОЕ
ЗАНЯТИЕ 3
Решение систем линейных уравнений методом Крамера и Гаусса
1. Метод Крамера.
Система
уравнений вида
 (3.1)
(3.1)
называется
системой
m
линейных уравнений с n
неизвестными.
Коэффициенты
этих уравнений записываются в виде
матрицы А,
называемой матрицей
системы,
а числа, стоящие в правой части системы,
образуют столбец В,
называемый столбцом
свободных членов.
Неизвестные системы так же записываются
в столбец, называемый столбец
неизвестных:
 ,
,
 ,
,
Используя
произведение матриц, можно записать
данную систему в матричном виде:
![]() .
.
Совокупность
чисел
![]() называетсярешением
называетсярешением
системы,
если каждое уравнение системы обращается
в равенство после подстановки в него
чисел
![]() вместо неизвестных
вместо неизвестных![]() .
.
Системы,
не имеющие решения, называются
несовместными.
Системы,
имеющие решения, называются совместными.
Заметим, что система может иметь
единственное решение, а может иметь
бесконечно много решений.
Для
нахождения единственного решения систем
с одинаковым количеством уравнений и
неизвестных есть метод, называемый
метод
Крамера.
Система
n
уравнений с n
неизвестными

имеет
единственное решение, если определитель
матрицы системы отличен от нуля.
Это решение находится по
формулам
Крамера:
![]() ,
,
(3.2)
где
– определитель матрицы системы, а k
– определитель матрицы, полученной
из матрицы системы заменой k-го
столбца столбцом свободных членов.
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Найти линейную комбинацию заданных матриц. Помогите пожалуйста моей подруге.
Котик
Знаток
(316),
закрыт
6 лет назад

Тадасана
Гений
(76838)
6 лет назад
Туповата у тебя полруга, прости…
E – единичная матрица, лямбда – число, ну и пусть вычтет у исходной лямбду из каждого элемента на нлавной диагонали.
I am going through Gilbert Strang’s Intro To Linear Algebra class. I believe I am misunderstanding how the questions in the textbook are written, however.
The first question of section 1.3 is:
Find the linear combination $3s_1 + 4s_2 +5s_3=b$
My understanding of a linear combination was that it was the multiplication of matrices itself that creates a linear combination of the columns.
So, is the answer here:
$begin{bmatrix}s_1 & s_2 & s_3end{bmatrix}begin{bmatrix}3\4\5end{bmatrix}$ = b?
I am confused on the rest of the question as well. It states to:
Write b as a matrix-vector multiplication multiplication $Sx$ with 3,4,5 in $x$. Compute the three dot products (row of S)$cdot x$ such that the following go into columns of S:
$\ s_1 = begin{bmatrix}1\1\1end{bmatrix}, s_2 = begin{bmatrix}0\1\1end{bmatrix}, s_3 = begin{bmatrix}0\0\1end{bmatrix} $
Then, is this asking me to set the question up in the following form:
$begin{bmatrix}1 & 0 & 0 \
1 & 1 & 0 \
1 & 1 & 1 end{bmatrix}begin{bmatrix}3\4\5end{bmatrix}$
And then solve to get
$b = begin{bmatrix}3 & 0 & 0 \
3 & 4 & 0 \
3 & 4 & 5 end{bmatrix}$?
I know this question is long winded and basic, but understanding what’s being asked would be really helpful for me
