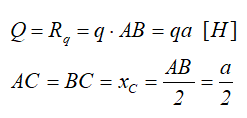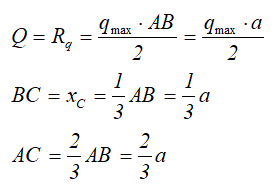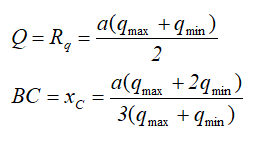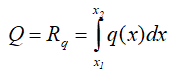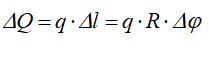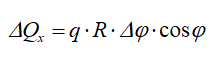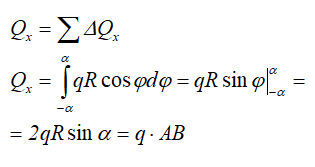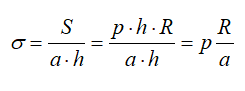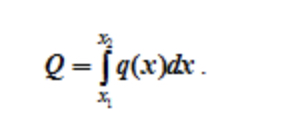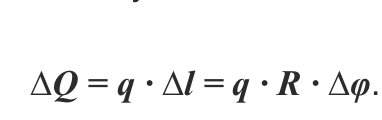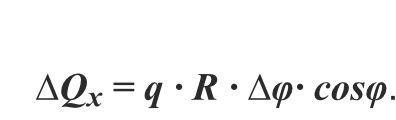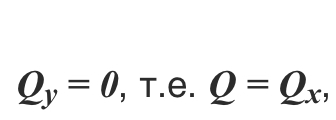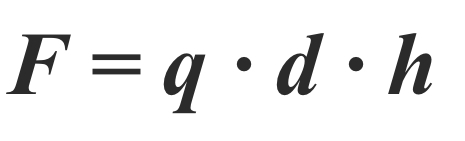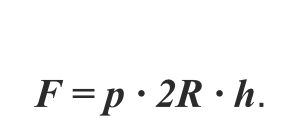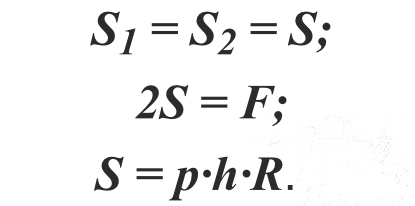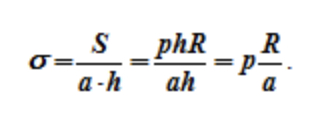Как найти линейную нагрузку

Распределенная нагрузка

Распределенной нагрузкой называют внешние или внутренние усилия, которые приложены не в одной точке твердого тела (т.е. не сосредоточены в одной точке), а равномерно, случайным образом или по заданному закону распределены по его определенной длине, площади (поверхности) или объему.

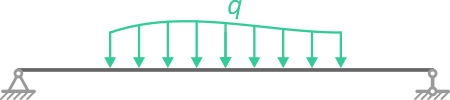
Рассмотрим виды распределенных нагрузок q: линейную, равномерную, треугольную (возрастающую или убывающую), трапециевидную, нелинейную, наклонную (направленную под углом) и замену их результирующей сосредоточенной силой — равнодействующей Q (R_q)

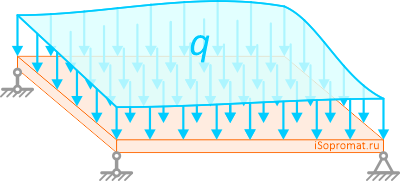
Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.

Это может быть собственный вес элемента конструкции, давление газа или воды, распределенный вес сыпучих материалов, ветровая нагрузка и тому подобное.

Обозначение распределенной нагрузки — q

Размерность:

• линейной нагрузки — Н/м,
• нагрузки распределенной по площади — Н/м²,
• объемной (например при учете собственного веса элементов конструкции) — Н/м³.

или кратные им, например кН/м.

Равнодействующая распределенной нагрузки

При решении некоторых задач технической и теоретической механики, распределенную нагрузку удобно заменять её равнодействующей, обозначаемой Q или R_q, которая для линейного случая распределения, определяется произведением интенсивности нагрузки q на её длину AB.

Равнодействующая распределенной нагрузки действует в точке, расположенной в центре тяжести фигуры, ограниченной профилем её распределения.

Рассмотрим способы замены распределенных нагрузок их равнодействующей.

Равномерно распределенная нагрузка

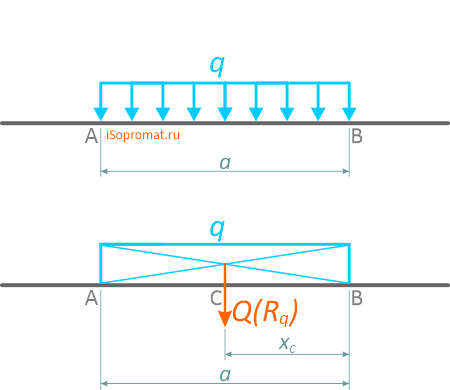
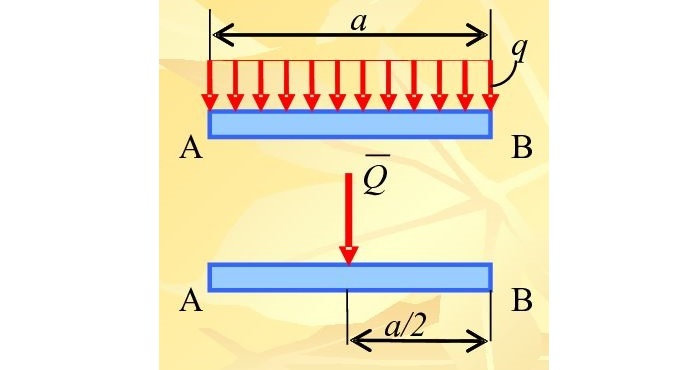
Равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м

может быть заменена сосредоточенной силой Q (R_q)

приложенной в центре (на пересечении диагоналей) прямоугольника, середине отрезка AB.

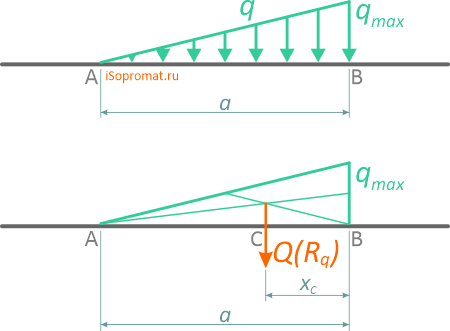
Линейно изменяющаяся (треугольная) нагрузка

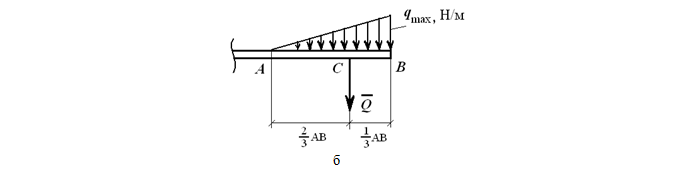
Треугольная, линейно изменяющаяся убывающая (возрастающая) нагрузка

может быть заменена равнодействующей силой, приложенной в точке C

Отметим, что центр тяжести треугольника находится на пересечении его медиан, на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин.

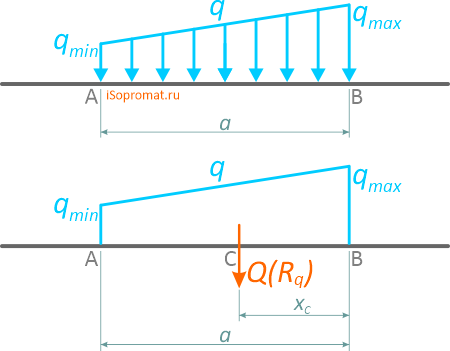
Трапециевидная распределенная нагрузка

Трапециевидная, равномерно убывающая или возрастающая нагрузка характеризуется длиной и двумя значениями интенсивности распределения нагрузки: минимальной q_min и максимальной q_max

Профиль такой нагрузки представляет собой трапецию.
Величина и положение равнодействующей Q в данном случае определяется по выражениям

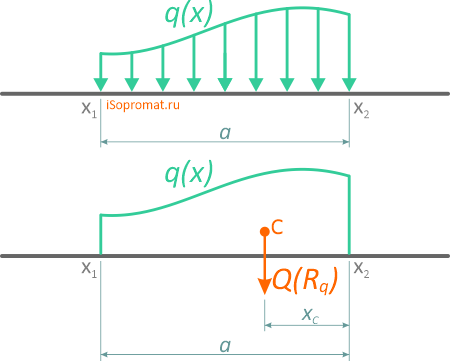
Нелинейная распределенная нагрузка

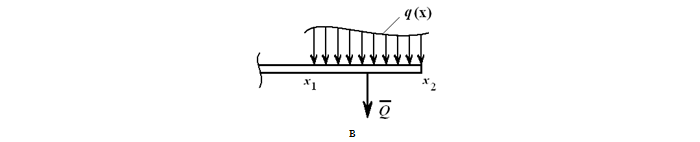
В произвольном общем случае, интенсивность распределения нагрузки по её длине может описываться одной или несколькими функциями.

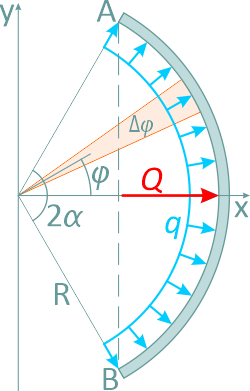
Зная функцию q(x), сосредоточенная эквивалентная (равнодействующая) сила рассчитывается по формуле

Эта сила также приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).

Для расчета точки приложения равнодействующей нагрузки необходимо вычислить координату положения центра тяжести фигуры, образуемой нагрузкой.

Наклонная распределенная нагрузка

В случаях, когда распределенная нагрузка приложена под определенным углом, величина равнодействующей определяется аналогично ранее описанным способам.

При этом угол наклона самой силы будет равен углу наклона нагрузки q.

Например, линия действия равнодействующей наклонной равномерно распределенной нагрузки будет пересекать ось балки ровно посередине между крайними точками её приложения.

Величина равнодействующей будет равна площади параллелограмма, образованного профилем нагрузки.

Как рассчитывается момент распределенной нагрузки

Распределенная нагрузка от давления

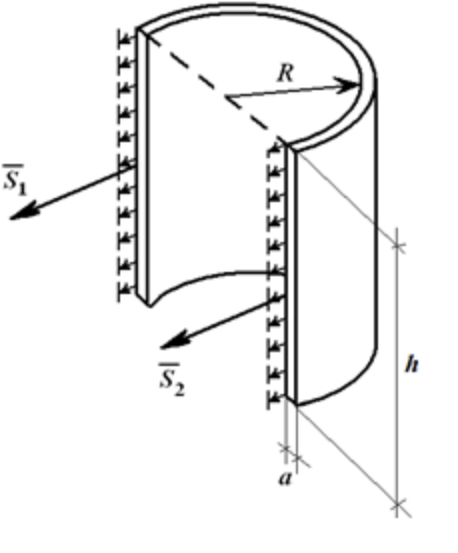
Примером распределенной нагрузки от давления может служить расчет усилий, разрывающих стенки баллона со сжатым газом.

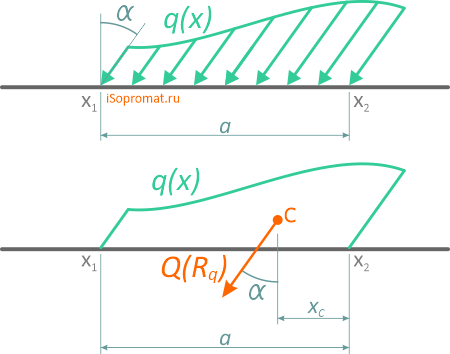
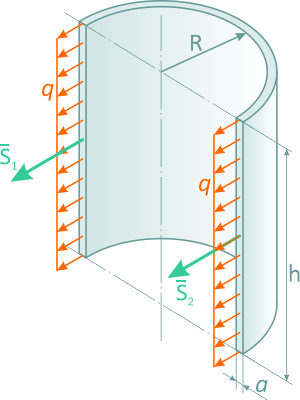
Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м];

где:
R – радиус трубы,
2α – центральный угол,
ось Ox – ось симметрии.

Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:

Проекция этой силы на ось Ox будет

В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:

Q_y = 0, т.е. Q = Q_x,

Тогда

где АВ – хорда, стягивающая концы дуги.

Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует равномерно распределенная нагрузка интенсивностью q = p [Н/м²].

Если цилиндр рассечен по диаметру, то равнодействующая этих сил равна

F = q ∙ d ∙ h

где, d – внутренний диаметр, или

F = p ∙ 2R ∙ h.

Тогда, разрывающие баллон по диаметру усилия:

S₁ = S₂ = S;
2S = F;
S = p∙h∙R.

Если принять что a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно

Примеры решения задач >
Уравнения равновесия системы сил >

Поверхностные и объёмные силы
представляют собой нагрузку, распределённую
по некоторой поверхности или объёму.
Такая нагрузка задаётся интенсивностью

,
которая представляет собой силу,
приходящуюся на единицу некоторого
объёма, или некоторой площади, или
некоторой длины.

Особое место при решении ряда
практически интересных задач занимает
случай плоской распределённой нагрузки,
приложенной по нормали к некоторой
балке. Если вдоль балки направить ось

,
то интенсивность будет функцией
координаты
и измеряется в Н/м. Интенсивность
представляет собой силу, приходящуюся
на единицу длины.

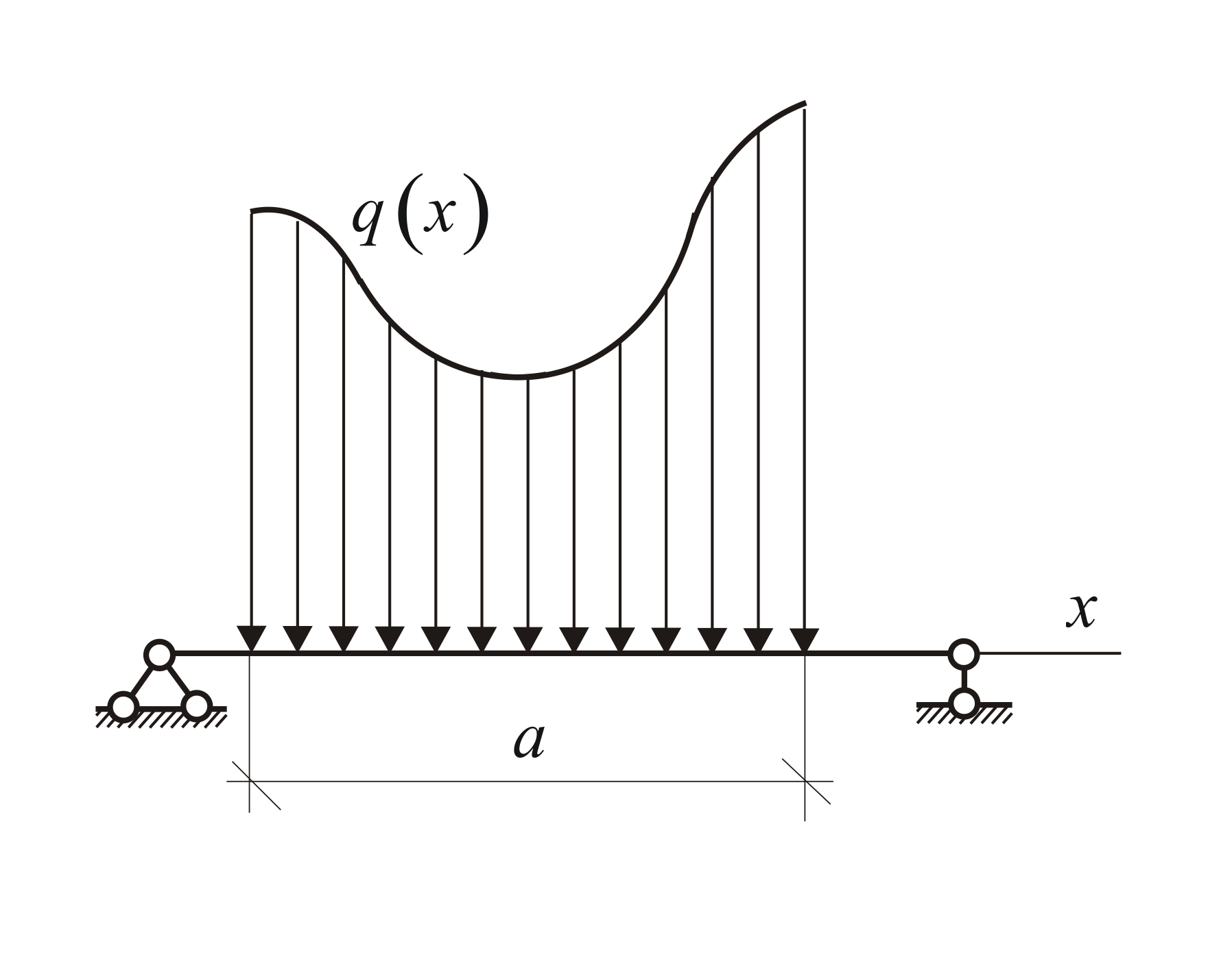
Плоская фигура, ограниченная балкой
и графиком интенсивности нагрузки,
называется эпюрой распределённой
нагрузки (Рис. 1.28). Если по характеру
решаемой задачи можно не учитывать
деформации, т.е. можно считать тело
абсолютно твёрдым, то распределённую
нагрузку можно (и нужно) заменить
равнодействующей.

Рис. 1.28		Рис. 1.29

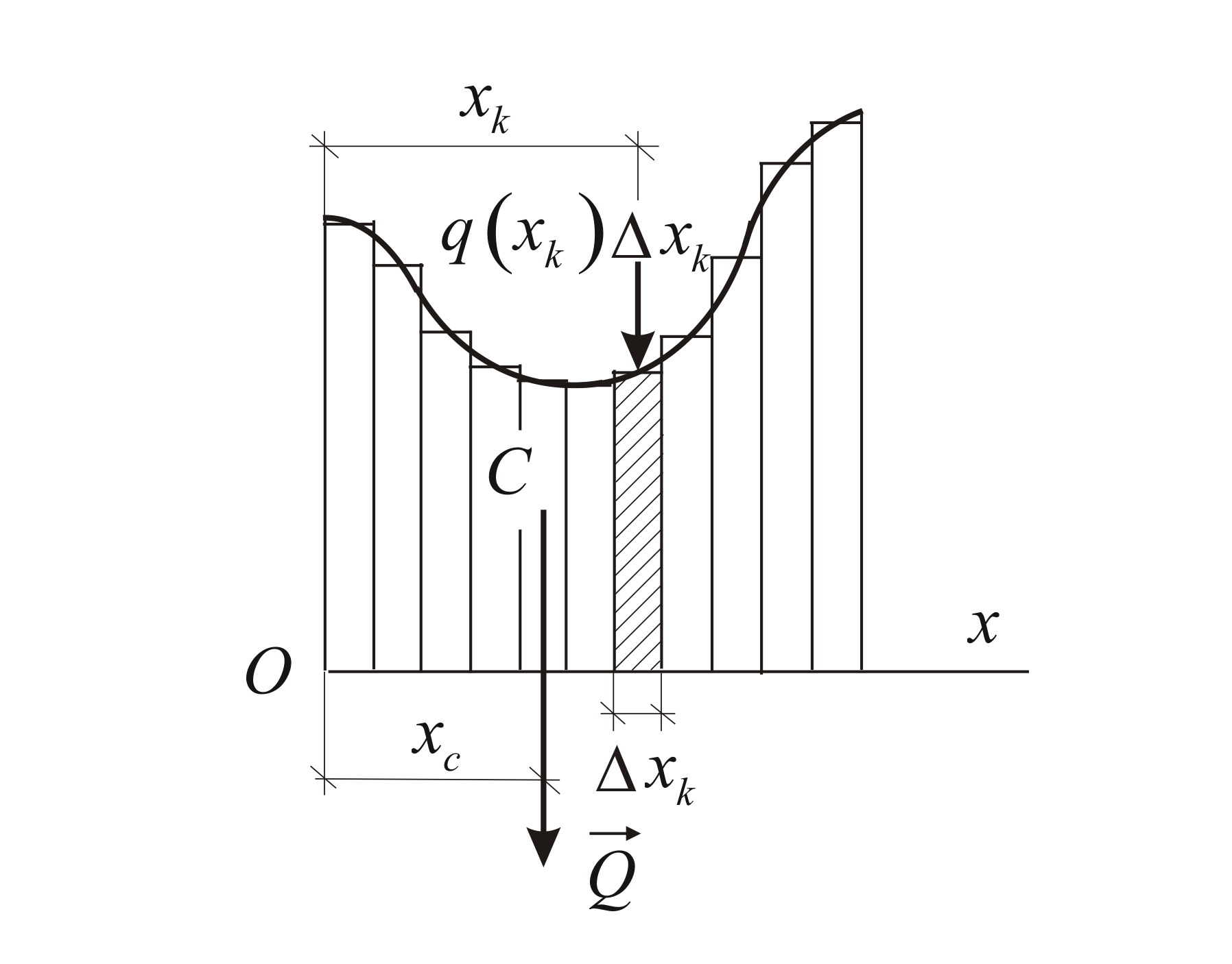
Разобьём балку на
отрезков длиной
,
на каждом из которых будем считать
интенсивность постоянной и равной
,
где
–координата отрезка
.
При этом кривая интенсивности заменяется
ломаной линией, а нагрузка, приходящаяся
на отрезок
,
заменяется сосредоточенной силой
,
приложенной в точке
(Рис. 1.29). Полученная система параллельных
сил имеет равнодействующую, равную
сумме сил, действующих на каждый из
отрезков, приложенную в центре
параллельных сил.

Понятно, что такое представление
тем точнее описывает реальную ситуацию,
чем меньше отрезок
,
т.е. чем больше число отрезков
.
Точный результат получаем, переходя к
пределу при длине отрезка
,
стремящейся к нулю. Предел, получаемый
в результате описанной процедуры,
представляет собой интеграл. Таким
образом, для модуля равнодействующей
получаем:

Для определения координаты точки

приложения равнодействующей используем
теорему Вариньона:

если система сил имеет равнодействующую,
то момент равнодействующей относительно
любого центра (любой оси) равен сумме
моментов всех сил системы относительно
этого центра (этой оси)

Записывая эту теорему для системы сил
в проекциях на ось
и переходя к пределу при длине отрезков,
стремящейся к нулю, получаем:

Очевидно, модуль равнодействующей
численно равен площади эпюры распределённой
нагрузки, а точка её приложения совпадает
с центром тяжести однородной пластины,
имеющей форму эпюры распределённой
нагрузки.

Отметим два часто встречающихся случая.

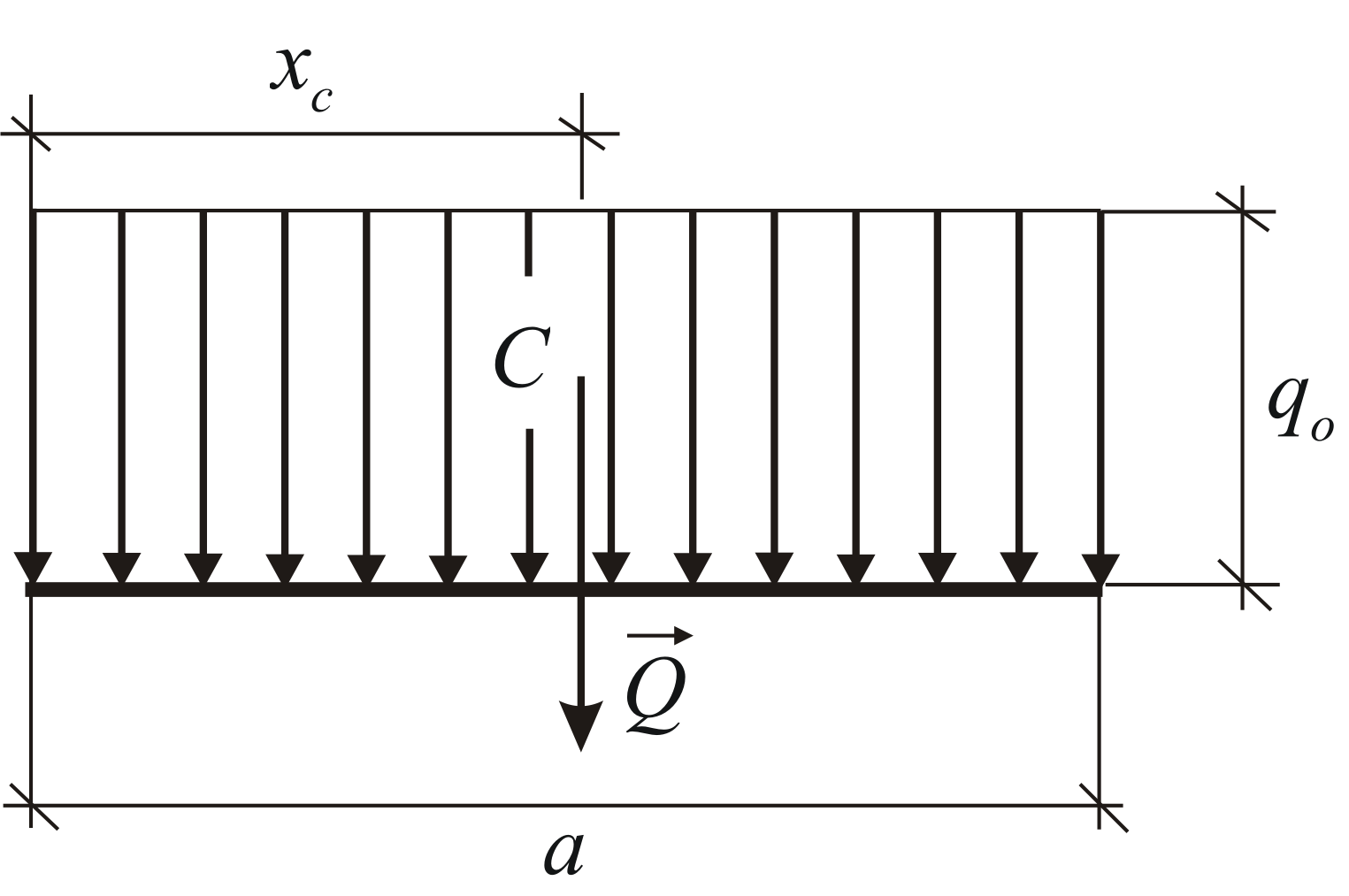
Равномерно распределённая нагрузка,(Рис. 1.30). Модуль равнодействующей и
координата её точки приложения
определяются по формулам:

В инженерной практике такая нагрузка
встречается довольно часто. Равномерно
распределённой в большинстве случаев
можно считать весовую и ветровую
нагрузку.

Рис. 1.30		Рис. 1.31

Линейно
распределённая нагрузка,(Рис. 1.31). В этом случае:

В
частности, давление воды на вертикальную
стенку прямо пропорционально глубине
.

Пример
1.5

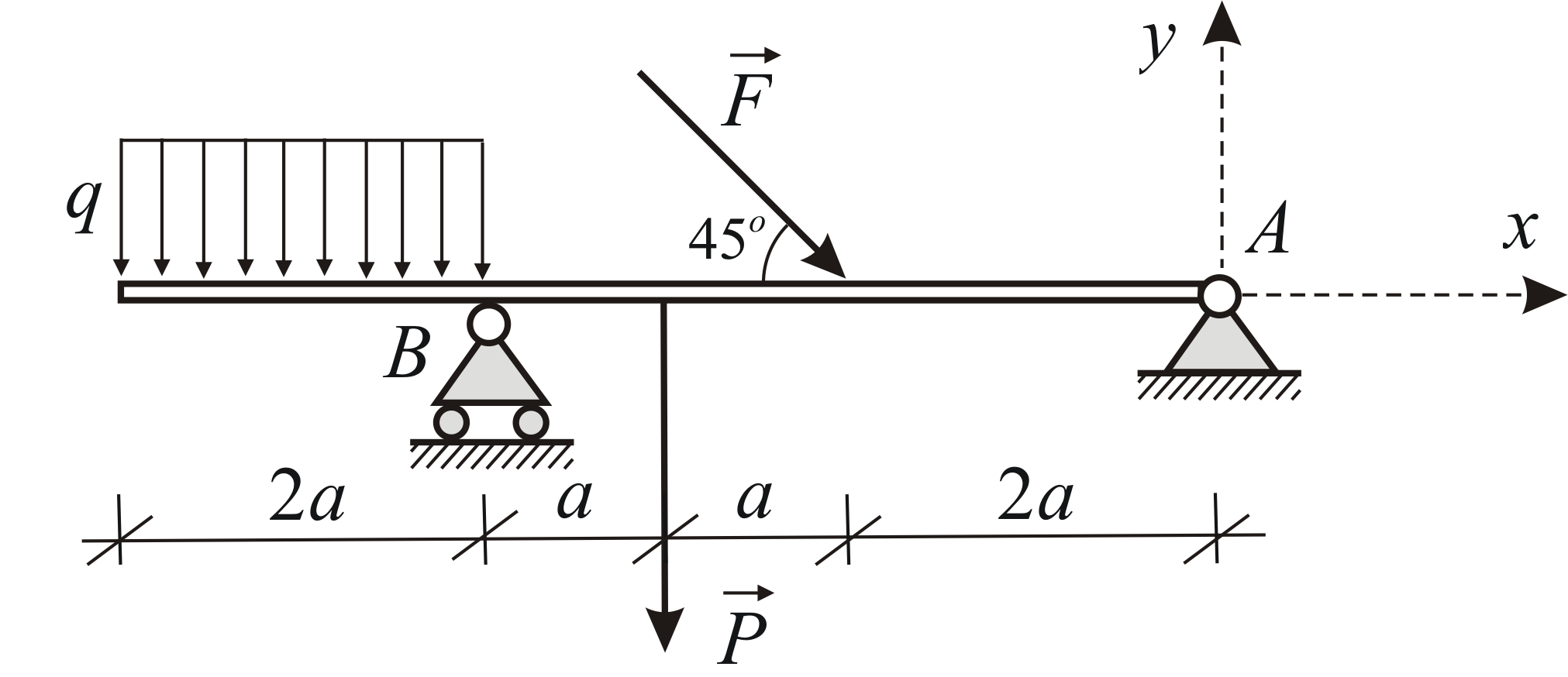
Определить реакции опор
ибалки, находящейся под действием двух
сосредоточенных сил и равномерно
распределённой нагрузки. Дано:

Рис. 1.32

Найдём равнодействующую распределённой
нагрузки. Модуль равнодействующей равен

плечо силы
относительно точкиравноРассмотрим равновесие балки. Силовая
схема представлена на Рис. 1.33.

Рис. 1.33

Условия
равновесия в рассматриваемом случае
имеют вид:

Пример
1.6

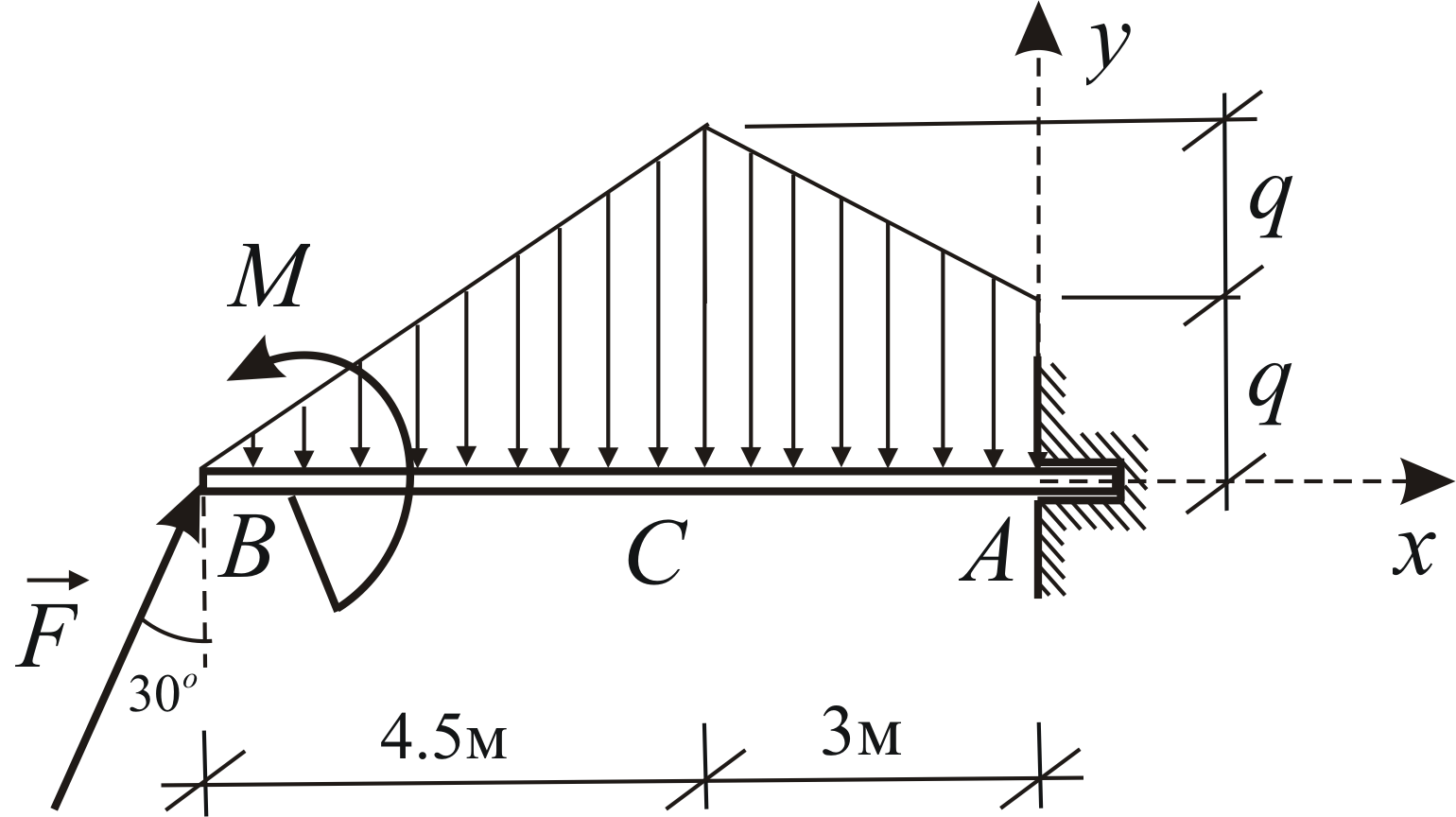
Определить реакцию заделки консольной
балки, находящейся под действием
сосредоточенной силы, пары сил и
распределённой нагрузки (Рис. 1.34).

Дано:

Заменим распределённую нагрузку тремя
сосредоточенными силами. Для этого
разобъём эпюру распределённой нагрузки
на два треугольника и прямоугольник.
Находим

Силовая схема представлена на Рис. 1.35.

Рис. 1.34		Рис. 1.35

Вычислим
плечи равнодействующих относительно
оси

Условия
равновесия в рассматриваемом случае
имеют вид:

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Что
называется интенсивностью распределённой
нагрузки?

2. Как
вычислить модуль равнодействующей
распределённой нагрузки?

3. Как
вычислить координату точки приложения
равнодействующей распределённой

нагрузки?

4. Чему
равен модуль и какова координата точки
приложения равномерно распределённой
нагрузки?

5. Чему
равен модуль и какова координата точки
приложения линейно распределённой
нагрузки?

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из
сборника задач И.В.Мещерского: 4.28;
4.29; 4.30; 4.33; 4.34.

Из
учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплекты СР-2; СР-3.

ПРАКТИЧЕСКИЕ
ЗАНЯТИЯ № 4-5

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #

  03.03.2015560.03 Кб15PSY – recommendation.pdf

• #
• #

Содержание:

1. Сосредоточенные силы и распределенные нагрузки
2. Плоская система параллельных сил
3. Равновесие системы тел
4. Статически обозначенные и статически неопределенные задачи
5. Методика решения задач на равновесие системы тел

Такие силы называются сосредоточенными. Однако в инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности или линии по тому или иному закону. Распределенные силы прежде всего характеризуются интенсивностью q, т.е. величиной силы, приходящейся на единицу поверхности или линии.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Сосредоточенные силы и распределенные нагрузки

Мы рассматривали силы, которые были представлены в виде вектора, приложенного к точке. Однако в природе существует большое количество взаимодействий тел, осуществляются не в точке и которые нельзя представить в виде вектора, приложенного к точке.

Такими силовыми факторами являются силы давления жидкости или газа в поверхность твердых тел, силы тяжести, как массовые силы, электромагнитные силы тому подобное. Поэтому в теоретической механике вводится понятие о распределенных силах, которые делятся на поверхностные и объемные.

Поверхностные силы действуют на некоторую поверхность тела. Объемные силы действуют на каждый элемент объема тела, рассматривается. Примером последних сил является сила притяжения.

В теоретической механике рассматривается воздействие на тело только сосредоточенных сил, приложенных к абсолютно твердым телам. А потому
распределенную нагрузку необходимо заменить его равнодействующей, то есть
сосредоточенной силой. Введем несколько общих положений.

Распределенная нагрузка характеризуется его интенсивностью , то есть величиной силы, приходящейся на единицу объема тела (в случае объемных сил), на единицу площади (в случае поверхностных сил) и на единицу длины (если поверхность, на которую действует нагрузка, можно считать линией, то есть шириной поверхности можно пренебречь). В последнем случае распределенная нагрузка называется плоской, на
силовых схемах оно изображается в виде эпюры элементарных сил, то есть графика интенсивности нагрузки, приложенная к линейному элементу тела.

В общем случае распределенная нагрузка изображается в виде определенной кривой, отражающей данный закон изменения интенсивности нагрузки на участке тела (рис. 1.20). Направление действия нагрузки показывается стрелками.

Сначала рассмотрим равномерно распределенную нагрузку и нагрузку, распределенную по линейному закону. Заменяем распределенную нагрузку сосредоточенной силой.

Рассмотрим эти два случая:

— равномерно распределенная нагрузка (или нагрузка, распределенная по закону прямоугольника) изображается на схемах в виде прямоугольника, размеры которого таковы: высота — это интенсивность нагрузки , длина — это длина l участка тела, на которой действует нагрузка. Стрелки показывают направление действия нагрузки (рис. 1.21). Для того, чтобы заменить эту нагрузку равнодействующей силой , надо определить ее. В данном случае

Q = q · l,

где q — интенсивность нагрузки, Н/м; l — длина участка тела, на которой приложенная нагрузка, м.

Точка C приложения равнодействующей силы  размещается посередине участка тела, на которой действует нагрузка. То есть , а направление совпадает с направлением распределенной нагрузки.

— нагрузка распределена по линейному закону (то есть по закону треугольника). В этом случае (рис. 1.22) интенсивность распределенной нагрузки на участке l меняется от 0 до максимального значения q_max. Равнодействующая сила  от этой нагрузки по величине равна

Точка C приложения равнодействующей  расположена на расстоянии  или , а направление совпадает с направлением нагрузки.

Плоская система параллельных сил

Когда линии действия всех сил параллельны, то всегда в плоскости можно так
расположить оси координат, одна из них будет обязательно параллельной заданным силам, а вторая — перпендикулярной. А потому, чтобы тело под действием плоской системы параллельных сил находилось в равновесии, необходимо приравнять к нулю алгебраическую сумму проекций всех сил на параллельную ось и алгебраическую сумму моментов всех сил относительно произвольной точки. В данном случае система условий равновесия (1.54) упрощается и будет иметь такой вид

Для равновесия тела, находящегося под действием системы параллельных сил
на плоскости, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил
на ось, параллельная силам, и алгебраическая сумма моментов всех сил относительно произвольной точки А плоскости равны нулю.

Для системы параллельных сил на плоскости можно использовать и такие условия равновесия

Для равновесия тела, находящегося под действием системы параллельных сил на плоскости, необходимо и достаточно, чтобы алгебраические суммы моментов всех
сил относительно любых двух точек плоскости равны нулю.

Однако для этих условиях существует ограничение: линия АВ, которой можно соединить
центры моментов, не должна быть параллельной силам.

Данные условия наиболее пригодны при расчетах двухопорных балок. Используя эти условия, составляют алгебраические суммы моментов всех сил относительно точек A и B, в которых установлены опоры балки.

Рассмотрим примеры задач на равновесие тела под действием плоской системы произвольных сил.

Пример:

Однородная балка АВ прямоугольного сечения весом 400 Н имеет один конец А, который закреплен шарнирно, и опирается на точечную опору O (рис. 1.23). Ко второму концу балки В подвешен груз весом 200 Н. Длина балки 4 м, точечная опора расположена на расстоянии ¾ длины балки от шарнирной опоры. Угол наклона балки к горизонту составляет α = 30º.

Определить реакции опор балки.

Краткое условие задачи:

G = 400 H ;

Q = 200 H ;

AB = 4 м;

AO = 3/4 AB = 3 м ;

α = 30º.

R_A = ?

R_о = ?

Решение.

Составляем расчетно–силовую схему задачи. Приложим к оси балки заданные активные силы: силу тяжести  самой балки и силу притяжения  груза. Сила притяжения балки приложена посередине балки в точке C (поскольку балка однородна) и направлена ​​вертикально вниз. Сила притяжения груза приложена к концу балки В и направлена ​​вертикально вниз.

Далее условно освобождаем балку от связей и заменяем их соответствующими реакциями связей. В точке A размещена неподвижная шарнирная опора, она имеет
две составляющие реакции _A и _A, которые расположены вдоль соответствующих осей
координат. В точке O — точечная опора, которая имеет одну реакцию _o, что направлена ​​перпендикулярно к балке.

Таким образом, балка находится в равновесии под действием плоской системы произвольных сил. Для решения этой задачи используем условия равновесия (1.54),

Поскольку оси координат x и y заданные по условию задачи, то составим соответствующие уравнения равновесия

Если подставить значения известных величин в эти уравнения равновесия, то получим

С третьего уравнения вычислим реакцию R_o:

R_o =   = 461,86 Н,

и подставим ее значение в первые два уравнения. Будем иметь

Х_А =   = R_o = 230,93 Н;

Y_А = 400 + 200 – 0,866 · 461,86 = 160,04 Н.

Поскольку определены две составляющие реакции, приложенные в точке A, — Х_А  и Y_А, то геометрическим добавлением можно вычислить модуль полной реакции R_A. А именно:

Таким образом определении все искомые реакции.

Ответ: R_A = 280,97 Н;

R_о = 461,86 Н.

Пример.

Определить реакции опоры однородной балки АВ прямоугольного сечения, один конец которого A жестко закреплен в стене и находящийся под действием сосредоточенной силы P = 4,0 kH, пары сил с моментом m = 2,0 kH · м и равномерно распределенной нагрузки интенсивностью q = 1,5 .  Длина балки АВ — 5 м, равномерно распределенная
нагрузка действует на участке 3 м от точки A. Угол наклона сосредоточенной силы к горизонту составляет α = 30º, оси x и y показаны на рис. 1.24.

Краткое условие задачи:

P = 4,0 kH;

m = 2,0 kH · м;

q = 1,5 ;

АВ = 5 м;

AС = 3 м;

α = 30º

R_A = ?

М_A = ?

Решение.

Составляем расчетно-силовую схему. Покажем все силы, приложенные к балке АВ. Прежде всего, это заданные активные силы — сила , приложена к концу балки В и направлена под углом α к горизонту. Равномерно распределенную нагрузка заменяем сосредоточенной силой , которая равна

= q · AC =1,5 · 3 = 4,5 kH .

Сила приложена посредине участка AC и направлена ​​в ту же сторону, что и сама нагрузка, то есть вертикально вниз. Покажем на силовой схеме пару сил, которая определяется моментом m.

Далее условно освобождаем балку от вязи и заменяем ее соответствующими реакциями вязи. В точке A — жесткое закрепление балки в стене, а потому оно имеет две составляющие реакции: _A, _A, которые расположены вдоль соответствующих осей
координат, и реактивный момент M_A. Направление этого неизвестного момента
показываем на силовой схеме произвольно, например, — против направления стрелки
часов. Если же при окончательном определении момента M_A получим отрицательный знак, то получим, что действительное направление момента — противоположно. Покажем на силовой схеме линейные и угловые размеры. Оси координат показаны на схеме.

Как видно из построенной расчетно–силовой схемы, балка находится под действием плоской системы произвольных сил. Используем условия равновесия (1.54). А именно            = 0.

Составим соответствующие уравнения равновесия

Если подставить значения известных величин в эти уравнения равновесия, то получаем

Из первого уравнения вычислим X_A:

X_A = 4,0 =  = 3,46 kH.

Из второго уравнения вычислим Y_A:

Y_A = 4,5 + 4,0 ·  = 6,50 kH.

С третьего уравнения вычислим M_A:

M_A = 2,0 + 4,5  + 4,0  · 5 = 2,0 + 6,75 + 10,0 = 18,75 kH.

Поскольку составляющие реакций X_A и Y_A, приложенных в точке A, вычислены, то можно найти модуль R_A полной реакции в точке A. Будем иметь

Таким образом, определены все искомые реакции.

Ответ: R_A = 4,30 kH; M_A = 18,75 kH.

Равновесие системы тел

Системой тел называется совокупность нескольких тел, или которые опираются друг на друга, или соединены шарнирами, которые дают возможность относительного движения тел.

При решении задач на систему тел различают силы внешние и внутренние.

Внешние силы — это силы взаимодействия тел данной системы с другими телами, которые не входят в состав системы.

Внутренние силы — это силы взаимодействия между отдельными телами, которые входят в состав данной системы. Внутренние силы существуют попарно, как действие и
противодействие.

Статически обозначенные и статически неопределенные задачи

Задача является статически обозначенной, если для нее можно составить такое
количество уравнений равновесия материальной системы, не меньше, чем число
неизвестных.

Задача, является статически неопределенной, если число уравнений равновесия
системы меньше, чем число неизвестных.

В теоретической механике рассматриваются только статически обозначенные
материальные системы.

Методика решения задач на равновесие системы тел

Равновесие системы тел можно рассматривать в целом под действием только
внешних сил. Но может так случиться, что количество уравнений равновесия будет
меньше, чем количество неизвестных. Тогда необходимо рассматривать равновесие
отдельных тел системы, условно разделяя ее обязательно по внутренним связям. Причем необходимо учитывать, что внутренние силы реакций входят попарно, как действие и противодействие.

Рассмотрим пример решения задач на равновесие системы тел.

Пример.

На трех-шарнирную арку А В С (рис. 1.25) действует вертикальная сила Р = 10 kH. Вес каждой части балки Q₁ = Q₂ = 6 kH. Определить реакции шарниров А, В, С арки, размеры которой данные на рисунке.

Решение.

Как видно из схемы, заданная система тел состоит из двух пиварок I и II, которые соединены шарниром в точке С. Составим расчетно–силовую схему, где покажем заданные активные силы Q₁, Q₂, и реакции связей: в точках A и B (неподвижные шарнирные опоры) — _A ,A и _В , В и в точке C (шарнирное соединение) — _C , ´_C и _{C ,} ´_С. Эти неизвестные реакции в точке С являются внутренними силами системы тел, а потому _C = ´_C  и _C = ´_С.

Покажем оси прямоугольной декартовой системы координат Axy.

Условно разделяем систему тел на два отдельных тела по шарниру С. Действие отброшенной части заменяем двумя реакциями _C и _C, которые равны

Теперь рассмотрим отдельно равновесие каждого тела, для чего составим две системы уравнений равновесия. Используем условия равновесия.

Для первого тела (левая половина арки):

 = 0; Х_А – Х_С = 0,

    = 0; Y_A + Y_C – Q₁ – P = 0,

  = 0; Х_С · 4 + Y_C · 5 – Q₁ · 1 – P · 4 = 0.

Для второго тела (правая половина арки):

 = 0; Х_B – Х´_С = 0,

    = 0; Y_B + Y´_C – Q₂ – P = 0,

 = 0; Q₂ · 1 – Х´_С · 4 + Y´_C · 5 = 0.

Как видно из полученных шести уравнений равновесия, в них содержатся шесть неизвестных: Х_А, Х_B, Х_С, Y_A, Y_B, Y_{C .}

Определим эти неизвестные величины. С третьего уравнения второй системы определим Y´_{C .} Перепишем это уравнение следующим образом:

5Y´_C = 4Х´_С – Q₂,

откуда находим реакцию Y´_C :

Поскольку численно Y´_C = Y_C , а Х_С = Х´_С, то подставив значения этих реакций в третье уравнение первой системы, получаем

или

8Х_С = Q₁ + Q₂ + 4P,

откуда

Теперь есть возможность определить неизвестную реакцию Y´_C . Подставив значение X_C в третье уравнение второй системы, будем иметь

Из первого уравнения первой системы имеем X_A = X_C = 6,5 kH. А с первого уравнения второй системы должны X_B = – X´_C = – 6,5 kH. Направление этой реакции противоположно показанному на силовой схеме. Из второго уравнения первой системы получаем

Y_A = Q₁ + P – Y_C = 6,0 + 10,0 – 4,0 = 12,0 kH.

Из второго уравнения второй системы вычислим последнюю неизвестную реакцию Y_B. Она будет равняться Y_B = Y´_C + Q₂ = 4,0 + 6,0 = 10,0 kH.

Таким образом вычислено все искомые величины.

Ответ:

X_A = 6,5 kH; Y_A = 12,0 kH; X_B = – 6,5 kH; Y_B = 10,0 kH; X_C = 6,5 kH; Y_C = 4,0 kH.

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Произвольная пространственная система сил
12. Плоская система сходящихся сил
13. Пространственная система сходящихся сил
14. Равновесие тела под действием пространственной системы сил
15. Естественный способ задания движения точки
16. Центр параллельных сил
17. Параллельные силы
18. Система произвольно расположенных сил
19. Кинематика
20. Кинематика твердого тела
21. Движения твердого тела
22. Динамика материальной точки
23. Динамика механической системы
24. Динамика плоского движения твердого тела
25. Динамика относительного движения материальной точки
26. Динамика твердого тела
27. Кинематика простейших движений твердого тела
28. Общее уравнение динамики
29. Работа и мощность силы
30. Обратная задача динамики
31. Поступательное и вращательное движение твердого тела
32. Плоскопараллельное (плоское) движение твёрдого тела
33. Сферическое движение твёрдого тела
34. Движение свободного твердого тела
35. Сложное движение твердого тела
36. Сложное движение точки
37. Плоское движение тела
38. Статика твердого тела
39. Равновесие составной конструкции
40. Равновесие с учетом сил трения
41. Центр масс
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

Взаимодействия с деталями, отдельными элементами и конструкциями механизма задается с помощью нагрузок. В плоскости задается интенсивность взаимодействия конструкции по длине, а в пространстве – по её площади.

Распределённая нагрузка на балку задается площадью, обозначается буквой q и измеряется в [H/м³] для объемной конструкции, в [H/м²] — для площади, для линейной – в [H/м].

Продемонстрируем это на рисунке:

Нагрузку также можно заменить тягой, рассредоточенной по всей поверхности. Значение определяется по формуле:

Q = q ∗ AB⌈H⌉

здесь AB является тяжестью, q – интенсивностью, которая измеряется в [H/м].

Примечательно, что сила приложена к середине данного отрезка AB.

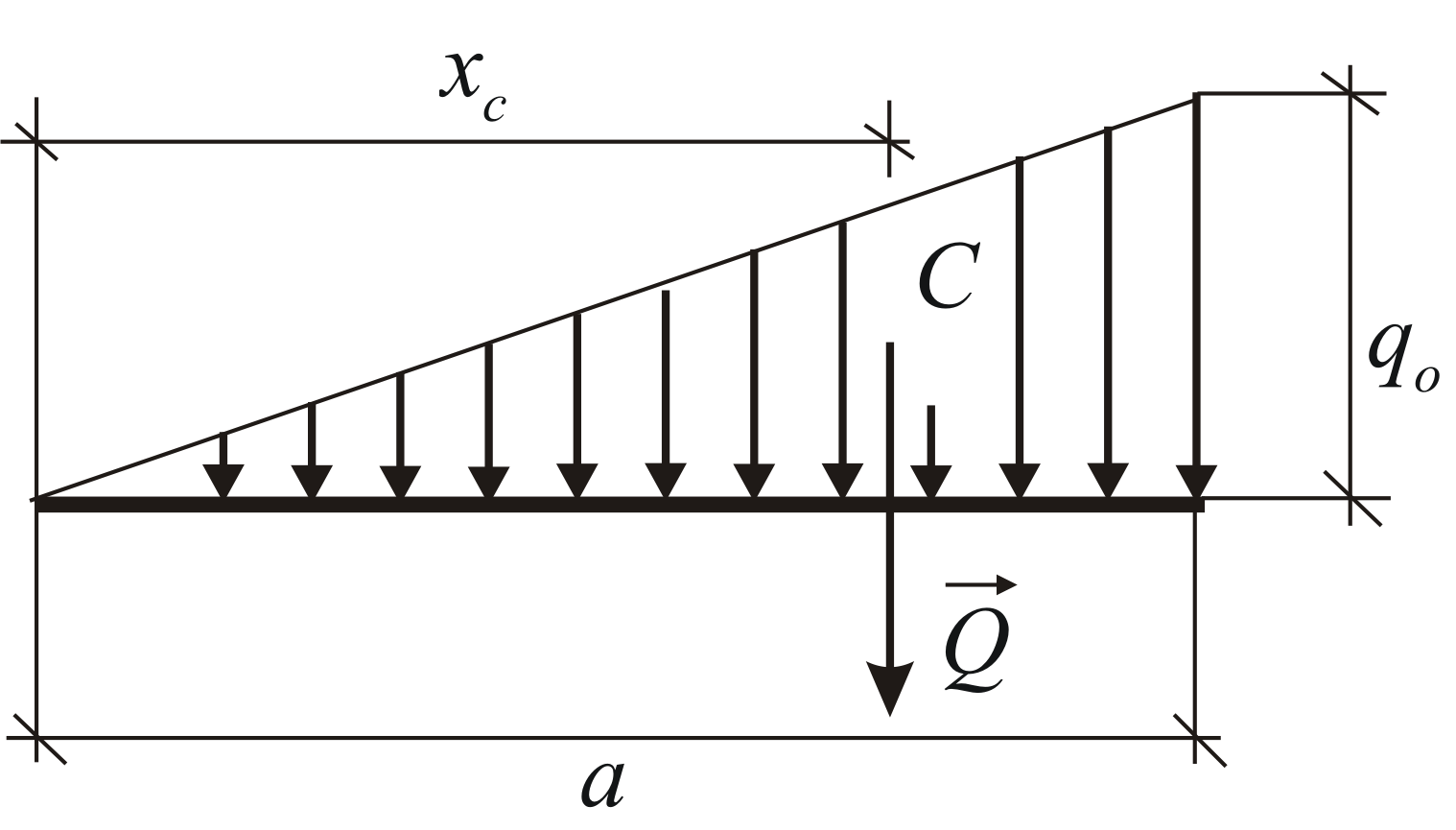
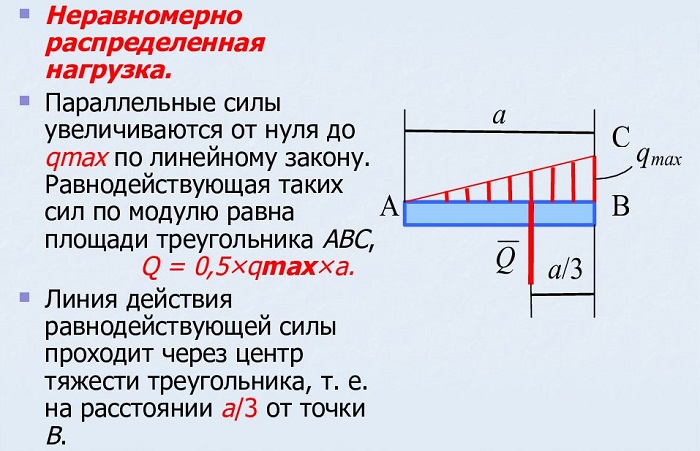
На данном рисунке представлен расчёт возрастающей нагрузки, которую можно заменить равнодействующей единицей, рассчитываемое по формуле:

Q = q_max ∗ AB/2

где q_max – максимальная интенсивность [Н/м]. 

Q приложена к точке C, где AC равно: AC = 2/3 AB 

Рассматривая функцию q(x), представленную на рисунке:

можно высчитать значение эквивалентной силы по формуле:

Равномерно и неравномерно распределенная нагрузка на балку

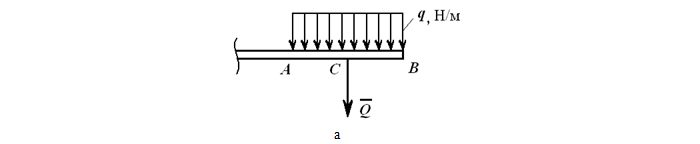
Распределение сил, которые лежат в одной плоскости, задается равномерно распределенной тяжестью. Основным обозначением является интенсивность q – предельная тяга, несущая равнодействующую на единицу длины нагруженного участка АВ длиной а. 

Единицы измерения распределённой нагрузки [Н/м].

Её также можно заменить на величину Q, которая приложена в середину AB. 

Составим формулу: Q = q∗a

Неравномерно распределённую нагрузку чаще всего упрощают, приводя её к эквивалентной равномерно распределенной, чтобы упростить расчеты.

При построении также следует учитывать максимальный прогиб балки, её прочность, расчетную опорную реакцию и моментальную опору.

Пример решения задач с распределенной нагрузкой

Рассмотрим пример распределенной нагрузки на балку. Им может послужить тяга, благодаря которой происходит разрыв стальной стенки баллона с некоторым газом.

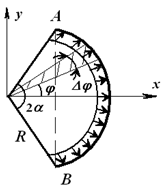
Для начала определяем результирующую давления в металлической трубе. Интенсивность равна q, радиус этого сектора трубы – R, ось симметрии Оx, а 2α – это центральный угол. Представим это на рисунке:

Выделим элемент сектора трубы ∆ϕ.

Затем определим единицу силы ∆Q. Она действует на плоскость дуги. Составим формулу:

Проекция результирующей тяги на ось Оx является:

Исходя из вышесказанного, можно найти проекцию этой же силы на ось Оy:

AB является хордой, которая стягивает дугу.

В нашей задаче сосуд – это ёмкость цилиндрической формы с высотой H, внутренним давлением P, действующим на стенки, и нагрузкой q = p [Н/м²]. 

Разделим цилиндр вдоль его диаметра. 

Исходя из этого, равнодействующая результирующих сил определяется по формуле:

где d – это внутренний диаметр цилиндра, h — его высота. 

Формулу также можно записать следующим образом:

Итак, почему баллон имеет способность разрываться? На его стенки действуют значения S1, S2, S3 (площади), а также F, p (плотность), h (высота цилиндра) и R (его радиус). Рассчитаем их по формулам:

 

Изобразим баллон в момент разрыва:

Учтём a – толщину ёмкости. Таким образом напряжение, которое растягивает баллон, (усилия распространяются в том числе на крышку и дно цилиндра) равно:

Важную роль при решении практических задач также играет эпюра распределенной нагрузки – плоская фигура, которая ограничена графиком. Величина, действующая на балку, называется интенсивностью – силой, которая распространяется на единицы площади, объема или длины.

Научные статьи на тему «Линейно‐распределенные нагрузки»

Определение опорных реакций в балке

при воздействии сосредоточенной силы Р образуется прогиб и углы поворота поперечных сечений, то есть линейные…
Рассмотрим алгоритм решения задач:

на расчетной схеме изображаем изгибающий момент, сосредоточенную и распределенную…
перемещений;
проводим проверку найденных значений и находим значения линейных и угловых перемещений…
мысленно отбросим опоры и на их месте появятся реакции, направленные вертикально;
если на схеме показа распределенная…
нагрузка, то ее заменяют на эквивалентную ей силу, которая равна площади эпюры нагрузки и приложена

Статья от экспертов

Идентификация линейной обобщенной нагрузки в трехфазной трехпроводной сети в задаче распределения фактических вкладов в точке общего присоединения

На основе матричного метода анализа электрических цепей определена структура эквивалентной схемы замещения обобщенной нагрузки. Предложен способ приближенного определения параметров эквивалентной схемы замещения обобщенной нагрузки. Выполнен анализ ошибок приближенного определения параметров эквивалентной схемы замещения обобщенной нагрузки применительно к задаче распределения фактических вкладов в точке общего присоединения.

Нагрузка в теоретической механике

вдоль заданного отрезка, согласно линейному закону, интенсивность $q$ будет представлять переменную…
определенной площадке, нагрузка таким образом будет распределенной….
Распределенная и сосредоточенная нагрузка
В реальности зачастую встречаются силы, которые приложены не…
Распределенная нагрузка с постоянной интенсивностью по всей длине участка считается равномерно распределенной…
Распределенная нагрузка с постоянной интенсивностью может заменяться сосредоточенной силой: $Q = ql$

Статья от экспертов

Распределенная инструментальная среда словарного морфологического анализа для обработки русского языка

В статье рассмотрен подход к масштабированию сервиса морфологического разбора слов естественного языка при обработке различных коллекций документов на русском языке. Выполнен обзор и критический анализ существующих решений. Сформированы требования к инструментальной среде словарного морфологического анализатора. Распределенная архитектура Web-сервиса морфологического анализа, предназначенного для обработки крупных коллекций документов на русском языке, представлена в виде структурной модели. Данная архитектура реализована в виде прототипа системы на языке программирования Ruby. Приведена структура используемого морфологического словаря в виде реляционной схемы. Испытания данного метода в распределенной вычислительной среде показали линейную масштабируемость предлагаемого решения. Конфигурация эксперимента включает систему генерации нагрузки в виде HTTP-запросов, систему балансировки нагрузки на рабочие узлы распределенной системы, серверы приложений с функционирующим анализатором и …