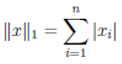Определение
1.
Линейной
оболочкой
заданной
конечной совокупности
элементов векторного пространства
n
над полем К называется множество всех
линейных комбинаций этих элементов с
коэффициентами из поля К. При этом сама
совокупность
называется порождающей
системой
данной линейной оболочки, а сама линейная
оболочка обозначается символом
.
Линейные оболочки
обладают следующими свойствами:
.
Линейная оболочка элементов векторного
пространства
n
является подпространством М векторного
пространства
n.
Данный
результат следует из определения
линейной оболочки: сумма
двух векторов из линейной оболочки
будет принадлежать линейной оболочки
(одна из линейных комбинаций), произведение
вектора из линейной оболочки также
будет принадлежать линейной оболочки.
.
Линейная оболочка может совпадать со
всем пространством Rn
(если образующая
система является базисом
в пространстве Rn
)
.
Линейная оболочка
является наименьшим подпространством,
содержащим элементы
.
Все остальные подпространства могут
только содержать вектора порождающей
системы или их возможные комбинации.
.
Если какой-нибудь элемент из порождающей
системы элементов
есть линейная комбинация остальных
элементов этой системы, то его можно
удалить из порождающей системы, не
изменив при этом линейной оболочки.
.
Если координатная матрица системы
образующих
имеет ранг р, где
,
то любая линейно независимая система
,
является базисом линейной оболочки
,
а сама линейная оболочка будет
подпространством размерности р,
.
Примеры.
-
Если
a,
b,
с – геометрические векторы, лежащие
на одной прямой. В этом случае линейная
оболочка L(а,b,c)=
L(a).Здесь
линейная оболочка является одномерным
пространством, которое состоит из всех
вектор, лежащих на прямой, причем вектор
а
–является базисом. -
Пусть
a,
b,
с – геометрические векторы, причем a,
b
не коллинеарны, с = а + b.
В этом случае линейная оболочка L(а,b,c)=
L(a,b).Здесь
линейная оболочка является двумерным
пространством, состоящем из всех
векторов, компланарных с векторами a
и b.
Вектора а,b
составляют базис в L(a,b).
Любой вектор из L
представляется в виде линейной комбинации
векторов а
и b.
Вообще,
в конечномерном пространстве R
всякое подпространство L
является линейной
оболочкой некоторой системы векторов.
Рассмотри
следующую задачу.
В евклидовом пространстве En
задана линейная оболочка
,
где k
n.
Требуется:
1)Найти
размерность и базис линейной оболочки
;
2)Выделить в линейной оболочке
ортогональный базис и
достроить
его до
ортонормированного базиса евклидова
пространства
En.
Если
схема решения первой задачи нам знакома,
то решение второй задачи строится на
следующем теоретическом результате.
Теорема
(Грама
– Шмидта)
Пусть
– система линейно независимых векторов
в евклидовом пространстве, где k
n,
являющихся образующей системой линейной
оболочки
.
Система векторов
,
описываемая формулами
,
,
,
. . .
где
коэффициенты
,
,
образует
ортогональный
базис
линейной оболочки
.
Доказательство.
Для
доказательства теоремы достаточно
доказать следующее утверждение: вектор
ортогонален вектору
.
Действительно,
умножая скалярно вектор
на вектор
,
получим
=

Следствие.
Результат теоремы дает
алгоритм последовательной ортогонализации
системы линейно независимых элементов
( так
называемый
метод Грама – Шмидта).
Пример
-
В
евклидовом пространстве E4
линейная оболочка
задана образующей системой векторов
с координатами

Требуется:
а)
найти размерность и базис линейной
оболочки
б)
указать в линейной оболочке
ортонормированный базис
и
достроить его до ортонормированного
базиса евклидова
пространства
E4.
Решение.
Рассмотрим координатную матрицу

Так как
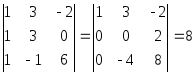
то
,
элементы
линейно независимы в E4
и образуют базис данной линейной
оболочки, являющейся подпространством
в E4.
Для
построения ортонормированного базиса
в E4
применим метод
ортогонализации
Грама-Шмидта. Получим
,
,
.
Записывая векторы
столбцами их координат, последовательно
найдем
.
Легко
проверить, что полученные элементы
попарно ортогональны. Найдем ортогональный
им вектор
.
Пусть

то неизвестные координаты
вектора Y4
найдутся из условий
,
,
.
Так
как
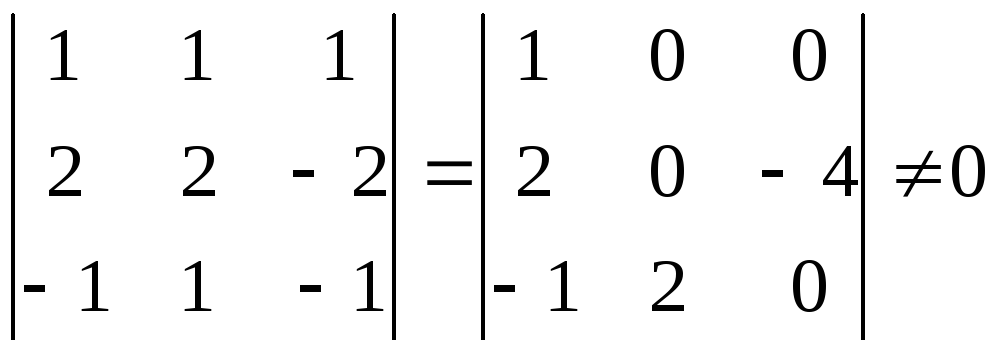
в последней системе неизвестные
можно взять в качестве базисных
неизвестных.
Если
для свободной (небазисной) неизвестной
,
то

Нормировав
найденные векторы
,
построим ортонормированный базис в E4:

Задача
решена.
В
завершении параграфа введем важное
определение.
Пусть
– – базис в En
и векторы
представлены в этом базисе своими
разложениями
.
Тогда
скалярное произведение этих векторов
имеет вид
или в матричной форме
,
где
– столбцы координат векторов
в базисе
а симметричная матрица
составлена из скалярных произведений
базисных векторов:

В
общем случае в качестве элементов
матрицы А рассматривают скалярные
произведения произвольной системы
векторов а1,
а2,…,
аn
Определение
3.
Определитель
матрицы А
скалярных произведений заданной системы
векторов
называют определителем
Грама.
Теорема
Произвольная
система
векторов,
заданных в ортонормированном
базисе,
будет линейно
независимой,
если ее определитель
Грама отличен от нуля.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 – 2 1 – 1 1 2 – 2 A = 3 – 2 1 2 1 2 3 – 1 – 2 = 3 · 1 · ( – 2 ) + ( – 2 ) · 2 · 3 + 1 · 2 · ( – 1 ) – 1 · 1 · 3 – ( – 2 ) · 2 · ( – 2 ) – 3 · 2 · ( – 1 ) = = – 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , – 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , – 1 , – 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 – 1 1 0 1 – 2 1
1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 – 2 – 1
1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , – 1 , – 2 ) a ( 2 ) = ( 0 , 2 , 1 , – 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства – e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n – некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 – x 1 ) · e ( 1 ) + ( x
2 – x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 – x 2 ) , . . . , ( x
n – x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , – 1 , 1 ) e ( 2 ) = ( 3 , 2 , – 5 ) e ( 3 ) = ( 2 , 1 , – 3 ) x = ( 6 , 2 , – 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 – 1 1 3 2 – 5 2 1 – 3
1 – 1 1 0 5 – 8 0 3 – 5
1 – 1 1 0 5 – 8 0 0 – 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 – 1 2 1 1 – 5 – 3 = – 1 ∆ x
1 = 6 3 2 2 2 1 – 7 – 5 – 3 = – 1 , x
1 ∆ = – 1 – 1 = 1 ∆ x
2 = 1 6 2 – 1 2 1 1 – 7 – 3 = – 1 , x
2 ∆ = – 1 – 1 = 1 ∆ x
3 = 1 3 6 – 1 2 2 1 – 5 – 7 = – 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) – координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
Линейные оболочки и подпространства
Определение. Подпространством 
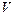
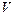

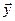
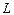
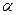
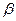
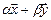
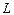
Утверждение. Подпространство само является линейным пространством.
Определение. Линейной оболочкой системы векторов 

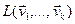
Утверждение. Линейная оболочка системы векторов является подпространством.
Определение. Пересечением двух подпространств и называется множество всех векторов, принадлежащих одновременно и ,и . Обозначается .
Определение. Суммой двух подпространств 



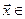

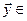

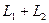
Утверждение. Сумма и пересечение подпространств 


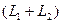

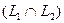




Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состоит только из нулевого вектора.
Примеры
1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами 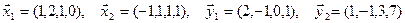
Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства 

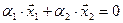
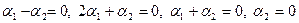
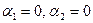

независимы и размерность подпространства 
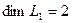

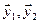
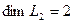
Вычислим теперь размерность пересечения подпространств 




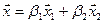

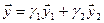
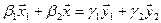
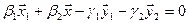

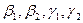
Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим 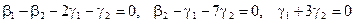
откуда 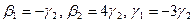
Полагая свободное неизвестное 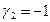
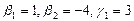
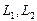
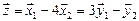
Размерность пересечения 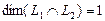
размерность суммы подпространств 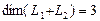

Задачи
3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами 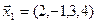
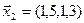

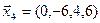
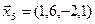
3.40. Найти размерность и какой-либо базис линейной оболочки векторов 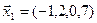
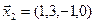
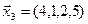
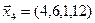
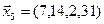
3.41. Является ли подпространством в указанном пространстве множество
а) векторов, выходящих из начала координат и заканчивающихся на фиксированной прямой, в пространстве R 2 ;
б) бесконечно малых числовых последовательностей в пространстве сходящихся последовательностей;
в) сходящихся к числу 
г) диагональных матриц в пространстве квадратных матриц того же порядка;
д) невырожденных матриц в пространстве симметричных матриц того же порядка;
е) дифференцируемых на интервале 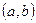
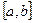
3.42. Почему не является подпространством в указанном пространстве множество
а) векторов, каждый из которых лежит на одной из координатных плоскостей, в пространстве R 3 ;
б) векторов из пространства R n , координаты которых удовлетворяют уравнению 
в) расходящихся числовых последовательностей в пространстве ограниченных последовательностей;
г) вырожденных матриц в пространстве квадратных матриц того же порядка;
д) монотонно возрастающих и ограниченных на множестве 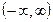
3.43. Найти размерность и какой-либо базис подпространства решений однородной системы:
а) 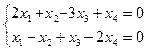
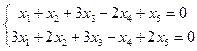
в) 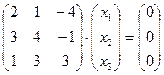
3.44. Доказать, что данное множество является подпространством в R n , найти его размерность и какой-либо базис:
а) все n-мерные векторы, координаты которых удовлетворяют уравнению 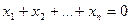
б) все n-мерные векторы, у которых первая координата равна нулю;
в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;
г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;
д) все n-мерные векторы, у которых координаты с нечетными номерами равны между собой.
3.45. Найти размерность суммы и пересечения подпространств, порожденных векторами 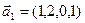
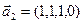
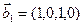
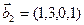
3.46. Найти размерность суммы и пересечения линейных оболочек векторов 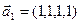
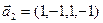
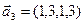

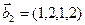
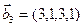
3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами 
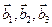
а) 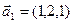
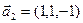
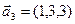
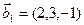
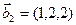
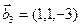
б) 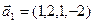
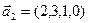
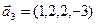
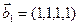
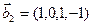
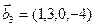
3.48. Найти базис суммы и пересечения линейных оболочек 
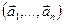

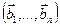
а) 
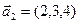
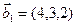
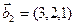
б) 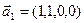
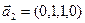
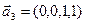
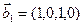
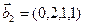
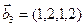
Является ли прямой сумма этих подпространств?
[spoiler title=”источники:”]
http://lektsii.org/10-6017.html
[/spoiler]
Пространство столбцов (также образ, область значений) матрицы 
Пусть 





Пространство строк определяется аналогично.
В данной статье рассматриваются матрицы над вещественными числами, то есть, пространства строк и столбцов являются подпространствами 

Обзор[править | править код]
Пусть 




[3],
равен числу опорных элементов в любом ступенчатом виде
,
равен наибольшему числу линейно независимых строк или столбцов матрицы
[4].
Пространство столбцов матрицы 

![{displaystyle A=[a_{1},dots ,a_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1211f89a00ba07d3dfaecb08c1219fff00e76ea)



Действие матрицы 







Концепция пространства столбцов может быть обобщена на матрицы, заданные над полем комплексных чисел 

Пример
Дана матрицы 
Её строки:
,
,
,
.
Следовательно, пространство строк матрицы 


![{displaystyle n=[6,-1,4,-4,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bcd6151d0fef4e3d0237a6ea5dbd089ec196314)


Пространство столбцов[править | править код]
Определение[править | править код]
Пусть 



Где 




Любая линейная комбинация столбцов матрицы 

Таким образом, пространство столбцов 


- Пример
- Если
, то её столбцы это
и
.
- Линейная комбинация
и
— это любой вектор, имеющий следующий вид:
Множество всех таких векторов образует пространство столбцов
. В данном случае пространство столбцов это в точности множество векторов
, удовлетворяющих уравнению
.
- В декартовой системе координат это множество соответствует некоторой плоскости, проходящей через начало отсчёт в трёхмерном пространстве.
Базис[править | править код]
Столбцы матрицы 
Например, дана такая матрица:
Столбцы этой матрицы не линейно независимы, что значит, что базис образует некоторое подмножество столбцов. Чтобы найти его, приведём 
[5]
Первый, второй и четвёртый столбцы линейно независимы, в то время как третий является линейной комбинацией первых двух (точнее, 
Стоит обратить внимание, что независимые столбцы это в точности столбцы, содержащие ведущие элементы, что позволяет сводить задачу поиска базиса в множестве столбцов к приведению матрицы к ступенчатому виду.
Алгоритм выше может быть использован для поиска зависимостей и нахождения базиса в любом множестве векторов. Также нахождение базиса пространства столбцов 

Размерность[править | править код]
Размерность пространства столбцов называется рангом матрицы. Ранг равен числу ведущих элементов в ступенчатом виде матрицы, а также наибольшему числу её линейно независимых столбцов. Например, ранг матрицы выше равен 
Так как пространство столбцов это образ соответствующего отображения, ранг матрицы равен размерности образа. Например, для отображения 

Размерность ядра матрицы равна числу столбцов, которые не содержат ведущих элементов[6]. Ранг и размерность ядра матрицы 

Связь с коядром[править | править код]
Коядро (левый аннулятор) матрицы 






Потому что строки 





Отсюда следует, что коядро 


Для матрицы над кольцами[править | править код]
Аналогичным образом пространство столбцов (иногда с уточнением как правое пространство столбцов) может быть определено для матриц над кольцом 
Где 


См. также[править | править код]
- Евклидово пространство
Примечания[править | править код]
Литература[править | править код]
- Anton, Howard (1987), Elementary Linear Algebra (5th ed.), New York: Wiley, ISBN 0-471-84819-0
- Axler, Sheldon Jay (1997), Linear Algebra Done Right (2nd ed.), Springer-Verlag, ISBN 0-387-98259-0
- Banerjee, Sudipto & Roy, Anindya (June 6, 2014), Linear Algebra and Matrix Analysis for Statistics (1st ed.), CRC Press, ISBN 978-1-42-009538-8
- Beauregard, Raymond A. & Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Company, ISBN 0-395-14017-X
- Lay, David C. (August 22, 2005), Linear Algebra and Its Applications (3rd ed.), Addison Wesley, ISBN 978-0-321-28713-7
- Leon, Steven J. (2006), Linear Algebra With Applications (7th ed.), Pearson Prentice Hall
- Meyer, Carl D. (February 15, 2001), Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8, <http://www.matrixanalysis.com/DownloadChapters.html> Архивная копия от 31 октября 2009 на Wayback Machine
- Poole, David (2006), Linear Algebra: A Modern Introduction (2nd ed.), Brooks/Cole, ISBN 0-534-99845-3
- Strang, Gilbert (July 19, 2005), Linear Algebra and Its Applications (4th ed.), Brooks Cole, ISBN 978-0-03-010567-8
Ссылки[править | править код]
- Weisstein, Eric W. Row Space (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Column Space (англ.) на сайте Wolfram MathWorld.
- Гилберт Стрэнг, MIT Linear Algebra Lecture on the Four Fundamental Subspaces на Google Video от MIT OpenCourseWare
- Khan Academy video tutorial
- Lecture on column space and nullspace by Gilbert Strang of MIT
- Row Space and Column Space
Линейная алгебра для исследователей данных
Время на прочтение
5 мин
Количество просмотров 14K

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».
Ирвинг Капланский
Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.
В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.
Произведения векторов
Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy
называется следующее вещественное число:
Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество
.
Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть
След
Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:
След обладает следующими свойствами:
-
Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.
-
Для любых матриц A,B ∈ ℝⁿˣⁿ: tr(A + B) = trA + trB.
-
Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.
-
Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.
-
Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).
Нормы
Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:
Заметим, что ‖x‖₂²=xᵀx.
Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:
-
Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).
-
f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).
-
Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).
-
Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)
Другими примерами норм являются норма l₁
и норма l∞
Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как
Нормы также могут быть определены для матриц, например норма Фробениуса:
Линейная независимость и ранг
Множество векторов {x₁, x₂, …, xₙ} ⊂ ℝₘ называют линейно независимым, если никакой из этих векторов не может быть представлен в виде линейной комбинации других векторов этого множества. Если же такое представление какого-либо из векторов множества возможно, эти векторы называют линейно зависимыми. То есть, если выполняется равенство
для некоторых скалярных значений α₁,…, αₙ-₁ ∈ ℝ, то мы говорим, что векторы x₁, …, xₙ линейно зависимы; в противном случае они линейно независимы. Например, векторы
линейно зависимы, так как x₃ = −2xₙ + x₂.
Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.
Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:
-
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.
-
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).
-
Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).
-
Для любых матриц A,B ∈ ℝᵐˣⁿ: rank(A + B) ≤ rank(A) + rank(B).
Ортогональные матрицы
Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м
атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.
Непосредственно из определений ортогональности и нормированности следует, что
Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n < m), но ее столбцы являются ортонормированными, то UᵀU = I, но UUᵀ ≠ I. Поэтому, говоря об ортогональных матрицах, мы будем по умолчанию подразумевать квадратные матрицы.
Еще одно удобное свойство ортогональных матриц состоит в том, что умножение вектора на ортогональную матрицу не меняет его евклидову норму, то есть
для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.
Область значений и нуль-пространство матрицы
Линейной оболочкой множества векторов {x₁, x₂, …, xₙ} является множество всех векторов, которые могут быть представлены в виде линейной комбинации векторов {x₁, …, xₙ}, то есть
Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,
Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть
Квадратичные формы и положительно полуопределенные матрицы
Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:
Заметим, что
-
Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как
(или просто A > 0), а множество всех положительно определенных матриц часто обозначают
.
-
Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как
(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают
.
-
Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной
-
, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx < 0.
-
Далее, симметричная матрица A ∈ 𝕊ⁿ называется отрицательно полуопределенной (
), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.
-
Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что
и
.
Собственные значения и собственные векторы
Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство
На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).
Перевод статьи был подготовлен в преддверии старта курса “Математика для Data Science”. Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.
-
ЗАПИСАТЬСЯ НА ДЕМОУРОК
Ну, вообщем я попробовал:
а)
У меня получилось вот такая ступенчатая матрица (для транспонированной изначальной матрицы):
[math]begin{pmatrix} 4 & -1 & frac{ 9 }{ 2 } & frac{ 5 }{ 2 } & frac{ 3 }{ 2 } \ 0 & 2 & 1 & 1 & 1 \ 0 & 0 & 7 & 1 & -1 \ 0 & 0 & 0 & 15 & -1 \ 0 & 0 & 0 & 0 & 0 end{pmatrix}[/math]
И такая для нетранспонированной:
[math]begin{pmatrix} 4 & 2 & -1 & -4 & 0 \ 0 & 14 & 1 & 36 & 16 \ 0 & 0 & 1 & -12 & -8 \ 0 & 0 & 0 & 1 & -frac{ 1 }{ 2 } \ 0 & 0 & 0 & 0 & 0 end{pmatrix}[/math]
(Просто я пока так и не понял, через какую делать правильно)
И вот дальше я не совсем понимаю, как найти базис линейной оболочки строк отсюда…
б)
Тут вроде получше, получилось, чем под а)
Решал по методу Гаусса, собственно ступенчатый вид нашел уже под буквой а), принял [math]x_{1},x_{2},x_{3},x_{4}[/math] за базисные, а [math]x_{5}[/math] и одна свободная осталась только [math]x_{5}[/math]. Получил фундаментальную систему решений:
[math]e=begin{pmatrix} 0 \ 0 \ 2 \ -frac{ 1 }{ 2 } \ 1 end{pmatrix}[/math]
Как я понимаю, это и будет базис решений однородной системы, так как все другие решения, через него выражаются.
Осталось с буквой а) разобраться…



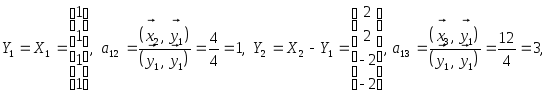







![{displaystyle r_{1}=[2,4,1,3,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b9baceafaf0af56855705d04af27bc9a2f7a04c)
![{displaystyle r_{2}=[-1,-2,1,0,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ee3686f197fbe6cdb790793bef7e0500aa15e91)
![{displaystyle r_{3}=[1,6,2,2,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/852213f4d0cc7cbdf4fdb5dc8275e2f04f10e0b6)
![{displaystyle r_{4}=[3,6,2,5,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c15eda77097540a4b9a280df76f2df00a10e203c)



![{displaystyle v_{1}=[1,0,2]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4beee6a0ba1b0983e0789869f4af16d1636770b)
![{displaystyle v_{2}=[0,1,0]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3713c3f3f5a3741781345901b9b8132390e76567)



![{displaystyle [x,y,z]in mathbb {R} ^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c95a23643f81cf94498b5f6774204860d12cab0)