Как найти линейную оболочку многочлена

Содержание

Линейная зависимость

Линейные комбинации. Линейная оболочка

Пусть $ S $ — некоторое подмножество элементов из $ M $ .

Определение 1. Линейной комбинацией¹⁾ элементов из $ S $ называют сумму $sum_{sin S}alpha_ss$ , где лишь конечное число элементов отлично от нуля. Элементы называются коэффициентами²⁾ линейной комбинации.

Пример 1. Кольцо многочленов $F[T]$ над полем $ F $ является, в частности, векторным пространством. Пусть $S={1,T,T^2, T^3,ldots,T^n,ldots}$ . Линейная комбинация этих векторов — это многочлен степени 2.

Предложение 1. Множество всех линейных комбинаций элементов из $ S $ является подмодулем в модуле $ M $ .

Определение 2. Пусть $ N $ — множество всех линейных комбинаций элементов из $ S $ , тогда $ N $ называется подмодулем, порожденным $ S $ , или $ R $ –линейной оболочкой³⁾ множества $ S $ , и обозначается . При этом $ S $ называют множеством образующих⁴⁾ для $ N $ .

В частном случае векторного пространства $ V $ над полем $ F $ данное определение можно переформулировать следующим образом:

Определение 2′. Линейной оболочкой⁵⁾ подмножества $ S $ линейного пространства $ V $ называется множество всех линейных комбинаций векторов из $ S $ . Говорят также, что оболочка порождена векторами $sin S$ , или что оболочка натянута на вектора $sin S$ .

Пример 2. В кольце многочленов $F[T]$ над полем $ F $ выберем множество $S={1,T,T^2, T^3,ldots,T^n,ldots}$ . Линейную оболочку $ S $ составляют всевозможные многочлены , то есть .

Пример 3. Кольцо многочленов от двух переменных можно рассматривать как левый модуль над кольцом . Пусть $S={1,T_1,T_1^2, T_1^3,ldots,T_1^n,ldots}$ , тогда -линейная оболочка множества $ S $ состоит из элементов , где . Таким образом, $langle s|sin Srangle_{F[T_2]}=F[T_1,T_2]$ .

Линейная зависимость

Определение 3. Набор элементов $ S $ модуля $ M $ называется линейно независимым⁶⁾ над $ R $ , если из равенства нулю линейной комбинации $underset{sin S}{sum}alpha_ss$ следует, что для всех $sin S$ . Если же существует соотношение $sum_{sin S}alpha_ss=0$ , в котором не все равны нулю, элементы из $ S $ называют линейно зависимыми⁷⁾.

Если в качестве модуля взять векторное пространство $ V $ и рассматривать конечные наборы , то определение линейной зависимости может быть переформулировано следующим образом:

Определение 3′. Система векторов пространства $ V $ называется линейно зависимой⁸⁾, если найдутся числа , не равные нулю одновременно и такие, что . В противном случае векторы называются линейно независимыми.

Пример 4. Если множество содержит нулевой элемент, то оно линейно зависимо.

Предложение 2. Пусть $ V $ — векторное пространство над полем $ F $ . Имеют место следующие утверждения:

система векторов с линейно зависимой подсистемой линейно зависима,
любая часть линейно независимой системы векторов линейно независима,
среди линейно зависимых векторов хотя бы один является линейной комбинацией остальных,
если один из векторов выражается через остальные, то векторы линейно зависимы,
если векторы линейно независимы, а — линейно зависимы, то — линейная комбинация векторов ,
если векторы линейно независимы и вектор нельзя через них выразить, то система линейно независима.

См. также

Литература

Наверх

Источник

Лекция
11

Связь
между базисами линейного пространства.

Линейные
подпространства

Матрица перехода от
базиса к базису. Связь координат одного
и того же вектора в двух базисах.
Линейные

подпространства.
Примеры

11.1. Связь между
базисами линейного пространства

Пусть
–
линейное пространство,
(I)
и
(II)
– два базиса в
.

Так как (I)
– базис, любой вектор из
,
в частности любой вектор системы (II),
можно представить в виде линейной
комбинации векторов системы (I),
т.е. найдутся такие числа
,
что

……………………………….
(11.1)

Определение 1.
Матрица

называется матрицей перехода от базиса
(I) к базису (II).

Замечание
1. Столбцы матрицы перехода
,
являются координатами в разложении
векторов

по базису (I).

Справедливость
этого замечания непосредственно следует
из равенств (11.1).

Замечание
2. Матрица перехода от
базиса к базису является невырожденной
матрицей.

Доказательство
этого факта опустим.

Справедливо
следующее утверждение.

Теорема 1. Пусть

– линейное пространство,

(I) и

(II) – два базиса в
,

– матрица перехода от (I)
к (II),
,

и
,
тогда

.
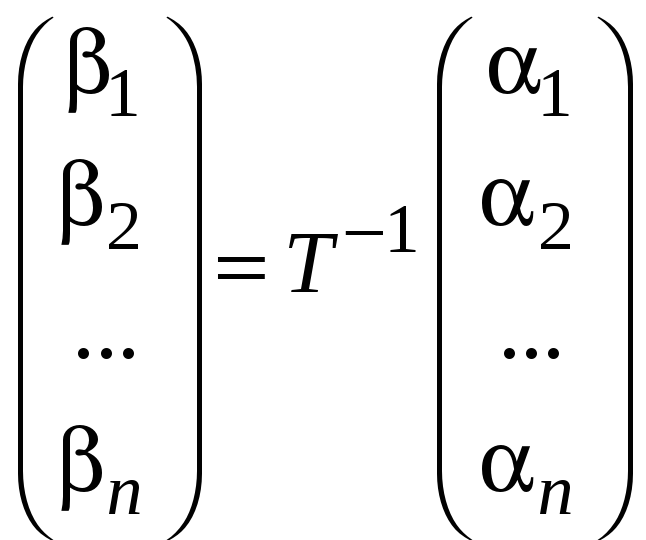
(11.2)

Доказательство.
Подставим в разложение

по базису (II) выражения

из (11.1), получим

Последнюю сумму
запишем развернуто:

По условию
,
используя теорему о единственности
разложения вектора по базису (теорема
3 в лекции 10), получим

……………………………………

что в матричном
виде выглядит как равенство

Отсюда следует

Теорема доказана.

Пример
1.

– линейное пространство всех геометрических
векторов плоскости,
(I)
– произвольный декартов базис,
(II)
– декартов базис, полученный поворотом
векторов

и

на угол

против хода часовой стрелки. Найти
матрицу перехода от (I) к
(II) и связь координат
одного и того же вектора в (I)
и (II).

Имеем
,

(рис. 11.1). Тогда

– матрица перехода
от (I) к (II).

Найдем
.

Формула (11.2) в этом
случае имеет вид

где

– координаты произвольного вектора

в базисе (I), а

– координаты этого же вектора в базисе
(II).

(Сравните с формулами
(5.24) в Лекции 5).

Пример
2.

– произвольное линейное пространство,
.
Векторы
,
и

заданы своими координатами в некотором
базисе
.
Доказать, что система

– базис в
,
и найти координаты вектора

в базисе
.

Сначала докажем,
что система

– базис. Рассмотрим линейную комбинацию
векторов

и
,
равную нулевому вектору
:

Покоординатно
последнее равенство запишется в виде
системы двух уравнений:

(11.3)

Определитель
системы (11.3)
,
следовательно, система (11.3) имеет
единственное решение
.

Итак, допустив,
что линейная комбинация векторов

и

равна
,
мы с необходимостью получили, что
коэффициенты этой линейной комбинации
равны нулю. Это означает, что система
векторов

линейно независима, а так как
,
векторы

являются базисом в
.
Обозначим этот базис (II).

Найдем матрицу
перехода от (I) к (II).

В силу определения
1

(координаты векторов

и

в (I) располагаем по
столбцам).

Обозначим через
координаты
вектора

в (II).

Воспользуемся
теоремой 1. Найдем
.
Имеем

и по формуле (11.2)
получим

Итак,
.

Упражнения.

1.

– линейное пространство многочленов
степени
.
Доказать, что система многочленов

образует базис в
.
Найти матрицу перехода от базиса

к этому базису и координаты многочлена

в нем.

2. В произвольном
линейном пространстве векторы

и

заданы своими координатами в некотором
базисе
:
,
,
,
.
Доказать, что система векторов

– базис в
,
и найти координаты

в этом базисе.

3. В произвольном
линейном пространстве

векторы
(I)
и
(II)
заданы своими координатами в некотором
базисе
,
,
,
,
,
.
Доказать, что системы (I)
и (II) являются базисами в
,
и найти матрицу перехода от (I)
к (II).

11.2. Линейные
подпространства

Определение 2.
Пусть

– линейное пространство. Непустое
подмножество

линейного пространства

()
называется линейным подпространством
в
,
если выполняются два условия:

1)
;

2)

при любом вещественном числе
.

Пример
3. Пусть

– линейное пространство всех
арифметических
-мерных
векторов
;

– совокупность всех векторов, у которых
первая и последняя компоненты равны
нулю, т.е. векторов вида
.

– подпространство в
.

Действительно,
пусть

и
,
следовательно, по определению

и
.
По правилу сложения векторов в

и, таким образом, сумма любых двух
векторов из

принадлежит
.

Пусть

и

– произвольное вещественное число.
Но

(так как
),
следовательно, по правилу умножения
вектора на число в

и вместе с любым вектором произведение
его на

тоже принадлежит
.
В соответствии с определением 2 это
означает, что

– линейное подпространство в
.

Замечание.
Если

– линейное
подпространство в
,
то

само является
линейным пространством относительно
введенных в

операций
сложения и умножения на число.

Действительно,
требования 1) и 2) в определении 2 означают,
что в

определены операции сложения векторов
и умножения вектора на число.

Аксиомы 1 и 2
выполняются в
,
так как они имеют место в
.
Убедимся в справедливости аксиомы 3.

Пусть
,
,
следовательно, согласно условию 2)
,
но по следствию 5 из аксиом в

,
таким образом,

и в

справедлива аксиома 3.

Пусть
,
.
Следовательно, согласно условию 2)
,
но по следствию 8 из аксиом в

,
таким образом,

и в

справедлива аксиома 4.

Аналогично
проверяется справедливость аксиом 5 –
8, следовательно,

– линейное пространство.

Пусть

– произвольное линейное пространство,

– некоторая система векторов в
.
Рассмотрим совокупность всех векторов
вида
,
где

принимают всевозможные вещественные
значения. Обозначим множество этих
векторов
.

называется линейной оболочкой
векторов
.

является подпространством в
.

Действительно,

(так как, например, сами векторы
,
,
принадлежат
).

Пусть
,
,
следовательно, по определению

такие, что
,

Имеем

и
.

Пусть
,

– произвольное вещественное число.

Имеем

и
.

Таким образом,
выполняются условия 1) и 2) определения
2 и

является линейным подпространством
в
.

Говорят, что

порождено системой векторов

или

“натянуто” на систему
.

Заметим, что само
линейное пространство

может рассматриваться как линейная
оболочка любого своего базиса.

Пример
4.

Найти
размерность и базис линейной оболочки
векторов
,
,
.

Найдем ранг матрицы,
строками которой являются данные векторы
,
,
:

~~.

Минор второго
порядка
,
следовательно, первые две строки матрицы
линейно независимы. Значит, векторы

и

составляют линейно независимую систему
векторов в
,
а следовательно, и в линейной оболочке
,
и вектор

через них линейно выражается. Тогда
любой вектор

тоже линейно выражается через

и
.
Векторы

и

являются базисом в
,
.

Упражнение.
–
линейное пространство арифметических
векторов
.
Найти размерность и все
базисы линейной оболочки векторов
,
,
,
.

143

Источник

Просьба окружить формулы (по крайней мере первые) знаками долларов. Увидите, что они станут смотреться гораздо лучше.

Независимость этих двух многочленов есть следствие того, что они не получаются друг из друга умножением на константу. Или, по-другому, если Вы составите их линейную комбинацию, то получить нулевой многочлен можто только если взять оба коэффициента равными нулю.

Ясно, что линейная оболочка этих двух многочленов будет включать в себя только многочлены не выше второй степени, но не все. Опишите, какому соотношению должны удовлетворять коэффициенты этого многочлена, чтобы он принадлежал этой оболочке.

Во второй задаче сначала докажите, что не может быть двух различных многочленов степени 3, которые бы совпадали в четырех точках. Затем подумайте, как в явном виде построить многочлен, заданный своими значениями в четырех точках. Вообще-то эта задача тут уже как-то обсуждалась, только для произвольной степени.

Источник

Как решить задачу по линейной алгебре:

Ксюша Некрасова

Ученик

(242),
закрыт

12 лет назад

Найдите размерность и базис линейной оболочки множества многочленов (1+t^3), t^3, 1, (t+t^2)
Что в таком линейном пространстве будет линейной оболочкой и базисом?

Лучший ответ

Я вышел родом из народа

Просветленный

(30667)

12 лет назад

Линейная оболочка – множество всех кубических многочленов от t, у которых коэффициенты при t^2 и t совпадают.
Размерность 3.
Базис – 1, t^3, t^2 + t

Остальные ответы

Булат 1

Оракул

(54366)

12 лет назад

Видно, что они линейно зависимы (1-й = 2-й + 3-й) , убираем, например, первый и эти уже линейно независимы, вот тебе и оболочка, и базис, и размерность

Похожие вопросы

Источник

Подпространства и линейные оболочки

Определение 1.3 Подмножество линейного пространства называется подпространством пространства , если вместе с любыми двумя векторами оно содержит их сумму, а вместе с любым вектором – результат умножения его на любое число.

Утверждение 1.1 Подмножество линейного пространства является подпространством тогда и только тогда, когда для любой системы векторов в оно содержит их произвольную линейную комбинацию.

Доказательство. Упражнение.

Примеры. 1) В пространстве всех геометрических векторов подмножество всех векторов, параллельных некоторой плоскости, будет подпространством, а подмножество всех векторов, концы которых лежат на некоторой плоскости, не будет подпространством.

2) Множество всех решений однородной линейной системы есть, как мы видели в первом семестре, векторное пространство, которое будет ни чем иным, как подпространством арифметического пространства (где в данном случае есть число неизвестных системы).

3) В пространстве рассмотрим подмножество всех многочленов степени, не превосходящей некоторого фиксированного . Сумма любых двух таких многочленов снова есть многочлен из заданного множества, равно как и результат умножения такого многочлена на произвольное число остается в данном множестве многочленов. Следовательно, множество многочленов степени не выше является подпространством пространства . Можно доказать, что система многочленов является базисом этого подпространства (упражнение!), и, таким образом, размерность данного подпространства многочленов равна . Мы имеем здесь, стало быть, пример конечномерного подпространства бесконечномерного линейного пространства.

Определение 1.4 Линейной оболочкой системы векторов некоторого линейного пространства называется множество всех линейных комбинаций векторов системы.