Как найти линейную оболочку системы векторов

Определение
1.
Линейной
оболочкой
заданной
конечной совокупности

элементов векторного пространства
ⁿ
над полем К называется множество всех
линейных комбинаций этих элементов с
коэффициентами из поля К. При этом сама
совокупность

называется порождающей
системой
данной линейной оболочки, а сама линейная
оболочка обозначается символом
.

Линейные оболочки
обладают следующими свойствами:

.
Линейная оболочка элементов векторного
пространства
ⁿ
является подпространством М векторного
пространства
ⁿ.

Данный
результат следует из определения
линейной оболочки: сумма
двух векторов из линейной оболочки
будет принадлежать линейной оболочки
(одна из линейных комбинаций), произведение
вектора из линейной оболочки также
будет принадлежать линейной оболочки.

.
Линейная оболочка может совпадать со
всем пространством Rⁿ
(если образующая
система является базисом
в пространстве Rⁿ
)

.
Линейная оболочка

является наименьшим подпространством,
содержащим элементы
.
Все остальные подпространства могут
только содержать вектора порождающей
системы или их возможные комбинации.

.
Если какой-нибудь элемент из порождающей
системы элементов

есть линейная комбинация остальных
элементов этой системы, то его можно
удалить из порождающей системы, не
изменив при этом линейной оболочки.

.
Если координатная матрица системы
образующих

имеет ранг р, где
,
то любая линейно независимая система
,
является базисом линейной оболочки
,
а сама линейная оболочка будет
подпространством размерности р,
.

Примеры.

1. Если
   a,
   b,
   с – геометрические векторы, лежащие
   на одной прямой. В этом случае линейная
   оболочка L(а,b,c)=
   L(a).Здесь
   линейная оболочка является одномерным
   пространством, которое состоит из всех
   вектор, лежащих на прямой, причем вектор
   а
   –является базисом.

2. Пусть
   a,
   b,
   с – геометрические векторы, причем a,
   b
   не коллинеарны, с = а + b.
   В этом случае линейная оболочка L(а,b,c)=
   L(a,b).Здесь
   линейная оболочка является двумерным
   пространством, состоящем из всех
   векторов, компланарных с векторами a
   и b.
   Вектора а,b
   составляют базис в L(a,b).
   Любой вектор из L
   представляется в виде линейной комбинации
   векторов а
   и b.

Вообще,
в конечномерном пространстве R
всякое подпространство L

является линейной
оболочкой некоторой системы векторов.

Рассмотри
следующую задачу.
В евклидовом пространстве Eⁿ
задана линейная оболочка
,
где k

n.
Требуется:

1)Найти
размерность и базис линейной оболочки
;
2)Выделить в линейной оболочке

ортогональный базис и

достроить
его до
ортонормированного базиса евклидова

пространства
Eⁿ.

Если
схема решения первой задачи нам знакома,
то решение второй задачи строится на
следующем теоретическом результате.

Теорема
(Грама
– Шмидта)

Пусть

– система линейно независимых векторов
в евклидовом пространстве, где k

n,
являющихся образующей системой линейной
оболочки
.
Система векторов
,
описываемая формулами

,

,

,
. . .

где
коэффициенты

,
,

образует
ортогональный
базис
линейной оболочки
.

Доказательство.
Для
доказательства теоремы достаточно
доказать следующее утверждение: вектор

ортогонален вектору
.

Действительно,
умножая скалярно вектор

на вектор
,
получим

==0

Следствие.
Результат теоремы дает
алгоритм последовательной ортогонализации
системы линейно независимых элементов
( так
называемый
метод Грама – Шмидта).

Пример

1. В
   евклидовом пространстве E⁴
   линейная оболочка
   
   задана образующей системой векторов
   
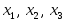
   с координатами

.

Требуется:

а)
найти размерность и базис линейной
оболочки

б)
указать в линейной оболочке

ортонормированный базис

и
достроить его до ортонормированного
базиса евклидова

пространства
E⁴.

Решение.
Рассмотрим координатную матрицу
.
Так как

,

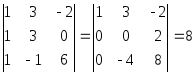то
,
элементы

линейно независимы в E⁴
и образуют базис данной линейной
оболочки, являющейся подпространством
в E⁴.

Для
построения ортонормированного базиса
в E⁴
применим метод
ортогонализации
Грама-Шмидта. Получим

,

,

.

Записывая векторы
столбцами их координат, последовательно
найдем

.

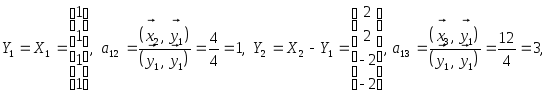
Легко
проверить, что полученные элементы

попарно ортогональны. Найдем ортогональный
им вектор
.

Пусть
,
то неизвестные координаты

вектора Y₄
найдутся из условий

,,.

Так
как
,
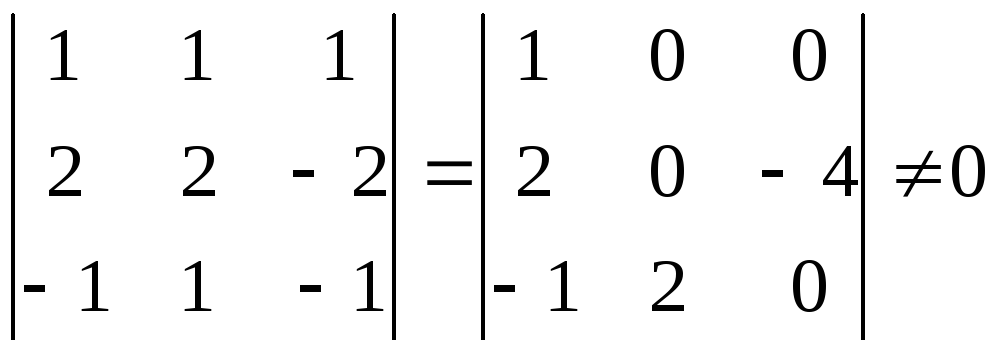в последней системе неизвестные

можно взять в качестве базисных
неизвестных.

Если
для свободной (небазисной) неизвестной
,
то
.

Нормировав
найденные векторы
,
построим ортонормированный базис в E⁴:

.

Задача
решена.

В
завершении параграфа введем важное
определение.

Пусть

– – базис в Eⁿ
и векторы

представлены в этом базисе своими
разложениями

.

Тогда
скалярное произведение этих векторов
имеет вид

или в матричной форме
,
где

– столбцы координат векторов

в базисе

а симметричная матрица

составлена из скалярных произведений
базисных векторов:

.

В
общем случае в качестве элементов
матрицы А рассматривают скалярные
произведения произвольной системы
векторов а₁,
а₂,…,
а_n

Определение
3.
Определитель
матрицы А
скалярных произведений заданной системы
векторов
называют определителем
Грама.

Теорема
Произвольная
система
векторов,
заданных в ортонормированном
базисе,
будет линейно
независимой,
если ее определитель
Грама отличен от нуля.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Линейные оболочки и подпространства

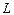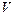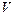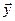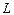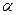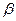Определение. Подпространством линейного пространства называется множество векторов из такое, что для любых двух векторови из и любых двух вещественных чисел и линейная комбинация 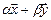также принадлежит .

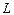Утверждение. Подпространство само является линейным про­странством.

Определение. Линейной оболочкой системы векторов называется множество всех линейных комбинаций векторов . Обозначается .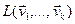

Утверждение. Линейная оболочка системы векторов является подпространством.

Определение. Пересечением двух подпространств и на­зывается множество всех векторов, принадлежащих одновре­менно и ,и . Обозначается .

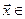
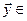
Определение. Суммой двух подпространств и называется множество всех векторов , представимых в виде , где , . Обозначается .

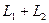Утверждение. Сумма и пересечение подпространств и являются линейными пространствами, и их размерности связаны равенством

+ = + .

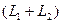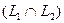Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состо­ит только из нулевого вектора.

Примеры

1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами .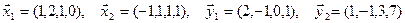

Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства , порождённого векторами , равенство нулю линейной комбинации 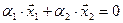, эквивалентное системе уравнений 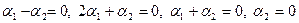, достигается лишь при условии 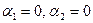. Следовательно, векторы линейно

независимы и размерность подпространства равна 2: 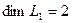. Для подпространства , порождённого векторами 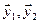, проводя аналогичный анализ, получим .

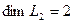Вычислим теперь размерность пересечения подпространств и . По определению векторы, составляющие пересечение, принадлежат одновременно обоим подпространствам. Произвольный вектор подпространства является линейной комбинацией базисных векторов : 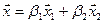. Аналогично для подпространства имеем 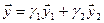, тогда условие принадлежности пересечению есть 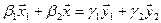или .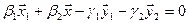

Это условие представляет собой систему уравнений относительно коэффициентов 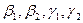. Составим матрицу системы и упростим её с помощью элементарных преобразований: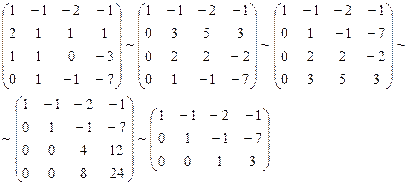

Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим ,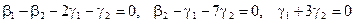

откуда .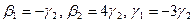

Полагая свободное неизвестное 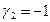, для остальных имеем

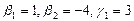. Итак, пересечение подпространств 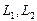имеет один базисный вектор

.

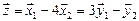Размерность пересечения 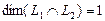. Следовательно, в соответствии с равенством

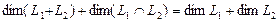
размерность суммы подпространств 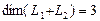. В качестве базиса суммы подпространств можно взять, например, векторы , дополненные вектором 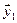. В линейной независимости векторов 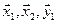убедиться нетрудно.

Задачи

3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами , , , , .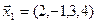

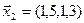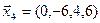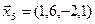3.40. Найти размерность и какой-либо базис линейной оболочки векторов , , , , .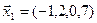

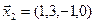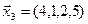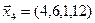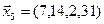3.41. Является ли подпространством в указанном пространстве множество

а) векторов, выходящих из начала координат и заканчиваю­щихся на фиксированной прямой, в пространстве R 2 ;

б) бесконечно малых числовых последовательностей в про­странстве сходящихся последовательностей;

в) сходящихся к числу последовательностей в простран­стве сходящихся последовательностей;

г) диагональных матриц в пространстве квадратных матриц того же порядка;

д) невырожденных матриц в пространстве симметричных мат­риц того же порядка;

е) дифференцируемых на интервале 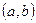функций в простран­стве функций, непрерывных на отрезке .

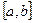3.42. Почему не является подпространством в указанном про­странстве множество

а) векторов, каждый из которых лежит на одной из коорди­натных плоскостей, в пространстве R 3 ;

б) векторов из пространства R n , координаты которых удовлетворяют уравнению ;

в) расходящихся числовых последовательностей в простран­стве ограниченных последовательностей;

г) вырожденных матриц в пространстве квадратных матриц того же порядка;

д) монотонно возрастающих и ограниченных на множестве 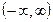функций в пространстве функций, ограниченных на том же множестве.

3.43. Найти размерность и какой-либо базис подпространства ре­шений однородной системы:

а) 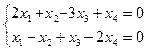; б) ;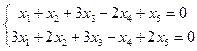

в) .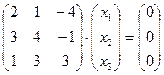

3.44. Доказать, что данное множество является подпространством в R n , найти его размерность и какой-либо базис:

а) все n-мерные векторы, координаты которых удовлетворя­ют уравнению ;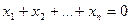

б) все n-мерные векторы, у которых первая координата равна нулю;

в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;

г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;

д) все n-мерные векторы, у которых координаты с нечетны­ми номерами равны между собой.

3.45. Найти размерность суммы и пересечения подпространств, порожденных векторам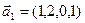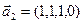и , и 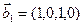, 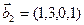. Является ли эта сумма прямой суммой?

3.46. Найти размерность суммы и пересечения линейных оболочек векторов 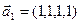, , 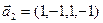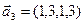и , , 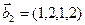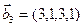. Является ли их cумма прямой?

3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами и 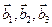, если

а) , , , , , ;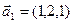

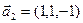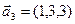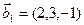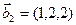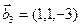б) , , , , , .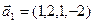

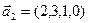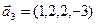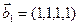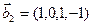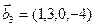3.48. Найти базис суммы и пересечения линейных оболочек 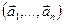и 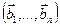, если

а) , , , ;

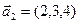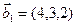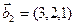б) , , , , , .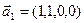

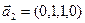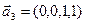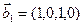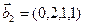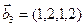Является ли прямой сумма этих подпространств?

Способы описания подпространств линейного пространства

Рассмотрим два важных способа описания линейных подпространств, которые условно будем называть внутренним и внешним. В первом (внутреннем) способе используется понятие линейной оболочки векторов, когда все элементы подпространства выражаются через некоторые его элементы (образующие). При втором (внешнем) способе применяются однородные системы уравнений. В этом случае подпространство описывается как пересечение некоторых содержащих его множеств. Для каждого способа описания подпространств укажем методики на хождения размерностей, базисов, алгебраических дополнений, пересечений и сумм подпространств.

Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству . Чтобы установить изоморфизм , достаточно выбрать в пространстве базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства .

Первый (внутренний) способ. Пусть в пространстве заданы столбцы . Напомним, что для систем столбцов были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.

Рассматривая линейную оболочку столбцов как линейное подпространство , заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства .

Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:

1) составить из данных столбцов матрицу размеров ;

2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;

3) определить размерность и базис подпространства

– количество ненулевых строк в матрице равняется размерности подпространства, т.е. ,

– столбцы матрицы , содержащие единичные элементы (в начале каждой “ступеньки”), определяют номера линейно независимых столбцов матрицы , т.е. искомый базис.

Таким образом, если подпространство задано своими образующими , то его размерность равна рангу системы столбцов , т.е. , а базисом служит максимальная линейно независимая подсистема образующих.

Второй (внешний) способ. Пусть подпространство задано как множество решений однородной системы уравнений с неизвестными. Множество решений системы уравнений можно рассматривать как пересечение подпространств , где — множество решений i-го уравнения системы . Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства , а базисом служит фундаментальная система решений однородной системы . Способы нахождения фундаментальной системы решений рассмотрены ранее.

Переход от одного способа описания подпространств к другому

Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов . Требуется составить такую однородную систему уравнений, множество решений которой совпадает с , т.е. . Для этого нужно выполнить следующие действия.

1. Из данных столбцов составить матрицу размеров , а затем блочную матрицу , приписав к матрице единичную матрицу n-го порядка.

2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу к виду , где — простейший вид матрицы .

3. Из последних строк матрицы составить матрицу .

4. Записать искомую систему уравнений .

Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид . Решаемую задачу можно сформулировать так: для каких векторов найдутся такие числа , чтобы выполнялось равенство . Другими словами, при каких неоднородная система ( уравнений с неизвестными ) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство . Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.

Пример 8.8. Подпространство задано линейной оболочкой столбцов . Составить систему уравнений, определяющую подпространство .

Решение. 1. Составляем матрицу и блочную матрицу:

2. Приводим левый блок к простейшему виду. Вычитаем первую строку из остальных, а затем к четвертой строке прибавляем вторую, умноженную на (-2):

Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер вый, умноженный на (-1), к третьему столбцу прибавим первый, умноженный на (-3), а затем второй, умноженный на (-1). Эти преобразования не изменяют правый блок полученной матрицы. Находим простейший вид Л матрицы и матрицу

3. Из последних строк матрицы составляем матрицу искомой системы.

4. Записываем систему уравнений Заданные в условии примера столбцы являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо .

Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными: . Требуется найти размерность и базис этого подпространства, т.е. представить его в виде линейной оболочки . Для этого нужно выполнить следующие действия.

1. Найти фундаментальную систему решений однородной системы . Искомая размерность .

2. Представить заданное пространство как линейную оболочку .

Первый пункт алгоритма удобно выполнять следующим образом:

– составить блочную матрицу , приписав к матрице единичную матрицу n-го порядка;

– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу к виду , где — простейший вид матрицы ;

– из последних столбцов матрицы составить фундаментальную матрицу .

Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.

Заметим, что решение поставленной задачи неоднозначно, так как существует много базисов одного и того же линейного подпространства.

Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений

Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6

Ее столбцы образуют фундаментальную систему решений. Размерность подпространства равна , .

2. Столбцы являются искомым базисом, так как они линейно независимы и .

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=sposoby-opisaniya-podprostranstv

[/spoiler]

Макеты страниц

Рассмотрим L – линейное пространство.

–  Сколько в L линейно независимых векторов.

–  Какой из смысл.

Определение: Линейное пространство L называется N-мерным, а число N – размерностью, если в L существует N линейно независимых векторов, причём любые N+1 векторов линейно зависимы.

Определение: В N-мерном линейном пространстве L любая совокупность(система) N линейно независимых векторов называется базисом.

, – базисные векторы.

Определение: если – базис в , то для любого существуют числа : . Это разложение вектора по базису.

Теорема 8: В данном базисе координаты вектора определены однозначно

Доказательство(от противного): Пусть в базисе два набора чисел для вектора

Так как линейно независимы, то все

Если в L существует любое число линейно независимых векторов, то L называется бесконечномерным линейным пространством.

Примеры базисов:

1)

2)

Базис Вейля

3)

.

4)

Подпространство и линейная оболочка

Пусть

L – множество

M – подмножество

Кроме того

L – линейное пространство

Тогда M – подпространство в L, если

Рассмотрим систему векторов .

Определение: Линейной оболочкой системы векторов называется множество всевозможных линейных комбинаций этих векторов. То есть: . Очевидно, что и является подпространством.

Пример: найти размерность и базис линейной оболочки , где

линейно независимы.

Операции над линейными пространствами.

– линейные пространства.

А)

Б)

А) Что такое .

Определение: линейное пространство L является прямой суммой и , если: выполняется одно из условий:

1)

2)

Теорема 9: Для того, чтобы , достаточно, чтобы

1)

2)

Тогда чтобы доказать, что, необходимо доказать, что – базис в L.

Рассмотрим:

Тогда .

Так как , то 0=0

< Предыдущая		Следующая >

Пусть L – n-мерное линейное пространство, в котором фиксирован некоторый базис е = (e₁ … е_n) и выбраны векторы a₁, …, a_k, b. Запишем разложение выбранных векторов по базису е:

a_j = ea_j, j = 1,k, b = eb,

где a_j = (a_1j … a_nj)^T , j = 1,k, b = (b₁ … b_n)^T – столбцы координат соответствующих векторов
. Пусть А – матрица типа n × k, составленная из координатных столбцов векторов a₁, …, а_k, а (A|b) – матрица, полученная из матрицы А добавлением справа еще одного столбца b.

Для вектора b возможны два случая:

1) вектор b принадлежит линейной оболочке span{a₁,…, a_k};

2) вектор b не принадлежит span{a₁,…,a_k}.

В первом случае добавление к системе векторов a₁, …, a_k вектора b не приводит к расширению линейной оболочки системы и, следовательно,

dimspan{a₁,… ,а_k} = dimspan{a₁,… ,а_k,b}.

По теореме 2.6 заключаем, что RgA = Rg(A|b).

Во втором случае, наоборот, добавление вектора b к системе векторов a₁, …, а_k приводит к расширению линейной оболочки, причем по теореме 2.5

dimspan{a₁,… ,а_k,b} = dimspan{a₁,… ,а_k} + 1,

так как

span{a₁,…, a_k, b} = span{a₁,…, a_k} ⊕ span{b}.

Следовательно, Rg(A|b) = RgA + 1.

Выясним теперь, что означают эти два случая “на координатном уровне”. В первом случае условие b ∈ span{a₁,… ,a_k} означает существование разложения

х₁а₁ +… + x_ka_k = b (2.8)

с некоторыми действительными коэффициентами x₁, …, x_k.
Записывая это векторное равенство в координатной форме, получаем систему линейных алгебраических уравнений (СЛАУ)

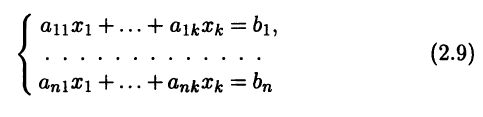
относительно переменных х = (х₁ … x_k)^T, которая в матричной форме имеет вид Ах = b. Существование разложения (2.8) означает, что полученная система имеет решение. Во втором случае представление (2.8) невозможно, т.е. система (2.9) не имеет решений.

Итак, следующие четыре утверждения эквивалентны между собой:

– b ∈ span{a₁,…,a_k};

– dimspan{a₁,… ,а_k,b} = dimspan{a₁,…,а_k};

– Rg(A|b) = RgA;

– система Ах = b из n линейных алгебраических уравнений относительно k неизвестных совместна.

Эквивалентность последних двух утверждений составляет содержание теоремы Кронекера – Капелли [III], которая верна для произвольных СЛАУ. Отметим, что любая система из п ли-нейных алгебраических уравнений относительно к неизвестных может быть получена как результат проведенных рассуждений. Для этого достаточно в качестве векторов a₁, …, a_k рассмотреть столбцы коэффициентов при неизвестных, а в качестве вектора b – столбец свободных членов. Все эти столбцы могут рассматриваться как n-мерные векторы в линейном арифметическом пространстве Rⁿ.

Таким образом, теорему Кронекера – Капелли можно переформулировать следующим образом: для того чтобы линейная оболочка системы векторов a₁, …, а_k совпадала с линейной оболочкой расширенной системы a₁, …, а_k, b, необходимо и достаточно, чтобы были равны размерности этих линейных оболочек.

Предположим, что квадратная СЛАУ Ах = b имеет решение при любом столбце b правых частей. Рассматривая столбцы матрицы А и столбец b как элементы a₁, …, a_n, b n-мерного линейного арифметического пространства и записывая СЛАУ в векторной форме

x₁a₁ + x₂a₂ + … + x_na_n = b,

заключаем, что линейная оболочка системы векторов a₁, …, а_n совпадает со всем линейным пространством Rⁿ. Из этого следует, что ранг этой системы векторов равен размерности линейного пространства n, а так как в системе ровно n векторов, то она, согласно теореме 2.6, линейно независима. Другими словами, столбцы матрицы А линейно независимы, а матрица А является невырожденной (см. теорему о базисном миноре [III]).

Таким образом, если квадратная СЛАУ Ах = b имеет решение при любой правой части, то матрица А системы невырождег на, а решение системы при любой правой части единственно.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ