Unit Converter
Enter the mass of an object and the characteristic length into the calculator to determine the linear density.
- All Density Calculators
- Sectional Density Calculator
- Surface Charge Density Calculator
- Density Calculator
- Average Density Calculator
- Copper Wire Weight Calculator
Linear Density Formula
The following formula is used to calculate a linear density.
- Where Ld is the linear density
- M is the mass
- L is the length
To calculate linear density, divide the total mass by the total length.
Linear Density Definition
A linear density is defined as the total mass per unit of length of an object. This is opposed to a normal density that is a mass per unit volume.
Is linear density constant?
Linear density is constant only if the mass of the object is constant along the length being measured. For example, if you are looking at a rod with even mass along the entire length, then no matter what section you look at the linear density will be constant.
Does linear density change with tension?
Yes, a linear density will change if tension is applied to an object. While the tension does not affect the mass, it will change the length of the object which would change the linear density.
What is a linear charge density?
A linear charge density is a measure of the total amount of charge per unit length of an electrical system or wire. More information can be found with this Surface Charge Density Calculator.
How to find linear density of a string?
First, you must measure the total mass of the string. Using an accurate scale, take the mass of the string. Next, you must straighten the string and measure the total length. Finally, use the formula Ld= M / L to calculate the linear density of the string.
Linear Density Example
How to calculate linear density?
- First, determine the length.
Measure the overall length or characteristic length of the object.
- Next, determine the mass.
Measure the mass of the length or section.
- Finally, calculate the linear density.
Calculate the linear density using the formula above.
FAQ
What is a linear density?
A linear density is a measure of the mass per unit length of an object.
Сосредоточенные и распределенные заряды
Заряды можно распределять по какой-либо области тел, тогда их называют распределенными. Когда же заряд целиком собран в одну точку, его называют точечным. Большинство школьных задач физики связано с точечными зарядами.
Сосредоточенный заряд
Электрический заряд, сосредоточенный в какой-либо точке пространства, называют точечным.
Рис. 1. Точечный заряд
Силу взаимодействия точечных зарядов можно вычислить, используя закон Кулона.
Распределенные заряды
Электрический заряд, так же, можно распределять по объему, площади, или длине. Такие заряды называют распределенными. Чтобы описать эти заряды, используют понятие плотности заряда.
Если заряд распределен по:
— объему, говорят о объемной плотности заряда;
— площади, употребляют поверхностную плотность;
— длине, используют линейную плотность.
Примечание: Плотности отрицательных зарядов записывают со знаком «минус».
Формула линейной плотности заряда
Рис. 2. Заряд распределен по длинному тонкому телу
[ large boxed {tau = frac{q}{L} } ]
( large q left(text{Кл} right) ) – заряд;
( large L left(text{м} right) ) – длина, по которой распределен заряд;
( large tau left(frac{text{Кл}}{text{м}} right) ) – линейная плотность заряда;
Формула поверхностной плотности заряда
Любая поверхность обладает площадью, распределяя по ней заряд, получим поверхностную его плотность.
Этот термин используют, например, для вычисления электрического поля заряженной плоскости, или плоского конденсатора (двух параллельных плоскостей).
Рис. 3. Заряд распределен по плоской поверхности
[ large boxed {sigma = frac{q}{S} } ]
( large S left(text{м}^{2} right) ) – площадь, по которой распределен заряд;
( large sigma left(frac{text{Кл}}{text{м}^{2}} right) ) – поверхностная плотность заряда;
Формула объемной плотности заряда
Функция, описывающая плотность распределения заряда в трехмерном пространстве, входит в одно из уравнений Максвелла.
Рис. 4. Заряд распределен по объему тела
[ large boxed {rho = frac{q}{V} } ]
( large V left(text{м}^{3} right) ) – объем, по которому распределен заряд;
( large rho left(frac{text{Кл}}{text{м}^{3}} right) ) – объемная плотность заряда;
Примечание:
Джеймс Клерк Максвелл (1831 — 1879) – талантливый шотландский математик и физик. Популяризатор науки, экспериментатор и конструктор научных приборов.
Описал электромагнитное взаимодействие с помощью своих уравнений (уравнения Максвелла). Система этих уравнений лежит в основе современной электродинамики.
Предсказал электромагнитные волны, обнаружил, что свет имеет электромагнитную природу и может создавать давление.
Занимался исследованиями в области молекулярной физики и термодинамики. Использовал математический аппарат статистики, получил температурное распределение скоростей молекул.
Проводил исследования в области астрономии и оптики, для планеты Сатурн провел анализ устойчивости колец.
Именно Максвелл заложил трехцветный принцип, который используется в цветной фотографии и телевидении.
Оценка статьи:
Загрузка…
Лине́йная пло́тность — физическая величина, определяемая отношением массы 
малого участка тела к его длине 
:
.
В случае однородного тела переход к пределу не требуется и
- ,
где 
и 
— масса и длина всего тела, соответственно. Понятие применяется преимущественно к протяжённым объектам (нитям, тонким стержням), когда изменения параметров в площади поперечного сечения незначимы. При отсутствии изгибов роль 
перенимет декартова координата вдоль объекта.
Единицей измерения в Международной системе единиц (СИ) является килограмм на метр (кг/м). В текстильной промышленности используются внесистемные единицы текс (г/км) и Денье (0,05г/450м, или 1/9 текс).
Термин «линейная плотность», как и просто «плотность», может использоваться не только для плотности массы, но и для плотности других физических величин — тогда это должно быть явно указано дополнительным словом. Например, говорят о линейной плотности заряда — пределе отношения электрического заряда, находящегося в элементе линии (заряженной нити), к длине этого элемента линии, который содержит данный заряд, когда длина этого элемента стремится к нулю.
В таком случае единицей измерения в СИ является кулон на метр (Кл/м).
См. также[править | править код]
- Теорема Гаусса
Для упрощения
математических расчетов электростатических
полей часто пренебрегают дискретной
структурой зарядов. Считают, что заряд
распределен непрерывно и вводят понятие
о плотности заряда.
Рассмотрим различные
случаи распределения зарядов.
1.Заряд
распределен вдоль линии.
Пусть на бесконечно малом участке
находится заряд
.
Введем величину
.
(1.5)
Величина
называется линейной плотностью заряда.
Ее физический смысл – заряд, приходящийся
на единицу длины.
2.Заряд
распределен по поверхности.
Введем поверхностную плотность заряда:
.
(1.6)
Её физический
смысл – заряд, приходящийся на единицу
площади.
3.Заряд
распределен по объёму.
Введем объёмную плотность заряда:
.
(1.7)
Её физический
смысл – заряд, сосредоточенный в единице
объёма.
Заряд,
сосредоточенный на бесконечно малом
участке линии, поверхности или в
бесконечно малом объёме можно считать
точечным. Напряжённость поля, создаваемого
им, определится формулой:
.
(1.8)
Для нахождения
напряжённости поля, создаваемого всем
заряженным телом, нужно применить
принцип суперпозиции полей:
.
(1.9)
В этом случае, как
правило, задача сводится к вычислению
интеграла.
1.3.Применение принципа суперпозиции к расчету электростатических полей. Электростатическое поле на оси заряженного кольца
Постановка
задачи.
Пусть имеется тонкое кольцо радиуса R,
заряженное с линейной плотностью заряда
τ.
Необходимо рассчитать напряжённость
электрического поля в произвольной
точке А,
расположенной на оси заряженного кольца
на расстоянии x
от плоскости кольца (рис. ).
Выберем
бесконечно малый элемент длины кольца
dl;
заряд dq,
находящийся на этом элементе равен dq=
τ·dl.
Этот заряд создает в точке А
электрическое поле напряжённостью
.
Модуль вектора напряжённости равен:
.
(1.10)
По
принципу суперпозиции полей напряжённость
электрического поля, создаваемого всем
заряженным телом, равна векторной сумме
всех векторов
:
.
(1.11)
Разложим
вектора
на составляющие: перпендикулярные оси
кольца (
)
и параллельные оси кольца (
).
.
(1.12)
Векторная
сумма перпендикулярных составляющих
равна нулю:
,
тогда
.
Заменяя сумму интегралом, получим:
.
(1.13)
Из
треугольника (рис.1.2) следует:
=
.
(1.14)
Подставим выражение (1.14) в формулу (1.13) и вынесем за знак интеграла постоянные величины, получим:
.
(1.15)
Так
как
,
то
.
(1.16)
С
учетом того, что
,
формулу (1.16) можно представить в виде:
.
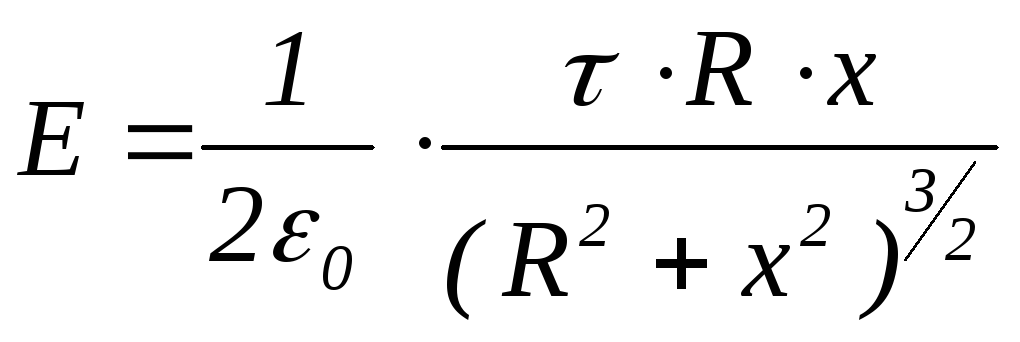(1.17)
1.4.Геометрическое описание электрического поля. Поток вектора напряжённости
Для
математического описания электрического
поля нужно указать в каждой точке
величину и направление вектора
,
то есть задать векторную функцию
.
Существует
наглядный (геометрический) способ
описания поля с помощью линий вектора
(силовых линий) (рис.13.).
Линии напряжённости
проводят следующим образом:
-
касательная
к линии в каждой точке должна совпадать
с направлением поля; -
число
линий пересекающих единичную площадку,
перпендикулярную к ним, должно быть
равно численному значению вектора
.
.
С
уществует
правило:
линии вектора напряжённости электрических
полей, создаваемых системой неподвижных
зарядов, могут начинаться или заканчиваться
лишь на зарядах либо уходить в
бесконечность.
На
рисунке 1.4 показано изображение
электростатического поля точечного
заряда с помощью линий вектора
,
а на рисунке 1.5 – изображение
электростатического поля диполя.
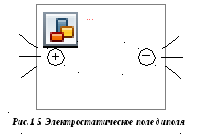
1.5.
Поток
вектора напряжённости электростатического
поля
П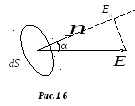
оместим
в электрическое поле бесконечно малую
площадку dS (рис.1,6).
Здесь
– единичный вектор нормали к площадке.
Вектор напряжённости электрического
поля
образует с нормалью
некоторый угол α.
Проекция вектора
на направление нормали равна En=E·cos
α .
Потоком вектора
через бесконечно малую площадку
называется скалярное произведение
,
(1.18)
или
.
(1.19)
Поток вектора
напряжённости электрического поля
является алгебраической величиной; его
знак зависит то взаимной ориентации
векторов
и
.
Поток
вектора
через произвольную поверхностьSконечной величины определится интегралом:
.
(1.20)
Е
сли
поверхность замкнутая, интеграл отмечают
кружочком:
.
(1.21)
Для замкнутых
поверхностей нормаль берется наружу
(рис.1.7).
Поток
вектора напряжённости имеет наглядный
геометрический смысл: он численно равен
числу линий вектора
,
проходящих через поверхностьS.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое плотность электрического заряда
Содержание
- 1 Типы зарядов
- 1.1 Связанные
- 1.2 Свободные
- 2 Точечный электрозаряд
- 3 Линейная плотность электрозаряда
- 4 Поверхностная плотность заряда
- 5 Объёмная плотность заряда
- 6 Заключение
- 7 Видео по теме
Физическую величину, характеризующую возможности тел быть первопричиной электромагнитного поля и участвовать в электромагнитных взаимодействиях с другими заряженными телами, называют электрическим зарядом. Различают электрозаряды точечные и распределенные в пространстве или области тела. Если основными параметрами точечного заряда является его знак (положительный или отрицательный) и абсолютная величина, то распределенный заряд характеризуется знаком и величиной плотности заряда.
Типы зарядов
Следует различать два типа зарядов — свободные и связанные.
Связанные
Такие электрозаряды находятся в составе нейтральных молекул либо это ионы (отрицательные и положительные), зафиксированные в узлах кристаллической решетки.
Свободные
Электрозаряды, свободно перемещающиеся на большие расстояния, создавая тем самым электрический ток, могут быть:
- Электрозаряды в вакууме или газовой среде.
- Электроны, вылетевшие с валентных орбит металлов.
- Ионы в электролитах.
- Электрозаряды на поверхности диэлектриков.
Точечный электрозаряд
По определению точечным считается электрозаряд, сосредоточенный в вакууме или в веществе (газе, жидкости, твердом теле), при этом его геометрические размеры намного меньше расстояний до ближайших заряженных частиц или тел, с которыми происходит электромагнитное взаимодействие. На ниже показано обозначение положительного точечного электрозаряда. В физике похожим понятием является материальная точка, которая необходима для решения задач в классической механике.
Единица измерения электрозаряда q в системе СИ — кулон (Кл) названа в честь французского естествоиспытателя Кулона. Электрозаряд в 1 Кл соответствует электрозаряду, прошедшему через поперечное сечение проводника при силе электротока 1 А за 1 секунду: [1 Кл] = [1 A] * [1 c].
Линейная плотность электрозаряда
Линейным называется физический объект, представляющий собой длинную нить с поперечным размером много меньше его длины.
Для этого случая распределения вводится понятие линейной плотности электрического заряда λ, которая равна:
Формула справедлива для электрозаряда, равномерно распределенного по длине. Когда он распределен по длине неравномерно, следует пользоваться дифференциальной версией формулы линейной плотности:
Поверхностная плотность заряда
В случае распределения электрозаряда на какой-либо поверхности площадью S для расчетов удобно использовать плотность поверхностного электрического заряда σ:
σ = q / S
Приведенная выше формула справедлива для электрозаряда, равномерно распределенного по площади. Для неравномерно распределенного по поверхности электрозаряда следует пользоваться дифференциальной версией формулы поверхностной плотности.
Объёмная плотность заряда
На картинке ниже показана ситуация распределения заряда в объеме объекта V. Для такого распределения применяется объемная плотность заряда ρ:
ρ= q / V
Как и в предыдущих случаях, формула применима для электрозаряда, равномерно распределенного в объеме. Для неравномерно распределенного в объеме электрозаряда следует пользоваться дифференциальной версией формулы объемной плотности.
Заключение
Несмотря на то, что электрические заряды по своей сути дискретны, понятие плотности электрозаряда помогает упростить расчёты, не внося значительных ошибок. Следует помнить, что в отличие от плотности физических тел (веществ) плотность электрозаряда может быть и положительной, и отрицательной, поскольку в природе присутствуют и «плюсы», и «минусы».
Видео по теме
