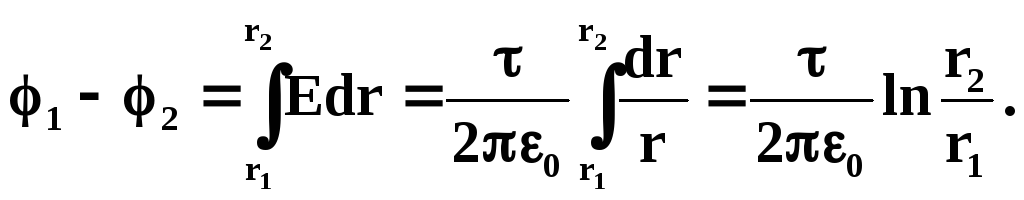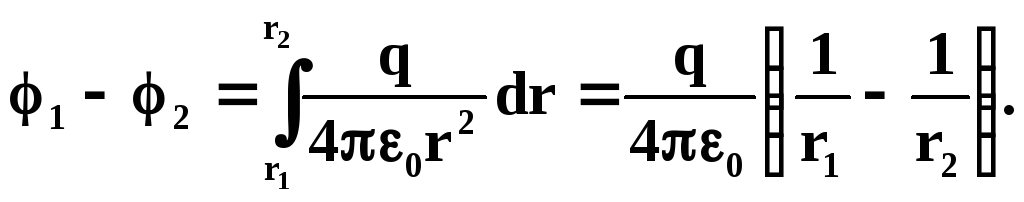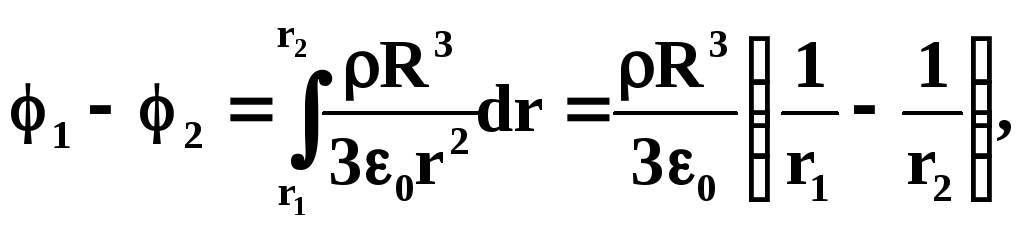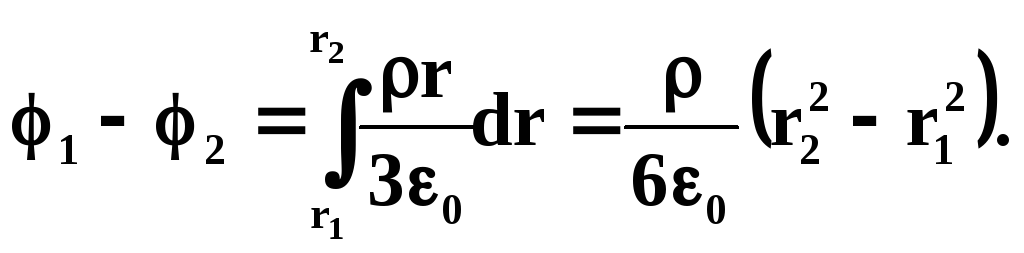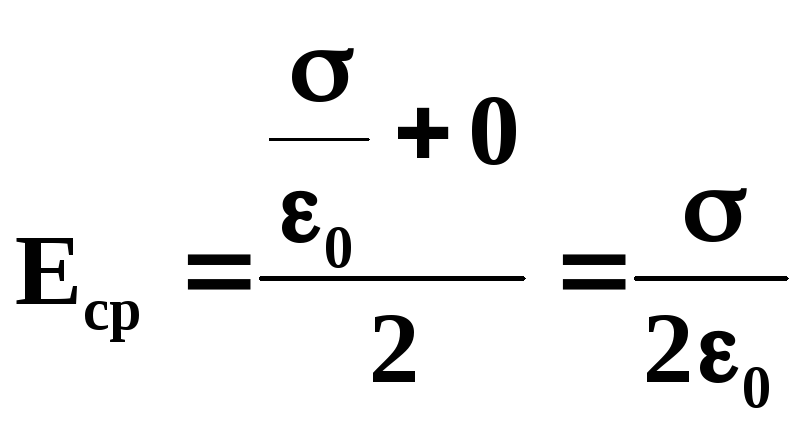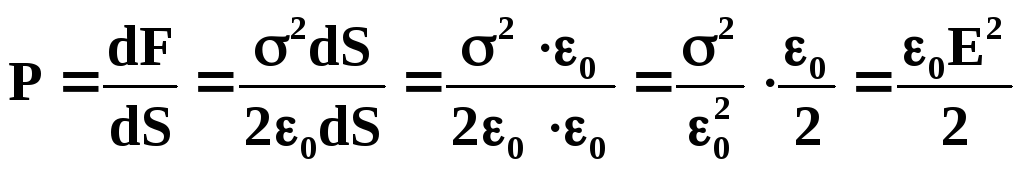Как найти линейную плотность заряда длинной нити

Решение.
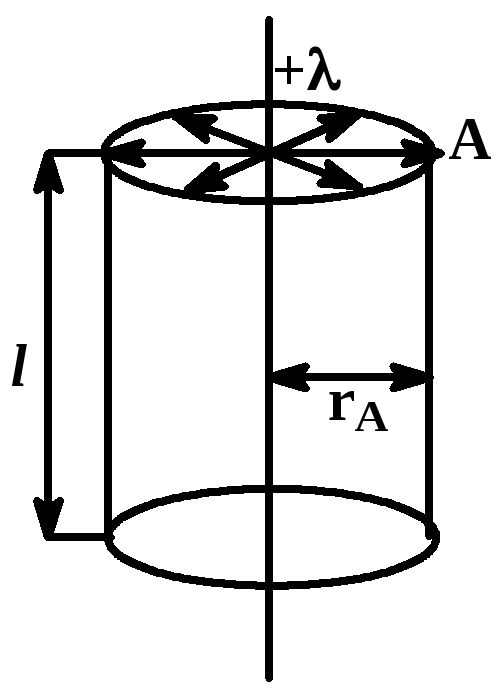
По теореме Гаусса поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду:

[ begin{align}
  & {{Phi }_{E}}=frac{Q}{varepsilon cdot {{varepsilon }_{0}}}(1),{{Phi }_{E}}=oint{{{E}_{n}}}cdot dS=Ecdot S=Ecdot 2cdot pi cdot rcdot l(2), \
 & Q=tau cdot l(3),frac{Q}{varepsilon cdot {{varepsilon }_{0}}}=Ecdot 2cdot pi cdot rcdot l,frac{tau cdot l}{varepsilon cdot {{varepsilon }_{0}}}=Ecdot 2cdot pi cdot rcdot l,E=frac{tau }{2cdot pi cdot varepsilon cdot {{varepsilon }_{0}}cdot r}(1). \
end{align} ]

Где: ε = 1 – диэлектрическая проницаемость воздуха, ε₀ = 8,854∙10^-12 Ф/м – электрическая постоянная.
Запишем уравнение элементарной работы, совершаемой внешними силами при перемещении заряда из точки 1 в точку 2.

[ begin{align}
  & dA=Fcdot dr(2),F=Qcdot E(3),dA=Qcdot Ecdot dr,dA=Qcdot frac{tau }{2cdot pi cdot varepsilon cdot {{varepsilon }_{0}}cdot r}cdot dr(4). \
 & A=intlimits_{{{R}_{1}}}^{{{R}_{2}}}{Qcdot frac{tau }{2cdot pi cdot varepsilon cdot {{varepsilon }_{0}}cdot r}cdot dr}=Qcdot frac{tau }{2cdot pi cdot varepsilon cdot {{varepsilon }_{0}}}cdot ln frac{{{R}_{2}}}{{{R}_{1}}}(5). \
 & tau =frac{Acdot 2cdot pi cdot varepsilon cdot {{varepsilon }_{0}}}{Qcdot ln frac{{{R}_{2}}}{{{R}_{1}}}}.tau =frac{-50cdot {{10}^{-6}}cdot 2cdot 3,14cdot 1cdot 8,85cdot {{10}^{-12}}}{1cdot {{10}^{-9}}cdot ln frac{2cdot {{10}^{-2}}}{5cdot {{10}^{-2}}}}=3032,77cdot {{10}^{-9}}. \
end{align} ]

Заряд перемещают против силовой линии поля, работа отрицательная.
Ответ:3,03∙10^-6 Кл/м, 3,03 мкКл/м.

Линейная
плотность заряда
– заряд, приходящийся на единицу длины:

Следовательно,

.

Разность потенциалов
между точками 1
и 2
поля, лежащими на расстоянии r₁
и r₂
от оси цилиндра:

3.
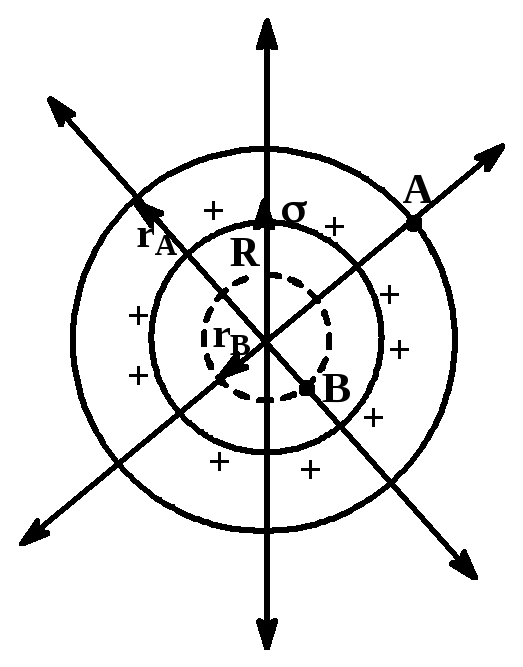
Поле заряженной сферической поверхности

Видно, что выражение
для
получилось таким же, как и для точечного
заряда.

Разность потенциалов

Шар, представляющий
собой диэлектрик, может быть внутри
равномерно заряжен с объемной плотностью

.
Поток векторачерез поверхность радиусомrR
(R
– радиус шара) равен
Заряд
внутри сферы радиусомr
равен:

.

По теореме Гаусса

и

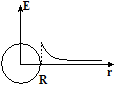
За пределами
равномерно заряженного шара выражение
для E_A
будет таким
же, как и полученное нами для полой сферы
,
только величинаq
будет
равняться V:

Разность потенциалов
для точек, лежащих на расстоянии rR
от центра шара:

и для точек, лежащих
на расстоянии rR
от центра шара:

2. Проводники в электрическом поле.

Проводниками
называют тела, которые хорошо проводят
электрический ток, в которых есть
свободные электрические заряды, способные
перемещаться по всему объему проводника.

Условия
равновесия зарядов на проводнике:

1. Напряженность
   поля внутри заряженного проводника
   должна быть равна нулю
   .
   В противном случае на заряды будет
   действовать электрическая сила,
   вызывающая их перемещение.

2. Избыточные заряды
   располагаются на поверхности проводника.
   В самом деле, при
   потокФ_Е вектора
   через любую замкнутую поверхность,
   проведенную внутри проводника, равен
   нулю. Из теоремы Гауссаследует,
   что приизбыточный заряд внутри проводника
   равен нулю:.

3. Потенциал поля
   внутри проводника постоянен, т.к. если
   ,
   то.

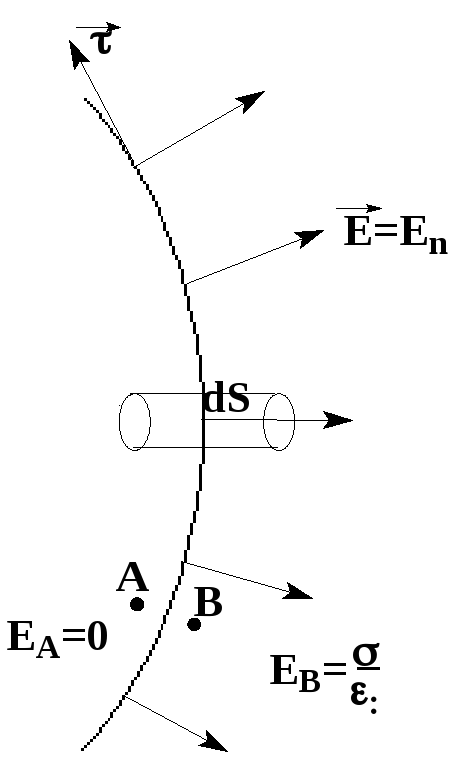
4. В каждой точке на
   поверхности заряженного проводника
   вектор напряженности направлен по
   нормали к поверхности. В противном
   случае вектор
   можно было бы разложить на две
   составляющие: нормальную к поверхностии направленную по касательной к
   поверхности:.
   Еслито на свободные заряды на поверхности
   проводника будет действовать электрическая
   сила, что заставит их перемещаться по
   поверхности проводника, при этом
   равновесие нарушится.

5. Поверхность
   проводника является эквипотенциальной
   поверхностью: потенциал во всех точках
   на поверхности проводника одинаков и
   равен потенциалу внутри проводника.

Поскольку внутри
проводника E=0,
а в непосредственной близости от
поверхности
,
то это значит, что при переходе из
проводника в пространство за проводником
(в воздух) значениеизменяется от 0 до.

Среднее значение
напряженности поля на поверхности
проводника получается равным:

Сила, с которой
поле проводника действует на заряд,
расположенный на его поверхности dS,
равна:

Давление, испытываемое
поверхностью проводника и обусловленное
избыточными зарядами на его поверхности,
равно:

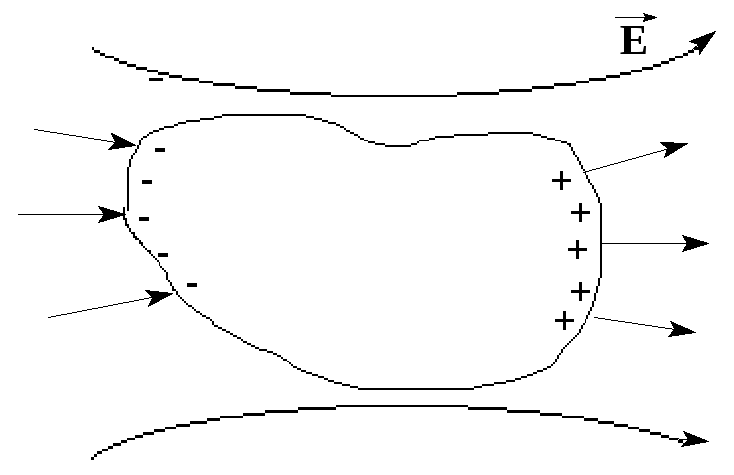
При помещении
незаряженного проводника в электрическое
поле имеющиеся на нем заряды приходят
в движение – на противоположных
поверхностях возникают избыточные
электрические заряды противоположных
знаков.

Возникающие на
поверхности заряды создают свое поле,
которое в точности равно внешнему, но
противоположно по направлению – внутри
проводника (в полости) поле отсутствует.

Перераспределение
зарядов в проводнике под действием
внешнего поля происходит до тех пор,
пока силовые линии не окажутся
перпендикулярными поверхности проводника.

Равенство нулю
напряженности поля в полости проводника
используют для реализации электрической
защиты, причем оказалось, что электрическая
защита получается достаточно хорошей
не только в случае сплошной металлической
оболочки, но и в случае использования
мелкой металлической сетки.

Соединение
проводником какого-либо тела с землей
называют заземлением. При заземлении
заряженных проводников, в том числе и
тела человека, они теряют заряд и их
потенциал будет равен потенциалу земли.
Заземление корпусов приборов и аппаратов
способствует их безопасной эксплуатации,
т.к. исключает возможность для персонала
оказаться под напряжением корпуса
аппарата и земли.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Лине́йная пло́тность — физическая величина, определяемая отношением массы малого участка тела к его длине :

.

В случае однородного тела переход к пределу не требуется и

,

где и — масса и длина всего тела, соответственно. Понятие применяется преимущественно к протяжённым объектам (нитям, тонким стержням), когда изменения параметров в площади поперечного сечения незначимы. При отсутствии изгибов роль перенимет декартова координата вдоль объекта.

Единицей измерения в Международной системе единиц (СИ) является килограмм на метр (кг/м). В текстильной промышленности используются внесистемные единицы текс (г/км) и Денье (0,05г/450м, или 1/9 текс).

Термин «линейная плотность», как и просто «плотность», может использоваться не только для плотности массы, но и для плотности других физических величин — тогда это должно быть явно указано дополнительным словом. Например, говорят о линейной плотности заряда — пределе отношения электрического заряда, находящегося в элементе линии (заряженной нити), к длине этого элемента линии, который содержит данный заряд, когда длина этого элемента стремится к нулю.

В таком случае единицей измерения в СИ является кулон на метр (Кл/м).

См. также[править | править код]

• Теорема Гаусса

Задача

Линейная плотность заряда бесконечной прямой нити τ = 0,2 мкКл/м. Определить работу сил поля A₁₂ по перемещению заряда q = 100 нКл из точки r₁ в точку r₂ = 2r₁. Электрическая постоянная равна ɛ₀ = 8,85·10⁻¹² Кл²/Нм².

Работа сил электростатического поля A₁₂ по перемещению заряда q равна:

Напряженность электростатического поля заряженной нити определялась ранее с помощью теоремы Гаусса и равна:

Учитывая связь напряженности и потенциала электростатического поля, можно записать:

Вставим под интеграл значение напряженности электростатического поля заряженной нити и получим:

Работа сил электростатического поля A₁₂ по перемещению заряда q= 100 нКл из точки r₁ в точку r₂= 2r₁ равна:

 Готовое решение: Заказ №8798

 Тип работы: Задача

Статус:  Выполнен (Зачтена преподавателем ВУЗа)

 Предмет: Физика

 Дата выполнения: 29.09.2020

 Цена: 227 руб.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

№1      6. Рассчитайте линейную плотность заряда длинной нити, если она притягивает точечный заряд 1 нКл, находящийся на расстоянии 1 мм, с силой 1 мкН.

Решение.

Проведём ось через нить, а ось – перпендикулярно нити через заряд.

Возьмём малый элемент нити с координатой. Его заряд:

где – линейная плотность заряда нити.

Элемент расположен от заряда на расстоянии:

Тогда сила взаимодействия элемента и заряда (по закону Кулона):