Для упрощения
математических расчетов электростатических
полей часто пренебрегают дискретной
структурой зарядов. Считают, что заряд
распределен непрерывно и вводят понятие
о плотности заряда.
Рассмотрим различные
случаи распределения зарядов.
1.Заряд
распределен вдоль линии.
Пусть на бесконечно малом участке
![]() находится заряд
находится заряд![]() .
.
Введем величину
![]() .
.
(1.5)
Величина
![]() называется линейной плотностью заряда.
называется линейной плотностью заряда.
Ее физический смысл – заряд, приходящийся
на единицу длины.
2.Заряд
распределен по поверхности.
Введем поверхностную плотность заряда:
![]() .
.
(1.6)
Её физический
смысл – заряд, приходящийся на единицу
площади.
3.Заряд
распределен по объёму.
Введем объёмную плотность заряда:
![]() .
.
(1.7)
Её физический
смысл – заряд, сосредоточенный в единице
объёма.
Заряд,
сосредоточенный на бесконечно малом
участке линии, поверхности или в
бесконечно малом объёме можно считать
точечным. Напряжённость поля, создаваемого
им, определится формулой:
![]() .
.
(1.8)
Для нахождения
напряжённости поля, создаваемого всем
заряженным телом, нужно применить
принцип суперпозиции полей:
![]() .
.
(1.9)
В этом случае, как
правило, задача сводится к вычислению
интеграла.
1.3.Применение принципа суперпозиции к расчету электростатических полей. Электростатическое поле на оси заряженного кольца
Постановка
задачи.
Пусть имеется тонкое кольцо радиуса R,
заряженное с линейной плотностью заряда
τ.
Необходимо рассчитать напряжённость
электрического поля в произвольной
точке А,
расположенной на оси заряженного кольца
на расстоянии x
от плоскости кольца (рис. ).

Выберем
бесконечно малый элемент длины кольца
dl;
заряд dq,
находящийся на этом элементе равен dq=
τ·dl.
Этот заряд создает в точке А
электрическое поле напряжённостью
![]() .
.
Модуль вектора напряжённости равен:
![]() .
.
(1.10)
По
принципу суперпозиции полей напряжённость
электрического поля, создаваемого всем
заряженным телом, равна векторной сумме
всех векторов
![]() :
:
![]() .
.
(1.11)
Разложим
вектора
![]() на составляющие: перпендикулярные оси
на составляющие: перпендикулярные оси
кольца (![]() )
)
и параллельные оси кольца (![]() ).
).
![]() .
.
(1.12)
Векторная
сумма перпендикулярных составляющих
равна нулю:
![]() ,
,
тогда![]() .
.
Заменяя сумму интегралом, получим:
![]() .
.
(1.13)
Из
треугольника (рис.1.2) следует:
![]() =
=![]() .
.
(1.14)
Подставим выражение (1.14) в формулу (1.13) и вынесем за знак интеграла постоянные величины, получим:
![]() .
.
(1.15)
Так
как
![]() ,
,
то
![]() .
.
(1.16)
С
учетом того, что
![]() ,
,
формулу (1.16) можно представить в виде:
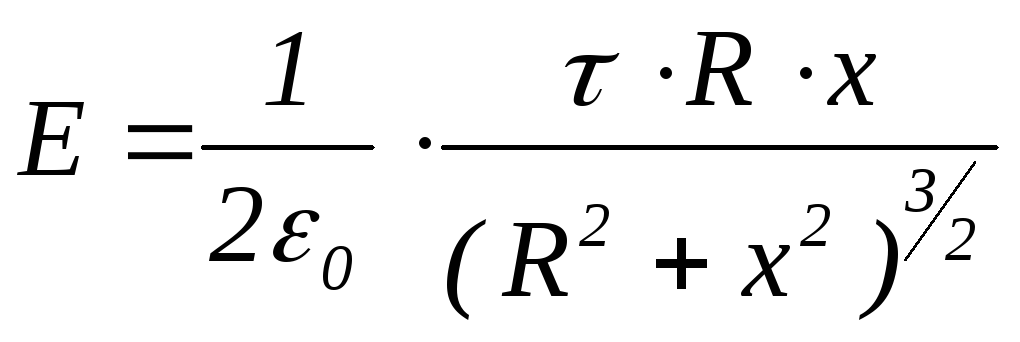 .
.
(1.17)
1.4.Геометрическое описание электрического поля. Поток вектора напряжённости
Для
математического описания электрического
поля нужно указать в каждой точке
величину и направление вектора
![]() ,
,
то есть задать векторную функцию![]() .
.
Существует
наглядный (геометрический) способ
описания поля с помощью линий вектора
![]() (силовых линий) (рис.13.).
(силовых линий) (рис.13.).
Линии напряжённости
проводят следующим образом:
-
касательная
к линии в каждой точке должна совпадать
с направлением поля; -
число
линий пересекающих единичную площадку,
перпендикулярную к ним, должно быть
равно численному значению вектора
 .
.
С
 уществует
уществует
правило:
линии вектора напряжённости электрических
полей, создаваемых системой неподвижных
зарядов, могут начинаться или заканчиваться
лишь на зарядах либо уходить в
бесконечность.
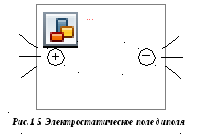
На
рисунке 1.4 показано изображение
электростатического поля точечного
заряда с помощью линий вектора
![]() ,
,
а на рисунке 1.5 – изображение
электростатического поля диполя.
1.5.
Поток
вектора напряжённости электростатического
поля
П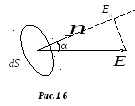 оместим
оместим
в электрическое поле бесконечно малую
площадку dS (рис.1,6).
Здесь
![]()
– единичный вектор нормали к площадке.
Вектор напряжённости электрического
поля
![]()
образует с нормалью
![]()
некоторый угол α.
Проекция вектора
![]()
на направление нормали равна En=E·cos
α .
Потоком вектора
![]() через бесконечно малую площадку
через бесконечно малую площадку
называется скалярное произведение
![]() ,
,
(1.18)
или
![]() .
.
(1.19)
Поток вектора
напряжённости электрического поля
является алгебраической величиной; его
знак зависит то взаимной ориентации
векторов
![]() и
и
![]() .
.
Поток
вектора
![]() через произвольную поверхностьSконечной величины определится интегралом:
через произвольную поверхностьSконечной величины определится интегралом:
![]() .
.
(1.20)
Е сли
сли
поверхность замкнутая, интеграл отмечают
кружочком:
![]() .
.
(1.21)
Для замкнутых
поверхностей нормаль берется наружу
(рис.1.7).
Поток
вектора напряжённости имеет наглядный
геометрический смысл: он численно равен
числу линий вектора
![]() ,
,
проходящих через поверхностьS.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На главную
страницу |
Мои темы
Заряженное кольцо
А я вот все
перерыл – и ни черта не могу найти формулу для электростатического поля в любой
точке плоскости заряженного (равномерно хотя бы) кольца.
Таков был вопрост
одного из участников форума на Мембране. Попробуем получить искомую формулу…
Пусть имеется: кольцо
радиуса r,
Заряженное с линейной плотностью заряда

Найдем напряженность,
создаваемую кольцом в точке, отстоящей на
R от центра кольца в плоскости кольца
(Рис. 1).

Для решения выберем
элементарный участок дуги кольца
dа
(точка А). На нем содержится заряд
![]() (1);
(1);
Этот заряд создает в
точке C элементарный
вектор напряженности dE.
 (2);
(2);
Найдем расстояние от
участка кольца до точки. Для этого используем тр.
OAC и теорему косинусов:
![]()
(3);
Теперь обратим внимание
на наличие симметричной точки
A’
и на то, что создаваемый этой точкой вектор также равен по модудю и направлен
симметрично оси х. Поэтому проекции векторов на ось «y»
компенсируются, а прекции на ось «x»
– удваиваются. Поэтому элементарный вектор напряженности, создаваемый ДВУМЯ
симметричными элементами кольца,
удваивается:
![]() (4);
(4);
Остается определить
cos(x).
Это легко сделать из рассмотрения тр.
ABC:
 (5);
(5);
Окончательно значение
проекции элементарного вектора напряженности будет иметь вид:

(6);
Для нахождения ПОЛНОГО
значения вектора напряженности в точке С,
необходимо
проинтегрировать выражение (6) по углу а в преднлпх от «0»
до
Pi.
При этом будут учтены ВСЕ заряды, находящиеся на кольце:
 (7);
(7);
И вот тут возникает
проблема. Ниже приводятся результаты интегрирования для функции
Z(a).

Вот и вылезли
эллиптические интегралы! А вот их расшифровка:

А главная проблема в
том, что эллиптические интегралы несводимы к обычным функциям. Таким образом,
ценность найденного решения, на мой взгляд, невелика.
Конечно, если
вычислитель умеет обращаться с такими функциями, это может помочь в расчетах. Но
я лично прдпочел бы воспользоваться одним из бесчисленных приемов числового
интегрирования выражения для
Z(a).
При разумном числе
разбиений процедура не займет много времени.
…Теперь понятно,
почему нигде нет стандартной формулы расчета параметров поля вокруг заряженного
кольца? Мне – да.

Рис. 2.
На Рис. 2 представлен график
напряженности как функция расстояния от произвольной точки до центра заряженного
кольца. Радиус кольца составляет 1000 ед. Красная линия представляет график
напряженности, создаваемой заряженной тем же зарядом сферой. При удалении
от кольца графики быстро сближаются. На первый взгляд может показаться, что
в
точке, соответствующей радиусу кольца, функция терпит разрыв. Но это не так.

Рис. 3
На Рис. 3
представлен график функции в непосредственной близости от кольца.
На самом кольце напряженность поля в
точности соответствует напряженности от заряженной проводящей сферы!

Рис. 4
На рис. 4.
представлен график функций вблизи отметки R=5*r.
Видно, насколько график искомой функции сблизился с графиком напряженности поля
заряженнрой сферы…
На главную
страницу |
Мои темы
![]()
Задача 1. Получить выражение для потенциала и напряженности
электрического поля на оси тонкого равномерно заряженного кольца
радиуса R . Линейная плотность заряда
.
const , показать, что при z R
Считая, что
потенциал поля кольца совпадает в пределе с потенциалом поля точечного
заряда.
1
Ведем цилиндрическую систему координат. Пусть ось совпадает с осью кольца и начало координат с центром кольца, – расстояние от центра коль
Ведем цилиндрическую систему координат. Пусть ось
с осью кольца и начало координат с центром кольца,
от центра кольца до точки наблюдения на оси.
dl
q
2 R
совпадает
– расстояние
Oz
z
dq dl Rd
– элемент длины тонкого кольца
Потенциал для точечного заряда
d
dq
4 0
(z)
2
0
Rd
R 2 z 2 4 0
R
4 0
1
1
R2 z 2
Напряженность поля кольца
d
1
R2 z 2
R
2 0
Ez (z)
1
R2 z 2
d
R
dz 2 0
E z (z) E z (z)
R
(z) (z)
z
2
z
2
3
2
Предельный случай
R
(z)
2 0
R
0
z
R
z
1
2
2
2 0
R z
1
2
R
1
z
z
R
R R
q 1
o
o
2 0 z
z 4 0 z
z
Использовали эквивалентную функцию
1 1
0
2
и
R
q
2
z R
Вывод. В предельном случае при
потенциал поля кольца совпадает с потенциалом поля точечного заряда
3
Задача 2. Получить выражение для напряженности электрического поля, создаваемое тонкой равномерно заряженной дугой окружности радиуса в е
Задача 2. Получить выражение для напряженности электрического
поля, создаваемое тонкой равномерно заряженной дугой окружности
радиуса R
в ее центре О. Линейная плотность заряда
.
4
В силу симметрии и принципа суперпозиции получаем, что
E x 0, E E y e y
Для точечного заряда
dq dl Rd
1
Rd 1
dE y dE cos
cos
cos
2
2
4 0 R
4 0 R
dq
0
0
cos d
Ey 2
sin
2 0 R
2
0 4 R 0
2
5
Задача 3. Найти силу взаимодействия отрезка длиной, равномерно заряженного с линейной плотностью заряда с точечным зарядом, находящимся н
Задача 3. Найти силу взаимодействия отрезка длиной l ,
равномерно заряженного с линейной плотностью заряда
с
точечным зарядом q 0
, находящимся на продолжении отрезка
на расстоянии a от ближайшего его конца.
Пусть ось Ox проходит через отрезок и точечный заряд. Начало
координат совпадает с началом отрезка. Тогда координата точечного
заряда равна
a l
dq dx
.
dq q0
1
dF
4 0 (l a x) 2
q0
q0 a dt
dx
F
2
2
4
4
0 (l a x)
0 l a t
0
l
6
Задача 4. Ось равномерно заряженного диска радиуса совпадает с осью. Центр диска находится в начала координат. Диск заряжен равномерно с по
Задача 4. Ось равномерно заряженного диска радиуса R совпадает
с осью Oz . Центр диска находится в начала координат. Диск
заряжен равномерно с поверхностной плотностью заряда.
Найти потенциал электрического поля, создаваемого диском в точках
оси. Рассмотреть предельный случай:
z R
7
Введем цилиндрическую систему координат
Рассмотрим точечный заряд
d
dq
4 0
dq dS rdrd
rdrd
1
4 0 r 2 z 2
r2 z2
1
2 R rdrd
2 R rdr
(z)
4 0 0 0 r 2 z 2 4 0 0 r 2 z 2
4 0
R2 z2
z2
dt
1/ 2
2 0
t
R z
2
2
z
8
Предельный случай
lim (z) lim
z
z 2
0
2
z
R
1 1
R 2 z 2 z lim
z
z 2
z
0
2
R2
z 1 R 2
R
1
q 1
o
2
2
z 4 0 z 16 0 z
z 2 2 z
z
0
Вывод. При z потенциал электрического поля заряженного
диска совпадает с точностью до константы с потенциалом поля
точечного заряда.
9
10. Задача 5. Найти потенциал ограниченной цилиндрической поверхности радиуса и длиной с зарядом, равномерно распределенным по поверхности.
Задача 5. Найти потенциал ограниченной цилиндрической
поверхности радиуса
R и длиной 2a с зарядом q
равномерно распределенным по поверхности.
,
Способ 1. Нахождение потенциала электрического поля, создаваемого
заряженной цилиндрической поверхностью через потенциал поля
заряженной окружности (тонкого кольца).
qкольца
кольца R
1
1
кольца(z)
, qкольца 2 R кольца
2
2
2
2
4 0 R z
2 0 R z
Рассматриваемая цилиндрическая поверхность – это совокупность
q
заряженных колец с зарядом dq
dz
2a
dq
q
2 R 2a
– заряд цилиндра
dz 2 Rd z
2a
z – координата кольца
10
11. Потенциала поля заряженной цилиндрической поверхности
(z)
a
q / 2a
4
0
a
1
R 2 (z z) 2
dz
a
a z (a z)2 R 2
q
d (z z)
q
ln
8 a 0 a R 2 (z z) 2 8 a 0 a z (a z) 2 R 2
Способ 2. Нахождение потенциала заряженной цилиндрической
поверхности через потенциал поля точечного заряда.
Цилиндрическая поверхность – это совокупность элементарных площадок
поверхности с зарядом
q
q
dq dS
2 R 2a
Rd dz
4 a
d dz
q 2 a
d dz
(z)
4 0 4 a 0 a R 2 (z z) 2
Точечным
зарядом
называется заряженное
тело, размерами которого можно пренебречь
по сравнению с расстояниями от этого
тела до других тел, несущих электрический
заряд.
Закон
Кулона:
Сила взаимодействия двух
неподвижных точечных зарядов
пропорциональна величине каждого из
зарядов и обратно пропорциональна
квадрату расстояния между ними.
Направление силы совпадает с соединяющей
эти заряды прямой.
где k
– коэффициент пропорциональности,q
1 иq
2
– величины
взаимодействующих зарядов,r
– расстояние между ними,e
12 – единичный вектор направленный от
заряда1
к заряду2
,F
12 – сила, действующая на заряд2
со
стороны заряда1
.
Коэффициент
k
определяется следующим
образом:
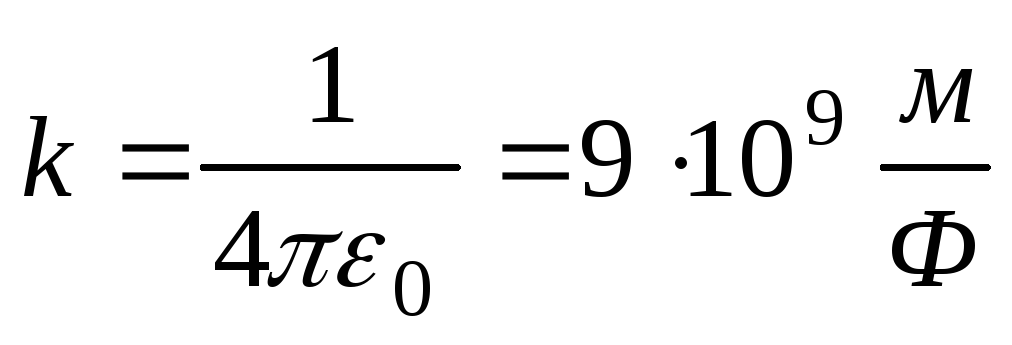 ,
,
где
0
= 8,85 10 -12 Ф/м – электрическая
постоянная.
Напряженность
поля
, создаваемого точечным зарядомq
прямо пропорциональна
заряду и обратно пропорциональна
квадрату расстояния от заряда до данной
точки поля:
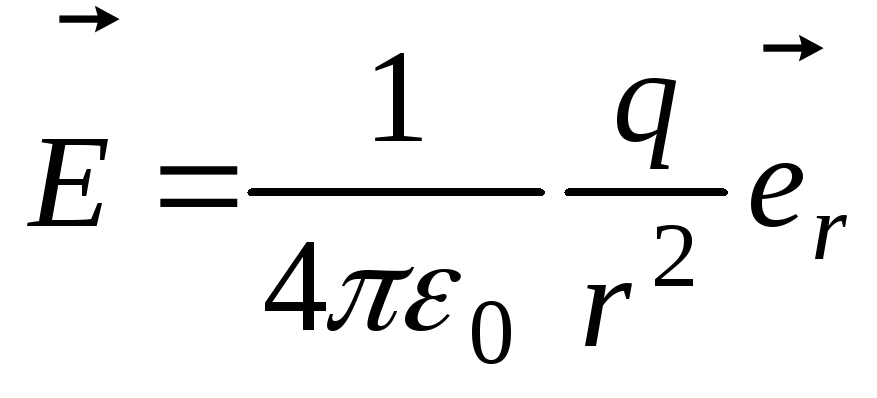 ,
,
вектор
направлен вдоль прямой, проходящей
через заряд и данную точку поля, от
заряда, если он положителен, и к заряду,
если он отрицателе.
Принцип
суперпозиции
: напряженность поля
системы зарядов равна векторной сумме
напряженностей полей, создаваемых
каждым зарядом в отдельности:
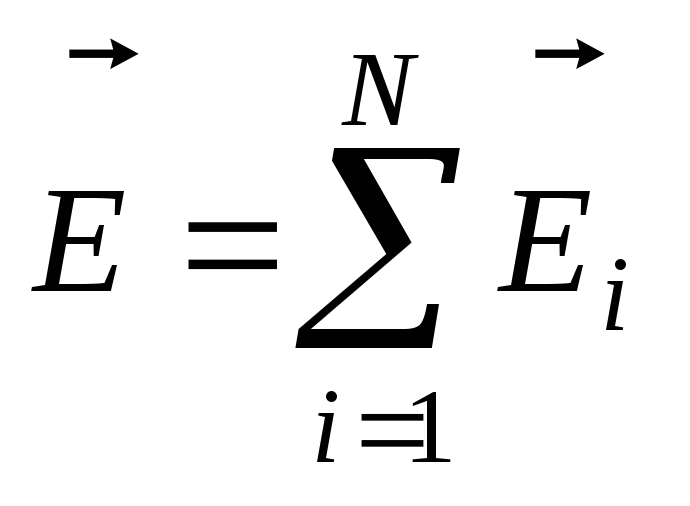 .
.
Потенциал
поля точечного заряда:
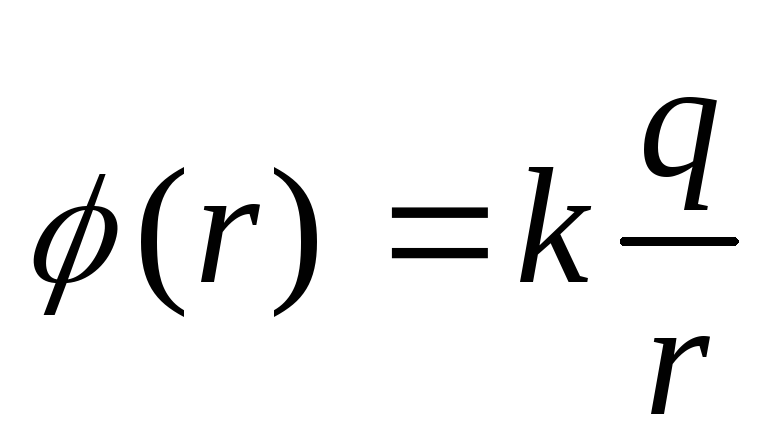 .
.
По принципу
суперпозиции потенциал системы точечных
зарядов равен:
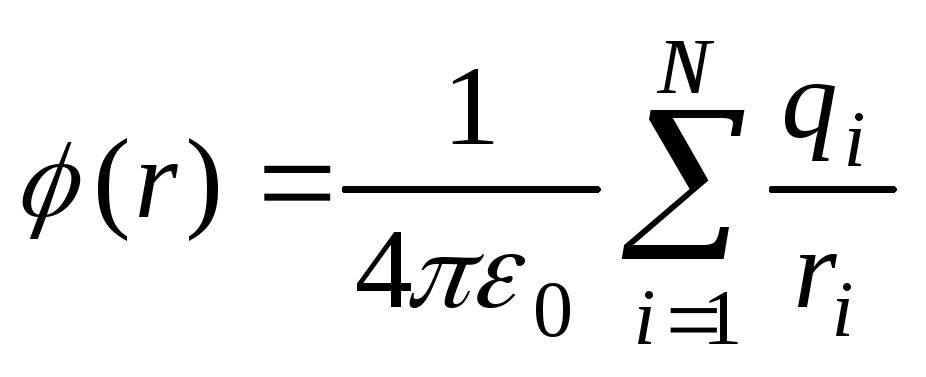 .
.
II. Примеры решения задач
Пример
1.1.
Тонкая проволока, представляющая
по форме четверть кольца радиусаR
,
заряжена равномерно зарядомq
.
Найти напряженность поля в центре
кривизны.
Решение.
Выбираем на
кольце элементарный заряд
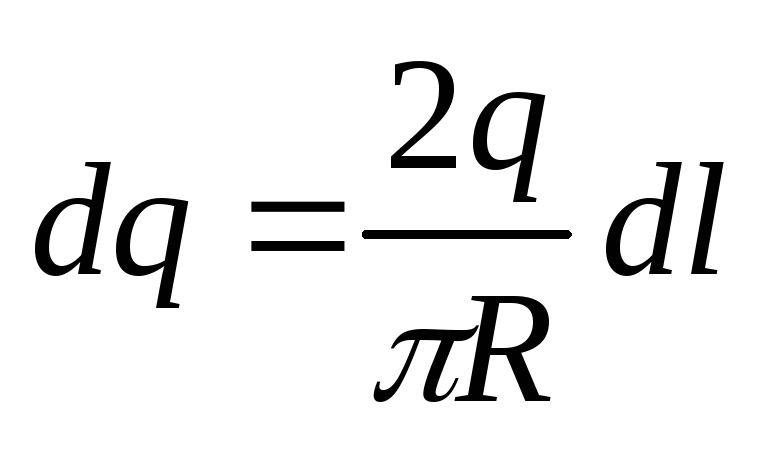 ,
,
где
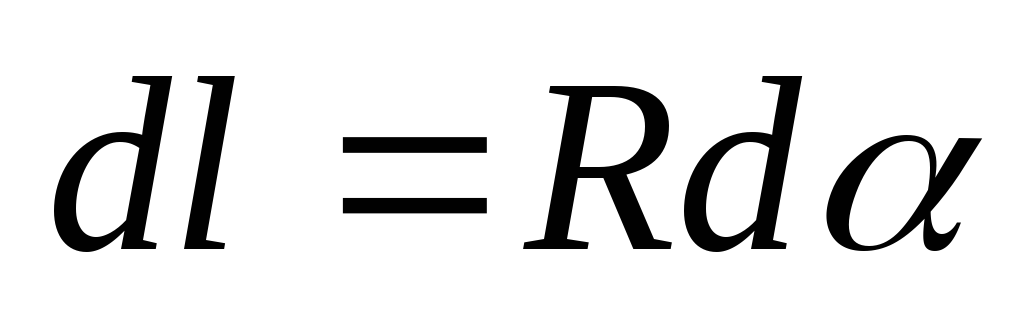 иd
иd
– угол под которым из центра кривизны
виден элементdl
.
Напряженность поля, создаваемого
этим элементарным зарядом, равна:
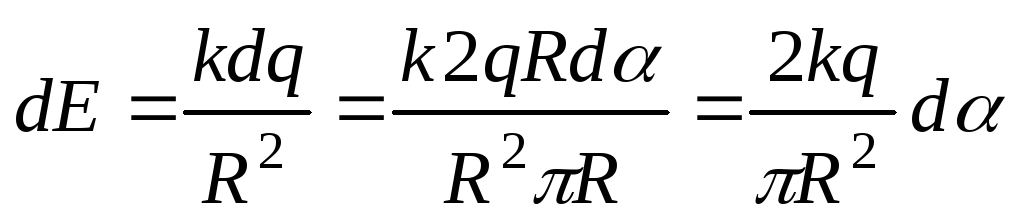 .
.
Введем оси
координат и находим проекции напряженности
поля на выбранные оси:
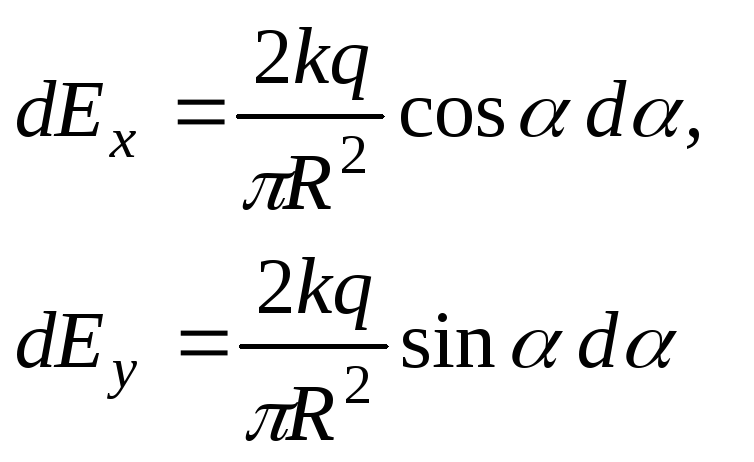 .
.
Тогда суммарная
напряженность будет равна:
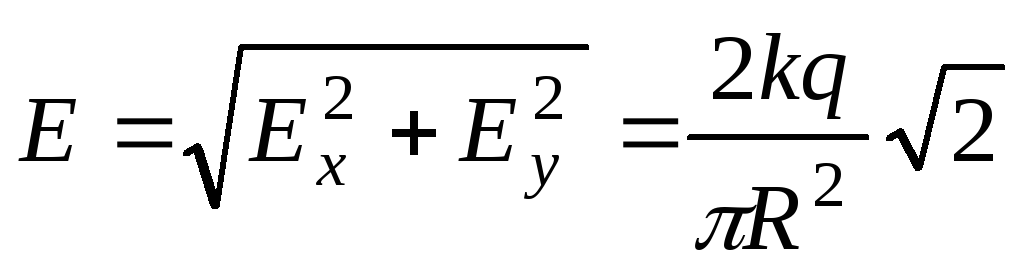 .
.
Вектор
напряженности направлен под углом 45к осих
.
Пример
1.2
Находящейся в вакууметонкий
прямой стержень длины 2а
заряжен
равномерно с зарядомq
.
Найти модуль напряженности электрического
поля как функцию расстоянияr
от центра стержня до точки прямой,
совпадающей с осью стержняr
>a
.
Решение.
Вводим
обозначения:
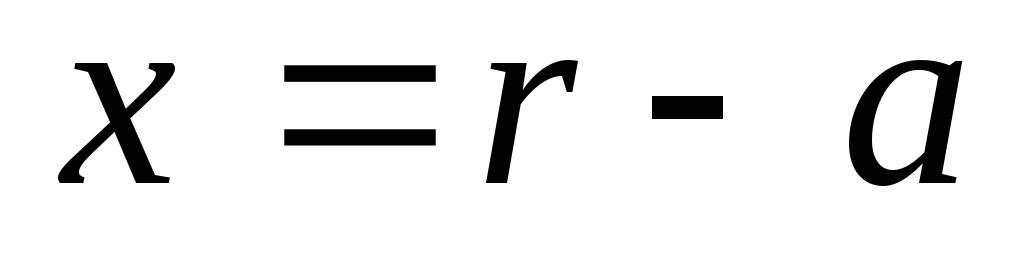 .
.
Выделим на стержне элементdl
,
заряд этого элемента равен:
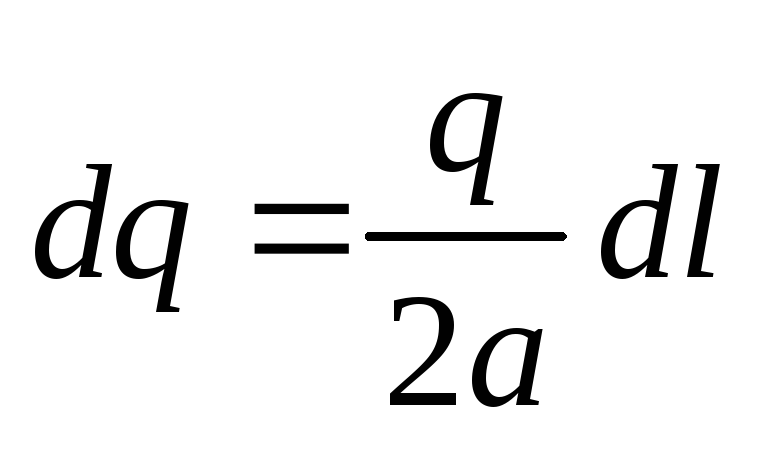 .
.
Напряженность поля, создаваемого в
точке наблюдения таким зарядом равна:
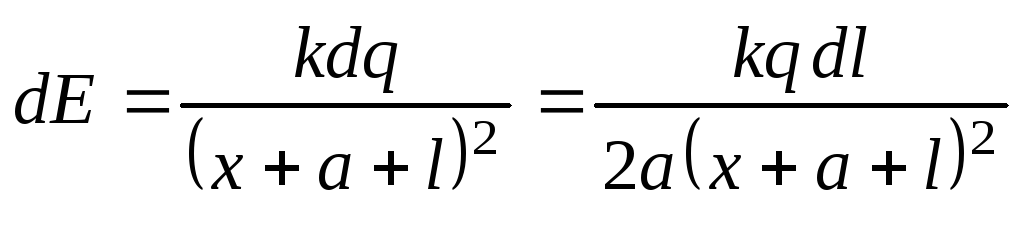 ,
,
где l
– расстояние от центра стержня до
элементаdl
. Поле,
создаваемое всем стерж7нем будет равно:
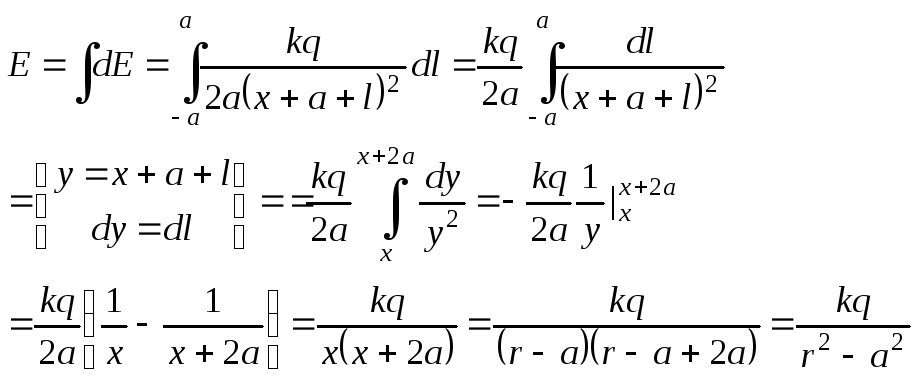
III. Задачи для самостоятельного решения
1.1.
Кольцо
радиусаRимеет зарядq.
Найти модуль напряженности электрического
поля на оси кольца как функцию расстоянияLдо его центра.
Ответ:
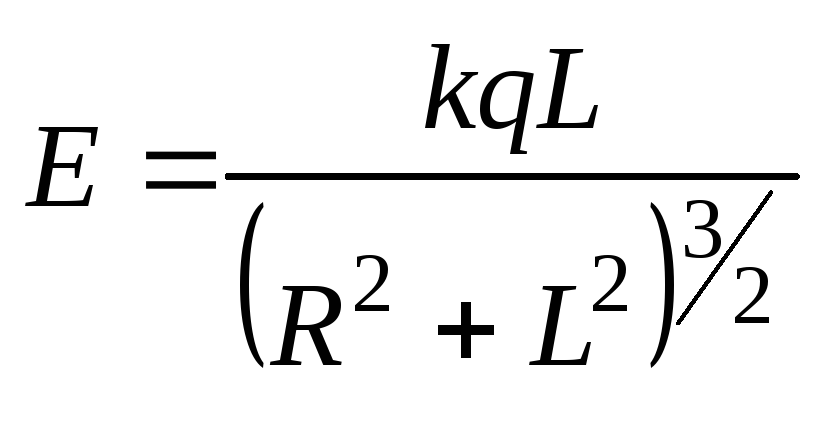 .
.
1.2.
Тонкая
проволока, представляющая по форме
кольцо радиусаR, заряжена
равномерно зарядомq.
Найти напряженность поля в центре
кольца.
Ответ:
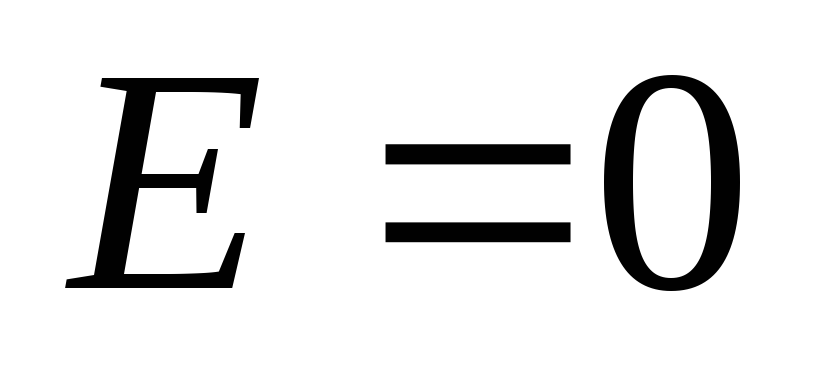 .
.
1.3.
Тонкое
полукольцо радиусаRимеет
положительный зарядq.
Найти напряженность в центре кривизны
этого полукольца.
Ответ:
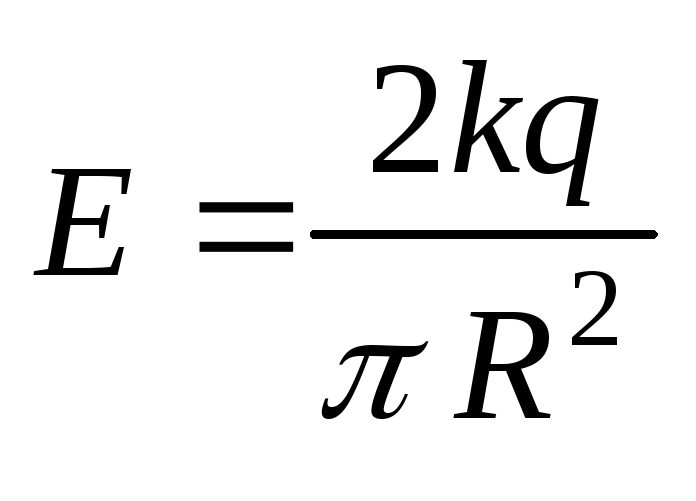 .
.
1.4.
Тонкая
проволока, представляющая по форме три
четверти кольца радиусаR,
заряжена равномерно зарядомq.
Найти напряженность поля в центре
кривизны.
Ответ:
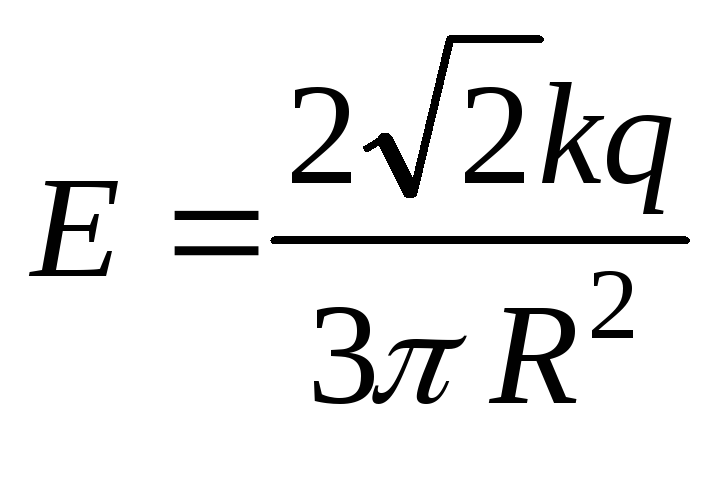 .
.
1.5.
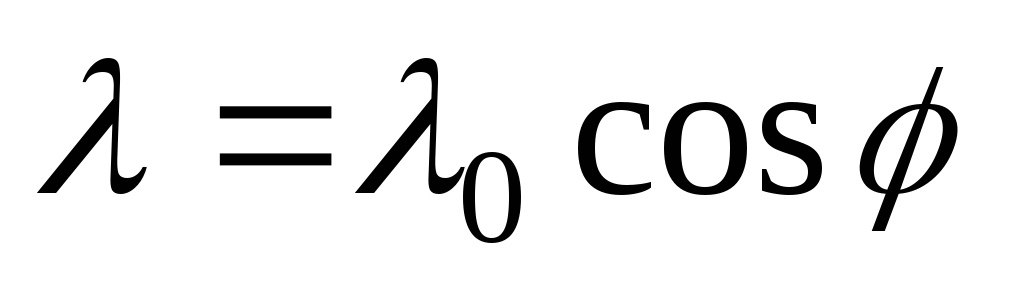 ,
,
где
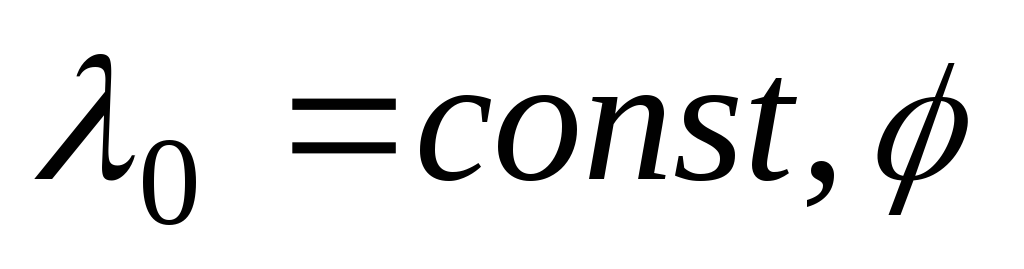 – азимутальный угол. Найти напряженность:
– азимутальный угол. Найти напряженность:
а) в центре кольца, б) на оси кольца в
зависимости от расстоянияL.
Ответ:
![]() .
.
1.6.
Тонкое
непроводящее кольцо радиусаRзаряжено с линейной плотностью
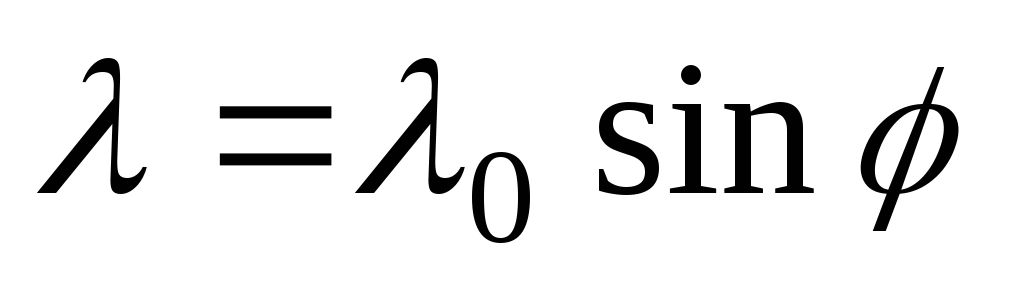 ,
,
где
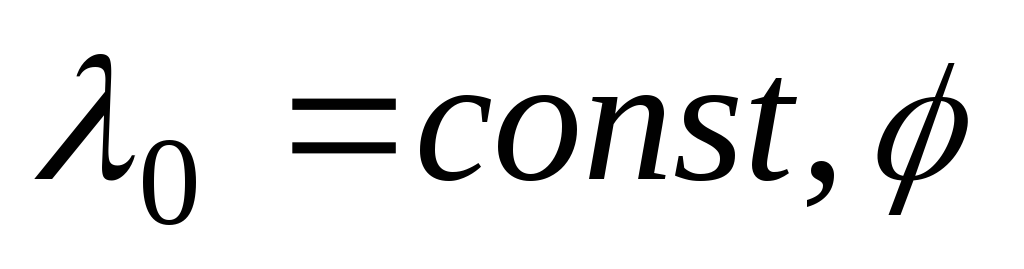 – азимутальный угол. Найти напряженность
– азимутальный угол. Найти напряженность
в центре кольца.
Ответ:
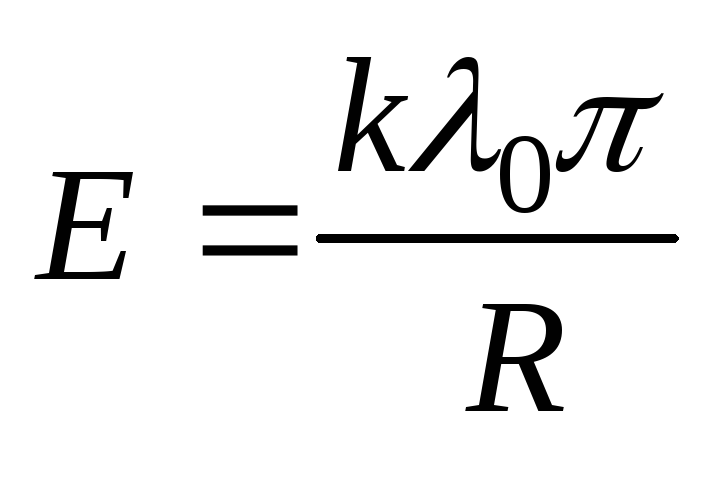 .
.
1.7.
Очень
длинная прямая нить заряжена с линейной
плотностью. Найти
модуль и направление напряженности
электрического поля в точке, которая
отстоит от нити на расстояниеLи находится на перпендикуляре к нити.
Ответ:
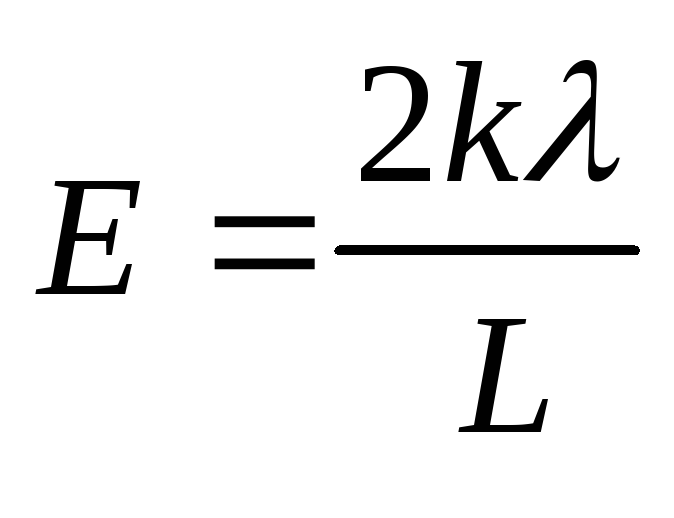 .
.
1.8.
Очень
длинная прямая нить заряжена с линейной
плотностью. Найти
модуль и направление напряженности
электрического поля в точке, которая
отстоит от нити на расстояниеLи находится на перпендикуляре к нити,
проходящем через один из ее концов.
Ответ:
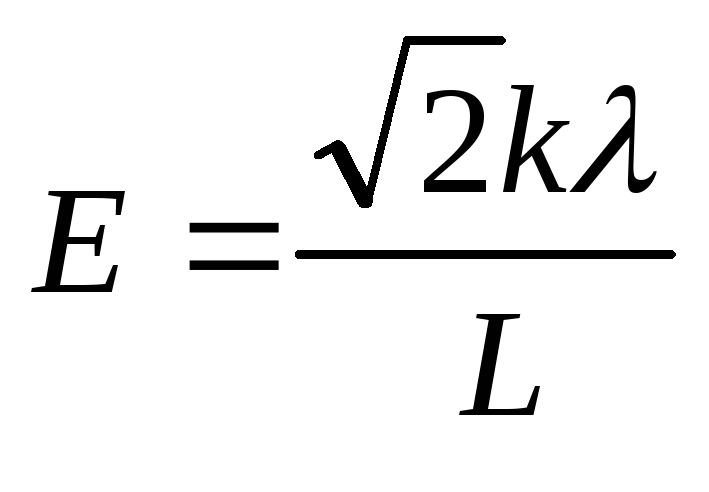 .
.
1.9.
Тонкий
прямой стержень длины 2а равномерно
заряжен с линейной плотностью.
НайтиE(L),
гдеL-расстояние от центра
стержня до точки прямой, перпендикулярной
стержню и проходящей через его центр.
Ответ:
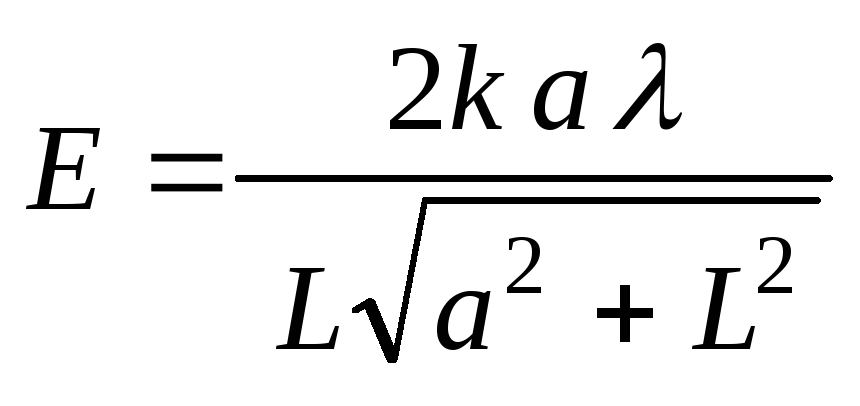 .
.
1.10.
Тонкий
прямой стержень длины 2а равномерно
заряжен с линейной плотностью.
НайтиE(L),
гдеL-расстояние от центра
стержня до точки прямой совпадающей с
осью стержня, если
 .
.
Ответ:
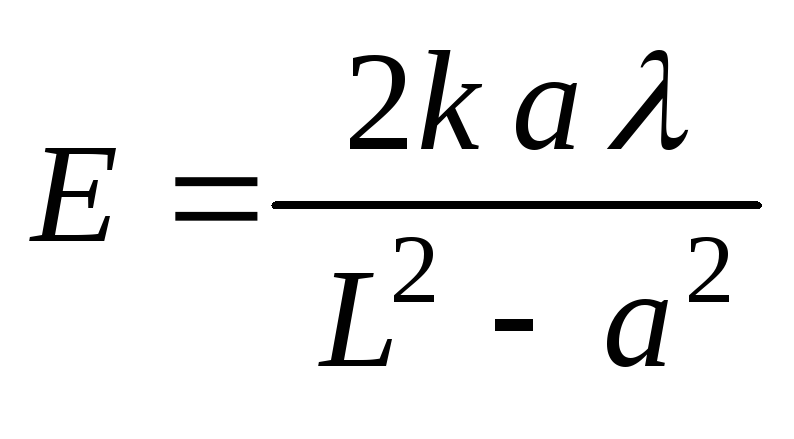 .
.
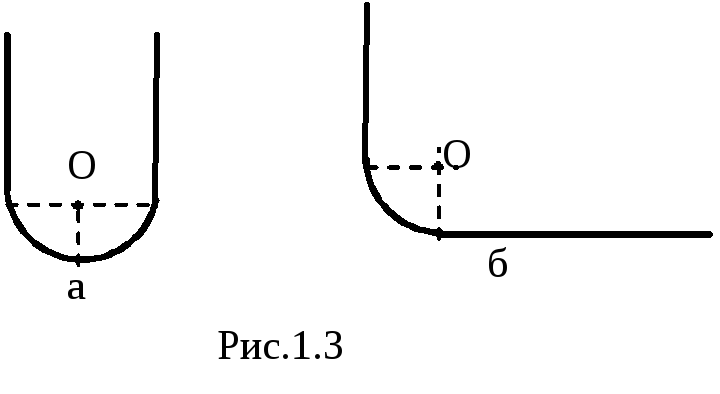
1.11.
Равномерно заряженная нить, на единицу
длины которой приходится заряд,
имеет конфигурацию, показанную на
рис.1.3. Радиус закругленияRгораздо меньше длинны нити. Найти модуль
напряженности электрического поля в
точке О.
Ответ:
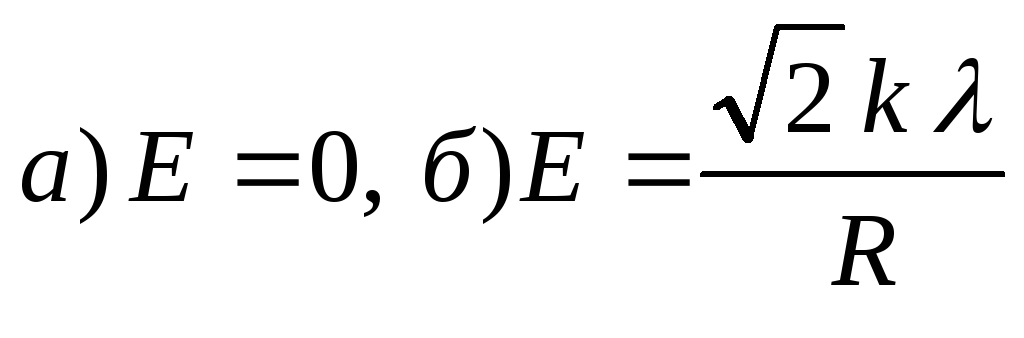 .
.
1.12.
Находящаяся в вакууме тонкая пластинка
радиусаRравномерно
заряжена с поверхностной плотностью. Найти модуль
напряженности электрического поля на
оси пластинки как функцию расстоянияLот ее центра.
Ответ:
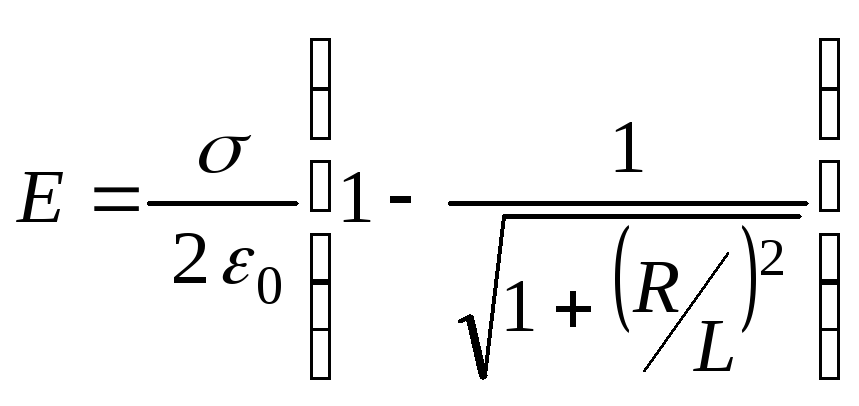 .
.
1.13
. Плоское
кольцо, внутренний радиус которого а,
внешний в, заряжено с поверхностной
плотностью. Найти
модуль напряженности электрического
поля на оси кольца как функцию расстоянияLот его центра.
О
 твет:
твет:
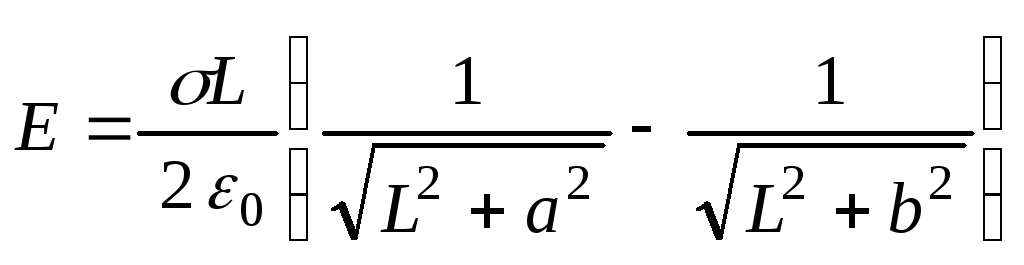 .
.
1.14.
Зарядqраспределен равномерно
по объему шара радиусаR.
Найти потенциал:
а) в центре
шара 0 ,
б) внутри шара(r),
в) вне шара(r),
гдеr- расстояние от центра
шара.
1.15.
Потенциал
поля внутри заряженного шара
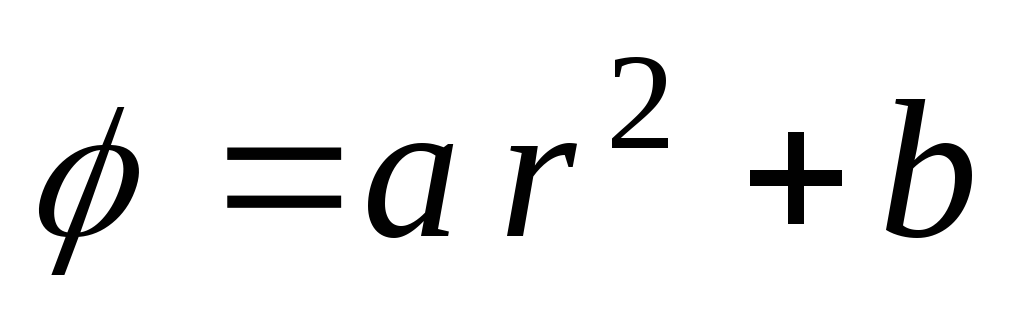 ,
,
гдеа
иb
–
постоянные. Найти зависимость объемной
плотности заряда(r)
от расстояния от центра шара.
Ответ:
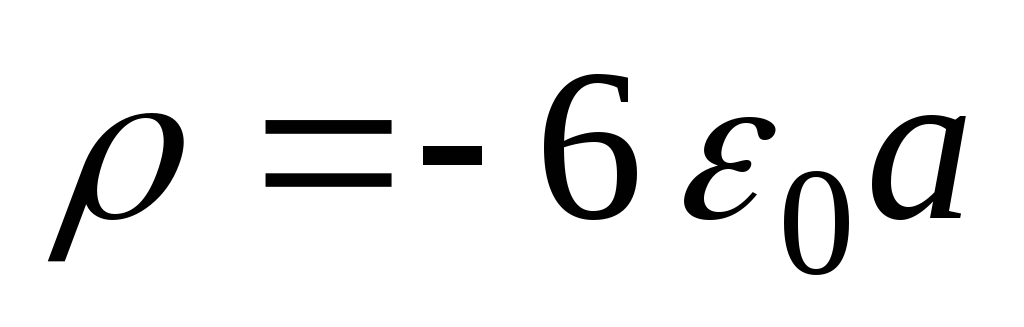 .
.
1.16.
По
сфере радиусаRравномерно
распределены заряды с поверхностной
плотностьюНайти
потенциал в зависимости от расстояния
до центра сферы.
Ответ:
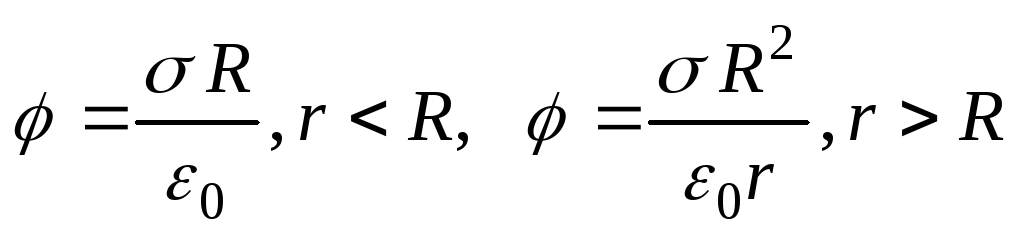 .
.
1.17
. Плоское
кольцо, внутренний радиус которогоа
,
внешнийb
, заряжено с
поверхностной плотностью.
Найти потенциал в центре кольца.
Ответ:
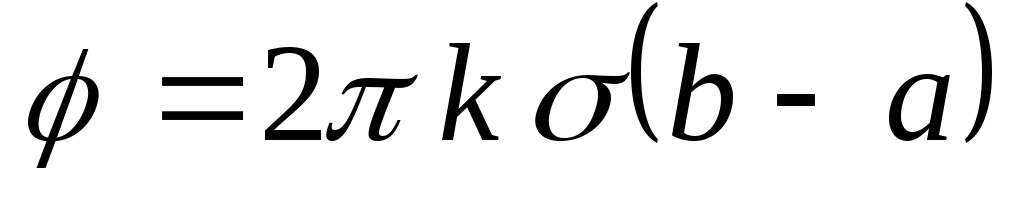 .
.
1.18.
Находящаяся в вакууме тонкая пластинка
радиусаRравномерно
заряжена с поверхностной плотностью. Найти потенциал
электрического поля на оси пластинки
как функцию расстоянияLот ее центра.
Ответ:
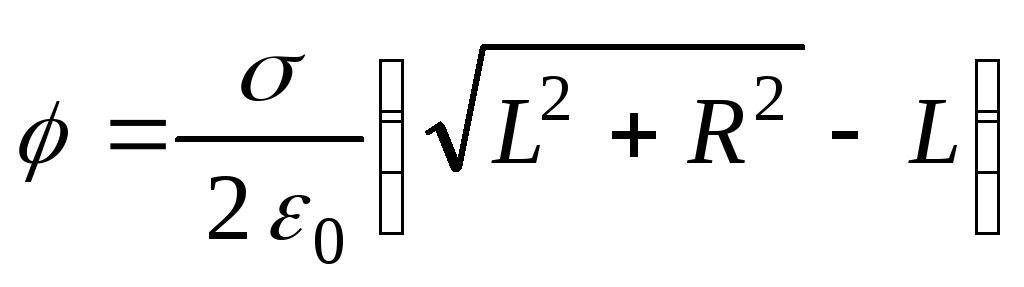 .
.
1.19
. Две
длинные одноименно заряженные нити
расположены на расстоянии
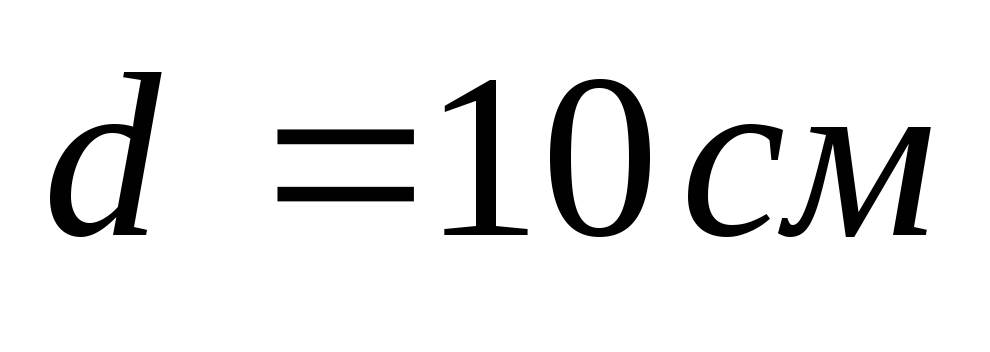 друг от друга. Линейная плотность заряда
друг от друга. Линейная плотность заряда
на нитях
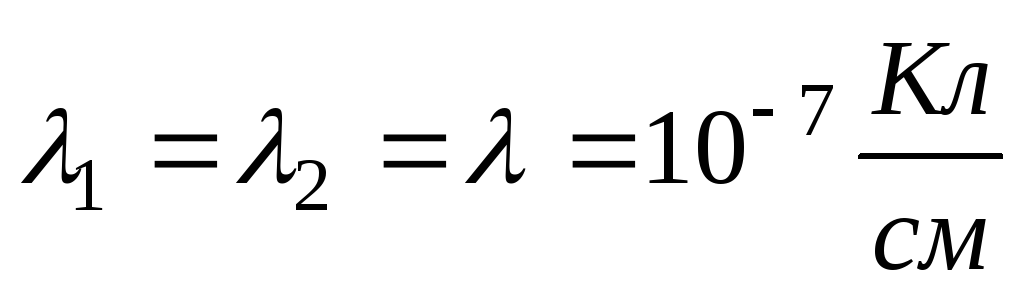 .
.
Найти величину и направление напряженности
результирующего электрического поля
в точке, находящейся на расстоянии
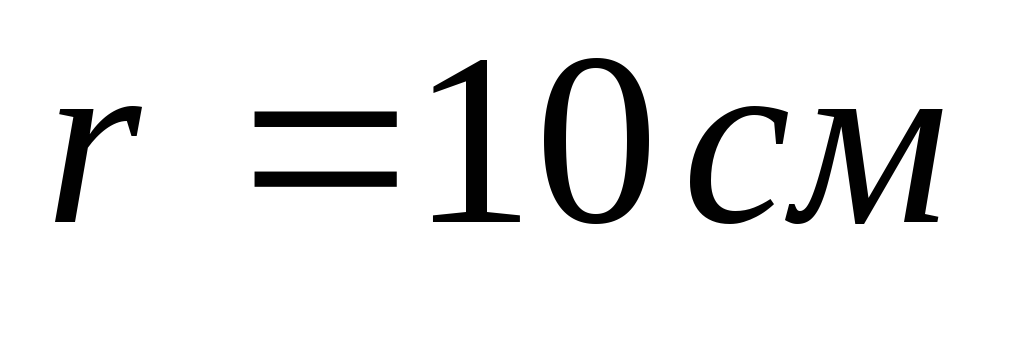 от каждой нити.
от каждой нити.
Ответ:
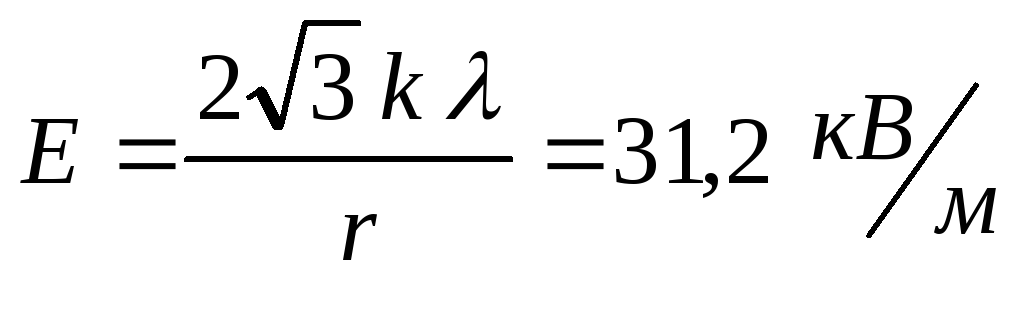 .
.
Пример расчета напряженности Электрического поля равномерно заряженного тонкого кольца
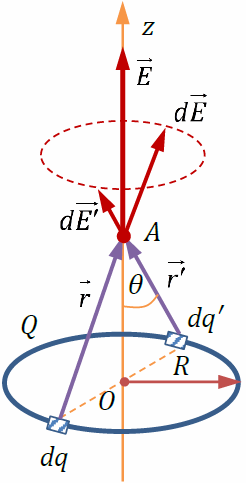 По тонкому кольцу равномерно распределён заряд Q
По тонкому кольцу равномерно распределён заряд Q
> 0. Находим напряжённость электрического поля в точке A
на оси кольца (OA
= z
). Разобьём кольцо на точечные заряды dq
(на рисунке показаны два малых заряда dq
и dq′
, равные по модулю и расположенные диаметрально противоположно). По принципу суперпозиции полей – где dE –
напряжённость электрического поля малого заряда dq
.
Векторы напряжённости электрического поля каждого из этих зарядов одинаковы по модулю и направлены так, что концы этих векторов образуют конус с вершиной в точке A
(штриховой линией показано основание этого конуса). Проекции этих векторов на плоскость кольца компенсируются, поэтому суммарный вектор направлен вдоль оси z
: E (при z
> 0). Вычислим Ez
. Напряжённость поля точечного заряда:
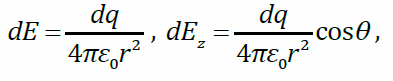
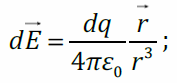 Величины r
Величины r
иθ (угол)
одинаковы для всех элементов dq
:
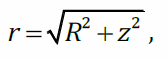
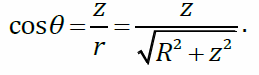 подставим
подставим 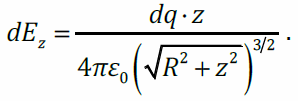
В этом выражении все величины – постоянные, кроме dq. Проинтегрируем по q:
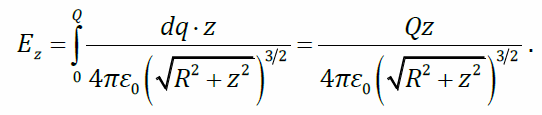
Поток вектора напряженности. Теорема Остроградского-Гауса для электростатического поля в вакууме. Применение теоремы к расчету напряженности поля. Пример: поле бесконечно большой равномерно заряженной плоскости.
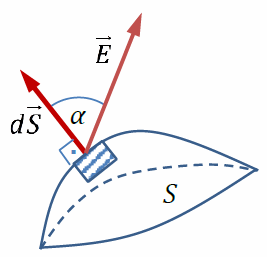 Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля
Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля
(Φ).
Элементарный поток
направлен по внешней нормали
к малому участку dS
(Если поверхность S
не замкнута, то выбор одного из двух направлений нормали произволен, при этом направление нормали для всех участков dS
должно быть одинаковым)
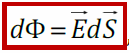
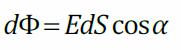
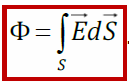
Полный поток
вектора сквозь поверхность S
E
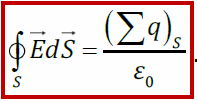
Теорема Остроградского-Гаусса для:
поток вектора напряжённости электрического поля сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охваченной этой поверхностью, делённой на ε
0:

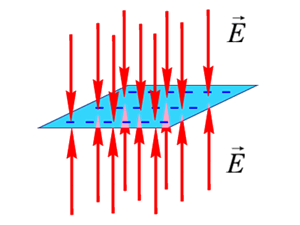
Поле равномерно заряженной бесконечной плоскости
:
, где – поверхностная плотность заряда.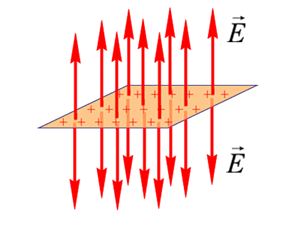
Работа сил электростатического поля по перемещению заряда. Потенциал электростатического поля. Связь между напряженностью поля и потенциалом. Понятие градиента. Методы расчета потенциала. Пример: потенциал на оси равномерно заряженного кольца.
I уравнение Максвелла для электростатического поля умножим на пробный заряд q
0:
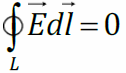
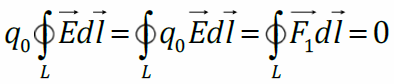
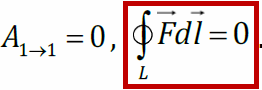 Работа электростатического поля по перемещению пробного заряда по произвольной замкнутой траектории равна нулю. Это означает, что электростатическое поле потенциально. Потенциальная энергия
Работа электростатического поля по перемещению пробного заряда по произвольной замкнутой траектории равна нулю. Это означает, что электростатическое поле потенциально. Потенциальная энергия
заряженной частицы в электростатическом поле равна работе внешних сил при перемещении этой частицы из точки, где потенциальная энергия принята равной нулю, в данную точку, или работе поля при этом перемещении: ![]() .Потенциальная энергия – характеристика и поля, и заряда:
.Потенциальная энергия – характеристика и поля, и заряда: ![]()
По тонкому проволочному кольцу равномерно распределен заряд с линейной плотностью τ = 100 пКл/м. Определить потенциал Φ электрического поля в центре кольца.
Эта задача была размещена посетителями в разделе Решаем вместе 8 октября 2007 года.
Решение:
 Потенциал в центре проволочного кольца определим по принципу суперпозиции, разбив кольцо на элементарные участки с зарядом qi. Получим формулу (на рисунке слева), в которой:
Потенциал в центре проволочного кольца определим по принципу суперпозиции, разбив кольцо на элементарные участки с зарядом qi. Получим формулу (на рисунке слева), в которой:
i — количество разбиений,
потенциал Φi, создаваемый в центре кольца элементарным зарядом qi, равен:
Из формулы линейной плотности заряда кольца
выразим:
Произведем суммирование Φ:
| Φ = | 1 | • | qiN | = | 1 | • | q | = | 2πτR | = | τ | . |
| 4πεo | R | 4πεo | R | 4πεoR | 2εo |
