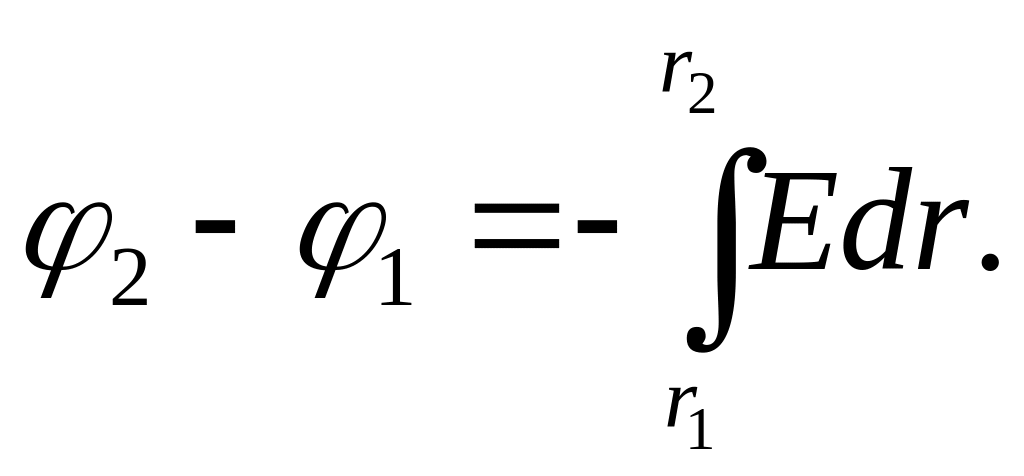Сосредоточенные и распределенные заряды
Заряды можно распределять по какой-либо области тел, тогда их называют распределенными. Когда же заряд целиком собран в одну точку, его называют точечным. Большинство школьных задач физики связано с точечными зарядами.
Сосредоточенный заряд
Электрический заряд, сосредоточенный в какой-либо точке пространства, называют точечным.
Рис. 1. Точечный заряд
Силу взаимодействия точечных зарядов можно вычислить, используя закон Кулона.
Распределенные заряды
Электрический заряд, так же, можно распределять по объему, площади, или длине. Такие заряды называют распределенными. Чтобы описать эти заряды, используют понятие плотности заряда.
Если заряд распределен по:
— объему, говорят о объемной плотности заряда;
— площади, употребляют поверхностную плотность;
— длине, используют линейную плотность.
Примечание: Плотности отрицательных зарядов записывают со знаком «минус».
Формула линейной плотности заряда
Рис. 2. Заряд распределен по длинному тонкому телу
[ large boxed {tau = frac{q}{L} } ]
( large q left(text{Кл} right) ) – заряд;
( large L left(text{м} right) ) – длина, по которой распределен заряд;
( large tau left(frac{text{Кл}}{text{м}} right) ) – линейная плотность заряда;
Формула поверхностной плотности заряда
Любая поверхность обладает площадью, распределяя по ней заряд, получим поверхностную его плотность.
Этот термин используют, например, для вычисления электрического поля заряженной плоскости, или плоского конденсатора (двух параллельных плоскостей).
Рис. 3. Заряд распределен по плоской поверхности
[ large boxed {sigma = frac{q}{S} } ]
( large S left(text{м}^{2} right) ) – площадь, по которой распределен заряд;
( large sigma left(frac{text{Кл}}{text{м}^{2}} right) ) – поверхностная плотность заряда;
Формула объемной плотности заряда
Функция, описывающая плотность распределения заряда в трехмерном пространстве, входит в одно из уравнений Максвелла.
Рис. 4. Заряд распределен по объему тела
[ large boxed {rho = frac{q}{V} } ]
( large V left(text{м}^{3} right) ) – объем, по которому распределен заряд;
( large rho left(frac{text{Кл}}{text{м}^{3}} right) ) – объемная плотность заряда;
Примечание:
Джеймс Клерк Максвелл (1831 — 1879) – талантливый шотландский математик и физик. Популяризатор науки, экспериментатор и конструктор научных приборов.
Описал электромагнитное взаимодействие с помощью своих уравнений (уравнения Максвелла). Система этих уравнений лежит в основе современной электродинамики.
Предсказал электромагнитные волны, обнаружил, что свет имеет электромагнитную природу и может создавать давление.
Занимался исследованиями в области молекулярной физики и термодинамики. Использовал математический аппарат статистики, получил температурное распределение скоростей молекул.
Проводил исследования в области астрономии и оптики, для планеты Сатурн провел анализ устойчивости колец.
Именно Максвелл заложил трехцветный принцип, который используется в цветной фотографии и телевидении.
Оценка статьи:
Загрузка…
Примеры решения задач
Пример
1. На тонком
стержне длиной l
= 20 см находится равномерно распределенный
электрический заряд. На продолжении
оси стержня на расстоянии а = 10 см от
ближайшего конца находится точечный
заряд q1
= 40 нКл, который взаимодействует со
стержнем с силой F
= 6 мкН. Определить линейную плотность
τ заряда на стержне.
Р
е ш е н и е. Сила взаимодействия F
заряженного стержня с точечным зарядом
q1
зависит от линейной плотности τ заряда
на стержне. Зная эту зависимость, можно
определить τ. При вычислении силы F
следует иметь в виду, что заряд на стержне
не является точечным, поэтому закон
Кулона непосредственно применить
нельзя. В этом случае можно поступить
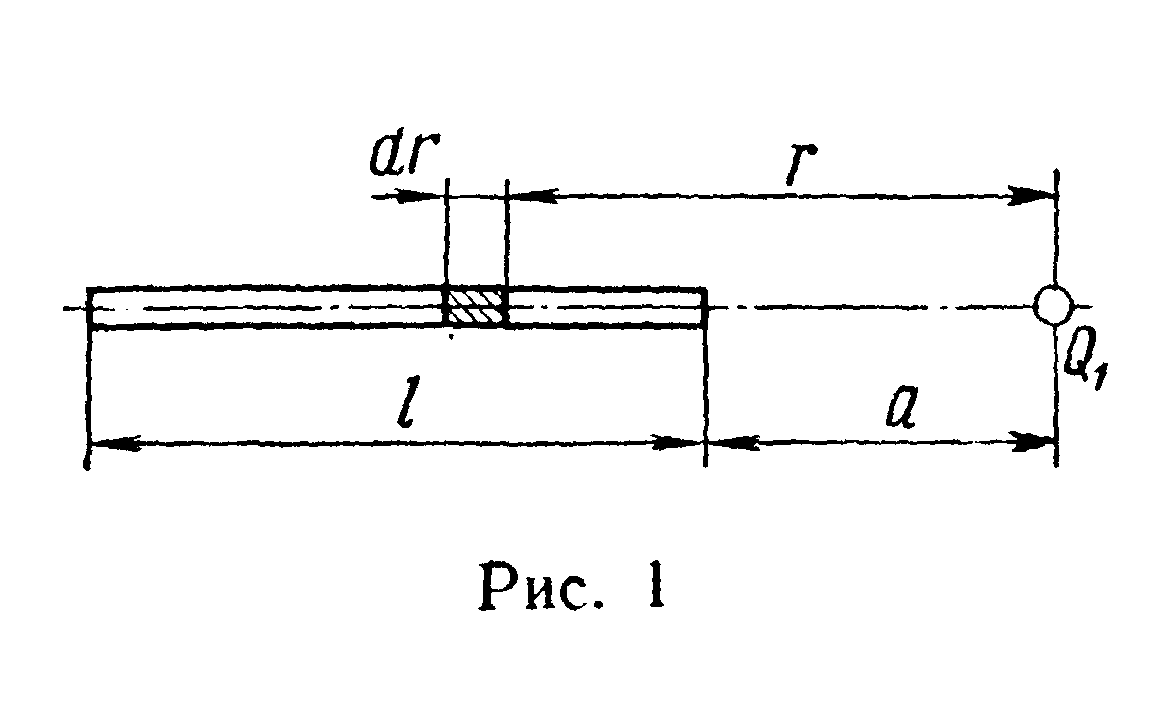
следующим образом. Выделим из стержня
(рис. 1) малый участок dr
с зарядом dq
= τdr.
Этот заряд можно рассматривать как
точечный. Тогда, согласно закону Кулона,
Интегрируя
это выражение в пределах от
до
+
,
получаем
откуда
Проверим,
дает ли расчетная формула единицу
линейной плотности электрического
заряда. Для этого в правую часть формулы
вместо символов величин подставим
их единицы:
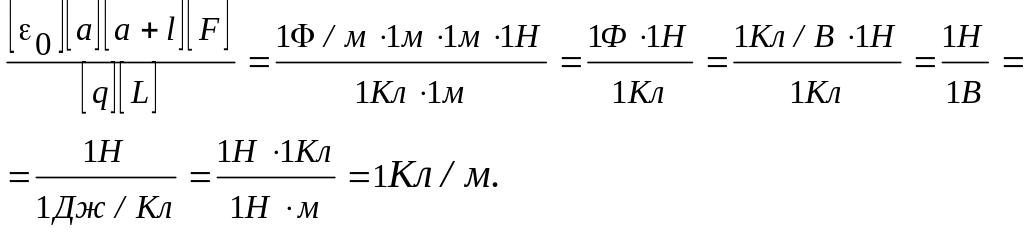
Найденная единица
является единицей линейной плотности
заряда.
Произведем
вычисления:
Пример
2. По тонкому
кольцу равномерно распределен заряд q
= 40 нКл с линейной плотностью τ = 50 нКл/м.
Определить напряженность
электрического поля, создаваемого этим
зарядом в точке А, лежащей на оси кольца
и удаленной от его центра на расстоянии,
равное половине радиуса.
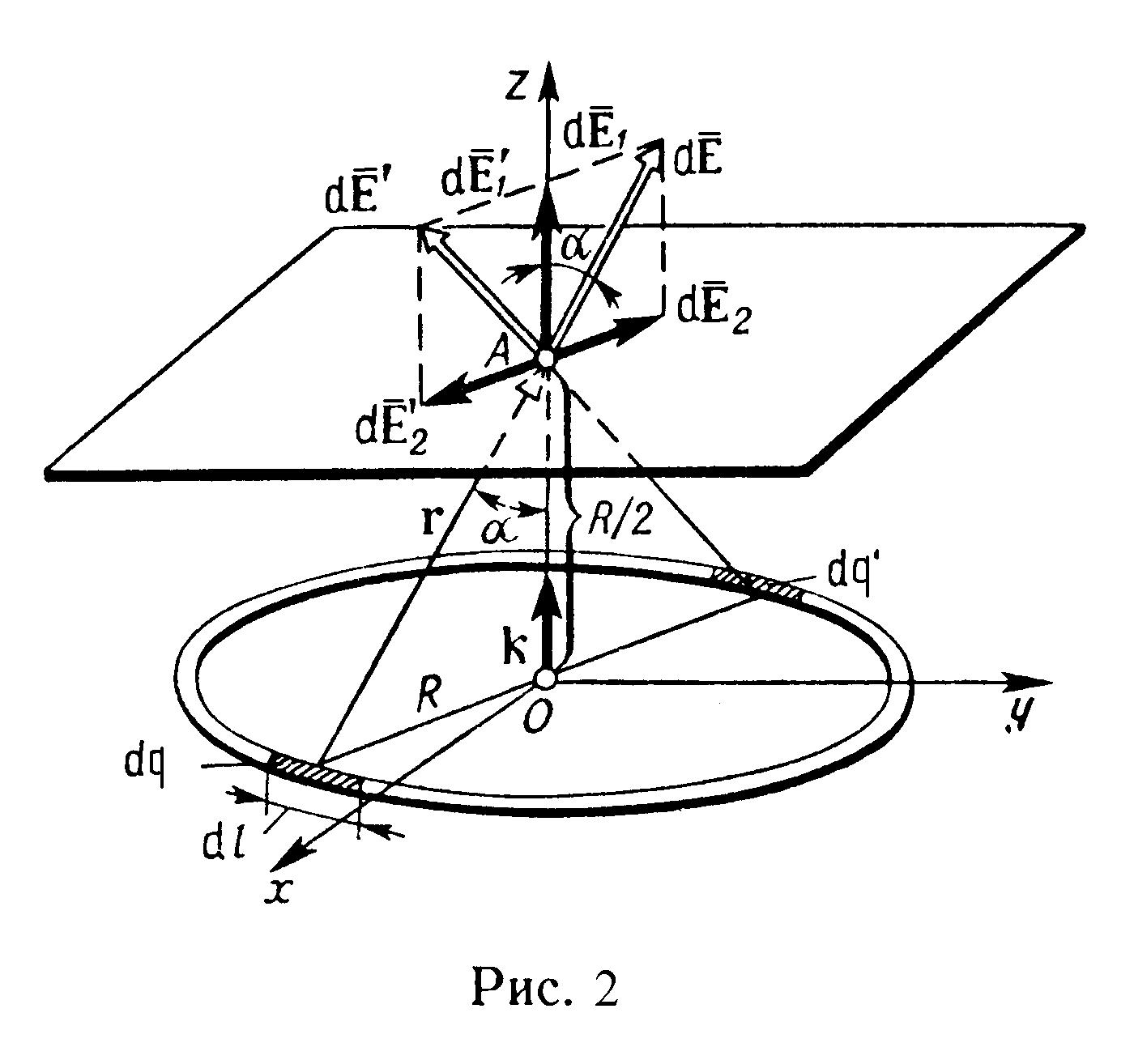
Р
е ш е н и е. Совместим координатную
плоскость xOy
с плоскостью кольца, а ось Oz
– с осью кольца (рис. 2). На кольце выделим
малый участок длиной dl.
Так как заряд dq=τdl,
находящийся на этом участке, можно
считать точечным, то напряженность d
электрического поля, создаваемого
этим зарядом, может быть записана в виде
где
–
радиус-вектор, направленный от элемента
dl
к точке А.
Разложим
вектор d
на две составляющие: d
1,
перпендикулярную плоскости кольца
(сонаправленную с осью Oz),
и d
2,
параллельную плоскости кольца
(плоскости xOy),
т. е.
.
Напряженность
электрического поля в точке А найдем
интегрированием:
где
интегрирование ведется по всем элементам
заряженного кольца. Заметим, что для
каждой пары зарядов dq
и dq`
(dq
= dq`),
расположенных симметрично относительно
центра кольца, векторы d
2
и d
2`
в точке А равны по модулю и противоположны
по направлению: d
2
= – d
2`.
Поэтому векторная сумма (интеграл)
Составляющие d
1
для всех элементов кольца сонаправлены
с осью Oz
(единичным вектором
),
т. е. d
1
=
dE1.
Тогда
Так
как
и
то
Таким
образом,
Из
соотношения q
= 2πRτ
определим радиус кольца R
= q/(2πτ).
Тогда
Модуль
напряженности
(1)
Проверим,
дает ли правая часть полученного
равенства единицу напряженности (В
/ м):
Выразим
физические величины, входящие в формулу
(1), в единицах СИ (τ = 5·10-8
Кл/м, q=4·10-8
Кл, ε0
= 8,85·10-12
Ф/м) и произведем вычисления:
П
ример
3. Две
концентрические проводящие сферы
радиусами R1
= 6 см и R2
= 10 см несут соответственно заряды q1
= 1нКл и q2
= – 0,5нКл. Найти напряженность Е поля в
точках отстоящих от центра сфер на
расстояниях r1
= 5 см, r2
= 9 см, r3
= 15 см. Построить график E(r).
Р
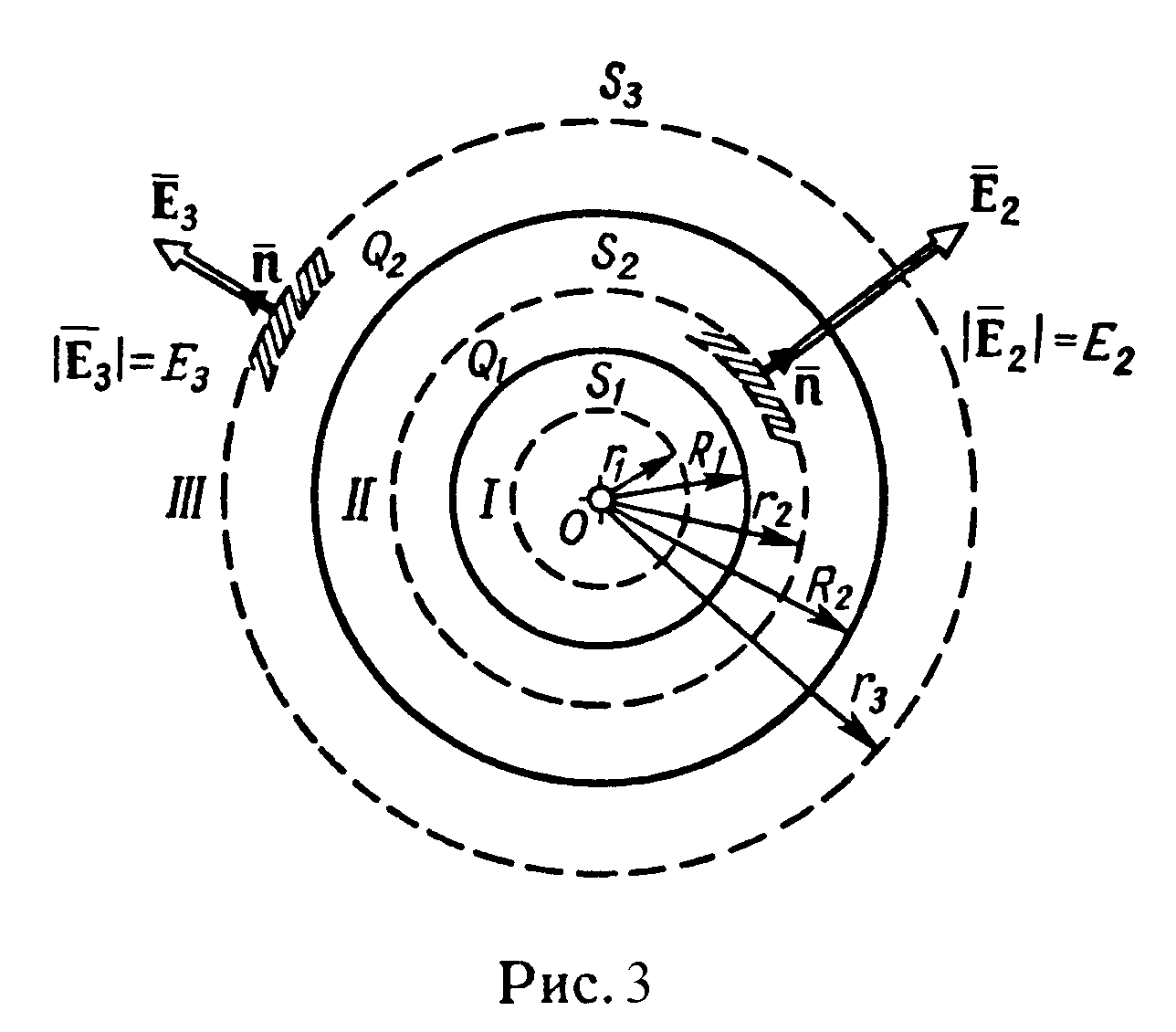
е ш е н и е. Заметим, что точки, в
которых требуется найти напряженности
электрического поля, лежат в трех
областях (рис. 3): области I
(r1<R1),
области II
(R1<r2<R2),
области III
(r2>R2).
1.
Для определения напряженности Е1
в области I
проведем гауссову поверхность S1
радиусом r1
и воспользуемся теоремой Остроградского
– Гаусса:
(так
как суммарный заряд, находящийся внутри
гауссовой поверхности, равен нулю).
Из соображений симметрии En=E1=const.
Следовательно,
и Е1
(напряженность поля в области I)
во всех точках, удовлетворяющих
условию r1<R1,
будет равна нулю.
2.
В области II
гауссову поверхность проведем радиусом
r2.
В этом случае (диэлектрическую
проницаемость среды будем считать
равной единице (вакуум))
(так
как внутри гауссовой поверхности
находится только заряд q1).
Так
как En
= E
= const,
то Е можно вынести за знак интеграла:
или
ES2
= q1/
.
Обозначив
напряженность Е для области II
через Е2,
получим
Е2
= q1/(
S2),
где
S2
= 4πr22
– площадь гауссовой поверхности. Тогда
(1)
3.
В области III
гауссова поверхность проводится радиусом
r3.
Обозначим напряженность Е области III
через Е3
и учтем, что в этом случае гауссова
поверхность охватывает обе сферы и,
следовательно, суммарный заряд будет
равен q1
+ q2.
Тогда
Е3
= (q1+q2)/4π
r32.
Заметив,
что q2<0,
это выражение можно переписать в виде
(2)
Убедимся
в том, что правая часть равенства (1) и
(2)дает единицу напряженности:
Выразим
все величины в единицах СИ (q1
= 10-9
Кл, q2=
– 0,5·10-9
Кл, r1=0,09
м, r2=0,15
м, 1/(4πε0)=9·109
м/Ф) и произведем вычисления:
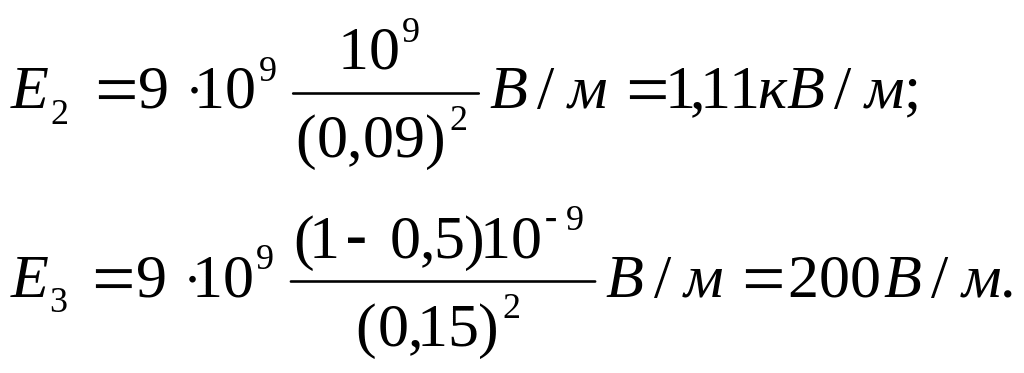
Построим
график E(r).
В области I(r1<R1)
Е = 0. В области II
(R1
r<R2)
E2(r)
изменяется по закону 1/r2.
В точке r
= R1
напряженность E2(R1)
= q1/(4π
R12)=2,25
кв/м. В точке r
= R2
(r
стремится к R2
слева) E2(R2)
= q1/(4π
R22)
= 0,9 кВ/м. В области III
(r>R2)
E3(r)
изменяется по закону 1/r2,
причем в точке r
= R2
(r
стремится к R2
справа) E3(R2)
= (q1
– |q2|/(4π
R22)
= 0,45 кВ/м. Таким образом, функция E(r)
в точках r
= R1
и r
= R2
терпит разрыв.
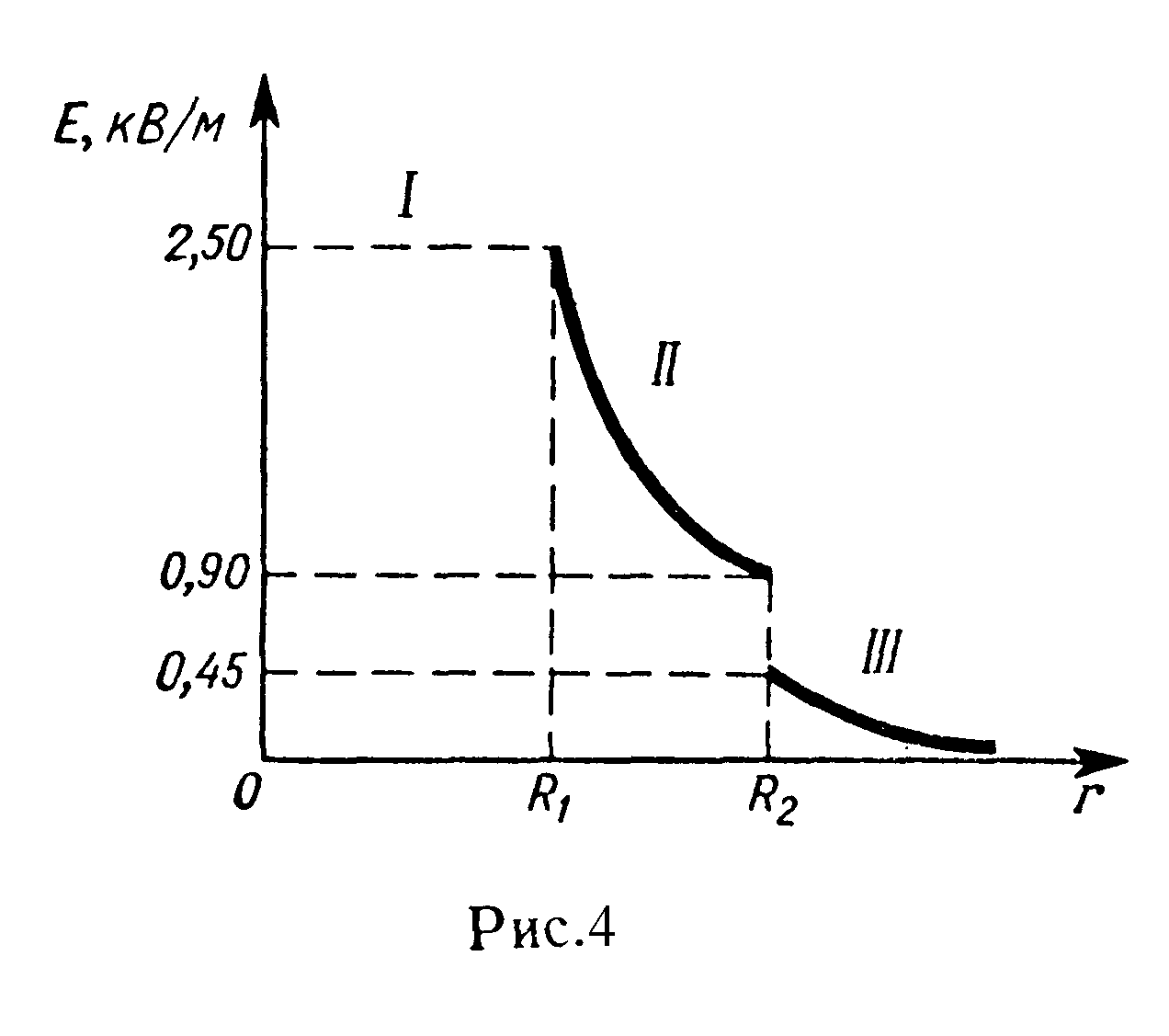
График
зависимости E(r)
представлен на рис. 4.
Пример
4. Электрическое
поле создано длинным цилиндром радиусом
R
= 1 см, равномерно заряженным с линейной
плотностью τ = 20 нКл/м. Определить разность
потенциалов двух точек этого поля,
находящихся на расстоянии
1
= 0,5 см и
2
= 2 см от поверхности цилиндра, в средней
его части.
Р
е ш е н и е. Для определения разности
потенциалов воспользуемся соотношением
между напряженностью поля и изменением
потенциала:
= – grad
φ.
Для поля с осевой симметрией, каким
является поле цилиндра, это соотношение
можно записать в виде
E
= – dφ/dr,
или dφ
= – Edr.
Интегрируя
это выражение, найдем разность потенциалов
двух точек, отстоящих на расстояниях
r1
и r2
от оси цилиндра:
(1)
Так
как цилиндр длинный и точки взяты вблизи
его средней части, то для выражения
напряженности поля можно воспользоваться
формулой напряженности поля, создаваемого
бесконечно длинным цилиндром:
E
= τ/(2π
r).
Подставив
выражение Е в (1), получим
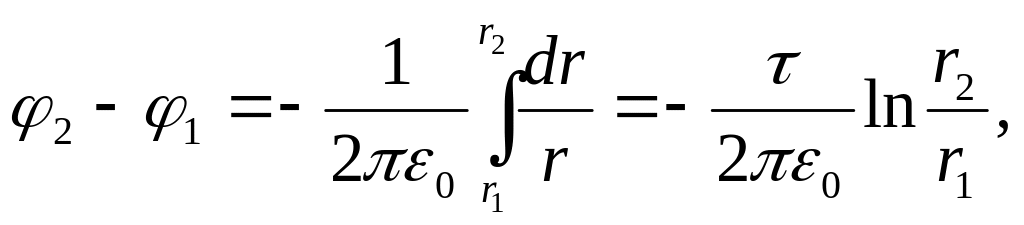
или
φ1
– φ2
= τ/(2π
)ln(r2/r1).
(2)
Произведем
подстановку, учитывая, что величины r1
и r2,
входящие в формулу (2) в виде отношения,
можно выразить в сантиметрах (r1
= R
+
= 1,5 см r2
= R
+
=
3 см):
φ1
– φ2
= 2 ·
10 –8
· 1,8
·
1010
ln(3/1,5)
= 3,6 ·102
·
2,3 ln2
В = 250 В.
Пример
5. Конденсатор
емкостью С1
= 3 мкФ был заряжен до разности потенциалов
U1
= 40 В. После отключения от источника тока
конденсатор соединили с другим
незаряженным конденсатором емкостью
С2
= 5 мкФ. Какая энергия
израсходуется на образование искры в
момент присоединения второго конденсатора?
Р
е ш е н и е. Энергия, израсходованная на
образование искры,
=
W1
– W2,
(1)
где
W1
– энергия, которой обладает первый
конденсатор до присоединения к нему
второго конденсатора; W2
– энергия, которую имеет батарея,
составленная из двух конденсаторов.
Энергия
заряженного конденсатора определяется
по формуле
W
= ½СU2,
(2)
где
С – емкость конденсатора или батареи
конденсаторов.
Выразив
в формуле (1) энергии W1
и W2
по формуле (2) и приняв во внимание,
что общая емкость параллельно соединенных
конденсаторов равна сумме емкостей
отдельных конденсаторов, получим
=
½ C1U12
– ½( C1
+
C2)U22,
(3)
где
U2
– разность потенциалов на зажимах
батареи конденсаторов.
Учитывая,
что заряд после присоединения второго
конденсатора остался прежним, выразим
разность потенциалов U2
следующим образом:
Подставив
выражение U2
в (3), найдем
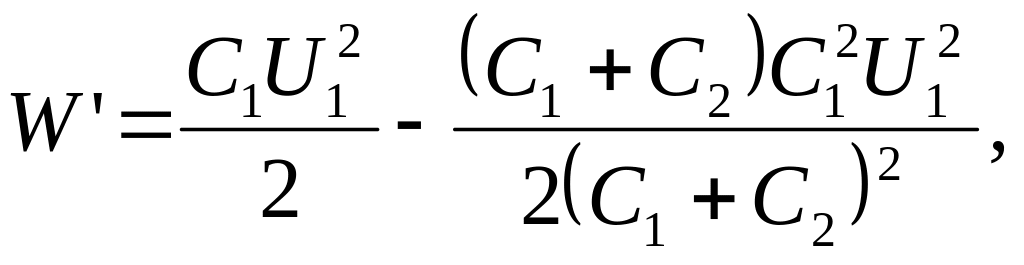
или
Произведем
вычисления:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Плотность заряда
Материал из Большого Справочника
| Плотность заряда (линейная, поверхностная, объемная) |
|
 |
|
| Размерность | L−1TI, L−2TI, L−3TI |
|---|---|
| Единицы измерения | |
| СИ | Кл/м, Кл/м2, Кл/м3 |
| Примечания | |
| скалярная величина |
Пло́тность заря́да — количество электрического заряда, приходящееся на единицу длины, площади или объёма. Таким образом определяются линейная, поверхностная и объёмная плотности заряда, которые в системе СИ измеряются в кулонах на метр (Кл/м), в кулонах на квадратный метр (Кл/м²) и в кулонах на кубический метр (Кл/м³), соответственно. В отличие от плотности вещества, плотность заряда может принимать не только положительные, но и отрицательные значения, поскольку существуют заряды обоих знаков.
Содержание
- 1 Плотность заряда в классической физике
- 2 Плотность заряда в квантовой механике
- 3 Определение плотности заряда через δ-функцию
- 4 Применение
- 5 См. также
- 6 Примечания
- 7 Литература
Плотность заряда в классической физике
Линейная, поверхностная и объёмная плотности электрического заряда обычно задаются функциями 



-
,
,
.
Плотность заряда в квантовой механике
В квантовой механике плотность заряда, например электрона в атоме, связана с волновой функцией 
-
,
причём волновая функция должна иметь нормировку:
-
.
Определение плотности заряда через δ-функцию
Иногда требуется записать объёмную плотность заряда для системы из точечных зарядов. Это может быть сделано с использованием δ-функции:
где сумма берётся по всем имеющимся зарядам, а 

Полный заряд, находящийся во всём пространстве, равен интегралу 
где интегрирование производится по всей четырёхмерной гиперплоскости, перпендикулярной к оси x0 (очевидно, что это и означает интегрирование по всему трёхмерному пространству). 
Применение
Функция распределения плотности заряда фигурирует в уравнениях Максвелла (
См. также
- Плотность тока
Примечания
- ↑ Ландау Л.Д., Лифшиц Е.М. Теория Поля, Том 2 из 10.. — 8 издание. — ФИЗМАТЛИТ, 2003. — С. 104. — 531 с. — ISBN 5-9221-0056-4.
Литература
- Сивухин Д. В. Общий курс физики. — Изд. 4-е, стереотипное. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — 656 с. — ISBN 5-9221-0227-3; ISBN 5-89155-086-5..