Как найти линейную скорость через период

Понятия и определения

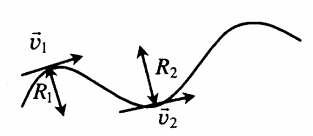
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Определение и формулы

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Определение и формулы

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Полезные факты

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Определение и формула

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с²). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10³ секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10⁶. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алиса Никитина | Просмотров: 21.8k

Что такое линейная скорость, единицы измерения

В международной системе СИ единицей измерения линейной скорости является производная от двух основных единиц:

• метр;
• секунда.

В международной системе СИ скорость измеряется в метрах в секунду (м/с). За единицу скорости принимают скорость равномерного движения, при которой путь в один метр тело преодолеет в течение одной секунды. Кроме того, скорость можно измерять в:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

• км/ч;
• км/с;
• см/с.

Связь между линейной и угловой скоростями

Скорость точки, которая совершает круговое движение, называется линейной скоростью, чтобы отделить это понятие от термина угловая скорость. Во время вращения абсолютно твердое тело в разных точках будет обладать неодинаковыми линейными скоростями, но значение угловой скорости остается стабильным.

Можно установить связь между линейной и угловой скоростью тела, вращающегося по окружности. Путь, который проходит точка, расположенная на окружности с радиусом R, составляет:

2πR

Исходя из того, что время одного оборота тела является периодом Т, модуль линейной скорости будет рассчитан по следующей формуле:

(v=frac{2pi R}{T}=2pi RV)

Зная, что:

(omega =2pi V)

получим справедливое равенство:

(v=omega R)

Данная формула демонстрирует увеличение линейной скорости тела при его удалении от оси вращения. К примеру, точки, которые движутся по земному экватору v=463 м/с, а точки, расположенные на широте города Санкт-Петербург, движутся со скоростью v=233 м/с. При нахождении на полюсах планеты скорость уменьшается до v=0.

Модуль центростремительного ускорения точки тела, которая совершает равномерные вращательные движения, определяют с помощью угловой скорости тела и радиуса окружности. Уравнение будет записано в следующем виде:

(a=frac{v^{2}}{R})

(v=omega R)

Таким образом, формула будет преобразована:

(a=omega ^{2}R)

Подытожив расчеты, можно записать все возможные равенства, справедливые для определения центростремительного ускорения:

(a=frac{v^{2}}{R}=omega ^{2}R=frac{4pi ^{2}}{T^{2}}R=4pi ^{2}V^{2}R)

Таким образом, рассматривают пару простейших движений, характерных для абсолютно твердого тела, включая поступательное и вращательное. При этом стоит отметить, что определить любое сложное движение, которое совершает абсолютно твердое тело, можно с помощью суммы двух независимых движений:

• поступательное;
• вращательное.

С помощью закона независимости движений описывают сложное движение абсолютно твердого тела.

Формулы для нахождения линейной скорости

Тело движется равномерно тогда, когда его скорость характеризуется постоянной величиной. Формула для расчета скорости такого движения будет иметь следующий вид:

V = st

где s является пройденным путем, то есть длиной линии;

t представляет собой время, в течение которого тело преодолевало указанный путь.

Основной формулой для определения линейной скорости является следующее равенство:

V = St

где S является путем,

t обозначает время, в течение которого тело преодолело путь S.

Иной вариант уравнения имеет такой вид:

V = lt

где l является путем,

t обозначает время, в течение которого тело преодолело дугу l.

В некоторых научных источниках скорость обозначают с помощью маленькой буквы v. Другим уравнением для расчета линейной скорости является равенство:

(v=2pi RT)

В данном случае 2π представляет собой полную окружность и составляет 360 угловых градусов. Вектор скорости направлен по касательной к траектории движении тела.

Модуль скорости

Числовое значение скорости может быть разным в зависимости от выбранной единицы измерения. Кроме числового значения, скорость характеризуется направлением. Числовое значение, которым обладает скорость, в физике называют ее модулем.

В случае, когда скорость обладает определенным направлением, такая величина является векторной. Таким образом, скорость представляет собой векторную физическую величину. Записывают модуль скорости в виде буквы v, а вектор скорости, как (vec{v})

Следует отметить, что такие величины, как путь, время, длина обладают только числовым значением. Они называются скалярными. Если тело движется неравномерно, то справедливо использовать в расчетах среднюю скорость.

Задачи с примерами решения

Задача №1

Тело совершает движение по окружности с ускорением 3 м/с в квадрате. Радиус окружности равен 40 метров. Необходимо определить линейную скорость движения тела.

Решение:

Ускорение в данном случае будет нормальным. Исходя из этого, определить линейную скорость тела можно с помощью формулы:

(a=frac{v^{2}}{R})

(v=sqrt{aR}=sqrt{40times 3}=10.9) м/с

Ответ: линейная скорость равна 10,9 м/с.

Задача №2

Поезд совершает равномерное движение. В течение 4 часов он преодолевает путь в 219 километров. Требуется рассчитать скорость движения поезда.

Решение:

Исходя из основной формулы для расчета линейной скорости, получим:

(v=frac{S}{t}=frac{219}{4}=54.75) км/ч

Ответ: скорость движения поезда составит 54.75 км/ч или 15.2 м/с.

Задача №3

Транспортное средство, работая на двигателе внутреннего сгорания, в течение 2,5 часов преодолевает расстояние в 213 километров. Требуется определить скорость движения транспорта.

Решение:

С помощью уравнения расчета скорости можно записать решение задачи:

(v=frac{S}{t}=frac{213}{2,5}=85.2) км/ч

Ответ: Скорость движение транспортного средства составляет 85.2 км/ч или 23.7 м/с.

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу для определения искомой величины.
3. Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

• Радиус окружности, по которой движется автомобиль: R = 100 м.
• Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

1. Записать исходные данные.
2. Определить, что нужно найти.
3. Записать формулу зависимости центростремительного ускорения от частоты.
4. Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
5. Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Движение материальной точки по окружности. Центростремительное ускорение.

Линейная и угловая скорости

Движение по окружности нас окружает постоянно – это может быть мотоциклист на мототреке, вращение грузика на веревке, движение по выгнутому круглому мосту, любой поворот на дороге тоже можно рассматривать, как движение по части окружности и т.д.

Давайте представим, что мы смотрим сверху на мототрек (см. рис.1.). Пусть точка (А) это мотоциклист, который движется с постоянной линейной скоростью (vec), и за какое-то время (t) он переместится по дуге окружности (^<’>) в точку (^<’>). Его пройденный путь будет равен длине дуги окружности (^<’>).

Определение Линейная скорость – это путь, который проходит мотоциклист за единицу времени (например, за секунду):

Понятно, что чем больший путь (большую длину дуги) успевает пройти тело за одно и тоже время, тем быстрее оно движется, тем больше его линейная скорость. Линейная скорость — это обычная скорость, к которой мы все привыкли. Обратите внимание, что вектор линейной скорости всегда направлен по касательной к траектории, в нашем случае – по касательной к окружности. Чуть позже нам это пригодится.

И так, при движении по окружности можно двумя способами измерять скорость – при помощи линейной скорости (какое расстояние проходит тело за единицу времени) и при помощи угловой скорости (на какой угол поворачивается тело за единицу времени). Эти скорости, очевидно, должны быть связаны между собой.

Но прежде чем, вывести это соотношение, представьте, что отрезок (AO) вращается по окружности (см.Рис.1.) и за время (t) переходит в отрезок (^<’>O) – точка (A) переходит в точку (^<’>), а точка (B) – в точку (^<’>).

При этом точка (A) проходит за время (t) расстояние равное длине дуги окружности (^<’>), а точка (B) за тоже самое время (ведь обе точки лежат все время на одной прямой) расстояние (^<’>).

А на какой угол успевают повернуться точки (A) и (B) за одно и тоже время (t)?

Из рисунка 1 видно, что они обе поворачиваются на один и тот же угол (Deltavarphi). А так как угловая скорость по определению, это отношение угла ко времени, то угловые скорости точек (A) и (B) одинаковые.

И так, что мы имеем – оказывается, что при удалении линейная скорость растет, а угловая скорость при этом не меняется. Тогда логичной выглядит следующая формула, связывающая угловую и линейную скорости:

где (V) – линейная скорость,

(omega) – угловая скорость,

(R) – радиус вращения.

Период и частота вращения

Важными характеристиками любого вращательного движения являются частота и период:

Определение Период – время, за которое тело совершает полный оборот.

В нашем примере с мотоциклистом, период – это время, за которое мотоциклист проезжает один полный круг.

Из курса геометрии вспоминаем, что длину дуги окружности можно посчитать как (2*pi*R), где (R) – радиус окружности. Тогда в случае равномерного движения период можно посчитать по формуле, как расстояние деленое на скорость: $$T=frac<2*pi*R>;$$ Подставив сюда формулу ((1)) для линейной скорости через угловую: $$T=frac<2*pi><omega>;$$ Где (V) –линейная скорость вращения.

В системе СИ период измеряется в ([^<-1>]).

Определение Частота – количество оборотов за единицу времени.

В случае с мотоциклистом, частота – это сколько кругов он успевает проехать, например, за один час. Обычно частоту измеряют в оборотах в секунду.

Период и частота вращения связаны между собой выражением: $$T=frac<1><nu>;$$ Отсюда можно получить формулы для частоты, подставив период: $$nu=frac<2*pi*R>=frac<omega><2*pi>;$$

Скорость точки, находящейся на краю вращающегося диска равна (V_A=15(м/с)), а точки, расположенной на 0,2 (м) ближе к центру вращения равна (V_B=10(м/с)). Найти частоту вращения и радиус диска.

Решение: Точка (А) находится дальше от центра на (20 (см)), а значит ее скорость больше, чем у точки (В). По условию так и есть. Так как обе точки находятся на одном радиусе, то угловые скорости у них одинаковые. Распишем угловые скорости для точек (А) и (В) и приравняем: $$omega_A=frac;$$ $$omega_B=frac;$$ $$omega_A=omega_B;$$ $$frac=frac;$$ Из условия (A0=BO+0.2): $$frac=frac;$$ $$frac<15>=frac<10>;$$ $$15*BO=(BO+0,2)*10;$$ $$5*BO=2;$$ $$BO=0,4.$$ Мы нашли радиус окружности по которой вращается точка (В), тогда радиус точки (А) будет на (0,2(м)) больше – (0,6(м)).

Для того, чтобы найти частоту, воспользуемся формулой: $$nu=frac<2*pi*R_A>=frac<15><2*3,14*0,6>=3,98(об/сек);$$ Ответ: (R=0,6(м)) и (nu=3,98(об/сек).)

Центростремительное (нормальное) ускорение

Вернемся к нашему примеру с мотоциклистом, двигающимся по мототреку в форму окружности. (См. Рис.3.) Для начала, представим, что линейная скорость у мотоциклиста постоянна, то есть он двигается равномерно, а значит его ускорение должно быть равно нулю. Это действительно так, но при движении по окружности (или любой другой криволинейной траектории) даже с постоянной скоростью возникает новый вид ускорения – центростремительное, еще его называют «нормальное», ускорение. Оно появляется по причине изменения направления вектором скорости.

На самом деле, для решения задач понимать природу центростремительного ускорения совсем необязательно. Достаточно просто помнить, что при любом криволинейном движении появляется такое ускорение. Его можно вычислить по формуле: $$a_n=frac;$$ где (V) –линейная скорость;

(R) – радиус окружности.

Подставим сюда линейную скорость через угловую – (V=omega*R). И получим еще одну формулу для центростремительного ускорения: $$a_n=omega^2*R;$$ Важно! Центростремительное ускорение всегда перпендикулярно скорости и направлено к центру окружности.

Тангенциальное ускорение

Теперь представим, что мотоциклист едет по круглому мототреку не с постоянной скоростью, а равноускорено/равнозамедлено. В этом случае говорят, говорят, что мотоциклист движется с тангенциальным ускорением.

Тангенциальное ускорение – это обычное ускорение, к которому мы привыкли в курсе кинематики. Оно показывает на сколько успевает измениться скорость за единицу времени, например, за секунду.

Тангенциальное ускорение всегда направлено по касательной к траектории. Если тело ускоряется, то оно сонаправлено с линейной скоростью, а если замедляется, то направлено в противоположную сторону. (см.Рис.3, показано синей стрелкой (vec>))

При равноускоренномравнозамедленном движении тангенциальное ускорение можно посчитать по формуле: $$a_<tau>=frac;$$ где (V_к) – конечная скорость;

(V_н) – начальная скорость;

(t) – время, за которое скорость изменилась с (V_н) до (V_к).

При любом неравномерном движение по криволинейной траектории (окружности), у тела обязательно есть два вида ускорений – нормальное, направленное к центру, перпендикулярно скорости, и тангенциальное, направленное по касательной к траектории. Нормальное ускорение отвечает за изменение направления вектора линейной скорости, а тангенциальное за изменение величины линейной скорости.

Если тело движется с постоянной скоростью, то тангенциальное ускорение равно (0).

Если тело движется по прямой, то нормальное ускорение равно (0).

Векторно сложим эти два ускорения по правилу параллелограмма, и получим вектор общего ускорения, которым обладает тело при движении по окружности. (см. Рис.3., фиолетовая стрелка (vec)).

Колесо радиуса R вращается с постоянной скоростью. Во сколько раз отличаются центростремительные ускорения двух точек расположенный на расстояниях (R/2) и (R/3) от центра колеса

Решение: Так как любая точка колеса вращается с одинаковой угловой скоростью (omega), то воспользуемся формулой для центростремительного ускорения через угловую скорость: $$a_n=omega^2*r;$$ Пусть точка А вращается по окружности радиусом (R/2), а точка В – (R/3). $$a_=omega^2*frac<2>;$$ $$a_=omega^2*frac<3>;$$ $$frac>>=frac<omega^2*frac<2>><omega^2*frac<3>>=frac<2>*frac<3>=1,5$$ Ответ:(frac>>=1.5.)

[spoiler title=”источники:”]

Движение по окружности с постоянной по модулю скоростью

http://sigma-center.ru/circularmotion

[/spoiler]

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Связь со вторым законом Ньютона

Как вывести формулу центростремительного ускорения

Движение по циклоиде*