I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Исследовательская работа «Определение линейной и угловой скоростей точки, равномерно движущейся по окружности»
ОГЭ 2021 по физике ›
1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.
При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.
2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ( T ) — время, в течение которого тело совершает один полный оборот. Единица периода — ( [,T,] ) = 1 с.
Частота обращения ( (n) ) — число полных оборотов тела за одну секунду: ( n=N/t ). Единица частоты обращения — ( [,n,] ) = 1 с-1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.
Связь между частотой и периодом обращения выражается формулой: ( n=1/T ).
Пусть некоторое тело, движущееся по окружности, за время ( t ) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ( varphi ).
Быстроту обращения тела характеризуют угловая и линейная скорости.
Угловая скорость ( omega ) — физическая величина, равная отношению угла поворота ( varphi ) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ( omega=varphi/t ). Единица угловой скорости — радиан в секунду, т.е. ( [,omega,] ) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ( 2pi ). Поэтому ( omega=2pi/T ).
Линейная скорость тела ( v ) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.
Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ( vec=l/t ). За один оборот точка проходит путь, равный длине окружности. Поэтому ( vec=2pi!R/T ). Связь между линейной и угловой скоростью выражается формулой: ( v=omega R ).
Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.
4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ( vec=frac<Deltavec> ) и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.
Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ( a=frac ). Так как ( v=omega R ), то ( a=omega^2R ).
При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности.
Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T
. Путь, который преодолевает точка — это есть длина окружности.
Общие понятия
Кинематика, входящая в состав механики, занимается изучением закономерностей движения. Под этим понятием понимается изменение положения тела относительно других объектов. Основная задача науки состоит в определении координат рассматриваемого предмета в любой момент. Кинематика изучает перемещение без учёта воздействия его вызвавшего. Любое движение считается относительным. Поэтому для его описания используют систему координат с начальной и конечной точкой отсчёта.
Для облегчения понимания процессов размерами исследуемого тела пренебрегают. Считая, что любой объект представляет собой совокупность материальных точек, повторяющих одинаковое движение при сравнении с друг другом. Существует несколько видов изменения положения. Различают их по траектории — воображаемой линии, повторяющей путь прохождения объекта. Сравнивая виды движения, выделяют два типа перемещения: прямолинейное и криволинейное.
Кроме этого, если рассматривать изменение положения во времени, движение можно различать по равномерности. При перемещении с постоянной скоростью движение называют равномерным, а при изменении её — неравномерным.
Более узкая классификация разделяет перемещение по характеру на следующие виды:
- равноускоренное — это перемещение, обусловленное движением тела, при котором ускорение будет постоянным по направлению;
- равнозамедленное — движение, при котором происходит отрицательное ускорение, до полного замедления объекта;
- равнопеременное — при таком виде перемещения скорость изменяется на одинаковое значение в любом промежутке времени;
- поступательное — если на перемещаемое тело нанести линии, они будут перемещаться параллельно сами себе;
- вращательное — это периодическое движение, при котором материальная точка описывает окружность.
Частным случаем криволинейного движения, то есть по траектории, отличной от прямой линии, является равномерное движение по окружности. Определение понятия включает в себя центростремительное ускорение и постоянную по модулю скорость. Под этим видом понимают изменение положения, при котором изменяется только направление скорости.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение тел
Под вращением понимают тип движения, при котором траектория перемещающегося тела представляет собой окружность. Вращение может происходить вокруг оси или вокруг фиксированной точки. Вращение колеса, планет по своим орбитам, спортсменов во время соревнований по фигурному катанию — все это примеры указанного типа движения.
По аналогии с линейным перемещением, главной формулой динамики вращения является следующая:
Здесь M и I — моменты силы и инерции, соответственно, α — ускорение угловое.
Для описания вращения удобно пользоваться не линейной, а угловой скоростью. Она определяется так:
Где θ — угол, на который тело повернулось за время t. С записанным ускорением α скорость ω связана следующим равенством:
Для измерения всех угловых величин используются радианы.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Основные понятия и законы динамики
Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой
Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано. Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется
инертностью.
Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией.
Инерциальными системами отсчёта
называют системы, в которых выполняется первый закон Ньютона.
Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса
— это мера инертности тела
Сила
— это количественная мера взаимодействия тел.
Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой: $F↖ <→>= m⋅a↖<→>$
Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.
Третий закон Ньютона:
Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению: $F_1↖ <→>= -F_2↖ <→>$
III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело A (см. рис.).
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места. Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости
записывают в виде где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.
При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения.
Различают трение покоя и трение скольжения.
Сила трения скольжения
подсчитывается по формуле где N — сила реакции опоры, µ — коэффициент трения. Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.
возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения
называют силы, с которыми любые два тела притягиваются друг к другу.
Закон всемирного тяготения:
любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Здесь R — расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.
называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.
— это сила, с которой все тела притягиваются к Земле: При неподвижной опоре вес тела равен по модулю силе тяжести: Если тело движется по вертикали с ускорением, то его вес будет изменяться. При движении тела с ускорением, направленным вверх, его вес Видно, что вес тела больше веса покоящегося тела.
При движении тела с ускорением, направленным вниз, его вес В этом случае вес тела меньше веса покоящегося тела.
называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила — сила тяжести.
Искусственный спутник Земли
— это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли На спутник Земли действует только одна сила — сила тяжести, направленная к центру Земли
Первая космическая скорость
— это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите. где R — расстояние от центра планеты до спутника. Для Земли, вблизи её поверхности, первая космическая скорость равна
1.3. Основные понятия и законы статики и гидростатики
Тело (материальная точка) находится в состоянии равновесия, если векторная сумма сил, действующих на него, равна нулю. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное.
Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это
устойчивое равновесие.
Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это
неустойчивое положение
; если никаких сил не возникает —
безразличное
(см. рис. 3). Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю. Здесь d —плечо силы.
Плечом силы
d называют расстояние от оси вращения до линии действия силы.
Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением
называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:
Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений. Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей где ρ — плотность жидкости, h — глубина проникновения в жидкость.
Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае Высоты столбов жидкости обратно пропорциональны плотностям:
представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой. Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют
силой Архимеда
Величину выталкивающей силы устанавливает
закон Архимеда
: на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом: где ρжидк — плотность жидкости, в которую погружено тело; Vпогр — объём погружённой части тела.
Условие плавания тела
— тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.
1.4. Законы сохранения
Импульсом тела
называют физическую величину, равную произведению массы тела на его скорость:
Импульс — векторная величина.
=кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы.
Это произведение силы на время её действия Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется
закон сохранения импульса
: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой
называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:
— это работа, совершённая в единицу времени:
Способность тела совершать работу характеризуют величиной, которую называют энергией.
Механическую энергию делят на
кинетическую и потенциальную.
Если тело может совершать работу за счёт своего движения, говорят, что оно обладает
кинетической энергией.
Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает
потенциальной энергией.
Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле где h — высота подъёма
Энергия сжатой пружины:
где k — коэффициент жёсткости пружины, x — абсолютная деформация пружины.
Сумма потенциальной и кинетической энергии составляет механическую энергию.
Для изолированной системы тел в механике справедлив
закон сохранения механической энергии
: если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
При равномерном движении по окружности вектор скорости тела меняется (скорость направлена по касательным к окружности), а модуль скорости тела (числовое значение) остается постоянным. Поэтому если один полный оборот тела по окружности обозначить как s (пройденный путь), а время, за которое он был совершен, как t, то найдем модуль скорости тела, движущегося равномерно по окружности:





Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Мгновенная и средняя скорости
Как найти линейную скорость? Формулу, согласно определению величины, можно записать следующую:
Где dl¯ — вектор перемещения тела за время dt. Эта скорость называется мгновенной, поскольку рассчитывается за чрезвычайно короткий промежуток времени dt. Мгновенная скорость в действительности является величиной не стабильной и постоянно меняющейся. Например, представим, что по дороге движется автомобиль. На первый взгляд можно полагать, что в любой момент времени его мгновенная скорость будет постоянной, однако, это не так. Мгновенная скорость испытывает колебания. Если спидометр автомобиля достаточно чувствителен, то он фиксирует эти колебания.
Формула линейной скорости средней ничем не отличается от таковой для мгновенной, однако, измеряется она за более длительный промежуток времени Δt:
В примере с автомобилем выше, хотя мгновенная скорость испытывает колебания, средняя скорость остается постоянной с определенной точностью на всем участке пути Δl¯.
При решении задач, как правило, используют среднюю скорость. Мгновенная же величина имеет смысл только в случае движения с ускорением.
Занимательный пример
Пусть имеется некая планета, которая совершила полтора оборота за сорок два часа, при этом метеостанция, располагающаяся на её экваторе, прошла путь равный 50 тыс. километров, делённых на час. Нужно определить линейную и угловую скорости планеты при её вращении вокруг собственной оси. Кроме этого, вычислить, чему равны сутки, и найти радиус планеты. При этом считать, что форма космического тела — идеальный шар.
Для решения задачи следует обозначить буквой эн число оборотов: n = 1,5, а t — время, за которое планета их совершила. Путь же, который прошла станция, можно представить в виде материальной точки и принять за l = 50 000 км. Найти же будет нужно линейную и угловую скорости. Кроме этого, по условию задачи нужно найти сутки, длина которых равняется периоду — полному обороту планеты вокруг оси.
В такой задаче необязательно переводить данные в систему СИ. Можно использовать километры и часы, так как в задании не требуется дать ответ в соответствии с СИ, тем более что метры и секунды использовать неудобно.
Первое, что можно найти, это линейную скорость, равную отношению пройденного пути ко времени: v = l / t = 50000 / 42. Решив дробь, примерный результат будет равняться 1190 км /ч. Теперь можно найти скорость угла поворота. Нужно разделить угол, на который изменилось положение точки, на время. Так как один полный оборот — это 2p, то полтора оборота будут составлять 3p. Тогда искомая скорость будет равняться: w = φ / t = 3p / 42 = 0,22 рад/ч.
Сутки, то есть период обращения, будут определяться как полный период вращения, который можно разделить на число оборотов за это время. Формула для расчёта будет выглядеть следующим образом: T = t / N. Подставив значения, можно найти искомый период. Он будет составлять: T = 42 / 1,5 = 28 часов.
Осталось вычислить радиус, который равняется отношению линейной скорости к угловой: R = v / w. Так как в качестве ответов записывались примерные значения, то для предотвращения арифметической ошибки подставлять уже найденные числа не следует. Поэтому лучше подставить алгебраические выражения. Тогда: R = (l /t) / (φ / t) = l / φ = 50000 / 3p = 5305 км. Задача решена.
[spoiler title=”источники:”]
http://svet202.ru/teoriya/formula-skorosti-cherez-radius.html
[/spoiler]
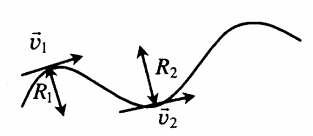
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Определение и формулы
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Определение и формулы
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные факты
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формула
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17763
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Или:
Отсюда:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 22k
Линейная скорость через угловую, теория и онлайн калькуляторы
Линейная скорость через угловую
Определение
Мгновенной (истинной) скоростью ($overline{v}$) называют векторную физическую величину, равную производной от вектора перемещения по времени ($t$):
[overline{v}={mathop{lim }_{Delta tto 0} frac{Delta overline{r}}{Delta t}=frac{doverline{r}}{dt} }left(1right).]
$Delta overline{r}$- вектор перемещения материальной точки, это перемещение точка совершает за отрезок времени $Delta t$.
Выражение линейной скорости через угловую скорость
Скорость называют мгновенной, так как ее значение показывает величину скорости в определенный момент времени.
Так как вектор перемещения $Delta overline{r}$ направлен по хорде, которая соединяет две близкие точки криволинейной траектории движения частицы, при уменьшении расстояния между этими точками, вектор $Delta overline{r}$ занимает положение касательной к линии, по которой движется частица. Из определения (1) следует, что мгновенная скорость направлена по касательной к траектории движения.
Скорость прохождения пути ($s$) определяют:
[v={mathop{lim }_{Delta tto 0} frac{Delta s}{Delta t}=frac{ds}{dt}left(2right). }]
Мгновенную скорость называют линейной тогда, когда хотят подчеркнуть ее отличие от угловой скорости.
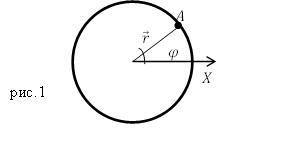
Если материальная точка движется по окружности, то ее положение характеризуют при помощи угла поворота ($varphi $), который образует радиус-вектор ($overline{r}$), определяющий положение рассматриваемой точки А с выделенным неизменным направлением от которого производят отсчет (рис.1).
Быстроту изменения угла поворота $varphi $ характеризуют при помощи такой физической величины как угловая скорость. Обычно угловую скорость обозначают буквой $omega $. Угловая скорость равна:
[omega =frac{dvarphi }{dt}left(3right).]
Вращение называют равномерным, если угловая скорость постоянна $omega =const$. При равномерном вращении $omega $ можно называть угловой частотой.
Линейная скорость движения точки по окружности связана с угловой скоростью. Пусть точка проходит путь равный длине дуги XA (рис.1). Этот путь обозначим $s$. Если радиус окружности равен$ R=const$, то длину дуги найдем как:
[s=Rvarphi left(4right).]
Продифференцируем обе части выражения (4) по времени, имеем:
[frac{ds}{dt}=frac{dleft(Rvarphi right)}{dt}=Rfrac{dvarphi }{dt}left(5right).]
Мы видим, что в левой части получена величина линейной скорости, в правой части радиус окружности умножен на угловую скорость:
[v=Romega left(6right).]
Формула (6) будет справедлива при движении точки по криволинейной траектории отличной от окружности, но в этом случае $R$ – радиус кривизны траектории в месте нахождения частицы.
В векторном виде выражение (6) записывают так:
[overline{v}=overline{omega }times overline{r}left(7right),]
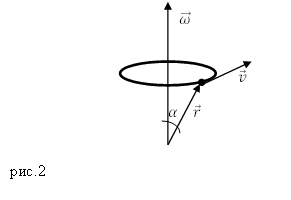
$overline{r}$ – вектор, соединяющий ось вращения и движущуюся точку (рис.2). Модуль скорости, используя формулу (7) найдем как:
[v=omega r{sin alpha left(8right), }]
где $alpha $ – угол между вектором угловой скорости и $overline{r}.$
Угловая скорость через линейную
Исходя из приведенных выше формул угловую скорость можно выразить через линейную. При движении по окружности:
[omega =frac{v}{R}left(9right).]
Или используя формулу (8) угловую скорость выразим как:
[omega =frac{v}{r{sin alpha }}left(10right).]
Примеры задач с решением
Пример 1
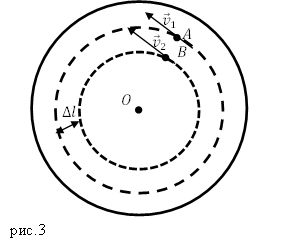
Задание. Диск равномерно вращается вокруг оси (O), перпендикулярной его плоскости, проходящей через его центр (рис.3). Линейная скорость точки A равна $v_1$, Точка B находится на расстоянии $Delta l$ ближе к оси и имеет лилейную скорость $v_2$. Какова угловая скорость вращения диска ($omega $)?
Решение. Основой для решения задачи будет формула:
[omega =frac{v}{R}left(1.1right).]
Угловые скорости движения точки A и B одинаковы (${omega }_A={omega }_B$), запишем выражение для каждой из этих скоростей используя (1.1):
[{omega }_A=frac{v_1}{R_1};; {omega }_B=frac{v_2}{R_2}left(1.2right).]
$R_1$ – расстояние от точки O до точки A; $R_2=R_1-Delta l$ – расстояние от точки B до точки O. Приравняем правые части выражений (1.2), выразим расстояние $R_1$:
[frac{v_1}{R_1}=frac{v_2}{R_1-Delta l}to R_1=frac{Delta lcdot v_1}{v_1-v_2}left(1.3right).]
Найдем угловую скорость точки A:
[{omega }_A=v_1cdot frac{v_1-v_2}{Delta lcdot v_1}=frac{v_1-v_2}{Delta l}.]
Ответ. Угловая скорость всех точек диска равна $omega =frac{v_1-v_2}{Delta l}$
Пример 2
Задание. Колесо радиусом R=1 м вращается так, что угол поворота изменяется в соответствии с
законом: $varphi left(tright)=2+5t^3(рад)$. Определите, какова линейная скорость точек обода колеса в момент времени,
равный $t’=1 (с)$.
Решение. В качестве основы для решения задачи воспользуемся формулой:
[v=Romega left(2.1right).]
Используя уравнение $varphi left(tright)$ и связь угла поворота и угловой скорости найдем $omega $:
[omega =frac{dvarphi }{dt}=frac{d}{dt}left(A+Bt^3right)=3Bt^2(2.2).]
Подставим результат (2.2) в (2.1), имеем:
[v=Rcdot 3Bt^2.]
Вычислим искомую скорость:
[v=1cdot 3cdot 5cdot 1^2=15 left(frac{м}{с}right).]
Ответ. $vleft(t’right)=15frac{м}{с}$
Читать дальше: масса и плотность вещества.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Что такое линейная скорость, единицы измерения
Определение
Скоростью при равномерном движении тела называют физическую величину, с помощью которой определяют путь, преодоленный телом за единицу времени.
В международной системе СИ единицей измерения линейной скорости является производная от двух основных единиц:
- метр;
- секунда.
В международной системе СИ скорость измеряется в метрах в секунду (м/с). За единицу скорости принимают скорость равномерного движения, при которой путь в один метр тело преодолеет в течение одной секунды. Кроме того, скорость можно измерять в:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- км/ч;
- км/с;
- см/с.
Связь между линейной и угловой скоростями
Скорость точки, которая совершает круговое движение, называется линейной скоростью, чтобы отделить это понятие от термина угловая скорость. Во время вращения абсолютно твердое тело в разных точках будет обладать неодинаковыми линейными скоростями, но значение угловой скорости остается стабильным.
Можно установить связь между линейной и угловой скоростью тела, вращающегося по окружности. Путь, который проходит точка, расположенная на окружности с радиусом R, составляет:
2πR
Исходя из того, что время одного оборота тела является периодом Т, модуль линейной скорости будет рассчитан по следующей формуле:
(v=frac{2pi R}{T}=2pi RV)
Зная, что:
(omega =2pi V)
получим справедливое равенство:
(v=omega R)
Данная формула демонстрирует увеличение линейной скорости тела при его удалении от оси вращения. К примеру, точки, которые движутся по земному экватору v=463 м/с, а точки, расположенные на широте города Санкт-Петербург, движутся со скоростью v=233 м/с. При нахождении на полюсах планеты скорость уменьшается до v=0.
Модуль центростремительного ускорения точки тела, которая совершает равномерные вращательные движения, определяют с помощью угловой скорости тела и радиуса окружности. Уравнение будет записано в следующем виде:
(a=frac{v^{2}}{R})
(v=omega R)
Таким образом, формула будет преобразована:
(a=omega ^{2}R)
Подытожив расчеты, можно записать все возможные равенства, справедливые для определения центростремительного ускорения:
(a=frac{v^{2}}{R}=omega ^{2}R=frac{4pi ^{2}}{T^{2}}R=4pi ^{2}V^{2}R)
Таким образом, рассматривают пару простейших движений, характерных для абсолютно твердого тела, включая поступательное и вращательное. При этом стоит отметить, что определить любое сложное движение, которое совершает абсолютно твердое тело, можно с помощью суммы двух независимых движений:
- поступательное;
- вращательное.
С помощью закона независимости движений описывают сложное движение абсолютно твердого тела.
Формулы для нахождения линейной скорости
Тело движется равномерно тогда, когда его скорость характеризуется постоянной величиной. Формула для расчета скорости такого движения будет иметь следующий вид:
V = st
где s является пройденным путем, то есть длиной линии;
t представляет собой время, в течение которого тело преодолевало указанный путь.
Определение
Линейной скоростью V называют физическую величину, которая демонстрирует путь, пройденный телом в течение определенного времени.
Основной формулой для определения линейной скорости является следующее равенство:
V = St
где S является путем,
t обозначает время, в течение которого тело преодолело путь S.
Иной вариант уравнения имеет такой вид:
V = lt
где l является путем,
t обозначает время, в течение которого тело преодолело дугу l.
В некоторых научных источниках скорость обозначают с помощью маленькой буквы v. Другим уравнением для расчета линейной скорости является равенство:
(v=2pi RT)
В данном случае 2π представляет собой полную окружность и составляет 360 угловых градусов. Вектор скорости направлен по касательной к траектории движении тела.
Модуль скорости
Числовое значение скорости может быть разным в зависимости от выбранной единицы измерения. Кроме числового значения, скорость характеризуется направлением. Числовое значение, которым обладает скорость, в физике называют ее модулем.
В случае, когда скорость обладает определенным направлением, такая величина является векторной. Таким образом, скорость представляет собой векторную физическую величину. Записывают модуль скорости в виде буквы v, а вектор скорости, как (vec{v})
Следует отметить, что такие величины, как путь, время, длина обладают только числовым значением. Они называются скалярными. Если тело движется неравномерно, то справедливо использовать в расчетах среднюю скорость.
Задачи с примерами решения
Задача №1
Тело совершает движение по окружности с ускорением 3 м/с в квадрате. Радиус окружности равен 40 метров. Необходимо определить линейную скорость движения тела.
Решение:
Ускорение в данном случае будет нормальным. Исходя из этого, определить линейную скорость тела можно с помощью формулы:
(a=frac{v^{2}}{R})
(v=sqrt{aR}=sqrt{40times 3}=10.9) м/с
Ответ: линейная скорость равна 10,9 м/с.
Задача №2
Поезд совершает равномерное движение. В течение 4 часов он преодолевает путь в 219 километров. Требуется рассчитать скорость движения поезда.
Решение:
Исходя из основной формулы для расчета линейной скорости, получим:
(v=frac{S}{t}=frac{219}{4}=54.75) км/ч
Ответ: скорость движения поезда составит 54.75 км/ч или 15.2 м/с.
Задача №3
Транспортное средство, работая на двигателе внутреннего сгорания, в течение 2,5 часов преодолевает расстояние в 213 километров. Требуется определить скорость движения транспорта.
Решение:
С помощью уравнения расчета скорости можно записать решение задачи:
(v=frac{S}{t}=frac{213}{2,5}=85.2) км/ч
Ответ: Скорость движение транспортного средства составляет 85.2 км/ч или 23.7 м/с.
Как найти линейную и угловую скорости движения точек экватора Земли по ее радиусу? Объясните как можно подробнее.
Для решения этой типовой задачи нам понадобятся две вещи: радиус окружности и период обращения точки по ней. В самой задаче этих данных, конечно же, нет, но подразумевается, что они нам известны. Ну или будут известны, когда мы найдем учебник или, еще лучше, спросим у гугла.
Итак, экваториальный радиус Земли – 6370 км, а период вращения вокруг своей оси – 24 часа.
Формулу линейной скорости выведем так: Если радиус равен RR, то точка за один оборот пройдет путь, равный длине окружности, т.е. равный 2πR2πR. Почему так? Ответ в геометрии за седьмой класс.
Далее. Путь этот она пройдет за время, равное периоду TT, а значит v=2πR/Tv = 2πR/T.
Ну а что такое угловая скорость? Это отношение угла поворота ко времени, за которое поворот совершен.
Полный оборот по окружности составляет 2π2π радиан по определению. Угловая скорость зависит от периода вращения, следовательно ω=2π/Tω = 2π/T. К сожалению, эта формула только для равномерного движения. К счастью, это наш случай.
Подставим известные величины в формулы и получим:
v=2πR/T=2⋅3.1415⋅6370⋅103м/24⋅602с=40022710м/86400с=463.22v = 2πR/T = 2 cdot 3.1415 cdot6370cdot10^3 м/ 24 cdot60^2 с = 40 022 710м/86 400с = 463.22м/с
ω=2⋅3.1415/24⋅602с=6.283рад/86400с=7,27⋅10−5ω = 2 cdot 3.1415/24cdot 60^2 с = 6.283рад/86 400с = 7,27cdot10^{-5} рад/с
Ответ: ν=463.22ν = 463.22 м/с, w=7,27⋅10−5w = 7,27cdot10^{-5} рад/с.
Теги: физика, механика, кинематика, вращение, задача
Тест по теме “Скорость движения точек экватора Земли”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат