Как найти линейную и угловую скорости движения точек экватора Земли по ее радиусу? Объясните как можно подробнее.
Для решения этой типовой задачи нам понадобятся две вещи: радиус окружности и период обращения точки по ней. В самой задаче этих данных, конечно же, нет, но подразумевается, что они нам известны. Ну или будут известны, когда мы найдем учебник или, еще лучше, спросим у гугла.
Итак, экваториальный радиус Земли – 6370 км, а период вращения вокруг своей оси – 24 часа.
Формулу линейной скорости выведем так: Если радиус равен RR, то точка за один оборот пройдет путь, равный длине окружности, т.е. равный 2πR2πR. Почему так? Ответ в геометрии за седьмой класс.
Далее. Путь этот она пройдет за время, равное периоду TT, а значит v=2πR/Tv = 2πR/T.
Ну а что такое угловая скорость? Это отношение угла поворота ко времени, за которое поворот совершен.
Полный оборот по окружности составляет 2π2π радиан по определению. Угловая скорость зависит от периода вращения, следовательно ω=2π/Tω = 2π/T. К сожалению, эта формула только для равномерного движения. К счастью, это наш случай.
Подставим известные величины в формулы и получим:
v=2πR/T=2⋅3.1415⋅6370⋅103м/24⋅602с=40022710м/86400с=463.22v = 2πR/T = 2 cdot 3.1415 cdot6370cdot10^3 м/ 24 cdot60^2 с = 40 022 710м/86 400с = 463.22м/с
ω=2⋅3.1415/24⋅602с=6.283рад/86400с=7,27⋅10−5ω = 2 cdot 3.1415/24cdot 60^2 с = 6.283рад/86 400с = 7,27cdot10^{-5} рад/с
Ответ: ν=463.22ν = 463.22 м/с, w=7,27⋅10−5w = 7,27cdot10^{-5} рад/с.
Теги: физика, механика, кинематика, вращение, задача
Тест по теме “Скорость движения точек экватора Земли”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
С какой скоростью вращается Земля вокруг своей оси? Не для кого не секрет, что смена дня и ночи технически вызвана вращением Земли. Но вам когда-нибудь приходило в голову с какой скоростью она вращается? И как посчитать эту скорость?
Если говорить о равномерном движении по окружности, можно выделить две скорости: угловую (ω) и линейную (v). Давайте найдем и ту, и другую для нашей прекрасной голубой планеты.
Угловая скорость вращения Земли
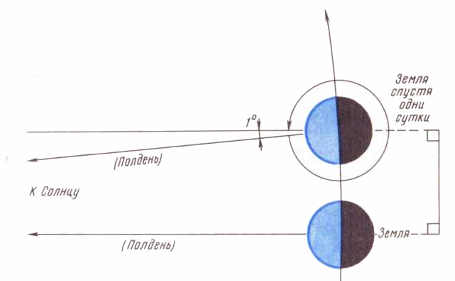
Угловая скорость определяет то, как быстро изменяется угол с течением в времени. Так как один полный оборот соответствует углу в 360о или 2π, а время, за которое он совершается есть период Т, то угловую скорость можно выразить как:
![]()
На всякий случай. Чтобы не было вопросов откуда берется 2π.
Один радиан соответствует углу с дугою равной радиусу. Соответственно чтобы посчитать количество радиан в окружности нам необходимо ее длину то есть 2πR, поделить на радиус R. R и R сокращаем и получаем 2π. Или приближенно 6.28.
Мы знаем, что в сутках 24 часа, а, следовательно, можно предположить, что период обращения Земли вокруг своей оси Т составит так же 24 часа. Но не торопитесь переводить это время в секунды и подставлять в уравнение, записанное выше. Так как Земля вращается еще вокруг солнца, то период обращения её вокруг собственной оси будет немного короче привычных нам солнечных суток и составит 23 часа 56 минут и 4 секунды. Это так называемые звездные сутки. В пересчете на секунды мы получаем: Т=86164 с.
Теперь можно найти угловую скорость:
![]()
Линейная скорость вращения Земли
Если говорить об угловой скорости, то она одинакова для любой точки нашей планеты. И не важно: пингвин в Антарктике, слон в Африке или Вы у себя дома, все будут иметь одинаковую угловую скорость. Но когда речь заходит о скорости линейной, то тут все наоборот. Она будет максимальна на экваторе и убывать к полюсам, так как напрямую зависит от радиуса окружности вращения. А это значит, что если вы залезете на табуретку вкрутить лампочку, то ваша линейная скорость увеличится. Строго говоря, линейная скорость описывает скорее не вращение Земли вокруг своей оси, она описывает вращение каких то отдельных её точек.
Рассчитать линейную скорость очень просто. По определению, скорость — это отношение пройденного пути ко времени, за которое этот путь был совершен. Если за один оборот мы проходим путь, равный длине окружности, а время движения будет ни что иное как период обращения Т, то, выразив длину окружности из известной школьной формулы: L= 2πR, мы получим уравнение для расчета линейной скорости:
![]()
Так как угловая скорость ![]() , то мы можем смело записать:
, то мы можем смело записать:
![]()
Радиус земли на экваторе R = 6378245 м, а значит линейная скорость там будет равна:![]() м/с.
м/с.
Для сравнения скорость звука в воздухе составляет 365 м/с. А это значит, что, сидя спокойно на стульчике где-нибудь в Африке или Индонезии мы будем двигаться со скоростями, превышающими звук. Если перевести эту величину в километры в час, то получится 1674 км/ч!!! В общем скорости сопоставимые со скоростями сверхзвуковой авиации.

Линейная скорость в зависимости от широты
Но это на экваторе. Ближе к полюсам, как я уже говорил, значение будет ниже. Так как радиус вращения будет снижаться.
Для того чтоб найти радиус вращения на той или иной широте. Необходимо косинус этой широты умножить на земной радиус.
К примеру, для Санкт-Петербурга соответствует шестидесятая северная широта. Косинус шестидесяти градусов как известно одна вторая. То есть радиус вращения будет вдвое меньше земного, а значит и линейная скорость будет так же в два раза меньше экваториальной, всего 837 км/ч.
А с какой линейной скоростью вращаетесь Вы??? Ответы можете писать в комментариях, а я с Вами прощаюсь. Всего хорошего, до скорых встреч.
Как известно, наша планета движется, и не только вокруг Солнца, но и вокруг своей оси. Вдобавок, мы знаем, что для любого движения характерна определённая скорость, которая может зависеть (как и само движение) от различных факторов. Следовательно, вращение Земли также имеет свою скорость.

Скорость — это векторная физическая величина, характеризующая быстроту перемещения материальной точки за любой отрезок времени относительно величины промежутка.
Скорость вращения Земли
Правда, земная скорость — вещь относительна. Так как для её расчёта нужна определённая точка отсчёта. Например, для того, чтобы вычислить с какой скоростью движется Земля вокруг своей оси, такой точкой является центр планеты.
Однако, говоря о подобном параметре земельного кружения, важно знать, что скорость разделяют на угловую и линейную.
Угловая скорость
Это величина, которая равна отношению угла тела к отрезку времени, затраченному на этот поворот. Можно сказать, что это быстрота изменения угла тела за промежуток времени. Выражается она в радианах в секунду, и для всех точек имеет постоянное значение.
Как выяснилось, на полный оборот нашей планеты вокруг своей оси требуется 23 часа 56 минут 4,09053 секунды. Проще говоря, одни звездные сутки.
Формула угловой скорости: отношение изменения угла за время.
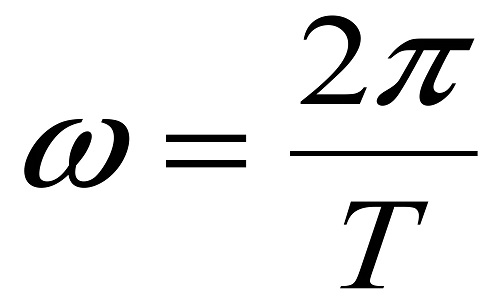
Так как земной оборот равен 360 градусов или 2π (2*3,14=6,28), а время этого оборота в секундах 86344, то угловая скорость вращения Земли вокруг своей оси приблизительно равна 7,26851851851-5с-1.
Линейная скорость
Такую характеристику применяют для того, чтобы выразить темп движения по окружности. Как известно, при круговом вращении тела его разные точки имеют разные скорости. Хотя угловая величина перемещения для них остаётся неизменной.
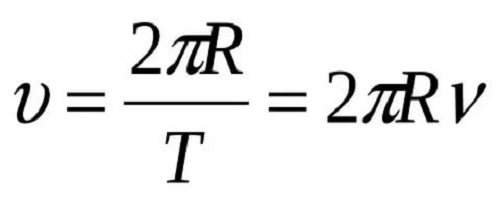
А это значит, что скорость вращения Земли равна примерно 465 м/сек. То есть расчет производится путём деления окружности на время, затраченное на весь оборот.
Однако скорость движения Земли изменяется, потому как её окружность также меняется относительно широты. Ведь радиус планеты уменьшается к полюсам. Соответственно, на разных широтах разный темп вращения. Другими словами, где меньший радиус медленнее и скорость. К примеру, на полюсах она почти нулевая, а на экваторе составляет 1674 км/час.
Для того, чтобы рассчитать скорость вращения Земли на другой широте, необходимо косинус выбранной широты умножить на экваторную скорость. Например, быстроту движения планеты на широте 30 градусов мы вычислим, если косинус 30 градусов, который равен 0,866, умножим на 1674. Таким образом, получаем 1449,7 км/час.
С какой скоростью Земля движется относительно Солнца
Поскольку наша планета, как и другие планеты звездной группы, движутся вокруг Солнца, у данного движение также есть своя скоростная величина.
На полный оборот вокруг главного светила уходит 365 дней 5 часов 48 минут и 46 секунд. Хотя мы привыкли округлять и говорить просто один год. Между прочим за каждый такой год накапливается по пять часов, так сказать, лишних. Но и им нашли место, их объединяют и каждому следующему четвертому году добавляют один день. Наверняка вы догадались, что такие года называются високосными.
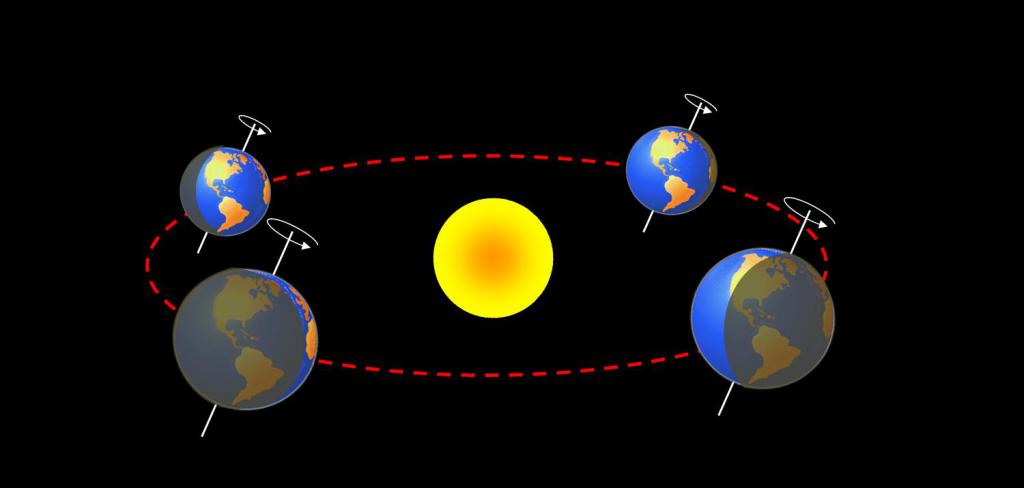
На основании данных о времени полного оборота планеты вокруг Солнца, не трудно вычислить с какой быстротой она движется относительно него. Следует учитывать, что двигаемся мы по орбите. А значит определяем с какой скоростью Земля летит именно по орбите.
Как рассчитать темп земного движения вокруг Солнца
Для этого необходимо радиус орбиты или расстояние до Солнца (≈150 млн км) умножить на 2π (23,14=6,28), что составляет 942 млн км. Все это разделим на время, затраченное на этот промежуток (365 дней 24 часа*3600 секунд=31 536 000 секунд). В итоге получаем 29,87 км в секунду.
Принято считать, что средняя скорость Земли по орбите (по окружности Солнца) равна 30 км/сек.
По данным учёных, скорость вращения Земли вокруг своей оси постепенно уменьшается. Причем наблюдаются пятилетние циклы то ускорения, то замедления движения планеты. Но объяснить по какой причине происходят такие изменения пока не получается. Поэтому за движением нашей планеты ведётся постоянное наблюдение и мониторинг. Возможно, отыщется какая-либо взаимосвязь данного явления.
Содержание материала
- Основные характеристики и формулы
- Видео
- Угловая скорость
- Вращение Земли
- Период и частота
- Мгновенная и средняя скорости
- Центростремительное ускорение
- Период и частота вращения
- Примеры задач с решением
Основные характеристики и формулы
Так как за период  угловое перемещение
угловое перемещение  рад, угловая скорость связана с периодом и частотой вращения:
рад, угловая скорость связана с периодом и частотой вращения:



Рис.1. Линейное и угловое перемещение при равномерном движении точки по окружности
Наряду с понятием угловой скорости для характеристики равномерного движения по окружности сохраняет смысл привычное для нас понятие скорости движения точки вдоль траектории, которое в данном случае называется линейной скоростью.
Модуль линейной скорости равен отношению длины дуги окружности  к промежутку времени, за который эта дуга пройдена.
к промежутку времени, за который эта дуга пройдена.
Линейная скорость тела, которое движется по окружности, не изменяется по модулю, а все время изменяется по направлению, и в любой точке траектории направлена по касательной к дуге этой окружности (рис.1).
Угловая и линейная скорости связаны между собой соотношением:

где  радиус окружности.
радиус окружности.
Кинематическое уравнение или закон движения точки по окружности:

Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.



Видео
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Мгновенная и средняя скорости

Как найти линейную скорость? Формулу, согласно определению величины, можно записать следующую:
v¯ = dl¯/dt.
Где dl¯ — вектор перемещения тела за время dt. Эта скорость называется мгновенной, поскольку рассчитывается за чрезвычайно короткий промежуток времени dt. Мгновенная скорость в действительности является величиной не стабильной и постоянно меняющейся. Например, представим, что по дороге движется автомобиль. На первый взгляд можно полагать, что в любой момент времени его мгновенная скорость будет постоянной, однако, это не так. Мгновенная скорость испытывает колебания. Если спидометр автомобиля достаточно чувствителен, то он фиксирует эти колебания.
Формула линейной скорости средней ничем не отличается от таковой для мгновенной, однако, измеряется она за более длительный промежуток времени Δt:
v¯ = Δl¯/Δt, где Δt>>dt.
В примере с автомобилем выше, хотя мгновенная скорость испытывает колебания, средняя скорость остается постоянной с определенной точностью на всем участке пути Δl¯.
При решении задач, как правило, используют среднюю скорость. Мгновенная же величина имеет смысл только в случае движения с ускорением.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Период и частота вращения
Важными характеристиками любого вращательного движения являются частота и период:
Определение Период – время, за которое тело совершает полный оборот.
В нашем примере с мотоциклистом, период – это время, за которое мотоциклист проезжает один полный круг.
Из курса геометрии вспоминаем, что длину дуги окружности можно посчитать как (2*pi*R), где (R) – радиус окружности. Тогда в случае равномерного движения период можно посчитать по формуле, как расстояние деленое на скорость: $$T=frac{2*pi*R}{V};$$ Подставив сюда формулу ((1)) для линейной скорости через угловую: $$T=frac{2*pi}{omega};$$ Где (V) –линейная скорость вращения.
В системе СИ период измеряется в ([{cек}^{-1}]).
Определение Частота – количество оборотов за единицу времени.
В случае с мотоциклистом, частота – это сколько кругов он успевает проехать, например, за один час. Обычно частоту измеряют в оборотах в секунду.
Период и частота вращения связаны между собой выражением: $$T=frac{1}{nu};$$ Отсюда можно получить формулы для частоты, подставив период: $$nu=frac{V}{2*pi*R}=frac{omega}{2*pi};$$
Пример 1
Скорость точки, находящейся на краю вращающегося диска равна (V_A=15(м/с)), а точки, расположенной на 0,2 (м) ближе к центру вращения равна (V_B=10(м/с)). Найти частоту вращения и радиус диска.
Примеры задач с решением
Пример 1
Задание. Диск равномерно вращается вокруг оси (O), перпендикулярной его плоскости, проходящей через его центр (рис.3). Линейная скорость точки A равна $v_1$, Точка B находится на расстоянии $Delta l$ ближе к оси и имеет лилейную скорость $v_2$. Какова угловая скорость вращения диска ($omega $)?
Решение. Основой для решения задачи будет формула: [omega =frac{v}{R}left(1.1right).]
Угловые скорости движения точки A и B одинаковы (${omega }_A={omega }_B$), запишем выражение для каждой из этих скоростей используя (1.1): [{omega }_A=frac{v_1}{R_1};; {omega }_B=frac{v_2}{R_2}left(1.2right).]
$R_1$ — расстояние от точки O до точки A; $R_2=R_1-Delta l$ — расстояние от точки B до точки O. Приравняем правые части выражений (1.2), выразим расстояние $R_1$: [frac{v_1}{R_1}=frac{v_2}{R_1-Delta l}to R_1=frac{Delta lcdot v_1}{v_1-v_2}left(1.3right).]
Найдем угловую скорость точки A: [{omega }_A=v_1cdot frac{v_1-v_2}{Delta lcdot v_1}=frac{v_1-v_2}{Delta l}.]
Ответ. Угловая скорость всех точек диска равна $omega =frac{v_1-v_2}{Delta l}$
Пример 2
Задание. Колесо радиусом R=1 м вращается так, что угол поворота изменяется в соответствии с законом: $varphi left(tright)=2+5t^3(рад)$. Определите, какова линейная скорость точек обода колеса в момент времени, равный $t’=1 (с)$.
Решение. В качестве основы для решения задачи воспользуемся формулой: [v=Romega left(2.1right).]
Используя уравнение $varphi left(tright)$ и связь угла поворота и угловой скорости найдем $omega $: [omega =frac{dvarphi }{dt}=frac{d}{dt}left(A+Bt^3right)=3Bt^2(2.2).]
Подставим результат (2.2) в (2.1), имеем: [v=Rcdot 3Bt^2.]
Вычислим искомую скорость: [v=1cdot 3cdot 5cdot 1^2=15 left(frac{м}{с}right).]
Ответ. $vleft(t’right)=15frac{м}{с}$
Читать дальше: масса и плотность вещества.

Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут! Узнать стоимость
Теги
|
Какая это скорость? Для измерения угловой скорости вращения Земли вокруг своей оси не нужно быть ученым. Каждый человек ведь знает, что Земля совершает полный оборот за сутки – приблизительно за 24 часа. Поэтому скорость вращения Земли – 1/24 обратного часа. Можно посчитать и в обратных секундах (то есть фактически в герцах), тогда получится очень маленькая величина. Если же требуется посчитать линейную скорость вращения Земли, но следует прежде всего учесть, что эта величина не постоянная, а изменяется от нуля на обоих географических полюсах до максимального значения на экваторе. То есть зависит от широты места. Линейную скорость вращения на экваторе тоже легко узнать, если знать его длину – примерно 40 тысяч километров (приблизительно эту величину определили еще в Древней Греции). То есть нужно 40000 км разделить на 24 ч, и тогда получится скорость около 1670 км/ч. Это больше, чем скорость звука в воздухе. система выбрала этот ответ лучшим Rafail 5 лет назад Если у Вас есть телескоп, подзорная труба или бинокль, или даже не имея ничего этого, Вы можете сделать даже сами. В какой-то момент направьте телескоп на какую-то звезду, зафиксируйте его (т.е исключите возможность самопроизвольного или при постороннем вмешательстве изменения положения) и запустите секундомер. На следующий день, наблюдая в телескоп, дождитесь когда звезда займёт то самое положение, которое было вчера и остановите секундомер. Он покажет время одного оборота Земли вокруг своей оси. Если у Вас нет телескопа, то Вы можете взять две пластиночки, просверлить в них по одному отверстию. Эти пластинки закрепить на дощечке перпендикулярно ей. Получится примитивная алидада. Используя её вместо телескопа, проведите те же самые измерения. Точность конечно будет поменьше, плюс-минус несколько секунд, но что значат несколько секунд по отношению к 86400 секундам (а именно столько секунд в сутках). Знаете ответ? |
