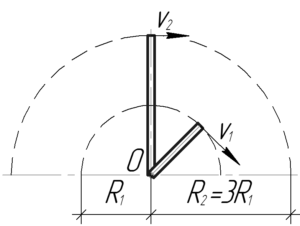
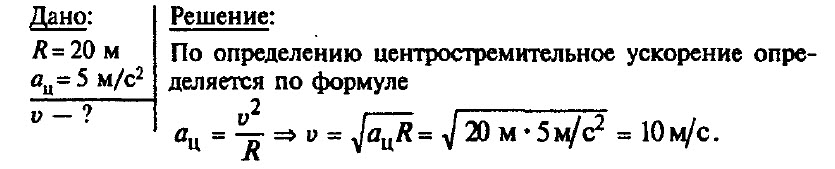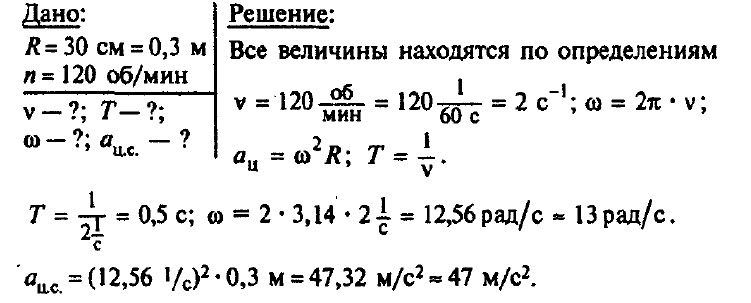Условие задачи:
Минутная стрелка часов в 3 раза длиннее секундной. Во сколько раз линейная скорость конца секундной стрелки больше линейной скорости конца минутной стрелки?
Задача №1.8.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(R_2=3R_1), (T_1=1) мин, (T_2=1) ч, (frac{upsilon_1}{upsilon_2}-?)
Решение задачи:
Линейную скорость конца любой стрелки можно определить по формуле:
[upsilon = omega R]
Циклическую частоту (omega) определим по известной формуле, зная период (T):
[omega = frac{{2pi }}{T}]
Суммируя все написанное:
[upsilon = frac{{2pi R}}{T}]
Тогда отношение скоростей равно:
[frac{{{upsilon _1}}}{{{upsilon _2}}} = frac{{2pi {R_1} cdot {T_2}}}{{{T_1} cdot 2pi {R_2}}} = frac{{{R_1}{T_2}}}{{{R_2}{T_1}}}]
Так как минутная стрелка длиннее секундной в 3 раза, то:
[frac{{{upsilon _1}}}{{{upsilon _2}}} = frac{{{R_1}{T_2}}}{{3{R_1}{T_1}}} = frac{{{T_2}}}{{3{T_1}}}]
Подставим в эту формулу периоды в единицах СИ и получим ответ.
[1; ч = 3600; с]
[1; мин = 60; с]
[frac{{{upsilon _1}}}{{{upsilon _2}}} = frac{{3600}}{{3 cdot 60}} = 20]
Ответ: в 20 раз.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.9 Колесо велосипеда делает 100 об/мин. Каков радиус колеса, если скорость
1.8.11 Тело движется по окружности с постоянной по модулю скоростью. Во сколько раз
1.8.12 Тело движется равномерно по окружности. Во сколько раз увеличится
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
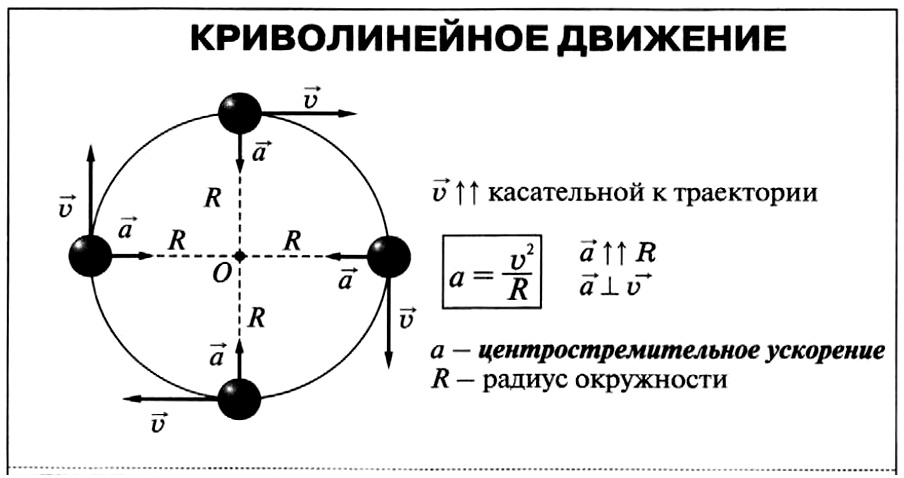
Криволинейное движение — механическое движение, траектория которого — кривые линии с произвольным ускорением и произвольной скоростью.
Угловая скорость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. [omega=dfracvarphi t=dfrac{2pi}{t}]
Период обращения — это время одного полного оборота.
Частота обращения — величина, обратная периоду. Частота показывает, сколько полных оборотов совершает материальная точка за секунду. [nu=dfrac1T]
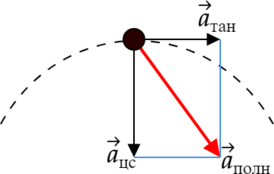
Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения.
Нормальное (центростремительное) ускорение — компонента ускорения, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной, направленное к центру кривизны траектории. [a_text{цс}=dfrac{v^2}{r}]
Полное ускорение тела, движущегося по окружности равно векторной сумме тангенциального и нормального ускорений. [overrightarrow a_text{полн}=overrightarrow a_text{тан}+overrightarrow a_text{цс}]
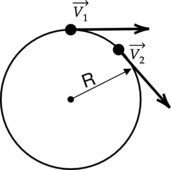
Два велосипедиста участвуют в кольцевой гонке, при чём отношение их линейных скоростей (displaystyle k= frac{upsilon_1}{upsilon_2} = 2). Найдите отношение угловых скоростей (displaystyle frac{omega _1}{omega _2}).
При движении по окужности линейная скорость связана с угловой следующей формулой: [upsilon=omega cdot R] Линейные скорости для велосипедистов 1 и 2: [upsilon_1=omega _1 cdot R] [upsilon_2=omega _2 cdot R] Поделив уравнения, получим отношение: [displaystyle frac{upsilon_1}{upsilon_2} = frac{omega _1}{omega _2} Rightarrow frac{omega _1}{omega _2} = k = 2]
Ответ: 2
Спутник движется по круговой орбите радиусом (R=670) км со скоростью (upsilon = 13,7) км/с. Чему равно центростремительное ускорение спутника? (Ответ дайте в метрах на секунду в квадрате, округлив до десятых)
Переведём данные в СИ:
(upsilon = 13700 text{ м/с})
(R = 6,7 cdot10^5 text{ м})
Центростремительное ускорение тела: [a_{text{цс}} = frac{upsilon^2}{R}] [a_{text{цс}} = frac{13700^2}{6,7cdot10^5} approx 280,1 text { м/с$^2$}]
Ответ: 280,1
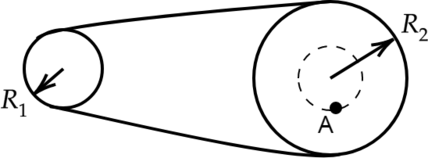
Два вращающихся вала соединены замкнутым нерастяжимым ремнём, котороый не проскальзывает относительно валов. Радиус первого вала равен (R_1), а второго вала — (R_2). Отношение угловой скорости в точке А к угловой скорости первого вала (k=0,25). Найдите отношение радиуса первого вала к радиусу второго.
Угловая скорость в точке А равна угловой скорости второго вала: [omega_A = omega_2 Rightarrow k = frac{omega_1}{omega_2}]
Так как валы связаны нерастяжимым ремнём, то линейные скорости на их ободах равны. Линейные скорости можно найти по формулам: [upsilon = omega_1 cdot R_1] [upsilon = omega_2 cdot R_2]
Отсюда: [omega_1 cdot R_1 = upsilon = omega_2 cdot R_2 Rightarrow frac{R_1}{R_2} = frac{omega_2}{omega_1} = 0,25]
Ответ: 0,25
Каково центростремительнное ускорение автомобиля, движущегося по закруглению 1000 м со скоростью 72 км/ч?
Центростремительное ускорение (нормальное): (displaystyle a_{text{цс}}=frac{upsilon^2}R=frac{(20 text{ м/с})^2}{1000 text{ м}}=0,4) м/с(^2)
Ответ: 0,4
Линейная скорость точки на ободе колеса радиусом 50 см равна 10 м/с. Чему равна линейная скорость точки, лежащей на том же радиусе, что и первая, но на 20 см ближе к центру колеса?
Угловая скорость равна: (displaystyle omega=frac{upsilon}R)
Для всех точек, находящихся на одном колесе угловая скорость одинаковая, поэтому можно записать: [omega=frac{upsilon_1}{R_1}=frac{upsilon_2}{R_2}] Отсюда получаем: [upsilon_2=frac{upsilon_1R_2}{R_1}=frac{10text{ м/с}cdot(0,5-0,2)text{ м}}{0,5text{ м}}=6 text{ м/с}]
Ответ: 6
Груз, подвешенный на нити длиной 2 м, отведён в сторону и отпущен. Нижнюю точку траектории он проходит со скоростью 1,4 м/с. Найдите центростремительное ускорение груза в нижней точке траектории. (Ответ дайте в метрах в секунду в квадрате и округлите до целых.)
Формула центростремительного ускорения: [a_{text{цс}}=frac{v^2}{R}=frac{1,4^2}{2}=1 text{ м/с$^2$}]
Ответ: 1
Линейная скорость конца стрелки часов (upsilon= 0,35cdot10^{-4}) м/с, ускорение конца стрелки (a = 0,61cdot10^{-7}) м/с(^2). Какая это стрелка – секундная, минутная, часовая? (В ответ запишите число: секундная – 1, минутная – 2, часовая – 3).
Формула для центростремительного ускорения: [displaystyle a_{mbox{цс}}=frac{upsilon^2}R] [R=frac{upsilon^2}{a_{mbox{цс}}}=frac{(0,35cdot10^{-4})^2}{0,61cdot10^{-7}}=0,02 mbox{ м}] Найдем период вращения стрелки: [T=frac{2pi R}{upsilon}=frac{2picdot0,02}{0,35cdot10^{-4}}=3600mbox{ с}] Следовательно, если период вращения стрелки равен 1 час, то это минутная стрелка.
Ответ: 2

УСТАЛ? Просто отдохни
Измерьте длину секундной и минутной стрелок своих часов и рассчитайте линейную скорость конца каждой стрелки.
reshalka.com
ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Движение по окружности. Номер №1652
Решение
Допустим длина секундной стрелки часов − 7 см, минутной стрелки − 5 см.
Дано:
R
м
=
7
см;
t
м
=
60
мин;
R
c
=
5
см;
t
с
=
60
с.
Найти:
v
м
и
н
− ?
v
с
− ?
СИ:
R
м
=
0
,
07
м;
t
м
=
3600
с;
R
c
=
0
,
05
м;
Решение:
Секундная стрелка делает один полный оборот за 60 секунд. Минутная стрелка делает один полный оборот за 60 минут (3600 секунд).
Найдем линейную скорость конца каждой стрелки:
v
=
2
π
R
t
;
v
м
=
2
∗
3
,
14
∗
0
,
07
3600
=
1
,
2
∗
10
−
4
м/с;
v
с
=
2
∗
3
,
14
∗
0
,
05
60
=
0
,
005
м/с;
Ответ:
1
,
2
∗
10
−
4
м/с; 0,005 м/с.

Длина секундной стрелки 15 мм.
1. Чему равна линейная скорость конца секундной стрелки?
2. Какой путь пройдёт стрелка за 45 секунд?
Длина минутной стрелки 12 мм.
1. Чему равна линейная скорость конца минутной стрелки?
2. Какой путь пройдёт стрелка за 30 минут?
Если можно полное решение и объяснение пожалуйста!
Светило науки – 85 ответов – 1702 помощи
1. V=S/t =2пR/t =2*3.14*0.015 / 60 = 0.00157 м/с =1.57 мм/с
2. S1 = 3/4 S = 3/4 2пr = 3/4 * 2*3.14*15 мм =70.65 мм =0.07 м
1. V =S/t =2пR/t =2*3.14*0.012 /3600=0.0000209 м/с=0.021 мм/с
2. S2 = 1/2 S = 1/2 *2пR = 1/2 * 2*3.14*12 мм =37.68 мм =0.038 м
Светило науки – 553134 ответа – 388270 раз оказано помощи
Длина секундной стрелки
r=15 мм. =0.015 м
длина окружности C=2пr
1. Чему равна линейная скорость конца секундной стрелки?
время движения по окружности t =60 c
линейная скорость v =C/t =2пr/t =2*3.14*0.015 / 60 = 0.00157 м/с =1.57 мм/с
2. Какой путь C1 пройдёт стрелка за 45 секунд?
45 сек – это 3/4 окружности
C1 = 3/4 C = 3/4 2пr = 3/4 * 2*3.14*15 мм =70.65 мм =0.07 м
Длина минутной стрелки R=12 мм. = 0.012 м
1. Чему равна линейная скорость конца минутной стрелки?
время движения по окружности t =60 мин =3600 c
линейная скорость v =C/t =2пR/t =2*3.14*0.012 /3600=0.0000209 м/с=0.021 мм/с
2. Какой путь C2 пройдёт стрелка за 30 минут?
30 мин – это 1/2 окружности
C2 = 1/2 C = 1/2 *2пR = 1/2 * 2*3.14*12 мм =37.68 мм =0.038 м
Если можно полное решение и объяснение пожалуйста!
Задачи на Движение тела по окружности с решениями
Формулы, используемые на уроках «Задачи на Движение тела по окружности».
Название величины |
Обозначение |
Единица измерения |
Формула |
Радиус окружности |
r |
м |
|
Линейная скорость (модуль) |
v |
м/с |
|
Центростремительное ускорение (модуль) |
a |
м/с2 |
|
Центростремительная сила (модуль) |
F |
Н |
|
Масса тела |
m |
кг |
|
Угловая скорость при равномерном вращении |
ω |
рад/с |
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Какова линейная скорость тела, движущегося по окружности радиусом 40 м с ускорением 2,5 м/с2 ?
Задача № 2.
С какой наибольшей скоростью может двигаться автомобиль массой 1 т на повороте радиусом 100 м, чтобы его не «занесло», если максимальная сила трения 4 кН?
Задача № 3.
Вентилятор вращается с постоянной скоростью и за две минуты совершает 2400 оборотов. Определите частоту вращения вентилятора, период обращения и линейную скорость точки, расположенной на краю лопасти вентилятора на расстоянии 10 см от оси вращения.
Задача № 4.
Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Задача № 5.
Велосипедист ехал со скоростью 25,2 км/ч. Сколько оборотов совершило колесо диаметром 70 см за 10 мин?
Задача № 6.
Минутная стрелка часов в 1,5 раза длиннее часовой. Определите, во сколько раз линейная скорость конца часовой стрелки меньше, чем линейная скорость конца минутной стрелки.
Задача № 7.
Автомобиль движется по закруглению дороги, радиус которой равен 20 м. Определите скорость автомобиля, если центростремительное ускорение равно 5 м/с2.
Задача № 8.
Шкив радиусом 30 см имеет частоту вращения 120 об/мин. Определите частоту, период обращения, угловую скорость шкива и центростремительное ускорение точек шкива, наиболее удаленных от оси вращения.
Задача № 9.
Для точек земной поверхности на широте Санкт-Петербурга (60°) определите линейную скорость и ускорение, испытываемое ими вследствие суточного вращения Земли. Радиус Земли считайте равным 6370 км.
Задача № 10.
ОГЭ
Точка движется равномерно по окружности. Как изменится её центростремительное ускорение, если скорость возрастёт вдвое, а радиус окружности вдвое уменьшится?
Задача № 11.
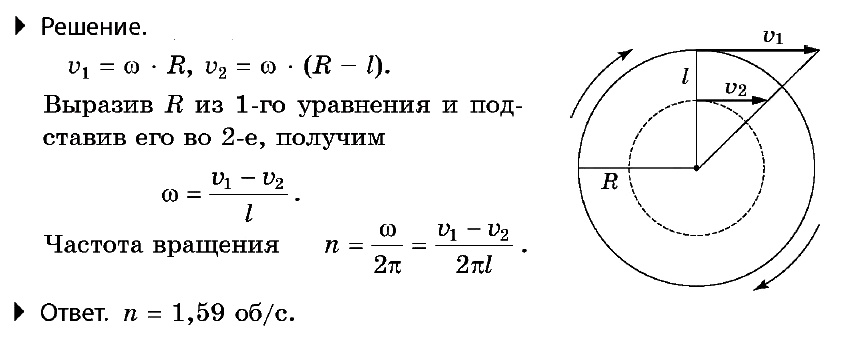
ЕГЭ
Линейная скорость точек обода вращающегося диска v1 = 3 м/с, а точек, находящихся на l = 10 см ближе к оси вращения, v2 = 2 м/с. Найти частоту вращения диска.
Задача № 12.
Груз, привязанный к шнуру длиной l = 50 см, описывает окружность в горизонтальной плоскости. Какой угол φ образует шнур с вертикалью, если частота вращения n = 1 с-1 ?
Рассуждение: На схеме покажем груз, подвешенный на нити и движущийся по окружности некого радиуса R в горизонтальной плоскости так, что нить составляет с вертикалью угол φ. На груз действуют две силы: 1) сила тяжести mg; 2) сила натяжения нити T. Так как груз не движется вдоль оси y, то запишем первый закон Ньютона в проекции на эту ось: T⋅• cos φ = mg. Поскольку груз описывается окружность, то второй закон Ньютона запишется так: T⋅• sin φ = ma.
Ответ: 60º.
Краткая теория для решения Задачи на Движение тела по окружности.
Это конспект по теме «ЗАДАЧИ на Движение тела по окружности». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Искусственные спутники планет.
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.