Как найти линейную скорость спутника земли

Четверг, 11 февраля, 2016

В космосе гравитация обеспечивает силу, из-за которой спутники (такие, как Луна) вращаются по орбитам вокруг более крупных тел (таких, как Земля). Эти орбиты в общем случае имеют форму эллипса, на чаще всего, этот эллипс не сильно отличается от окружности. Поэтому в первом приближении можно считать орбиты спутников круговыми. Зная массу планеты и высоту орбиты спутника над Землей, можно рассчитать, какой должна быть скорость движения спутника вокруг Земли.

Расчет скорости движения спутника вокруг Земли

Вращаясь по круговой орбите вокруг Земли, спутник в любой точке своей траектории может двигаться только с постоянной по модулю скоростью, хотя направление этой скорости будет постоянно изменяться. Какова же величина этой скорости? Её можно рассчитать с помощью второго закона Ньютона и закона тяготения.

Для поддержания круговой орбиты спутника массы в соответствии со вторым законом Ньютона потребуется центростремительная сила: , где — центростремительное ускорение.

Как известно, центростремительное ускорение определяется по формуле:

   

где — скорость движения спутника, — радиус круговой орбиты, по которой движется спутник.

Центростремительную силу обеспечивает гравитация, поэтому в соответствии с законом тяготения:

   

где кг — масса Земли, м³⋅кг^-1⋅с^-2 — гравитационная постоянная.

Подставляя все в исходную формулу, получаем:

   

Выражая искомую скорость , получаем, что скорость движения спутника вокруг Земли равна:

   

Это формула скорости, которую должен иметь спутник Земли на заданном радиусе (т.е. расстоянии от центра планеты) для поддержания круговой орбиты. Скорость не может меняться по модулю, пока спутник сохраняет постоянный орбитальный радиус, то есть пока он продолжает обращаться вокруг планеты по круговой траектории.

При использовании полученной формулы следует учитывать несколько деталей:

• В качестве радиуса нужно использовать расстояние от центра Земли, а не высоту над поверхностью.
  Следовательно, расстояние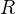 в формуле – это расстояние между центрами двух тел. В том случае, если известна высота спутника над поверхностью Земли, то для нахождения 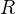к этой высоте нужно прибавить радиус Земли, который приблизительно равен 6400 км.
• Данная формула верна для спутников, находящихся за пределами атмосферы.
  Однако в случае искусственных спутников это не совсем так. Даже на высоте 600 км от Земли имеет место определённое сопротивление воздуха. Постепенно это сопротивление, т.е. трение о воздух, заставляет спутники снижаться, и в конце концов они сгорают при входе в атмосферу. На высоте менее 160 км орбита спутника существенно понижается при каждом обороте вокруг Земли из-за сопротивления воздуха.
• Скорость спутника на круговой орбите не зависит от его массы.
  Если представить себе, что сопротивлением воздуха можно пренебречь, и Луна обращается вокруг Земли на расстоянии 640 км, то для сохранения орбиты она должна двигаться с такой же точно скоростью, что и искусственный спутник на той же высоте, хотя масса и размеры Луны намного больше.

Искусственные спутники Земли, как правило, обращаются вокруг планеты на высоте от 500 до 2000 км от поверхности планеты. Рассчитаем, с какой скоростью должен двигаться такой спутник на высоте 1000 км над поверхностью Земли. В этом случае км. Подставляя числа, получаем:

 км/с.

Материал подготовлен репетитором по математике и физике в Москве, Сергеем Валерьевичем

Искусственный спутник обращается вокруг Земли по окружности на высоте h=3,6 Мм. Определить линейную скорость v спутника. Радиус R Земли

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,279
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,949
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу для определения искомой величины.
3. Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

• Радиус окружности, по которой движется автомобиль: R = 100 м.
• Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

1. Записать исходные данные.
2. Определить, что нужно найти.
3. Записать формулу зависимости центростремительного ускорения от частоты.
4. Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
5. Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Вычислите угловую и линейную скорости орбитального движения спутника Земли, если период его обращения 121, 16 мин, а высота полета 1700 км?

Физика | 10 – 11 классы

Вычислите угловую и линейную скорости орбитального движения спутника Земли, если период его обращения 121, 16 мин, а высота полета 1700 км.

121, 16 мин = 7269, 6 секунд.

Радиус обращения равен 6371 км (радиус Земли) + 1700 км = 8071 км.

Определите среднюю орбитальную скорость спутника, если средняя высота его орбиты над Землей 1200 км, а период обращения 105 мин?

Определите среднюю орбитальную скорость спутника, если средняя высота его орбиты над Землей 1200 км, а период обращения 105 мин.

Средняя высота движения спутника над поверхностью Земли равна 1700км?

Средняя высота движения спутника над поверхностью Земли равна 1700км.

Определите скорость обращения спутника вокруг Земли.

(Считать радиус Земли равным 6400км).

Искусственный спутник Земли (ИСЗ) движется по круговой орбите на высоте 630 км с периодом обращения 97, 5 мин?

Искусственный спутник Земли (ИСЗ) движется по круговой орбите на высоте 630 км с периодом обращения 97, 5 мин.

Радиус Земли≈ 6400 км.

Определите линейную скорость и центростремительное ускорение ИСЗ.

Вычислите орбитальную скорость спутника на высоте, равной двум земным радиусам над поверхностью Земли?

Вычислите орбитальную скорость спутника на высоте, равной двум земным радиусам над поверхностью Земли.

Спутник движется по круговой орбите на высоте 600км, период его обращения вокруг Земли 97, 5 мин?

Спутник движется по круговой орбите на высоте 600км, период его обращения вокруг Земли 97, 5 мин.

Определите скорость и ускорение спутника.

При равноускоренном движении тела по окружности остается постоянной 1) линейная скорость 2) угловая скорость 3) период обращения 4) частота обращения?

При равноускоренном движении тела по окружности остается постоянной 1) линейная скорость 2) угловая скорость 3) период обращения 4) частота обращения!

Скажите правильный ответ пожалуйста!

Период обращения искусственного спутника земли T = 96, 2мин определить угловую скорость , с которой он двигался?

Период обращения искусственного спутника земли T = 96, 2мин определить угловую скорость , с которой он двигался.

Рассчитайте скорость движения и период обращения искусственного спутника Земли с круговой орбитой , высота которой над поверхностью Земли = 300 км(радиус земли = 6 400 км)?

Рассчитайте скорость движения и период обращения искусственного спутника Земли с круговой орбитой , высота которой над поверхностью Земли = 300 км(радиус земли = 6 400 км).

Искусственный спутник обращается вокруг Земли по окружности на высоте 300 км?

Искусственный спутник обращается вокруг Земли по окружности на высоте 300 км.

Определить линейную скорость спутника и период его вращения.

С каким центростремительным ускорением и с какой скоростью движется искусственный спутник Земля, если высота его орбиты над поверхностью Земли 1200 км, а период обращения 105 мин?

С каким центростремительным ускорением и с какой скоростью движется искусственный спутник Земля, если высота его орбиты над поверхностью Земли 1200 км, а период обращения 105 мин?

Считайте, что спутник движется по круговой орбите с постоянной скоростью.

На этой странице вы найдете ответ на вопрос Вычислите угловую и линейную скорости орбитального движения спутника Земли, если период его обращения 121, 16 мин, а высота полета 1700 км?. Вопрос соответствует категории Физика и уровню подготовки учащихся 10 – 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Тк диск сделал четверть оборота, следовательно перемещение любой точки на краю диска равно четверти длины окружности S = 2 * Pi * R / 4 = 2 * 3. 14 * 1 / 4 = 1. 57 метра.

A = F / m = q * E / m = 0, 1 * 10 ^ – 6810 * 10 ^ 3 / 2 * 10 ^ – 3 = 5 м / с2.

1. Единицей пути является метр. Ответ : а 2. S = Ut S = 15× 7200 = 108000 м = 108 км. Ответ : в 3. M = Vp ; V = Sl m = Slp = 0. 000001× 10× 8900 = 0. 089 кг = 89 г Ответ : в.

1. Единицей пути является метр 2. 108 км 3. 89 г.

По модулю : a = | V – Vo | / t = | 10 – 15 | / 5 = 5 / 5 = 1 м / с².

Так как скорость вычисляется по формуле V = sqrt(3 * R * T / M), то при увеличении подкоренного выражения в 9 раз, значение скорости увеличится в 3 раза.

Вода не сохраняет свою фотрму и объем только в газообразном состоянии.

В газообразном состоянии .

S = a * b , где а и b – стороны стены S = 50 b = 0, 010км = 10 м a = 50 / 10 = 5м – сторона a (высота стены) Ответ : 5м или 0. 005 км.

Vo = 4 м / с v = 24 м / с t1 = 5 c t2 = 10 c a1 = ? A2 = ? = = = Ускорения этих тел различны a1 = (v – vo) / t1 = (24 – 4) / 5 = 4 м / с² a2 = (v * vo) / t2 = (24 – 4) / 10 = 2 м / с² = = = = = = = = = = = = = = = = = = = = = = = = =.

[spoiler title=”источники:”]

http://fizika.my-dict.ru/q/3028759_vycislite-uglovuu-i-linejnuu-skorosti-orbitalnogo/

[/spoiler]

---

---

Нашли ошибку? Сообщите в комментариях (внизу страницы)

Раздел: Физика Полное условие: 168. Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте h=1000 км. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными. Решение, ответ задачи 13420 из ГДЗ и решебников: Этот учебный материал представлен 1 способом: Для просмотра в натуральную величину нажмите на картинку Идея нашего сайта – развиваться в направлении помощи ученикам школ и студентам. Мы размещаем задачи и решения к ним. Новые задачи, которые недавно добавляются на наш сайт, временно могут не содержать решения, но очень скоро решение появится, т.к. администраторы следят за этим. И если сегодня вы попали на наш сайт и не нашли решения, то завтра уже к этой задаче может появится решение, а также и ко многим другим задачам. основной поток посетителей к нам – это из поисковых систем при наборе запроса, содержащего условие задачи

Счетчики: 4795 | Добавил: Admin

Добавить комментарий Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ]