Как найти линейную скорость точек земной поверхности

Найти линейную скорость v точек земной поверхности на географической широте

Найти линейную скорость v и центростремительное ускорение а точек на поверхности земного шара: на экваторе; на широте φ =60°. Радиус Земли R принять равным 6400 км.

Дано:

R = 6400 км = 6,4·10 4 м

Решение:

Линейная скорость связна с угловой

Угловая скорость вращения Земли

Период вращения Земли

Ответ:

Источник

Пример решения задачи.

1.За промежуток времени τ = 10 с точка прошла половину окружности радиуса R = 160 см. Вычислить за это время: а) среднюю скорость ; б) модуль среднего вектора скорости | |; в) модуль среднего вектора полного ускорения | |, если точка двигалась с постоянным тангенциальным ускорением.

Поместим начало координат в точке 1 (рис.1.4).Тогда за время τ точка переместилась из положения 1 в положение 2 и вектор перемещения будет r₂₁ , а пройденный путь, т.е. длина траектории, равен половине длины окружности. По определению средней скорости , где в нашем случае Δs = πR, Δt = τ. Тогда , а численное значение = 0,5 м/c.

Средний вектор скорости по определению , а его модуль . В нашем случае , и тогда . Численное значение | | = 0,32 м/c.

Средний вектор полного ускорения , где Δv = v₂—v₁ – приращение вектора скорости за время Δt, а его модуль . Из рисунка видно, что вектора v₂ и v₁ антиколлинеарны и | v₂—v₁| = v₂+v₁. Из условия задачи известно, что w_τ – постоянно, а, следовательно, скорость по модулю линейно зависит от времени, т.е. v(t ) = v₁+ w_τt. При такой зависимости средняя скорость может быть определена как , откуда 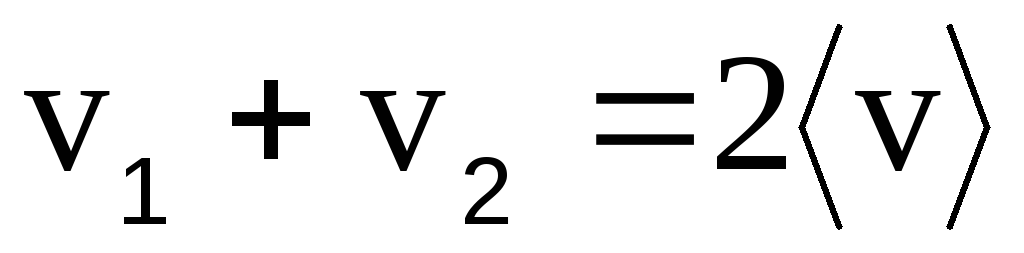. Подставляя это уравнение в формулу для определения модуля среднего вектора ускорения, получим: . Подставив численные значения, получим .

2.Диск радиусом R = 10 см вращается так, что зависимость угла поворота диска от времени задается уравнением  = А+Вt 3 (А = 2 рад, В = 4 рад/с 3 ). Определить угол , при котором полное ускорение составит с радиусом диска угол α = 45 0 .

Модуль полного ускорения , где нормальная составляющая a_n направлена вдоль радиуса диска, а тангенциальная составляющая a_ направлена по касательной к диску. Из рисунка 1.5 видно, что

.

Когда угол α = 45 0 , a_n = a_ и tgα = 1.

Найдем a_n и a_. a_n =  2 R, где  — угловая скорость: . Тогда

.

a_ = εR, где ε – угловое ускорение: . Следовательно,

.

Приравнивая a_n и a_, найдем момент времени, когда угол между полным ускорением и радиусом диска будет равен 45 0 :

.

Подставив полученное значение в формулу зависимости угла поворота диска от времени, получим

.

Подставив численные значения, получим  = 3,67 рад.

Список задач.

1.1. Точка прошла половину пути со скоростью v₀ . Оставшуюся часть пути она половину времени двигалась со скоростью v₁ , а последний участок — со скоростью v₂ . Найти среднюю за все время движения скорость точки.

Ответ: = 2v₀(v₁+ v₂)/(2v₀+ v₁+ v₂).

1.2. Две частицы, 1 и 2 , движутся с постоянными скоростями v₁ и v₂. Их радиус-векторы в начальный момент равны r₁ и r₂. При каком соотношении между этими четырьмя векторами частицы испытают столкновение друг с другом?

1.3. Два пловца должны попасть из точки А на одном берегу реки в прямо противоположную точку В на другом берегу. Для этого один из них решил переплыть реку по прямой АВ, другой же — все время держать курс перпендикулярно к течению, а расстояние, на которое его снесет, пройти пешком по берегу со скоростью u. При каком значении u оба пловца достигнут точки В за одинаковое время, если скорость течения v₀ = 2,0 км/ч и скорость каждого пловца относительно воды v₁ = 2,5 км/ч?

1.4. Лодка движется относительно воды со скоростью, в n = 2,0 раза меньшей скорости течения реки. Под каким углом к направлению течения лодка должна держать курс, чтобы ее снесло течением как можно меньше?

Ответ: θ = arcsin (1/n)+/2 = 120 O .

1.5. Точка движется вдоль оси х со скоростью, проекция которой v_x как функция времени описывается графиком (рис. 1.6). Имея в виду, что в момент t = 0 координата точки х = 0, начертить примерные графики зависимостей от времени ускорения а_x, координаты х и пройденного пути s.

Ответ: см.рис. 1, 7.

1.6. Точка движется в плоскости xy по закону 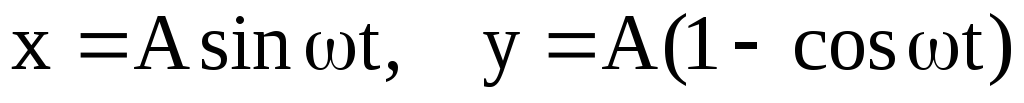, где А и  — положительные постоянные. Найти:

а) путь s, пройденный точкой за время ;

б) угол между скоростью и ускорением точки.

Ответ: a) s = A; б) /2.

1.7. В момент t = 0 частица вышла из начала координат в положительном направлении оси х, Ее скорость меняется со временем по закону v = v_o(1-t/), где v_o—вектор начальной скорости, модуль которого v₀ = 10,0 см/с,  = 5,0 с. Найти: а) координату х частицы в моменты времени 6,0, 10 и 20 с;

б) моменты времени, когда частица будет находиться на расстоянии

10,0 см от начала координат;

Ответ: а) x = v₀t (1-t/2); б) 1,1, 9 и 11 с.

1.8. Радиус точки A относительно начала координат меняется со временем t по закону r = сti-bt 2 j, где с и b — положительные постоянные, i и j— орты осей x и y. Найти: а) уравнение траектории точки y(x) ; изобразить ее график; б) зависимости от времени векторов скорости v, ускорения а и модулей этих величин; в) зависимость от времени угла  между векторами v и а; г) средний вектор скорости за первые t секунд движения и модуль этого вектора.

Ответ: a) y = -x 2 b/с 2 ; б) v = сi-2btj, а = -2bj, v = , а = 2b;

в) tg  = с/2bt; г) v = сi-btj, v = .

1.9. Пушка и цель находятся на одном уровне на расстоянии 5,10 км друг от друга. Через сколько времени снаряд с начальной скоростью 240 м/с достигнет цели в отсутствие сопротивления воздуха?

Ответ: Через 0,41 или 0,71 мин в зависимости от начального угла.

1.10. Шарик начал падать с нулевой начальной скоростью на гладкую наклонную плоскость, составляющую угол 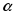с горизонтом. Пролетев расстояние h, он упруго отразился от плоскости. На каком расстоянии от места падения шарик отразится второй раз?

Ответ: L = 8h sin.

1.11. Точка движется по окружности со скоростью v = bt, где b = 0,50 м/с 2 . Найти ее полное ускорение в момент, когда она пройдет n = 0,10 длины окружности после начала движения.

Ответ: a = b= 0,8 м/с 2 .

1.12. Колесо вращается вокруг неподвижной оси так, что угол  его поворота зависит от времени как  = bt 2 , где b = 0,20 рад/с 2 . Найти полное ускорение a точки A на ободе колеса в момент t = 2,5 с, если линейная скорость точки A в этот момент v = 0,65 м/с.

Ответ: a = (v/t)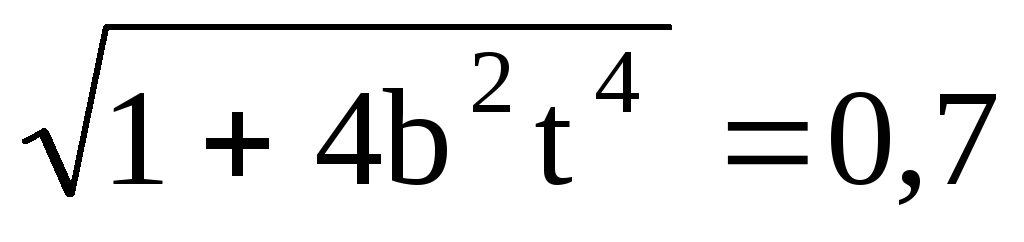м/с 2 .

1.13. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением ε = bt, где b = 2,010 -2 рад/c 3 . Через сколько времени после начала вращения вектор полного ускорения произвольной точки тела будет составлять угол α = 60 O с ее вектором скорости?

Ответ: t =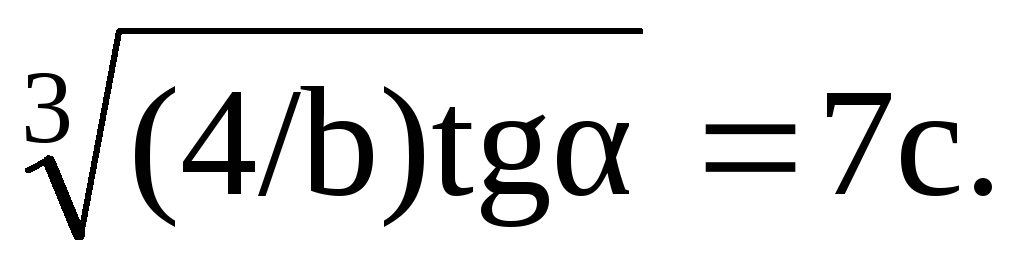

1.14. Твердое тело вращается вокруг неподвижной оси по закону , где а = 6,0 рад/c, b = 2,0 рад/с. Найти:

а) средние значения угловой скорости и углового ускорения за промежуток времени от t = 0 до остановки;

б) угловое ускорение в момент остановки тела.

Ответ: а)  = 2а/3 = 4 рад/с, ε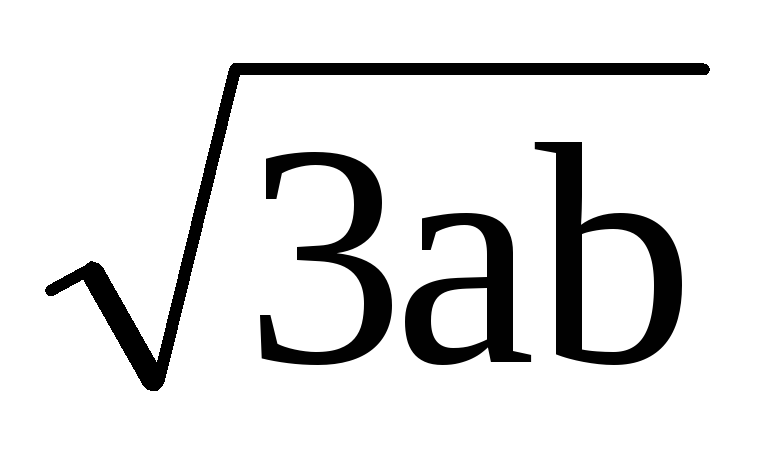 = = 6 рад/c 2 ; б) = 12 рад/c.

1.15. Снаряд вылетел со скоростью v = 320 м/с, сделав внутри ствола n = 2,0 оборота. Длина ствола L = 2,0 м. Считая движение снаряда в стволе равноускоренным, найти его угловую скорость вращения вокруг оси в момент вылета.

Ответ:  = 2nv/l = 2,010 3 рад/с.

1.16. Найти угловое ускорение ε колеса, если известно, что через время t = 2 c после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол α = 60 0 с вектором ее линейной скорости.

Ответ: рад/c.

1.17. Найти линейную скорость v точек земной поверхности на географической широте φ, вызванную суточным вращением Земли вокруг своей оси.

Ответ: v = 1670cos φ км/c.

1.18. Якорь электромотора, вращавшегося с частотой N оборотов в секунду, двигаясь после выключения тока равнозамедленно, остановился, сделав n оборотов. Найти угловое ускорение якоря после выключения тока.

Ответ: ε = πN 2 /n.

1.19. Автомобиль движется со скоростью 60 км/ч. Сколько оборотов в секунду делают его колеса, если они катятся по шоссе без скольжения, а внешний диаметр покрышек колес равен 60 см.

1.20. Разматывая веревку и вращая без скольжения вол ворота, ведро опускается в колодец с ускорением 1 м/c 2 . С каким угловым ускорением вращается вал ворота? Как зависит от времени угол поворота вала? Радиус вала ворота равен 25 см.

Ответ: ε = 4 рад/c 2 ; φ = 2t 2 рад.

2. Д И Н А М И К А М А Т Е Р И А Л Ь Н О Й Т О Ч К И

Источник

Условие задачи:

Радиус Земли равен 6400 км. Какую скорость имеют точки земной поверхности на широте 60° из-за суточного вращения Земли?

Задача №2.5.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(R=6400) км, (alpha=60^circ), (upsilon-?)

Решение задачи:

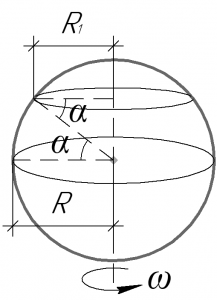Изобразим на схеме все точки Земли, находящиеся на широте 60°. Все эти точки составляют окружность, радиус которой равен (R_1). Из рисунка видно, что:

[{R_1} = R cdot cos alpha ;;;;(1)]

Понятно, что период обращения всех точек равен периоду вращения Земли (T) вокруг своей оси, т.е. 24 часам. Запишем формулу определения периода для всех точек на широте 60°:

[T = frac{{2pi {R_1}}}{upsilon }]

Здесь (upsilon) – искомая линейная скорость.

Учитывая (1), имеем:

[T = frac{{2pi R cdot cos alpha }}{upsilon }]

В итоге решение задачи в общем виде выглядит так:

[upsilon  = frac{{2pi R cdot cos alpha }}{T}]

Переведем период вращения и радиус Земли в систему СИ:

[24; ч = 24 cdot 60 cdot 60 ; с = 86400; с]

[6400; км = 6,4 cdot {10^6}; м]

Посчитаем ответ:

[upsilon  = frac{{2 cdot 3,14 cdot 6,4 cdot {{10}^6} cdot cos 60^circ }}{{86400}} = 232,6; м/с = 837,3; км/ч]

Ответ: 837,3 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.5.19 Определить минимальный период обращения спутника нейтронной звезды. Её плотность
2.5.21 На каком расстоянии от центра Земли (в долях радиуса Земли R) ускорение свободного
2.5.22 Радиус Земли равен 6400 км. На каком расстоянии от поверхности Земли сила притяжения

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Чему равна линейная скорость точки поверхности земли

Человечество всегда интересовало движение Земли и ее взаимодействие со вселенной. Одним из параметров, который определяет движение Земли, является линейная скорость точки поверхности Земли.

Линейная скорость

Линейная скорость — это физическая величина, которая выражает скорость точки на плоскости в километрах в час. В нашем случае, это скорость точки на поверхности Земли.

Линейная скорость зависит от радиуса кривизны пути и угловой скорости вращения. В случае Земли, это означает, что линейная скорость зависит от расстояния от центра Земли и скорости вращения Земли.

Радиус Земли

Для ответа на вопрос о линейной скорости точки на поверхности Земли, мы сначала должны узнать радиус Земли. Это физическая константа и составляет примерно 6371 километр.

Скорость вращения Земли

Земля вращается на своей оси каждые 23 часа, 56 минут и 4.1 секунд. Скорость вращения Земли в области экватора составляет примерно 1670 километров в час (или 465 метров в секунду), медленно уменьшаясь по мере того, как мы приближаемся к полюсам.

Линейная скорость точки на поверхности Земли

Чем дальше от экватора, тем ниже линейная скорость точки на поверхности Земли. Это происходит из-за уменьшения радиуса кривизны пути, когда мы движемся к полюсам.

Для того, чтобы вычислить линейную скорость точки на поверхности Земли в конкретном месте, необходимо умножить скорость вращения Земли в этой точке на радиус Земли в этом месте.

Линейная скорость точки на поверхности Земли может быть вычислена как V = rω, где V — линейная скорость, r — радиус Земли в данной точке и ω — угловая скорость вращения Земли в этой точке.

Например, линейная скорость точки на экваторе составляет примерно 1670 километров в час, а линейная скорость точки на полюсах — 0.

Заключение

Линейная скорость точки на поверхности Земли является важным параметром, определяющим движение Земли и ее взаимодействие со вселенной. Она зависит от радиуса кривизны пути и скорости вращения Земли. Чем дальше от экватора, тем меньше линейная скорость точки на поверхности Земли.

• линейная скорость зависит от радиуса кривизны пути и скорости вращения Земли
• для вычисления линейной скорости нужно умножить скорость вращения Земли на радиус Земли в данной точке
• линейная скорость на экваторе — примерно 1670 километров в час, на полюсах — 0

Чему равна линейная скорость точки поверхности земли

Линейная скорость точки поверхности Земли – это один из наиболее фундаментальных параметров движения планеты, описывающих ее движение в пространстве. Зная скорость, можно рассчитать много разных параметров и сделать выводы о взаимодействии Земли с другими небесными телами. Давайте попробуем разобраться, что такое линейная скорость точки поверхности Земли и как ее можно рассчитать.

Что такое линейная скорость?

Линейная скорость точки поверхности Земли – это скорость движения точки на ее поверхности относительно центра Земли. Иными словами, это скорость, с которой движется точка на поверхности Земли в любой момент времени. Единица измерения линейной скорости – метры в секунду.

Чтобы понять, что такое линейная скорость, рассмотрим простой пример. Представьте себе, что вы сидите на вращающемся стуле и вращаете его вокруг своей оси. Если вы тянетесь к центру стула, то это приводит к увеличению скорости вращения стула и, следовательно, к увеличению вашей линейной скорости. Если же вы отдаляетесь от центра стула, то скорость вращения уменьшается, и линейная скорость также уменьшается.

Как рассчитать линейную скорость точки поверхности Земли?

Рассчитать линейную скорость точки поверхности Земли можно с помощью формулы:

v = 2πR/T

Где:

• v – линейная скорость;
• R – радиус Земли (приблизительно 6 371 км);
• T – период вращения Земли вокруг своей оси (приблизительно 24 часа, то есть 86 400 секунд).

Таким образом, рассчитать линейную скорость точки поверхности Земли можно подставив все значения в формулу:

v = 2π x 6 371 км / 86400 с = приблизительно 465 м/с

То есть, линейная скорость точки поверхности Земли составляет приблизительно 465 м/с, это очень быстро, но для нашей жизни это медленно и ее очень трудно почувствовать.

Заключение

Таким образом, линейная скорость точки поверхности Земли равна приблизительно 465 м/с. Это скорость, с которой движется точка на поверхности Земли, относительно ее центра. Зная этот параметр, можно рассчитать много других параметров движения планеты, сделать выводы о взаимодействии Земли с другими небесными телами и прочие расчеты. Линейная скорость очень важна в науке и астрономии, и ее понимание является ключом к пониманию многих астрономических явлений и процессов.

Чему равна линейная скорость точки поверхности земли?

В наше время наука и технологии достигли такого более высокого уровня, что люди быстро стали перемещаться между континентами и странами за считанные часы. С данного момента, путешествия стали более доступными, облегченными и удобными. Но вопросы, связанные с подобными перемещениями, всегда оставались открытыми, и один из них это линейная скорость движения точки поверхности земли.

Что такое линейная скорость?

Для начала разберемся, что такое линейная скорость. Линейная скорость — это скорость точки, движущейся вдоль прямой линии, и измеряется в м/с (метры в секунду).

Линейная скорость точки на поверхности Земли зависит от ее широты (угла от экватора, измеряемого в градусах) и угловой скорости Земли вокруг своей оси. Угловая скорость Земли зависит от ее периода вращения вокруг своей оси, который равен 23 часам, 56 минутам и 4,091 секундам. Это период, который называется сидерическим днем.

Что такое широта?

Широта — это угол между экватором и данной точкой на карте. Этот угол измеряется в градусах, минутах и секундах. В радианах широта равна градусам, умноженным на 0,01745329252.

Графически это можно представить так: экватор — это линия, которая пересекает земной шар на его самом широком месте. Линии широт проходят параллельно экватору, однако расстояние между ними постоянно меняется (уменьшается) с приближением к северному или южному полюсу.

Как определить линейную скорость движения точки поверхности Земли?

Скорость движения точки поверхности Земли можно вычислить, зная ее широту и угловую скорость вращения Земли.

1. Сначала необходимо вычислить радиус Земли. Радиус Земли равен примерно 6 378 км.
2. Затем необходимо вычислить угловую скорость вращения Земли. Угловая скорость Земли — это 360 градусов, деленных на время вращения Земли вокруг своей оси, приблизительно равное 23 часам, 56 минутам и 4,091 секундам.
3. Далее можно вычислить линейную скорость точки на поверхности Земли, используя формулу v = r * ω * cos(широта), где v — линейная скорость, r — радиус Земли, ω — угловая скорость вращения Земли, а cos(широта) — косинус угла между экватором и точкой, измеренный в радианах.

Итог

Таким образом, линейная скорость точки на поверхности Земли зависит от ее широты и угловой скорости Земли. Угловая скорость Земли зависит от ее периода вращения, который составляет примерно 23 часа, 56 минут и 4,091 секунды. Вычислить линейную скорость точки на поверхности Земли можно, зная ее широту и используя формулу v = r * ω * cos(широта). Учтите, что на экваторе линейная скорость составляет примерно 1670 км/ч, а на полюсах — ноль.