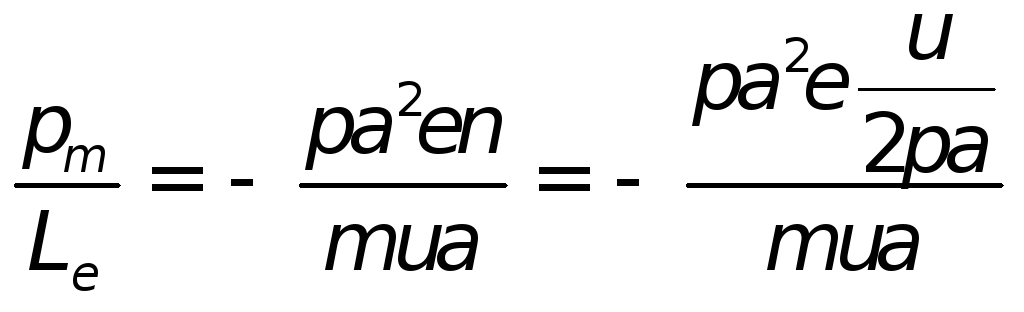Как найти линейную скорость вращения электрона

По теории Бора электрон в атоме водорода вращается вокруг ядра

Условие задачи:

По теории Бора электрон в атоме водорода вращается вокруг ядра по круговой орбите радиусом 0,53·10 -10 м. Определить скорость движения электрона по орбите.

Задача №6.1.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

Атом водорода содержит один электрон, вращающийся вокруг ядра. Ядро водорода состоит из одного протона (то есть нейтронов вообще нет). Заряд протона равен по абсолютному значению заряду электрона (то есть элементарному заряду (e)). Тогда по закону Кулона силу взаимодействия между ядро атома водорода и электроном можно найти по формуле:

В этой формуле (k) – коэффициент пропорциональности, равный 9·10 9 Н·м 2 /Кл 2 , (e) – элементарный заряд, равный 1,6·10 -19 Кл.

Эта сила сообщает электрону центростремительное ускорение (a_ц), запишем второй закон Ньютона:

Здесь (m) – масса электрона, она равна 9,1·10 -31 кг.

Центростремительное ускорение (a_ц) можно выразить через линейную скорость электрона на орбите (upsilon) и радиус этой орбиты (r):

Подставим выражения (1) и (3) в равенство (2), тогда:

Откуда искомая скорость электрона (upsilon) равна:

Произведём расчёт численного ответа:

Ответ: 2186 км/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Найти угловую скорость вращения электрона вокруг ядра

UptoLike

В первом приближении можно считать, что электрон в атоме водорода движется по круговой орбите с линейной скоростью v. Найти угловую скорость ω вращения электрона вокруг ядра и его нормальное ускорение а_n. Считать радиус орбиты r = 0,5·10 -10 м и линейную скорость электрона на этой орбите v = 2,2·10 6 м/с.

ОПРЕДЕЛЕНИЯ

• векторная величина, характеризующая быстроту вращения твердого тела

• движение вокруг своей оси по окружности

• стабильная отрицательно заряженная элементарная частица с зарядом 1,6·10 -19 Кл и массой 9·10 -31 кг

• положительно заряженная массивная центральная часть атома, состоящая из протонов и нейтронов

самая малая частица химического элемента, она является носителем его свойств. Состоит атом из электронов и положительно заряженного ядра. У атома размеры порядка 10 -10 м, а порядок энергии связи внешних электронов равен 10 эВ.

Шпаргалка по общей электронике и электротехнике.

5. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ.

В некоторых электровакуумных приборах используется движение электронов в магнитном поле.

Рассмотрим случай, когда электрон влетает в однородное магнитное поле с начальной скоростью v0, направленной перпендикулярно магнитным силовым линиям. В этом случае на движущийся электрон действует так называемая сила Лоренца F, которая перпендикулярна вектору нО и вектору напряженности магнитного поля Н. Величина силы F определяется выражением: F= еv0Н.

При v0 = 0 сила Рравна нулю, т. е. на неподвижный электрон магнитное поле не действует.

Сила F искривляет траекторию электрона в дугу окружности. Поскольку сила F действует под прямым углом к скорости нО, она не совершает работы. Энергия электрона и его скорость не изменяются по величине. Происходит лишь изменение направления скорости. Известно, что движение тела по окружности (вращение) с постоянной скоростью получается благодаря действию направленной к центру центростремительной силы, которой именно и является сила F.

Направление поворота электрона в магнитном поле в соответствии с правилом левой руки удобно определяется по следующим правилам. Если смотреть в направлении магнитных силовых линий, то электрон движется по часовой стреле. Иначе говоря, поворот электрона совпадает с вращательным движением винта, который ввинчивается по направлению магнитных силовых линий.

Определим радиус r окружности, описываемой электроном. Для этого воспользуемся выражением для центростремительной силы, известным из механики: F = mv20/r. Приравняем его значению силы F = еv0Н: mv20/r = еv0Н. Теперь из этого уравнения можно найти радиус: r= mv0/(еН).

Чем больше скорость электрона v0, тем сильнее он стремится двигаться прямолинейно по инерции и радиус искривления траектории будет больше. С другой стороны, с увеличением Н растет сила F, искривление траектории возрастает и радиус окружности уменьшается.

Выведенная формула справедлива для движения в магнитном поле частиц с любыми массами и зарядом.

Рассмотрим зависимость rот mи е. Заряженная частица с большей массой mсильнее стремится лететь по инерции прямолинейно и искривление траектории уменьшится, т. е. rстанет больше. А чем больше заряд е, тем больше сила F и тем сильнее искривляется траектория, т. е. ее радиус становится меньше.

Выйдя за пределы магнитного поля, электрон дальше летит по инерции по прямой линии. Если же радиус траектории мал, то электрон может описывать в магнитном поле замкнутые окружности.

Таким образом, магнитное поле изменяет только направление скорости электронов, но не ее величину, т. е. между электроном и магнитным полем нет энергетического взаимодействия. По сравнению с электрическим полем действие магнитного поля на электроны является более ограниченным. Именно поэтому магнитное поле применяется для воздействия на электроны значительно реже, нежели электрическое поле.

[spoiler title=”источники:”]

http://zzapomni.com/katalog/1-54-nayti-uglovuyu-skorost-vrashcheniya-elektrona-vokrug-yadra

http://ur-consul.ru/Bibli/SHpargalka-po-obshchyeyi-elyektronikye-i-elyektrotyekhnikye.5.html

[/spoiler]

Условие задачи:

По теории Бора электрон в атоме водорода вращается вокруг ядра по круговой орбите радиусом 0,53·10^-10 м. Определить скорость движения электрона по орбите.

Задача №6.1.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(r=0,53 cdot 10^{-10}) м, (upsilon-?)

Решение задачи:

Атом водорода содержит один электрон, вращающийся вокруг ядра. Ядро водорода состоит из одного протона (то есть нейтронов вообще нет). Заряд протона равен по абсолютному значению заряду электрона (то есть элементарному заряду (e)). Тогда по закону Кулона силу взаимодействия между ядро атома водорода и электроном можно найти по формуле:

[{F_{эл}} = frac{{k{e^2}}}{{{r^2}}};;;;(1)]

В этой формуле (k) – коэффициент пропорциональности, равный 9·10⁹ Н·м²/Кл², (e) – элементарный заряд, равный 1,6·10^-19 Кл.

Эта сила сообщает электрону центростремительное ускорение (a_ц), запишем второй закон Ньютона:

[{F_{эл}} = m{a_ц};;;;(2)]

Здесь (m) – масса электрона, она равна 9,1·10^-31 кг.

Центростремительное ускорение (a_ц) можно выразить через линейную скорость электрона на орбите (upsilon) и радиус этой орбиты (r):

[{a_ц} = frac{{{upsilon ^2}}}{r};;;;(3)]

Подставим выражения (1) и (3) в равенство (2), тогда:

[frac{{k{e^2}}}{{{r^2}}} = frac{{m{upsilon ^2}}}{r}]

[frac{{k{e^2}}}{r} = m{upsilon ^2}]

Откуда искомая скорость электрона (upsilon) равна:

[upsilon = esqrt {frac{k}{{mr}}} ]

Произведём расчёт численного ответа:

[upsilon = 1,6 cdot {10^{ – 19}} cdot sqrt {frac{{9 cdot {{10}^9}}}{{9,1 cdot {{10}^{ – 31}} cdot 0,53 cdot {{10}^{ – 10}}}}} = 2185660;м/с approx 2186;км/с]

Ответ: 2186 км/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.1.6 Два заряженных шара одинакового радиуса, массой 0,3 кг каждый, расположены
6.1.8 В атоме водорода электрон движется вокруг протона с угловой скоростью
6.1.9 Два одинаковых шара, массы которых 600 г и радиусы – 20 см, имеют

(Буланчук О.Н., каф.
физики ПГТУ )

Опыты Штерна и Герлаха. Спин электрона.

При
движении электрона (как заряженной
частицы) вокруг ядра он создает некоторый
электрический ток. Этот ток (а также
аналогичные токи в молекулах) получил
название молекулярного тока. Однако
если существует электрический ток, то
в соответствии с законом Био-Саварра-Лапласа
он должен создавать в окружающем
пространстве магнитное поле, величина
которого определяется магнитным моментом
тока.
Покажем, что магнитный момент электрона
в атоме связан с его механическим
моментом (орбитальным моментом импульса).

Будем
полагать, что электрон движется по
окружности. Тогда сила тока в атоме:
магнитный
момент по определению равен.
Частота вращения электронамомент импульса для круговой орбиты.
Отношение магнитного момента к
механическому будет равно:

—гиромагнитное
соотношение

Таким
образом, орбитальный магнитый и
механический момент оказываются связаны
соотношением:

С
учетом того, что проекция механического
момента на выделенное направление
из получим:

,

где
—магнетон
Бора. Т.е., проекция магнитного момента
оказывается кратной магнетону Бора.

Если
механический момент равен нулю, то и
магнитный момент также равен нулю ().
В 1921 Штерн и Герлах поставили опыты, в
которых измерялся магнитный (а значит
механический) момент атома (точнее
электронов в атоме). Опыты Штерна и
Герлаха относятся к числу основополагающих
экспериментов атомной физики. Идея
опыта: по величине расщепления пучка,
проходящего между полюсами постоянного
магнита, определялась сила,
действующая на атом в неоднородном
магнитном поле. Затем по величине силы
рассчитывался магнитный момент атома.
С помощью такой методики удалось
экспериментально подтвердить существование
магнитных моментов у атомов и их
пространственное квантование.

В
одномерном случае

.

Для
наблюдения эффекта необходимо, чтобы
неоднородность поля
была
достаточно велика на расстояниях порядка
размеров атома. Для этого северный полюс
магнита был изготовлен в виде призмы с
острым ребром вдоль направления пучка,
а в южном была проточена канавка в том
же направлении. Если пропускать между
магнитными полюсами атомы водорода
(или другие атомы с одним валентным
электроном всостоянии)
в основном состоянии для которых,
то в этом случае из следует чтои на экране должна была наблюдаться
одна полоса. На самом деле оказалось
две.

При этом расчеты
показали, что магнитный момент оказался
в два раза больше, чем определяемый по
формуле . С точки зрения классической
физики такой результат был невозможен.
Объяснение опыта было предложено в
1925г. Гаудсмитом и Уленбеком, которые
предположили наличие у электрона
собственного магнитного и механического
момента – спина. Спин можно представить
как свойство электрона (заряженного
шарика) вращающегося вокруг своей оси
подобно волчку. Однако такая простая
модель в данном случае оказывается
неправильной. Зная магнитный, а значит
и механический момент электрона можно,
используя формулу
(где–момент
инерции электрона-шарика), рассчитать
угловую и линейную скорость вращения
электрона вокруг оси. При этом оказывается,
что скорость вращения поверхности
электрона в 300 раз больше скорости
света, что противоречит специальной
теории относительности. Это означает,
что спин – внутреннее свойство электрона
(и других элементарных частиц), например,
такое же как заряд и масса, которому
нельзя сопоставить классического
аналога.

Результаты
измерений показали, что спин электрона
равен

,

где
—
спиновое магнитное квантовое число:.

.

–cпиновое
квантовое число,

Таким
образом, волновая функция электрона в
атоме водрода должна зависеть от 4-х
квантовых чисел:
.
В простейшем случае ее можно представить
в виде,
где—спиновая
волновая функция. Кратность вырождения
в этом случае увеличивается в два раза.

Для
фотона
.
С понятием спина связано понятие
спиральности частиц—знака проекции
спина на направление импульса.

Замечание:
спин электрона является релятивистским
свойством. Дирак показал, что существование
спина является следствием учета
релятивистских эффектов в уравнении
Шредингера (релятивистское волновое
уравнения Дирака).

Учёные
из Национального института стандартов
США (NIST) создали микроскопический
осциллятор, который может использоваться
в мобильных телефонах, устройствах
беспроводной связи и радарах. Отличие
нового прибора в том, что его габариты
в сотни раз меньше существующих устройств
и сравнимы с толщиной человеческого
волоса.

Новый
осциллятор может генерировать
электрические колебания с частотой от
5 до 40 гигагерц. Принцип его действия
основан на периодическом изменении
спина электронов в магнитных плёнках,
разделённых слоем диамагнетика. Процесс
происходит автоматически, частота
колебаний зависит от величины протекающего
по плёнкам тока.

Активная
область экспериментального прибора,
построенного учёными из NIST, имеет площадь
в несколько квадратных микрон. Осциллятор
очень недорог и прост в изготовлении,
так что в ближайшем будущем можно ожидать
революции в области беспроводных
коммуникаций.

Соседние файлы в папке лекции БОН

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #