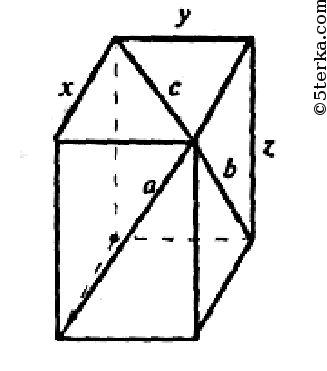
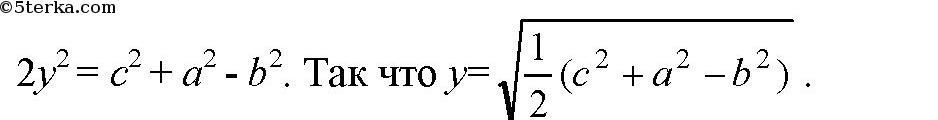Пусть х, у, z линейные размеры прямоугольного параллелепипеда. Тогда по теореме Пифагора:
Сложим первые два уравнения и вычтем третье:
Аналогично:
и
Санечка69
9 лет назад
Светило науки – 5643 ответа – 53043 помощи
линейные размеры – это длина(а), ширина(b) и высота(с).
У прямоугольного параллелепипеда всех этих ребер (длины, ширины и высоты) по 4. Значит, а+b+с=180:4=45. Но по условию а:b:с=4:5:6, т. е. а=4х, b=5х, с=6х.
Составим и решим уравнение 4х+5х+6х=45
15х=45
х=45:15
х=35
Значит а=4*3=12 (см), b=5*3=15 (см), с=3*6=18 (см)
(2 оценки)
Содержание
- Объем параллелепипеда
- Понятие объема
- Объем прямоугольного параллелепипеда
- Что такое линейные размеры прямоугольного параллелепипеда?
- Диагонали трех граней прямоугольного параллелепипеда сходящиеся в одной вершине равны 5, 6, 7?
- В прямоугольном параллелепипеде линейные размеры 10 см, 22 см, 16 см?
- Размеры кирпича 40см, 20см, 10см?
- Размеры кирпича 40 см, 20см, 10см?
- Что такое прямоугольный параллелепипед?
- Размеры одного кирпича 40см, 20см, 10см?
- Что такое РЕБРО прямоугольного параллелепипеда ?
- Что такое объём прямоугольного параллелепипеда ?
- Помогите сроочно))))Найти площадь полной поверхности прямоугольного параллелепипеда, если его диагональ больше линейных размеров на 10 см, 9 см и 1 см соответственно?
- Размеры кирпича 40см, 20см, 10см?
- Прямоугольный параллелепипед. Что это такое?
- Определение параллелепипеда
- Свойства параллелепипеда
- Прямой параллелепипед
- Прямоугольный параллелепипед
- Свойства прямоугольного параллелепипеда
- Диагонали прямоугольного параллелепипеда: теорема
- Куб: определение, свойства и формулы
- Решение задач
- Самопроверка
Объем параллелепипеда
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см 3 ), кубический миллиметр (1 мм 3 ), кубический метр (1 м 3 ).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
Два свойства объёма
- У равных тел равные объёмы. Если два тела одинаковы и имеют равные единицы измерения — их объёмы равны. Например, у двух одинаковых пакетов сока равные объемы.
- Если геометрическое тело состоит из нескольких геометрических тел, то его объём равен сумме объёмов этих тел.
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Объем прямоугольного параллелепипеда
Прямоугольный параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.
Прямоугольным параллелепипедом называют параллелепипед, у которого основание — прямоугольник, а боковые ребра образуют с основаниями прямые углы.
Формула объема прямоугольного параллелепипеда
Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты:
V = a × b × h
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
Источник
Что такое линейные размеры прямоугольного параллелепипеда?
Математика | 10 — 11 классы
Что такое линейные размеры прямоугольного параллелепипеда.
Длина, ширина, высота — линейные измерения.
Диагонали трех граней прямоугольного параллелепипеда сходящиеся в одной вершине равны 5, 6, 7?
Диагонали трех граней прямоугольного параллелепипеда сходящиеся в одной вершине равны 5, 6, 7.
Найдите линейные размеры параллелепипеда.
В прямоугольном параллелепипеде линейные размеры 10 см, 22 см, 16 см?
В прямоугольном параллелепипеде линейные размеры 10 см, 22 см, 16 см.
Найти полную поверхность.
Размеры кирпича 40см, 20см, 10см?
Размеры кирпича 40см, 20см, 10см.
Из таких кирпечей сложен параллелепипед Чему равны размеры и объём такого параллелепипеда.
Всего 4 кирпича.
Размеры кирпича 40 см, 20см, 10см?
Размеры кирпича 40 см, 20см, 10см.
Из таких кирпичей сложен параллелепипед.
Чему равны размеры и объем такого параллелепипеда?
Что такое прямоугольный параллелепипед?
Что такое прямоугольный параллелепипед?
Размеры одного кирпича 40см, 20см, 10см?
Размеры одного кирпича 40см, 20см, 10см.
Из таких кирпичей сложен параллелепипед.
Чему равны размер и объём такого параллелепипеда?
Что такое РЕБРО прямоугольного параллелепипеда ?
Что такое РЕБРО прямоугольного параллелепипеда ?
Что такое объём прямоугольного параллелепипеда ?
Что такое объём прямоугольного параллелепипеда ?
Помогите сроочно))))Найти площадь полной поверхности прямоугольного параллелепипеда, если его диагональ больше линейных размеров на 10 см, 9 см и 1 см соответственно?
Помогите сроочно))))Найти площадь полной поверхности прямоугольного параллелепипеда, если его диагональ больше линейных размеров на 10 см, 9 см и 1 см соответственно.
Размеры кирпича 40см, 20см, 10см?
Размеры кирпича 40см, 20см, 10см.
Из таких кирпичей сложен параллелепипед.
Чему равны размер и объём такого параллелепипеда?
На этой странице сайта, в категории Математика размещен ответ на вопрос Что такое линейные размеры прямоугольного параллелепипеда?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.
Источник
Прямоугольный параллелепипед. Что это такое?
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение параллелепипеда
Начнем с того, что узнаем, что такое параллелепипед.
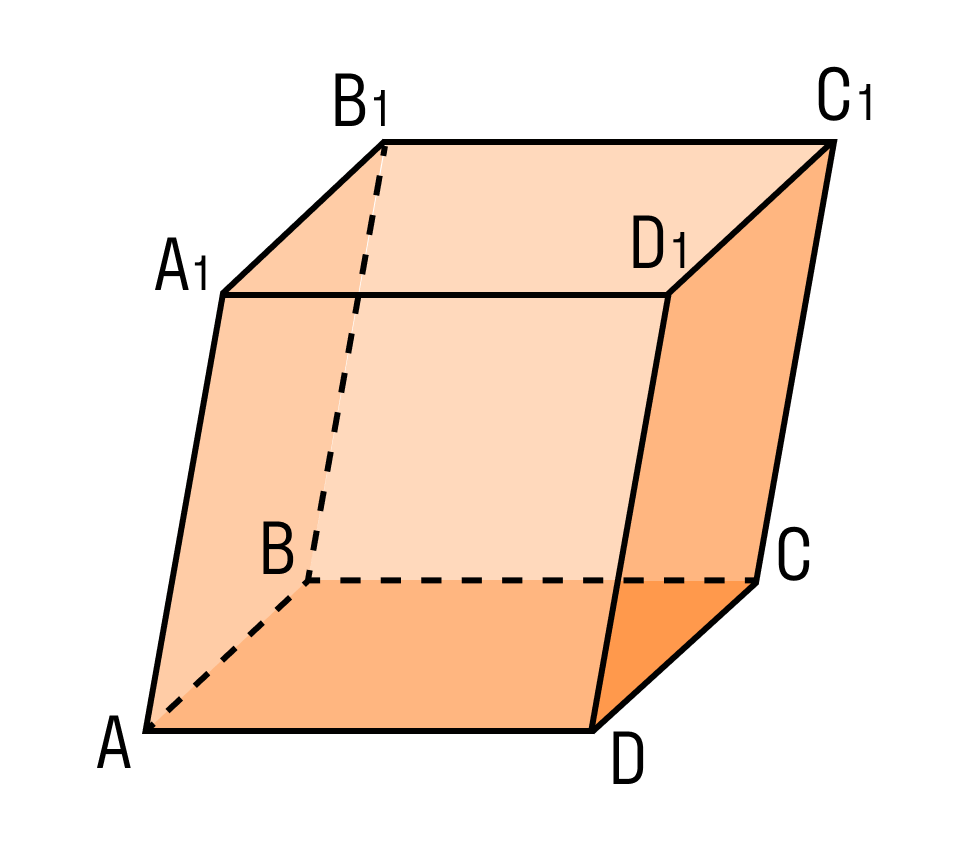
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.
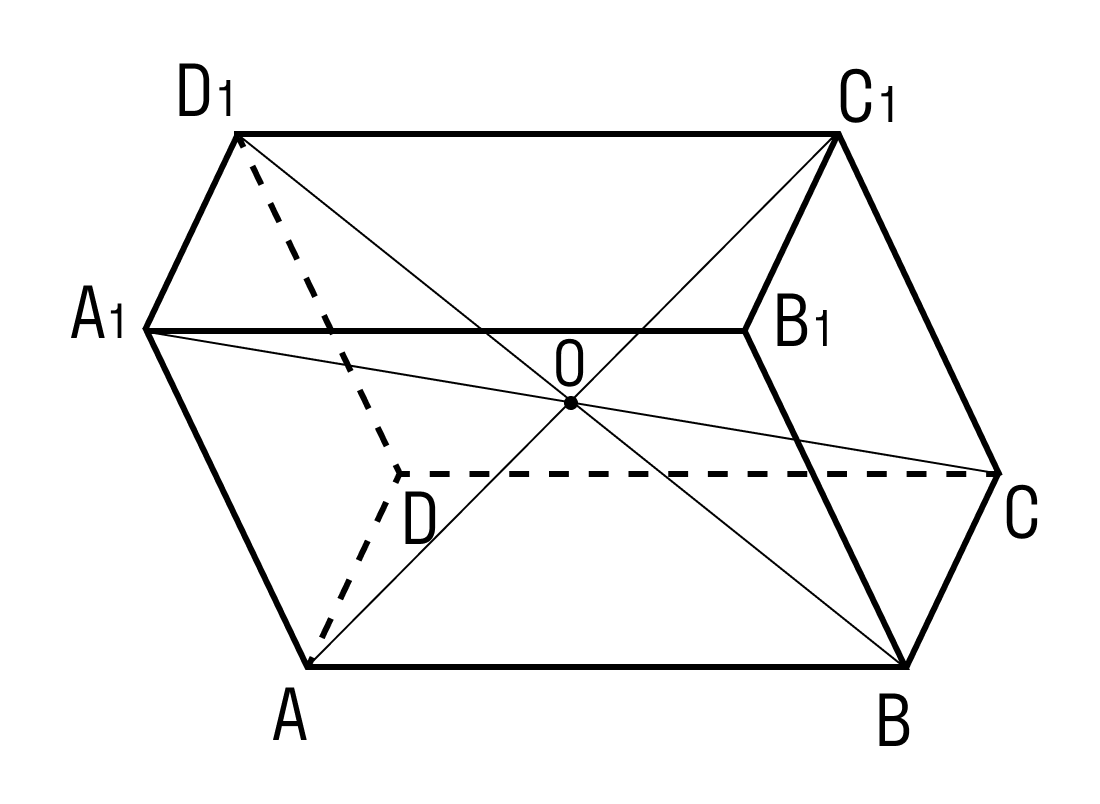
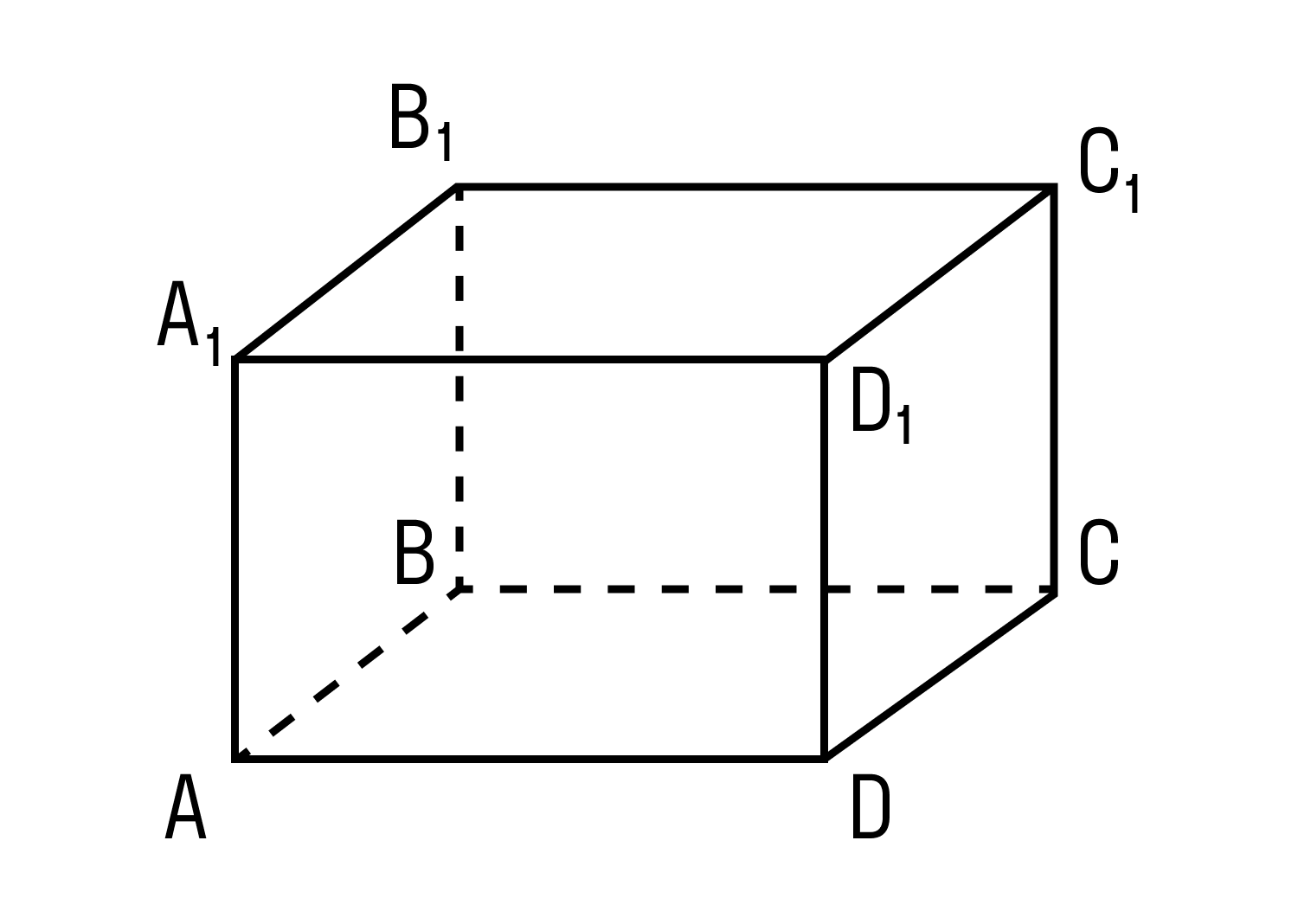
На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
- Противолежащие грани параллелепипеда равны и параллельны друг другу.
- Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- Параллелепипед симметричен относительно середины его диагонали.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
Свойства прямого параллелепипеда:
- Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
- Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
- Высота прямого параллелепипеда равна длине бокового ребра.
- Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
- Диагонали прямого параллелепипеда точкой пересечения делятся пополам.
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
- Площадь боковой поверхности прямого параллелепипеда
Sб = Ро*h
Ро — периметр основания
h — высота - Площадь полной поверхности прямого параллелепипеда
Sп = Sб+2Sо
Sо — площадь основания - Объем прямого параллелепипеда
V = Sо*h
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
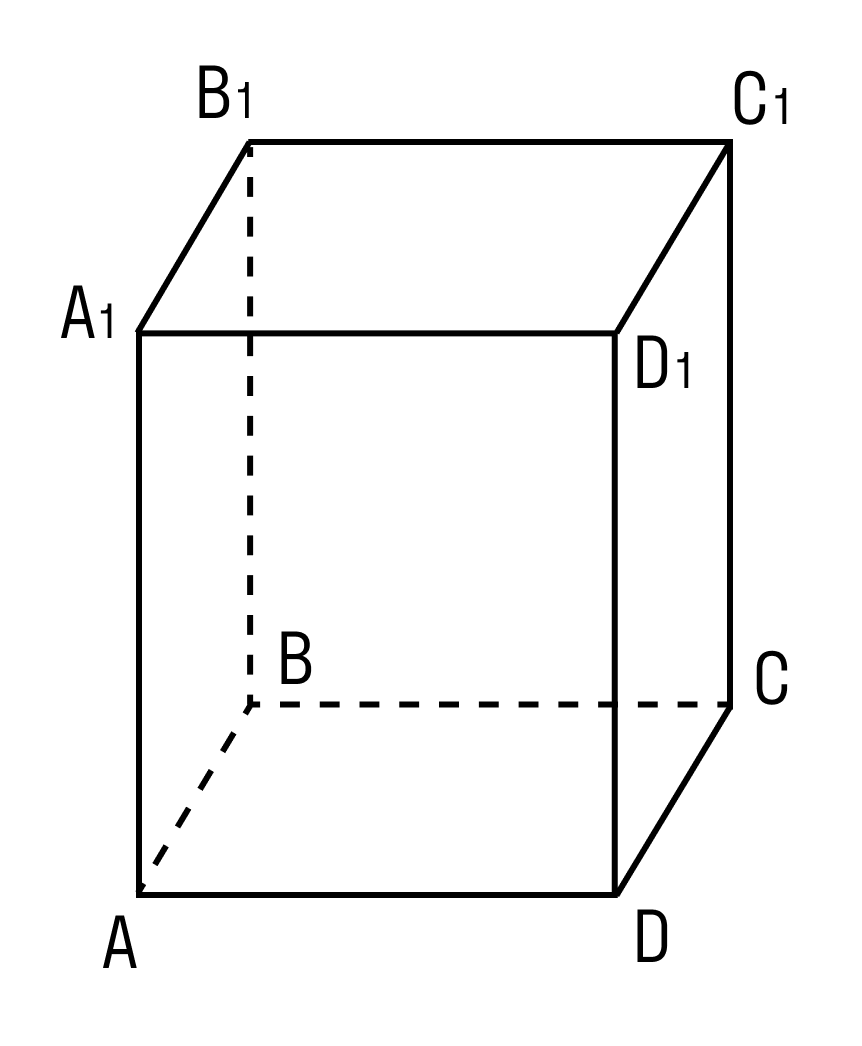
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
- Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
- Противолежащие грани параллелепипеда попарно параллельны и равны.
- Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
- Диагонали прямоугольного параллелепипеда равны.
- В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы прямоугольного параллелепипеда:
- Объем прямоугольного параллелепипеда
V = a · b · h
a — длина, b — ширина, h — высота - Площадь боковой поверхности
Sбок = Pосн·c=2(a+b)·c
Pосн — периметр основания, с — боковое ребро - Площадь поверхности
Sп.п = 2(ab+bc+ac)
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
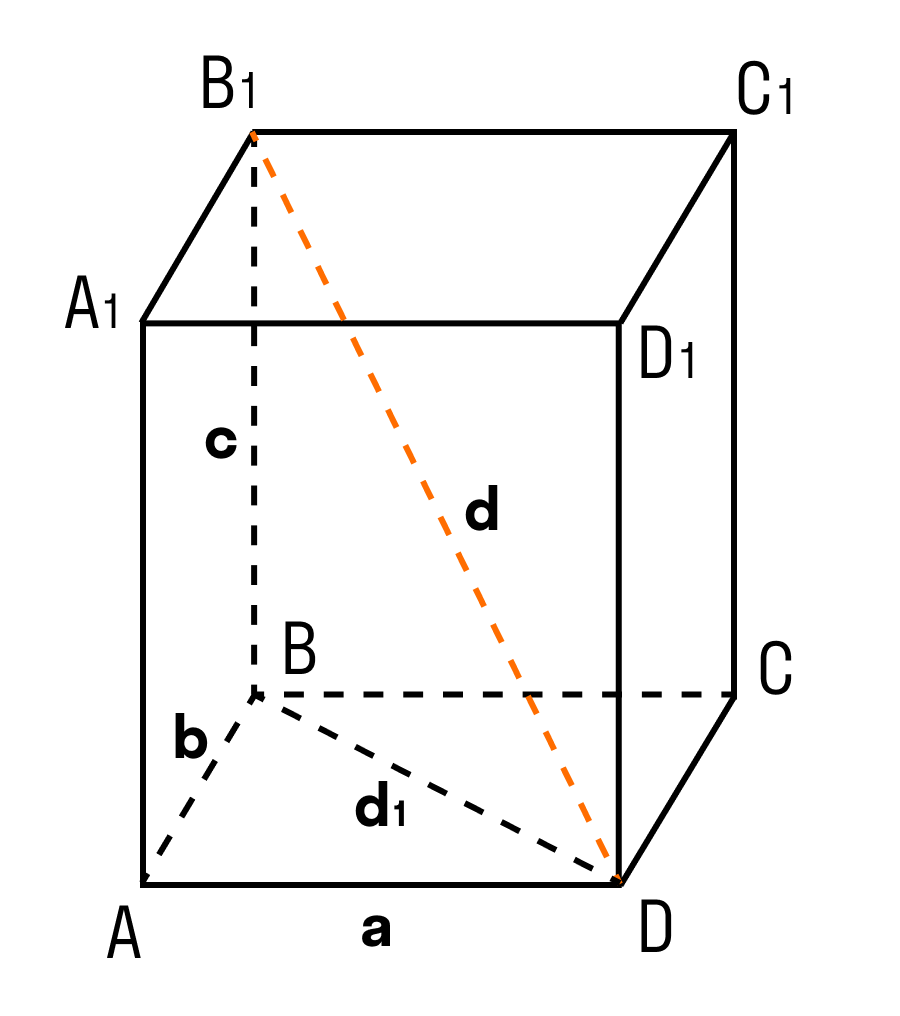
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
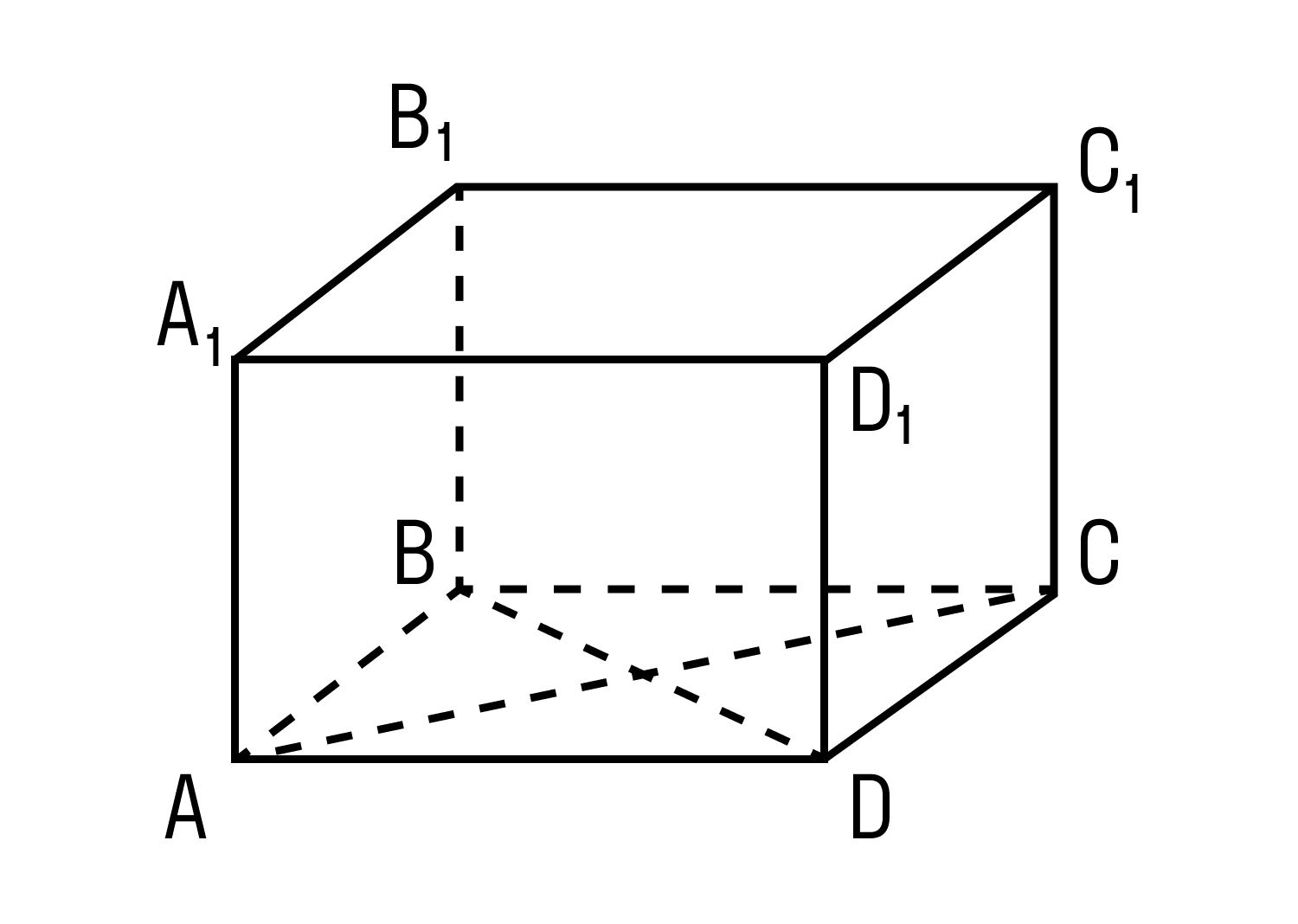
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.
Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = d₁² + c² = a² + b² + c²
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
У нас есть отличные дополнительные онлайн занятия по математике для учеников с 1 по 11 классы, записывайся!
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.
Свойства куба:
- В кубе 6 граней, каждая грань куба — квадрат.
- Противолежащие грани параллельны друг другу.
- Все углы куба, образованные двумя гранями, равны 90°.
- У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
- Диагонали куба равны.
- Диагональ куба в √3 раз больше его ребра.
- Диагональ грани куба в √2 раза больше длины ребра.
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
- Объем куба через длину ребра a
V = a3 - Площадь поверхности куба
S = 6a2 - Периметр куба
P = 12a
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
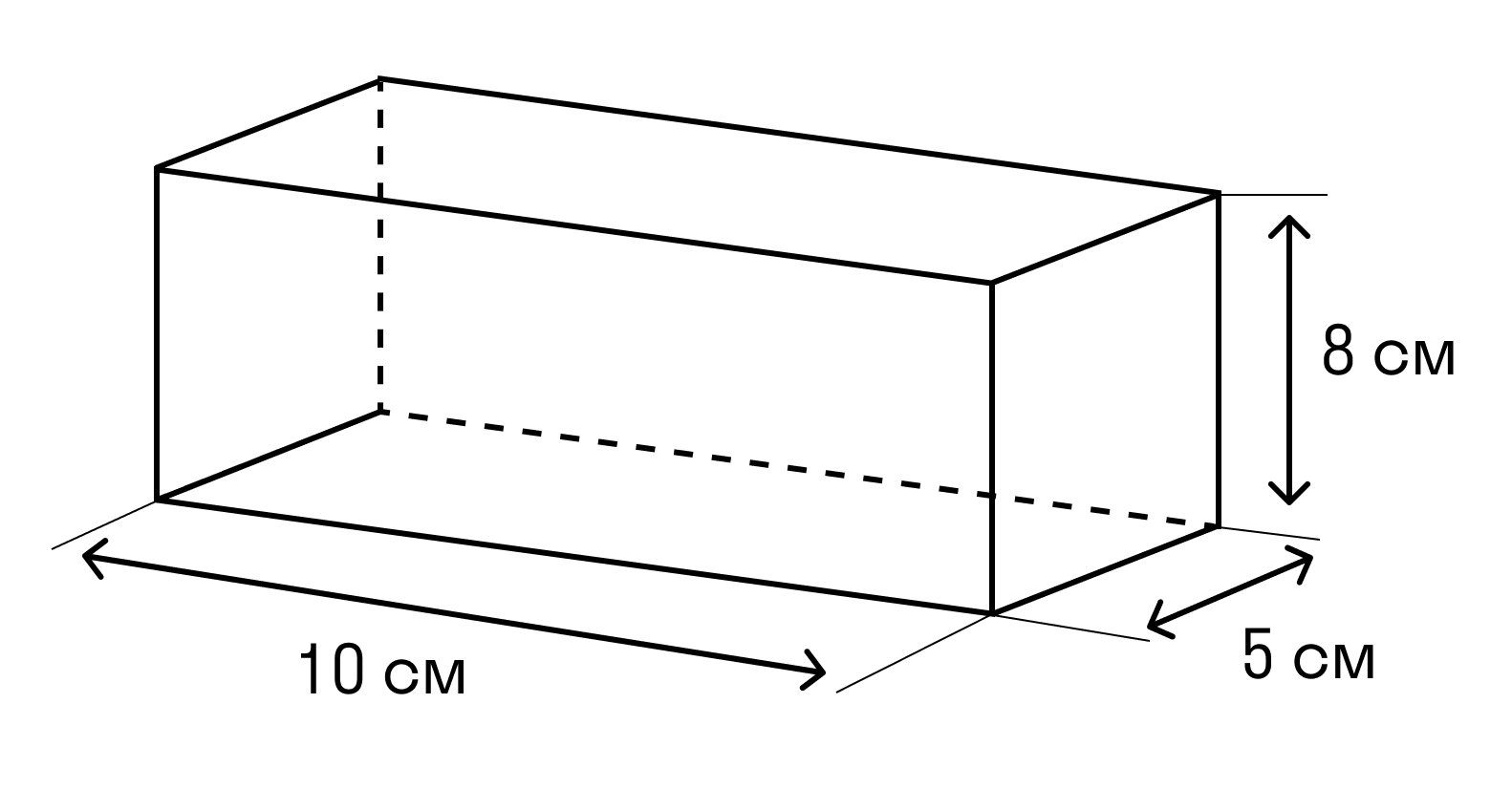
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.
Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.
Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.
Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.
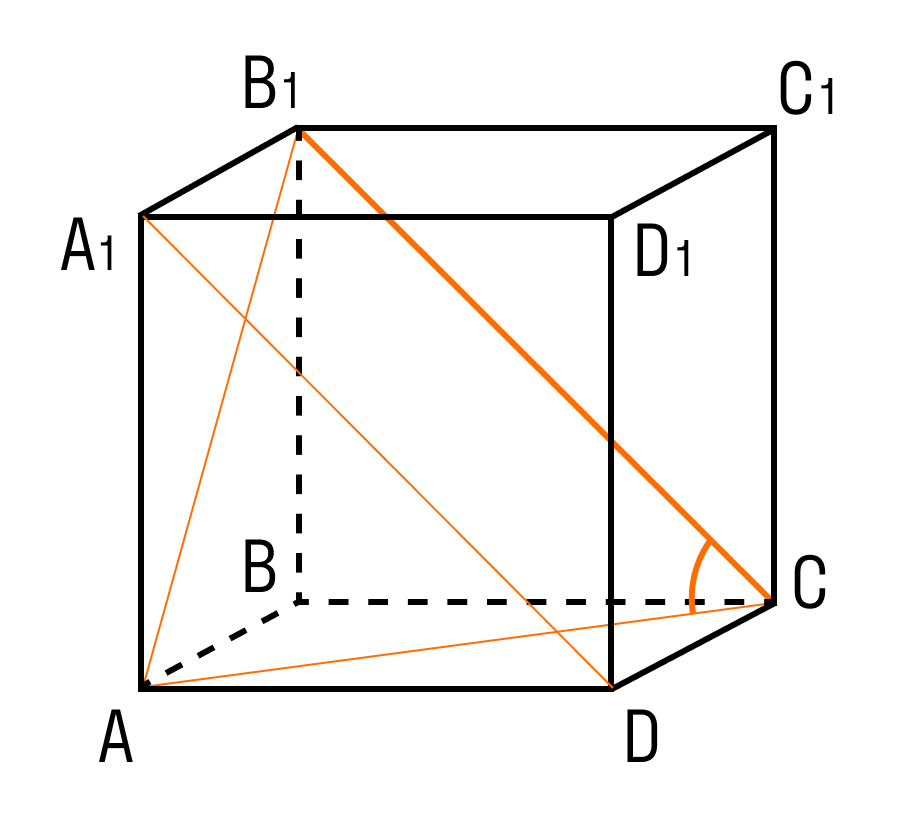
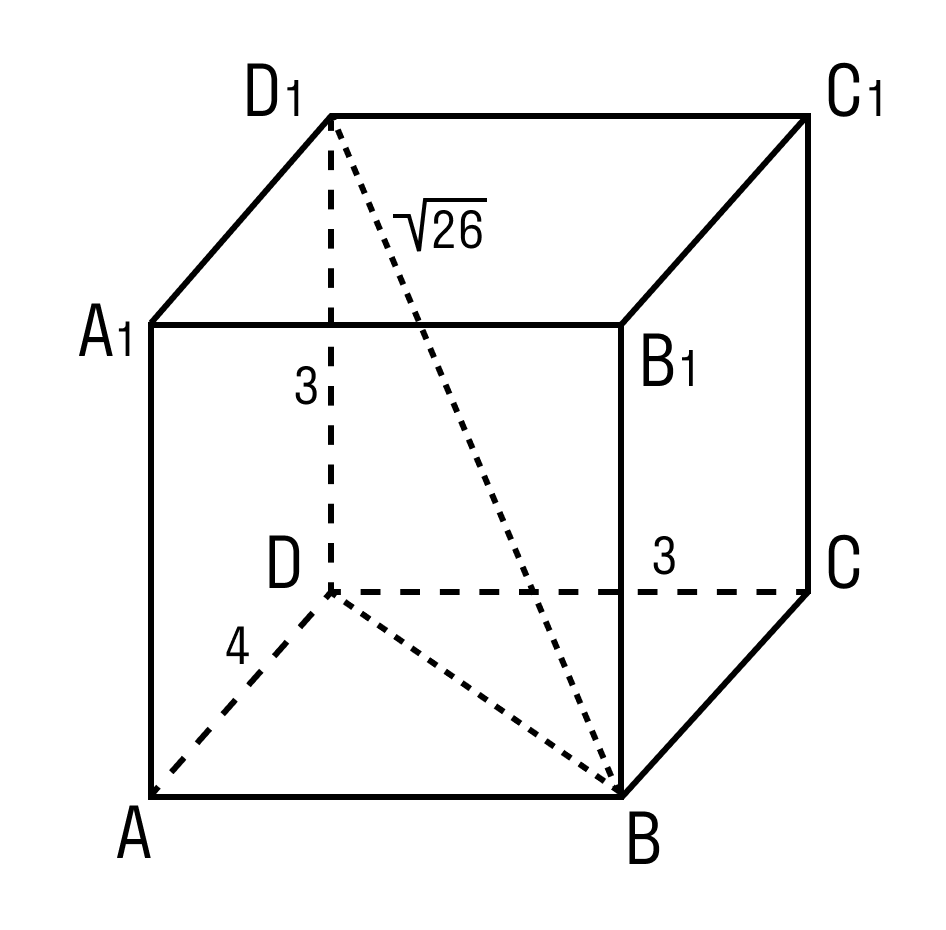
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Нужно найти длину ребра A1B1.
В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.
По теореме Пифагора:
BD1 2 = DD1 2 + BD 2
BD 2 = BD1 2 – DD1 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 — AD 2 = (√17)2 — 4 2 = 1
A1B1 = AB.
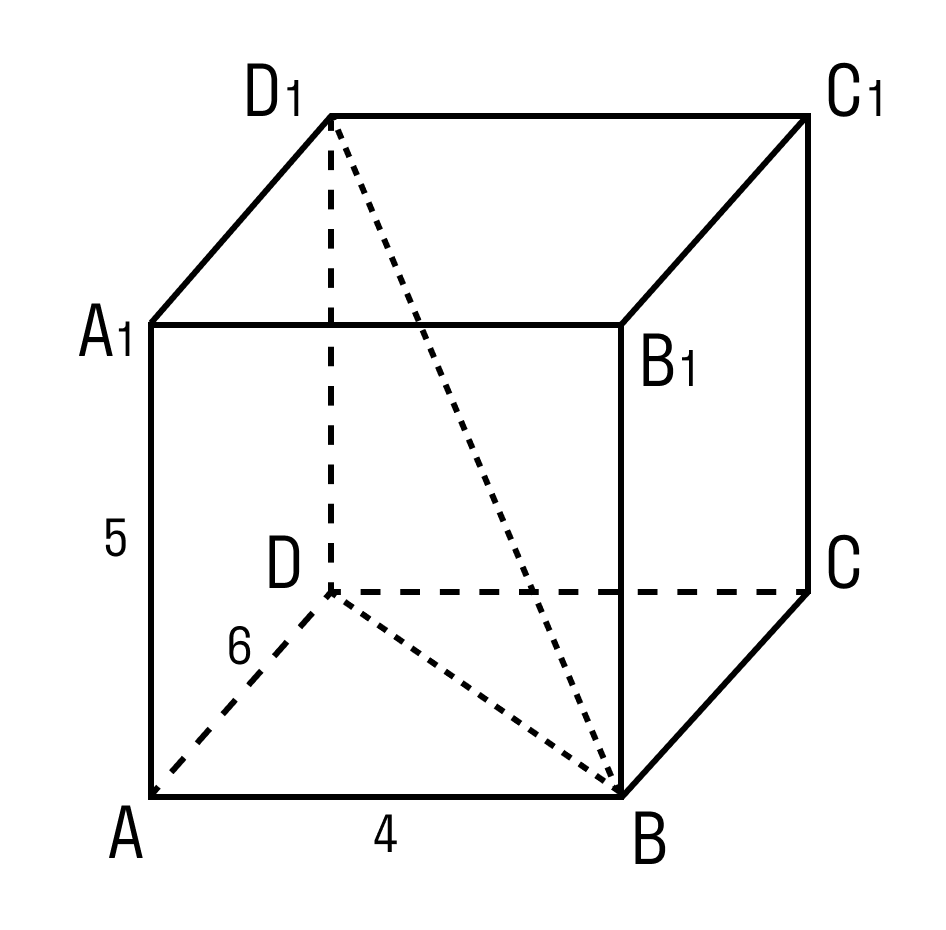
Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.
В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD1 2 = 52 + 25 = 77.
Самопроверка
Теперь потренируйтесь самостоятельно — мы верим, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
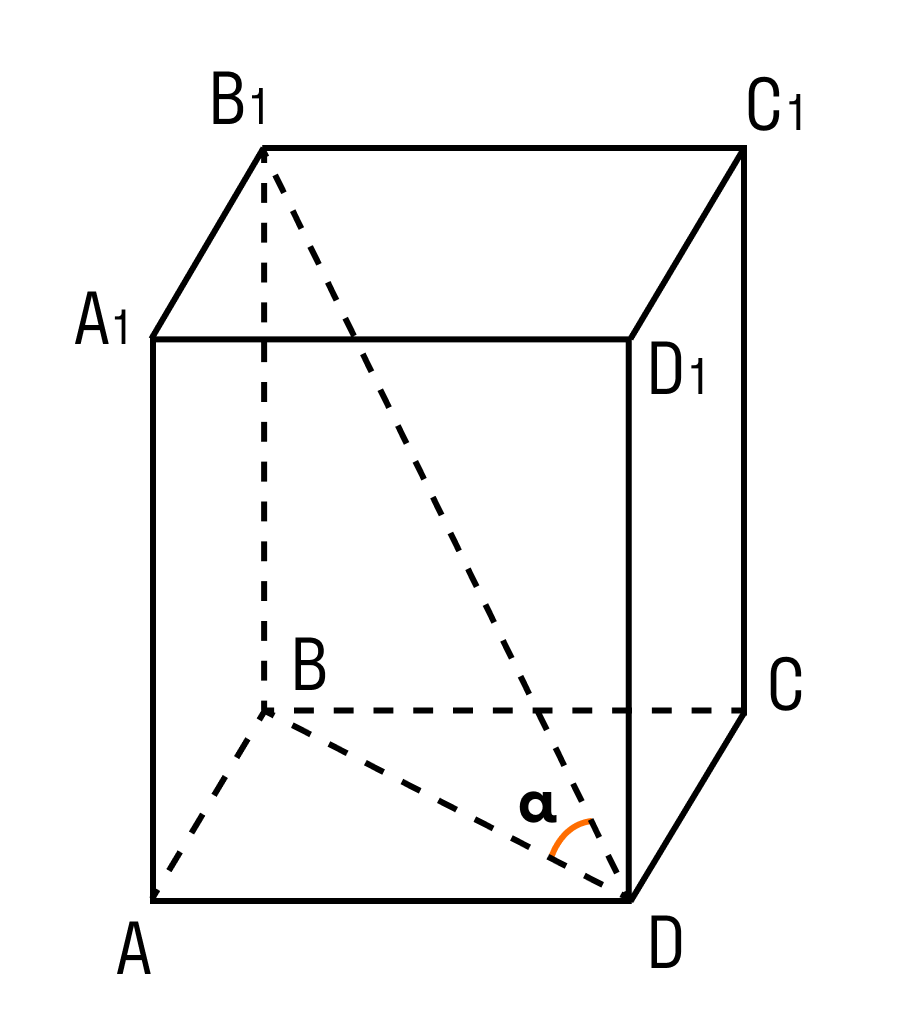
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:
- прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
- параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
- основание прямоугольного параллелепипеда — прямоугольник;
- три измерения прямоугольного параллелепипеда: длина, ширина, высота;
- диагональ параллелепипеда равна сумме квадратов его измерений.
Источник
Adblock
detector
Найди верный ответ на вопрос ✅ «Найти линейные размеры прямоугольного параллелепипеда, если сумма длин всех сторон его ребер равна 180 см. А линейные размеры относятся как …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Математика » Найти линейные размеры прямоугольного параллелепипеда, если сумма длин всех сторон его ребер равна 180 см. А линейные размеры относятся как 4:5:6.
Найдите правильный ответ на вопрос ✅ «Найти линейные размеры прямоугольного параллелепипеда, если сумма длин всех сторон его ребер равна 180 см. А линейные размеры относятся как …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Главная » Математика » Найти линейные размеры прямоугольного параллелепипеда, если сумма длин всех сторон его ребер равна 180 см. А линейные размеры относятся как 4:5:6.