Как найти линейный радиус планеты

1. Каким образом греческий учёный Эратосфен определил размеры Земли?

Идея Эратосфена заключается в следующем. На одном и том же географическом меридиане земного шара выберем две точки $O_1$ и $O_2.$ Обозначим длину пути меридиана $O_1O_2$ через $l,$ а её угловое значение через $n$ (в градусах). Тогда длина пути $1°$ меридиана $l_0$ будет равна:

$$l_0=dfrac{l}{n},$$

а длина всей окружности меридиана:

$$L=360°·l_0=dfrac{360°·l}{n}=2pi R,$$

где $R$ — радиус земного шара. Отсюда $R=dfrac{180°·l}{pi n}.$

2. Как определяют длину дуги меридиана триангуляционным методом?

Длина дуги определяется путём вычислений, требующих измерения только сравнительно небольшого расстояния — базиса и ряда углов. По обе стороны дуги $O_1O_2$, длину которой необходимо определить, выбирается несколько точек $A, B, C, …$ на взаимных расстояниях до 50 км с таким расчётом, чтобы из каждой из них были видны по меньшей мере две другие точки.

Длину базиса очень тщательно измеряют специальными мерными лентами. Измеренные углы в треугольниках и длина базиса позволяют по тригонометрическим формулам вычислить стороны треугольников, а по ним — длину дуги $О_1О_2$ с учётом её кривизны.

3. Что понимают под горизонтальным параллаксом?

Определение расстояний до тел Солнечной ситсемы основано на измерении их горизонтальных параллаксов. Горизонтальный параллакс — угол $p,$ под которым со светила виден радиус Земли, перпендикулярный к лучу зрения.

4. Как определить расстояние до светила, зная его горизонтальный параллакс?

Зная горизонтальный параллакс светила, можно определить его расстояние $D.$ Расстояние до светила $D=S=dfrac{R_⊕}{sin p},$ где $R_⊕$ — радиус Земли. Приняв $R_⊕$ за единицу, можно выразить расстояние до светила в земных радиусах.

5. Что такое астрономическая единица?

Для измерения расстояний в пределах Солнечной системы используют астрономическую единицу (а.е.), которая равна среднему расстоянию Земли от Солнца(1 а.е. ≈ 149 600 000 км).

6. В чём состоит радиолокационный метод определения расстояний до небесных тел?

Расстояние до объекта по времени прохождения радиолакационного сигнала можно определить по формуле $S=dfrac{1}{2}ct,$ где $S$ — расстояние до объекта; $c$ — скорость светы; $t$ — время прохождения сигнала до объекта и обратно.

7. на каком расстоянии от Земли находится небесное тело, если его горизонтальный параллакс равен 1′?

Для нахождения расстояния применим формулу:

$$D=dfrac{206265”}{p”}R_⊕.$$

Приняв радиус Земли $6371, км,$ получим $D=1, 314, 114, 315, км,$ или $8.8, а.е.$

8. Определите линейный радиус Луны, если во время наблюдений стало известно, что её горизонтальный параллакс в это время равен 57′ а угловой радиус — 15,5′ Радиус Земли принять равным 6400 км.

Дано:

$p = 57′,$
$ρ = 15.5′,$
$R_З = 6400, км.$

$R – ?$

Решение:

Найдём расстояние $D$ до Луны:

$D=dfrac{R_З}{sin p};$ $D=dfrac{6400}{sin 0.95°} approx 3.86 · 10^5, км.$

Вычислим линейный радиус:

$R=D·sin ρ;$ $R = 3.86 · 10^5 · sin 0.26° approx 1752, км.$

Ответ: $1752, км.$

9. Определите диаметр Меркурия, если при прохождении по диску Солнца его угловой диаметр оказался 11.0″, а горизонтальный параллакс в этот момент равен 14.3″.

Дано:

φ=28°.varphi=28°.

Найти:

aМ−?a_М-?

Решение:

sin⁡φ=aМaЗ.sin varphi=dfrac{a_М}{a_З}.

aМ=a⊕⋅sin⁡(28°)=0.4694…≈=0.47 а. е.a_М=a_opluscdot sin(28°)=0.4694…approx=0.47text{ а. е.}

Ответ: aМ=0.47 а. е.a_М=0.47text{ а. е.}

Присоединяйтесь к Telegram-группе @superresheba_11,
делитесь своими решениями и пользуйтесь материалами, которые присылают другие участники группы!

Угол, под которым
с Земли виден диск светила, называется
его угловым
диаметром.
Угловые диаметры некоторых небесных
тел (Солнца, Луны, планет) можно определить
непосредственно из наблюдений.

Рис. 2.4. Определение
линейных размеров светил.

Если известен
угловой диаметр (или радиус) светила и
его расстояние от Земли, то легко
вычислить его истинный диаметр (или
радиус) в линейных мерах. Действительно,
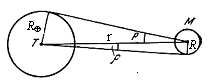
если (рис. 2.4) —
угловой радиус светила М, r
— расстояние между центрами светила и
Земли, р — горизонтальный экваториальный
параллакс светила, а R_
и R — линейные
радиусы Земли Т и светила М, то

,

(2.12)

а, учитывая, что
угол 
мал и

:

,

(2.13)

где

— угловой
радиус, выраженный в угловых секундах.

С учетом формулы (2.9) соотношение (2.13)
может быть приведено к следующему виду:

,

(2.14)

т.е.
чтобы вычислить
линейный радиус небесного тела, необходимо
измерить его угловой радиус и горизонтальный
параллакс.

Форму небесных тел можно определить,
измеряя различные диаметры их дисков.
Если тело сплющенное, то один из его
диаметров окажется больше, а один —
меньше всех других диаметров. Измерения
диаметров планет показали, что помимо
Земли сплющенную форму имеют Марс,
Юпитер, Сатурн, Уран и Нептун.

Линейные размеры
и форма небесных тел, угловые размеры
которых непосредственно измерить нельзя
(например, малые планеты и звезды),
определяются специальными методами.

§ 2.5. Измерение расстояний до звезд

Т.к. звезды удалены
от нас на огромные расстояния, то их
суточное параллактическое смещение
исключительно мало, поэтому оно не может
быть измерено.

Расстояния до
звезд определяются по их годичному
параллактическому смещению,
которое обусловлено перемещением
наблюдателя (вместе с Землей) по земной
орбите (рис. 2.5).

Рис. 2.5. Годичный
параллакс звезд.

Угол, под которым
со звезды был бы виден средний радиус
земной орбиты при условии, что направление
на звезду перпендикулярно к радиусу,
называется годичным
параллаксом звезды
.
Если СТ = а_
есть средний радиус земной орбиты, МС
= r
— расстояние звезды М
от Солнца С
(гелиоцентрическое
расстояние),
а угол 
— годичный параллакс звезды, то из
прямоугольного треугольника СТМ
имеем

.

(2.15)

Годичные параллаксы
звезд меньше 1“, и поэтому, учитывая,
что

,
получим:

,

(2.16)

где

— годичный
параллакс, выраженный в угловых секундах.

Расстояние r
по этим формулам получается в тех же
единицах, в которых выражено среднее
расстояние а_
Земли от Солнца.

Т.к. звезды находятся
на очень больших расстояниях от Земли,
то их гелиоцентрические расстояния и
расстояния от Земли будем считать
одинаковыми.

Расстояние,
соответствующее годичному параллаксу
в 1“,
называется парсеком.

Если расстояния
до звезд измерять в парсеках (пс),
то

.

(2.17)

Кроме этого,
расстояния до звезд измеряют также в
световых
годах.

Световой год
— расстояние,
которое свет проходит за один год,
распространяясь со скоростью около 300
000 км/с.

Запишем соотношения
между единицами расстояния в астрономии:

1 пс
= 3,1¹³
км
= 206 265 а.е.
= 3,26 светового
года;

1 световой
год = 9,46¹²
км =
63 240 а.е.;

1 а.е.=
149,6 
10⁶
км.

Расстояния до
небесных тел, находящихся за пределами
Солнечной системы, обычно выражаются
в парсеках, килопарсеках (1 000 пс)
и мегапарсеках (1 000 000 пс),
а также в световых годах.

Установлено, что
ближайшей к Солнцу звездой является
звезда Проксима
Центавра, которая имеет годичный
параллакс 
= 0“,772.
Следовательно, она находится от нас на
расстоянии 1,3 пс
или 4,2 светового
года.

Современные
астрономические приборы позволяют в
настоящее время измерить годичные
параллаксы, не меньшие 0“,005.
Это дает возможность определить
расстояния методом годичного параллакса,
не превышающие 200 пс.
Расстояния до более далеких объектов
определяются другими способами.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Определить географическую широту двух пунктов оказывается гораздо проще, чем измерить расстояние между ними. Зачастую непосредственное измерение кратчайшего расстояния между этими пунктами оказывается невозможным из-за различных естественных препятствий (гор, рек и т. п.). Поэтому применяется способ, основанный на явлении параллактического смещения и предусматривающий вычисление расстояния на основе измерений длины одной из сторон (базиса — BC) и двух углов B и C в треугольнике ABC (рис. 3.9).

Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя.

Чем дальше расположен предмет, тем меньше его параллактическое смещение, и чем больше перемещение наблюдателя (базис измерения), тем больше параллактическое смещение.

Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус.

Предмет: астрономия

Учитель: Кузина Маргарита Викторовна, МБОУ «Гимназия №
11 г. Ельца»

Уровень образования: базовый

Тема: « Определение расстояний и размеров тел в
Солнечной системе»

Тип урока:   изучение и первичное закрепление 
новых знаний и способов деятельности.

Время проведения: 1 полугодие

Участники: 11Б

Цель:  Познакомить
с различными способами определения расстояний до небесных тел Солнечной
системы.

Образовательные задачи урока:

1. Вычисление расстояний до небесного тела
   Солнечной системы.
2. Решение задачи на определение расстояний
3. Совершенствование работы с подвижной картой звездного
   неба.

Развивающие задачи урока:

1. Формирование умения подбора литературы,
   выделения главного из отобранного материала
2. Развитие творческих способностей обучающихся

Воспитательные задачи урока:

1. Формирование активного отношения у изучению
   материала
2. Содействие формированию мировоззренческой
   идеи о познаваемости мира.

Оборудование:

·        
техническое оснащение: компьютер,
мультимедийный проектор, компакт диск с записью музыки

·        
наглядные пособия: демонстрационная
карта звёздного неба, подвижные карты звёздного неба (у каждого ученика)

·        
программное обеспечение:программы Microsoft Word, Photoshop, Power Point, Internet Explorer.

Ключевые слова: триангуляция, параллактическое смещение, горизонтальный параллакс,
радиолокация, астрономическая единица

Литература:

Астрономия. Базовый уровень. 11 класс:
учебник/ Б.А. Воронцов-Вельяминов, Е.К.Страут. – М.: Дрофа, 2018. – 238.

Астрономия. 11 класс. Методическое пособие к
учебнику Б.А. Воронцова-Вельяминова, Е.К.Страута «Астрономия. Базовый уровень.
11 класс»/ М.А.Кунаш. – М.: Дрофа, 2018, 217с.

 Астрономия. 11 класс: поурочные планы по
учебнику Е.П.Левитана, – Волгоград: Учитель, 2007

Аннотация Межпредметная связь: Градусная и радианная меры угла, смежные и
вертикальные углы. Шар и сфера (математика, 5, 7, 10, 11 кл.). Расстояние от
Земли до Луны и Солнца. Сравнительные размеры Солнца и Земли, Земли и Луны
(природоведение, 5 кл). Скорость распространения электромагнитных волн. Метод
радиолокации (физика, 11 кл).

Длительность
урока: 45 мин.

План урока.

1. Орг. момент
2. Постановка целей и задач.
3.  Изучение нового материала
• сообщения учащихся, 
• решение задач,
• работа с презентацией
4. Закрепление новых знаний

·        
проверка усвоения материала,

·        
работа с подвижной картой звездного неба

1. Д.з. Итог урока

Ход урока.

1. Организационный момент.
2. Постановка целей и задач.

Сегодня на уроке
мы:

Поговорим о форме 
и размерах Земли;

Узнаем, как
Эратосфен измерил радиус Земли

Рассмотрим способы
измерения больших расстояний

Для этого вы:

прослушаете
сообщения одноклассников

просмотрите
презентацию

решите задачи

определите место
планеты на подвижной карте звездного неба.

1. Изучение нового материала

Эпиграфом к нашему
уроку я взяла четверостишие

Вот дотошные наши
земляне!

Всё измерить бы
нам, рассчитать.

И от центра Земли
расстоянье

К центру Солнца
сумели узнать.

Используя третий закон Кеплера, среднее расстояние всех планет
от Солнца можно выразить через среднее расстояние Земли от Солнца. Определив
его в километрах, можно найти в этих единицах все расстояния в Солнечной
системе.

Но есть и другие варианты. Разобраться в этом нам помогут сообщения,
подготовленные одноклассниками

1)     
Градусные измерения и триангуляция

Эратосфен — греческий ученый, живший в
египетском городе Александрии с 276 года по 196 год до нашей эры. Работал он в
Александрийском мусейоне. Отчасти это был музей, отчасти научный центр того
времени.

т проезжих путешественников Эратосфен услышал
о необычном явлении, которое они наблюдали в Сиене, городе, расположенном далеко
к югу от Александрии. Путешественники рассказали, что в полдень первого дня
лета — в самый тельный день в году — в Сиене исчезали тени. Солнце в это время
стояло прямо над головой, лучи его падали на землю отвесно вниз. Внимательно
вглядываясь в воду водоема, можно было рассмотреть отражение Солнца на дне.

Эратосфен съездил в Сиену и убедился в этом
сам. Вернувшись в Александрию, он обнаружил, что и в самый длительный день года
в полдень стены мусейона продолжали отбрасывать тень на землю. Основываясь на
этом простом наблюдении, он смог вычислить окружность Земли.
Вычисления окружности Эратосфен знал, что из – за громадного расстояния
от Земли до Солнца, лучи последнего достигают и Сиены и Александрии
параллельными лучами. То есть лучи Солнца, падающие на землю в Александрии,
параллельны лучам, падающим на землю в Сиене в то же время. Если бы Земля была
плоской, то тени исчезали бы на ней повсеместно 21 июня. Но так как, рассуждал
он, Земля искривлена, то в Александрии, удаленной от Сиены на 500
миль (1 миля равна 1,609 километра) к северу, местные стены и колонны
наклонены по отношению к сиенским стенам и колон нам под некоторым углом. Итак,
в полдень первого дня лета Эратосфен измерил тень, отбрасываемую обелиском,
стоявшим неподалеку от мусейона. Зная высоту обелиска, он смог легко вычислить
длину линии, соединяющей вершину обелиска и конец тени. Получился воображаемый
треугольник. После того как треугольник был «очерчен», оставалось, используя
известные к тому времени правила геометрии, вычислить его углы. И Эратосфен их
вычислил. Он нашел, что угол отклонения обелиска от солнечного луча составляет
чуть больше 7 градусов. Так как в Сиене вертикальные предметы не отбрасывали
тени, то угол между ними и солнечным лучом составлял ноль градусов. Короче, никакого
угла не было. Это означало, что Александрия отстоит по земной окружности от
Сиены на 7 градусов. Такой угол между городами — это 1/50 часть окружности.
Всякая окружность содержит 360 градусов, земная окружность в этом смысле не
исключение. Эратосфен умножил расстояние между Сиеной и Александрией — 500
миль — на 50 и получил значение окружности Земли. Оно оказалось равным 25
тысячам миль. Современные ученые, измерившие с помощью высококлассной техники
окружность Земли, нашли ее равной 24 894 тысяч миль. Все таки Эратосфен
оказался первоклассным ученым, а не дилетантом.

Источник: http://www.voprosy-kak-i-pochemu.ru/eratosfen-i-okruzhnost-zemli/
.

2)     
Параллактическое смещение

Классическим способом определения расстояний был и остается
угломерный геометрический способ. Им определяют расстояния и до далеких звезд,
к которым метод радиолокации неприменим. Геометрический способ основан на
явлении параллактического смещения.                                                                                       Параллактическим
смещением называется изменение направления на предмет при перемещении
наблюдателя

3)Объяснение учителя

а) Измерить расстояние от Земли до Солнца удалось лишь во второй
половине XVIII в., когда впервые был определен
горизонтальный параллакс Солнца.  Угол, под которым со светила виден радиус
Земли, перпендикулярный к лучу зрения, называется горизонтальным параллаксом.

D=R/sin p

1 рад = 206265’’

При малых углах sin р = p, если угол р выражен в радианах.
Если р выражен в секундах дуги, то вводится множитель

где 206265 — число секунд в одном радиане.

Тогда

Знание этих соотношений упрощает вычисление расстояния по
известному параллаксу:

б) Определение размеров тел

Если углы и ρ малы, то синусы пропорциональны углам, и
можно написать:

Этот способ определения размеров светил применим только тогда,
когда виден диск светила.

в) С 40-х годов нашего века радиотехника позволила определять
расстояния до небесных тел посредством радиолокации, о которой вы знаете из
курса физики. Советские и американские ученые уточнили радиолокацией расстояния
до Меркурия, Венеры, Марса и Юпитера.

1. Закрепление новых знаний

1)     
упр 11 (1)

Чему равен
горизонтальный параллакс Юпитера, наблюдаемого с Земли в противостоянии, если
Юпитер в 5 раз дальше от Солнца, чем Земля?

2)     
 

1. Д.з. Итог урока

п 13, упр. 11 (2,
4)

Заполните таблицу

Цель	Требуемые параметры (что нужно знать для достижения поставленной цели)
Вычисление радиуса Земли
Вычисление расстояния до тела Солнечной системы

Д.з. 

http://tepka.ru/astronomiya

Пример решения задачи

Задача. На каком расстоянии от Земли находится Сатурн,
когда его горизонтальный параллакс равен 0,9″?

Зная расстояние D до светила и измерив его угловой радиус , можно вычислить его
линейный радиус r: r=Dsin или r=D, если угол выражен в радианах.

Пример решения задачи

Задача. Чему равен линейный диаметр Луны, если она видна с
расстояния 400 000 км под углом примерно 0,5°?

1. Закончите предложения

Для измерения расстояний в пределах Солнечной системы
используют астрономическую единицу (а. е.), которая равна среднему
расстоянию от Земли до Солнца.

1 а.е. = 149
600 000 км

Расстояние до объекта по времени прохождения радиолокационного
сигнала можно определить по формуле , где S = 1/2·ct, где S —
расстояние до объекта, c — скорость света, t — время прохождения светила.

2. Дайте определения понятиям «параллакс» и «базис»;
на рисунке 10.1 покажите эти величины

Параллакс — угол p, под которым из недоступного места
(точка C) будет виден отрезок AB, называемый базисом.

Базис — тщательно измеренное расстояние от точки A
(наблюдатель) до какой-либо достигнутой для наблюдения точки B.

3. Как с помощью понятий параллакса и базиса
определить расстояние до удаленного недоступного объекта С (рис. 10.1)?

По величине базиса и прилегающим к нему углам треугольника ABC
найти расстояние AC. При измерениях на Земле этот метод называют триангуляцией.

4. Угол, под которым со светила S виден радиус Земли,
перпендикулярный лучу зрения, называется горизонтальным параллаксом p (рис,
10.2). Определите расстояния: а) до Луны, если ее горизонтальный параллакс p =
57′; б) до Солнца, горизонтальный параллакс которого p = 8,8″

Решение.

Вариант 2.

1. Сигнал, посланный радиолокатором к Венере, возвратился
назад через t — 4 мин 36 с. На каком расстоянии в это время находилась Венера в
своем нижнем соединении?

Ответ: 41 млн км.

2. На какое расстояние к Земле подлетал астероид Икар, если
его горизонтальный параллакс в это время был p = 18,0″?

Ответ: 1,22 млн км.

3. С помощью наблюдений определили, что угловой радиус Марса p
= 9,0″, а горизонтальный параллакс p = 16,9″. Определите линейный радиус Марса.

Ответ: 3390 км.

http://superresheba.by

I. Опрос учащихся (5-7 минут). Диктант.
 

1. Ученый, создатель гелиоцентрической системы
   мира. (Н. Коперник)
2. Ближайшая точка орбиты ИСЗ. (Перигей)
3. Значение астрономической единицы. (1 а.
   е.=149600000км )
4. Основные законы небесной механики. (4
   закона-3Вт и 3-й закон Коперника)
5. Планета, открытая на «кончике пера».
   (Нептун)
6. Значение круговой (I космической) скорости
   для Земли. (7,9 км/с)
7. Отношение квадратов периодов обращения двух
   планет равно 8. Чему равно отношение больших полуосей этих планет? (2)
8. В какой точке эллиптической орбиты ИСЗ имеет
   минимальную скорость? (В апогее)
9. Немецкий астроном, открывший законы движения
   планет (И. Кеплер)
10. Формула третьего закона Кеплера, после
    уточнения И. Ньютона.
11. Вид орбиты межпланетной станции, посланной
    для облета Луны. (Эллипс)
12. Чем отличается первая космическая скорость
    от второй. (в раз >)
13. В какой конфигурации находится Венера, если
    она наблюдается на фоне диска Солнца? (Соединение нижнее)
14. В какой конфигурации Марс ближе всего к
    Земле. (В противостоянии)
15. Виды периодов движения Луны = (временных)?
    (Сидерический, синодический).

II Новый материал

1) Определение расстояний до небесных тел.
     В астрономии нет единого универсального способа
определения расстояний. По мере перехода от близких небесных тел к более
далеким одни методы определения расстояний сменяют другие, служащие, как
правило, основой для последующих. Точность оценки расстояний ограничивается
либо точностью самого грубого из методов, либо точностью измерения
астрономической единицы длины (а. е.).
1-й способ: (известен) По третьему закону Кеплера можно
определить расстояние до тел СС, зная периоды обращений и одно из расстояний. 

    Приближённый
метод.

2-й способ: Определение
расстояний до Меркурия и Венеры в моменты элонгации (из прямоугольного
треугольника по углу элонгации).
3-й способ: Геометрический (параллактический).
  Пример: Найти неизвестное
расстояние АС.
  [АВ] – Базис – основное известное расстояние, т. к. углы САВ и СВА –
известны, то по формулам тригонометрии (теорема синусов) можно в ? найти
неизвестную сторону, т. е. [CА]. Параллактическим  смещением называется
изменение направления на предмет при перемещении наблюдателя.
  Параллакс- угол (АСВ), под которым из недоступного места виден
базис (АВ – известный отрезок). В пределах СС за базис берут
экваториальный радиус Земли R=6378км.

     Пусть К – местонахождение
наблюдателя, из которого светило видно на горизонте. Из рисунка видно, что из
прямоугольного треугольника гипотенуза, расстояние D равно: ,
так как при малом значении угла если выражать величину угла в радианах и
учитывать, что угол выражен в секундах дуги, а 1рад =57,3⁰=3438’=206265″,
то и получается вторая формула.

Угол (ρ) под которым со светила, находящегося на
горизонте (? R – перпендикулярно лучу зрения) был бы виден экваториальный
радиус Земли называется горизонтальным экваториальным параллаксом светила.
Т.к. со светила никто наблюдать не будет в силу объективных причин, то
горизонтальный параллакс определяют так:

1. измеряем высоту светила в момент верхней
   кульминации из двух точек земной поверхности, находящихся на одном
   географическом меридиане и имеющем известные географические широты.
2. из полученного четырехугольника вычисляют
   все углы (в т. ч. параллакс).

Из истории: Первое
измерение параллакса (параллакса Луны) сделано в 129г до НЭ Гиппархом
(180-125, Др. Греция).
    Впервые расстояния до небесных тел (Луны, Солнца, планет)
оценивает    Аристотель (384-322, Др. Греция) в 360г до НЭ в
книге «О небе» →слишком не точно, например радиус Земли в 10000
км.
    В 265г до НЭ Аристарх Самосский (310-230, Др.
Греция) в работе «О величине и расстоянии Солнца и Луны» определяет расстояние
через лунные фазы. Так расстояния у него до Солнца (по фазе Луны в 1 четверти
из прямоугольного треугольника, т. е. впервые использует базисный метод:
ЗС=ЗЛ/cos 87º≈19*ЗЛ). Радиус Луны определил в 7/19 радиуса Земли, а Солнца в
6,3 радиусов Земли (на самом деле в 109 раз). На самом деле угол не 87º а
89º52′ и поэтому Солнце дальше Луны в 400 раз. Предложенные расстояния
использовались многие столетия астрономами.
    В 240г до НЭ ЭРАТОСФЕН (276-194, Египет)
произведя измерения 22 июня в Александрии угла между вертикалью и направлением
на Солнце в полдень (считал, что раз Солнце очень далеко, то лучи параллельны)
и используя записи наблюдений в тот же день падения лучей света в глубокий
колодец в Сиене (Асуан) (в 5000 стадий = 1/50 доли земной окружности (около
800км) т. е. Солнце находилось в зените) получает разность углов в 7º12′ и
определяет размер земного шара, получив длину окружности шара 39690
км (радиус=6311км). Так была решена задача определения размера Земли,
используя астрогеодезический способ. Результат не был произведён до 17 века,
лишь астрономы Багдадской обсерватории в 827г немного поправили его ошибку.
   В 125г до НЭ Гиппарх довольно точно определяет (в
радиусах Земли) радиус Луны (3/11 R_⊕) и расстояние до Луны
(59 R_⊕).
Точно определил расстояние до планет, приняв расстояние от Земли до Солнца за
1а.е., Н. Коперник.
    Наибольший горизонтальный
параллакс имеет ближайшее тело к Земле – Луна. Р_?=57’02^“;
а для Солнца   Р_¤=8,794^“
Задача 1: учебник Пример № 6 – Найти расстояние от
Земли до Луны, зная параллакс Луны и радиус Земли.
Задача 2 : (самостоятельно). На каком расстоянии от Земли
находится Сатурн, если его параллакс 0,9″. [из формулы
D=(206265/0,9)*6378= 1461731300км = 1461731300/149600000≈9,77а.е.]
4-й способ Радиолокационный: импульс→объект →отраженный
сигнал→время. Предложен советскими физиками Л.И. Мандельштам и Н.Д.
Папалекси. Быстрое развитие радиотехники дало астрономам возможность
определять расстояния до тел Солнечной системы радиолокационными методами. В
1946г была произведена первая радиолокация Луны Баем в Венгрии и в США, а в
1957-1963гг — радиолокация Солнца (исследования солнечной короны проводятся с
1959г), Меркурия (с 1962г на ll= 3.8, 12, 43 и 70
см), Венеры, Марса и Юпитера (в 1964 г. на волнах l = 12 и 70
см), Сатурн (в 1973 г. на волне l = 12.5
см) в Великобритании, СССР и США. Первые эхо-сигналы от солнечной короны были
получены в 1959 (США), а от Венеры в 1961 (СССР, США, Великобритания). По
скорости распространения радиоволн с = 3 × 10⁵ км/сек
и по промежутку времени t (сек) прохождения радиосигнала с Земли
до небесного тела и обратно легко вычислить расстояние до небесного тела.
V_ЭМВ=С=299792458м/с≈3*10⁸
м/с.

     Основная трудность в
исследовании небесных тел методами радиолокации связана с тем, что
интенсивность радиоволн при радиолокации ослабляется обратно пропорционально
четвертой степени расстояния до исследуемого объекта. Поэтому радиолокаторы,
используемые для исследования небесных тел, имеют антенны больших размеров и
мощные передатчики. Например, радиолокационная установка центра дальней
космической связи в Крыму имеет антенну с диаметром главного зеркала 70
м и оборудована передатчиком мощностью несколько сотен кВт на волне 39
см. Энергия, направляемая к цели, концентрируется в луче с углом раскрыва 25′.
    Из радиолокации Венеры, уточнено значение астрономической
единицы:    1 а. е.=149 597 870 691 ± 6м ≈149,6 млн.км., что
соответствует Р_¤=8,7940″. Так проведенная в Советском Союзе обработка данных
радиолокационных измерений расстояния до Венеры в 1962-75гг (один из первых
удачных экспериментов по радиолокации Венеры провели сотрудники Института
радиотехники и электроники АН СССР в апреле 1961г антенной дальней космической
связи в Крыму, l= 39 см) дала значение 1 а.е. =149597867,9 ±0,9
км. XVI Генеральная ассамблея Международного астрономического союза приняла в
1976г значение 1 а.е.=149597870±2 км. Путем радиолокации с КА определяется
рельеф поверхности планет и их спутников, составляются их карты.
  Основные антенны, используемые для радиолокации планет:
   = Евпатория, Крым, диаметр 70
м, l= 39 см;
   = Аресибо, Пуэрто Рико, диаметр 305
м, l= 12.6 см;
   = Голдстоун, Калифорния, диаметр 64
м, l = 3.5 и 12.6 см, в бистатическом режиме прием осуществляется на
системе апертурного синтеза VLA.

     С изобретение Квантовых генераторов (лазера)
в 1969г произведена первая лазерная локация Луны (зеркало для отражения лазерного
луча на Луне установили астронавты США «Ароllо – 11» 20.07.69г), точность
измерения составили ±30 см. На рисунке показано расположение лазерных уголковых
отражателей на Луне, установленных при полете КА “Луна-17, 21” и
“Аполлон – 11, 14, 15”. Все, за исключением отражателя Лунохода-1
(L1), работают и сейчас.
Лазерная (оптическая) локация нужна для:
-решение задач космических исследований.
-решение задач космической геодезии.
-выяснения вопроса о движении земных материков и т.д.
   

2) Определение размеров небесных тел.

а) Определение радиуса Земли.
 

АОВ=n=φА-φВ(разность географических широт) е=АВ – длина дуги вдоль меридиана т.к. е10=е/n=2πR/3600 ,то  [форм 21].  Аналогичным способом в 240г до НЭ (рисунок выше) определяет радиус Земли географ Эратосфен.   L/800=3600/7,20

б) Определение
размера небесных тел.

Р- параллакс. ρ – угловой радиус светила Из прямоугольных треугольников дважды используя формулу R=r. sin ρ (чертёж) получим  [форм. 22]

III. Закрепление материала

1. Пример 7 (стр.
   51).
2. CD- “Red Shift
   5.1” – Определить на данный момент удаленность нижних (планет земной
   группы, верхних планет, планет гигантов) от Земли и Солнца в а.е.
3. Угловой радиус Марса 9,6″, а
   горизонтальный параллакс 18″. Чему равен линейный радиус Марса? [Из
   формулы 22 получим 3401,6 км. (фактически 3396
   км)].
4. Каково расстояние между лазерным отражателем
   на Луне и телескопом на Земле, если импульс возвратился через 2,43545с? [
   из формулы R=(c^.t)/2 R=3^.10^8.2,43545/2≈365317500,92м≈365317,5км]
5. Расстояние от Земли до Луны в перигее
   363000км, а в апогее 405000км. Определите горизонтальный параллакс Луны в
   этих положениях. [ из формулы D=(206265″/p)*R_⊕ отсюда р=(206265″/D)*R_⊕; р_А=(206265″/405000)*6378≈3248,3″≈54,1′,
   р_П= (206265″/363000)*6378≈3624,1″≈60,4′].
6. Тест с картинками по
   главе 2.
7. Дополнительно,
   для тех кто сделал – кроссворд.

Планета СС  [Меркурий] Ближайшая к Земле точка орбиты ИСЗ  [перигей] Ученый, создатель гелиоцентрической системы мира  [Коперник] Угол под которым со светила виден R Земли  [параллакс] Ученый, направивший первым в 1609г телескоп на небо [Галилей] Сторона горизонта  [север]

Итог:
1) Что такое параллакс?
2) Какими способами можно определить расстояние до тел СС?
3) Что такое базис? Что принимается за базис для определения расстояния до тел
СС?
4) Как зависит параллакс от удаленности небесного тела?
5) Как зависит размер тела от угла?
6)  Оценки

Домашнее задание: §11;
вопросы и задания стр. 52, стр. 52-53 знать и уметь. Повторить полностью вторую
главу. СР№6, ПР№4.
Можно задать по данному разделу подготовить кроссворд, опросчик, реферат об
одном из ученых-астрономов или истории астрономии (один из вопросов или
направлений).
   Можно предложить практическую работу
“Определение размера Луны”.
   В период полнолуния, используя две соединенные под прямым углом линейки,
определяются видимые размеры лунного диска: поскольку треугольники KCD и КАВ
подобны, из теоремы о подобии треугольников следует, что: АВ/СD=KB/KD. Диаметр
Луны АВ = (CD^.KB)/KD. Расстояние от Земли до Луны берёте из
справочных таблиц (но лучше, если сумеете вычислить его сами).

http://www.astro.websib.ru/metod/tem-2/

Наименование разделов и тем	Содержание учебного материала, лабораторные  работы и практические занятия, самостоятельная работа обучающихся	Объем часов	Уровень освоения
Законы движения небесных тел. Определение расстояний и размеров тел в Солнечной системе.	Законы Кеплера. Определение расстояний и размеров тел в Солнечной системе. Горизонтальный параллакс.  Формулирование законов Кеплера. Воспроизведение формул для определения расстояний и размеров тел в Солнечной системе. Воспроизведение определений терминов и понятий (паралактическое смещение, горизонтальный параллакс). Применение полученных знаний для решения задач на законы Кеплера, на определение расстояний и линейных размеров тел.	2	2

Тема 3.2. Законы движения небесных тел. Определение расстояний и размеров тел в Солнечной системе.

3.2.1. Законы движения небесных тел.

Важную роль в формировании представлений о строении Солнечной системы сыграли также законы движения планет, которые были открыты Иоганном Кеплером (1571—1630) и стали первыми естественнонаучными законами в их современном понимании. Работы Кеплера создали возможность для обобщения знаний по механике той эпохи в виде законов динамики и закона всемирного тяготения, сформулированных позднее Исааком Ньютоном. Многие ученые вплоть до начала XVII в. считали, что движение небесных тел должно быть равномерным и происходить по «самой совершенной» кривой— окружности. Лишь Кеплеру удалось преодолеть этот предрассудок и установить действительную форму планетных орбит, а также закономерность изменения скорости движения планет при их обращении вокруг Солнца.

В своих поисках Кеплер исходил из убеждения, что «в мире правит число», высказанного еще Пифагором. Он искал соотношения между различными величинами, характеризующими движение планет, — размеры орбит, период обращения, скорость. Кеплер действовал фактически вслепую, чисто эмпирически. Он пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы, длиной сторон описанных и вписанных в орбиты планет многоугольников Иоганн Кеплер и т. д.

Кеплеру необходимо было построить орбиты планет, перейти от экваториальной системы координат, указывающих положение планеты на небесной сфере, к системе координат, указывающих ее положение в плоскости орбиты. Он воспользовался при этом собственными наблюдениями планеты Марс, а также многолетними определениями координат и конфигураций этой планеты, проведенными его учителем Тихо Браге.Орбиту Земли Кеплер считал (в первом приближении) окружностью, что не противоречило наблюдениям. Для того чтобы построить орбиту Марса, он применил способ, который показан на рисунке 3.5.

Пусть нам известно угловое расстояние Марса от точки весеннего равноденствия во время одного из противостояний планеты — его прямое восхождение  α₁, которое выражается углом Т₁М₁ где Т₁ — положение Земли на орбите в этот момент, а М₁ — положение Марса. Очевидно, что спустя 687 суток (таков звездный период обращения Марса) планета придет в ту же точку своей орбиты. Если определить прямое восхождение Марса на эту дату, то, как видно из рисунка 3.5, можно указать положение планеты в пространстве, точнее, в плоскости ее орбиты. Земля в этот момент находится в точке Т₂, и, следовательно, угол T₂M₁ есть не что иное, как прямое восхождение Марса — α₂. Повторив подобные операции для нескольких других противостояний Марса, Кеплер получил еще целый ряд точек и, проведя по ним плавную кривую, построил орбиту этой планеты.

Изучив расположение полученных точек, он обнаружил, что скорость движения планеты по орбите меняется, но при этомрадиус-вектор планеты за равные промежуткивремени описывает равные площади.Впоследствии эта закономерность получила название второго закона Кеплера.

Этот закон, который часто называют законом площадей, иллюстрируется рисунком 3.6. Радиус-вектором называют в данном случае переменный по своей величине отрезок, соединяющий Солнце и ту точку орбиты, в которой находится планета. АА₁ ВВ₁ и СС₁ — дуги, которые проходит планета за равные промежутки времени. Площади заштрихованных фигур равны между собой.

Согласно закону сохранения энергии, полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остается неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергий планеты, которая движется вокруг Солнца, неизменна во всех точках орбиты и равна полной энергии. По мере приближения планеты к Солнцу возрастает ее скорость — увеличивается кинетическая энергия, но вследствие уменьшения расстояния до Солнца уменьшается энергия потенциальная.

Установив закономерность изменения скорости движения планет, Кеплер задался целью определить, по какой кривой происходит их обращение вокруг Солнца. Он был поставлен перед необходимостью сделать выбор одного из двух возможных решений:     1) считать, что орбита Марса представляет собой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с наблюдениями (из-за ошибок наблюдений) на 8′; 2) считать, что наблюдения таких ошибок не содержат, а орбита не является окружностью. Будучи уверенным в точности наблюдений Тихо Браге, Кеплер выбрал второе решение и установил, что наилучшим образом положения Марса на орбите совпадают с кривой, которая называется эллипсом, при этом Солнце не располагается в центре эллипса. В результате был сформулирован закон, который называется первым законом Кеплера.

Каждая планета обращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.

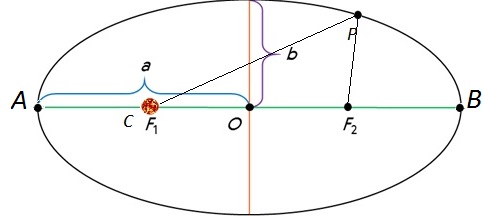
Как известно, эллипсом называется кривая, у которой сумма расстояний от любой точки Р до его фокусов есть величина постоянная. На рисунке 3.6 обозначены: О – центр эллипса; F и F₁ — фокусы эллипса; АВ — его большая ось. Половина этой величины (а), которую обычно называют большой полуосью, характеризует размер орбиты планеты. Ближайшая к Солнцу точка А называется перигелий, а наиболее удаленная от него точка В — афелий. Отличие эллипса от окружности характеризуется величиной его эксцентриситета: е = OS/OA. В том случае, когда эксцентриситет равен О, фокусы и центр сливаются в одну точку — эллипс превращается в окружность.

Примечательно, что книга, в которой в1609 г. Кеплер опубликовал первые два открытых им закона, называлась «Новая астрономия, или Физика небес, изложенная в исследованиях движения планеты Марс…».

Оба этих закона, опубликованные в 1609 г., раскрывают характер движения каждой планеты в отдельности, что не удовлетворило Кеплера. Он продолжил поиски «гармонии» в движении всех планет, и спустя 10 лет ему удалось сформулировать третий закон Кеплера.

Квадраты звездных периодов обращения планет относятся между собой, как кубы больших полуосей их орбит.

Формула, выражающая третий закон Кеплера, такова:

где Т₁ и Т₂ — периоды обращения двух планет; а₁ и а₂ — большие полуоси их орбит.

Вот что писал Кеплер после открытия этого закона: «То, что 16 лет тому назад я решил искать, <…> наконец найдено, и это открытие превзошло все мои самые смелые ожидания…»

Действительно, третий закон заслуживает самой высокой оценки. Ведь он позволяет вычислить относительные расстояния планет от Солнца, используя при этом уже известные периоды их обращения вокруг Солнца. Не нужно определять расстояние от Солнца каждой из них, достаточно измерить расстояние от Солнца хотя бы одной планеты. Величина большой полуоси земной орбиты — астрономическая единица (а. е.) — стала основой для вычисления всех остальных расстояний в Солнечной системе.

Пример решения задач

Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось ее орбиты?

3.2.2. Определение расстояний и размеров тел в Солнечной системе.

Представление о Земле как о шаре, который свободно, без всякой опоры находится в космическом пространстве, является одним из величайших достижений науки древнего мира.

Считается, что первое достаточно точное определение размеров Земли провел греческий ученый Эратосфен (276— 194 до н. э.), живший в Египте. Идея, положенная в основу измерений Эратосфена, весьма проста: измерить длину дуги земного меридиана в линейных единицах и определить, какую часть полной окружности эта дуга составляет. Получив эти данные, можно вычислить длину дуги в 1°, а затем длину окружности и величину ее радиуса, т. е. радиуса земного шара. Очевидно, что длина дуги меридиана в градусной мере равна разности географических широт двух пунктов: φ_B – φ_A.

Для того чтобы определить эту разность, Эратосфен сравнил полуденную высоту Солнца в них в один и тот же день. Измерив высоту Солнца h_B(рис. 3.8) в полдень 22 июня в Александрии, где он жил, Эратосфен установил, что Солнце отстоит от зенита на 7,2°. В этот день в полдень в городе Сиена (ныне Асуан) Солнце освещает дно самых глубоких колодцев, т. е. находится в зените h_A.

Следовательно, длина дуги составляет 7,2°. Расстояние между Сиеной (А) и Александрией (В) около 5000 греческих стадий — l.

Стадией в Древней Греции считалось расстояние, которое проходит легко вооруженный греческий воин за тот промежуток времени, в течение которого Солнце, коснувшееся горизонта своим нижним краем, целиком скроется за горизонт.

Несмотря на кажущееся неудобство такой единицы и достаточную громоздкость словесного определения, ее введение выглядело вполне оправданным, учитывая, что строгая периодичность небесных явлений позволяла использовать их движение для счета времени.

Обозначив длину окружности земного шара через L, получим такое выражение: 

откуда следует, что длина окружности земного шара равняется 250 000 стадий.

Точная величина стадии в современных единицах неизвестна, но, зная, что расстояние между Александрией и Асуаном составляет 800 км, можно полагать, что 1 стадия = 160 м. Это означает, что результат, полученный Эратосфеном, практически не отличается от современных данных, согласно которым длина окружности Земли составляет 40 000 км.

Эратосфен ввел в практику использование терминов «широта» и «долгота». Видимо, появление этих терминов связано с особенностями формы карт того времени: они повторяли по очертаниям побережье Средиземного моря, которое длиннее по направлению запад-восток (по долготе), чем с севера на юг (по широте).

Определить географическую широту двух пунктов оказывается гораздо проще, чем измерить расстояние между ними. Зачастую непосредственное измерение кратчайшего расстояния между этими пунктами оказывается невозможным из-за различных естественных препятствий (гор, рек и т. п.). Поэтому применяется способ, основанный на явлении параллактического смещения и предусматривающий вычисление расстояния на основе измерений длины одной из сторон (базиса — ВС) и двух углов В и С в треугольнике ABC(рис. 3.9).

Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя.

Чем дальше расположен предмет, тем меньше его параллактическое смещение, и чем больше перемещение наблюдателя (базис измерения), тем больше параллактическое смещение.

Для определения длины дуги используется система треугольников — способ триангуляции, который впервые был применен еще в 1615 г. Пункты в вершинах этих треугольников выбираются по обе стороны дуги на расстоянии 30 — 40 км друг от друга так, чтобы из каждого пункта были видны по крайней мере два других. Основой для вычисления длин сторон во всех этих треугольниках является размер базиса АС (рис. 3.10). Точность измерения базиса длиной в 10 км составляет около 1 мм. Во всех пунктах устанавливают геодезические сигналы — вышки высотой в несколько десятков метров. С вершины сигнала с помощью угломерного инструмента (теодолита) измеряют углы между направлениями на два-три соседних пункта. Измерив углы в треугольнике, одной из сторон которого является базис, геодезисты получают возможность вычислить длину двух других его сторон. Проводя затем измерение углов из пунктов, расстояние между которыми вычислено, можно узнать длину двух очередных сторон в треугольнике. Зная длину сторон этих треугольников, можно определить длину дуги АВ.

В какой степени форма Земли отличается от шара, выяснилось в конце XVIII в. Для уточнения формы Земли Французская академия наук снарядила сразу две экспедиции. Одна из них работала в экваториальных широтах Южной Америки в Перу, другая — вблизи Северного полярного круга на территории Финляндии и Швеции. Измерения показали, что длина одного градуса дуги меридиана на севере больше, чем вблизи экватора. Последующие исследования подтвердили, что длина дуги одного градуса меридиана увеличивается с возрастанием географической широты. Это означало, что форма Земли — не идеальный шар: она сплюснута у полюсов. Ее полярный радиус на 21 км короче экваториального.

Для школьного глобуса масштаба 1:50 000 000 отличие этих радиусов будет всего 0,4 мм, т. е. совершенно незаметно.

Отношение разности величин экваториального и полярного радиусов Земли к величине экваториального называется сжатием. По современным данным оно составляет 1/298 или 0,0034. Это означает, что сечение Земли по меридиану будет не окружностью, а эллипсом, у которого большая ось проходит в плоскости экватора, а малая совпадает с осью вращения.

В XX в. благодаря измерениям, точность которых составила 15 м, выяснилось, что земной экватор также нельзя считать окружностью. Сплюснутость экватора составляет всего 1/30 000 (в 100 раз меньше сплюснутости меридиана). Более точно форму нашей планеты передает фигура, называемая эллипсоидом, у которого любое сечение плоскостью, проходящей через центр Земли, не является окружностью.

В настоящее время форму Земли принято характеризовать следующими величинами:

• экваториальный радиус – 6378,160 км;
• полярный радиус – 6356,777 км;
• сжатие эллипсоида – 1 : 298,25;
• средний радиус – 6371,032 км;
• длина окружности экватора – 40075,696 км.

13.2 Определение расстояний в Солнечной системе.

Горизонтальный параллакс

Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определен горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является ее радиус.

Горизонтальным параллаксом (р) называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения (рис. 3.11).

Из треугольника OASможно выразить величину — расстояние OS = D:

,

где R— радиус Земли. По этой формуле можно вычислить расстояние в радиусах Земли, а зная его величину, — выразить расстояние в километрах.

Очевидно, что чем дальше расположен объект, тем меньше его параллакс. Наибольшее значение имеет параллакс Луны, который меняется в связи с тем, что Луна обращается по эллиптической орбите, и в среднем составляет 57′. Параллаксы планет и Солнца значительно меньше. Так, параллакс Солнца 8,8Ѕ. Такому значению параллакса соответствует расстояние до Солнца, примерно равное 150 000 000 км. Это расстояние принимается за одну астрономическую единицу (1 а. е.) и используется при измерении расстояний между телами Солнечной системы.

Известно, что для малых углов sin p ≈ p, если угол р выражен в радианах. В одном радиане содержится 206 265Ѕ. Тогда, заменяя sin р на р и выражая этот угол в радианной мере, получаем формулу в виде, удобном для вычислений:

или (с достаточной точностью)

Во второй половине XX в. развитие радиотехники позволило определять расстояния до тел Солнечной системы посредством радиолокации. Первым объектом среди них стала Луна. Затем радиолокационными методами были уточнены расстояния до Венеры, Меркурия, Марса и Юпитера. На основе радиолокации Венеры величина астрономической единицы определена с точностью порядка километра. Столь высокая точность определения расстояний — необходимое условие для расчетов траекторий полета космических аппаратов, изучающих планеты и другие тела Солнечной системы. В настоящее время благодаря использованию лазеров стало возможным провести оптическую локацию Луны. При этом расстояния до лунной поверхности измеряются с точностью до сантиметров.

Пример решения задач.

На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0,9″?

13.4. Определение размеров светил

Зная расстояние до светила, можно определить его линейные размеры, если измерить его угловой радиус ρ (рис. 3.12).

Формула, связывающая эти величины, аналогична формуле для определения параллакса:

Учитывая, что угловые диаметры даже Солнца и Луны составляют примерно 30′, а все планеты видны невооруженному глазу как точки, можно воспользоваться соотношением: sin ρ ≈ ρ. Тогда:

 и .

Следовательно,

.

Если расстояние Dизвестно, то

где величина ρ выражена в радианах.

Пример  решения задач

Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 30′?