Как найти линейный ток в треугольнике

П

Рис. 3. 11. 3.12.

ри соединении треугольником (рис.
4.11.) каждая фаза приемника подключена
к двум линейным проводам, поэтому каждое
фазное напряжение равно соответствующему
линейному напряжению.

Таким образом,
соединение треугольником следует
применять тогда, когда каждая фаза
трехфазного приемника рассчитана на
напряжение, равное номинальному линейному
напряжению сети.

Рис. 4.11.

Фазные токи
,,в общем случае не равны линейным токам,,и могут быть найдены по следующим
соотношениям:

,
,.

Линейные токи
,,могут быть определены через значения
фазных токов. Из первого закона Кирхгофа
запишем:

,
,.

Использую указанные
соотношения и имея векторы фазных токов,
можно построить векторную диаграмму
линейных токов (рис. 4.12.).

При симметричной
нагрузке соединением «треугольник»
равны в отдельности активные и полные
реактивные сопротивления всех фаз
,

Однако, как правило,
однофазные приемники подключаются не
одновременно. Нагрузку можно считать
симметричной лишь тогда, когда включены
все приемники. Для каждой фазы могут
быть использованы все методы расчета,
рассмотренные ранее применительно к
однофазной цепи с одним источником.
Зная, например, фазные напряжения и
сопротивления, можно по закону Ома найти
фазные токи по формулам
,,

При симметричной
нагрузке,
,-фазные токи равны друг другу и сдвинуты
по фазе относительно соответствующих
фазных напряжений на одинаковые углы.

В

Рис. 3. 13.

екторная диаграмма фазных напряжений
и токов на рис. 4.13. показывает, что при
симметричной нагрузке векторы фазных
токов равны по величине и сдвинуты по
фазе относительно друг друга на угол.

Векторы линейных
токов
изображают результирующими векторов
фазных токов, как показано на рис. 4.13.
Из векторной диаграммы следует, что_.

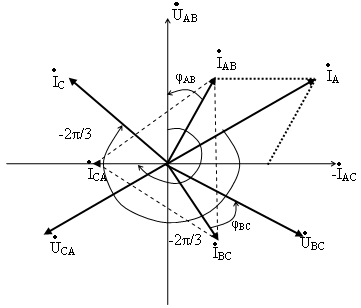
Рис. 4.13.

Такое же соотношение
существует между любыми другими фазными
и линейными токами. Поэтому можно
написать, что при симметричной нагрузке

_.

Зная фазные
напряжения, токи и углы сдвига фаз между
ними, либо токи и сопротивления, можно
найти фазные мощности. Например, мощности
фазы АВ будут равны

Таким же путем
находим мощности фаз ВС и СА. В силу
равенства напряжений, токов, углов
сдвига фаз и сопротивлений при симметричной
нагрузке
,,.

При симметричной
нагрузке активная Р,
реактивная Q
и полная S
мощности трехфазного приемника
,,

.

В качестве
номинальных напряжений и токов трехфазных
приемников указываются обычно линейные
напряжения и токи. Учитывая это, мощности
трехфазных приемников желательно также
выражать через линейные напряжения и
токи
,,_.

4.6. Несимметричные нагрузки при соединении треугольником

Несимметричной
нагрузкой считают такую, при которой
активное или реактивное сопротивление
хотя бы одной из фаз не равно сопротивлениям
других фаз (рис. 4.14.) r_AB
= r_BC
= r_C;
X_AB=X_BC≠X
_CA.
В таком
случае при несимметричной нагрузке Z_AB
≠ Z_BC
≠ Z_CA.

Фазные токи, углы
сдвига фаз между фазными напряжениями
и токами, а также мощности могут быть
определены по формулам

,
,

Так как,
а при несимметричной нагрузкеZ_AB
≠ Z_BC
≠ Z_CA,
то.

Рис. 4.14.

Углы сдвига фаз
между фазными токами и напряжениями
зависят от величины и характера
сопротивлений фаз и могут быть определены
следующим образом
;;.

Т.о., при несимметричной
нагрузке фазные токи, углы сдвига фаз
и фазные мощности в общем случае
различные.

Зная фазные
напряжения, токи и углы сдвига фаз между
ними, либо токи и сопротивления, можно
найти фазные мощности. Например, мощности
фазы AB

Активные и реактивные
мощности приемника
;
.

Векторная диаграмма
при несимметричной нагрузке для случая,
когда в фазе AB
имеется активное сопротивление, в фазе
BC
– активное и индуктивное сопротивления,
фазе CA
– активное и емкостное сопротивления,
приведена на рис. 4.15. Построение векторов
линейных токов произведено в соответствии
с выражениями
,
,.

Если
кроме фазных токов, требуется определить
линейные токи, то их можно так же
определить по векторной диаграмме, не
прибегая к решению задачи в комплексной
форме.

Рис. 4.15.

О

Рис. 3. 15.

тключение нагрузки одной из фаз
можно считать частным случаем
несимметричной нагрузки, при которой
сопротивление отключенной фазы равно
бесконечности. Так при отключении фазыCA
сопротивление Z
_CA
= ∞. При этом, ток
;
фазные токи,
а также углыφ_AB,
φ _BC
не изменятся, а линейные токи
уменьшатся и будут равны
,
_.

Всем привет мои дорогие друзья, подписчики, и все кто читает эту статью. Сегодня я хочу ответить на часто задаваемый вопрос новичков и студентов: “Чем отличается фазные напряжения и токи от линейных”. Я отвечу по простому, чтобы этот материал мог понять каждый, поэтому не надо говорить, что я где-то использовал не правильную терминологию.

Начну по порядку. Существует в основном две схемы подключения трехфазных источников питания и их потребителей, это звезда и треугольник. Есть еще зигзаг, но его я рассматривать не буду. И мы будем ориентироваться по схеме соединения источника.

Первый вариант это звезда. Как вы видите на схеме, концы или начала обмоток соединяют между собой и существует центральная четвертая точка, так называемая нулевая точка трансформатора или генератора, которую обычно с сетях электроснабжения заземляют. Такие сети называют – с глухозаземленной нейтралью.

Если мы говорим про фазное напряжение, то это напряжение на одной обмотке, или как в нашем случае, это между фазой и нейтралью источника. Линейное напряжение – это напряжение между линиями, то есть между двух фаз. В этой схеме линейное напряжение больше фазного в квадратный корень из 3 раз. То есть получается линейное напряжение равно квадратный корень из трех умноженное на фазное напряжение.

Про ток – тоже самое. Фазный ток – это ток в одной обмотке фазы. А линейный ток – это ток в линии одной фазы. Получается, что ток протекающий в обмотке источника и по одной фазе линии равны. И мы можем записать формулу, что линейный ток равен фазному.

Рассмотрим второй вариант, это схема соединения треугольником. Здесь нет нейтрали, и конец одной обмотки подключен к началу другой. Здесь картина полностью противоположенная.

Фазное напряжение – это напряжение на одной обмотке. А линейное, между двумя фазами. Получается, что на обмотке и между ее двумя фазами напряжение одно и тоже, поэтому мы можем записать это в формулу, что линейное напряжение равно фазному.

Теперь рассмотрим как протекает ток. Фазный ток, это ток протекающий по одной обмотке. А линейный по одной фазе, и как вы заметили, что ток в этой системе будет отличаться. Линейный ток равен квадратному корню из трех умноженное на фазный ток.

Если Вам понравилась эта статья, то поставьте ей лайк, а также не забудьте подписаться на наш канал. Всего Вам доброго, до новых встреч

Как найти линейный ток в трехфазной цепи?

На фазах нагрузки находят линейные напряжения источника питания. Фазные токи в нагрузке определяют с помощью закона Ома для участка цепиIф = Uф/zф, где Uф – фазное напряжение на нагрузке (соответствующее линейное напряжение источника питания); zф – полное сопротивление соответствующей фазы нагрузки.

Как найти ток в трехфазной цепи?

На практике применяется формула, в которой ток и напряжение обозначают линейные величины и для соединения в звезду и в треугольник. В первое уравнение подставим Uф=U/1,73, а во второе Iф=I/1,73, получим общую формулу P=1,73·U·I·cosфи.

Как определить линейные токи?

При соединении в звезду с нулевым проводом можно получить два напряжения: линейное напряжение Uл между проводами отдельных фаз и фазное напряжение Uф между фазой и нулевым проводом (рис. 2). Соотношение между линейным и фазным напряжениями выражается следующим образом: Uл=Uф∙√3.

Что такое линейный ток?

Линейный ток — ток, протекающий по линейному проводу. При соединении звездой линейный ток равен фазному. При работе по нулевому проводу протекает ток, равный векторной сумме трех линейных токов: IА, IB и IC.

Как найти фазное напряжение?

При соединении в звезду с нулевым проводом можно получить два напряжения: линейное напряжение Uл между проводами отдельных фаз и фазное напряжение Uф между фазой и нулевым проводом (рис. 2). Соотношение между линейным и фазным напряжениями выражается следующим образом: Uл=Uф∙√3.

Что такое фазное напряжение?

Uф — фазное напряжение — это напряжение между началом и концом фазной обмотки или приемника энергии. Другими словами можно сказать: фазное напряжение — это напряжение между ли-нейным и нулевым проводами. При симметричной нагрузке нулевой провод практически не нужен, т.

Что такое косинус фи?

Коэффициент мощности cos фи (φ) определяется как отношение полезной мощности к полной. Математически это определение часто записывают в виде кВт/кВА, где числитель – активная (действительная) мощность, а знаменатель – кажущаяся (активная + реактивная, полная) мощность.

Как узнать ток двигателя по мощности?

Зная номинальную мощность двигателя (из паспорта) можно определить его номинальный ток. При включении двигателя в трехфазную сеть 380 В номинальный ток можно посчитать по следующей формуле: Iн = Pн/(√3Uн х η х сosφ), где Pн — номинальная мощность двигателя в кВт, Uн — напряжение в сети, в кВ (0,38 кВ).

Как рассчитать мощность трехфазного автомата?

Расчет мощности трехфазного автомата

1. Для расчета мощности номинала трехфазного автомата необходимо суммировать всю мощность электроприборов, которые будут подключены через него. …
2. L1 5000 W + L2 5000 kW + L3 5000W = 15000 W.
3. Полученные ваты переводим в киловатты:
4. 15000 W / 1000 = 15 kW.
5. Полученное число умножаем на 1,52 и получаем рабочий ток А.

Какой из токов в схеме линейный какой фазный?

Так, токи, протекающие в каждой фазе, именуют фазными и условно обозначают IА, IB, IC либо условно Iф. Токи в ветвях нагрузки именуют линейными. … При сугубо активной нагрузке токи идентичны с напряжениями по фазе, а при индуктивной либо емкостной нагрузке, токи могут опережать или отставать от напряжения.

Как измерить линейные и фазные напряжения?

КРАТКО: Линейное напряжение измеряется между фазой и фазой, а фазное между фазой и нулём. Линейное напряжение больше фазного в √3 или в 1,73 раза. Нагрузка к трёхфазной сети может быть подключена по трём или четырем проводам.

В каком соотношении находятся линейные и фазные напряжения?

больше фазных, а при соединении треугольником равны. Этот фактор необходимо учитывать при подключении нагрузки, чтоб не произошло аварийных ситуаций и выхода оборудования из строя. Линейные напряжения тоже сдвинуты друг относительно друга на угол 1200 или 2π/3.

Что такое звезда в электрике?

В трехфазных цепях применяют два вида соединений генераторных обмоток – в звезду и треугольник (рис. 1). При соединении в звезду все концы фазных обмоток соединяют в один узел, называемый нейтральной или нулевой точкой, и обозначают, как правило, буквой O.

Чему равно фазное напряжение в треугольнике?

180, линейное напряжение создает каждая фазная обмотка. У потребителя, соединенного треугольником, линейное напряжение подключается к зажимам фазного сопротивления. Следовательно, при соединении треугольником фазное напряжение равно линейному: Uл = Uф.

Задачи на трехфазные цепи

Трехфазные электрические цепи получили широкое распространение в промышленности, благодаря своим немалым преимуществам перед другими системами электрических цепей. К ним относятся – экономичность передачи энергии, относительная простота создания вращающегося магнитного поля, а также возможность получения двух значений напряжения. Основными потребителями трехфазных систем являются асинхронные двигатели, а основными источниками – трехфазные генераторы.

В разделе электротехники трехфазным цепям переменного тока посвящено немало задач, рассмотрим решение некоторых из них.

Задача 1

Обмотки трехфазного генератора соединены по схеме “звезда”, э.д.с. в них 220 В. Построить векторные диаграммы и определить линейные напряжения для схемы соединения, в которой в одной точке сходятся: a) X Y Z б) X B Z в) X B C . Начала обмоток – A,B,C, концы обмоток – X,Y,Z. Принять нагрузку на генераторе равной нулю.

а) Для данной схемы соединения векторная диаграмма будет выглядеть следующим образом

Линейные напряжения в данном случае будут равны и определяться как

б) Так как обмотка BY подключена началом в нейтральную точку, то вектор напряжения оказывается повернутым на 180 относительно нормального положения.

Линейные напряжения в данном примере будут разными по значению

в) В данном случае относительно нормального положения повернуты вектора двух обмоток – BY и CZ.

Как и в предыдущем примере, линейные напряжения не будут равны

Задача 2

К зажимам приемника подсоединён трехфазный генератор, как показано на схеме. Определить показания амперметров A₁,A₂ и фазные токи зная, что U_л=380В, R=50 Ом, x_L=35 Ом.

Определим комплексные значения сопротивления (для удобства вычислений будем переводить в показательную форму)

Напряжения в фазах будет равно

Токи в фазах

Ток в нейтральном проводе равен (для удобства сложения сначала переведем из показательной формы в алгебраическую, а затем наоборот)

Соответственно, показания амперметров будут следующими:

К зажимам приемника, подсоединён трехфазный генератор, обмотки которого соединены по схеме “треугольник”. Определить фазные и линейные токи, показания вольтметра, зная, что линейное напряжение равно 220 В, R=25 Ом, x_L=x_C=10 Ом.

Как и в предыдущей задаче, в первую очередь определим комплексы сопротивлений

Фазное напряжение при данном соединении будет равно линейному, следовательно

Фазные токи при несимметричной нагрузке не равны

Для определения линейных токов представим фазные токи в алгебраической форме комплексного числа

Сумма линейных токов

Равенство нулю суммы линейных токов является свойством любой трёхфазной системы.

Чтобы определить показания вольтметра, найдём сумму падений напряжения на x_L и R в соответствующих обмотках.

Так решаются задачи на трехфазные цепи . Спасибо за внимание! Читайте также – задачи на цепи переменный ток

Примеры решения задач на расчет цепей при соединении треугольником

Пример №1

Задача

В трехфазную сеть с U_Л = 380 В включен соединенный треугольником трехфазный асинхронный двигатель мощностью P = 5 кВт, КПД двигателя равен η_Н = 90%, коэффициент мощности cos φ_Н = 0,8. Определить фазные и линейные токи двигателя, параметры его схемы замещения R_Ф, X_Ф, построить векторную диаграмму. Включить ваттметры для измерения активной мощности и найти их показания.

Анализ и решение задачи

Двигатель является активно-индуктивным потребителем энергии, его схема замещения приведена на рис. 2

Расчет активной мощности и токов, потребляемых двигателем из сети.

В паспорте двигателя указывается механическая мощность на валу; потребляемая активная мощности двигателя

P = P_Н / η = 500 / 0.9 = 5560 Вт.

Для симметричной нагрузки, какой является двигатель,

P = 3 U_Ф I_Ф cos φ и I_Ф = P / (3 U_Ф cos φ).
I_Ф = 5560 / (3 · 380 · 0,8) = 6,09 А.
I_Л = I_Ф = · 6,09 = 10,54 А.

Расчет параметров схемы замещения двигателя.

Z_Ф = U_Ф / I_Ф = 380 / 6,09 = 62,4 Ом; R_Ф = Z_Ф cos φ = 62,4 · 0,8 = 49,9 Ом;
X_Ф = Z_Ф sin φ_Ф = 62,4 · 0,6 = 37,4 Ом; cos φ_Ф = cos φ_Н = 0,8.

Построение векторной диаграммы.

Линейные напряжения строятся в виде симметричной звезды, они же являются в данном случае фазными напряжениями. Фазные токи отстают от напряжений на угол φ_Ф, линейные токи строятся по фазным на основании уравнений, составленных по первому закону Кирхгофа:

Векторная диаграмма показана на рис. 3

Схема включения ваттметров.

В трехпроводных сетях часто для измерения активной мощности применяется схема двух ваттметров, один из вариантов которой показан на рисунке 4. Показания ваттметра определяются произведением напряжения, приложенного к его катушке напряжения, на ток в токовой катушке и косинус угла между ними:

Активная мощность трехфазной цепи равна алгебраической сумме показаний приборов: P = P₁ + P₂ = 1573 + 3976 = 5549 Вт.

На рисунке 5 показано еще два варианта подключения приборов по схеме двух ваттметров.

При симметричной нагрузке можно измерить мощность одним ваттметром, подключив его обмотку напряжения к соответствующему фазному напряжению сети (если доступна нейтральная точка) или создав искусственную точку (рис. 6), при этом прибор измеряет мощность одной фазы, мощность всей цепи P_цепи = 3 P_W.

Пример № 2

Задача

К источнику с U_Л = 220 В подключена соединенная треугольником осветительная сеть. Распределение нагрузки по фазам: P_AB = 2200 Вт, P_BC = 3300 Вт, P_CA = 4400 Вт. Вычислить активную мощность, потребляемую схемой из сети, фазные и линейные токи приемников.

Анализ и решение задачи

Активная мощность всей нагрузки равна сумме мощностей фаз:

P = P_AB + P_BC + P_CA = 2200 + 3300 + 4400 = 9900 Вт.

Расчет фазных токов. Т.к. осветительная сеть имеет cos φ = 1, для любой фазы I_Ф = P_Ф / U_Ф, поэтому:

Аналитический расчет линейных токов выполняется комплексным методом на основании 1-го закона Кирхгофа; определим их графически, построив векторную диаграмму (рис. 7, а)

Из диаграммы следует: I_A = 27,6 А; I_B = 22,8 А; I_C = 26,6 А.

Задание 1. Выполните расчет трехфазной цепи по условиям задачи 1.

В трехфазную сеть с U_Л = 380 В включен по схеме треугольник асинхронный двигатель, имеющий Z_Ф = 19 Ом, cos φ_Ф = 0,8. Найти линейные токи и активную мощность, потребляемую двигателем из сети.

Ответ: 34,6 А; 18,2 кВт.

Задание 2. Выполните расчет трехфазной цепи по условиям задачи 2.

Трехфазная печь включена в сеть с U_Л = 380 В по схеме треугольник. Найти линейный ток и мощность печи, если R_Ф = 10 Ом. Как изменятся линейный ток и мощность печи, если ее включить в ту же сеть по схеме звезда?

Ответ: 65,7 А; 43,2 кВт; 21,9 А; 14,4 кВт.

Контрольные вопросы

1. Начертите схему соединения потребителей по способу «треугольник» и подключения их к трехфазной сети.

2. Как определить общую активную Р, реактивную Q и полную S мощности электроприемников в несимметричной трехфазной цепи при их соединении треугольником?

3. Как определить общую активную Р, реактивную Q и полную S мощности электроприемников в симметричной трехфазной цепи при их соединении треугольником?

4. Как определить активную Рф, реактивную Qф и полную Sф мощности для отдельной фазы?

5. Запишите соотношение между фазными и линейными токами при соединении «треугольником»?

6. Запишите соотношение между фазными и линейными напряжениями при соединении «треугольником»?

7. Опишите, что произойдет в системе трехфазного питания при обрыве одного из линейных проводов.

Трехфазные цепи

Содержание:

Общие сведения о трёхфазных цепях

Трёхфазная электрическая цепь может быть представлена как совокупность трёх однофазных цепей, в которой действуют ЭДС одной и той же частоты, сдвинутые относительно друг друга на одну треть периода или, что то же самое, на угол .

Эти три составные части трёхфазной цепи называются фазами и им будем приписывать буквенные обозначения А, В, С. Таким образом, термин “фаза” в электротехнике обозначает два понятия: угол, определяющий стадию периодического процесса, и составную часть трёхфазной цепи.

Изобразим трёхфазную цепь, фазы которой не связаны друг с другом (рис. 1). Такую трёхфазную цепь называют несвязанной (в настоящее время не применяется).

Фазы изображены под углом 120° для того чтобы подчеркнуть, что напряжения источников сдвинуты относительно друг другу на одну треть периода. Следовательно,

Кривые, изображающие эти напряжения, показаны на рис. 2.

При равенстве амплитуд напряжений и одинаковых сопротивлениях нагрузки Z в фазах токи также равны по величине и сдвинуты относительно друг друга на одну треть периода, образуя так называемый трёхфазный ток. Сумма этих токов в любой момент времени равна нулю:

Поэтому, если три провода, по которым токи возвращаются к источникам, объединить в один, то ток в этом проводе будет равен нулю. При отсутствии в проводе тока излишним в данном случае является и сам провод, от него можно отказаться, перейдя к схеме рис. 3.

В результате этого достигается экономия материала проводов; кроме того, по сравнению с несвязанной трёхфазной цепью исключаются потери мощности от токов в обратном проводе.

Возможно вам будут полезны данные страницы:

Трёхфазная цепь (рис. 3), фазы которой соединены электрически, представляет одну из разновидностей так называемых связанных трёхфазных цепей.

Необходимо отметить, что для получения связанной трёхфазной цепи не требуются отдельные однофазные генераторы, а используется один трёхфазный генератор.

Обмотки трёхфазного генератора могут быть соединены либо звездой, либо треугольником. При соединении звездой концы обмоток соединяют в общую точку, которую называют нейтральной. Начало обмоток обозначают Л, В, С; концы -х, у, z (рис. 4, а).

Начала обмоток соединяют с нагрузкой линейными проводами, по которым идут линейные токи.

Будем в дальнейшем пользоваться следующей терминологией: ЭДС, индуктируемые в обмотках генератора или трансформатора, напряжения на зажимах обмоток и токи в них называть фазными ЭДС, напряжениями и токами, а напряжения между линейными проводами и токи в них – линейными напряжениями и токами. Па схеме (рис. 4, a) , – комплексы фазных напряжений генератора; – комплексы линейных напряжений. Абсолютные значения этих напряжений являются их модулями, т.е.

Связь между линейными и фазными напряжениями устанавливается на основании второго закона Кирхгофа:

Топографическая векторная диаграмма линейных и фазных напряжений генератора приведена на рис. 4, б.

Из векторной диаграммы следует, что при соединении генератора звездой линейные напряжения равны по величине и сдвинуты относительно друг друга на угол .

Па основании геометрических соображений легко показать, что между фазными и линейными напряжениями при соединении звездой существует следующее соотношение:

Действительно из треугольника (рис. 4, б) следует

При соединении генератора треугольником конец первой фазы соединяется с началом второй фазы, конец второй – с началом третьей, конец третьей – с началом первой (рис. 5, а).

Топографическая диаграмма напряжений приведена на рис. 5, я. Векторная диаграмма напряжений показана на рис. 5, б.

Общие точки соединённых обмоток генератора выводятся на зажимы, к которым присоединяются линейные провода или нагрузка.

Нагрузка (потребитель) в трёхфазной цепи также может быть соединена звездой или треугольником.

Симметричный режим работы трёхфазной цепи

Трёхфазные цепи представляют собой разновидность цепей синусоидального тока и поэтому расчёт и исследование их производятся теми же методами, что и для однофазных цепей. Расчёт трёхфазной цепи, так же как и расчёт всякой сложной цепи, ведётся обычно в комплексной форме. Ввиду того что фазные ЭДС и напряжения генератора сдвинуты относительно друг друга на 120°, для краткости математической записи применяется фазовый оператор – комплексная величина:

Умножение вектора на оператор а означает поворот вектора на 120° в положительном направлении (против хода часовой стрелки), соответственно умножение вектора на означает поворот вектора на 240° в положительном направлении или, что то же самое, поворот вектора на 120° в отрицательном направлении:

Три вектора образуют симметричную трёхфазную систему векторов. При этом . При помощи оператора а можно, например, записать напряжения фаз трёхфазной системы как

Па практике применяются различные комбинации соединений, например, генератор и нагрузка соединяются звездой, генератор может быть соединен звездой, а нагрузка – треугольником и т.д.

На рисунке 6, а показано соединение нагрузки звездой. Па схеме обозначены: – линейные токи; -фазные напряжения нагрузки; Z-сопротивления нагрузки.

В этой схеме комплексы фазных напряжений источника и комплексы фазных напряжений нагрузки соответствующих фаз равны между собой, т.е.

Векторная диаграмма напряжений и токов имеет вид, показанный на рис. 6, б. Ток в каждой фазе отстаёт от напряжения той же фазы на угол

где R и X- активное и реактивное сопротивления фаз.

Ток в каждой из фаз находят так же, как и в однофазной цепи. Например, в фазе А

Соответственно токи в фазах В и С выражаются через ток :

Таким образом, при симметричном режиме работы трёхфазной цепи задача сводится к расчёту одной из фаз аналогичш расчёту однофазной цепи.

Линейное напряжение определяется как разности соответствующих фазных напряжений. Например:

При соединении нагрузки треугольником (рис. 7, а) сопротивления отдельных фаз находятся под линейными напряжениями, поэтому фазные токи в них определяются по закону Ома:

Линейные токи определяются на основании первого закона Кирхгофа. Так, линейный ток фазы А равен

т.е. линейный ток отстаёт по фазе на 30° от тока , причём модуль его в раз больше фазного тока .

Таким образом, при симметричном режиме работы цепи имеет место следующее соотношение:

Векторная диаграмма линейных напряжений и токов при соединении нагрузки треугольником показана на рис. 7, б. Как и при соединении звездой, угол сдвига фаз равен

Активная мощность симметричной трёхфазной цепи равна

При соединении нагрузки звездой

Поэтому активная мощность трёхфазной цепи, выраженная через линейные токи и линейные напряжения,

При соединении нагрузки треугольником

Активная мощность трёхфазной цепи будет такой же:

Следовательно, независимо от схемы соединения нагрузки

Аналогично, реактивная мощность

и полная мощность симметричной треугольной цепи

При этом коэффициент мощности определяется из соотношения

где – угол сдвига фазного тока относительно соответствующего фазного напряжения.

Измерение мощности в трёхфазной цепи

Для измерения мощности в трёхфазной цепи с нейтральным проводом простейшим является метод трёх ваттметров (рис. 12). При таком соединении каждый из ваттметров измеряет активную мощность одной фазы приёмника (нагрузки). Активная мощность всей трёхфазной цепи равна сумме показаний трёх ваттметров:

Если нагрузка симметрична, достаточно произвести измерение одним ваттметром:

При отсутствии нейтрали провода достаточно иметь два ваттметра. В соответствии с (6) для схемы рис. 13 комплекс мощности всей цепи может быть записан как

При выводе формулы (6) не делалось никаких предположений о симметрии цепи; следовательно, данный метод

измерения двумя ваттметрами применим как в случае симметричной, так и в случае несимметричной трёхфазной системы.

Показания ваттметров следующие:

Мощность всей трёхфазной цепи

т.е. равна сумме показаний отдельных ваттметров.

Измерение реактивной мощности в трёхфазных цепях производится с помощью специальных измерителей реактивной мощности, подобных по устройству ваттметрам. В симметричной трёхфазной цепи измерение реактивной мощности может быть произведено, кроме того, с помощью ваттметров активной мощности. В этом случае ваттметр может быть включён в схему, как показано на рис. 14.

Поскольку при симметричной нагрузке как при соединении треугольником, так и при соединении звездой угол между линейным напряжением и линейным током равен 90° – , то показание ваттметра будет

Для получения суммарной реактивной мощности показание ваттметра нужно умножить на :

где В данном случае , т.е. нагрузка носит индуктивный характер.

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

[spoiler title=”источники:”]

http://poisk-ru.ru/s52946t22.html

http://natalibrilenova.ru/trehfaznyie-tsepi/

[/spoiler]