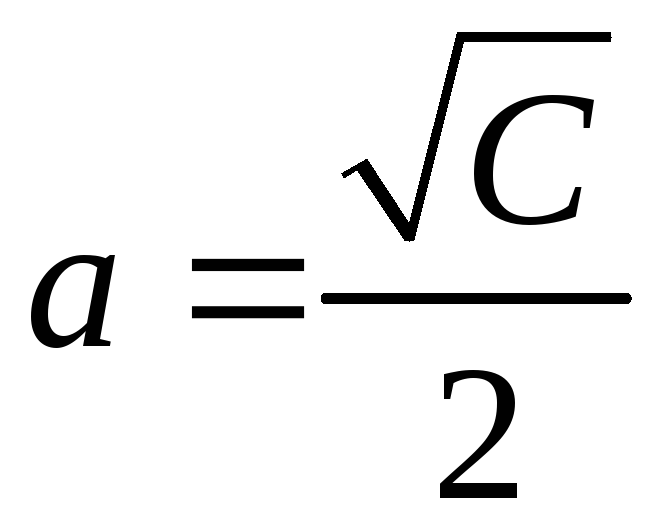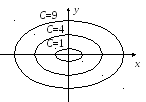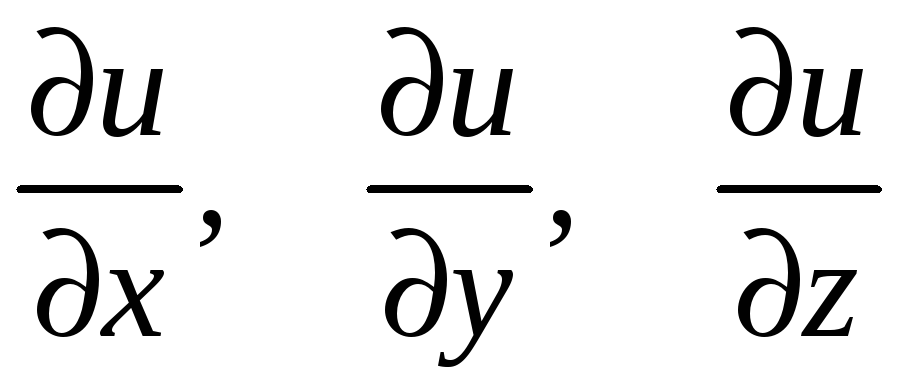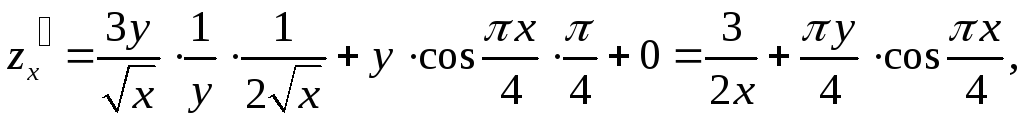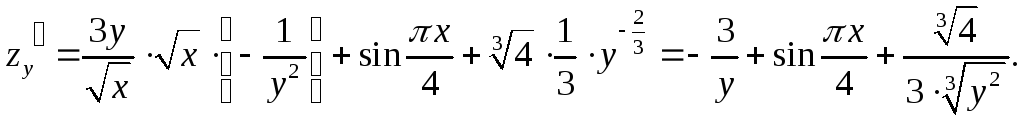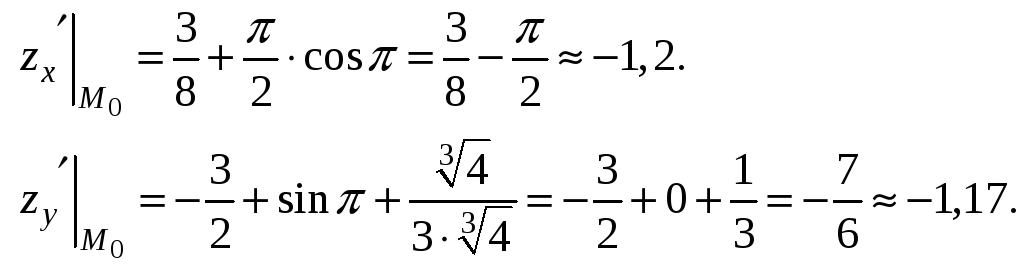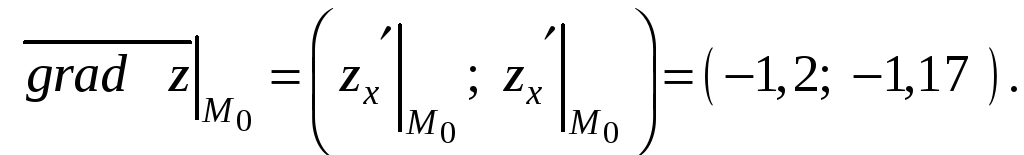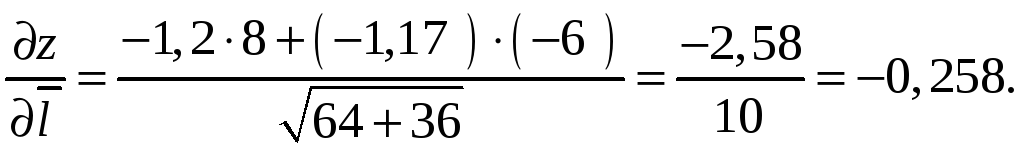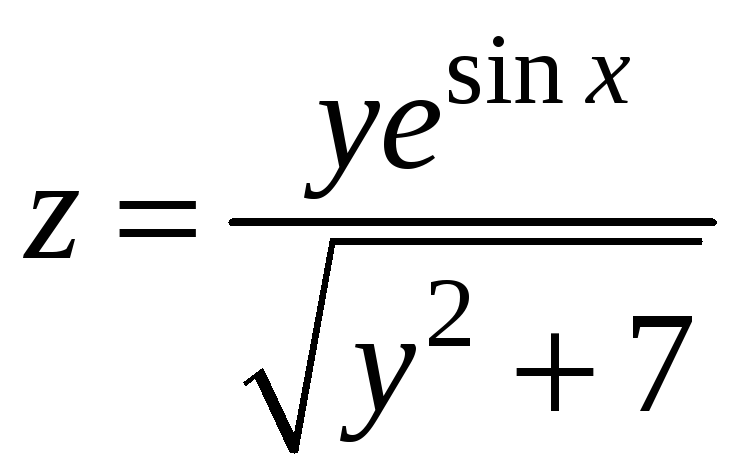Как найти линии уровня для функции онлайн

Найти уравнение и построить линии функций

Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции

Что умеет находить этот калькулятор:

• Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
• Умеет определять точки пересечения графика функции с осями координат: Да
• Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
• Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
• Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
• Горизонтальные асимптоты графика функции: Да
• Наклонные асимптоты графика функции: Да
• Четность и нечетность функции: Да

Правила ввода выражений и функций

3.14159.. e Число e – основание натурального логарифма, примерно равно

2,7183.. i Комплексная единица oo Символ бесконечности – знак для бесконечности

© Контрольная работа РУ – калькуляторы онлайн

Функции нескольких переменных

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Пусть: z – переменная величина с областью изменения R; R- числовая прямая; D – область на координатной плоскости R2.

Любое отображение D->R называют функцией двух переменных с областью определения D и пишут z = f(x;y).

Если каждой паре (х; у) двух независимых перемен­ных из области D по некоторому правилу ста­вится в соответствие одно определенное значение z из R, то переменную величину z называют функцией двух не­зависимых переменных х и у с областью определения D и пишут

Аналогичным образом определяются функции многих переменных

П р и м е р 1. Найти и изобразить область определения функции

Область определения – есть плоскость хОу за исключением точек, лежащих на параболе у = х2, см. рисунок.

П р и м е р 2. Найти и изобразить область определения функции

Область определения – есть часть плоско­сти, лежащая внутри круга радиуса г = 3 , с центром в начале координат, см. рисунок.

П р и м е р 3. Найти и изобразить область определения функции

Область определения – есть часть плоско­сти, в которой абсцисса и ордината ка­ждой точки имеют одинаковые знаки, т. е. это часть плоскости, лежащая в пер­вом и третьем координатных углах, см. рисунок.

К числу функций нескольких переменных относятся производственные функции.

Производственными функциями называют функ­ции, представляющие зависимости величин объемов вы­пускаемой продукции от переменных величин затрат ре­сурсов.

Производственные функции применяются не только в микроэкономических, но и в макроэкономических рас­четах.

Простейшая производственная функция – функция зависимости объема произведенной работы V от объемов трудовых ресурсов R и вложенного в производство капи­тала К

2.ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ФУНКЦИИ ДВУХ

2.1.График функции двух переменных

Рассмотрим в пространстве прямоугольную систему координат и область D на плоскости хОу. В каждой точке М(х;у) из этой области восстановим перпендикуляр к плос­кости хОу и отложим на нем значение z = f(x; у). Геомет­рическое место полученных точек

является пространственным графиком, функции двух переменных.

Это некоторая поверхность.

Равенство z = f(x; у) называется уравнением этой по­верхности.

Функция двух переменных имеет наглядную геомет­рическую интерпретацию. Для функции числа перемен­ных n > 2 аналогом поверхности является гиперповерх­ность (n + 1) – мерного пространства, не имеющая геомет­рической интерпретации.

Линией уровня функции двух переменных z = f(x; у) называется линия f(x; у) = С (С = const) на плоскости хОу, в каждой точке которой функция сохраняет постоянное значение С.

Линия уровня представляет собой сечение поверхности графика функции двух переменных z = f(x; у) плоскостью z = С.

Поверхностью уровня функции трех переменных

u = f(x; у; z) называется поверхность в R3 (трехмерном про­странстве), в каждой точке которой функция сохраняет постоянное значение f(x;y;z) = C (С = const).

П р и м е р. Найти и построить линии уровня функции

Решение.

Линии уровня z = С данной функции имеют уравнения

Это окружности с центром в начале координат, радиусом R = C1/2 и уравнением

x2 + y2 = R2, см. рисунок.

Линии уровня позволяют представить рассматриваемую поверхность, дающую в сечении плоскостями z = C концентрические окружности.

При построении графика функции часто пользуются методом сечений.

П р и м е р. Построить график функции и найти .

Решение. Воспользуемся методом сечений.

– в плоскости – парабола.

– в плоскости –парабола.

– в плоскости – окружность.

Искомая поверхность – параболоид вращения.

Расстоянием между двумя произвольными точками и (евклидова) пространства называется число

Множество точек называется открытым кругом радиуса с центром в точке r.

Открытый круг радиуса ε с центром в точке A называется – ε – окрестностью точки А.

Найти и изобразить графически область определения функции:

Построить линии уровня функций:

3. ПРЕДЕЛ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

Основные понятия математического анализа, введен­ные для функции одной переменной, распространяются и на функции нескольких переменных.

О п р е д е л е н и е:

Постоянное число А называется пределом функции двух переменных z = f(x;у) при х —> х0, у —> у0, если для лю­бого

ε >0 существует δ >0 такое, что |f(х; у) – А| 0 – постоянное число.

Постоянное число А называется пределом функции двух переменных f(x;y) = f(M) при стремлении точки М к точке М0, если для любого ε >0 можно найти такое число г >0, что как только расстояние |М0М| 0.

Предел отношения при Δs—>0 называется произ-

водной функции z = f(х; у) в точке (х; у) по направлению вектора и обозначается

Переходя к этому пределу, получим

(*)

Таким образом, зная част­ные производные функции

z = f(x; у) можно найти произ­водную этой функции по любому направлению, а каждая частная производная является частным случаем произ­водной по направлению.

П р и м е р. Найти производную функции

в точке М(1;0) в направлении, составляющем с Ох угол в 30°.

Следовательно, функция z = f(x;y) в данном направлении возрастает.

Градиентом функции z = f(x; у) называется вектор , координатами которого являются соответствующие частные производные данной функции

Связь между производной функции по направлению и градиентом этой функции осуществляется соотношени­ем

т. е. производная функции z = f(x;y) в данном направле­нии равна проекции градиента функции на направле­ние дифференцирования.

Градиент функции в каждой точке направлен по нормали к соответствующей линии уровня данной функ­ции.

Направление градиента функции в данной точке есть направление наибольшей скорости возрастания функции в этой точке.

Линии и поверхности уровня

Содержание:

Линии и поверхности уровня

Понятие линии и поверхности уровня:

Для характеристики функций двух переменных вводится понятие линий уровня.

Определение 2. Линией уровня функции z = f (x, y) называется совокупность всех точек на плоскости Oxy, для которых выполняется условие f (x, y) = C.

Линии уровня можно получить, пересекая поверхность z = f (x, y) плоскостями z = C, где С = соnst.

Пример 1. Найти линии уровня функции z = x 2 + y 2 .

Решение.
Пусть z = C. x 2 + y 2 = C (C ≥ 0),

В этом случае линиями уровня является множество концентрических окружностей с центром в начале координат и радиусом С (рис. 2) .Аналогично вводится понятие поверхности уровня для функции трех переменных u = f (x, y, z), (f (x, y, z) = C).

Пример 2. Найти поверхности уровня функции u = x 2 + y 2 + z 2 .

Решение. Пусть u = C. Тогда x 2 + y 2 + z 2 = C (C ≥ 0) — это множество сфер с центром в точке O(0; 0; 0) и радиусом C.

Поверхности второго порядка

Наиболее изучены поверхности в курсе аналитической геометрии — поверхности второго порядка. В общем случае уравнение такой поверхности имеет вид:
a₁₁ x 2 + 2a₁₂ xy + a₂₂ y 2 + 2a₁₃ xz + 2a₂₃ yz + a₃₃ z 2 + 2a₁₄ x + 2a₂₄ y + 2a₃₄ z + a₄₄ = 0.

В зависимости от значений коэффициентов получают различные поверхности второго порядка.

Например:
1) — конус;

2) — полусфера;

Рис. 4.

3) — эллиптический параболоид;

Рис. 5.

4) — гиперболический параболоид;

рис.6

5) — трехосный эллипсоид.

Рис. 7.

Для изучения поверхностей в трехмерном пространстве применяется метод сечений. Суть этого метода такова: пересекаем заданную поверхность плоскостями x = C₁, y = C₂, z = C₃. В результате получим некоторые кривые, характеризующие поверхность.

Пример 3. z = x 2 + y 2 . Пусть z = C₁ (C₁ ≥ 0). Получим уравнение x 2 + y 2 = C₁ (уравнение окружности). Положим y = C₂ , тогда — уравнение параболы в плоскости Оxz, которая смещена на единиц вверх по оси Oz. Положим x = C₃ , получим уравнение
Получили уравнение параболы в плоскости Оyz, которая смещена на единиц вверх по оси Оz. Из этих исследований вытекает, что графиком функции z = x 2 + y 2 является параболоид вращения вокруг оси Оz.

Гиперповерхности уровня

Пусть задана функция от n переменных u = f (x₁, x₂, . x_n) . Если положить u = C, то получим уравнение f (x₁, x₂, . x_n) = C, которое называется уравнением гиперповерхности уровня в пространстве R n . Например: Если u = C, то уравнение является уравнением гиперсферы в R n с центром в точке O (0,0, . 0) и радиусом .

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

[spoiler title=”источники:”]

http://pandia.ru/text/78/481/32586.php

http://natalibrilenova.ru/linii-i-poverhnosti-urovnya/

[/spoiler]

Основные функции

• : x^a

модуль x: abs(x)

Построение графиков функций

Сервис поддерживает возможность построения графиков функций как вида , так и вида . Для того, чтобы построить график функции на отрезке нужно написать в строке: f[x],{x, a, b}. Если Вы хотите, чтобы диапазон изменения ординаты был конкретным, например , нужно ввести: f[x],{x, a, b},{y, c, d}.

Примеры

• x^2+x+2, {x,-1,1};
• x^2+x+2, {x,-1,1},{y,-1,5};
• Sin[x]^x, {x,-Pi,E};
• Sin[x]^x, {x,-Pi,E},{y,0,1}.

Если Вам требуется построить сразу несколько графиков на одном
рисунке, то перечислите их, используя союз
«И»:f[x]&&g[x]&&h[x]&&…&&t[x],{x,
a, b}.

Примеры

• x&&x^2&&x^3, {x,-1,1},{y,-1,1};
• Sin[x]&&Sin[5x]&&Sin[10x]&&Sin[15x], {x,-5,5}.

Для того, чтобы построить график функции на прямоугольнике , нужно написать в строке: f[x, y],{x, a, b},{y, c, d}. К сожалению, диапазон изменения аппликаты пока что нельзя сделать конкретным. Тем не менее, интересно отметить, что при построении графика функции Вы получите не только поверхность, которую она определяет, но и «контурную карту» поверхности (линии уровня).

Примеры

• Sin[x^2+y^2],{x,-1,-0.5},{y,-2,2};
• xy,{x,-4,4},{y,-4,4}.

Консультации по учебе, на самой крупной бирже
студенческих работ !

Калькулятор для нахождения линий уровня функции `z=3x//y` двух переменных

Линиями уровня функции z=3x/y двух переменных являются.

Для решения задач необходимо зарегистрироваться.

 Линии на плоскости xOy,
заданные уравнениями
,
где С – произвольная константа,
называются линиями уровня функции
.

Линии уровня являются линиями пересечения
поверхности, заданной функцией

и плоскости z = C,
параллельной плоскости xOy.
С помощью линий уровня можно изучать
форму поверхности, заданной функцией
.

Пример 9.2. Найти линии уровня и
определить форму поверхности, заданной
уравнением
.

Решение. Уравнения линий уровня в
данном случае имеют вид
.
При C < 0 уравнение

дает пустое множество решений
(следовательно, вся поверхность
расположена выше плоскости xOy).
При C = 0 уравнению
линии уровня удовлетворяет только одна
точка x = 0, y
= 0 (с плоскостью xOy
поверхность пересекается только вначале
координат). При C >
0 линии уровня являются эллипсами
,
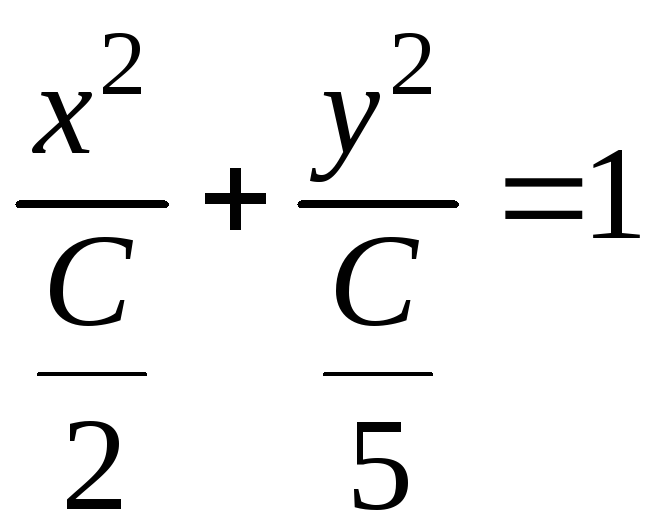
с полуосями

и
.
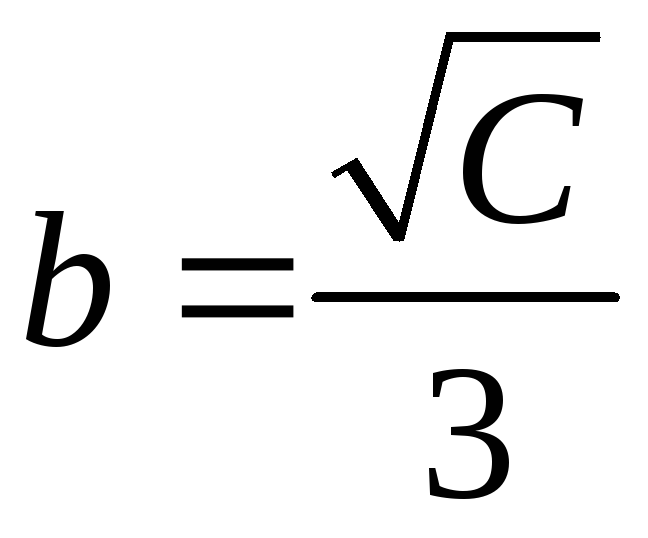
Линии уровня, соответствующие различным
значениям С, изображены на рис.
9.3. Поверхность, заданная уравнением
,
называется эллиптическим параболоидом
(рис. 9.4).

Рис.9.3 Рис. 9.4

§9.3. Частные производные первого порядка

Пусть в некоторой области D
плоскости xOy задана
функция
,
и пусть

– некоторая точка области D.

 Частной производной функции

в точке

по переменной x
(обозначается

или
)
называется

,
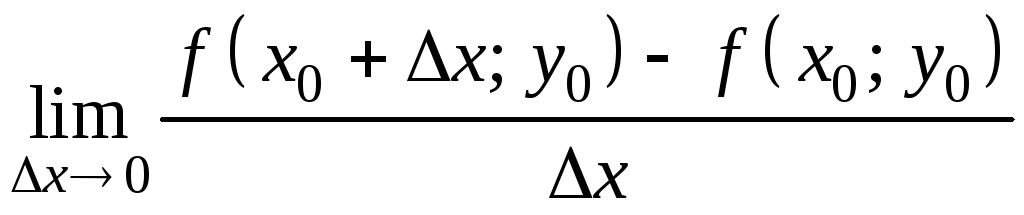
(9.1)

если данный
предел существует и конечен.

 Частной производной функции

в точке

по переменной y
(обозначается

или
)
называется

,
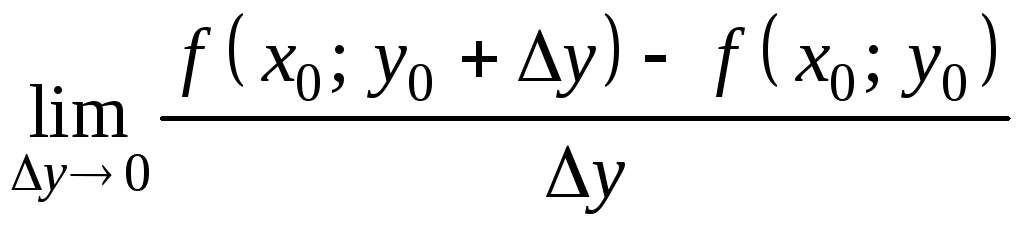
(9.2)

если данный
предел существует и конечен.

 Частной производной функции n
переменных

в точке

по переменной x_i
называется

,
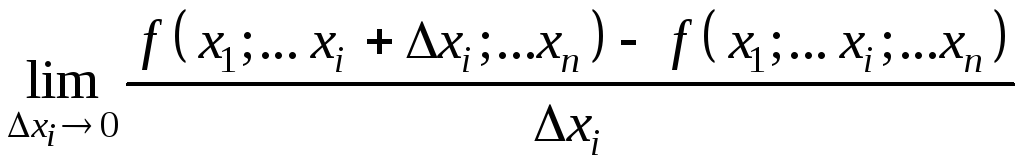
(9.3)

если данный
предел существует и конечен.

Как видно из формул (9.1) – (9.3), частные
производные определяются аналогично
тому, как определялась производная
функции одной переменной. При вычислении
предела приращение получает только
одна из переменных, остальные переменные
приращения не получают и остаются
постоянными. Следовательно, частные
производные можно вычислять по тем же
правилам, что и обычные производные,
обращаясь со всеми свободными переменными
(кроме той, по которой производится
дифференцирование) как с константами.

Пример 9.3. Найти частные производные
функции

.

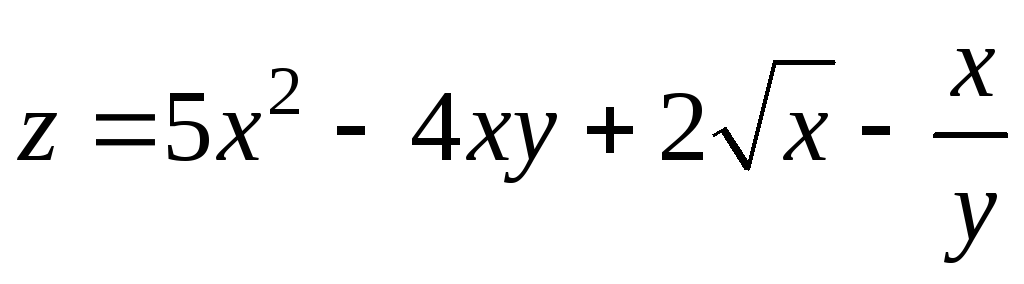
Решение.
.

.

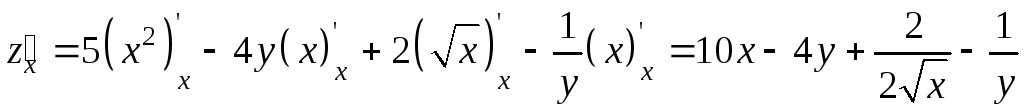
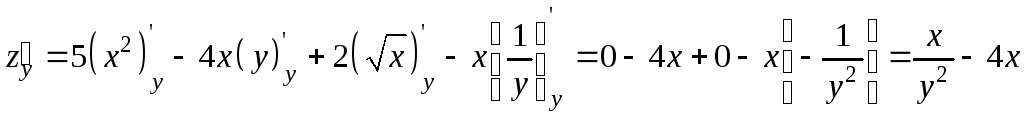
Пример 9.4. Найти частные производные
функции
.

Решение. При дифференцировании
данной функции по переменной x
мы пользуемся правилом дифференцирования
степенной функции, а при нахождении
частной производной по переменной y
– правилом дифференцирования показательной
функции:

,

.

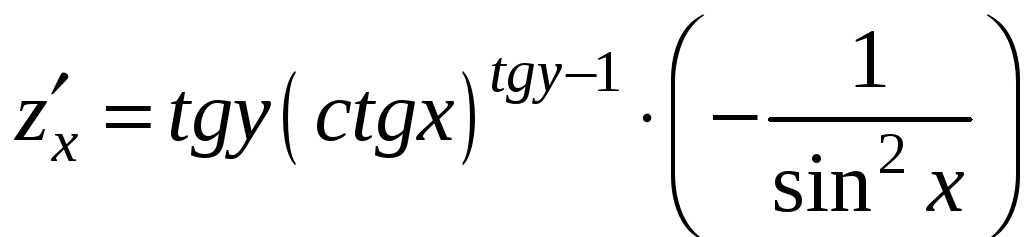
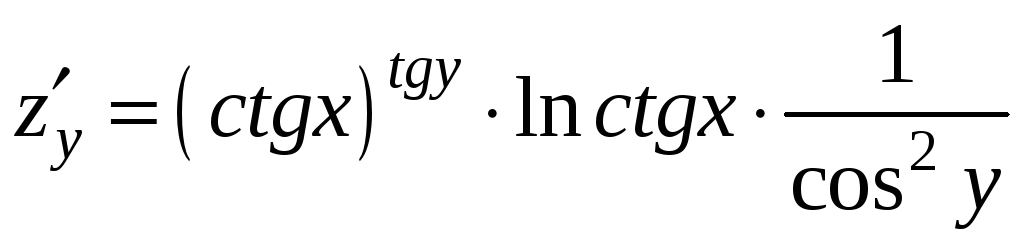
Пример 9.5. Вычислить частные
производные

функции

в точке
.

Решение. Применяя правило
дифференцирования сложной функции,
найдем частные производные

,

,

.

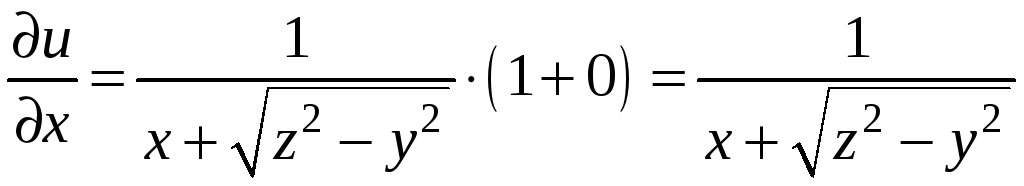
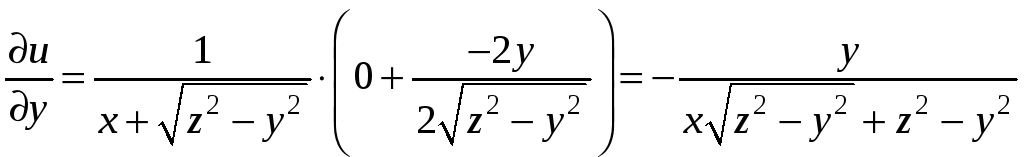
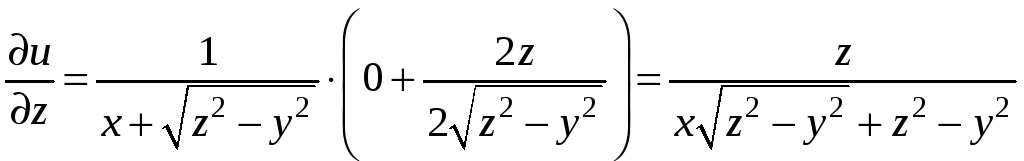
Подставляя в частные производные
координаты точки М, получим

,

,

.

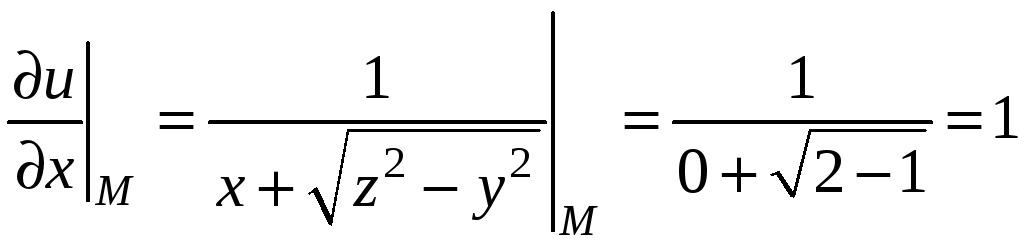
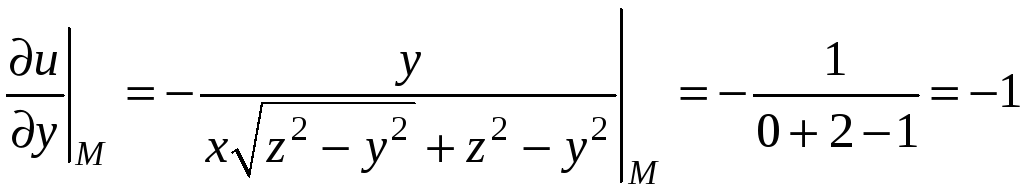
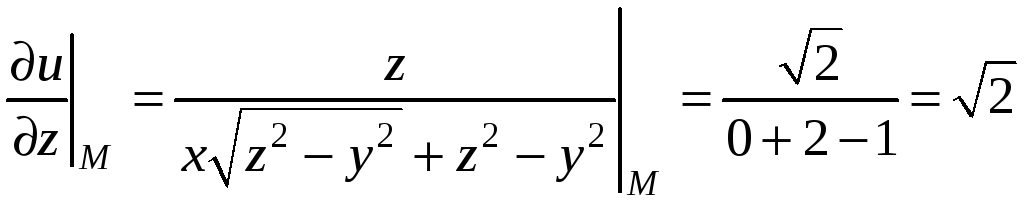
§9.4. Градиент функции нескольких переменных. Производная по направлению

 Градиентом функции

в точке

называется вектор, составленный из
частных производных данной функции,
вычисленных в данной точке:

.
(9.4)

 Если в точке

градиент функции

отличен от нулевого вектора, то он
направлен в сторону наибольшего
возрастания данной функции в точке М₀.
Это означает, что существует такое
достаточно малое число 
> 0, что в точке
,
находящейся от точки

на расстоянии r < 
(),
приращение функции

будет максимальным, если направление
вектора

совпадает с направлением вектора
.

 Производной функции

в точке

по направлению вектора

называется проекция вектора градиента
данной функции, вычисленного в точке
М₀, на данное направление

.
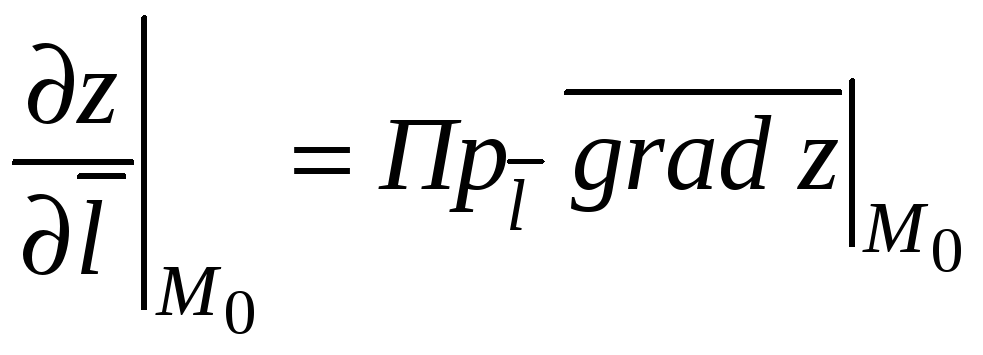
(9.5)

Из формулы (9.5) следует, что по знаку
производной по направлению в точке М₀
можно определить поведение функции
(возрастание или убывание) в данной
точке и в данном направлении. Угол между
векторами

и

острый (функция в данном направлении
возрастает), тогда и только тогда, когда
производная по направлению вектора

в точке М₀ больше нуля. Угол
между векторами

и

тупой (функция в данном направлении
убывает), тогда и только тогда, когда
производная по направлению вектора

в точке М₀ меньше нуля.

Вычисляя проекцию вектора на вектор в
соответствие с формулой (2.6) первой
части пособия, получим

.
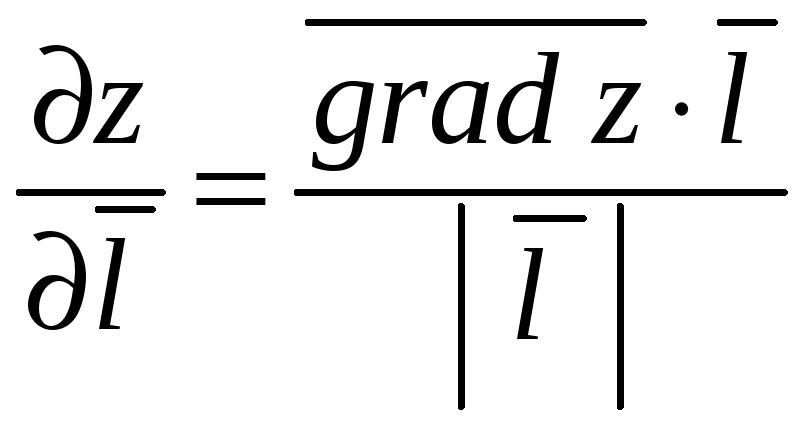
(9.6)

Замечая, что
,
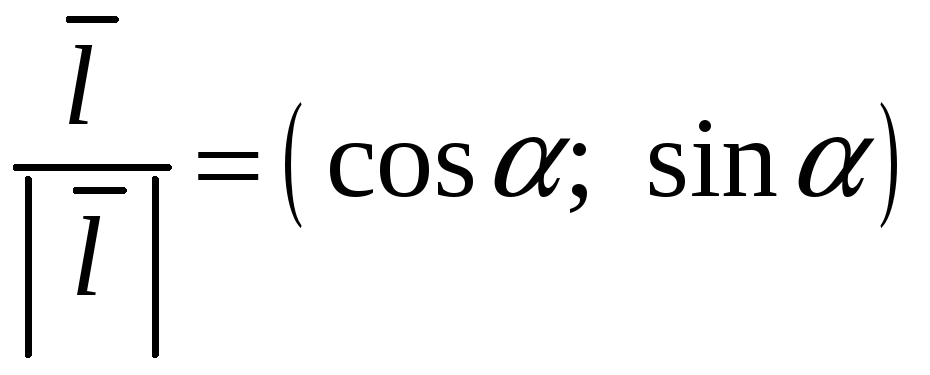
где 
– угол, который вектор

образует с осью OX,
получим еще одну формулу для вычисления
производной по направлению вектора

. (9.7)

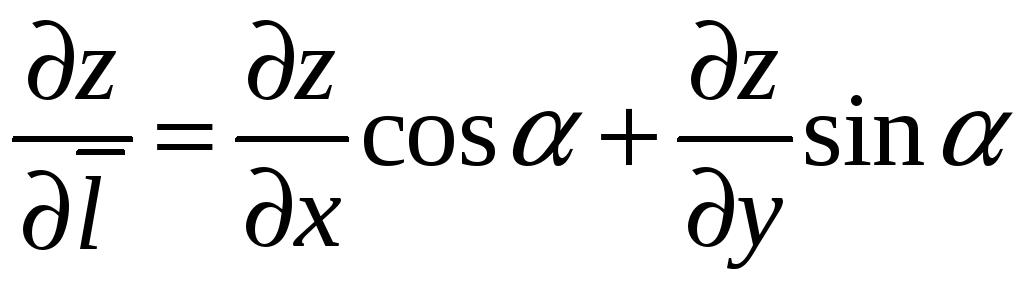
Пример 9.6. Найти градиент функции

в точке М₀(4; 2) и производную
по направлению вектора

Решение. Найдем частные производные

Вычислим значения частных производных
в точке М₀:

Градиент функции в точке М₀
найдем по формуле (9.4):

Производную функции в точке М₀
по направлению вектора

найдем по формуле (9.6):

Пример 9.7. В точке М₀(0; 1)
вычислить производную функции

по направлению биссектрисы второго
координатного угла и сделать вывод о
поведении функции в данном направлении.

Решение. Найдем частные производные
функции
:

,

.

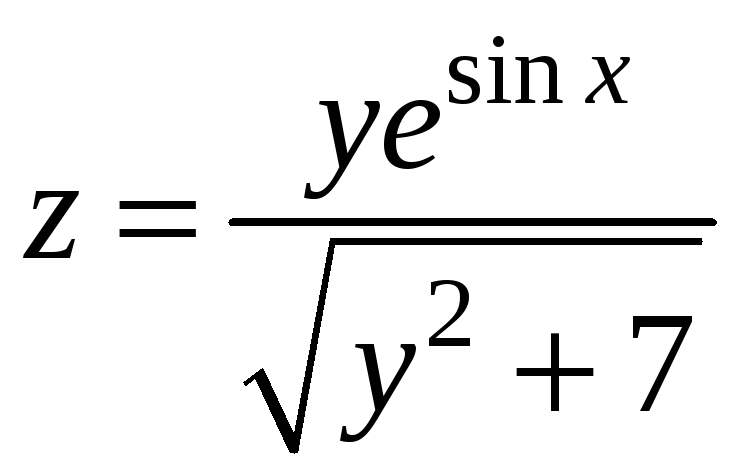
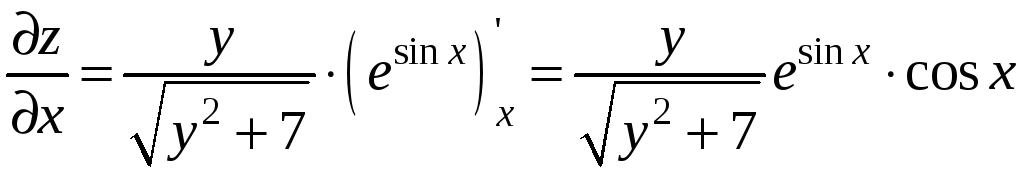
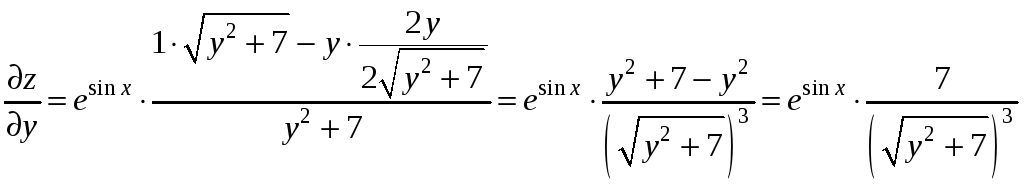
Вычислим значения частных производных
и градиент функции в точке М₀:

,

,

.

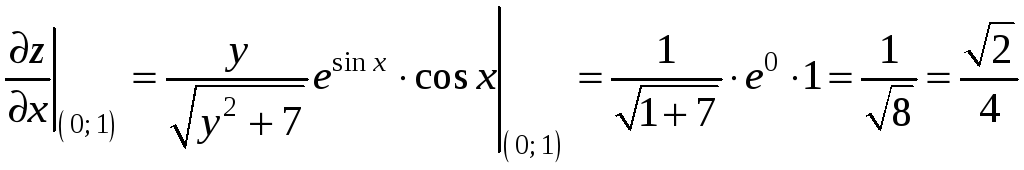
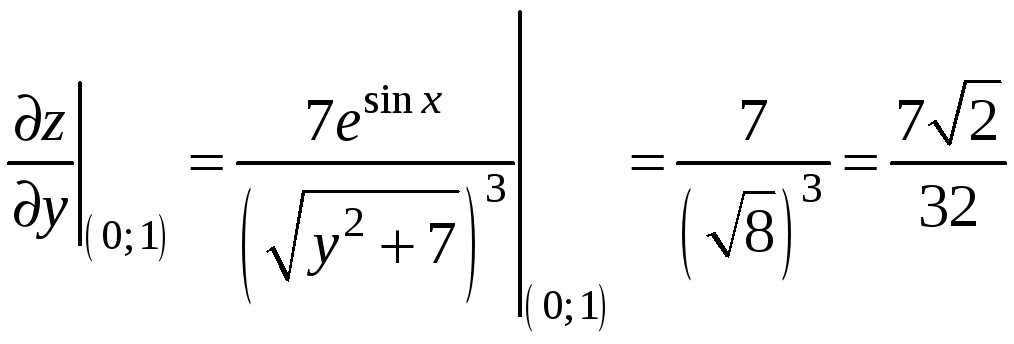
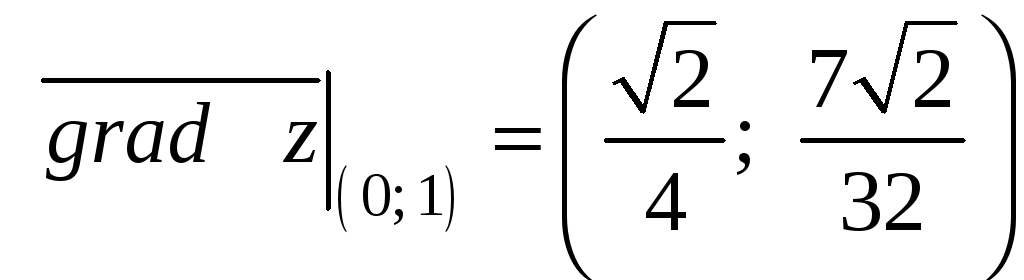
Производную функции в точке М₀
по направлению биссектрисы второго
координатного угла (данное направление
составляет с осью OX
угол 
= 135)
найдем по формуле (9.7):

.

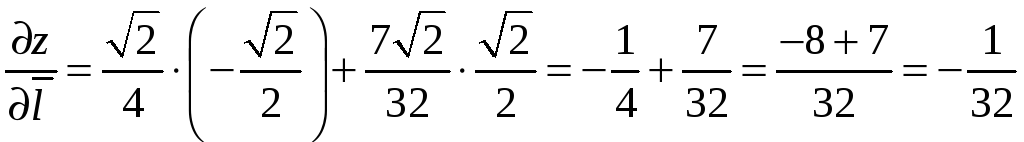
Так как прозиводная по данному
направлению отрицательна, то, следовательно,
в точке М₀ по выбранному
направлению функция убывает.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #