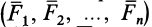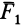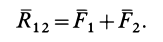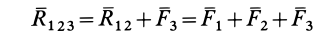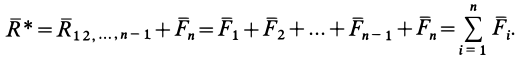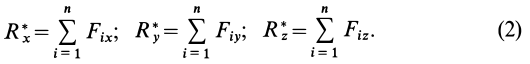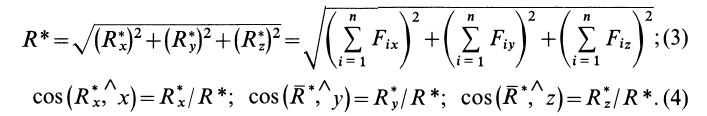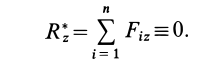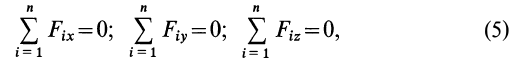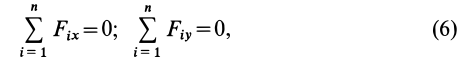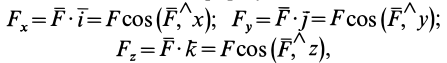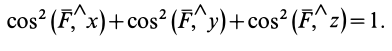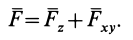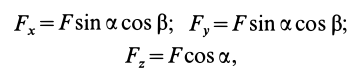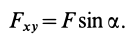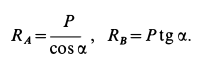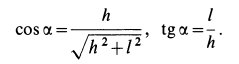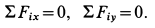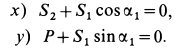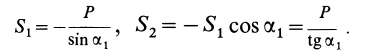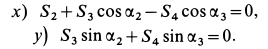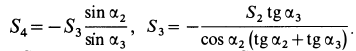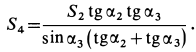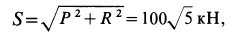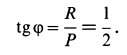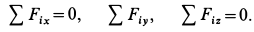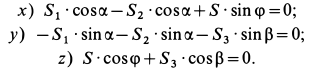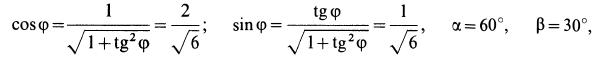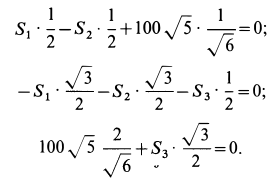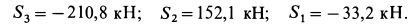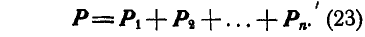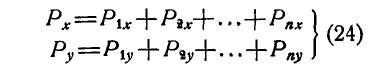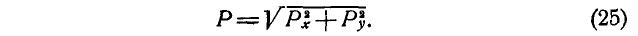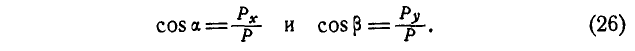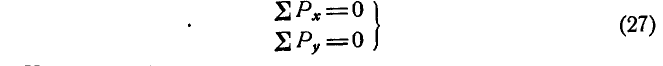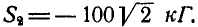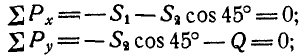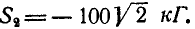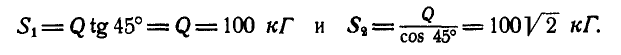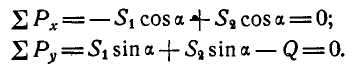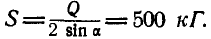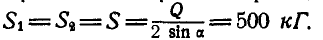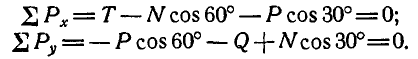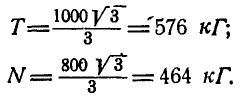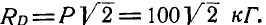Линией действия силы
Предмет
Механика
Разместил
🤓 menctexpulo1986570
👍 Проверено Автор24
называется прямая, вдоль которой действует сила.
Научные статьи на тему «Линией действия силы»
Моменты в теоретической механике
Плоскую систему при этом представляют силы, чьи линии действия лежат в одной плоскости….
Пространственную систему – силы, у которых линии действия не лежат в одинаковой плоскости….
Систему сходящихся сил представляют силы, чьи линии действия будут пересекаться в одной точке….
В произвольной системе линии действия сил не будут пересекаться в одной точке….
силы переносится вдоль линии ее действия.

Статья от экспертов
Влияние направления линии действия силы тяги на сопротивление плуга
В статье приведен анализ взаимного воздействия плуга и стенки борозды и влияние направления силы тяги на сопротивление плуга. Обосновывается и предлагается смещение плуга на тракторе, обеспечивающее меньшее трение о стенку борозды.
Рычаг
Основные понятия, используемые для описания принципа действия рычага – линия действия силы и плечо силы…
Линией действия силы называют прямую, проходящую через вектор силы….
Плечом силы называют кратчайшее расстояние от оси рычага или точки опоры до линии действия силы….
Линия действия силы и плечо силы
На рис. 2 линии действия сил $F_1$ и $F_2$ задаются их направляющими…
О перпендикуляр на линию действия силы $F_2$, получим отрезок ОВ – плечо силы $F_2$.

Статья от экспертов
К решению задачи об определении равновесных форм деформированных линий стержня моделированием чистого изгиба при действии продольной силы
Записаны уравнения, моделирующие чистый изгиб стержня по деформируемой схеме. Получены решения для тонкого стержня.
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек
Часть
2. СТАТИКА
Введение в статику
Статику
можно разделить на элементарную (или
геометрическую) и аналитическую.
Аналитическая статика рассматривается
в Ч. 4 Элементы
аналитической механики.
Все
материальные тела в той или иной степени
деформируемы, т.е. расстояние между
точками этих материальных тел изменяется.
В тех случаях, когда этими деформациями
можно пренебречь, т. е. они достаточно
малы, то материальное тело рассматривается
как НМС, расстояние между точками которой
не изменяется.
Элементарная
статика представляет собой в основном
статику НМС, а так же статику МС, состоящей
из нескольких НМС. Как было сказано во
введении в теоретическую механику,
мерой механического взаимодействия
является сила.
В
статике изучаются: операции
над силами, позволяющие приводить
системы сил к простейшим системам, и
условия равновесия этих систем.
Система
сил находится в равновесии, если под ее
действием тело остается в покое или
двигается по инерции, т. е. совершает
поступательное, равномерное и прямолинейное
движение.
Так
как сила, действующая на НМС, как будет
показано далее, есть вектор скользящий,
то к изложению элементарной статики
может быть применен богатый материал
геометрии скользящих векторов.
В
основе элементарной статики лежат шесть
аксиом, которые будут изложены в главе
1. Аксиомы – это истины, принимаемые без
математического доказательства и
подтверждаемые повседневным опытом.
Все же остальные положения статики
выводятся и доказываются исходя из этих
аксиом.
Глава
1. Основные определения, аксиомы
1.1.
Силы, связи
Определение:
Силой
называется мера механического
взаимодействия, характеризующая
интенсивность и направление этого
взаимодействия.
Из
определения следует, что сила есть
вектор
(рис.1).
Рис.1
Определения:
Точкой
приложения силы
называется точка, в которой приложена
сила.
Линией
действия силы
называется прямая, по которой направлена
сила.
Свободным
называется материальное тело (МТ, СМТ,
МС, НМС, АТТ),
на перемещения которого не наложено
никаких ограничений.
Несвободным
называется материальное тело (МТ, СМТ,
МС, НМС, АТТ),
на перемещения которого наложены
ограничения.
Связями
называются
тела, ограничивающие перемещения
рассматриваемого материального тела.
Активными
или заданными
силами
называются силы,
изменяющие
или стремящиеся изменить характер
механического движения материального
тела.
Пассивными
силами или
силами реакции
связи
называются силы, являющиеся мерой
механического взаимодействия между
несвободным материальным телом и связью.
Силы
реакции связи не могут вызвать механическое
движение и возникнуть при отсутствии
активных сил.
Системой
сил
называется совокупность сил, рассматриваемых
вместе.
Произвольной
или пространственной системой сил
называется система, линия действия всех
сил которой как угодно расположены в
пространстве.
Плоской
системой сил
называется система, линии действия всех
сил которой расположены в одной плоскости.
Системой
сходящихся сил называется
система, линии действия всех сил которой
пересекаются в одной точке.
Системой
параллельных сил
называется система, линии действия всех
сил которой параллельны.
Эквивалентными
системами сил
называются такие системы сил, при замене
одной из которых на другую состояние
свободного телa
не изменится.
‘
Равнодействующей
силой,
рассматриваемой системы сил, называется
сила, эквивалентная этой системе сил.
‘
.
Уравновешенной
системой сил
(эквивалентной нулю) называется система
сил, которая, будучи приложенной к
свободному телу, не изменяет его
состояния.
‘
0.
1.2.
Аксиомы статики
Аксиома
двух уравновешенных сил
Аксиома
1: Система
двух сил, действующих на свободную НМС
(МТ), будет уравновешенной
,
когда силы равны по модулю и противоположно
направлены по одной прямой (рис. 2).
Рис.
2
Аксиома
о добавлении (отбрасывании)
уравновешенной
системы сил
Аксиома
2: Состояние
свободной НМС (МТ) не изменится, если к
действующей на НМС (МТ) системе сил
добавить или от нее отнять уравновешенную
систему сил.
Следствие:
Состояние НМС не изменится, если силу,
приложенную к какой-либо ее точке,
перенести вдоль линии действия силы в
любую другую точку НМС, лежащую на линии
действия этой силы.
Доказательство:
Пусть на НМС
действует сила
в точке O1.
Приложив на основании аксиомы 2 к НМС в
точке O2
уравновешенную систему двух сил, равных
по модулю заданной силе и лежащих на
линии ее действия (рис. 3), получим:
Рис. 3.
Таким
образом, сила
– вектор скользящий.
Аксиома
(правило) параллелограмма сил
Аксиома
3: Система
двух сил, приложенных к точке НМС или к
МТ, всегда имеет равнодействующую,
приложенную в этой же точке и совпадающую
по величине и направлению с диагональю
параллелограмма, построенного на этих
силах (рис. 4).
‘
или
,
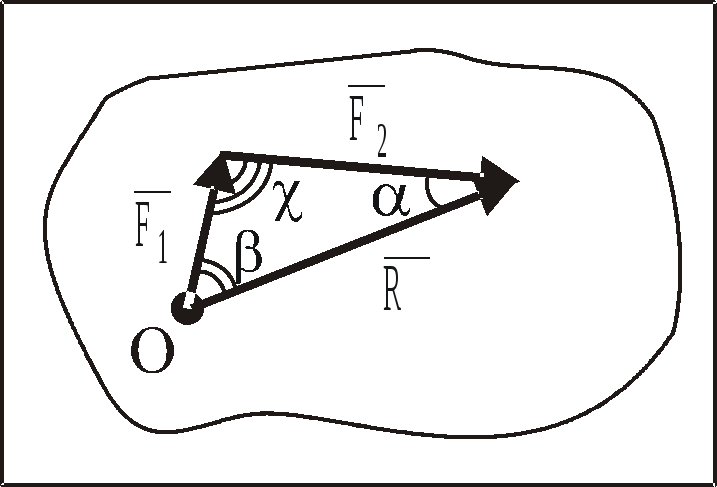
Из
правила параллелограмма следует правило
треугольника сложения сил (рис. 5).
Рис.
4 Рис.
5
.
Используя аксиому 3 – правило
параллелограмма, можно решить и обратную
задачу: разложение силы на две составляющие
силы, которая в отличие от прямой задачи
имеет бесконечное множество решений.
Аксиома
действия и противодействия
Аксиома
4: Силы, с
которыми действуют друг на друга две
НМС (МТ), всегда равны по величине и
направлены по одной прямой в противоположные
стороны.
Аксиома
связей (принцип освобождаемости)
Аксиома
5: Всякую
несвободную НМС (МТ) можно рассматривать
как свободную, отбросив (условно) связи
и заменив их действие реакциями связи
(пассивными силами).
Аксиома
затвердевания
Аксиома
6: Равновесие
несвободной МС не нарушится, если на
нее наложить дополнительные связи.
1.3.
Моменты силы относительно точки и оси
Пусть
имеются сила
,
приложенная в точке какой-либо НМС,
точка О и ось .
Тогда можно дать определения моментам
силы относительно точки и оси и установить
связь между ними.
1.3.1. Момент силы
относительно точки
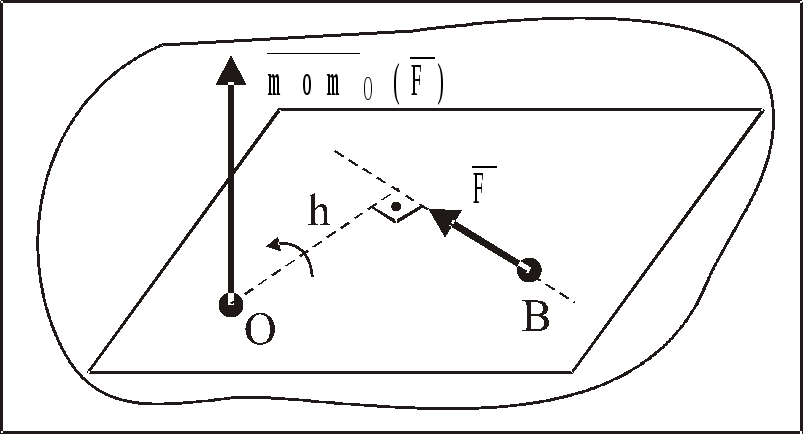
Определение:
Моментом силы относительно точки
называется вектор, приложенный в этой
точке, равный по величине произведению
величины силы на кратчайшее расстояние
от точки до линии действия силы (называемое
плечом), направленный перпендикулярно
к плоскости, проходящей через точку и
силу, по правилу правого винта, т. е. в
ту сторону, откуда совершаемый силой
поворот тела, относительно точки виден
против хода часовой стрелки (рис. 6).
Рис. 6
.
(1.1)
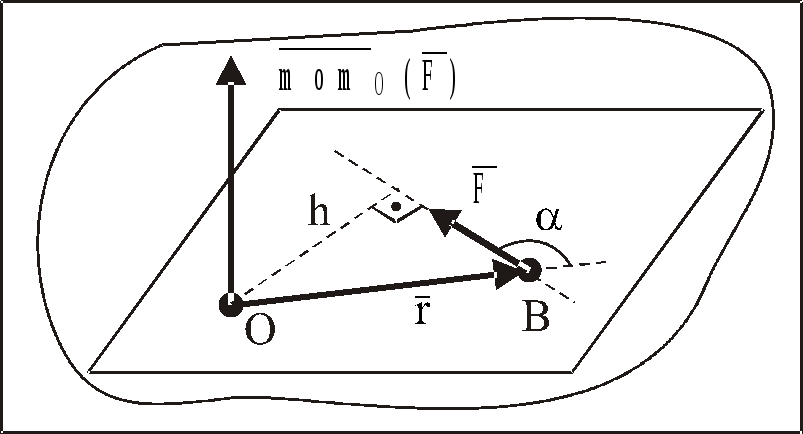
Введем
в рассмотрение радиус-вектор
,
определяющий положение точки B
– точки приложения силы
(рис. 7).
Рис. 7
При
рассмотрении векторного произведения
векторов
и
,
оказывается, что
а)
;
б)
плоскости, в которой находятся
;
в)
составляют правую тройку векторов, т.
е. если смотреть с конца третьего вектора,
поворот от первого ко второму вектору
виден против хода часовой стрелки.
Таким образом, можно сделать следующий
вывод:
.
(1.2)
В
случае плоской системы сил величину
момента силы относительно точки, лежащей
в плоскости действия сил, можно
рассматривать как алгебраическую
величину, равную взятому со знаком плюс
или минус произведению модуля силы на
плечо:
.
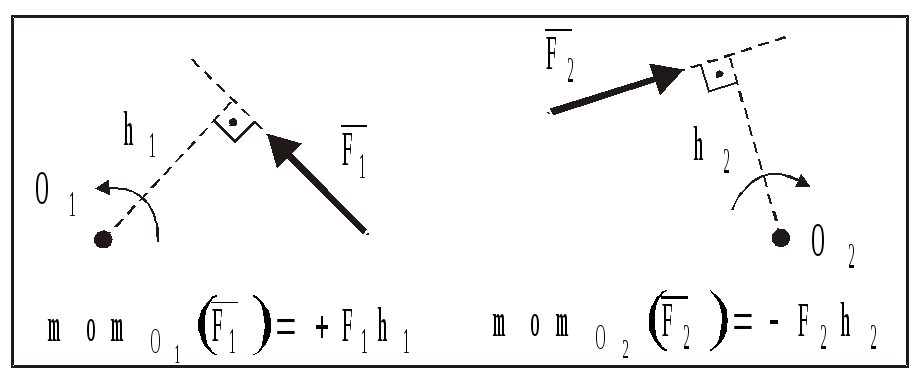
При
этом величина момента берется со знаком
плюс, если сила стремится осуществить
поворот тела относительно точки против
хода часовой стрелки и со знаком минус
в противоположном случае (рис. 8).
Рис.
8
1.3.2. Момент силы
относительно оси
Определение:
Моментом силы относительно оси
называется взятая со знаком плюс или
минус величина момента проекции силы
на плоскость, перпендикулярную оси,
относительно точки пересечения оси и
плоскости:
.
(1.3)
Момент
берется со знаком плюс, если, смотря с
конца положительного направления оси,
видно, что проекция силы стремится
осуществить поворот тела относительно
оси против хода часовой стрелки. В
противном случае момент берется со
знаком минус (рис. 9).
Рис.
9
Момент
силы относительно оси не зависит от
выбора плоскости, перпендикулярной
оси.
Момент
силы относительно оси равен нулю, если:
-
=0
, т.е. сила параллельна оси, -
h=0
, т.е. линия действия силы пересекает
ось.
1.3.3.
Связь между моментами силы
относительно
точки и оси
Момент
силы относительно оси равен
проекции на эту ось момента силы
относительно любой точки, лежащей на
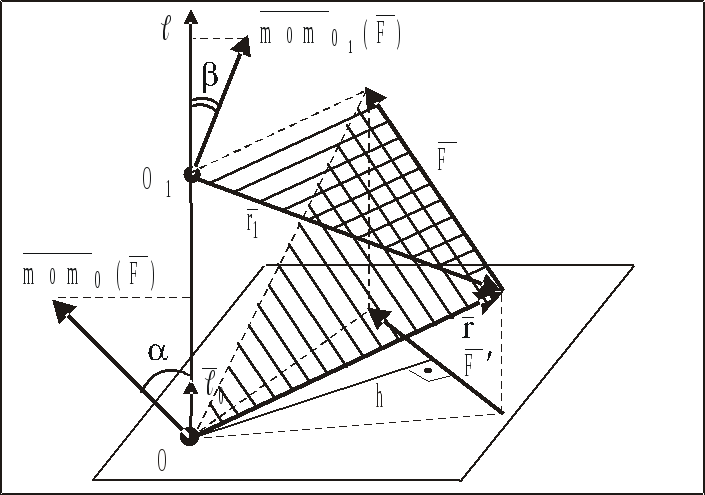
этой оси (рис. 10):
.
(1.4)
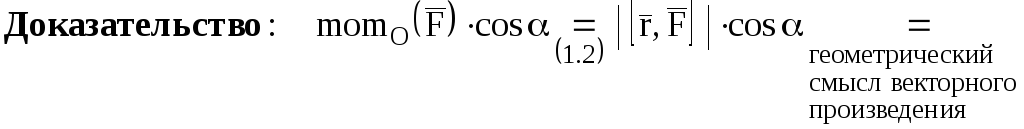
Осталось доказать, что связь между
моментами силы относительно точки и
оси не зависит от выбора точки на оси.
Рис.
10
Возьмем
вторую точку на оси О1
(рис. 11) и единичный орт

оси ,
тогда
Здесь
.
Рис.
11
Зависимость
между моментами силы относительно оси
и точки иногда принимается в качестве
определения момента силы относительно
оси, которое эквивалентно определению,
данному в пункте 1.3.2.
1.3.4.
Моменты силы относительно начала
координат
и
координатных осей декартовой системы
координат
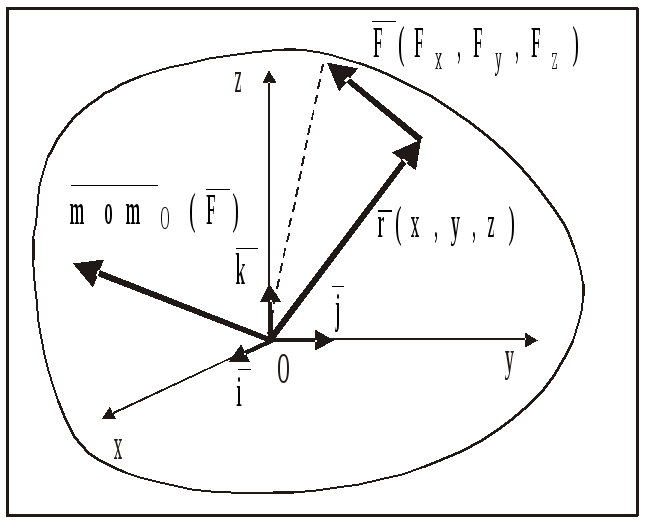
Запишем
выражение для момента силы
относительно начала координат О в виде
определителя (рис. 12):
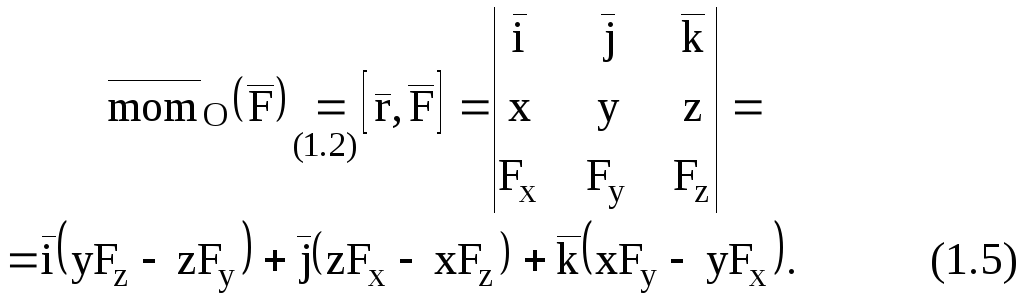
Спроектировав
выражение (1.5) на оси декартовой системы
координат, с учетом связи между моментами
силы относительно точки и оси, получим:
(1.6)
Рис.
12
173
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дано определение силы в механике. Описаны факторы, определяющие действие на тело силы: направление, точка приложения и численное значение. Сформулированы второй и третий Законы Ньютона. Дано понятие равнодействующей силы.
 Сила в механике
Сила в механике
Определение силы
Твердые тела могут вступать во взаимодействие, в результате которого изменяется характер их движения. Мерой этого взаимодействия является физическая величина, которую называют силой.
Сила – векторная величина, количественная мера механического взаимодействия физических тел, приводящего к изменению их скорости или к их деформациям.
Действие силы на тело определяется тремя факторами:
- направлением;
- точкой приложения;
- численным значением.
Это означает, что сила является векторной величиной (вектором).
Обозначение силы
На схемах вектор силы обозначается отрезком, на конце которого ставится стрелка. Начало отрезка указывает точку приложения силы, а стрелка указывает направление действия силы. Длина отрезка в выбранном масштабе соответствует численному значению силы (рис.1).
В тексте чаще всего сила обозначается латинской буквой F со стрелкой или чертой над ней. Чтобы различать силы, их обозначают посредством нижнего индекса, который ставится после буквы F. Например: Fтяж — сила тяжести; Fупр — сила упругости; Fтр — сила трения; Fм — сила тяги мышц. Иногда за конкретным видом силы стандартно закрепляется определенная буква латинского алфавита, например буква Р (со стрелкой сверху) обозначает вес тела.
Точка приложения силы
При расчетах очень важно знать точку приложения силы. В прикладной механике такие силы называют сосредоточенными. Например, точкой приложения силы тяжести является центр масс (центр тяжести) тела. Также, зная направление и точку приложения силы, можно определить линию действия силы.
Прямая, вдоль которой направлена сила, проходящая через точку ее приложения называется линией действия силы.
Численное значение силы
Численное значение силы (модуль) измеряется в Ньютонах (Н).
С точки зрения механики, все силы возникают при взаимодействии двух или более тел, и у каждой силы есть противодействующая ей сила. Об этом говорит третий закон Ньютона.
Третий закон Ньютона
«Силы, с которыми действуют два тела друг на друга, равны по численному значению и противоположны по направлению. При этом одна сила приложена к одному телу, другая – к другому».
Третий закон Ньютона записывается в следующем виде: F1= — F2.
Второй закон Ньютона (основной закон динамики)
«Ускорения, которые силы сообщают телам, прямо пропорциональны величинам этих сил и обратно пропорциональны массам тел и направлены в сторону действия сил».
Это позволяет определить численное значение силы, если известна масса тела и его ускорение по формуле: F=m*a.
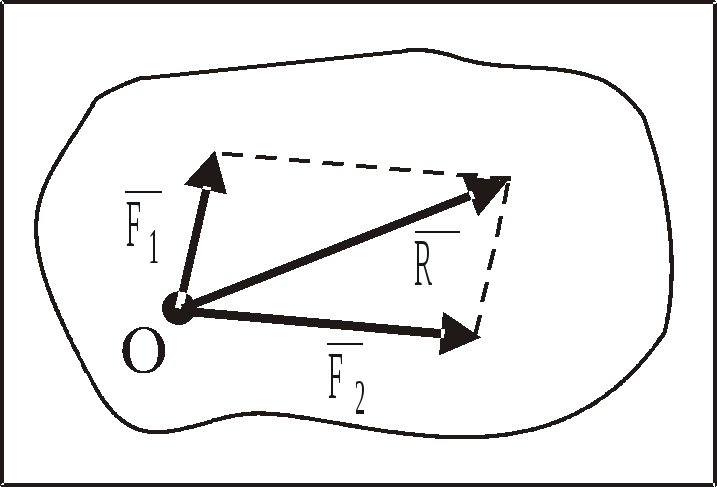
Равнодействующая сила
Если на тело действует несколько сил, приложенных к одной точке, можно найти равнодействующую (результирующую) силу, действие которой на тело эквивалентно воздействию на тела нескольких сил.
Равнодействующая сила – это сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Так как сила – это векторная величина, к ней можно применять правила операции над векторами, например, сложение. Чтобы найти равнодействующую силу, необходимо сложить два или несколько векторов (рис.2).
Для анализа силовых упражнений, необходимо познакомится с некоторыми видами сил:
- силой тяжести,
- весом тела,
- силой реакции опоры,
- силой упругости,
- силой тяги мышц.
С уважением, А.В. Самсонова
Похожие записи:
Мышечно-сухожильный комплекс
Приведена рецензия на книгу В.Т.Тураева и В.В. Тюпа «Мышечно-сухожильный комплекс: анатомия, биомеханика, спортивная практика» зав. кафедрой биомеханики НГУ…
Сила тяжести
Дано определение силы тяжести. Показано, что сила тяжести является частным случаем силы гравитации. Описаны факторы, определяющие силу тяжести:…
Звенья тела человека как рычаги
Дано описание опорно-двигательного аппарата (ОДА) человека как системы рычагов. Приведен пример расчета силы двуглавой мышцы плеча…
Типы телосложения (соматотип) по Башкирову
Описана краткая биография П.Н. Башкирова и его научные труды. Дается классификация типов телосложения человека: долихоморфного (астенического), мезоморфного…
Типы телосложения (конституции) по Э. Кречмеру
Описана биография Эрнста Кречмера – немецкого психиатра и психолога, разработавшего типологию тела человека. Дано описание типов телосложения…
Типы конституции женщин по И.Б. Галанту
Описана биография известного советского психиатра И.Б.Галанта, предложившего естественную систему конституциональных типов женщин. Дана характеристика предложенных И.Б.Галантом конституциональных…
Содержание:
Система сходящихся сил:
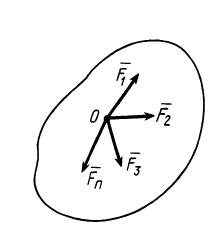
Рассмотрим одну из важных систем сил — систему сходящихся сил. Для этой системы сил следует рассмотреть приведение ее к простейшему виду и установить условия равновесия.
Системой сходящихся сил (или пучком сил) называют такую систему сил, линии действия которых пересекаются в одной точке — центре пучка. Сходящиеся системы сил могут быть пространственными и плоскими, т. е. расположенными в одной плоскости.
Приведение к равнодействующей силе
Рассмотрим общий случай пространственной системы сходящихся сил. Так как сила, действующая на твердое тело, есть вектор скользящий, то можно считать, что силы системы
Применяя к первым двум силам пучка
Затем по правилу параллелограмма складываем силы 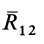
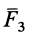
Рис. 12
Рис. 13
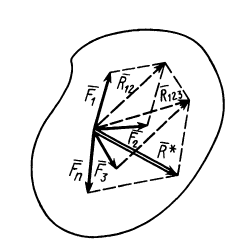
и т. д. Продолжая процесс векторного сложения сил для всех 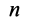
Таким образом, система 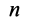
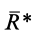
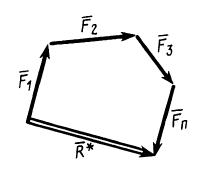
Процесс последовательного применения к силам правила параллелограмма, или их векторного сложения, приводит к построению силового многоугольника из заданных сил. В силовом многоугольнике конец одной из сил служит началом другой (рис. 14). Равнодействующая сила 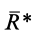
Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской— плоской. Для плоской системы сходящихся сил равнодействующую силу можно определить графически путем построения замыкающей силового многоугольника в выбранном для сил масштабе. Для пространственной системы сходящихся сил пришлось бы силовой многоугольник строить в пространстве из стержней.
Рис. 14
Итак, система сходящихся сил в общем случае приводится к одной силе—равнодействующей этой системы сил, которая изображается замыкающей силового многоугольника, построенного на силах системы. Линия действия равнодействующей силы проходит через центр пучка параллельно замыкающей силового многоугольника.
Для аналитического определения равнодействующей силы следует выбрать систему прямоугольных осей координат и воспользоваться известной из геометрии теоремой о том, что проекция замыкающей любого многоугольника на какую-либо ось равна алгебраической сумме проекций составляющих его сторон на ту же ось.
Так как равнодействующая сила 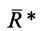
Проецируя векторы векторного равенства на прямоугольные оси координат, согласно теореме о проекции замыкающей получим
По проекциям определяем модуль равнодействующей силы и косинусы углов ее с осями координат по формулам
В формуле (3) перед квадратным корнем всегда берут знак плюс, так как определяется модуль равнодействующей силы.
В случае плоской системы сходящихся сил одну из координатных осей, обычно 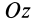
Условия равновесия системы сходящихся сил
Для равновесия системы сходящихся сил, приложенных к твердому телу, замыкающая силового многоугольника, изображающая равнодействующую силу, должна обратиться в точку, т. е. конец последней силы в многоугольнике должен совпасть с началом первой силы. Такой силовой многоугольник называют замкнутым (рис. 15). Получено условие равновесия сходящихся сил в геометрической форме: для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым. Для случая трех сходящихся сил при равновесии должен быть замкнутым силовой треугольник, построенный из трех сил.
Рис. 15
Для определения неизвестных сил при равновесии более предпочтительным является использование условий равновесия системы сходящихся сил в аналитической форме. Так как при равновесии системы сходящихся сил равнодействующая сила должна быть равна нулю (силовой многоугольник замкнут), то из этого следует, что равно нулю подкоренное выражение в (3), состоящее из суммы положительных величин. Таким образом, равны нулю квадраты каждой из величин подкоренного выражения, а следовательно, равны нулю и сами величины. Получаем условия равновесия пространственной системы сходящихся сил в аналитической форме:
т. е. для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны нулю.
В случае плоской системы сходящихся сил одну из осей координат, обычно 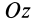
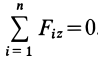
т. е. для равновесия плоской системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных координатных осей, лежащих в плоскости сил, были равны нулю.
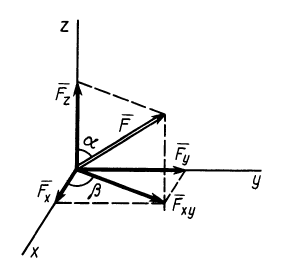
Проецирование силы на оси координат
Если дана сила 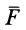
где 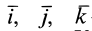
Из трех углов независимыми являются только два.
Рис. 16
При проецировании силы на прямоугольные оси координат целесообразно использовать тоже два угла. Для этого предварительно силу разлагают на две взаимно перпендикулярные составляющие, одна из которых параллельна какой-либо оси координат, например 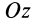
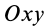
Проецируя векторы векторного равенства на координатные оси, имеем
так как
При проецировании использованы только два угла: 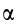
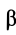
Векторные величины 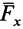
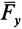
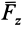
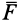
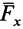
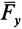
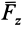
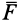
Пример 1.
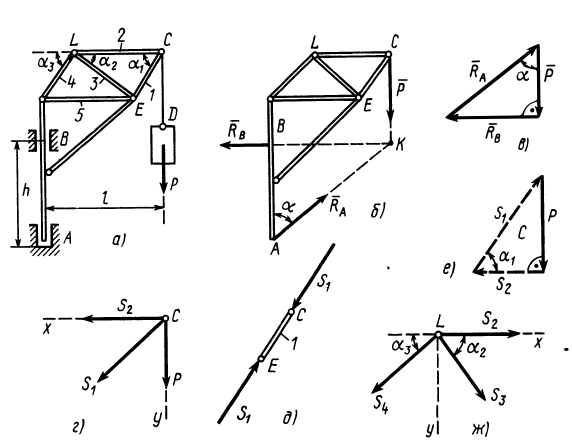
Подъемный кран, имеющий вертикальную ось вращения 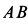
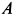
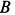
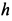
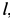
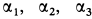
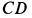
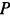
Решение. Считая кран твердым телом, освободим его от связей, которыми являются подпятник и подшипник, заменив их силами реакций связей. Сила реакции подшипника (цилиндрический шарнир) перпендикулярна его оси. Направление силы реакции подпятника заранее не известно и подлежит определению. На весь кран, находящийся в равновесии, действуют три силы: 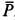
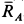
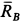
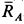
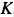
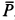
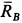
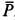
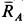
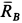
Рис. 17
Из геометрического треугольника
Для определения усилий в стержнях 1 и 2 применим метод вырезания узлов. Для этого рассмотрим равновесие отдельного шарнира или узла С. На этот узел действуют сила Р через трос и силы реакций стержней 1 и 2, которые следует мысленно отбросить. Силы реакций стержней на узел должны быть направлены по стержням, так как на эти стержни между их шарнирами другие силы не действуют. Стержни являются шарнирными. (Условимся силы реакций стержней направлять от узла (рис. 17, г) и знак вектора у сил на рисунке не ставить, чтобы не увеличивать без необходимости число обозначений для одинаковых по числовому значению сил.)
Выбрав в точке 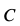

Эти условия в рассматриваемом случае принимают форму в проекциях на оси:
Из полученных уравнений получаем:
Знак 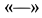
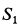

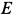

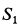
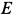

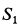
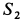
На узел 
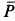
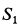
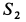
Из уравнений равновесия или силового треугольника можно определить только две неизвестные силы. Поэтому при дальнейшем решении задачи следует переходить к рассмотрению равновесия узла, на который действуют не более двух неизвестных сил. Таким узлом является узел 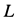
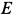
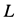
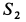
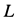
Из этих уравнений находим
Подставляя в выражение для 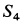
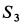
Усилие 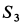
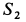
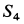
Для узла 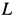
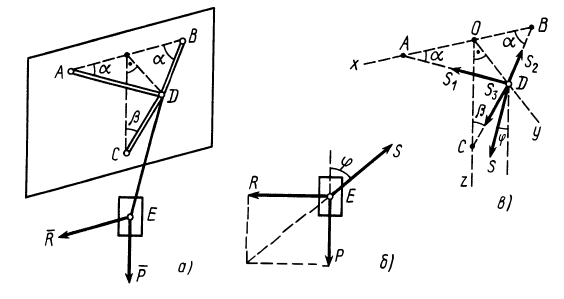
Пример 2.
Груз с силой тяжести 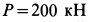
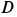
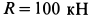
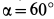
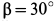
Решение. На находящийся в равновесии груз 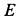
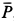
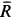
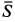
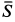
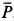
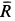
так как силы 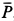
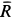
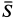
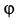
Рассмотрим равновесие шарнира 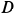
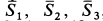
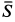
В рассматриваемом случае для выбранных осей координат имеем:
Рис. 18
Так как
то система уравнений принимает форму
Решая эту систему уравнений, получаем:
Усилия в стержнях направляли от рассматриваемого узла и получили 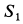
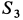
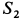
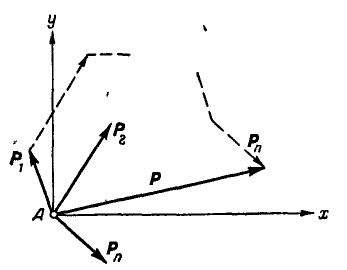
Силы, сходящиеся в одной точке
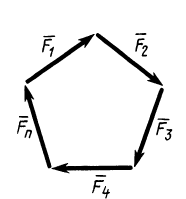
Если на точку А действуют n сил, расположенных в одной плоскости (рис. 22), то эти силы можно сложить геометрически, построив многоугольник векторов, который в нашем случае называется многоугольником сил.
Рис. 22.
Обозначая равнодействующую сил через Р, можем написать:
Проектируя равнодействующую и составляющие на координатные оси, проведенные через точку А, по формуле (3) имеем:
Величину равнодействующей находим по формуле (7):
Направление равнодействующей определяем по формулам (6):
Может оказаться, что при построении многоугольника сил конец последней силы совпадет с началом первой; в этом случае многоугольник сил получается замкнутым, равнодействующая сила равна нулю и силы находятся в равновесии. Таким образом, геометрическое условие равновесия сил, приложенных к точке, заключается в том, что многоугольник этих сил должен быть замкнут.
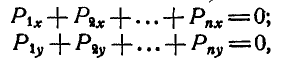
В этом случае Р=0, а поэтому и 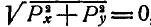
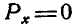
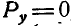
или сокращенно:
Уравнения (27) называются уравнениями равновесия сил, приложенных к точке, и выражают аналитические условия равновесия этих сил.
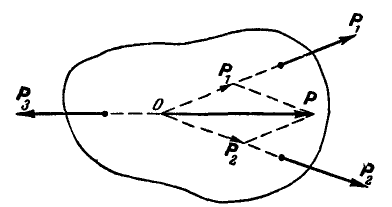
Рассмотрим равновесие трех сил 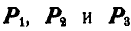
Рис. 23.
Пусть в точке О пересекаются линии действия любых двух сил, например 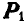
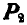
Теперь на тело уже действуют две силы Р и А, равновесие которых по аксиоме 2 возможно, если они будут направлены по одной прямой.
Отсюда заключаем, что три силы, действующие на тело, и расположенные в одной плоскости, могут находиться в равновесии только тогда, когда их линии действия пересекаются в одной точке.
- Заказать решение задач по теоретической механике
Задача 1.
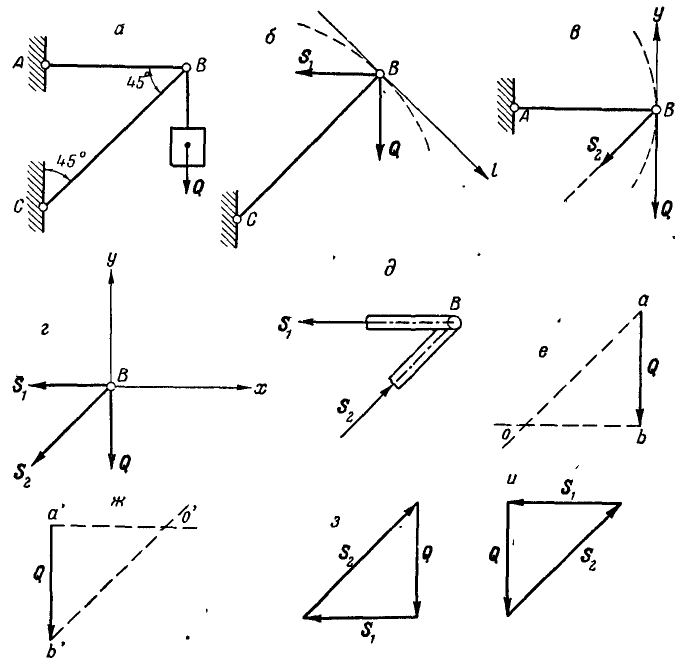
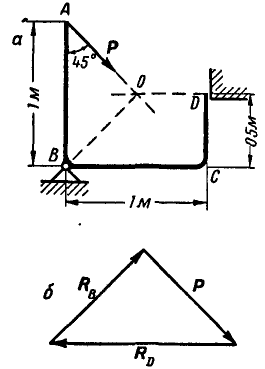
К точке В шарнирного кронштейна АВС (рис. 24, а) подвешен груз Q = 100 кГ. Определить усилия 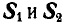
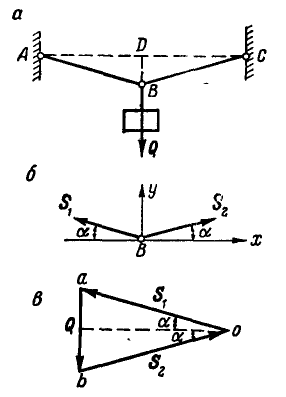
Решение. Для определения усилия 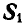
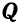
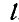
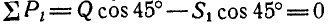
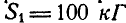
Для нахождения усилия 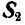
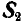
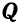
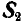
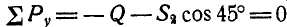
При решении этой задачи можно было бы освободиться одновременно от обеих связей ВА и ВС, вводя взамен их реакции связей 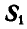
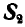
Тогда для свободной точки В можно написать два уравнения равновесия (27) в виде:
отсюда находим, что 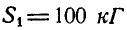
Знак минус у 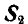
Рис. 24.
При неподвижной точке В реакция направленная от узла, будет растягивать стержень, а реакция 58, направленная к узлу, будет сжимать стержень, что ясно видно из чертежа.
Решим теперь эту задачу геометрическим способом. Все силы, заданные и реактивные, действующие на точку В, взаимно уравновешиваются, а поэтому многоугольник этих сил должен быть замкнут. На этом основании проводим вектор, равный силе 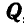
Так как многоугольник сил, действующих на точку В, должен быть замкнут, то стрелки всех сил в полученном многоугольнике сил, в нашем случае – треугольнике (рис. 24, е или 24, ж), должны быть расположены в одном направлении. Исходя из заданного направления силы 
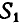
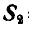
Выбрав один из полученных треугольников сил, замечаем, что сила 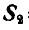
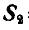
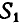
При решении дальнейших задач аналитическим способом стрелки неизвестных реакций стержней будём направлять всегда от рассматриваемого нами узла; тогда знак минус у модуля реакции какого-либо стержня будет указывать на то, что рассматриваемый нами стержень сжат.
Задача 2.
Определить усилия в стержнях АВ и ВС при действии в шарнире В силы Q=100 кГ, если АВ = ВС =5 м, BD = 0,5 м и шарниры А и С расположены на одной горизонтали (рис. 25, а).
Рис. 25.
Решение. Решим сначала задачу аналитическим способом, для чего рассмотрим равновесие точки В, находящейся под действием трех сил: заданной силы 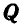
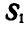
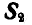
Применяя уравнения равновесия (27), имеем:
Из первого уравнения находим: 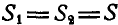
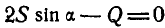
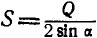
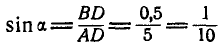
Знак плюс у S указывает на то, что оба стержня ВА и ВС растянуты.
Для решения этой задачи геометрическим способом, построим треугольник равновесия 0ab (рис. 25,в), из которого сразу находим правильное направление реакции 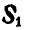
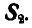
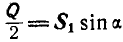
Задача 3.
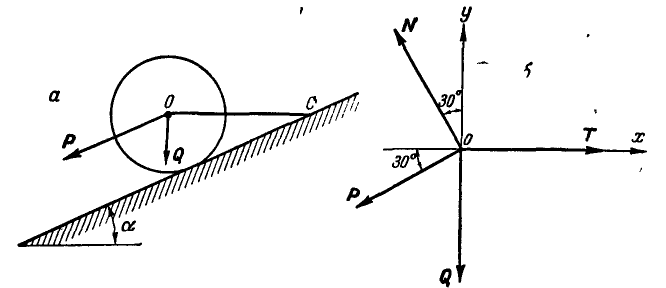
Однородный цилиндр (рис. 26,а) весом 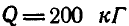
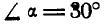
Рис. 26.
Решение. Решим задачу аналитическим способом. Освободившись от связей (рис. 26,6) и составляя для точки О уравнения равновесия (27), имеем:
Подставляя вместо Р и Q их значения и решая полученные уравнения, находим неизвестные силы:
Задача 4.
Жесткое колено ABCD (рис. 27,а), могущее вращаться вокруг шарнира В, опирается в точке D на гладкий уступ. Пренебрегая весом колена, определить реакции связей в точках В и D, если в точке А колена приложена сила Р=100 кГ.
Рис. 27.
Решение. Так как колено находится в равновесии, то три силы, действующие в точках А, В и D, должны пересекаться в одной точке. Продолжаем линию действия силы Р и реакции в точке D, направленной перпендикулярно к плоскости уступа, до взаимного пересечения в точке О; тогда линия действия реакции шарнира В пройдет обязательно через точку О. На рисунке 27, б дано построение треугольника равновесия трех сил 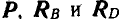
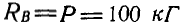
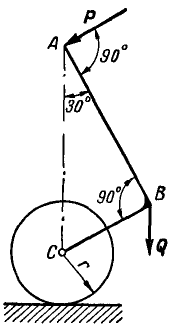
Задача 5.
При подъеме плуга на стоянке (рис. 30) поворачивают коленчатый рычаг АВС, вращая рукоятку силой Р. Какова при этом должна быть величина силы Р, если вес части плуга, передающейся на коленчатый рычаг, вращающийся вокруг шарнира В, равен Q = 30 кГ, длина рукоятки АВ = 0,6 м и радиус колеса плуга г = 0,25 м.
Рис. 30.
Решение. Строим для сил, приложенных к коленчатому рычагу, треугольник равновесия. Из подобия треугольника равновесия и соответствующего треугольника на чертеже находим силу Р.
Ответ: Р = 11 кГ.
- Моменты силы относительно точки и оси
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Аксиомы и теоремы статики
- Приведение системы сил к простейшему виду
- Плоское движение тела
- Принцип виртуальных перемещений
Словосочетания «момент силы» и «вращательный момент» — это синонимы. Можно употреблять любой из них.
Сила может заставлять тело двигаться:
- поступательно,
- или вращательно.
В этой статье будем рассматривать вращательное движение.
Рекомендую также ознакомиться со статьей о видах механического движения (откроется в новой вкладке).
Что такое линия действия силы
Линия действия – это прямая линия, на которой лежит вектор.
Провести эту линию легко. Приложить линейку к вектору и пунктиром провести прямую, продолжив ее в обе стороны от вектора.
Рис. 1. Линия (пунктир), на которой лежит вектор, называется линией действия вектора
Что такое плечо силы и как его нарисовать
Предположим, нужно с помощью ключа закрутить гайку (см. рис. 2).
Рис. 2. Красная точка, вокруг которой вращается ключ — это центр гайки
Винт, на который накручена гайка – это ось вращения. Ключ может вращаться вокруг красной точки. Для упрощения назовем ее кратко: «точка вращения».
Примечание:
Ось вращения проходит перпендикулярно плоскости рисунка через красную точку. Используем вместо оси вращения термин «точка вращения» для простоты.
Рассмотрим следующий рисунок (см. рис. 3)
Рис. 3. Плечо силы – это перпендикуляр ( l ). Он соединяет линию действия силы с точкой вращения
На рисунке 3 черная стрелка – это вектор силы, которая вращает ключ. Пунктир – линия действия силы. Из красной точки к линии действия силы проведен перпендикуляр. Этот перпендикуляр, обозначенный ( l ), называется плечом силы.
Перпендикуляр к линии действия легко провести с помощью прямоугольного треугольника (см. рис. 4):
Рис. 4. Один катет приложим к линии действия силы, вдоль второго проведем перпендикуляр к точке вращения
Плечо силы проводят так:
- взять прямоугольный треугольник;
- приложить один из катетов к линии действия;
- провести перпендикуляр к точке вращения, используя второй катет;
Момент силы, формула
Момент силы (вращательный момент) можно вычислить, когда известны сила и ее плечо.
Перемножим силу на плечо силы, получим момент силы.
[ large boxed { M = F cdot l } ]
( M left( H cdot text{м} right) ) – момент силы (вращательный момент);
( F left( H right) ) – сила, которая вращает тело;
( l left( text{м} right) ) – плечо этой силы;
Примечание:
Отрезок, не перпендикулярный силе, плечом силы не является. Сила и ее плечо всегда перпендикулярны!
Еще одна формула для момента силы
Вращательный момент можно рассчитать еще одним способом.
Для этого вместо плеча силы нужно использовать:
- величину ( d ) и
- угол ( gamma ) между силой и этим расстоянием.
Величина ( d ) – это расстояние между двумя точками:
- точкой, к которой приложена сила
- и точкой, вокруг которой происходит вращение.
Рис. 5. Момент силы можно рассчитать, зная: — силу; — расстояние между точками приложения силы и вращения; — угол между силой и этим расстоянием
На рисунке 5: черная стрелка – это вектор вращающей силы ( vec{ F } ); красная линия – это расстояние ( d ) между точкой приложения силы и точкой вращения.
[ large boxed { M = F cdot d cdot sin(gamma) } ]
Этой формулой во многих случаях пользоваться удобнее, чем формулой, содержащей ( l ) плечо силы.
Когда момент силы обращается в ноль
Рассмотрим внимательнее формулу для момента силы.
[ M = F cdot d cdot sin(gamma) ]
В правой части формулы находятся три множителя: ( F ) , (d) и ( sin(gamma) )
Если любой из трех множителей будет равен нулю, то правая часть уравнения обратится в ноль.
Левая часть уравнения, при этом, также, обратится в ноль. Потому, что между левой и правой частями записан знак равенства.
Кратко: Вращательный момент будет нулевым в любом из таких случаев:
- ( F = 0) – когда вращающая сила отсутствует;
- (d = 0 ) – когда сила приложена к точке вращения;
- ( sin(gamma) = 0 ) – когда сила ( F ) и величина (d ) лежат на одной прямой. В таком случает, угол между величинами ( F ) и (d ) равен нулю;
Действительно: ( sin(0) = 0 ), такое будет, когда ( F || d )
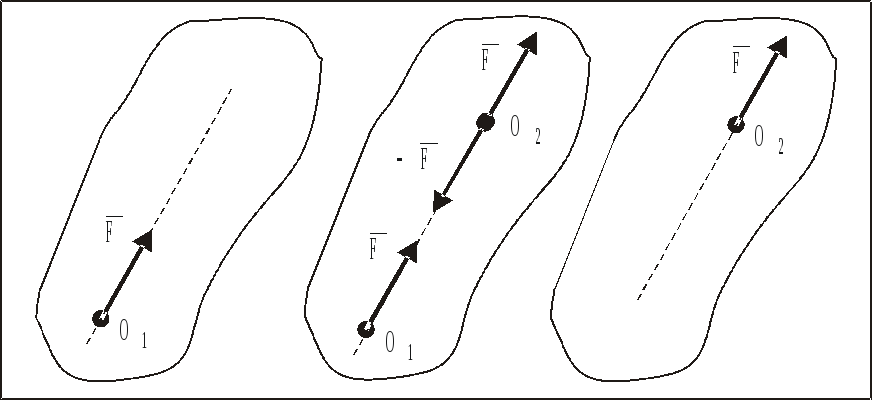
Эти три случая изображены на рисунке 6.
Рис. 6. Сверху вниз представлены три случая, в которых вращательный момент обращается в ноль
На рисунке 6: черная стрелка – это вектор силы, красная линия – это расстояние между точкой приложения силы и точкой вращения.
Сверху вниз представлены три случая для нулевого вращательного момента.
- В верхней части рисунка сила отсутствует;
- Средняя часть рисунка соответствует случаю, когда сила (черная стрелка) приложена к точке, вокруг которой тело может вращаться;
- Внизу — сила ( F ) параллельна величине (d ) — расстоянию между точкой приложения силы и точкой вращения.


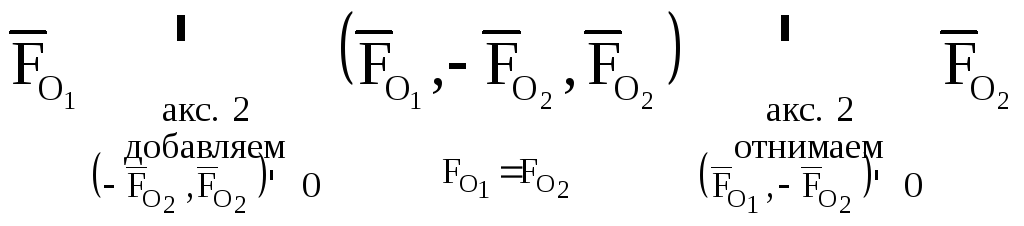

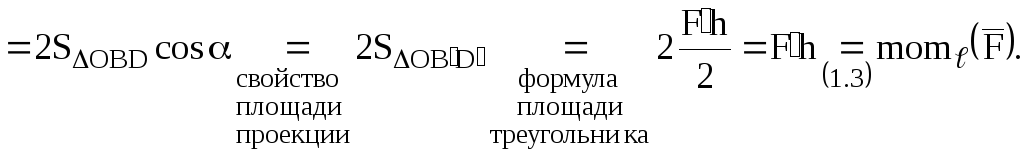


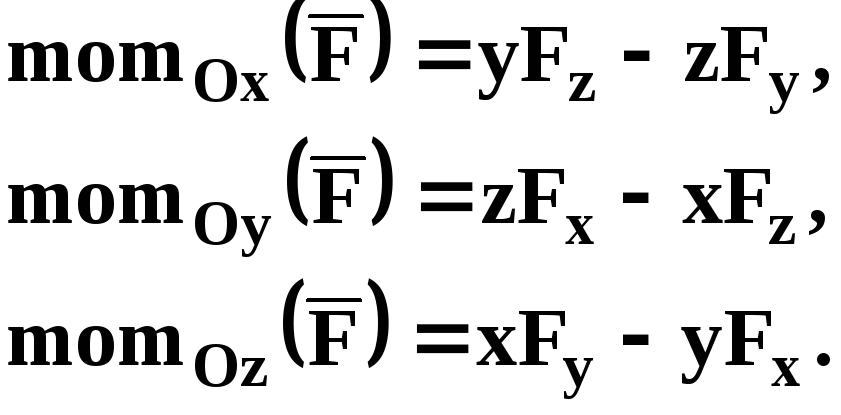
 Сила в механике
Сила в механике