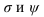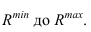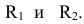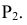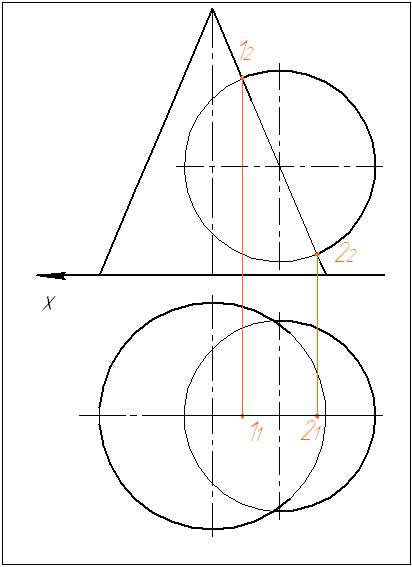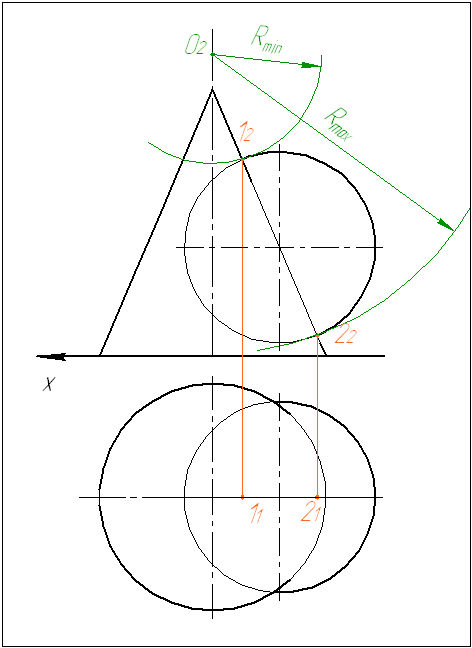Как найти линию пересечения двух тел

Содержание:

Взаимное пересечение поверхностей:

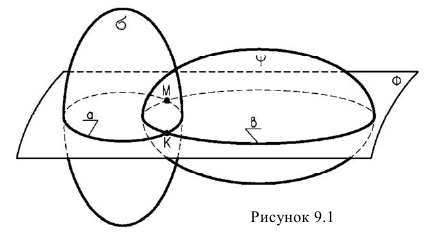
При пересечении поверхностей образуется линия, которую принято называть линией взаимного пересечения поверхностей. Эта линия пересечения принадлежит одновременно двум поверхностям. Поэтому построение линии пересечения сводится к определению точек одновременно принадлежащих обеим поверхностям. Для нахождения таких точек используется в общем случае метод вспомогательных секущих поверхностей. Сущность способа заключается в следующем: Пусть задано две поверхности

Общий алгоритм построения линии пересечения поверхностей:

1. Введем вспомогательную поверхность Ф.
2. Строим линии пересечения поверхности Ф с поверхностями
3. Определяем точки пересечения К и М, простроенных линий a и b
4. Многократно повторяя эту операцию, найдем ряд точек, принадлежащих одновременно двум поверхностям.
5. Соединяем последовательно точки с учетом видимости.

В качестве посредников могут быть приняты как поверхности, так и плоскости, но целесообразно выбирать такие, которые дают наиболее простые линии пересечения с заданными поверхностями.

Взаимное пересечение поверхностей

Линия, общая для двух пересекающихся поверхностей – линия пересечения.

Чтобы определить проекцию линии пересечения, необходимо найти проекции точек, общих для этих поверхностей. Их находят способом вспомогательных секущих плоскостей или вспомогательных сфер.

Если рёбра призмы или ось вращения цилиндра перпендикулярны какой-либо из плоскостей проекций, то на этой плоскости проекций линия пересечения совпадает с контуром основания призмы или цилиндра.

Пересечение двух многогранников

Для построения линии пересечения двух многогранников необходимо определить точки пересечения ребер первого многогранника с гранями второго, затем ребер второго с гранями первого. Полученные точки соединить отрезками прямой с учетом видимости. На рисунке 9.2 заданы поверхности трехгранной призмы DEFD’E’F’ и трехгранной пирамиды SABC. Так как призма F, фронтально-проецирующая, фронтальная проекция линии пересечения совпадает с гранями призмы, поэтому необходимо построить только горизонтальную проекцию. Для этого определяем точки пересечения ребер пирамиды с гранями призмы. Ребро SC пересекает грани призмы в точках I и 2, ребро SB – в точках 3 и 4, ребро SA не пересекает призму. Затем определяем точки пересечения ребер призмы с гранями пирамиды.

По чертежу видим, что только ребро DD’ пресекает поверхность пирамиды. Для определения точек пересечения 5 и б через ребро DD’ проводим горизонтальную плоскость, которая пересекает пирамиду по треугольнику. Точки 5 и 6 получаем, как пересечение DD’ с построенным треугольником.

Полученные точки соединяем с учетом видимости. Видимой считается тот отрезок прямой, который принадлежит двум видимым граням поверхностей.

Как видим, линия пересечения двух многогранников представляет собой пространственную ломаную линию.

В том случае, когда обе гранные поверхности общего положения, последовательность соединения точек вызывает затруднение. Поэтому для соединения точек используется диаграмма Ананова – условные развертки поверхностей (см. учебник).

Пересечение гранной и кривой поверхности

Линия пересечения гранной и кривой поверхности, представляет собой пространственную кривую линию, с точками излома на ребрах многогранника.

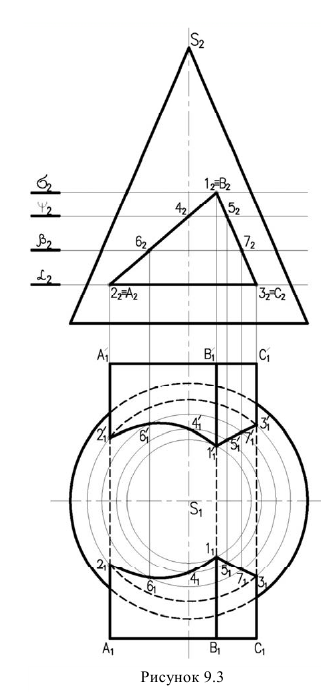
Поэтому сначала определяем точки пересечения ребер многогранника с кривой поверхностью, а затем промежуточные точки и соединяем их с учетом видимости. На рисунке 9.3 заданы поверхности трехгранной призмы и кругового конуса.

Так как призма фронтально-проецирующая, фронтальная проекция линии пересечения совпадает с проекцией боковых граней призмы, поэтому необходимо построить только горизонтальную проекцию линии пересечения.

Сначала определяем точки пересечения ребер призмы с поверхностью конуса, а затем находим промежуточные точки, принадлежащие линиям пересечения. Для нахождения точек пересечения, используем горизонтальные плоскости посредники, так как они пересекают конус по окружностям, а призму но прямым линиям. Как видим, в данном случае линия пересечения распадается на две отдельные части.  

Пересечение двух кривых поверхностей. Метод вспомогательных секущих плоскостей

Линия пересечения двух кривых поверхностей, представляет пространственную кривую линию. Поэтому для ее построения необходимо определить ряд точек принадлежащих этой лини.

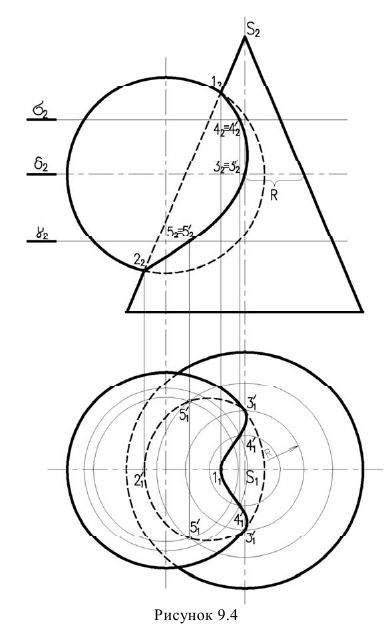
На рисунке 9.4 заданы поверхности конуса и сферы. Точки строятся при помощи горизонтальных плоскостей посредников, которые рассекают обе поверхности но окружностям.

Обязательно находим опорные точки, к которым относятся высшая и низшая точки линии пересечения и точки границы видимости. Так как оси поверхностей лежат в одной фронтальной плоскости, контурные образующие поверхностей пересекаются в точках 1 и 2 — это и будет высшая и низшая точки. Точки границы видимости лежат на экваторе сферы, поэтому точки 3 и 3′ находим с помощью вспомогательной горизонтальной плоскости, проходящей через центр сферы. Она рассекает сферу по экватору, а конус но параллели радиуса R.

Взаимно пересекаясь, они и дают точки 3 и 3′ фронтальную проекцию определяем по вертикальной линии связи на плоскости 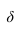Затем берем еще две вспомогательные плоскости расположенные выше и ниже плоскости и выполняя, аналогичные построения определяем точки 4 и 5 и 5′. Полученные точки соединяем с учетом видимости.  

• Заказать чертежи

Пересечение поверхностей вращении. Метод вспомогательных секущих сфер

Способ вспомогательных секущих сфер применяется при следующих условиях:

1. Пересекающиеся поверхности являются поверхностями вращения.
2. Оси этих поверхностей пересекаются.
3. Оси поверхностей параллельны одной из плоскостей проекций.

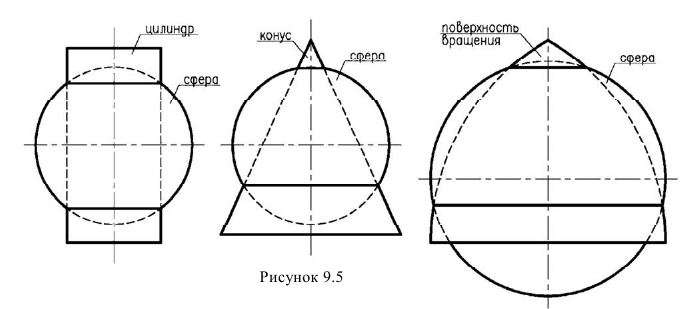
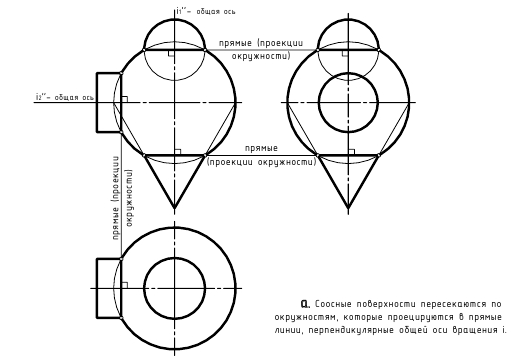
Перед рассмотрением этого способа разберем понятие соосных поверхностей. Соосными называются поверхности вращения, имеющие общую ось. Соосные поверхности пересекаются по окружностям перпендикулярным оси вращения.

На рисунке 9.5 приведены некоторые из них.

Именно то, что поверхности пересекаются по окружностям, которые проецируются в линии и используется в методе сфер.

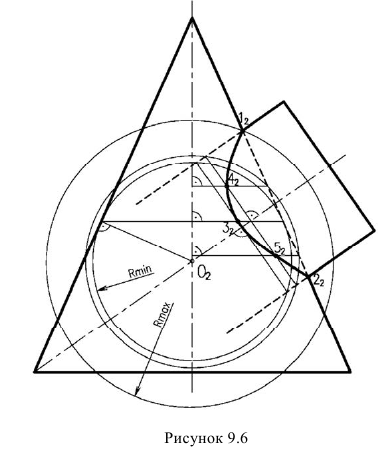
Рассмотрим пример на рисунок 9.6. Даны поверхности вращения – конус и цилиндр. Так как оси лежат в одной плоскости, можно определить точки пересечения контурных образующих в точках 1 и 2, как в предыдущем примере.

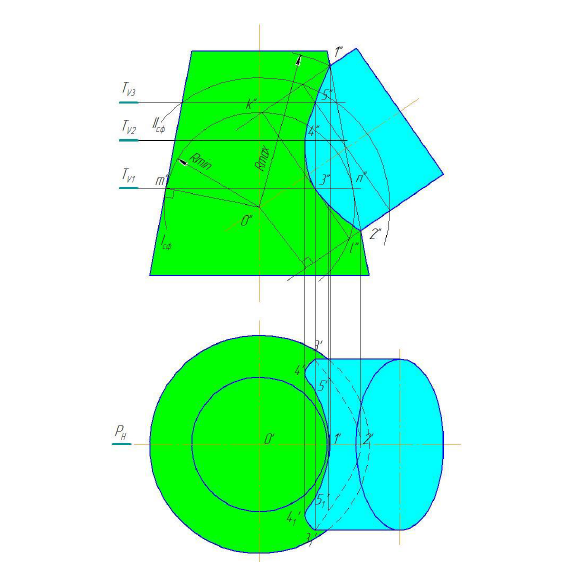
Однако, для нахождения промежуточных точек, вспомогательные секущие плоскости не подходят, т.к. горизонтальные плоскости рассекут цилиндр по эллипсам, фронтально-нроецирующие – конус по эллипсам. А сам эллипс строить непросто. Поэтому именно в этом случае удобно использовать в качестве посредников – сферы. За центр вспомогательных сфер, принимается точка пересечения осей заданных поверхностей. Далее необходимо определить, размеры радиусов вспомогательных секущих сфер. Максимальный радиус сферы

В данном случае минимальная сфера вписана в конус. Минимальная сфера касается поверхности конуса по окружности, а цилиндр пересекает по окружности. Нужно, иметь ввиду, что проекции окружностей пересечения перпендикулярны осям вращения. Эти две окружности пересекаются в точке 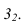. Фактически таких точек две, они совпадают на фронтальной проекции. Для построения промежуточных точек берем вспомогательные сферы радиусов в пределах от

Они пересекают и поверхность цилиндра, и поверхность конуса по окружностям, которые пересекаясь даюг промежуточные точки. Полученные точки соединяются плавной линией.

Здесь построена только фронтальная проекция. Для построения горизонтальной проекции, если это необходимо, точки строят как лежащие на окружностях полученных радиусов.  

Теорема Монжа

Рассмотрим вариант, когда минимальная сфера касается двух поверхностей вращения. В этом случае для построения линии пересечения поверхностей используется теорема Г. Монжа, которая формулируется так:

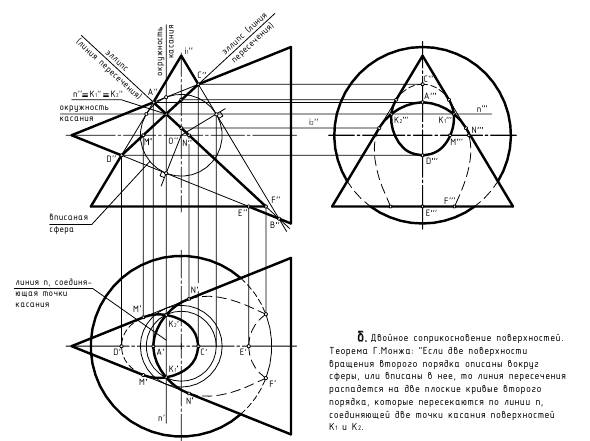
Если две поверхности вращении второго порядка описаны около третьей или вписаны в нее, то линии их пересечении распадается на две плоские кривые второго порядка. Плоскости этих кривых проходит через прямую, соединяющую точки пересечении линий касании.

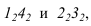
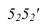
В соответствии с этой теоремой линии пересечения конуса и цилиндра описанного около сферы (рисунок 9.7) будут плоскими кривыми -эллипсами, фронтальные проекции которых изображаются прямыми проходящими через – точки линий пересечения окружностей касания.

Пересечение поверхностей вращения с многогранниками

Внешние и внутренние формы большинства предметов образуются сочетанием нескольких поверхностей. Пересекаясь между собой, они образуют линии, которые принято называть линиями перехода.

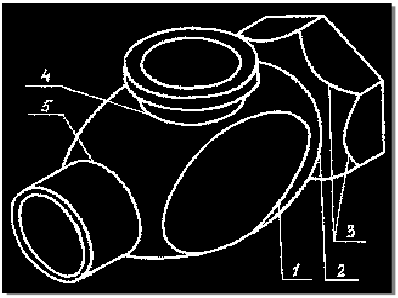
На рис. 9.1 изображена деталь с несколькими линиями перехода. Линия 1 является границей между плоской и торовой поверхностями, 2 – торовой и конической, 3 – конической и плоскими (гранями призмы), 4 и 5 – торовой поверхностью корпуса и цилиндрическими поверхностями патрубков.

Рисунок 9.1 – Корпус с линиями перехода

Линия пересечения многогранника с телом вращения в общем случае состоит из отдельных участков кривых линий, получающихся при пересечении граней многогранника с поверхностью вращения. Точки перехода от одного участка к другому находятся в пересечении ребер многогранника с телом вращения и называются точками излома. Участок линии пересечения может быть и прямой линией в случае пересечения линейчатой поверхности вращения гранью многогранника по образующей.

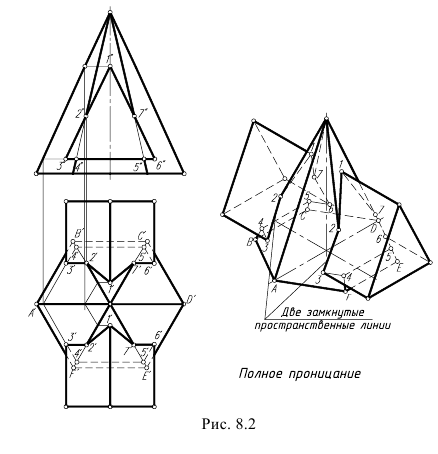
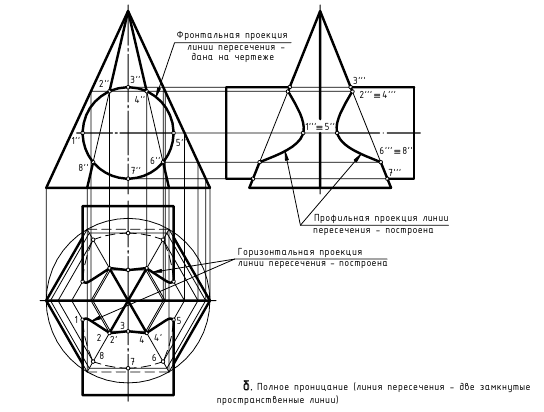
При проницании (полном пересечении) получаются две замкнутые линии пересечения. Они могут быть плоскими (поверхность вращения проницает одну грань) или пространственными, состоящими из нескольких плоских кривых с точками излома в местах пересечения поверхности вращения ребрами многогранника.

При врезании (неполном пересечении) получается одна замкнутая пространственная линия.

Таким образом, в соответствии с указанным выше, задачи данной темы решаются по следующему плану:

• Определяются точки излома линии пересечения, являющиеся точками пересечения ребер многогранника с поверхностью вращения;
• Находятся точки принадлежащие линиям пересечения отдельных граней многогранника с телом вращения. При этом сначала следует найти характерные (опорные) точки кривых. Это точки, проекции которых отделяют видимую часть проекции линии пересечения от невидимой, это проекции наивысших и наинизших точек линии пересечения, ближайших и наиболее удаленных, крайних слева и справа на проекциях линии пересечения;
• Определение видимости линии пересечения поверхностей и их очерков. Видимость проекций участков линии пересечения определяется из условия расположения их на видимой стороне каждой поверхности.

При построении точек линии пересечения многогранников с телами вращения используют вспомогательные секущие плоскости. Их располагают так, чтобы они пересекали данные поверхности по простым для построения линиям (прямым или окружностям).

Рассмотрим линии пересечения поверхности прямой трехгранной призмы с поверхностью конуса вращения. Боковые грани призмы являются фронтально-проецирующими плоскостями, а ось конуса перпендикулярна горизонтальной плоскости проекций.

Призму можно рассматривать, как три плоскости, проходящие через ее грани, а задача сводится к нахождению линий пересечения этих плоскостей с конусом.

Рисунок 9.2 – Пересечение трехгранной призмы с конусом

Пример. Построить линию пересечения поверхности тора с поверх-ностью трехгранной призмы (рис. 9.3).

Решение. Боковые грани призмы являются фронтально-проецирующими плоскостями и фронтальная проекция линии пересечения совпадают с проекцией боковой поверхности призмы. Из фронтальной проекции видно, что в данном случае имеет место проницание тора призмой (две замкнутые линии пересечения).

На рис. 9.3 рассмотрен пример пересечения поверхностей тора и треугольной призмы [2].

По двум заданным проекциям строим третью – профильную.

Рисунок 9.3 – Построение линии пересечения трехгранной призмы с тором

Заданная призма – горизонтально-проецирующая. Так как грани призматического отверстия перпендикулярны горизонтальной плоскости проекций, то на чертеже известна горизонтальная проекция линии пересечения, она совпадает с вырожденной проекцией поверхности призмы.

Следовательно, линия пересечения совпадает с горизонтальной проекцией основания призмы.

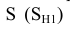
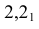
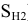
Определяем характерные точки: самую близкую точку 1 фронтальной плоскостью и самые далекие – и 3 фронтальной плоскостью S ().

Определяем промежуточные точки 4 и 5 при помощи вспомогательных фронтальных плоскостей .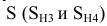

Соединяем полученные точки плавной кривой линией с учетом видимости.

Пересечение поверхностей вращения

Линия пересечения двух поверхностей вращения в общем случае представляет пространственную кривую, которая может распадаться на две и более части. Эти части могут быть, в частности, и плоскими кривыми и даже прямыми линиями.

Линию пересечения поверхностей обычно строят по ее отдельным точкам. Точки подразделяются на характерные (опорные) и промежуточные (случайные).

Общим способом построения этих точек является способ вспомогательных секущих поверхностей – посредников. При пересечении данных поверхностей вспомогательной поверхностью определяются линии пересечения ее с данными поверхностями, в пересечении этих линий получаются точки, принадлежащие искомой линии пересечения.

Наиболее часто в качестве поверхностей-посредников применяются плоскости или сферы.

Для определения линии пересечения часто пользуются вспомогательными секущими поверхностями. Поверхности-посредники пересекают данные поверхности по линиям, которые, в свою очередь, пересекаются в точках линии пересечения данных поверхностей.

Секущие поверхности-посредники выбираются так, чтобы они, пересекаясь с данными поверхностями, давали простые для построения линии, например прямые и окружности.

Из общей схемы построения линии пересечения поверхностей выделяют два основных метода – метод секущих плоскостей и метод секущих сфер.

Способ вспомогательных секущих плоскостей

В качестве вспомогательных секущих плоскостей чаще всего используют плоскости, параллельные одной из плоскостей проекций.

Положение их выбирают таким, чтобы они пересекали заданные поверхности по простейшим линиям – прямым или окружностям.

Этот способ рекомендуется применять, если сечениями заданных поверхностей одной и той же плоскостью являются прямыми линиями или окружностями. Такая возможность существует в трех случаях:

1. Если образующие (окружности) расположены в общих плоскостях уровня;
2. Если в общих плоскостях уровня оказываются прямолинейные образующие линейчатой поверхности и окружности циклической;
3. Линейчатые каркасы заданных поверхностей принадлежат общим плоскостям уровня или пучкам плоскостей общего положения.

Пересечение цилиндрической и торовой поверхности

Если одна из поверхностей является цилиндрической проецирующей поверхностью, то построение линии пересечения упрощается, так как в этом случае одна проекция линии пересечения совпадает с окружностью – проекцией цилиндра на перпендикулярную плоскость проекций.

На рис. 9.4 построена линия перехода между цилиндром и тором. Так как поверхность цилиндра перпендикулярна плоскости Н, то горизонтальная проекция линии перехода известна. Она совпадает с горизонтальной проекцией цилиндра. Фронтальную и профильную проекции строим по принадлежности точек линии перехода не проецирующей поверхности тора.

Рисунок 9.4 – Построение линии пересечения цилиндра с тором

Линия пересечения заданных поверхностей представляет собой пространственную кривую линию, имеющую фронтальную плоскость симметрии, образованную пересекающимися поверхностями цилиндра и тора.

Рассмотрим линию пересечения поверхности сферы с поверхностью конуса вращения (Рисунок 9.5).

Точки 1 и 7, расположенные на очерках фронтальных проекций конуса и сферы, очевидны и определяются без дополнительных построений.

Точка 4 на экваторе сферы построена с помощью горизонтальной плоскости, пересекающей конус по окружности. В пересечении горизонтальных проекций этой окружности и экватора находится горизонтальная проекция 4′ точки 4 и фронтальная 4” проекции точки 4 определим с помощью линии связи. Точка 4 на горизонтальной проекции разделяет кривую на видимую и невидимую части.

Точки 2, 3, 5 и 6, расположенные в промежутке между характерными точками 1,4 и 7 строим аналогично. С помощью линий связи определим фронтальные и горизонтальные проекции этих точек.

Рисунок 9.5 – Построение линии пересечения конуса и сферы

Особые случаи пересечения

Пересечение соосных поверхностей вращения

Соосными называют поверхности вращения, оси которых совпадают. Линия пересечения таких поверхностей строится на основании теоремы о пересечении соосных поверхностей вращения: соосные поверхности вращения пересекаются между собой по окружностям.

Если ось вращения соосных поверхностей перпендикулярна к какой либо плоскости проекций, то линия их пересечения проецируется на эту плоскость в виде окружности, а на другую плоскость проекций – в прямую линию.

75

На рис. 9.6 даны примеры пересечения соосных поверхностей вращения (ось вращения параллельна горизонтальной плоскости). На рис. 9.6, а приведены сфера и конус, б – сфера и цилиндр, в – сфера и тор.

Рисунок 9.6 – Пересечение соосных поверхностей вращения

Теорема Монжа для пересекающихся поверхностей вращения

Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания.

Для этого случая пересечения поверхностей вращения необходимо выполнение трех условий:

• пересекающиеся поверхности должны быть поверхностями вращения;
• оси поверхностей должны пересекаться;
• плоскость, образованная осями поверхностей, должна быть параллельна одной из плоскостей проекций.

Рисунок 9.7 – Пересечение поверхностей вращения по теореме Монжа

Это положение подтверждается теоремой Монжа: Если две поверхности второго порядка могут быть вписаны или описаны около третьей поверхности второго порядка, то пространственная кривая их пересечения четвертого порядка распадается на две плоские кривые второго порядка.

Способ вспомогательных секущих сфер

При построении линии пересечения поверхностей вращения не всегда удается подобрать секущие плоскости так, чтобы они пересекали поверхности по линиям, проекции которых были бы прямыми или окружностями. В некоторых таких случаях в качестве секущих поверхностей (посредников) целесообразно применять сферы. Этот способ основан на свойстве сферы пересекаться с любой поверхностью вращения, ось которой проходит через центр сферы по окружности.

Чтобы сфера одновременно пересекала две поверхности по окружностям, проецирующимся в прямые линии, необходимо выполнить условия:

• Оси поверхностей вращения должны пересекаться (точку пересечения принимают за центр вспомогательных концентрических сфер).
• Оси поверхностей вращения должны располагаться параллельно какой-либо плоскости проекций.

Пример. Построить проекции линии пересечения поверхностей конуса и цилиндра (рис. 9.8) [1].

Заданы прямой усеченный конус и наклонный цилиндр – тела вращения. Их оси параллельны фронтальной плоскости проекций и пересекаются в точке О(о′,о), т.е. соблюдены условия метода сфер.

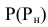
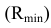
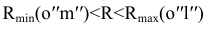
Как и в предыдущих задачах, найдем проекции характерных точек. Точка 1 – самая высокая, точка 2 – самая низкая. Чтобы убедится в этом проведем через оси тел вспомогательную фронтальную плоскость . Эта плоскость рассекает рассматриваемые тела по крайним очерковым образующим, которые на фронтальную плоскость проекции проецируются без искажения и, пересекаясь между собой, образуют искомые точки 1′, 2′. С помощью вспомогательных сфер найдем другие точки линии пересечения заданных поверхностей. Для определения радиуса наименьшей сферы из центра О(о′) проведем две нормали, перпендикулярные очерковым образующим этих тел и большей нормалью выполним эту сферу. Эта сфера будет наименьшей , проведенной в большем теле, поэтому поверхности конуса она касается по окружности, которая проецируется на фронтальную плоскость проекций в виде отрезка m′′n′′, а поверхность наклонного цилиндра пересекает по окружности, фронтальная проекция которой также проецируется в прямую линию k′′l′′. В пересечении k′′l′′ и m′′n′′ получим точку 3′′ – самую глубокую точку пересечения. Для нахождения промежуточных точек проведем ряд концентрических сфер, радиусы которых должны находится в пределе , и аналогично точке 3′′ находим необходимые промежуточные точки.

Рисунок 9.8 – Построение линии пересечения конуса и цилиндра

Учитывая, что сфера минимального радиуса всегда касается той поверхности, которая пронизывается другой, соединим найденные фронтальные проекции плавной кривой. Получим фронтальную проекцию линии пересечения. В нашем случае сфера радиусом 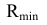касается поверхности конуса, значит, поверхность цилиндра пронизывает поверхность конуса.

Построим горизонтальную проекцию линии пересечения. Т.к. точки 1′′, 2′′ лежат на очерковой образующей конуса, то горизонтальные проекции этих точек находятся на оси конуса, т.е. на горизонтальной проекции этой образующей. Для нахождения горизонтальных проекций точек 3′, 4′, 5′ воспользуемся горизонтальными плоскостями 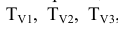, проведенными через эти точки соответственно. Каждая плоскость рассекает поверхность конуса по окружности, которая на горизонтальной плоскости проекций не искажается. По линиям связи найдем горизонтальные проекции точек 3′, 4′, 5′.

Для правильного соединения точек определим их видимость. Границей видимости на плоскости Н является точка 4′′, лежащая на осевой фронтальной проекции цилиндра. Горизонтальные проекции ее 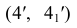находятся на очерковых образующих цилиндра. Соединив плавной кривой найденные точки, получим горизонтальную проекцию линии пересечения рассматриваемых тел.

Способ вспомогательных секущих плоскостей

Суть способа – вспомогательная секущая плоскость одновременно пересекает поверхности каждого тела и образует фигуры сечения, контуры которых пересекаются. Точки пересечения контуров соединяют.

Этот способ применим тогда, когда контуры отдельных сечений представляют прямые линии или окружности.

Точки 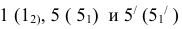являются очевидными – это точки пересечения очерковых и оснований конусов. Найдём соответствующие вторые проекции этих точек.

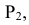
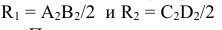
Проведём горизонтальную плоскость которая рассечет оба конуса. В сечении конусов будут окружности причем их фронтальными проекциями являются прямые. Построим горизонтальные проекции этих сечений – окружности радиусом

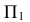
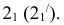
На пересечении этих окружностей сечений на  определим горизонтальную проекцию общей точки – Фронтальную проекцию точек 2 и 2 определим по линиям связи на секущей плоскости

Проведём еще ряд горизонтальных секущих плоскостей и определим проекции других промежуточных точек линии пересечения, которые соединим лекальной кривой с учётом видимости.

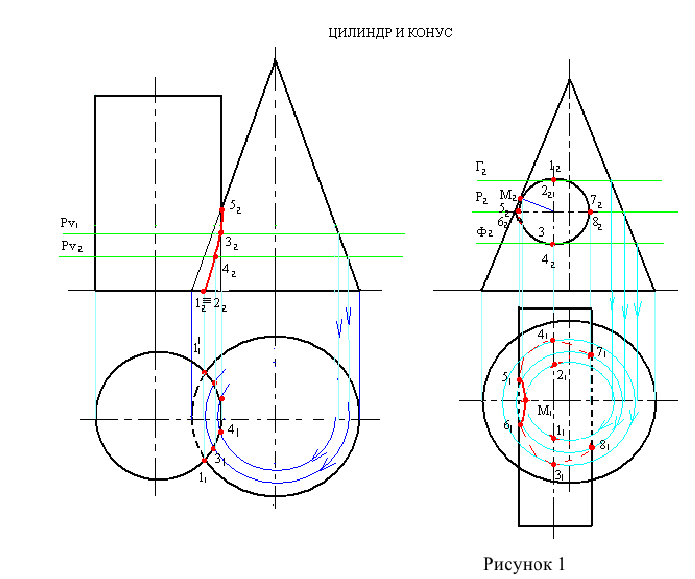
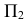
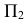
При взаимном пересечении конуса и цилиндра (рисунок 1) ось вращения цилиндра перпендикулярна . Значит, на линия пересечения совпадет с контуром основания цилиндра, т.е. фронтальной проекцией линии пересечения будет являться фронтальная проекция цилиндра.

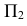
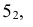
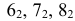
Построив горизонтальную проекцию линии пересечения, на на 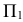пересечении горизонтальной оси симметрии цилиндра с проекцией цилиндра наметим точки – точки границы видимости линии пересечения, лежащие на экваторе цилиндра.

На точки линии пересечения, лежащие выше экватора будут видимы, а точки, лежащие ниже экватора – невидимы.

Способ вспомогательных сфер

Этот метод можно применять при соблюдении следующих условий :

• пересекающиеся поверхности должны быть поверхностями вращения;
• их оси должны пересекаться ; точка пересечения осей является центром вспомогательных сфер;
• их оси должны быть // какой-либо плоскости проекций.

Сфера 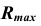проходит через самую дальнюю очевидную точку.

Сфера , должна касаться образующей большего тела, а меньшее тело -пересекать.

Сфера определяется как большее расстояние от центра сфер до образующих обоих тел – перпендикуляры из центра сфер к очерковым образующим. Больший перпендикуляр и будет являться радиусом минимальной сферы.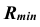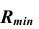

Сфера пересекает тела по окружностям, проецирующимся на одну из плоскостей проекций отрезком.

1.    Определяем очевидные точки

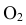
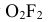
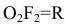
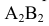
2.    Восстанавливаем перпендикуляры из центра сфер к очерковым образующим цилиндра и конуса. Перпендикуляр к цилиндру больше, чем перпендикуляр к образующей конуса. Значит, и будет являться радиусом минимальной сферы. На проводим из центра этим радиусом R окружность, которая рассечет и конус и цилиндр по окружностям, фронтальной проекцией которых будут прямые – сечение конусаи сечение цилиндра

На пересечении этих сечений определяем фронтальную проекцию точки 3 – .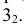

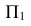
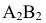
3.    На строим горизонтальную проекцию сечения конуса, на котором находится точка 3 -окружность радиусом / 2, на которой по линии связи определяем точки

1.    Проводим ещё ряд секущих сфер радиусом больше минимальной и меньше максимальной и определяем другие промежуточные точки линии пересечения, которые соединяем лекальной кривой с учётом видимости.

Большее тело поглощает меньшее.

2.    Видимость линии пересечения определяем следующим образом:

Элементы технического рисования

Технический рисунок – это наглядное изображение, выполненное по правилам аксонометрических проекций от руки, на глаз, соблюдая пропорции. Им пользуются на производстве для иллюстрации чертежей.

Обычно технический рисунок выполняется в изометрии.

Выполнение рисунка модели или детали начинается с проведения аксонометрических осей. Затем рисуется основание и строятся габаритные очертания -прямоугольные параллелепипеды. Деталь мысленно расчленяют на отдельные геометрические элементы, постепенно вырисовывая все элементы.

Технические рисунки получаются более наглядными, если их покрыть штрихами. При нанесении штрихов считают, что лучи света падают на предмет справа и сверху или слева и сверху.

Взаимное пересечение поверхностей с примерами

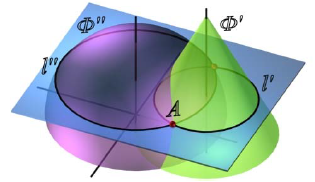
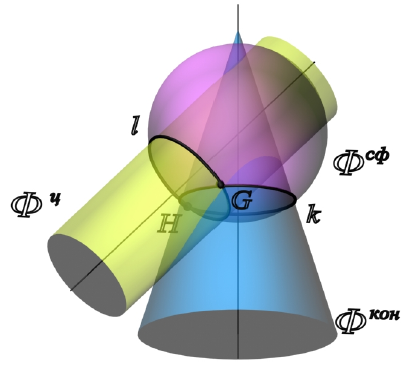
Алгоритм решения задач по определению линии пересечения поверхностей Ф’ и Ф” (рис. 9.1) в целом аналогичен решению второй позиционной задачи и состоит в следующем:

1. Обе заданные поверхности Ф’ и Ф” рассекают третьей, вспомогательной плоскостью или поверхностью P.
2. Определяют линии пересечения каждой заданной поверхности со вспомогательной: Ф’ × P =l’, Ф” × P =l”.
3. Определяют точки пересечения полученных линий l’×l” = A и A’. Точки A и a´ принадлежат обеим поверхностям.
4. Проведя несколько вспомогательных поверхностей, находят достаточное количество точек и соединяют их плавной лекальной кривой, которая и является искомой линией пересечения поверхностей.
5. Определяют видимость поверхностей и линии их пересечения.

Рис. 9.1. Пересечение поверхностей

В качестве вспомогательных поверхностей P следует выбирать поверхности – плоскости или сферы, которые пересекают обе заданные поверхности по наиболее простым для построения линиям – прямым или окружностям. Кроме того, если в сечении поверхности получаются окружности, они должны проецироваться на одну из плоскостей проекций без искажения.

Определение точек линии пересечения поверхностей начинают с построения так называемых опорных точек. К ним относятся:

• точки пересечения очерковых образующих, если образующие лежат в одной плоскости,
• точки, лежащие на очерковых образующих поверхностей,
• точки, лежащие в общей плоскости симметрии,
• экстремальные (верхние – нижние, правые – левые) по отношению к плоскостям проекций, к центру концентрических сфер.

При соединении точек следует иметь ввиду, что проекции линии пересечения не могут выходить за пределы общей площади – площади наложения – проекций пересекающихся поверхностей. Видимыми будут те участки линии пересечения, которые принадлежат видимым частям обеих поверхностей.

Способ вспомогательных параллельных плоскостей

Этот способ заключается в том, что обе поверхности рассекаются параллельными плоскостями уровня. Этот способ применяют лишь в тех случаях, когда вспомогательные плоскости рассекают поверхности по простым линиям – прямым или окружностям, которые проецируются на соответствующую плоскость проекций без искажения.

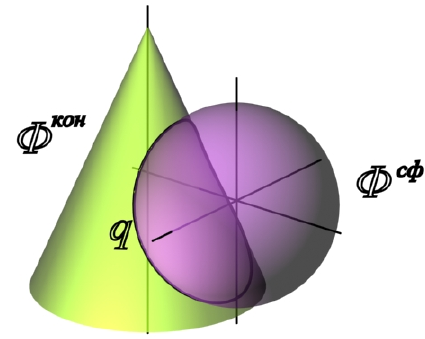
Рассмотрим построение линии пересечения прямого кругового конуса и сферы (рис. 9.2).

Рис. 9.2. Линия пересечения поверхностей прямого кругового конуса и сферы

Фронтальные плоскости уровня пересекают поверхность конуса по гиперболам, следовательно, для решения данной задачи нужно применить горизонтальные плоскости уровня, которые рассекают обе данные поверхности по окружностям.

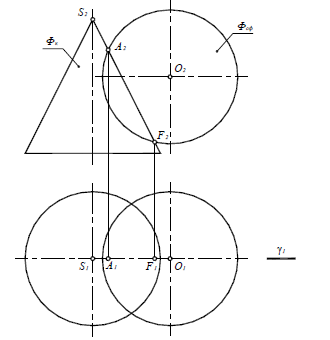
Решение задачи начинают с построения опорных точек. Конус и сфера имеют общую плоскость симметрии γ(γ₁), параллельную плоскости П₂. Поэтому высшая точка A и низшая точка F линии пересечения получаются как результат пересечения очерковых образующих конуса и сферы (рис. 9.3).

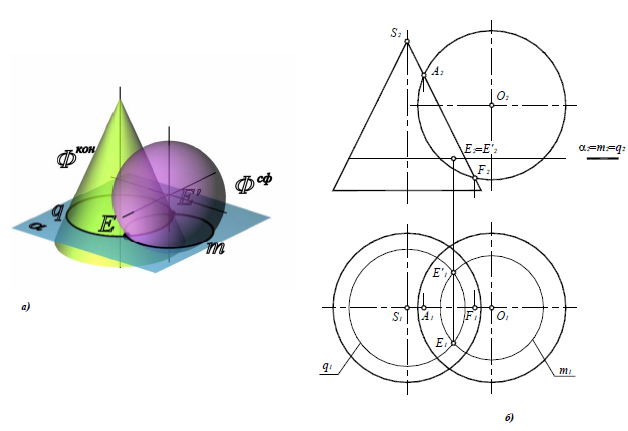
Остальные точки определяются с помощью горизонтальных плоскостей уровня. Более подробно разберем построение точек E и E'(рис. 9.4).

1.    Пересечь обе поверхности вспомогательной горизонтальной плоскостью уровня α(а₂). Плоскость а(а₂) пересекает сферу по окружности m(m₁,m₂), а конус – по окружности q(q₁,q₂):
m(m₁ ,m ₂)=Ф ^сф 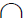а (а₂);
q(q₁ ,q₂) =Ф^к 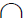а (u₂).
 

2.    Построив горизонтальные проекции окружностей m и q, определить точки их пересечения E и E’:
E₁= m₁ × q₁; E₂=E₁E₂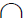α2.
E’₁=m₁ × q₁; E’₂=E_lE₂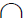α2.

Рис. 9.3. Определение опорных точек линии пересечения поверхностей

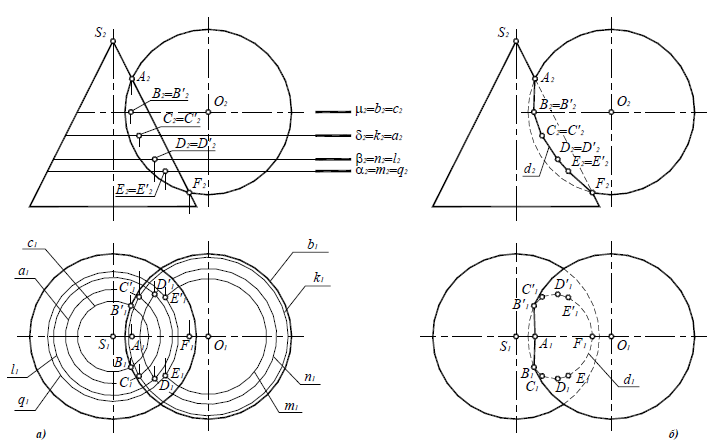
3.    Аналогичным образом определяются остальные точки, формирующие линию пересечения (рис. 9.5,а). Они получены с помощью горизонтальных плоскостей уровня β(β₂), δ(δ₂) и μ(μ₂). Пределы этих плоскостей по высоте определяют высшая и низшая опорные точки линии пересечения поверхностей. Плоскость μ(μ₂)рассекает поверхность сферы по очерковой образующей b (b₂, b₂),поэтому полученные точки В и В’ являются опорными, ограничивающими линию пересечения поверхностей по ширине.

4.    Последовательно соединить одноименные проекции полученных точек плавной лекальной кривой. Полученная линия не должна выходить за пределы области перекрытия проекций данных поверхностей.

5.    Определить видимость линии пересечения поверхностей и их очерковых образующих.

Поверхность конуса на горизонтальной плоскости проекций полностью видима, следовательно, видимость линии пересечения определяется по поверхности сферы. Видима будет та часть сферы, которая на П₂ лежит выше очерковой образующей b₂.Точки В и В’ на очерковой образующей сферы являются точками смены видимости линии пересечения на плоскости проекций П₁.
Искомая линия пересечения поверхностей конуса и сферы d(d₁,d₂) (кривая второго порядка), полученная способом вспомогательных секущих плоскостей, приведена на рис 9.5,б.

Рис. 9.4. Определение промежуточных точек линии пересечения поверхностей:
а – наглядное изображение;
б – комплексный чертеж

Рис. 9.5. Определение линии пересечения поверхностей способом вспомогательных параллельных плоскостей:
а – определение промежуточных точек;
б – искомая линия пересечения

Способ вспомогательных сфер

При построении линии пересечения двух поверхностей способом вспомогательных сфер возможны два случая. В одном из них используются сферы, проведенные из одного, общего центра (концентрические), а в другом -сферы, проведенные из разных центров (эксцентрические).

Способ концентрических сфер

Этот способ применяется для построения линии пересечения поверхностей вращения произвольного вида, при условии, что оси этих поверхностей пересекаются.

В основу способа концентрических сфер положено свойство сферы с центром на оси какой-либо поверхности.

Если центр сферы находится на оси любой поверхности вращения, то сфера соосна с поверхностью вращения и в их пересечении получатся окружности (рис. 9.6).

Рис.    9.6. Соосные поверхности вращения:
a- наглядное изображение;
б – на комплексном чертеже

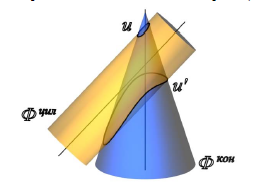
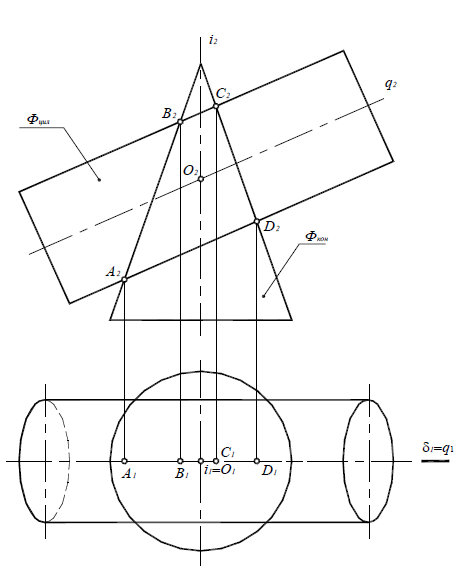
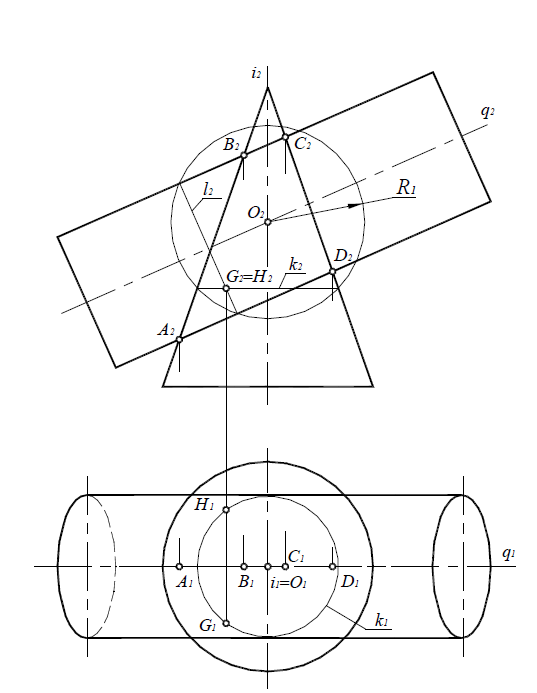
Рассмотрим способ концентрических сфер на примере построения линии пересечения цилиндра и конуса вращения, оси которых i(i₁,i₂) и q(q₁,q₂) пересекаются и точка пересечения осей обозначена через O (O₁ ,O₂)(рис. 9.7).

Рис. 9.7. Линия пересечения поверхностей цилиндра и прямого кругового конуса

Точка пересечения осей поверхностей принимается за центр вспомогательных концентрических сфер.

Алгоритм решения задачи об определении линии пересечения поверхностей состоит в следующем:

1.    Определить опорные точки (рис. 9.8). Так как обе данные поверхности имеют общую плоскость симметрии δ(δ₁), параллельную плоскости проекций П₂, то их очерковые образующие, по отношению к плоскости П₂,пересекаются. Точки A(A₁,A₂), B(B₁,B₂), C(C₁,C₂) и D(D₁,D₂) пересечения этих образующих являются точками видимости линии пересечения поверхностей.

2.    Определить радиусы максимальной и минимальной сфер, необходимых для определения точек линии пересечения.

Радиус максимальной сферы R_max равен расстоянию от центра вспомогательных сфер до наиболее удаленной точки пересечения очерковых образующих, в данном случае Rmax=O₂A₂ (рис. 9.9).

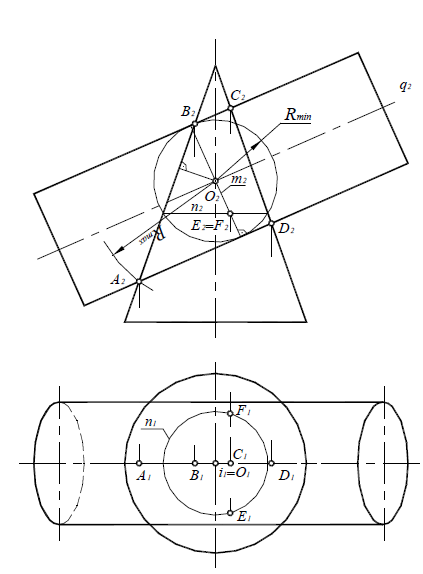
Чтобы определить радиус минимальной сферы R_min, необходимо провести через точку O₂ нормали к очерковым образующим данных поверхностей. Тогда больший из отрезков этих нормалей и будет R_min. В этом случае сфера минимального радиуса будет касаться одной из данных поверхностей, а со второй – пересекаться.

В данном случае сферой минимального радиуса является сфера, касающаяся цилиндрической поверхности (см. рис. 9.9).

Сфера радиусом R_min касается цилиндрической поверхности по окружности m, которая на фронтальной проекции изображается в виде прямой m₂, перпендикулярной q₂(m₂q₂). Эта же сфера пересекает коническую поверхность по двум окружностям. Но, в данном случае, нам интересна только окружность n, так как только она дает решение. Эта окружность n изображается на фронтальной проекции в виде прямой n₂, перпендикулярной i₂(n2i₂). Точки E и Fпересечения этих окружностей будут принадлежать обеим поверхностям:

m₂×n₂ =E₂, F₂.

Чтобы построить горизонтальные проекции точек Е и F следует воспользоваться окружностью n, содержащей данные точки, так как она не искажается на плоскости проекций П₁:

E₁ ,F ₁∈ n₁.

Рис. 108. Определение опорных точек линии пересечения поверхностей

Рис. 9.9. Определение радиусов максимальной и минимальной сфер.

Для построения промежуточных точек линии пересечения проводят несколько концентрических сфер с центром в точке O, причем радиус R этих сфер должен изменяться в пределах R_min< R < R_max.

Рассмотрим определение точек линии пересечения на примере сферы радиусом R1 (R_min1max) (рис. 9.10, 9.11).

Рис. 9.10. Определение промежуточных точек линии пересечения поверхностей

Сфера радиусом R₁ пересекает цилиндрическую поверхность по окружности l, которая на фронтальной проекции изображается в виде прямой l₂, перпендикулярной q₂( 1₂q₂). Эта же сфера пересекает коническую поверхность по окружности k, которая изображается на фронтальной проекции в виде прямой k₂, перпендикулярной i₂(k₂i₂). Точки G и Hпересечения этих окружностей будут точками искомой линии пересечения:

1₂×k₂=G₂, H₂.

Чтобы построить горизонтальные проекции точек G и H, следует воспользоваться окружностью k, содержащей данные точки, так как она не искажается на плоскости проекций Π₁: G₁∈ k ₁.

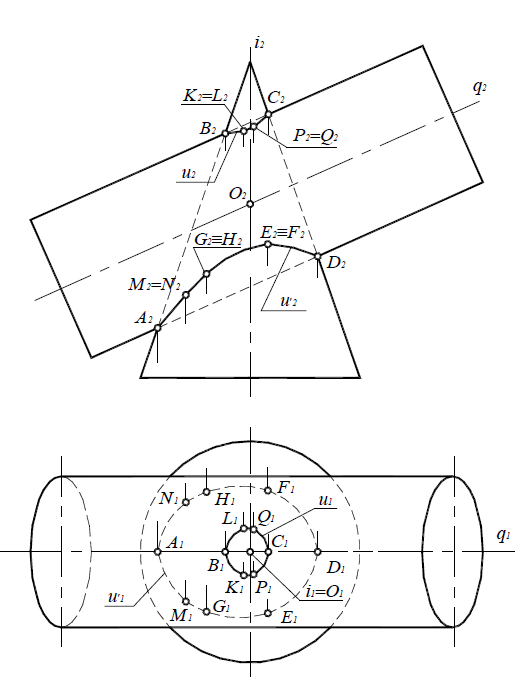
4.    Аналогичным образом определить все остальные точки искомой линии пересечения. Последовательно соединить полученные точки плавной лекальной кривой. В данном случае линия пересечения поверхностей цилиндра и конуса представляет собой две кривые второго порядка u(u₁,u₂) и u( u’₁ ,u ₂) (рис. 9.12).

Горизонтальная проекция линии пересечения поверхностей симметрична относительно плоскости δ(δ₁) – общей плоскости симметрии данных поверхностей. Эта плоскость была указана ранее (см. рис. 9.8).

Рис. 9.11. Определение промежуточных точек линии пересечения поверхностей

5.    Определить видимость линии пересечения поверхностей и их очерковых образующих. На фронтальной плоскости проекций видимы будут те точки линии пересечения, которые лежат перед горизонтальной проекцией очерковых образующих, проекции которых совпадают с плоскостью симметрии δ(δ₁), – точки A, M, G, E, D и B, K, P, C. На горизонтальной плоскости проекций линия u(u₁,u₂) видима, так как все ее точки лежат выше фронтальной проекции оси вращения цилиндра q(q₂), а линия u(u₁ ,u₂)будет невидима, поскольку все ее точки лежат ниже фронтальной проекции образующих, совпадающих с проекцией оси вращения цилиндра q(q₂).

Рис. 9.12. Линия пересечения поверхностей цилиндра и конуса

Пересечение поверхностей

Пересечение поверхностей и способы построения линий пресечения

Линия пересечения принадлежит обеим пересекающимся поверхностям и образуется множеством их общих точек. Следовательно, построение линии пересечения поверхностей сводится к построению этих общих точек.

При пересечении поверхностей вращения порядок линии пересечения определяется умножением порядков пересекающихся поверхностей. Например, если пересекаются круговой конус (поверхность 2-го порядка) и сфера (поверхность 2-го порядка), то линия пересечения является кривой 4-го порядка.

Определение способа построения линии пересечения зависит от взаимного расположения пересекающихся поверхностей, а также от их расположения относительно плоскостей проекций. Из всех возможных вариантов пересечения поверхностей геометрических тел в зависимости от их взаимного расположения можно выделить четыре случая, которые позволяют определить и представить форму линии пересечения поверхностей:

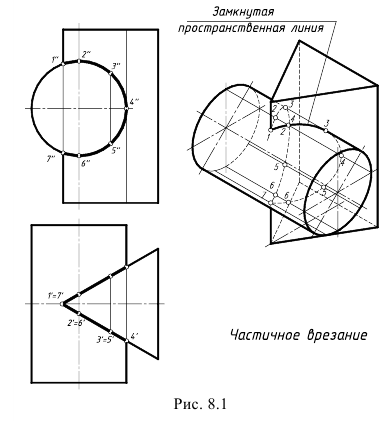
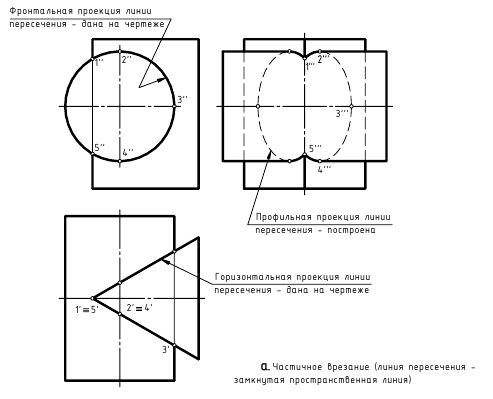
I случай. Частичное врезание (рис. 8.1). В этом случае линией пересечения является одна замкнутая пространственная линия.

II случай. Полное проницание (рис. 8.2). В этом случае линией пересечения являются две замкнутые пространственные линии.

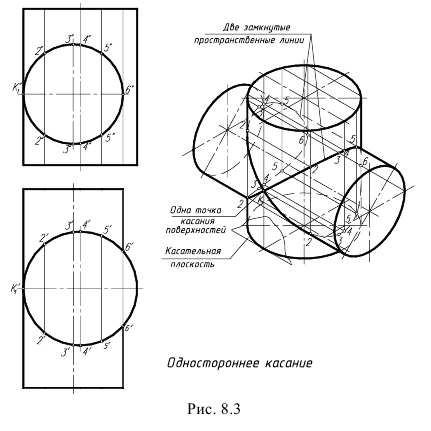
III случай. Одностороннее соприкосновение (рис. 8.3). В этом случае поверхности соприкасаются в одной общей точке K₁ и линия их пересечения, проходя через эту точку, распадается на две замкнутые пространственные линии (поверхности имеют одну общую касательную плоскость).

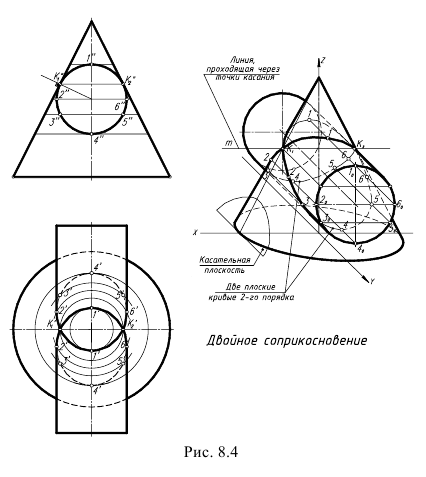
IV случай. Двойное соприкосновение (рис. 8.4).

В этом случае поверхности имеют две точки соприкосновения K₁ и K₂ и линия их пересечения распадается на две плоские кривые в соответствии с теоремой 2 (С. А. Фролов «Начертательная геометрия» [23]): «Если две поверхности вращения второго порядка имеют касание в двух точках, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую m, соединяющую точки касания» (поверхности имеют две общие касательные плоскости).

В зависимости от расположения пересекающихся геометрических тел относительно плоскостей проекций и участия в пересечении геометрических тел, имеющих проецирующую поверхность (как призма или цилиндр) или не имеющих проецирующей поверхности (пирамида, конус, шар, тор, тороид, наклонная призма или наклонный цилиндр, глобоид и др.), следует выбрать оптимальный способ построения проекций линии пересечения поверхностей на чертеже.

По этим признакам способы построения линий пересечения поверхностей можно объединить в две группы:

Первая группа: частные случаи пересечения поверхностей, когда для построения линий пересечения не требуется применения специальных способов, а используется частное положение пересекающихся геометрических тел относительно плоскостей проекций.

Вторая группа: общие случаи пересечения поверхностей, когда для построения линий пересечения требуется применить специальные способы посредников.

Частные случаи пересечения поверхностей

K первой группе частных случаев пересечения поверхностей относятся следующих четыре случая:

1-й случай: пересечение геометрических тел, боковые поверхности которых являются проецирующими, то есть, перпендикулярны какой-либо плоскости проекций.

2-й случай: пересечение геометрических тел, у одного из которых боковая поверхность является проецирующей.

3-й случай: пересечение соосных поверхностей вращения, т. е. имеющих общую ось вращения.

4-й случай: пересечение поверхностей вращения второго порядка, описанных вокруг сферы (по теореме Г. Монжа).

Рассмотрим на примерах построение проекций линий пересечения поверхностей геометрических тел в четырех частных случаях первой группы.

Следует отметить, что перечисленные частные случаи пересечения поверхностей наиболее часто встречаются при формообразовании различных реальных деталей.

1-й частный случай

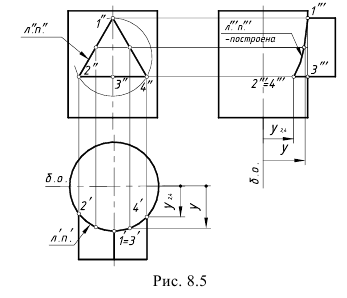
На рис. 8.5 показан пример построения проекций линии пересечения поверхностей горизонтально-проецирующего цилиндра и фронтально-проецирующей прямой правильной треугольной призмы, то есть пересекаются два геометрических тела, боковые поверхности которых занимают относительно плоскостей проекций проецирующее положение.

Характерный признак 1-го частного случая: на заданных проекциях тел определяются две проекции искомой линии пересечения:

– фронтальная проекция (л”п”) линии пересечения 1″-2″-3″-4″ совпадает с вырожденной в ломаную линию боковой поверхностью призмы;

– горизонтальная проекция (л’п’) линии пересечения 1′-2′-3′-4′ совпадает с участком окружности, которая является вырожденной проекцией боковой поверхности цилиндра.

Следовательно, требуется достроить только профильную проекцию (л'”п”‘) линии пересечения, построив профильные проекции обозначенных точек по их принадлежности одному из тел (в данной задаче – цилиндру), и соединить их плавной кривой с учетом ее видимости на поверхностях.

2-й частный случай

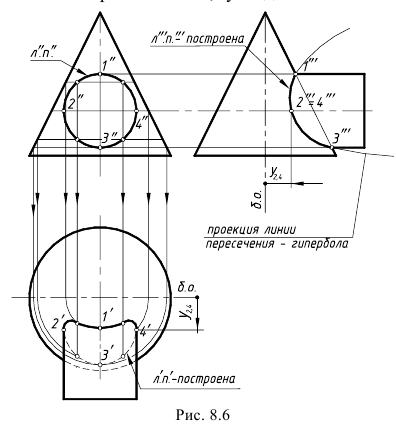
На рис. 8.6 показан пример построения проекций линии пересечения поверхностей прямого кругового конуса и фронтально-проецирующего цилиндра, то есть пересекающихся геометрических тел, у одного из которых боковая поверхность проецирующая.

Характерный признак 2-го частного случая: на заданных проекциях тел определяется одна проекция линии пересечения:

– фронтальная проекция (л”п”) линии пересечения 1″-2″-3″-4″ совпадает с окружностью, которая является вырожденной проекцией боковой поверхности цилиндра.

Следовательно, требуется достроить горизонтальную (л’п’) и профильную (л”‘п”‘) проекции линии пересечения, построив горизонтальные и профильные проекции обозначенных точек по их принадлежности конусу, и соединить построенные на проекциях точки плавными кривыми линиями с учетом их видимости на поверхностях.

!!! На профильную проекцию предмета пространственная кривая линия пересечения 4-го порядка проецируется в виде участка гиперболы.

3-й частный случай

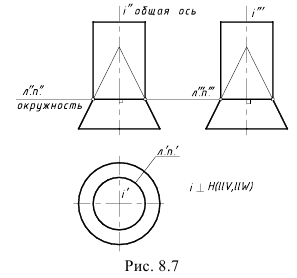
Пересечение соосных геометрических тел. Соосными называются геометрические тела вращения, имеющие общую ось вращения «i». Поверхности соосных тел пересекаются по окружностям, перпендикулярным их общей оси. Если общая ось «i» соосных геометрических тел является прямой проецирующей (т. е. она перпендикулярна какой-либо одной плоскости проекций, а двум другим параллельна), то окружность пересечения проецируется дважды в прямую линию, перпендикулярную их общей оси, на те плоскости проекций, которым эта общая ось параллельна.

На рис. 8.7 показан пример построения линии пересечения соосных геометрических тел – конуса и горизонтально-проецирующего цилиндра, имеющих общую горизонтально-проецирующую ось i (ось перпендикулярна H и параллельна V и W). Линией пересечения является окружность, фронтальная (л”п”) и профильная (л”‘п”‘) проекции которой представляют собой прямые линии, перпендикулярные их общей оси i и проходящие через точки пересечения фронтальных и профильных очерков поверхностей. Горизонтальная проекция этой окружности пересечения л’п’) совпадает с вырожденной горизонтальной проекцией боковой поверхности цилиндра.

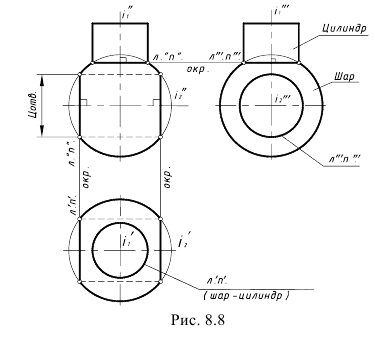
На рис. 8.8 показан пример построения линий пересечения двух пар соосных поверхностей:

– поверхности шара и горизонтально-проецирующего цилиндра, соосных относительно горизонтально-проецирующей оси i₁, окружности пересечения которых проецируются в прямые линии на фронтальную и профильную проекции;

– поверхности шара и сквозного профильно-проецирующего цилиндрического отверстия Ц_отв в шаре, соосных относительно профильно-проецирующей оси i₂, окружности пересечения которых проецируются в прямые линии на фронтальную и горизонтальную проекции.

4-й частный случай

Пересечение поверхностей вращения второго порядка, описанных вокруг сферы (по теореме Г. Монжа).

Напоминаем, к поверхностям вращения второго порядка относятся круговые цилиндр и конус, шар, эллипсоиды, параболоид и одно-, двуполостные гиперболоиды.

Эллиптические цилиндры и конусы, а также наклонный круговой конус – это не поверхности вращения!

Все торы (открытый, закрытый и самопересекающийся), глобоиды и тороиды относятся к поверхностям вращения четвертого порядка!

В 4-м частном случае имеет место двойное соприкосновение пересекающихся поверхностей вращения второго порядка, описанных вокруг сферы, и построение линии пересечения основано на теореме 2 (С. А. Фролов «Начертательная геометрия» [23]):

Теорема 3, известная как теорема Г. Монжа, вытекает из теоремы 2: «Если две поверхности вращения второго порядка описаны вокруг третьей поверхности второго порядка или вписаны в нее, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки касания».

Практическое применение теоремы возможно в том случае, когда две поверхности вращения второго порядка описаны вокруг сферы или вписаны в нее.

Использовать теорему Г. Монжа для построения на чертеже линии пересечения поверхностей можно при наличии в задаче четырех обязательных графических условий:

1. Пересекаются поверхности вращения второго порядка.
2. Оси поверхностей вращения должны пересекаться (точка пересечения – центр вписанной сферы).
3. Поверхности описаны вокруг общей сферы или вписаны в нее.
4. Общая плоскость симметрии, проходящая через оси поверхностей, является плоскостью уровня.

При соблюдении этих четырех условий на одной из заданных проекций можно построить проекции двух плоских кривых, на которые распадается искомая линия пересечения:

• – плоские кривые проецируются в отрезки прямых линий на ту проекцию предмета, которая расположена на плоскости проекций, параллельной общей плоскости симметрии поверхностей;
• – точки пересечения очерков поверхностей на этой проекции принадлежат искомой линии пересечения и через эти точки проходят прямые, в которые проецируются плоские кривые пресечения;
• – прямые, как проекции плоских кривых, пересекаются в точке, с которой совпадают проекции двух точек K₁≡K₂ соприкосновения поверхностей и соответственно проекция прямой m(m’, m”), соединяющей эти точки соприкосновения (точки касания).

!!! Точки касания (соприкосновения) поверхностей K₁(K₁“) и K₂(K₂“) определяются на пересечении проекций окружностей касания вписанной сферы с каждой из поверхностей.

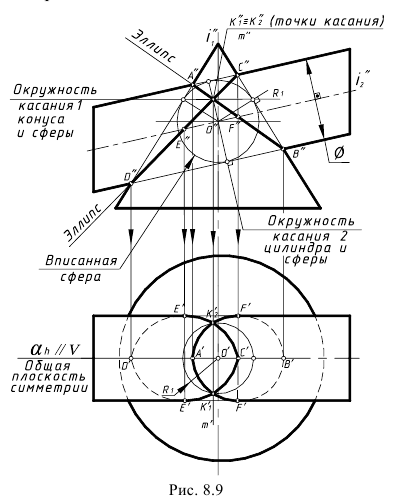
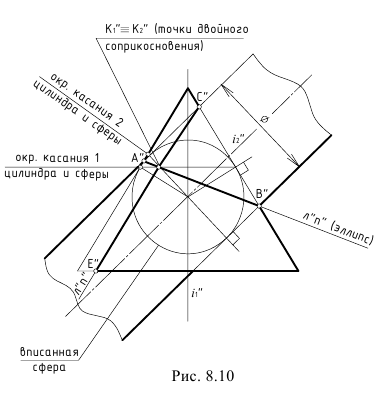
На рис. 8.9 показан пример построения проекций линии пересечения поверхностей вращения второго порядка – прямого кругового конуса и наклонного кругового цилиндра, описанных вокруг общей сферы. Для решения задачи использована теорема Г. Монжа, поскольку здесь соблюдены все четыре обязательных условия ее применения:

1. Пересекаются прямой круговой конус и круговой наклонный цилиндр, т. е. поверхности вращения второго порядка.
2. Оси конуса и цилиндра пересекаются в точке O(O”).
3. Обе поверхности описаны вокруг общей для них сферы с центром точке O(O”).
4. Общая плоскость симметрии поверхностей α(α_H) является фронтальной плоскостью уровня (//V).

Построение проекций линии пересечения поверхностей по теореме Г. Монжа выполняется по следующему графическому алгоритму:

1-е действие. Определить проекцию предмета, на которую плоские кривые проецируются в отрезки прямых линий: в данной задаче это фронтальная проекция, так как общая плоскость симметрии α(α_Н) параллельна фронтальной плоскости проекций V.

2-е действие. Построить фронтальные совпадающие проекции K₁≡K₂ точек соприкосновения заданных поверхностей, лежащих на пересечении проекций окружностей касания вписанной сферы с каждой из поверхностей (прямые линии – проекций этих окружностей касания – строятся как линии пересечения соосных поверхностей, так как вписанная сфера образует две пары соосных поверхностей – конус/сфера с общей осью i₁ и цилиндр/сфера с общей осью i₂. На чертеже проекции этих окружностей касания проходят через точки, полученные на пересечении перпендикуляров, проведенных из точки О(О”) – центра вписанной сферы – к образующим конуса (окружность касания 1) и цилиндра (окружность касания 2).

3-е действие. Отметить на фронтальной проекции точки A(A”), B(B”), C(C”) и D(D”) пересечения очерков поверхностей и построить фронтальные проекции плоских кривых пересечения 2-го порядка, соединив прямыми линиями A-B(A”-B”) и C-D(C”-D”) противоположные точки пересечения очерков (обе прямые обязательно должны пройти через построенные проекции точек соприкосновения поверхностей K₁≡K₂ (K”₁≡K”₂);

4-е действие. Построить горизонтальные проекции двух плоских кривых пересечения – эллипсов, по горизонтальным проекциях обозначенных точек A, B, C, D, K₁ и K₂, построенных по принадлежности поверхности конуса; обозначить и построить точки E(E’) и F(F’), которые лежат на очерковых образующих горизонтальной проекции цилиндра и определяют границу видимости кривых на горизонтальной проекции предмета, а также отметить и построить необходимое количество промежуточных точек (здесь не обозначены).

5-е действие. Оформить фронтальный и горизонтальный очерки пресекающихся поверхностей.

!!! Построение точек соприкосновения K₁≡K₂ поверхностей особенно важно в задачах, где по условию нельзя определить одну из четырех точек пересечения очерков поверхностей. Совпадающие проекции точек соприкосновения в этом случае определят направление одной из двух прямых линий – проекций плоских кривых пересечения (рис. 8.10). В данном случае проекция плоской кривой линии пересечения CE проведена через точки C и K₁≡K₂. Точка E определяется на основании конуса.

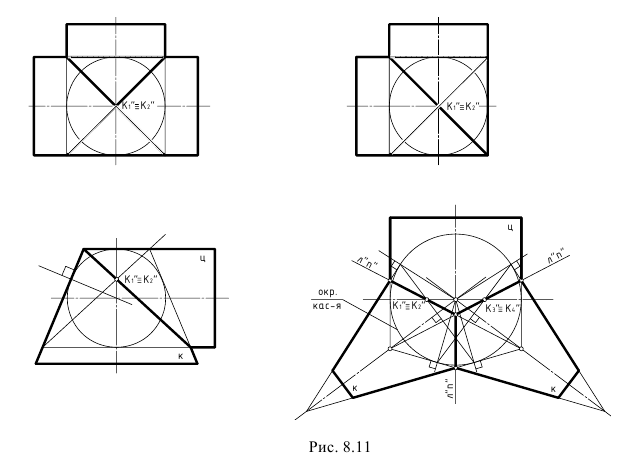
На рис. 8.11 показаны примеры построения линий пересечения поверхностей второго порядка, описанных вокруг сферы, с применением теоремы Г. Монжа. Они часто встречаются при конструировании различных переходов цилиндрических и конических труб, или пересечений отверстий в деталях.

Общие случаи пересечения поверхностей и способы построения линий пересечения поверхностей

Ко второй рассматриваемой группе относятся общие случаи пересечения геометрических тел, боковые поверхности которых могут занимать относительно плоскостей проекций непроецирующее положение (это наклонные призмы и цилиндры), а также геометрические тела, поверхности которых непроецирующие – это конус, сфера, торы, глобоид, эллипсоид, параболоид и гиперболоиды. Сюда же относятся наклонный эллиптический цилиндр, имеющий круговые сечения, и наклонный круговой конус.

Для построения линий пересечения поверхностей в этом случае применяются специальные способы вспомогательных посредников – плоскостей уровня или поверхностей (сфер, цилиндров, конусов), из которых мы рассматриваем следующие:

1. способ вспомогательных секущих плоскостей уровня;
2. способ вспомогательных концентрических сфер;
3. способ вспомогательных эксцентрических сфер.

Применение одного из указанных способов для построения линий пересечения поверхностей геометрических тел возможно при наличии некоторых обязательных графических условий расположения геометрических тел относительно плоскостей проекций и зависит от того, какие именно геометрические тела пересекаются в конкретной задаче.

Линия пересечения поверхностей является общей для обеих поверхностей и образуется множеством общих точек, которые строятся с помощью вспомогательных посредников.

Предварительно требуется выполнить графический анализ условия задачи для выбора рационального способа ее решения, определить проекцию предмета, на которой следует начинать решение задачи, и границы введения посредников.

Для построения проекций точек, принадлежащих линии пересечения поверхностей, способом посредников следует применять общий для всех рассматриваемых способов графический алгоритм.

Графический алгоритм I:

1-е действие. Ввести вспомогательную плоскость или поверхность-посредник.

2-е действие. Построить вспомогательные линии пересечения плоскости – или поверхности-посредника с каждой из заданных поверхностей.

3-е действие. Определить точки пересечения построенных вспомогательных линий пересечения – эти точки принадлежат искомой линии пересечения.

Рассмотрим на примерах применение различных способов вспомогательных посредников для построения проекций линий пересечения поверхностей.

Способ вспомогательных секущих плоскостей уровня

Применение способа вспомогательных секущих плоскостей рационально при наличии двух графических условий:

1. Общая плоскость симметрии пересекающихся геометрических тел является плоскостью уровня; при соблюдении этого условия точки пересечения очерков поверхностей принадлежат искомой линии пересечения и определяют верхнюю и нижнюю границу введения плоскостей-посредников на соответствующей проекции предмета.

2. Сечениями геометрических тел в одной из плоскостей уровня должны быть простые в построении линии пересечения – прямые линии (образующие) или окружности; эту плоскость уровня и следует выбрать в качестве посредника.

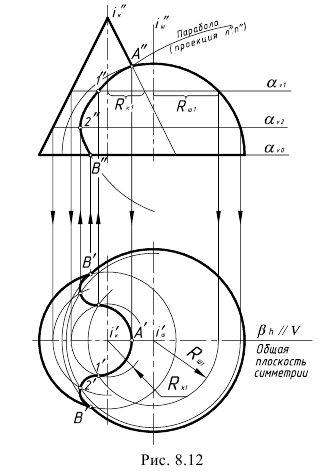
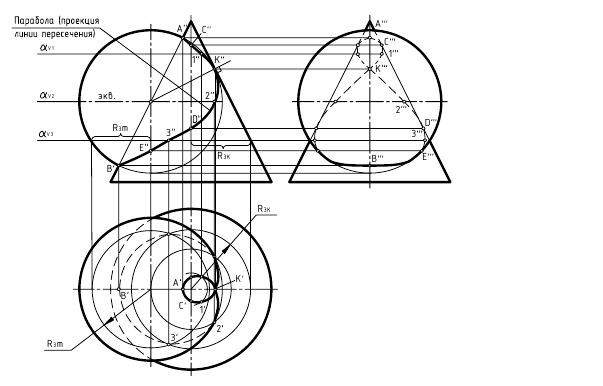
На рис. 8.12 показан пример построения проекций линии пересечения прямого конуса и половины шара.

Для решения задачи требуется предварительно выполнить графический анализ заданных проекций предмета:

А. Выбираем для решения задачи способ вспомогательных секущих плоскостей, так как здесь соблюдены два графических условия его применения:

– общая плоскость симметрии β(β_Н) геометрических тел – конуса и полушара – является фронтальной плоскостью уровня (первое условие применения);

– горизонтальные плоскости уровня, которые пересекают поверхности конуса и полушара по окружностям, выбираем в качестве вспомогательных плоскостей-посредников (второе условие применения).

Б. Решение задачи, то есть введение плоскостей-посредников, начинаем на фронтальной проекции предмета, так как общая плоскость симметрии геометрических тел является фронтальной плоскостью уровня.

В. Определяем границы введения плоскостей-посредников – это точка А(А”) пересечения фронтальных очерков и точки B(B’,B”) пересечения окружностей оснований конуса и полушара, лежащие в горизонтальной плоскости уровня α(α_Vо).

Построить проекции точек искомой линии пересечения, выполнив действия предложенного графического алгоритма I:

1-е действие. Ввести на фронтальной проекции предмета первую вспомогательную секущую горизонтальную плоскость-посредник α(α_V1) произвольно и ниже точки А(А”).

2-е действие. Построить на горизонтальной проекции предмета вспомогательные окружности радиусами R_к1 и R_ш1, по которым секущая плоскость-посредник α(α_V1) пересекает поверхности конуса и шара.

3-е действие. Определить на пересечении построенных вспомогательных окружностей горизонтальные проекции точек 1(1′), принадлежащих линии пересечения; фронтальные совпадающие проекции 1(1″) этих точек определяются по линии связи на фронтальной проекции плоскости-посредника α(α_V1).

3.1. Повторить действия основного графического алгоритма, введя вторую плоскость-посредник α₂(α_V2), и построить проекции точек 2(2′,2″) и т. д.

Дополнительные действия:

4-е действие. Соединить проекции построенных точек на фронтальной и горизонтальной проекциях предмета плавными кривыми линиями с учетом их видимости на проекциях: на фронтальную проекцию предмета пространственная кривая пересечения проецируется в видимую плоскую кривую второго порядка (участок параболы), поскольку горизонтальная проекция предмета имеет фронтальную симметрию; на горизонтальную проекцию предмета – в участок видимой кривой 4-го порядка сложной формы.

5-е действие. Оформить очерки поверхностей на заданных проекциях предмета с учетом их относительной видимости:

• – на фронтальной проекции – очерк конуса существует влево от точки А(А”), а очерк шара вправо от точки А(А”) (несуществующие очерки конуса и шара оставить тонкими линиями);
• – на горизонтальной проекции – окружность основания конуса существует влево от точек В(B’), а окружность основания шара существует вправо от точек В(B’) (несуществующие части окружностей оснований конуса и шара оставить тонкими линиями).

!!! Способ вспомогательных секущих плоскостей позволяет строить одновременно две проекции искомой линии пересечения.

Способ вспомогательных концентрических сфер

Основанием для применения сферы в качестве вспомогательной поверхности-посредника являются две ее характерные особенности:

• – в сфере можно провести через ее центр бесконечное количество осей;
• – сфера может быть соосна любой поверхности вращения; соосные поверхности пересекаются по окружностям, проекции которых легко построить (см. рис. 8.7 и 8.8).

Сфера-посредник образует две пары соосных поверхностей с каждой из заданных поверхностей. Каждая образованная пара соосных поверхностей пересекается по соответствующим окружностям, которые проецируются в прямые, перпендикулярные общей оси каждой пары, и проходят через точки пересечения очерков каждой пары соосных поверхностей.

Применение способа вспомогательных концентрических сфер для построения линии пересечения поверхностей возможно при наличии трех следующих графических условий:

1. Пересекаются поверхности вращения (кроме открытого и закрытого тора).
2. Общая плоскость симметрии пересекающихся поверхностей является плоскостью уровня; при этом условии точки пересечения очерков на проекции предмета, изображенного на параллельной общей плоскости симметрии плоскости проекций, принадлежат искомой линии пересечения.
3. Оси поверхностей пересекаются; точка пересечения осей является центром всех вспомогательных сфер.

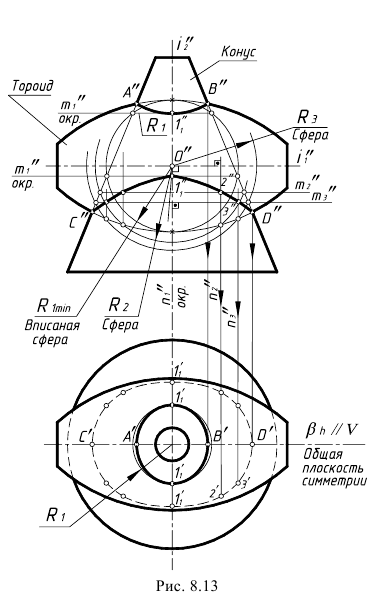
На рис. 8.13 показан пример построения проекций линии пересечения усеченного конуса и тороида (самопересекающийся тор).

Рассмотренный способ вспомогательных секущих плоскостей здесь применять не следует, так как ни одна плоскость уровня не пересекает поверхности одновременно по окружностям (одно из условия применения).

Для решения задачи требуется предварительно выполнить графический анализ заданных проекций предмета.

А. Выбираем для решения задачи способ вспомогательных концентрических сфер, так как здесь соблюдены три графических условия его применения:

• – пересекаются поверхности вращения – прямой круговой конус и тороид  (самопересекающийся тор);
• – общая плоскость симметрии геометрических тел β(β_Н) является фронтальной плоскостью уровня;
• – оси поверхностей пересекаются в точке O(O”) – центр всех вспомогательных сфер.

Б. Решение задачи, то есть введение вспомогательных сфер-посредников начинаем на фронтальной проекции предмета, так как общая плоскость симметрии является фронтальной плоскостью уровня и точки A(A”), B(B”), C(C”) и D(D”) пересечения фронтальных очерков принадлежат линии пересечения.

В. Определяем границы введения сфер – это точки C(C”) и D(D”) пересечения фронтальных очерков пересекающихся геометрических тел. Построить проекции точек линии пересечения, выполнив действия предложенного графического алгоритма I.

1-е действие. Ввести на фронтальной проекции вспомогательную сферу-посредник минимального радиуса R_1min, с центром в точке O(O”), вписанную в тороид (минимальная сфера-посредник должна вписываться в одну из поверхностей, а с другой поверхностью – пересекаться).

2-е действие. Построить проекции вспомогательных окружностей пересечения двух пар соосных поверхностей, образованных сферой-посредником с каждой заданной поверхностью:

• – первая пара соосных поверхностей – сфера-посредник и тороид – имеют горизонтальную общую ось i₁” и пересекаются по окружности касания n₁“, которая проецируется в прямую линию (совпадает с осью конуса);
• – вторая пара соосных поверхностей – сфера-посредник и конус имеют вертикальную общую ось вращения i₂” и пересекаются по двум вспомогательным окружностям m₁“, которые проецируются в прямые линии;

3-е действие. Определить точки 1(1₁“) пересечения построенных проекций вспомогательных окружностей m₁” и n₁“, которые принадлежат искомым линиям пересечения (по две пары совпадающих точек).

!!! Здесь имеет место случай полного проницания (II случай), и линия пересечения распадается на две замкнутые кривые.

Дополнительные действия:

4-е действие. Повторить действия основного графического алгоритма, введя вспомогательные сферы большего радиуса R₂ и R₃ с тем же центром в точке О(О”), и построить следующие пары точек 2(2″) и 3(3″).

4.1. Достроить горизонтальные проекции построенных точек линии пересечения по принадлежности параллелям конуса.

4.2. Соединить проекции построенных точек на фронтальной и горизонтальной проекциях предмета плавными кривыми линиями с учетом их видимости на проекциях (только линия пересечения D’-3′-2′-1₁‘-C’ будет невидимой на горизонтальной проекции предмета).

5-е действие. Оформить очерки поверхностей на заданных проекциях предмета с учетом их относительной видимости.

Способ вспомогательных эксцентрических сфер

Наименование способа говорит о том, что вспомогательные сферы имеют разные центры, которые и нужно определять в процессе построения проекций линии пересечения поверхностей.

Способ вспомогательных эксцентрических сфер для построения линии пересечения поверхностей возможно применять при наличии трех следующих графических условий:

1. Пересекаются:

• – поверхности вращения 4-го порядка, т. е. торовые поверхности – открытый или закрытый тор;
• – поверхности эллиптических цилиндра и конуса, имеющие круговые сечения.

2. Общая плоскость симметрии поверхностей является плоскостью уровня.

3. Оси поверхностей пересекаются или скрещиваются.

Поскольку в этом способе центр каждой вспомогательной сферы нужно определять графическими построениями, первое действие графического алгоритма для построения проекций точек линии пересечения дополняется построением центра каждой вспомогательной сферы.

Порядок графических действий для построения линий пересечения способом вспомогательных эксцентрических сфер показан на двух примерах.

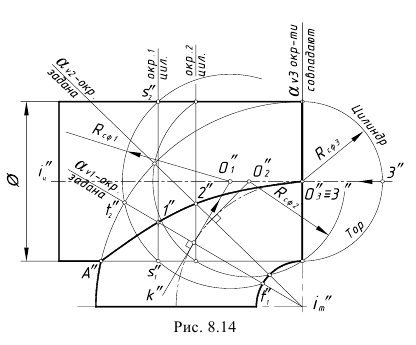
На рис. 8.14 показан пример построения проекции линии пересечения профильно-проецирующего цилиндра с поверхностью четвертой части открытого тора. Задача решается способом вспомогательных эксцентрических сфер, так как здесь соблюдены три необходимых условия для применения этого способа:

• – одна из пересекающихся поверхностей – открытый тор, имеющий круговые сечения во фронтально-проецирующих плоскостях, проходящих через его ось вращения i”_m;
• – общая плоскость симметрии поверхностей – фронтальная плоскость уровня (подразумевается), поэтому точка A(A”) пересечения фронтальных очерков принадлежит искомой линии пересечения;
• – оси поверхностей i_ц и i_m скрещиваются.

Построение проекций точек линии пересечения поверхностей выполняется на заданной фронтальной проекции предмета по предлагаемому графическому алгоритму II.

Графический алгоритм II.

1-е действие. Ввести вспомогательную сферу, выполнив предварительно следующие графические действия.

1.1. Задать произвольное круговое сечение поверхности тора фронтально-проецирующей плоскостью α_V1, проходящей через его ось i”_m; окружность t₁-t₂, (ее проекция – прямая линия t”₁-t”₂) – это заданная линия пересечения тора с искомой вспомогательной сферой, центр которой должен лежать на перпендикуляре к проекции этой окружности – прямой t”₁-t”₂ (хорда окружности, в которую проецируется вспомогательная сфера).

1.2. Провести к прямой t”₁-t”₂ через ее середину перпендикуляр k” и на его пересечении с осью цилиндра i”_ц определить центр первой вспомогательной сферы – точку O”₁.

1.3. Провести окружность – проекцию вспомогательной сферы-посредника – с центром в точке O”₁, радиус которой R_сф.1 определяется расстоянием от точки О”₁ до одной из крайних точек t”₁ или t”₂ прямой t”₁-t”₂.

2-е действие. Построить проекцию окружности пересечения построенной сферы-посредника с поверхностью соосного ей цилиндра – это прямая s”₁-s”₂, проходящая через точки s”₁ и s”₂ пересечения очерков цилиндра и сферы-посредника.

3-е действие. Определить на пересечении построенных проекций заданной окружности t”₁-t”₂ и построенной окружности s”₁-s”₂ совпадающие точки 1(1″), принадлежащие искомой линии пересечения заданных поверхностей.

Дополнительные действия:

4-е действие. Повторить действия графического алгоритма и построить достаточное количество точек линии пересечения. В данном примере дополнительными сечениями вспомогательных плоскостей α_V2 и α_V3 и вспомогательными сферами R_сф.2 и R_сф.3 с центрами O₂ и O₃ построены точки 2 и 3, принадлежащие линии пересечения. Причем в плоскости α_V3 окружности сечений совпадают и совпадающие точки 3 делят существование этих окружностей на две половины – верхняя часть принадлежит цилиндру, а нижняя – тору.

5-е действие. Соединить на фронтальной проекции точки A”-1″-2″-3″ линии пересечения плавной видимой кривой.

6-е действие. Оформить очерки поверхностей на заданной проекции.

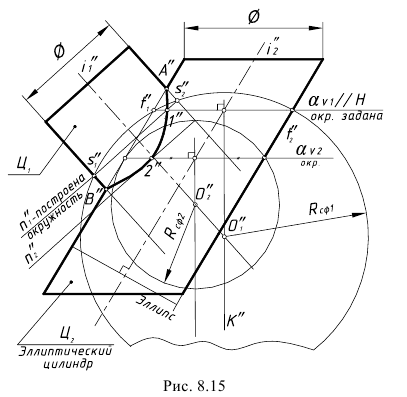
На рис. 8.15 показан пример построения линии пересечения наклонного кругового цилиндра Ц₁ с осью i”₁ и наклонного эллиптического цилиндра с осью i”₂, у которого есть круговые сечения в горизонтальных плоскостях уровня.

Выполнить графический анализ условия и исключить нерациональный способ решения задачи.

Рассмотренный способ вспомогательных секущих плоскостей применять не следует, так как на заданной фронтальной проекции ни одна плоскость уровня не пересекает поверхности одновременно по окружностям или образующим (одно из условий применения).

Рассмотренный способ вспомогательных концентрических сфер применять нельзя, так как проведенные сферы с центром в точке пересечения осей образуют соосные пары только с одной заданной поверхностью Ц₁ (одно из условий применения).

Выбираем для решения задачи способ вспомогательных эксцентрических сфер, так как здесь соблюдены три условия его применения:

• – пересекаются наклонный круговой цилиндр Ц₁ и эллиптический цилиндр Ц₂ (поверхность не вращения);
• – общая плоскость симметрии поверхностей является фронтальной плоскостью уровня (подразумевается);
• – оси поверхностей i₁ и i₂ – пересекаются.

Решение задачи, то есть введение сечений цилиндра Ц₂ (параллельных заданному) горизонтальными плоскостями уровня α, начинаем на фронтальной проекции предмета, так как общая плоскость симметрии является фронтальной плоскостью уровня и точки A(A”) и B(B”) пересечения фронтальных очерков принадлежат линии пересечения.

Определяем границы введения сечений цилиндра Ц₂ – это точки A(A”) и B(B”) пересечения фронтальных очерков пересекающихся геометрических тел.

Построить проекции точек линии пересечения поверхностей, выполнив действия предложенного графического алгоритма II.

Графический алгоритм II.

1-е действие. Ввести вспомогательную сферу, выполнив предварительные графические действия.

1.1. Задать произвольное круговое сечение эллиптического цилиндра Ц₂ горизонтальной плоскостью α_V1 – прямую t₁-t₂. Эта заданная линия t₁-t₂ – окружность пересечения эллиптического цилиндра с искомой вспомогательной сферой, центр которой лежит на перпендикуляре, проведенном из середины этой прямой.

1.2. Провести к прямой t₁-t₁ через ее середину перпендикуляр k” и на пересечении с осью i₁ кругового цилиндра Ц₁ определить точку О₁ – центр первой вспомогательной сферы-посредника.

1.3. Провести окружность сферы-посредника радиусом R_сф.1, который определяется расстоянием от точки О”₁ до одной из точек t”₁ или t”₂ прямой t₁-t₂.

2-е действие. Построить проекцию окружности пересечения сферы посредника с соосной ей поверхностью кругового цилиндра Ц₁ – это прямая s₁-s₂, проходящая через точки пересечения очерков сферы и цилиндра.

3-е действие. Определить на пересечении заданной окружности t₁“-t₂” и построенной окружности s₁“-s₂” совпадающие точки 1(1″), принадлежащие искомой линии пересечения.

Дополнительные действия.

4-е действие. Повторить действия графического алгоритма II и построить проекции точек 2(2″);

5-е действие. Соединить на фронтальной проекции точки А”-1″-2″-B” линии пересечения плавной видимой кривой.

6-е действие. Оформить очерки поверхностей на заданной проекции.

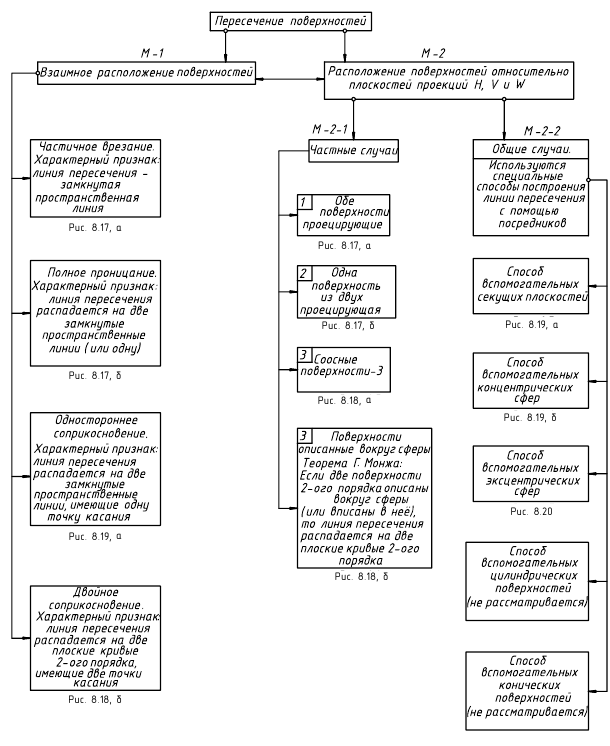
Структуризация материала восьмой лекции в рассмотренном объеме схематически представлена на рис. 8.16 (лист 1). На последующих листах 2–5 приведены иллюстрации к этой схеме для быстрого визуального закрепления изученного материала при повторении (рис. 8.17–8.20).

Пересечение поверхностей:

Частный случай 1. Обе пересекающиеся поверхности проецирующие

Частный случай 2. Одна из двух пересекающихся поверхностей проецирующая

Частный случай 3. Соосные поверхности вращения (с общей осью i)

Частный случай 4. Пересечение поверхностей вращения 2-го порядка, описанных вокруг сферы

Общие случаи пересечения поверхностей:

1. Способ вспомогательных секущих плоскостей

а. Одностороннее касание (две замкнутые пространственные линии пересечения касаются в одной точке К)

Графический алгоритм:

1. Ввести плоскость-посредник (горизонтальная плоскость α/α_V3).
2. Построить линии пересечения плоскости-посредника с каждой поверхностью (окружности радиусом R_3К и R_3m).
3. Определить точки (3), принадлежащие искомой линии пересечения (на пересечении построенных окружностей радиусами R_3К и R_3m).
4. Повторить алгоритм необходимое число раз.
5. Способ вспомогательных концентрических сфер

б. Частичное врезание (линия пересечения – замкнутая пространственная линия)

Графический алгоритм:

1. Ввести сферу-посредник (R_1min минимальная вписанная сфера-посредник)
2. Построить линии пересечения сферы-посредника с каждой поверхностью (касательная окр.1 и окр.1, пересечение соосных поверхностей)
3. Определить точки 1, принадлежащие искомой линии пересечения (на пересечении построенных проекций окружностей 1)
4. Повторить алгоритм необходимое число раз, увеличивая радиусы сфер-посредников
5. Способ вспомогательных эксцентрических сфер

в. Полное проницание (линия пересечения распадается на две замкнутые пространственные линии)

Графический алгоритм:

I. Предварительные действия для определения центра вспомогательной сферы-посредника

1. Задать проекцию окружности (прямая S_1-S₂), по которой вспомогательная плоскость α/α_V1) пересекает поверхность открытого тора.

2. Провести через середину этой проекции перпендикуляр к ней до пересечения с осью конуса – на пересечении определяется центр первой сферы-посредника О₁(О”).

II. Основные действия

3. Ввести сферу-посредник радиусом R₁ с центром в т. О₁(О₁“).

4. Построить линии пересечения сферы-посредника с каждой поверхностью (заданная окружность S₁ -S₂ и две построенные окружности n₁ и n₂).

5. Определить точки 1₁” и 1₂”, принадлежащие искомой линии пересечения (на пересечении линий S₁ -S₂ (S₁“-S₂“) и n₁” и n₂”.

Образец взаимного пересечения поверхностей

Линия пересечения двух поверхностей – это геометрическое место точек, принадлежащих одновременно обеим поверхностям.

Общим способом построения точек, принадлежа­щих кривой взаимного пере­сечения поверхностей, является способ вспомогательных поверхностей посредников. Этот способ заключается в следующем.

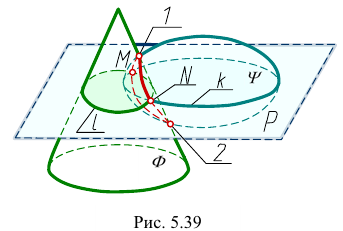
Пусть даны некоторые взаимно пересекающиеся по­верхности 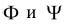(рис. 5.39).

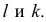
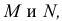
Введем плоскость-посредник Р, которая пересечет поверхности по линиям Пересечение линий даст точки принадлежащие кривой пересечения. Применяя ряд посредников, получаем семейство точек линии пересечения. В качестве посредников наиболее часто применяют плоскости и шаровые поверхности – сферы. В зависимости от вида поверхностей посредников можно выделить следующие способы построения линии пересечения двух поверхностей:

• а) способ вспомогательных секущих плоскостей;
• б) способ вспомогательных сфер.

При построении линии взаимного пересечения поверхностей не­обходимо сначала строить опорные точки кривой. Эти точки дают пределы линии пересечения. Между ними и следует определять промежуточные (случайные) точки.

28

МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Филиал государственного
образовательного учреждения

высшего
профессионального образования

«Уфимский
государственный нефтяной

технический
университет»

Филиал УГНТУ в г.
Салавате

Кафедра «Оборудование
предприятий нефтехимии и нефтепереработки»

Учебно-методическое
пособие

к выполнению
расчетно-проектировочной работы
«Взаимное пересечение тел»

для студентов
специальности 240801.65

очной и очно-заочной
форм обучения

Уфа 2010

Пособие предназначено
для самостоятельной работы студентов
при выполнении расчетно-графической
работы «Взаимное пересечение тел».
Пособие содержит варианты заданий и
примеры выполнения задачи. Рекомендуется
для студентов очной и заочной форм
обучения при изучении дисциплины
«Начертательная геометрия. Инженерная
графика»

Составитель Алушкина
Т.В., доц. канд. техн. наук

Рецензенты:

© Уфимский
государственный нефтяной технический
университет, 2010

Расчетно-графическая
работа № 2

Часть 2. Взаимное
пересечение тел

Цель работы:

Освоить основные
приемы построения линии пересечения
геометрических тел. Изучить метод
вспомогательных плоскостей и метод
сфер. Научиться пользоваться ими при
решении комплексных задач.

Для выполнения
работы необходимо знать основные
положения начертательной геометрии:

-понятия кривой
линии;

-понятия опорных
точек;

-сущность способа
вспомогательных плоскостей;

-сущность метода
концентрических сфер и область его
применения;

– сущность метода
эксцентрических сфер и область его
применения.

Работа состоит
из двух задач, при решении которых
необходимо уметь:

-пользоваться
указанными методами;

-уметь находить
опорные точки, точки видимости;

-находить проекции
точек принадлежащих поверхности.

Работа выполняется
на формате А2. Исходные данные, рамка,
штамп выполнить простым карандашом в
соответствии с ГОСТами ЕСКД. Дополнительные
построения выполнять цветными карандашами
или пастой (синей, зеленой и т.д.), конечный
результат построений выделить красным
цветом.

Все надписи на
чертеже выполняются простым карандашом
шрифтом №5, индексы – шрифт №3,5.

Исходные данные
к задаче 1 представлены в Приложении
А, к задаче 2 – в Приложении Б.

Метод вспомогательных
секущих плоскостей

Метод используется
для определения проекций линий пересечения
двух геометрических тел: многогранника
и поверхности вращения, двух многогранников,
двух поверхностей вращения.

При решении задач
на взаимное пересечение поверхностей
следует помнить следующие положения:

1. Чтобы найти
точку, принадлежащую линии пересечения
необходимо оба геометрических тела
рассечь вспомогательной плоскостью
так, чтобы в сечении плоскостью
образовались простые фигуры – отрезок,
окружность, треугольник, прямоугольник.
Рассматривается пересечение простых
фигур и определяются общие точки.
Использование нескольких вспомогательных
плоскостей позволяет определить ряд
точек линии пересечения. Соединять
можно только те точки, которые находятся
на одной грани многогранника.

2. Если боковая
поверхность цилиндра или призмы занимает
относительно плоскости проекций
проецирующее положение (образующие
поверхности перпендикулярны этой
плоскости проекций), то одна проекция
линии пересечения уже есть и она совпадает
с проекцией поверхности.

3. Если линия,
принадлежащая поверхности, видна не
полностью, то точки перехода от видимой
части линии пересечения к невидимой
располагаются на очерке геометрического
тела. Видимая часть линии пересечения
должна быть видимой одновременно для
двух геометрических тел.

4. Чтобы найти
верхнюю или нижнюю точку линии пересечения
(конуса и многогранника), соответствующей
грани с конусом, нужно взять плоскость,
которая должна проходить через вершину
конуса перпендикулярно грани многогранника
(ребрам многогранника).

5. Чтобы найти
верхнюю или нижнюю точку линии пересечения
(сфера и цилиндр), необходимо провести
вспомогательную плоскость через оси
двух поверхностей.

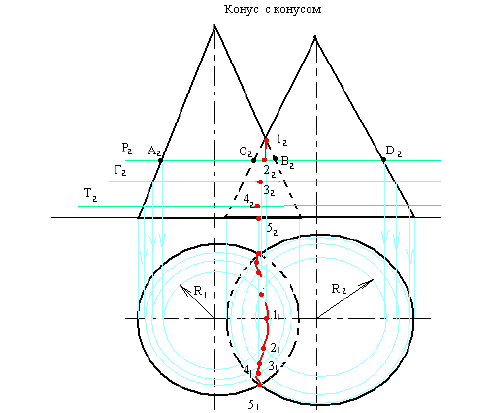
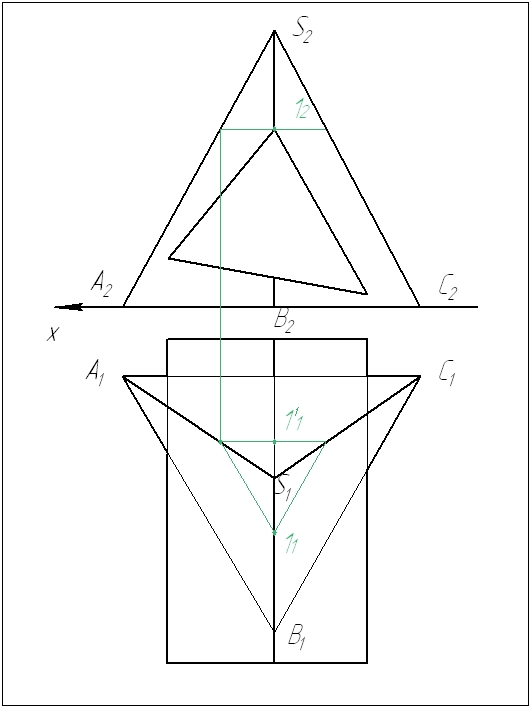
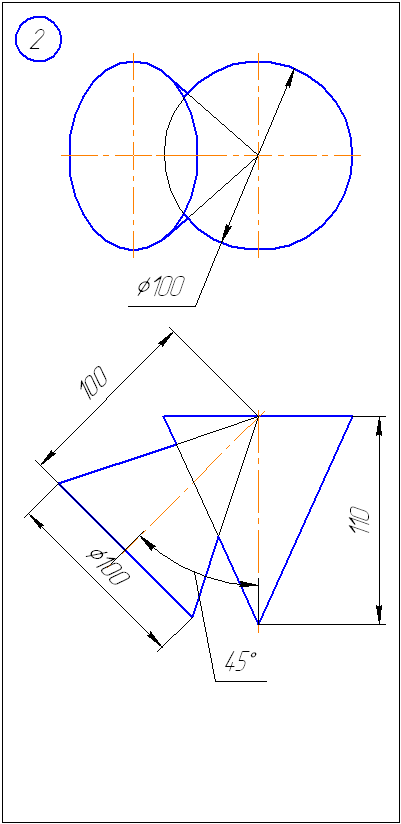
Условие задачи 1:

Построить проекции
линии пересечения двух геометрических
тел. При решении задачи использовать
метод вспомогательных секущих плоскостей.

Рисунок 1

Алгоритм решения
задачи:

1 В данной задаче
образующие (ребра) призмы расположены
перпендикулярно плоскости проекций
П₂,
следовательно, одна готовая проекция
линии пересечения уже есть – на плоскости
П₂.

При решении задачи
в первую очередь необходимо найти
опорные точки – это высшая и низшая
точки, либо точки, которые можно определить
без дополнительных построений. Находим
высшую точку 1.

Определяем остальные
опорные точки – 2 и 3.

2 Между опорными
точками проводим вспомогательную
секущую плоскость так, чтобы в сечении
образовались простые фигуры: треугольник
(для пирамиды) и прямоугольник (для
призмы). Пересечение этих фигур дает
нам искомые точки 4 и 5.

3 В случае, если
находится линия пересечения поверхностей
вращения необходимо проводить несколько
вспомогательных плоскостей. Для
определения линии пересечения гранных
поверхностей достаточно найти точки
пересечения граней с ребрами и получим
проекции ломанной линии пересечения.

4 Соединяем точки
в последовательности, определенной на
фронтальной плоскости проекций.
Определяем видимость полученной линии
пересечения.

Метод сфер

Существуют две
разновидности метода сфер:

– метод концентрических
сфер;

-метод эксцентрических
сфер.

Для каждого из
этих методов существует ряд ограничений
по области применения. Метод сфер
применим, если:

– оба геометрических
тела являются поверхностями вращения;

– оси поверхностей
лежат в плоскости, параллельной плоскости
проекций.

Сущность метода
сфер заключается в следующем:

На пересечении
осей поверхностей берется центр сфер.
Проводится сфера произвольного радиуса.
Сфера пересекает поверхности по
окружностям, которые на эпюре вырождаются
в отрезки. Рассматриваем пересечение
отрезков, ищем общие точки. Найденные
точки будут принадлежать искомой линии
пересечения поверхностей. Проводим
следующую вспомогательную сферу,
построения повторяем, и т.д. Найденные
точки соединяем плавной кривой.

Рассмотрим варианты
пересечения поверхностей.

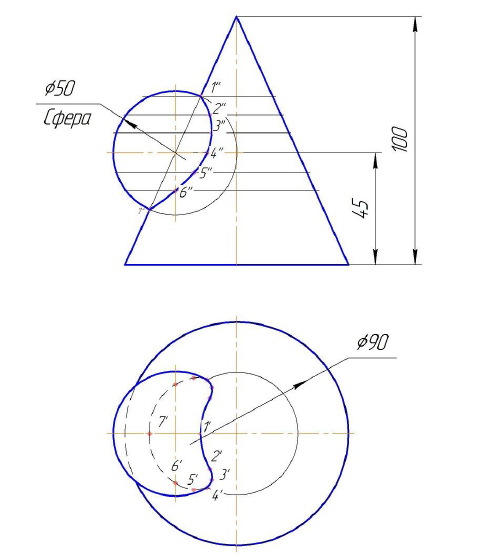
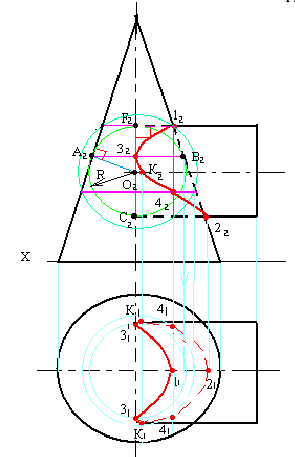
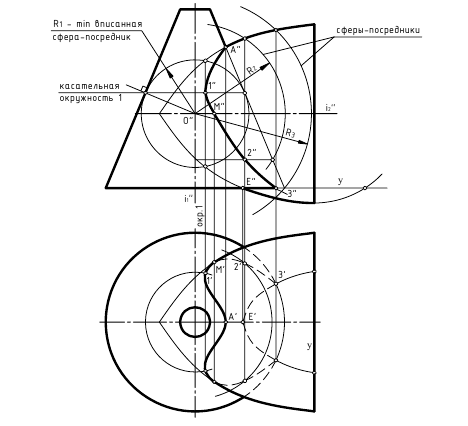
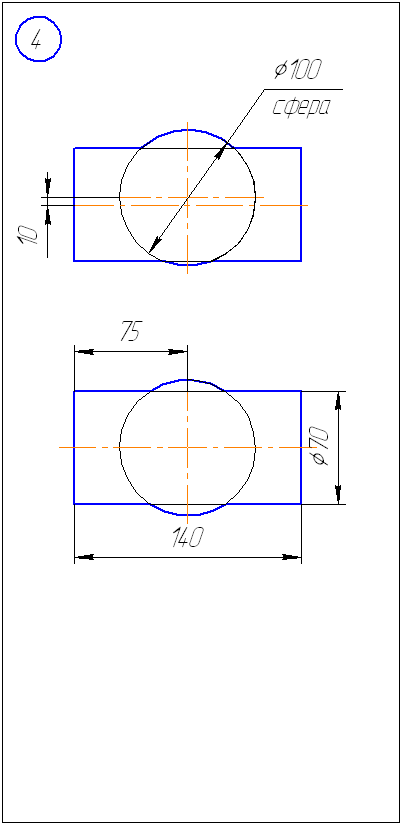
Задача 1.
Построить линию пересечения двух
поверхностей, одна из которых – сфера.
Определить видимость. Задачу решить
методом концентрических сфер.

Рисунок

Решение:

Данную задачу
можно отнести к частному случаю. Таким
способом можно решать задачу только в
случае, если одно из тел – сфера.

1. Определяем
опорные точки: высшую 1 и низшую 2. Находим
их проекции.

2. На оси конуса
произвольно выбираем точку О₂
– центр сфер. Определяем величину
минимально допустимого радиуса сферы:

.

Определяем
максимально допустимый радиус сферы:

.

Диапазон значений
радиусов сфер:

.

3. Проводим
вспомогательную сферу. Определяем
пересечение сферы с поверхностями как
точки пересечения очерков поверхностей
с дугой. Проводим отрезки и определяем
их точку пересечения.

4. Проводим следующую
сферу. Построения повторяем.

5. Соединяем
полученные точки плавной кривой.

6. Достраиваем
горизонтальную проекцию линии пересечения.
Для этого рассматриваем найденные точки
как точки, принадлежащие поверхности
конуса. Полученные точки соединяем
плавной кривой с учетом видимости.

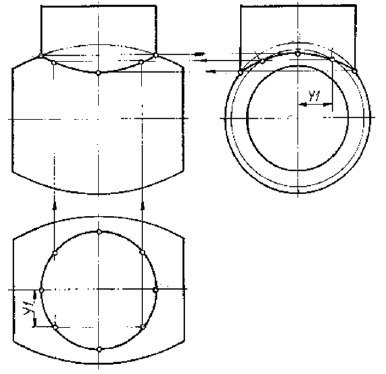
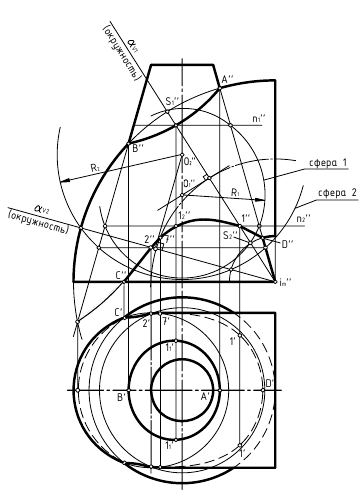
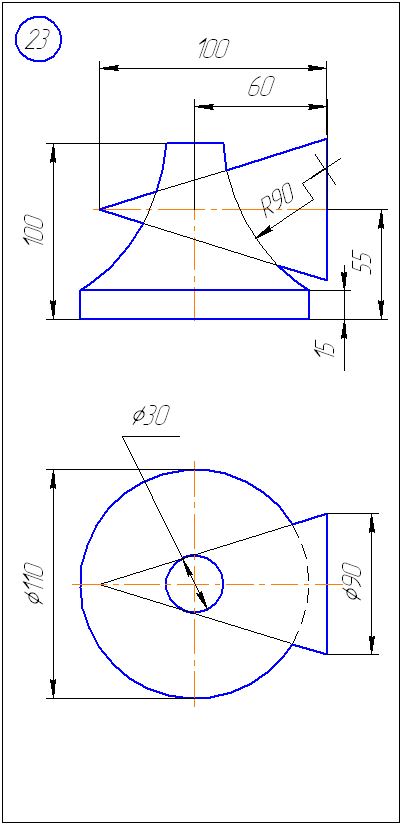
Задача 2. Построить
проекции линии пересечения поверхностей.
Определить видимость. Задачу решить
методом концентрических сфер.

Рисунок

Решение:

1. Определяем
опорные точки, как точки пересечения
очерков поверхностей.

2. Определяем центр
сфер – как точку пересечения осей.

3. Определяем
максимально возможный радиус сферы

4. Определяем
минимально возможный радиус сферы. Для
этого из центра сферы проводим
перпендикуляры к образующим поверхностей.

5. Вписываем сферу
минимального радиуса. Сфера касается
поверхности конуса по окружности и
пересекает поверхность цилиндра по
окружности. Обе этих окружности на эпюре
вырождаются в отрезки. Рассматриваем
пересечение отрезков, ищем общие точки.

6. Вписываем сферу
произвольного радиуса R.
Построения повторяем.

7. Количество
вписанных сфер должно быть не менее
трех. Полученные таким образом точки,
соединяем плавной кривой.

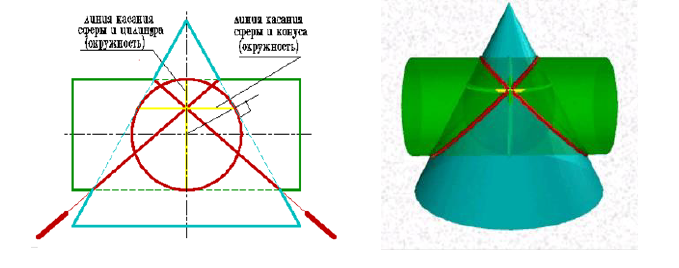
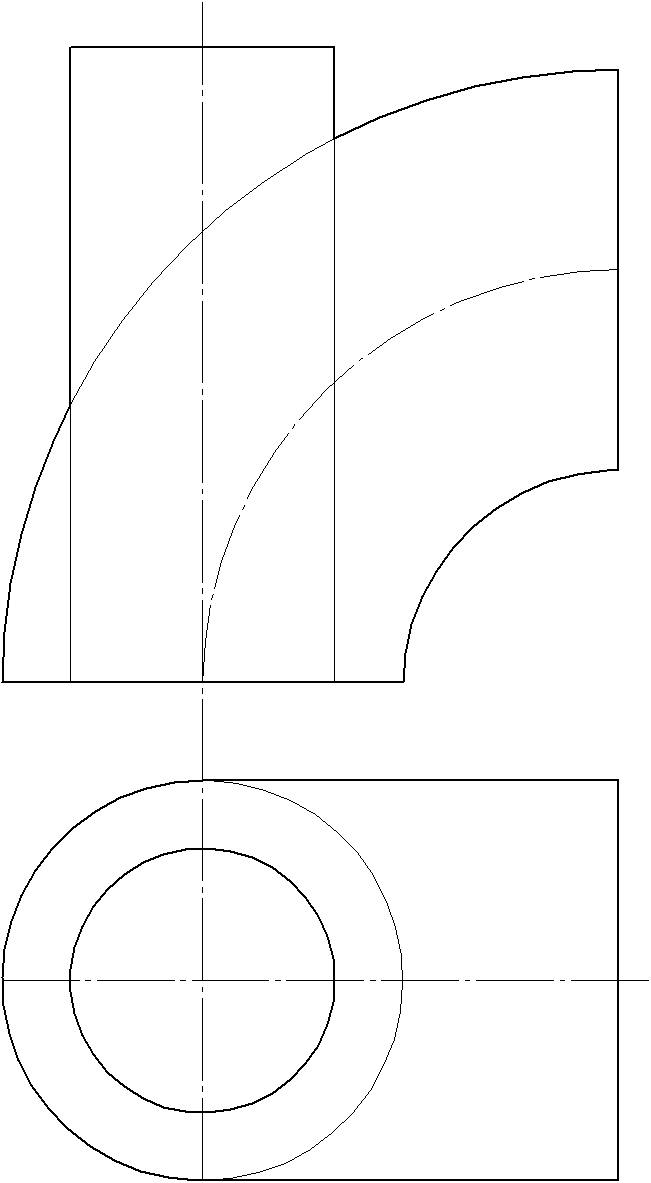
Задача 3.
Построить проекции линии пересечения
тора с цилиндром. Определить видимость.
Задачу решить методом эксцентрических
сфер.

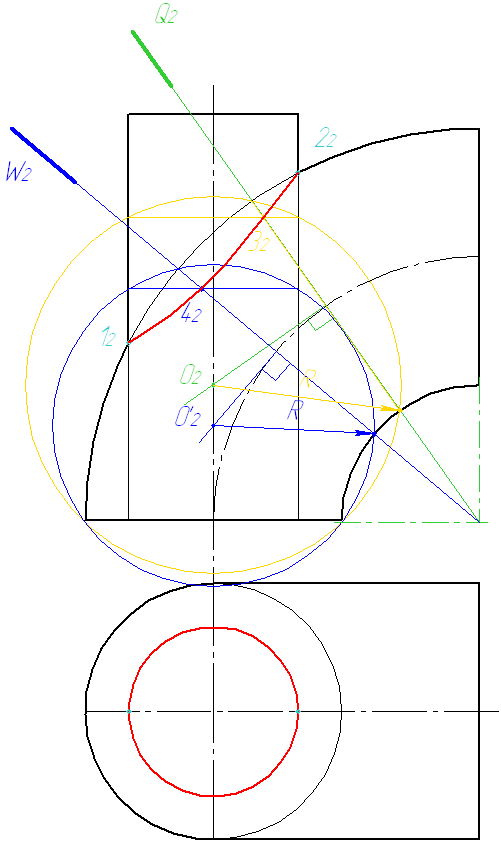
Рисунок

Метод эксцентрических
сфер применим, если:

– оба геометрических
тела поверхности вращения;

– оси поверхностей
лежат в плоскости, параллельной плоскости
проекций;

– одна из поверхностей
– тор.

Решение:

1. Определяем
опорные точки как точки пересечения
очерков.

2. Проводим
проецирующую плоскость в интервале
между опорными точками. Из точки
пересечения проецирующей плоскости с
осью тора восстанавливаем перпендикуляр
до пересечения осью цилиндра. Получим
точку О – центр сфер.

3 Из центра О₂
проводим сферу радиуса R.
Сфера будет пересекать поверхности
цилиндра и тора по окружностям, которые
на эпюре вырождаются в отрезки. Искомая
точка лежит на пересечении полученных
отрезков.

4. Проводим следующую
проецирующую плоскость. Построения
повторяем.

5 Количество сфер
выбирается самостоятельно, но не менее
трех.

Соединяем полученные
точки плавной кривой. Находим вторую
проекцию линии пересечения.

Приложение А –
Варианты заданий к задаче 1 (метод секущих
плоскостей)

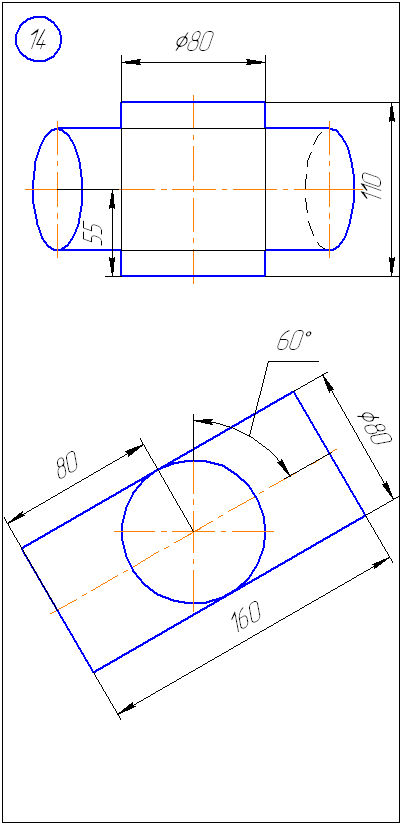
Приложение Б –
Варианты заданий к задаче 2 (метод сфер)

Соседние файлы в папке РГР Нач геом

• #
• #
• #
• #

Пересечение в евклидовой геометрии — точка или кривая, общие для двух или более объектов (таких как кривые, плоскости и поверхности). Простейший случай — пересечение двух различных прямых на плоскости, которое либо является одной точкой, либо не существует, если прямые параллельные.

Задача нахождения пересечения плоскостей — двумерных линейных геометрических объектов, встроенных в многомерное пространство — сводится к решению системы линейных уравнений.

В общем случае, пересечение определяется системой нелинейных уравнений, которая може быть решена численно, например, с использованием метода Ньютона. Задачи о пересечении прямой и конического сечения (круг, эллипс, парабола и т. д. ) или квадрики (сфера, цилиндр, гиперболоид и т. д. ) приводят к квадратным уравнениям, которые легко решаются. Пересечения между квадриками приводят к уравнениям четвёртой степени, которые можно решить алгебраически.

На плоскости[править | править код]

Две линии[править | править код]

Для определения точки пересечения двух непараллельных прямых:

можно использовать, например, правило Крамера, или подставляя переменную, координаты точки пересечения :

.

(Если , то эти линии параллельны, а это значит, что эти формулы нельзя использовать, так как они предполагают деление на 0.)

Два отрезка[править | править код]

Для двух непараллельных линейных отрезков и эта точка не обязательно является точкой пересечения (см. диаграмму), потому что точка пересечения соответствующих линий не обязательно должна содержаться в линейных отрезках. Для проверки ситуации используются параметрические представления линий:

Отрезки пересекаются только в общей точке соответствующих линий, если соответствующие параметры удовлетворяют условию .
Параметры являются решением линейной системы

Его можно решить для s и t с помощью правила Крамера (см. выше). Если выполняется условие , то вставляется или в соответствующее параметрическое представление и получается точка пересечения .

Пример: Для отрезков и получается линейная система

и . Это означает: линии пересекаются в точке .

Примечание: Рассматривая прямые, а не отрезки, определяемые парами точек, каждое условие может быть опущено, и метод даёт точку пересечения линий (см. выше).

Линия и круг[править | править код]

Для пересечения отрезка и окружности решают линейное уравнение для x или y и подставляют в уравнение окружности и получают решение (используя формулу квадратного уравнения) с:

,

,

если . Если это условие выполняется со строгим неравенством, то существуют две точки пересечения; в этом случае прямая называется секущей линией окружности, а отрезок прямой, соединяющий точки пересечения, называется хордой окружности.

Если выполняется , то существует только одна точка пересечения и прямая касается окружности. Если слабое неравенство не выполняется, линия не пересекает окружность.

Если середина круга не является началом координат^[1], можно рассматривать пересечение прямой и параболы или гиперболы.

Две окружности[править | править код]

Определение точек пересечения двух окружностей:

сводится к предыдущему случаю пересечения прямой и окружности. Путём вычитания двух данных уравнений получается линейное уравнение:

Эта особая линия является радикальной осью двух окружностей.

Особый случай ; в этом случае начало координат — это центр первого круга, а второй центр лежит на оси абсцисс (см. диаграмму^{[уточнить]}). Уравнение радикальной прямой упрощается до:
а точки пересечения можно записать как с

В случае окружности не имеют общих точек.
В случае окружности имеют одну общую точку, а радикальная ось является общей касательной.

Любой общий случай, как написано выше, можно превратить сдвигом и поворотом в частный случай.

Пересечение двух кругов (внутренности двух окружностей) образует форму, называемую линзой^[en].

Два конических сечения[править | править код]

Задача пересечения эллипса, гиперболы, параболы с другим коническим сечением сводится к системе квадратных уравнений, которую в частных случаях легко решить, исключив одну координату. Специальные свойства конических сечений могут быть использованы для получения решения. В общем, точки пересечения могут быть определены путём решения уравнения с помощью итерации Ньютона. Если а) обе коники заданы неявно (посредством уравнения), необходима двумерная итерация Ньютона; б) одна неявно, а другая параметрически — необходимо, чтобы была задана 1-мерная итерация Ньютона.

Две плавные кривые[править | править код]

Две кривые в (двумерном пространстве), которые непрерывно дифференцируемы (то есть нет резкого изгиба),
имеют точку пересечения, если они имеют общую точку плоскости и имеют в этой точке

a: разные касательные (трансверсальное пересечение) или

b: касательная линия общая, и они пересекают друг друга (касание пересечения, см. диаграмму).

Если обе кривые имеют общую точку S и касательную, но не пересекают друг друга, они просто «касаются» в точке S.

Поскольку касания пересечений возникают редко и с ними трудно справиться, следующие соображения не учитывают этот случай. В любом случае ниже предполагаются все необходимые дифференциальные условия. Определение точек пересечения всегда приводит к одному или двум нелинейным уравнениям, которые можно решить с помощью итерации Ньютона. Список возникающих случаев следующий:

• Если заданы обе кривые явно: , приравнивание их даёт уравнение

• Если заданы обе кривые параметрически:

Приравнивая их, получаем два уравнения с двумя переменными:

• Если заданы одна кривая параметрически, а другая неявно:

Это простейший случай помимо явного. Нужно вставить параметрическое представление в уравнение кривой , и получится уравнение:

• Если заданы обе кривые неявно:

Здесь точка пересечения — это решение системы

Любая итерация Ньютона требует удобных начальных значений, которые можно получить, визуализировав обе кривые. Параметрически или явно заданная кривая может быть легко визуализирована, потому что для любого параметра t или x соответственно легко вычислить соответствующую точку. Для неявно заданных кривых эта задача не так проста. В этом случае необходимо определить точку кривой с помощью начальных значений и итерации^[2].

Примеры:

1: и окружность (см диаграмму).

Итерация Ньютона для функции

должна быть выполнена. В качестве начальных значений можно выбрать −1 и 1.5.

Точки пересечения: (−1.1073, −1.3578), (1.6011, 4.1046)

2:

(см диаграмму).

Итерация Ньютона

должна быть выполнена, где является решением линейной системы

в точке . В качестве начальных значений можно выбрать (−0.5, 1) и (1, −0.5).

Линейная система может быть решена по правилу Крамера.

Точками пересечения являются (−0.3686, 0.9953) и (0.9953, −0.3686).

Два многоугольника[править | править код]

Если кто-то хочет определить точки пересечения двух многоугольников, можно проверить пересечение любой пары линейных сегментов многоугольников (см. выше). Для многоугольников с большим количеством сегментов этот метод довольно трудоёмок. На практике алгоритм пересечения ускоряется с помощью оконных тестов. В этом случае можно разделить многоугольники на маленькие подполигоны и определить наименьшее окно (прямоугольник со сторонами, параллельными осям координат) для любого подполигона. Перед началом трудоёмкого определения точки пересечения двух отрезков линии любая пара окон проверяется на наличие общих точек^[3]

В пространстве (три измерения)[править | править код]

В трёхмерном пространстве есть точки пересечения (общие точки) между кривыми и поверхностями. В следующих разделах мы рассматриваем только трансверсальное пересечение.

Линия и плоскость[править | править код]

Пересечение прямой и плоскости в общем положении в трёх измерениях является точкой.

Обычно линия в пространстве представляется параметрически , а плоскость — уравнением . Вставка представления параметра в уравнение даёт линейное уравнение

для параметра точки пересечения .

Если линейное уравнение не имеет решения, либо прямая лежит на плоскости, либо параллельна ей.

'x1,y1,z1, x2,y2,z2, x3,y3,z3 - координаты заданной плоскости
'x4,y4,z4, x5,y5,z5 - координаты заданной прямой

'Коэффициенты для уравнения плоскости
A = y1*(z2 - z3) + y2*(z3 - z1) + y3*(z1 - z2)
B = z1*(x2 - x3) + z2*(x3 - x1) + z3*(x1 - x2)
C = x1*(y2 - y3) + x2*(y3 - y1) + x3*(y1 - y2)
D = -1*(x1*(y2*z3 - y3*z2) + x2*(y3*z1 - y1*z3) + x3*(y1*z2 - y2*z1))

'Нормальный вектор к заданной плоскости
xN = A
yN = B
zN = C

'Вспомогательный вектор
xV = x1-x4
yV = y1-y4
zV = z1-z4

'Расстояние до плоскости по нормали
dist1 = xN*xV + yN*yV + zN*zV

'Вспомогательный вектор
xW = x5-x4
yW = y5-y4
zW = z5-z4

'Приближение к плоскости по нормали
dist2 = xN*xW + yN*yW + zN*zW

'Проверка на параллельность
IF dist1 <> 0 THEN 'Прямая не принадлежит плоскости
	IF dist2 <> 0 THEN 'Прямая не параллельна плоскости

		'Вспомогательное отношение
		ratio = dist1/dist2

		'Вспомогательный вектор
		xW = xW*ratio
		yW = yW*ratio
		zW = zW*ratio

		'Искомые координаты
		x0 = x4 + xW
		y0 = y4 + yW
		z0 = z4 + zW
	END IF
END IF

Три плоскости[править | править код]

Если линия определяется двумя пересекающимися плоскостями и должна пересекаться третьей плоскостью , необходимо оценить общую точку пересечения трёх плоскостей.

Три плоскости с линейно независимыми нормальными векторами имеют точку пересечения

Для доказательства следует установить используя правила тройного скалярного произведения. Если тройное скалярное произведение равно 0, то плоскости либо не имеют тройного пересечения, либо это прямая (или плоскость, если все три плоскости одинаковы).

Кривая и поверхность[править | править код]

Аналогично плоскому случаю следующие случаи приводят к нелинейным системам, которые могут быть решены с использованием 1- или 3-мерной итерации Ньютона^[4]:

• параметрическая кривая и

параметрическая поверхность

• параметрическая кривая и

неявная поверхность

Пример:

параметрическая кривая и

неявная поверхность (см. рисунок).

Точки пересечения: (−0.8587, 0.7374, −0.6332), (0.8587, 0.7374, 0.6332).

Пересечение линии и сферы^[en] — это частный случай.

Как и в случае линии и плоскости, пересечение кривой и поверхности в общем положении состоит из дискретных точек, но кривая может частично или полностью содержаться на поверхности.

Прямая и многогранник[править | править код]

Две поверхности[править | править код]

Две трансверсально пересекающиеся поверхности дают кривую пересечения^[en]. Самый простой случай — линия пересечения двух непараллельных плоскостей.

Примечания[править | править код]

Литература[править | править код]

• Erich Hartmann. Geometry and Algorithms for Computer Aided Design. — Darmstadt University of Technology, 2003.

Содержание:

1. Пересечение прямой линии с поверхностями тел
2. Линии пересечения и перехода
3. Общие правила построения линий пересечения поверхностей
4. Пересечение поверхностей цилиндра и призмы
5. Пересечение цилиндрических поверхностей
6. Пересечение  поверхностей многогранников
7. Пересечение  поверхностей цилиндра и конуса
8. Пересечение  поверхностей сферы и цилиндра
9. Пересечение  поверхностей тора и цилиндра
10. Построение линий пересечения поверхностей способом вспомогательных сфер

Взаимное пересечение поверхностей. Поверхности могут взаимно пересекаться. При этом линии одной поверхности пересекаются с другой поверхностью и образуют точки, которые в совокупности представляют линию пересечения.

Пересечение прямой линии с поверхностями тел

Конструкции деталей можно рассматривать как сочетание различных геометрических тел. Необхо­димо уметь строить линии пересечения поверхнос­тей этих тел. Пример, где требуется подобное по­строение, показан на рис. 195, на котором изо­бражен бункер, ограниченный цилиндрической поверхностью А, пересекающейся с конической поверхностью Б и поверхностью пирамиды В.

В зависимости от вида поверхностей тел линии пересечения могут быть лекальными кривыми или ломаными.

Для решения задач на построение линий пере­сечения поверхностей необходимо предварительно усвоить построение точек пересечения прямой с поверхностями различных геометрических тел.

Рис. 195

Если прямая пересекается с поверхностью тела, получаются две точки, одновременно принадлежа­щие как поверхности тела, так и прямой линии. Такие точки называются точками входа и выхода (рис. 196. а; точки N и М). Для нахождения этих точек выполняются построения в следующем по­рядке.

Через данную прямую проводят вспомогатель­ную плоскость (обычно проецирующую). Напри­мер, на рис. 196, а, где изображено пересечение прямой АВ с поверхностью пирамиды, через пря­мую проведена вспомогательная горизонтально-проецирующая плоскость Р. Затем находят линии пересечения вспомогательной плоскости с повер­хностью данного геометрического тела (линии КС и ЕD). На пересечении полученных линий с за­данной прямом находят искомые точки (точки N и М).

На комплексном чертеже точки входа и выхода определяют следующим образом (рис. 196. б). Горизонтальные проекции kс и ed прямых КС и ED совпадают с горизонтальным следом плоскости Р_H. Фронтальные проекции точек k‘, с’, е’ и d‘ определяют, пользуясь вертикальными линиями связи, проведенными из точек k, с, е и d до пере­сечения с фронтальными проекциями основания пирамиды. Соединяют точки k‘ с с’ и е’ с d‘ прямыми. На пересечении фронтальных проекций найденных прямых с проекцией а’Ь’ данной пря­мой получают фронтальные проекции n‘ и т’ искомых точек входа и выхода. Проведя через них вертикальные линии связи, находят горизонталь­ные проекции п и т этих точек.

Рис. 196

В некоторых частных случаях можно обой­тись без применения вспомогательной плоскос­ти. Например, точки входа и выхода прямой АВ с поверхностью прямого кругового цилин­дра (рис. 197, а) определяют следующим образом.

Горизонтальная проекция цилиндрической по­верхности представляет собой окружность, поэто­му горизонтальные проекции всех точек, располо­женных на цилиндрической поверхности, в том числе и двух искомых точек, будут расположены на этой окружности (рис. 197, а).

Фронтальные проекции  n‘ и m‘ искомых точек определяют, проводя через точки n и m верти­кальные линии связи до встречи с данной фрон­тальной проекцией а’Ь’ прямой АВ.

На рис. 197, б, в показано построение точек входа и выхода прямой АВ и поверхности прямого кругового конуса. Через прямую АВ проводят вспомогательную плоскость Р, проходящую через вершину конуса. Плоскость Р пересечет конус по образующим SH₃ SH_4.

На комплексном чертеже изображение плос­кости Р строят следующим образом. На прямой АВ берут произвольную точку К и соединяют ее с вершиной S конуса прямой линией. Две пересе­кающиеся прямые АВ и SK определяют плоскость Р.

Чтобы найти точки входа и выхода, необходимо построить горизонтальные проекции образующих SH₃ и SH₄. Для этого продолжим s’k’ и а’b‘ до пересечения с осью х в точках h‘₂  и h‘₁. Опустим линию связи из точки k‘ до пересечения с ab, полученную точку k соединим с s. Продлим гори­зонтальную проекцию прямой SK до пересечения с линией связи, опушенной из точки h‘₂, получим точку h₂. Из точки h‘₁ проведем линию связи до пересечения с продолжением прямой ab, получим точку h₁. Через следы h₁ и h₂ пройдет горизон­тальный след плоскости Р. Точки h₁ и h₂  соеди­ним прямой и получим горизонтальный след Р_Н  плоскости Р.

Основание конуса является горизонтальным следом конической поверхности. Поэтому, опреде­лив точки пересечения этого следа со следом Р_Н плоскости Р, можно найти и те две образующие, по которым коническая поверхность пересекается вспомогательной плоскостью Р. На комплексном чертеже горизонтальная проекция основания ко­нуса (окружность) пересекается со следом Р_Н в точках h₃ и h₄. Эти точки соединяют с вершиной s и получают следы sh₃ и sh₄ образующих SH₃ и SH₄.

На пересечении найденных образующих с дан­ной прямой АВ находят искомые точки М и N — точки входа и выхода прямой АВ с конической поверхностью.

Горизонтальные проекции точек т и n находят на пересечении горизонтальных проекций обра­зующих sh₃ и sh₄ с горизонтальной проекцией прямой ab. Через точки m и n проводят вертикальные линии связи до пересечения а’b‘ и нахо­дят фронтальные проекции т‘ и n‘ точек входа и выхода.

Рис. 197

Точки входа и выхода прямой АВ с повер­хностью сферы (рис. 198) находят, проведя через прямую АВ вспомогательную фронтально-проецирующую плоскость Р.

Вспомогательная плоскость Р пересекает сферу по окружности, которая проецируется на плос­кость Н в виде эллипса, что затрудняет построе­ние. Поэтому в данном случае необходимо приме­нить способ перемены плоскостей проекций. Но­вую плоскость проекций выбирают так, чтобы вспомогательная плоскость Р была бы ей парал­лельна, т.с. следует провести новую ось проекций x₁ так. чтобы она была параллельна фронтальной проекции а’b‘ прямой АВ (для упрощения по­строении на рис. 198 ось x₁ проведена через про­екцию а’b‘).

Затем необходимо построить новую горизон­тальную проекцию a₁b₁ прямой АВ и новую го­ризонтальную проекцию окружности диаметра D, по которой плоскость Р пересекает сферу. На пересечении новых горизонтальных проекций двух искомых точек m_} и n_} Обратным построе­нием определяем фронтальные т’ и n‘ и горизон­тальные т и п проекции точек входа и выхода.

Рис. 198

Линии пересечения и перехода

Многие детали машин представляют собой кон­струкции из пересекающихся геометрических тел. Общая линия пересекающихся поверхностей на­зывается линией пересечения.

На чертежах линии пересечения поверхностей изображаются сплошной основной линией (рис. 199, а). В местах перехода поверхностей литых и штампованных деталей нет четкой линии пересечения. Воображаемая линия пересечения называется линией перехода и условно изобража­ется на чертежах сплошной тонкой линией. Эта линия начинается и заканчивается в точках пере­сечения продолжения контура взаимно пересека­ющихся поверхностей (рис. 199. б).

Рис. 199

Встречаются детали, имеющие всевозможные линии пересечения и перехода поверхностей. Особенно много линий перехода у поверхностей дета­лей, изготовленных литьем.

На рис. 200, а на приборе для испытания твер­дости видны линии переходов различных повер­хностей.

Кожух и крышка смесительного аппарата (рис. 200. б) имеют разнообразные линии перехо­да. Здесь можно видеть линии взаимного пересе­чения цилиндрических и других поверхностей.

Построение линий пересечения и перехода поверхностей при выполнении чертежей трубопрово­дов, вентиляционных устройств, резервуаров, кожухов машин, станков требует точности.

Рис. 200

Общие правила построения линий пересечения поверхностей

Метод построения линий пересечения повер­хностей тел заключается в проведении вспомога­тельных секущих плоскостей и нахождении от­дельных точек линий пересечения данных повер­хностей в этих плоскостях.

Построение линии пересечения поверхностей тел начинают с нахождения очевидных точек. Например, на рис. 201, где изображены линии пересечения призмы с конусом, такими точками являются точки А и В. Затем определяют харак­терные точки, расположенные, например, на очерковых образующих поверхностей вращения или крайних ребрах, отделяющих видимую часть линий перехода от невидимой. На рис. 201 это точки С и D. Они располагаются на крайних ребрах верхней горизонтальной грани призмы.

Все остальные точки линии пересечения назы­ваются промежуточными (например, точки Е и F). Обычно их определяют с помощью вспомога­тельных параллельных секущих плоскостей (рис. 201, а).

В качестве вспомогательных плоскостей выби­рают такие плоскости, которые пересекают обе заданные поверхности по простым линиям — пря­мым или окружностям, причем окружности до­лжны располагаться в плоскостях, параллельных плоскостям проекций.

В данном примере плоскость Р рассекает конус по окружности (рис. 201, в), с помощью которой находят горизонтальные проекции точек е и f.

Во всех случаях. перед тем как строить линию пересечения поверхностей на чертеже, необходи­мо представить себе эту линию в пространстве (рис. 201, б).

Рис. 201

Пересечение поверхностей цилиндра и призмы

На рис. 202 показано построение проекции линий пересечения поверхности треугольной при­змы с поверхностью прямого кругового цилиндра. Боковые грани призмы перпендикулярны плоскос­ти V (рис. 202, а), поэтому фронтальная проекция линий пересечения поверхностей этих тел совпа­дает с фронтальной проекцией основания призмы. Горизонтальные проекции линий пересечения поверхностей совпадают с горизонтальной проек­цией цилиндра и являются окружностью. Про­фильные проекции точек А и Е находим по гори­зонтальным и фронтальным проекциям с по­мощью линий связи. Для построения проекций промежуточных точек В, С, D используем вспомо­гательные секущие плоскости Р_V, Р_V1 и Р_V2, c помощью которых находим фронтальные проек­ции b‘, с’. d‘ точек B, С. D.

В данном примере можно обойтись без вспомо­гательных секущих плоскостей, намечая произво­льно на фронтальной проекции точки b‘, с’, d‘.

Опуская линии связи на горизонтальную проек­цию, находим горизонтальные проекции с, Ь, d точек С, В, D. На профильной проекции с помощью линий связи находим проекции Ь”, с”, d“.

На рис. 202, б показано построение изометри­ческой проекции. После построения изометричес­кой проекции цилиндра, используя размеры т и п (рис. 202, а), строят изометрическую проекцию основания призмы, на котором находят точки 1, 2. 3. 4. 5. От этих точек откладывают расстояния 1“е”. 2“d“ и т.п., взятые с профильной проекции комплексного чертежа, и находят точки А, В. С, D. Е

На изометрической проекции линия пересече­ния поверхностей цилиндра и призмы получается соединением точек А, В. С, D, Е, которые строят­ся но координатам, взятым с комплексного чертежа.

Рис. 202

Пересечение цилиндрических поверхностей

При выполнении машиностроительных черте­жей наиболее часто встречается случай пересече­ния двух цилиндрических поверхностей, оси кото­рых расположены под углом 90⁰.

Разберем пример построения линии пересече­ния поверхностей двух прямых круговых цилин­дров. оси которых перпендикулярны к плоскостям проекций (рис. 203, а).

В начале построения, как известно, находим проекции очевидных точек 1, 7 и 4.

Построение проекций промежуточных точек показано на рис. 203, б. Если в данном примере применить общий способ построения линий пере­сечения с помощью вспомогательных взаимно параллельных плоскостей, пересекающих обе цилин­дрические поверхности по образующим, то на пересечении этих образующих будут найдены искомые промежуточные точки линии пересече­ния (например, точки 2, 3, 5 на рис. 203, а). Од­нако в данном случае выполнять такое построение нет необходимости по следующим соображениям.

Горизонтальная проекция искомой линии пере­сечения поверхностей совпадает с окружностью — горизонтальной проекцией большого цилиндра. Профильная проекция линии пересечения также совпадает с окружностью — профильной проекци­ей малого цилиндра. Таким образом, фронталь­ную проекцию искомой линии пересечения легко найти по общему правилу построения кривой линии по точкам, когда две проекции точек извес­тны. Например, по горизонтальной проекции точ­ки 3 (рис. 203, б) находят профильную проекцию 3″. Но двум проекциям 3 и 3″ определяют фрон­тальную проекцию 3′ точки 3. принадлежащей линии пересечения цилиндров.

Построение изометрической проекции пересека­ющихся цилиндров начинают с построения изометрической проекции вертикального цилин­дра. Далее через точку а₁ параллельно оси х про­водят ось горизонтального цилиндра. Положение точки О₁ определяется величиной h₁, взятой с комплексного чертежа (рис. 203, б). Отрезок, равный h, откладываем от точки О вверх по оси z (рис. 203, в). Откладывая от точки О₁ по оси горизонтального цилиндра отрезок l, получим точку О₂ — центр основания горизонтального цилиндра.

Изометрическая проекция линии пересечения поверхностей строится по точкам с помощью трех координат. Однако в данном примере искомые точки можно построить иначе.

Так, например, точки 3 и 2 строят следующим образом. От центра О₂ (рис. 203, в) вверх, парал­лельно оси z, откладывают отрезки т и п, взятые с комплексного чертежа. Через концы этих отрез­ков прямые, параллельные оси у, до пересечения с основанием горизонтального цилиндра в точках 3₁ и 2₁. Затем из точек 1…3 проводят прямые, параллельные оси х, и на них откладывают отрез­ки, равные расстоянию от основания горизонтального цилиндра до линии пересечения, взятые с фронтальной или горизонтальной проекции комплексного чертежа. Конечные точки этих отрезков будут принадлежать линии пересечения. Через полученные точки проводят по лекалу кривую, выделяя се видимые и невидимые части.

Рис. 203

Пример взаимного пересечения цилиндрических поверхностей с осями, перпендикулярными друг к другу, приведен на рис. 204, а. Одна цилиндрическая поверхность корпуса имеет вертикальную ось, а другая (половина цилиндра) — горизонталь­ную.

Если диаметры пересекающихся цилиндричес­ких поверхностей одинаковы. то профильная про­екция линии пересечения представляет собой две пересекающиеся прямые (рис. 204, б).

Если пересекающиеся цилиндрические поверхности имеют оси, расположенные под углом, отличным от прямого угла, то линию их пересечения строят с помощью вспомогательных секущих плоскостей или другими способами (например, способом сфер).

Рис. 204

Пересечение  поверхностей многогранников

При пересечении двух многогранников линия пересечения поверхностей представляет собой ломаную линию.

Если ребра двух призм взаимно перпендикуляр­ны (рис. 205, а), то линия пересечения призм строится следующим образом.

Горизонтальная и профильная проекции линии пересечения совпадают соответственно с горизон­тальной проекцией пятиугольника (основания одной призмы) и с профильной проекцией четырехугольника (основания другой призмы). Фрон­тальную проекцию ломаной линии пересечения строят по точкам пересечения ребер одной призмы с гранями другой.

Например, взяв горизонтальную 1 и про­фильную 1″ проекции точки 1 пересечения ребра пятиугольной призмы с гранью четырех­угольной (рис. 205, а) и пользуясь известным приемом построения, с помощью линии связи можно легко найти фронтальную проекцию 1′ точки 1, принадлежащей линии пересечения призм.

Изометрическая проекция двух пересекающих­ся призм (рис. 205, б) может быть построена по координатам соответствующих точек.

Например, изометрическую проекцию двух точек 5 и 5₁, симметрично расположенных на левой грани пятиугольной призмы, строят так. Принимая для удобства построений за начало координат точку О, лежащую на верхнем основа­нии пятиугольной призмы, откладываем влево от О по оси х отрезок ОЕ, величину которого берут с комплексного чертежа на фронтальной или горизонтальной проекции. Далее из точки Е вниз параллельно оси z откладываем отрезок EF, рав­ный а, и, наконец, от точки F влево и вправо параллельно оси у откладываем отрезки F5 и F5_1, равные с/2.

Далее от точки F параллельно оси х откладыва­ем отрезок n, взятый с комплексного чертежа. Через его конец проводим прямую, параллельную оси у, и откладываем на ней отрезок, равный с. Вниз параллельно оси z откладываем отрезок, равный Ь, и параллельно у — отрезок, равный k. В результате получаем изометрию основания че­тырехугольной призмы.

Рис. 205

Точки 1 и 4 на ребрах пятиугольной призмы можно построить, используя только одну коорди­нату z.

Примеры, где требуются подобные построения, показаны на рис. 206, на которых видны линии пересечения поверхностей призм.

Рис. 206

Линию пересечения поверхностей четыреху­гольной призмы с четырехугольной пирамидой (рис. 207, а) строят по точкам пересечения ребер одного многогранника с гранями другого многогранника.

Например, проекции точек 1 и 3 искомой ли­нии пересечения находят следующим образом. Фронтальные проекции 1‘ и 3′ очевидны. Про­фильные проекции 1“ и 3“ и горизонтальные 1 и 3 находят с помощью линий связи. Аналогично находят точки 2 и 4.

Линию пересечения поверхностей четыреху­гольной призмы с четырехугольной пирамидой (рис. 207, а) строят по точкам пересечения ребер одного многогранника с гранями другого многогранника.

Например, проекции точек 1 и 3 искомой ли­нии пересечения находят следующим образом. Фронтальные проекции 1‘ и 3′ очевидны. Про­фильные проекции 1“ и 3“ и горизонтальные 1 и 3 находят с помощью линий связи. Аналогично находят точки 2 и 4.

На рис. 207, б и в показана последовательность построения диметрической проекции. Сначала строят пирамиду. Для построения призмы от точ­ки О откладывают отрезок ОО₁, взятый с фрон­тальной проекции комплексного чертежа (О’ О’₁ ). и получают точку О₁ (рис. 207, б). Через точку О₁ проводят параллельно оси х ось симметрии призмы и по ней от точки откладывают вправо и влево половины высоты призмы. Через точки О₂ и О₃ проводят прямые, параллельные осям у и z, на которых откладывают соответственно половину и целую длину диагоналей четырехугольника основания призмы. Соединив концы диагоналей прямыми, получают диметрическую проекцию основания призмы.

Диметрические проекции точек пересечения 2. 4, б. 8 ребер призмы и пирамиды получаются без дополнительных построений (рис. 207, в).

Диметрические проекции точек пересечения 1, 3, 5. 7 ребер пирамиды с гранями призмы находят по координатам известным способом.

В этом примере диметрические проекции точек 1, 3, 5 и 7 можно построить иначе. От середины левого основания призмы — точки О₂ — отклады­ваем вверх и вниз по оси z соответственно отрезки т и n, взятые с комплексного чертежа. Через концы отрезков т и n проводят прямые, парал­лельные оси у, до пересечения с контуром основания призмы в точках А, В, С и D. Через эти точ­ки проводят прямые, параллельные оси х, до пе­ресечения с ребрами пирамиды. В результате по­лучают искомые точки 1, 3, 5 и 7.

Рис. 207

На рис. 208 показан корпус оптического компа­ратора, который имеет элементы пересечения поверхностей пирамид и призм. На рисунке видна линия пересечения поверхностей этих тел.

Рис. 208

Пересечение  поверхностей цилиндра и конуса

Пример пересечения поверхностей цилиндра и конуса показан на рис. 209, б. Построение линии пересечения поверхностей прямого кругового усе­ченного конуса, имеющего вертикальную ось, с цилиндром, расположенным горизонтально, пока­зано на рис. 209, а. Оси цилиндра и конуса пере­секаются в точке О₁ и лежат в одной плоскости.

Как и ранее, сначала определяют проекции очевидных 1, 7 и характерных 4, 10 точек линии пересечения.

Для определения промежуточных точек прово­дят вспомогательные горизонтальные секущие плоскости Р₁…Р₅. (рис. 209, а). Они будут рассе­кать конус по окружности, а цилиндр по образую­щим (рис. 209, б). Искомые точки линии пересе­чения находятся на пересечении образующих с окружностями.

Для определения горизонтальных проекций точек пересечения из центра O₁ проводят горизонтальные проекции дуг окружностей (рис. 209, а), по которым вспомогательные плос­кости Р₁…Р₅ пересекают конус. Размеры радиусов этих дуг окружностей взяты с профильной про­екции.

Так как профильные проекции точек 1“… 12“ известны, то, проводя линии связи до пересечения с соответствующими дугами окружностей, находят горизонтальные проекции точек 1… 12. Используя линии связи, по двум имеющимся проекциям, профильной и горизонтальней, находим фронталь­ные проекции точек пересечения 1‘…12’.

Полученные на фронтальной и горизонтальной проекциях точки, принадлежащие к линии пере­сечения. обводят по лекалу.

На горизонтальной проекции часть линии пере­сечения будет видимой, а часть — невидимой. Границу этих частей линии пересечения определяют с помощью вспомогательной секущей плос­кости Р₃, проведенной через ось цилиндра. Точки, расположенные над плоскостью Р₃ (см. профиль­ную проекцию), будут на плоскости Н видимы, а точки, расположенные под плоскостью Р_3,— неви­димы.

Изометрическую проекцию пересекающихся поверхностей цилиндра и конуса вычерчивают в такой последовательности. Вначале выполняют изометрическую проекцию конуса (рис. 209, в). Затем от центра О нижнего основания конуса по его оси вверх откладывают координату ОО₁ = h и получают точку О₁, через которую проводят ось цилиндра параллельно изометрической оси х. От точки О₁ по этой оси откладывают координату х = О₁О₂ точки О₂ — центра окружности основания цилиндра.

Для построения линии пересечения находят изометрические проекции точек этой линии с помощью их координат, взятых с комплексного чертежа. За начало координат принимается точка О₂ (центр основания цилиндра). Параллельно оси у проводят до пересечения с овалом следы плос­костей сечения с координатами по оси z, взятых с профильной проекции. Из полученных точек А, В, С… параллельно оси х проводят прямые — об­разующие цилиндра, на них откладывают ко­ординаты Al, В2, …, взятые с фронтальной проекции комплексного чертежа, и получают точки 2… 12, принадлежащие искомой линии пере­сечения.

Через найденные точки проводят кривую ли­нию по лекалу.

Рис. 209

На рис. 210 показана деталь. Линию пересечения конической поверхности с цилиндрической строят описанным выше спосо­бом.

Рис. 210

Построение линии пересечения поверхностей цилиндра и конуса, оси которых параллельны (рис. 211), аналогично построению, рассмотренно­му на рис. 209.

Выбирают вспомогательные горизонтальные плоскости, например Р₁, Р₂ и Р₃, которые пересекают конус и цилиндр по окружностям (рис. 211, б). Диаметр окружностей, образованных в результате пересечения этих плоскостей с ци­линдрам, одинаков и равен D; диаметры окруж­ностей, полученных в результате пересечения плоскостей с конусом, — различные. Взаимное пересечение горизонтальных проекций этих ок­ружностей дают искомые горизонтальные проек­ции точек 1…9 линии пересечения (рис. 211, а). Фронтальные проекции 1’…9′ этих точек находят с помощью линий связи на фронтальных следах Р_V1, Р_V2, Р_V3 вспомогательных плоскостей. Про­фильные проекции точек строят по двум их извес­тным проекциям.

Характерными точками в данном примере явля­ются: высшая точка линии пересечения — точка 5, нахождение проекций которой начинают с име­ющейся горизонтальной проекции, и точки 1, 9

Точки 1 и 9 получились от пересечения основа­ний цилиндра и конуса.

Построение изометрической проекции пересекающихся конуса и цилиндра (рис. 211, в) выполня­ется по этапам, подробно описанным в предыдущем примере (см. рис. 209, в). Построение начи­нается проведением изометрических осей конуса и цилиндра, затем их оснований (эллипсов) с центрами на расстоянии друг от друга, определяе­мом координатой n₃. Для построения линий пере­сечения находят изометрические проекции точек этой линии с помощью координат, взятых с чер­тежа.

Рис. 211

На рис. 212 показана деталь, имеющая форму двух цилиндров, пересекающихся с конусом. Оси цилиндра и конуса параллельны.

Рис. 212

Примеры пересечения поверхностей даны на рис. 213. Линии пересечения показаны красным цветом.

Рис. 213

Пересечение  поверхностей сферы и цилиндра

Прямой круговой цилиндр, расположенный перпендикулярно плоскости Н, пересекается с шаром, центр которого расположен на оси цилин­дра, по окружности, которая изображается на фронтальной проекции отрезком прямой (рис 214). Проводя через точки А и В пересече­ния контурных образующих цилиндра и очерка шара вспомогательную горизонтальную плоскость Р, заметим следующее. Плоскость Р пересечет как цилиндр, так и шар по окружности одинакового диаметра, которая расположена в проецирующей плоскости. Следовательно, се фронтальная проек­ция будет изображаться в виде прямой а’b’.

При пересечении поверхности конуса или по­верхности вращения с шаром, центр которого расположен на оси этих поверхностей, также по­лучается окружность (рис. 214, а).

Если центр шара расположен вне оси цилиндра (рис. 214, б), то для построения линии пересече­ния применяют вспомогательные горизонтальные плоскости. Например, вспомогательная горизонтальная плоскость Р пересекает цилиндр по ок­ружности радиуса r, а шар — по окружности ради­уса R. Точки пересечения а и b горизонтальных проекций этих окружностей принадлежат горизонтальной проекции линии пересечения. Фронтальные проекции а’ и b‘ строят, используя ли­нии связи.

Одной из характерных точек данной линии пересечения является верхняя точка D. Горизон­тальная проекция этой точки находится на пере­сечении прямой, соединяющей центры окружнос­тей радиусов r и R с горизонтальной проекцией основания цилиндрической поверхности. Для по­строения фронтальной проекции точки D через точку d проводят дугу радиуса r₁, строят фрон­тальную проекцию дуги (отрезок прямой, парал­лельной оси х) и с помощью линии связи находят точку d’.

Рис. 214

Пересечение  поверхностей тора и цилиндра

Патрубок, форма которого образована пересека­ющимися поверхностями тора и цилиндра, пока­зан на рис. 215. Выполнен комплексный чертеж с построением линии пересечения поверхностей и тора, и цилиндра. В этом примере очевидные точки 1 и 5. Для определения проекций промежу­точных точек используют вспомогательные плос­кости Р_Н и P_Н1, параллельные фронтальной плос­кости проекции. Например, плоскость Р_Н пересе­кает поверхность тора по окружности радиуса R, а поверхность цилиндра — по двум образующим Взаимное пересечение этих образующих с дугою окружности радиуса R дает на фронтальной про­екции две точки 2′ и 4′, принадлежащие искомой линии пересечения.

Рис. 215

Построение линий пересечения поверхностей способом вспомогательных сфер

Для построения линии пересечения поверхнос­тей вместо вспомогательных секущих плоскостей при определенных условиях удобно применять вспомогательные сферические поверхности.

В отличие от метода вспомогательных секущих плоскостей метод вспомогательных сфер имеет преимущество, так как при построении фронтальной проекции линии пересечения поверхностей не используются две другие проекции пересекающих­ся поверхностей (рис. 216).

Вспомогательные сферические поверхности для построения линий пересечения поверхностей тел можно применять лишь при следующих условиях:

а) пересекающиеся поверхности должны быть поверхностями вращения;

б) оси поверхностей вращения должны пересе­каться; точка пересечения осей является центром вспомогательных сфер;

в) оси поверхностей вращения должны быть параллельны какой-либо плоскости проекций.

Примеры применения вспомогательных сфери­ческих поверхностей показаны на рис. 216, а и б.

На рис. 216, а дано построение фронтальных проекций линии пересечения поверхностей двух цилиндров, оси которых пересекаются под острым углом.

Вспомогательные сферические поверхности проводят из точки О’ пересечения осей цилин­дров.

Построим, например, фронтальную проекцию некоторой промежуточной точки линии пересече­ния. Для этого из точки О’ проводят сферичес­кую поверхность радиуса R, которая на данной проекции изобразится в виде окружности этого же радиуса. Окружность радиуса R пересечет горизонтальный цилиндр по окружностям диаметра АС и ВD, а наклонно расположенный цилиндр — по окружностям диаметра АВ.

В пересечении полученных проекций окружнос­тей — отрезков а’b’ и c‘d‘— находят проекцию 2′ промежуточной точки линии пересечения.

Вводя еще целый ряд вспомогательных сфери­ческих поверхностей, можно построить необходи­мое число точек линии пересечения.

Пределы радиусов сферических поверхностей находят следующим образом (рис. 216, а и б): наибольшая окружность сферической поверхности должна пересекаться с контурными образующими 1—1 и II— II цилиндра и наименьшая должна быть касательной к одной из данных пересекающихся поверхностей и пересекаться с образующими дру­гой поверхности.

Рис. 216

Если поверхности двух конусов (рис. 217, а) описаны около шара, то они касаются шара по двум окружностям; эти окружности пересекаются в двух точках, которые проецируются на фрон­тальную плоскость проекций в точку р’. Плоскости, в которых лежат эти окружности, пересекают­ся по прямой, соединяющей точки пересечения линий касания конусов с шаром. Окружности проецируются на фронтальную плоскость проек­ций в виде прямых линий.

Соединив очевидную точку s’ пересечения конусов с точкой р‘, получим линию пересечения конусов с шаром, которая представляет собой фронтальную проекцию эллипса.

Разберем второй подобный пример. Если два прямых круговых цилиндра с осями, пересекаю­щимися в точке О’ (рис. 217, б), описаны около шара с центром в точке О, то фронтальная про­екция шара будет окружностью, касательной к контурным образующим цилиндров. Линии пере­сечения поверхностей этих цилиндров представля­ют собой эллипсы, фронтальные проекции кото­рых изображаются в виде прямых линий а’b‘ и c’d’.

Рис. 217

Примеры и образцы решения задач:

• Решение задач по инженерной графике
• Решение задач по начертательной геометрии

Услуги по выполнению чертежей:

1. Заказать чертежи
2. Помощь с чертежами
3. Заказать чертеж в компасе
4. Заказать чертеж в автокаде
5. Заказать чертежи по инженерной графике
6. Заказать чертежи по начертательной геометрии
7. Заказать черчение

Учебные лекции:

1. Инженерная графика
2. Начертательная геометрия
3. Оформление чертежей
4. Чертеж общего вида и сборочный чертеж
5. Техническое рисование
6. Машиностроительные чертежи
7. Геометрические построения
8. Деление окружности на равные части
9. Сопряжение линий
10. Коробовые кривые линии
11. Построение уклона и конусности
12. Лекальные кривые
13. Параллельность и перпендикулярность
14. Методы преобразования ортогональных проекций
15. Поверхности
16. Способы проецирования
17. Метрические задачи
18. Способы преобразования чертежа
19. Кривые линии
20. Кривые поверхности
21. Трёхгранник Френе
22. Проецирование многогранников
23. Проецирование тел вращения
24. Развёртывание поверхностей
25. Проекционное черчение
26. Проецирование
27. Проецирование точки
28. Проецирование отрезка прямой линии
29. Проецирование плоских фигур
30. Способы преобразования проекций
31. Аксонометрическое проецирование
32. Проекции геометрических тел
33. Сечение геометрических тел плоскостями и развертки их поверхностей
34. Сечение полых моделей
35. Разрезы
36. Требования к чертежам деталей
37. Допуски и посадки
38. Шероховатость поверхностей и обозначение покрытий
39. Разъемные и неразъемные соединения деталей
40. Передачи и их элементы