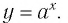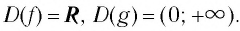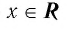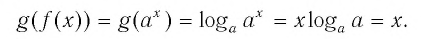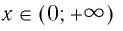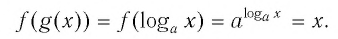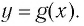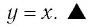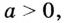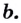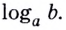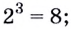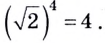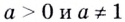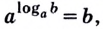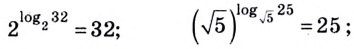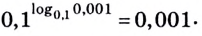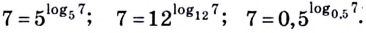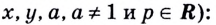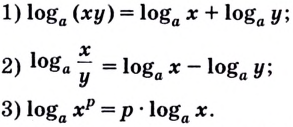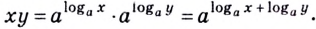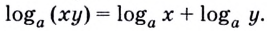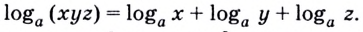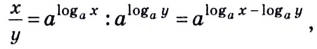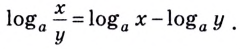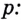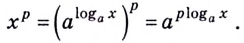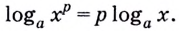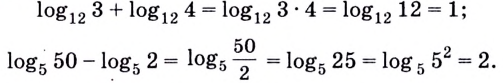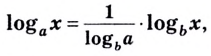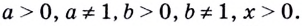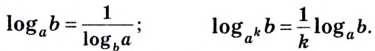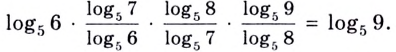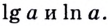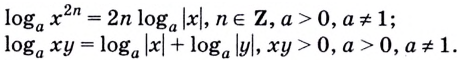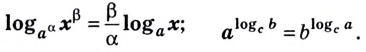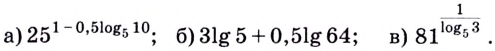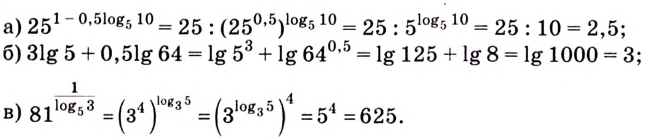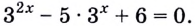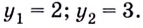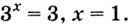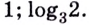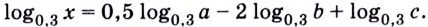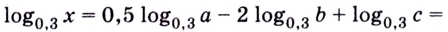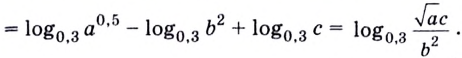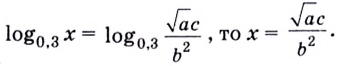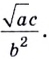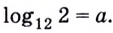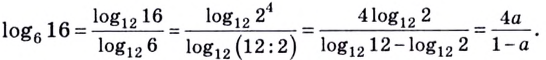Как найти логарифм числа
На практике чаще всего применяются десятичные логарифмы, которые принято называть стандартными. Для их нахождения составлены специальные таблицы, используя которые можно найти значение логарифма любого положительного числа с той или иной точностью, предварительно приведя его к стандартному виду. Для решения большинства задач вполне достаточны четырехзначные таблицы Брадиса с точностью до 0,0001, которые содержатся мантиссы десятичных логарифмов. Характеристику можно легко найти по одному виду числа. Обращение с таблицами весьма простое.
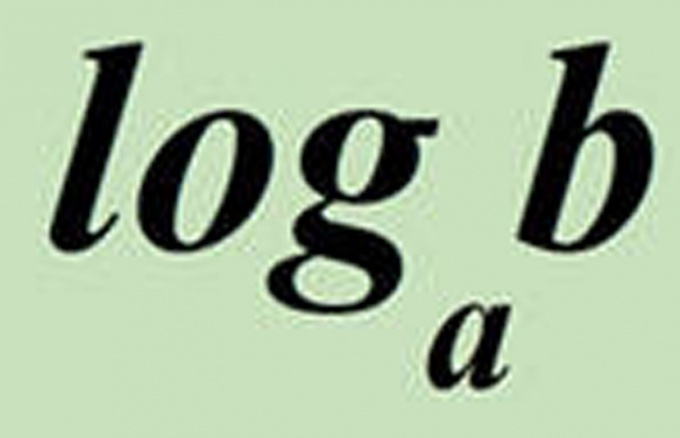
Вам понадобится
- – формула перехода от одного основания логарифма к другому;
- – четырехзначные математические таблицы Брадиса.
Инструкция
Приведите логарифм к стандартному виду, если его основание не равно 10. Используйте формулу перехода от одного основания к другому.
Найдите характеристику логарифма. Если число больше или равно единице, то сосчитайте количество цифр в целой части данного числа. Отнимите из этого количества единицу и получите значение характеристики. Например, у логарифма числа 56,3 характеристика равна 1. Если число является десятичной дробью, меньшей 1, то сосчитайте в ней количество нулей до первой цифры, отличной от нуля. Сделайте отрицательным подученное значение характеристики. Например, у логарифма числа 0,0002 характеристика равна -4.
Определите число для нахождения мантиссы как целое. Проигнорируйте в данном числе запятую, если она есть и отбросьте все нули, стоящие в конце числа. Положение запятой в десятичном числе и последние нули никаким образом не влияют на величину мантиссы. Запишите образовавшееся целое число. Например, у логарифма числа 56,3 оно равно 563. В зависимости от того, сколько цифр содержится в этом числе, зависит алгоритм работы с четырехзначными таблицами. Существует три типа алгоритмов.
Найдите мантиссу логарифма, выполнив следующие действия, если число для ее нахождения является трехзначным. Найдите в четырехзначных математических таблицах Брадиса таблицу XIII «Мантиссы десятичных логарифмов». Перейдите на строчку, содержащую в первом столбце «N» эти две первые цифры числа, по которому ищется мантисса. Например, если имеем число 563, то ищите строчку, где в первом столбе стоит 56. Затем продвигайтесь по этой строчке вправо до ее пересечения со столбцом, номер которого совпадает с третьей цифрой исходного числа. В нашем примере это столбец с номером 3. На пересечении найденной строки и столбца находится значение мантиссы. Мантисса, найденная по числу 563 равна 0,7505.
Найдите мантиссу логарифма, выполнив следующие действия, если число для ее нахождения состоит из двух или одной цифры. Припишите мысленно к этому числу такое количество нулей, чтобы оно стало трехзначным. Если число равно 56, то получается 560. Найдите мантиссу по полученному трехзначному числу. Для этого выполните действия из шага 4. Мантисса по числу 560 равна 0,7482.
Найдите мантиссу логарифма, выполнив следующие действия, если число для ее нахождения является четырехзначным. Найдите мантиссу для числа, изображенного первыми тремя цифрами данного числа. Для этого выполните действия из шага 4. Затем передвигайтесь по горизонтальной строке от найденной мантиссы в правую часть таблицы, расположенную за вертикальной жирной чертой и содержащей поправки на четвертую цифру. Найдите в области поправок столбец с номером, совпадающим с четвертой цифрой числа. Прибавьте поправку, находящуюся на пересечении строки и столбца, к мантиссе, найденной по трехзначному числу. Например, если число для нахождения мантиссы равно 5634, то мантисса по 563 равна 0,7505. Поправка по цифре 4 равна 3. Окончательный результат равен 0,7508.
Найдите мантиссу логарифма, выполнив следующие действия, если число для ее содержит более четырех цифр. Округлите число до четырех знаков так, чтобы все цифры, начиная с пятой, были нулями. Отбросьте последние нули и найдите мантиссу по четырехзначному числу. Для этого выполните действия из шага 7.
Найдите логарифм числа как сумму характеристики и мантиссы. В рассматриваемом примере логарифм числа 56,3 равен 1,7505.
Видео по теме
Источники:
- Таблицы десятичных логарифмов
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как использовать логарифмические таблицы
3 методика:Как читать логарифмическую таблицуКак найти антилогарифмПеремножение чисел с помощью логарифмической таблицы
До появления компьютеров и калькуляторов люди считали логарифмы с помощью логарифмических таблиц. Эти таблицы по-прежнему могут использовать для быстрого вычисления логарифмов или умножения больших чисел.
Шаги
Метод 1 из 3: Как читать логарифмическую таблицу
-
1
Что такое логарифм. 102 = 100. 103 = 1000. Степени 2 и 3 являются логарифмами с основанием 10 (или десятичными логарифмами) чисел 100 и 1000.[1] Иначе говоря, ab = c может быть записано, как logac = b. То есть, сказать “10 в степени 2 равно” – это все равно, что сказать “логорифм 100 с основанием 10 равен 2”. Логарифмические таблицы используют логарифм с основанием 10, поэтому а = 10.- Перемножьте два числа, сложив показатели их степеней. Например: 102 * 103 = 105, или 100 * 1000 = 100,000.
- Натуральный логарифм (ln) имеет основание е. е – это константа, равная 2.718. Число е используется в разных областях математики и физики. В таблице можно использовать как десятичные, так и натуральные логарифмы.
-
2
Определите характеристики числа, натуральный логарифм которого вы хотите определить. 15 находится между 10 (101) и 100 (102), поэтому его логарифм будет находиться между 1 и 2. 150 находится между 100 (102) и 1000 (103), поэтому его логарифм будет находиться между 2 и 3. Смысл использования логарифмической таблицы как раз состоит в поиске точного значения, то есть дробной части числа (значения после запятой). То, что находится до запятой (1 в первом случае, 2 во втором), является характеристикой. -
3
Найдите нужную строку, используя колонку слева. Эта колонка показывает первые 2 или, если это большая таблица, 3 цифры числа, логарифм которого вы ищете. Если вы ищете логарифм числа 15,27, вам нужна строка 15. Если вы ищете логарифм числа 2,57, отправляйтесь на строку 25.- Иногда числа на этой строки будут с запятыми, поэтому вы будете искать 2,5, а не 25. Вы можете игнорировать запятую, так как это не повлияет на ответ.[2]
- Также игнорируйте запятую в числе, логарифм которого вы ищете, так как дробная часть логарифма от 1,527 не отличается от дробной части логарифма 152,7.
-
4
После того, как вы нашли строку, найдите правильную колонку. Вам нужна колонка с номером, равным следующей цифре в вашем числе. Например, если вы ищете логарифм числа 15,27, номер строки равен 15, а номер колонки равен 2. Таким образом, на пересечении колонки и строки окажется число 1818. Запишите его. -
5
Если в вашей логарифмической таблице есть таблица среднего расхождения, найдите в ней колонку с номером, равным следующей цифре в вашем числе. Для числа 15,27 это будет номер 7. В данный момент, вы находитесь на пересечении 15 строки и 2 колонки. Теперь переместитесь на пересечение строки 15 и колонки таблицы среднего расхождения 7. Таким образом, на пересечении колонки и строки окажется число 20. Запишите его. -
6
Сложите два числа, полученные на предыдущих этапах. Для числа 15,27 это будет 1838. Это дробная часть логарифма числа 15,27. -
7
Добавьте характеристику. Поскольку 15 находится между 10 и 100 (101 и 02), логарифм 15 находится между 1 и 2. Следовательно, характеристика этого числа равна 1. Соедините характеристику и дробную часть, чтобы получить результат. Итак, логарифм 15,27 равен 1,1838.
Метод 2 из 3: Как найти антилогарифм
-
1
Что такое таблица антилогарифмов. Используйте эту таблицу, если вам известно значение логарифма числа, но не само число. В формуле 10n = x n – это обычный десятичный логарифм х. Если вам известно значение х, вы можете найти n с помощью таблицы логарифмов. Если вам известно n, вы можете найти х с помощью таблицы антилогарифмов.- Антилогарифм также известен как обратный логарифм.
-
2
Запишите характеристику. Это число перед запятой. Если вы ищете антилогарифм числа 2,8699, характеристикой будет 2. Мысленно уберите ее из своего числа, она понадобится позже. -
3
Найдите строку, соответствующую дробной части. У числа 2,8699 дробная часть – это ,8699. В большинстве антилогарифмических таблиц, так же как и в большинстве логарифмических, в левой колонке только два числа, поэтому вам следует искать ,86. -
4
Найдите колонку с номером, равным следующей цифре в вашей дробной части. Для числа 2,8699 вам нажно найти пересечение строки ,86 и колонки 9. Это даст вам число 7396. Запишите его. -
5
Если в вашей антилогарифмической таблице есть таблица среднего расхождения, найдите в ней строку с номером, соответствующим первым цифрам дробной части, то есть ,86. Затем, в таблице среднего расхождения найдите колонку с номером, равным следующей цифре в дробной части вашего числа, то есть 9. На пересечении строки с номером ,86 и колонки таблицы среднего расхождения 9 будет число 15. Запишите его. -
6
Сложите два числа из предыдущих шагов. В нашем примере, 7396 и 15. Их сумма равна 7411. -
7
Используйте характеристику. В нашем случае 2. Это значит, что ответ расположен между 102 и 103, или между 100 и 1000. Чтобы наше число 7411 попало в промежуток между 100 и 1000, запятая должна находиться после первых 3 цифр. Итак, наш результат 741,1.
Метод 3 из 3: Перемножение чисел с помощью логарифмической таблицы
-
1
Как перемножать числа, используя их логарифмы. Мы знаем, что 10 * 100 = 1000. Запишем это выражение, используя степени: 101 * 102 = 103. Мы также знаем, что 1 + 2 = 3. Таким образом, 10x * 10y = 10x + y. То есть, сумма логарифмов двух разных чисел равна логарифму произведения этих чисел. Мы можем перемножить два числа с одинаковым основанием, складывая их степени. -
2
Найдите логарифмы чисел, которые вы хотите перемножить. Для поиска логарифма используйте метод, описанный ранее. Например, если вы хотите умножить 15,27 но 48,54, найдите их логарифмы, равные соответственно 1,1838 и 1,6861. -
3
Сложите эти числа, чтобы найти логарифм решения. В этом примере сложите 1,1838 и 1,686, чтобы получить 2,8699. Это число является логарифмом вашего ответа. -
4
Воспользуйтесь антилогарифмической таблицей, чтобы найти решение исходной задачи. Следуйте ранее описанному методу. Для этого примера ответ равен 741,1.
Советы
- Выполняйте вычисления на листке бумаги, а не в уме, так как числа могут быть довольно громоздкими.
- Внимательной прочитайте Оглавление страницы. В логарифмической книге около 30 страниц, и использование неправильной страницы приведет вас к неправильному ответу.
Предупреждения
- Убедитесь, что данные из одной строки. Иногда можно случайно перепутать строки и колонки из-за их маленького размера.
- Данные методы подходят для поиска логарифмов с основанием 10.
- Большинство таблиц имеет точность до 3-4 знаков. Если вы посчитаете антилогарифм числа 2,8699 на калькуляторе, то получите ответ, округленный до 741,2, хотя таблицы дадут вам 741,1. Это зависит от округлений в таблицах. Если вам нужен более точный ответ, используйте калькулятор вместо таблиц.
Что вам понадобится
- Логарифмическая таблица или книга
- Листок бумаги
Download Article
Download Article
- Quick Instructions
- In-Depth Instructions
- Finding the Anti-Log
- Multiplying Numbers
- Video
- Q&A
- Tips
- Warnings
- Things You’ll Need
|
|
|
|
|
|
|
|
Before computers and calculators, logarithms were quickly calculated using logarithmic tables.[1]
These tables can still be useful for quickly calculating logarithms or multiplying large numbers, once you figure out how to use them.
-
1
Choose the correct table. To find loga(n), you’ll need a loga table. Most log tables are for base-10 logarithms, called “common logs.”[2]
- Example: log10(31.62) requires a base-10 table.
-
2
Find the correct cell. Look for the cell value at the following intersections, ignoring all decimal places:[3]
- Row labeled with first two digits of n
- Column header with third digit of n
- Example: log10(31.62) → row 31, column 6 → cell value 0.4997.
Advertisement
-
3
Use smaller chart for precise numbers. Some tables have a smaller set of columns on the right side of the chart. Use these to adjust answer if n has four or more significant digits:
- Stay in same row
- Find small column header with fourth digit of n
- Add this to previous value
- Example: log10(31.62) → row 31, small column 2 → cell value 2 → 4997 + 2 = 4999.
-
4
Prefix a decimal point. The log table only tells you the portion of your answer after the decimal point. This is called the “mantissa.”[4]
- Example: Solution so far is ?.4999
-
5
Find the integer portion. Also called the “characteristic”. By trial and error, find integer value of p such that
and
.
Advertisement
-
1
Understand what a logarithm is. 102 is 100. 103 is 1000. The powers 2 and 3 are the base-10 logarithms of 100 and 1000.[5]
In general, ab = c can be rewritten as logac = b. So, saying “ten to the power of two is 100” is equivalent to saying “the base-ten log of 100 is two.” Each logarithmic table is only usable with a certain base (a in the equation above). By far the most common type of log table uses base-10 logs, also called the common logarithm.- Multiply two numbers by adding their powers. For example: 102 * 103 = 105, or 100 * 1000 = 100,000.
- The natural log, represented by “ln”, is the base-e log, where e is the constant 2.718. This is a useful number in many areas of math and physics. You can use natural log tables in the same way that you use common, or base-10, log tables.
-
2
Identify the characteristic of the number whose log you want to find. Let’s say you want to find the base-10 log of 15 on a common log table. 15 lies between 10 (101) and 100 (102), so its logarithm will lie between 1 and 2, or be 1.something. 150 lies between 100 (102) and 1000 (103), so its logarithm will lie between 2 and 3, or be 2.something. The .something is called the mantissa; this is what you will find in the log table. What comes before the decimal point (1 in the first example, 2 in the second) is the characteristic.
-
3
Slide your finger down to the appropriate row on the table using the leftmost column. This column will show the first two or, for some large log tables, three digits of the number whose logarithm you’re looking up. If you’re looking up the log of 15.27 in a normal log table, go to the row marked 15. If you’re looking up the log of 2.57, go to the row marked 25.
- Sometimes the numbers in this row will have a decimal point, so you’ll look up 2.5 rather than 25. You can ignore this decimal point, as it won’t affect your answer.
- Also ignore any decimal points in the number whose logarithm you’re looking up, as the mantissa for the log of 1.527 is no different from that of the log of 152.7.
-
4
On the appropriate row, slide your finger over to the appropriate column. This column will be the one marked with the next digit of the number whose logarithm you’re looking up. For example, if you want to find the log of 15.27, your finger will be on the row marked 15. Slide your finger along that row to the right to find column 2. You will be pointing at the number 1818. Write this down.
-
5
If your log table has a mean difference table, slide your finger over to the column in that table marked with the next digit of the number you’re looking up. For 15.27, this number is 7. Your finger is currently on row 15 and column 2. Slide it over to row 15 and mean differences column 7. You will be pointing at the number 20. Write this down.
-
6
Add the numbers found in the two preceding steps together. For 15.27, you will get 1838. This is the mantissa of the logarithm of 15.27.
-
7
Add the characteristic. Since 15 is between 10 and 100 (101 and 102), the log of 15 must be between 1 and 2, so 1.something, so the characteristic is 1. Combine the characteristic with the mantissa to get your final answer. Find that the log of 15.27 is 1.1838.
Advertisement
-
1
Understand the anti-log table. Use this when you have the log of a number but not the number itself. In the formula 10n = x, n is the common log, or base-ten log, of x. If you have x, find n using the log table. If you have n, find x using the anti-log table.
- The anti-log is also commonly known as the inverse log.
-
2
Write down the characteristic. This is the number before the decimal point. If you’re looking up the anti-log of 2.8699, the characteristic is 2. Mentally remove it from the number you’re looking up, but make sure to write it down so you don’t forget it – it will be important later.
-
3
Find the row that matches the first part of the mantissa. In 2.8699, the mantissa is .8699. Most anti-log tables, like most log tables, have two digits in the leftmost column, so run your finger down that column until you find .86.
-
4
Slide your finger over to the column marked with the next digit of the mantissa. For 2.8699, slide your finger along the row marked .86 to find the intersection with column 9. This should read 7396. Write this down.
-
5
If your anti-log table has a table of mean differences, slide your finger over to the column in that table marked with the next digit of the mantissa. Make sure to keep your finger in the same row. In this case, you will slide your finger over to the last column in the table, column 9. The intersection of row .86 and mean differences column 9 is 15. Write that down.
-
6
Add the two numbers from the two previous steps. In our example, these are 7396 and 15. Add them together to get 7411.
-
7
Use the characteristic to place the decimal point. Our characteristic was 2. This means that the answer is between 102 and 103, or between 100 and 1000. In order for the number 7411 to fall between 100 and 1000, the decimal point must go after three digits, so that the number is about 700 rather than 70, which is too small, or 7000, which is too big. So the final answer is 741.1.
Advertisement
-
1
Understand how to multiply numbers using their logarithms. We know that 10 * 100 = 1000. Written in terms of powers (or logarithms), 101 * 102 = 103. We also know that 1 + 2 = 3. In general, 10x * 10y = 10x + y. So, the sum of the logarithms of two different numbers is the logarithm of the product of those numbers. We can multiply two numbers of the same base by adding their powers.[6]
-
2
Look up the logarithms of the two numbers you want to multiply. Use the method above to find the logarithms. For example, if you want to multiply 15.27 and 48.54, you would find the log of 15.27 to be 1.1838 and the log of 48.54 to be 1.6861.
-
3
Add the two logarithms to find the logarithm of the solution. In this example, add 1.1838 and 1.6861 to get 2.8699. This number is the logarithm of your answer.
-
4
Look up the anti-logarithm of the result from the above step to find the solution. You can do this by finding the number in the body of the table closest to the mantissa of this number (8699). The more efficient and reliable method, however, is to find the answer in the table of anti-logarithms, as described in the method above. For this example, you will get 741.1.
Advertisement
Add New Question
-
Question
How do I find the log of a cube?
Triple the log of the number that has been cubed.
-
Question
How do I find logs for 3.14?
Multiply 3.14 with 10 to get 31.4, then find log (31.4), which is roughly 1.4969. Now, divide this by 10 to get your log with base 10.
-
Question
How do I find the log of a single digit?
Say you want to find the log of 9. You know that 9 = 9.0 = 9.00 and so on. Now that you have the correct number of significant digits, you can use a log table as long as you deal with decimal points correctly.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Always do the calculations on a sheet of paper and not mentally, as these are large and complicated numbers and they can get tricky.
-
Read the page heading carefully. A log book has about 30 pages and using the wrong page will give the wrong answer.
Thanks for submitting a tip for review!
Advertisement
-
Most tables are only accurate to three or four digits. If you find the anti-log of 2.8699 using a calculator, the answer will round to 741.2, but the answer you get using log tables is 741.1. This is due to rounding in the tables. If you need a more precise answer, use a calculator or another method rather than log tables.
-
Use the methods described in this article for common log, or base-ten log, tables, and make sure the numbers you’re looking up are in base-ten format, or scientific notation.
-
Make sure that the readings are from the same row. Sometimes, we may mix up rows and columns because of the small size and close spacing.
Advertisement
Things You’ll Need
- logarithmic table or log book
- spare sheet of paper.
References
About This Article
Article SummaryX
To use logarithmic tables for a base-10 logarithm, start by making sure you have the correct log table, called a “common log.” Then, scan the “n” column on the far left for the first two digits of the number. From there, move to the right to find the column labeled with the third digit of the number, and find the cell where the row and column intersect. The cell contains the digits of the number that are after the decimal point, or the “mantissa.” Once you have the mantissa, count the number of places after the decimal point and subtract one to find the integer. If you need to learn more, such as how to find the anti-log of your logarithm, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,111,866 times.
Reader Success Stories
-
“I was searching the document for use of log tables. This was required for preparing Standard Operating Procedure…” more
Did this article help you?
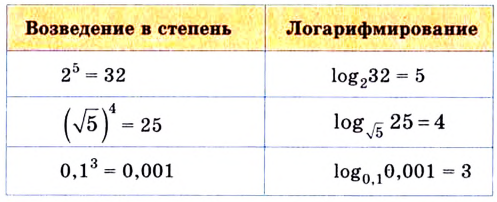
Логарифмом положительного числа (c) по основанию (a) ((a>0, aneq1)) называется показатель степени (b), в которую надо возвести основание (a), чтобы получить число (c) ((c>0)), т.е.
(a^{b}=c) (Leftrightarrow) (log_{a}{c}=b)
Объясним проще. Например, (log_{2}{8}) равен степени, в которую надо возвести (2), чтоб получить (8). Отсюда понятно, что (log_{2}{8}=3).
|
Примеры: |
(log_{5}{25}=2) |
т.к. (5^{2}=25) |
||
|
(log_{3}{81}=4) |
т.к. (3^{4}=81) |
|||
|
(log_{2})(frac{1}{32})(=-5) |
т.к. (2^{-5}=)(frac{1}{32}) |
Аргумент и основание логарифма
Любой логарифм имеет следующую «анатомию»:

Аргумент логарифма обычно пишется на его уровне, а основание – подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».
Как вычислить логарифм?
Чтобы вычислить логарифм – нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?
Например, вычислите логарифм: а) (log_{4}{16}) б) (log_{3})(frac{1}{3}) в) (log_{sqrt{5}}{1}) г) (log_{sqrt{7}}{sqrt{7}}) д) (log_{3}{sqrt{3}})
а) В какую степень надо возвести (4), чтобы получить (16)? Очевидно во вторую. Поэтому:
(log_{4}{16}=2)
б) В какую степень надо возвести (3), чтобы получить (frac{1}{3})? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени).
(log_{3})(frac{1}{3})(=-1)
в) В какую степень надо возвести (sqrt{5}), чтобы получить (1)? А какая степень делает любое число единицей? Ноль, конечно!
(log_{sqrt{5}}{1}=0)
г) В какую степень надо возвести (sqrt{7}), чтобы получить (sqrt{7})? В первую – любое число в первой степени равно самому себе.
(log_{sqrt{7}}{sqrt{7}}=1)
д) В какую степень надо возвести (3), чтобы получить (sqrt{3})? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень – это степень (frac{1}{2}).
(log_{3}{sqrt{3}}=)(frac{1}{2})
Пример: Вычислить логарифм (log_{4sqrt{2}}{8})
Решение:
|
(log_{4sqrt{2}}{8}=x) |
Нам надо найти значение логарифма, обозначим его за икс. Теперь воспользуемся определением логарифма: |
|
|
((4sqrt{2})^{x}=8) |
Что связывает (4sqrt{2}) и (8)? Двойка, потому что и то, и другое число можно представить степенью двойки: |
|
|
({(2^{2}cdot2^{frac{1}{2}})}^{x}=2^{3}) |
Слева воспользуемся свойствами степени: (a^{m}cdot a^{n}=a^{m+n}) и ((a^{m})^{n}=a^{mcdot n}) |
|
|
(2^{frac{5}{2}x}=2^{3}) |
Основания равны, переходим к равенству показателей |
|
|
(frac{5x}{2})(=3) |
Умножим обе части уравнения на (frac{2}{5}) |
|
|
(x=1,2) |
Получившийся корень и есть значение логарифма |
Ответ: (log_{4sqrt{2}}{8}=1,2)
Зачем придумали логарифм?
Чтобы это понять, давайте решим уравнение: (3^{x}=9). Просто подберите (x), чтобы равенство сработало. Конечно, (x=2).
А теперь решите уравнение: (3^{x}=8).Чему равен икс? Вот в том-то и дело.
Самые догадливые скажут: «икс чуть меньше двух». А как точно записать это число? Для ответа на этот вопрос и придумали логарифм. Благодаря ему, ответ здесь можно записать как (x=log_{3}{8}).
Хочу подчеркнуть, что (log_{3}{8}), как и любой логарифм – это просто число. Да, выглядит непривычно, но зато коротко. Потому что, если бы мы захотели записать его в виде десятичной дроби, то оно выглядело бы вот так: (1,892789260714…..)
Пример: Решите уравнение (4^{5x-4}=10)
Решение:
|
(4^{5x-4}=10) |
(4^{5x-4}) и (10) никак к одному основанию не привести. Значит тут не обойтись без логарифма.
Воспользуемся определением логарифма: |
|
|
(log_{4}{10}=5x-4) |
Зеркально перевернем уравнение, чтобы икс был слева |
|
|
(5x-4=log_{4}{10}) |
Перед нами линейное уравнение. Перенесем (4) вправо. И не пугайтесь логарифма, относитесь к нему как к обычному числу. |
|
|
(5x=log_{4}{10}+4) |
Поделим уравнение на 5 |
|
|
(x=)(frac{log_{4}{10}+4}{5}) |
Вот наш корень. Да, выглядит непривычно, но ответ не выбирают. |
Ответ: (frac{log_{4}{10}+4}{5})
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы ((a>0, aneq1)). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
Натуральный логарифм: логарифм, у которого основание – число Эйлера (e) (равное примерно (2,7182818…)), и записывается такой логарифм как (ln{a}).
То есть, (ln{a}) это то же самое, что и (log_{e}{a}), где (a) – некоторое число.
Десятичный логарифм: логарифм, у которого основание равно 10, записывается (lg{a}).
То есть, (lg{a}) это то же самое, что и (log_{10}{a}), где (a) – некоторое число.
Основное логарифмическое тождество
У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:
Это свойство вытекает напрямую из определения. Посмотрим как именно эта формула появилась.
Вспомним краткую запись определения логарифма:
если (a^{b}=c), то (log_{a}{c}=b)
То есть, (b) – это тоже самое, что (log_{a}{c}). Тогда мы можем в формуле (a^{b}=c) написать (log_{a}{c}) вместо (b). Получилось (a^{log_{a}{c}}=c) – основное логарифмическое тождество.
Остальные свойства логарифмов вы можете найти здесь. С их помощью можно упрощать и вычислять значения выражений с логарифмами, которые «в лоб» посчитать сложно.
Пример: Найдите значение выражения (36^{log_{6}{5}})
Решение:
|
(36^{log_{6}{5}}=) |
Сразу пользоваться свойством (a^{log_{a}{c}}=c) мы не можем, так как в основании степени и в основании логарифма – разные числа. Однако мы знаем, что (36=6^{2}) |
|
|
(=(6^{2})^{log_{6}{5}}=) |
Зная формулу ((a^{m})^{n}=a^{mcdot n}), а так же то, что множители можно менять местами, преобразовываем выражение |
|
|
(=6^{2cdotlog_{6}{5}}=6^{log_{6}{5}cdot2}=(6^{log_{6}{5}})^{2}=) |
Вот теперь спокойно пользуемся основным логарифмическим тождеством. |
|
|
(=5^{2}=25) |
Ответ готов. |
Ответ: (25)
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что (log_{2}{4}) равен двум. Тогда можно вместо двойки писать (log_{2}{4}).
Но (log_{3}{9}) тоже равен (2), значит, также можно записать (2=log_{3}{9}) . Аналогично и с (log_{5}{25}), и с (log_{9}{81}), и т.д. То есть, получается
(2=log_{2}{4}=log_{3}{9}=log_{4}{16}=log_{5}{25}=log_{6}{36}=log_{7}{49}…)
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как (log_{2}{8}), или как (log_{3}{27}), или как (log_{4}{64})… Здесь мы как аргумент пишем основание в кубе:
(3=log_{2}{8}=log_{3}{27}=log_{4}{64}=log_{5}{125}=log_{6}{216}=log_{7}{343}…)
И с четверкой:
(4=log_{2}{16}=log_{3}{81}=log_{4}{256}=log_{5}{625}=log_{6}{1296}=log_{7}{2401}…)
И с минус единицей:
(-1=) (log_{2})(frac{1}{2})(=) (log_{3})(frac{1}{3})(=) (log_{4})(frac{1}{4})(=) (log_{5})(frac{1}{5})(=) (log_{6})(frac{1}{6})(=) (log_{7})(frac{1}{7})(…)
И с одной третьей:
(frac{1}{3})(=log_{2}{sqrt[3]{2}}=log_{3}{sqrt[3]{3}}=log_{4}{sqrt[3]{4}}=log_{5}{sqrt[3]{5}}=log_{6}{sqrt[3]{6}}=log_{7}{sqrt[3]{7}}…)
И так далее.
Любое число (a) может быть представлено как логарифм с основанием (b): (a=log_{b}{b^{a}})
Пример: Найдите значение выражения (frac{log_{2}{14}}{1+log_{2}{7}})
Решение:
|
(frac{log_{2}{14}}{1+log_{2}{7}})(=) |
Превращаем единицу в логарифм с основанием (2): (1=log_{2}{2}) |
|
|
(=)(frac{log_{2}{14}}{log_{2}{2}+log_{2}{7}})(=) |
Теперь пользуемся свойством логарифмов: |
|
|
(=)(frac{log_{2}{14}}{log_{2}{(2cdot7)}})(=)(frac{log_{2}{14}}{log_{2}{14}})(=) |
В числителе и знаменателе одинаковые числа – их можно сократить. |
|
|
(=1) |
Ответ готов. |
Ответ: (1)
Смотрите также:
Логарифмические уравнения
Логарифмические неравенства
Содержание:
Множеством (областью) значений показательной функции
Такое значение аргумента единственное, так как если 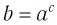
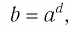
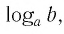
Таким образом, равенство 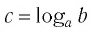
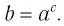
Определение:
Пусть 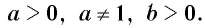
Приведем несколько примеров:
Нахождение логарифма числа называется логарифмированием.
Обозначим 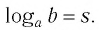
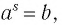
Это равенство называется основным логарифмическим тождеством.
Согласно этому тождеству, например, имеем: 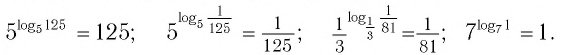
Например:
История логарифма
Логарифмы были изобретены в 1614 г. шотландским математиком Д. Непером (1550—1617) и независимо от него на 6 лет позднее швейцарским механиком и математиком И. Бюрги (1552—1632).
Оба исследователя хотели найти новое удобное средство арифметических вычислений, но их определения логарифма различны и у обоих не похожи на современные. Понимание логарифма как показателя степени с данным основанием впервые появилось в XVIII в. в работах английского математика В. Гардинера (1742). Широкому распространению этого определения логарифма более других содействовал Jl. Эйлер, который впервые применил в этой связи и термин «основание».
Термин «логарифм» принадлежит Неперу. Он возник из сочетания греческих слов логос — отношение и аритмос — число. Слово «логарифм», таким образом, означало «число отношения».
Пример:
а) Записать число 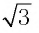
б) Записать число -5 в виде логарифмов по основанию 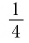
Решение:
а) По определению логарифма имеем:
б) По определению логарифма имеем:
Пример:
Между какими целыми числами находится число
Решение:
Пусть 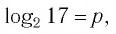
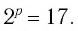
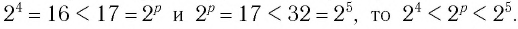
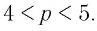
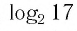
Ответ:
Пример:
Решить уравнение:
Решение:
а) Поскольку 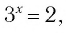
б)
Ответ:
Логарифмы по основанию 10 имеют особое название — десятичные логарифмы. Десятичный логарифм числа b обозначается 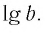
▲ Особое обозначение и название имеют не только десятичные логарифмы, но и логарифмы, основанием которых является число е:
Такие логарифмы называются натуральными.
Логарифмы по основанию е позволяют выражать математическую зависимость, которая характеризует многие биологические, химические, физические, социальные и другие процессы. По-видимому, этим объясняется и название «натуральные логарифмы», т. е. естественные (этот термин ввел в 1659 г. итальянский математик П. Менголи). Натуральные и десятичные логарифмы имели большое значение для облегчения вычислений в XVII—XX вв. до создания мощных современных вычислительных средств. Натуральные логарифмы имеют и большое теоретическое значение.▲
Основные свойства логарифмов
Теорема:
При любых положительных значениях b и с верно равенство:
Доказательство:
Докажем утверждение (1).
По основному логарифмическому тождеству
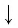
Таким образом, имеем:
Отсюда по следствию из п. 2.3 получаем равенство (1).
Докажем утверждение (2). Преобразуем левую часть равенства (2):
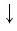
Заметим, что равенство (2) можно доказать тем же способом, что и равенство (1), — сделайте это самостоятельно.
Равенство (1) означает, что логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
Равенство (2) означает, что логарифм дроби с положительными. числителем и знаменателем равен разности логарифмов числителя и знаменателя.
Замечание. Равенства, доказанные в теореме 1 (как и другие равенства этого пункта), являются тождествами. Действительно, каждое из них превращается в верное числовое равенство при любых значениях a, b и с, для которых входящие в равенство выражения имеют смысл.
Теорема:
При любых значениях s и положительных значениях b верно равенство
Доказательство:
По основному логарифмическому тождеству
Таким образом, имеем
Отсюда по следствию из п. 2.3 получаем равенство (3).
Следствие 1. Если числа 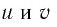
Следствие 2. При любом целом 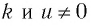
Пример №1
Найти значение выражения:
Решение:
Ответ:
Теорема:
При любых значениях 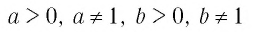
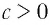
Доказательство:
Способ 1. По основному логарифмическому тождеству имеем
Прологарифмировав левую и правую части этого тождества по основанию а, получим
Применив тождество (3), имеем
Так как 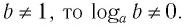
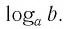
Способ 2. Пусть 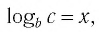
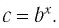
Откуда имеем
Итак,
Тождество (6) называется формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Обычно в таблицах, калькуляторах даются значения логарифмов по основанию 10, а когда нужно найти значение логарифма по другому основанию, пользуются формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Следствием из тождества (6) при основании а = с является формула
(убедитесь в этом самостоятельно).
Пример №2
Найти значение выражения, если
Решение:




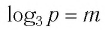
6)


Ответ:
Следствие 3. Имеют место тождества:
Тождества (8) и (9) можно доказать, используя уже доказанные тождества из этого пункта.
Пример №3
Упростить выражение
Решение:
Используя определение логарифма, представим числа 1 и 3 в виде логарифмов по основанию 2:
Ответ:
Развитие науки, прежде всего астрономии, уже в XVI в. привело к необходимости громоздких вычислений при умножении и делении многозначных чисел. Эти вычислительные проблемы были в некоторой степени решены с открытием логарифмов и созданием таблиц логарифмов.
Логарифмическая функция
Рассмотрим выражение 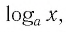
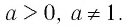
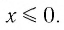
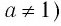
Определение:
Логарифмической функцией называется функция вида 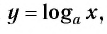
Область определения логарифмической функции — это естественная область определения выражения 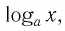
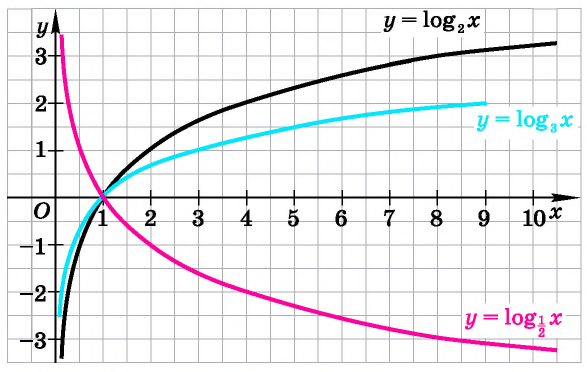
Графики некоторых логарифмических функций изображены на рисунке 34. Эти изображения (как и для графиков других функций) можно было получить, строя их по точкам. Отметим некоторые особенности изображенных графиков.
График функции 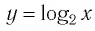
Когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» опускается вниз. А когда значения аргумента х увеличиваются, то график «медленно» поднимается вверх (ем. рис. 34). Аналогично для любой функции 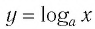
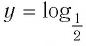
Заметим, что когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» поднимается вверх. А когда значения аргумента х увеличиваются, то график «медленно» опускается вниз. Аналогично для любой функции 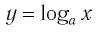
Теорема (о свойствах логарифмической функции 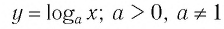
- Областью определения логарифмической функции является интервал
- Множеством (областью) значений логарифмической функции является множество R всех действительных чисел.
- Логарифмическая функция не имеет ни наименьшего, ни наибольшего значений.
- График логарифмической функции пересекается с осью абсцисс в точке (1; 0) и не пересекается с осью ординат.
- Значение аргумента х = 1 является нулем логарифмической функции.
- 6. При а > 1 логарифмическая функция принимает отрицательные значения на интервале (0; 1) и принимает положительные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
и принимает положительные значения на интервале (0; 1).
- Логарифмическая функция не является ни четной, ни нечетной.
- При а > 1 логарифмическая функция возрастает на всей области определения. При 0 < а < 1 логарифмическая функция убывает на всей области определения.
- Логарифмическая функция не является периодической.
Изображение графика логарифмической функции позволяет наглядно представить эти свойства.
Множество (область) значений логарифмической функции — проекция ее графика на ось Оу, а на рисунках 35 и 36 видно, что эта проекция есть ось Оу. Это значит, что для любой точки 
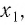
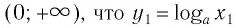
Множество (область) значений логарифмической функции — это множество всех действительных чисел, а в нем нет ни наименьшего числа, ни наибольшего (свойство 3).
График логарифмической функции проходит через точку (1; 0) и лежит в правой полуплоскости (свойства 4, 5).
При а > 1 график логарифмической функции лежит в IV координатном угле, когда 
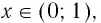
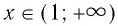
Область определения логарифмической функции — интервал 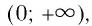
На рисунке 35 видно, что при а > 1 логарифмическая функция возрастает на области определения, а на рисунке 36 видно, что при 0 < а < 1 логарифмическая функция убывает на области определения (свойство 8).
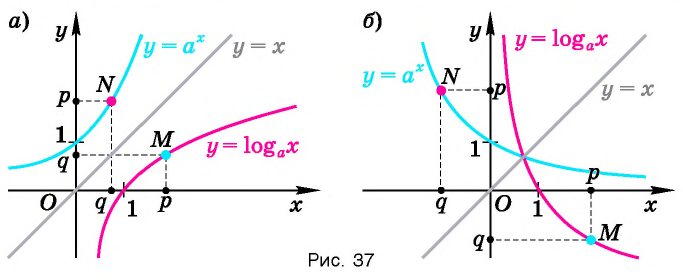
Пусть точка 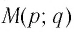
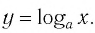
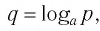
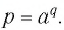
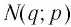
Заметим, что точки 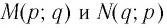
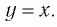
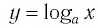
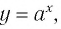
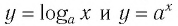
Последнее утверждение дает возможность, зная график функции 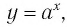
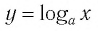
▲ Симметричность графиков функций 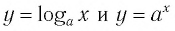
Функции 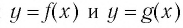
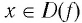
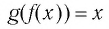
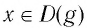
Покажем, что показательная и логарифмическая функции с одним, и тем же основанием а взаимно обратны.
Пусть 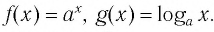
Для любого
Для любого
Покажем, что графики взаимно обратных функций 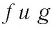
Пусть точка 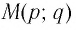
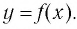
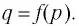
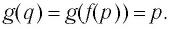
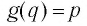
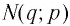
Таким образом, каждой точке М на графике функции 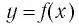
- Заказать решение задач по высшей математике
Логарифмы и их свойства
В предыдущем параграфе вы находили корни уравнения вида 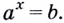
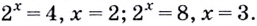
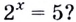
Для записи корней показательного уравнения используют понятие «логарифм» и соответствующий символ. Корнем уравнения 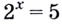
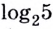
Рассмотрим общий случай-.
Пусть 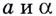
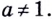
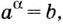
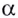
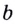
Логарифмом числа 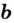
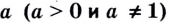
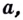
Логарифм числа 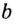
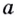
Примеры:
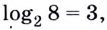
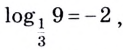
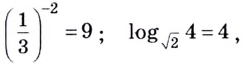
Основанием логарифма может быть произвольное положительное число, кроме единицы. Как известно, если 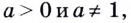
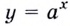
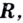
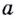
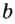
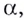
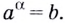
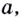
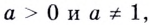
Полезно помнить, что для каждого
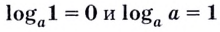
Нахождение логарифма числа называют логарифмированием. Эта операция обратная к операции возведения в степень с соответствующим основанием.
Согласно определению логарифма, если 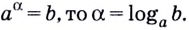
которое называют основным логарифмическим тождеством. Оно правильное для любых положительных
Например:
С помощью основного логарифмического тождества любое положительное число можно представить в виде степени, имеющей заданное основание.
Например:
Докажем ещё несколько важных свойств логарифмов (для положительных
1) По основному логарифмическому тождеству и основному свойству степени
Итак, 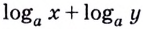
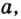
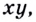
Эту формулу можно обобщить на три и более множителя:
Кратко говорят: логарифм произведения равен сумме логарифмов множителей.
2) Доказательство аналогичное предыдущему:
отсюда
Кратко говорят: логарифм частного равен разности логарифмов делимого и делителя.
3) Возведём обе части тождества 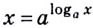
Итак,
Доказанные формулы можно использовать и справа налево, например:
В логарифмах переходить от одного основания к другому можно при помощи формулы перехода
где
Докажем эту формулу. Поскольку положительные числа 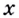
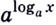
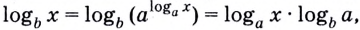
Обратите внимание! Как следствия из формулы перехода можно получить следующие формулы:
Докажите их самостоятельно.
Пример №4
Упростите выражение 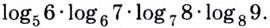
Решение:
Сведём все логарифмы к основанию 5. Имеем:
Особенно часто используют логарифмы по основаниям 10 и 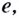
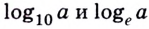
Рассмотренные в параграфе свойства логарифмов правиль-1 ные при условии, что переменные принимают положительные значения. С помощью модуля можно расширить использование некоторых формул. Например:
Для преобразования выражений, решения уравнений и неравенств используют и другие формулы, содержащие логарифмы:
Докажите их самостоятельно.
Пример №5
Вычислите:
Решение:
Пример №6
Решите уравнение:
Решение:
Пусть 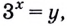
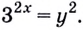
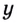
Получим: 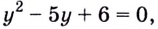
Поскольку 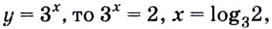
Ответ.
Пример №7
Найдите 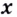
Решение:
Поскольку
Ответ.
Пример №8
Вычислите 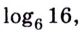
Решение:
Ответ.
- Корень из числа – нахождение и вычисление
- Теория множеств – виды, операции и примеры
- Числовые множества
- Вектор – определение и основные понятия
- Бесконечно убывающая геометрическая прогрессия
- Периодические дроби
- Степень с рациональным показателем
- Степень с действительным показателем











































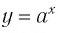
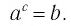
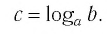
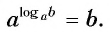
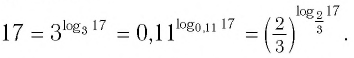
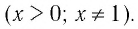
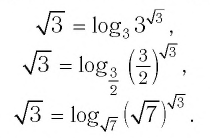
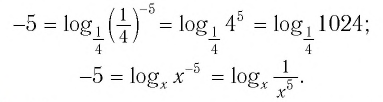
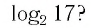
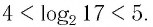
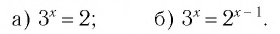
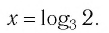
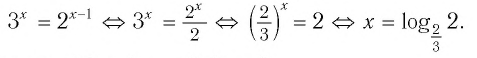
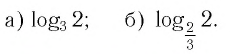
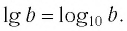
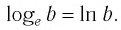
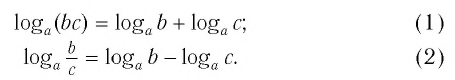
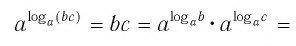
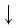
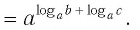
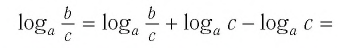
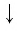
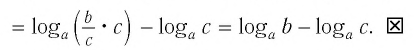

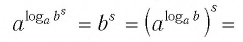
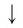
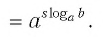
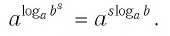

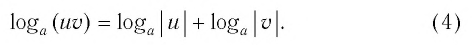
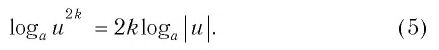
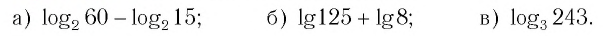
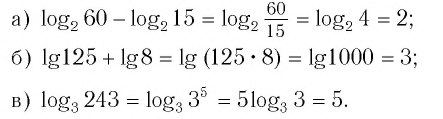
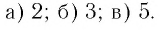

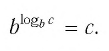
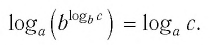
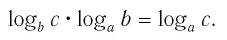

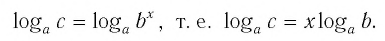
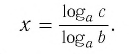
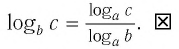

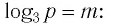
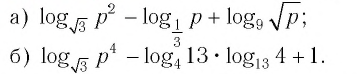
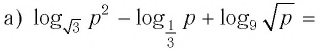
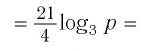
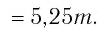
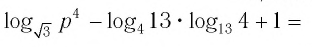
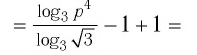
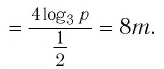

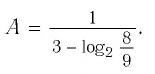
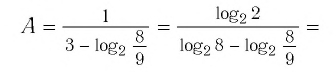
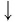
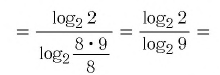
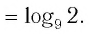
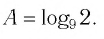
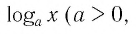
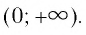
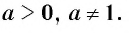
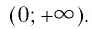
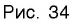
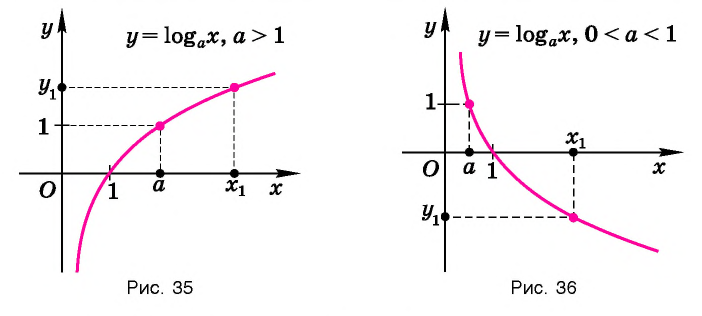
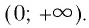
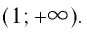 И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале 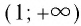 и принимает положительные значения на интервале (0; 1).
и принимает положительные значения на интервале (0; 1).