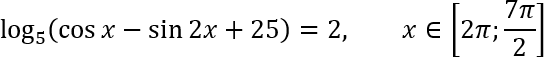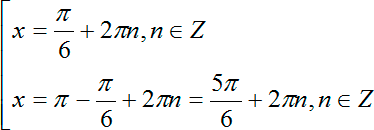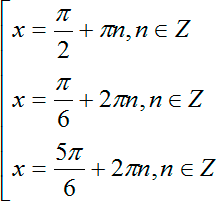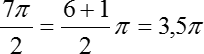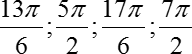Логарифмы синусов углов близких к 90° и косинусов малых углов (Таблица Брадиса 16)
Логарифмы синусов любого угла, содержащего целое число градусов и минут, берется из таблица Брадиса 15, если угол заключается между 0° и 14°, и из таблица Брадиса 16, если он заключается между 14° и’90°. В готовом виде таблицы Брадиса 16 даёт только логарифмы синусов углов через 0,1° = 6′, для других нужна интерполяция, вводящая поправку на разность между данным углом и ближайшим табличным. Эта поправка берётся из соответствующего столбца справа (курсив). Она прибавляется к ближайшему меньшему табличному логарифму, если данный угол превосходит ближайший меньший табличный на 1, 2, 3 минуты, и отнимается от ближайшего большего в остальных случаях. Например, lg sin 20°38′ = 1,5470, так как 5463 + 7=5470, a lg sin 20°41′ =1,5481, так как 5484 — 3=5481.
Так же данная таблица служит для разыскания логарифмов косинусов, причём надо пользоваться нумерацией градусов справа, минут — снизу, и не забывать, что при возрастании острого угла его косинус убывает. Подыскание косинусов можно устранить, заменяя их синусами дополнительных углов.
Читайте также — как пользоваться таблицами Брадиса
Смотрите — все таблицы Брадиса
| ЛОГАРИФМЫ СИНУСОВ УГЛОВ |
|||||||||||||||
| А | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 14° | 1,3837 | 3867 | 3897 | 3927 | 3957 | 3986 | 5 | 10 | 15 | ||||||
| 4015 | 4044 | 4073 | 4102 | 1,4130 | 75° | 5 | 10 | 14 | |||||||
| 15° | 1,4130 | 4158 | 4186 | 4214 | 4242 | 4269 | 5 | 9 | 14 | ||||||
| 4296 | 4323 | 4350 | 4377 | 1,4403 | 74° | 4 | 9 | 13 | |||||||
| 16° | 1,4403 | 4430 | 4456 | 4482 | 4508 | 4533 | 4 | 9 | 13 | ||||||
| 4559 | 4584 | 4609 | 4634 | 1,4659 | 73° | 4 | 8 | 13 | |||||||
| 17° | 1,4659 | 4684 | 4709 | 4733 | 4757 | 4781 | 4805 | 4829 | 4853 | 4876 | 4900 | 72° | 4 | 8 | 12 |
| 18° | 4900 | 4923 | 4946 | 4969 | 4992 | 5015 | 5037 | 5060 | 5082 | 5104 | 5126 | 71° | 4 | 8 | 11 |
| 19° | 5126 | 5148 | 5170 | 5192 | 5213 | 5235 | 5256 | 5278 | 5299 | 5320 | 1,5341 | 70° | 4 | 7 | 11 |
| 20° | 1,5341 | 5361 | 5382 | 5402 | 5423 | 5443 | 5463 | 5484 | 5504 | 5523 | 5543 | 69° | 3 | 7 | 10 |
| 21° | 5543 | 5563 | 5583 | 5602 | 5621 | 5641 | 5660 | 5679 | 5698 | 5717 | 5736 | 68° | 3 | 6 | 10 |
| 22° | 5736 | 5754 | 5773 | 5792 | 5810 | 5828 | 5847 | 5865 | 5883 | 5901 | 5919 | 67° | 3 | 6 | 9 |
| 23° | 5919 | 5937 | 5954 | 5972 | 5990 | 6007 | 6024 | 6042 | 6059 | 6076 | 6093 | 66° | 3 | 6 | 9 |
| 24° | 6093 | 6110 | 6127 | 6144 | 6161 | 6177 | 6194 | 6210 | 6227 | 6243 | 1,6289 | 65° | 3 | 6 | 8 |
| 25° | 1,6259 | 6276 | 6292 | 6308 | 6324 | 6340 | 6356 | 6371 | 6387 | 6403 | 6418 | 64° | 3 | 5 | 8 |
| 26° | 6418 | 6434 | 6449 | 6465 | 6480 | 6495 | 6510 | 6526 | 6541 | 6556 | 6570 | 63° | 3 | 5 | 8 |
| 27° | 6570 | 6585 | 6600 | 6615 | 6629 | 6644 | 6659 | 6673 | 6687 | 6702 | 6716 | 62° | 2 | 5 | 7 |
| 28° | 6716 | 6730 | 6744 | 6759 | 6773 | 6787 | 6801 | 6814 | 6828 | 6842 | 6856 | 61° | 2 | 5 | 7 |
| 29° | 6856 | 6869 | 6883 | 6896 | 6910 | 6923 | 6937 | 6950 | 6963 | 6977 | 1,6990 | 60° | 2 | 4 | 7 |
| 30° | 1,6990 | 7003 | 7016 | 7029 | 7042 | 7055 | 7068 | 7080 | 7093 | 7106 | 7118 | 59° | 2 | 4 | 6 |
| 31° | 7118 | 7131 | 7144 | 7156 | 7168 | 7181 | 7193 | 7205 | 7218 | 7230 | 7242 | 58° | 2 | 4 | 6 |
| 32° | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 7326 | 7338 | 7349 | 7361 | 57° | 2- | 4 | 6 |
| 33° | 7361 | 7373 | 7384 | 7396 | 7407 | 7419 | 7430 | 7442 | 7453 | 7464 | 7476 | 56° | 2 | 4 | 6 |
| 34° | 7476 | 7487 | 7498 | 7509 | 7520 | 7531 | 7542 | 7553 | 7564 | 7575 | 1,7586 | 55° | 2 | 4 | 6 |
| 35° | 1,7586 | 7597 | 7607 | 7618 | 7629 | 7640 | 7650 | 7661 | 7671 | 7682 | 7692 | 54° | 2 | 4 | 5 |
| 36° | 7692 | 7703 | 7713 | 7723 | 7734 | 7744 | 7754 | 7764 | 7774 | 7785 | 7795 | 53° | 2 | 3 | 5 |
| 37° | 7795 | 7805 | 7815 | 7825 | 7835 | 7844 | 7854 | 7864 | 7874 | 7884 | 78,93 | 52° | 2 | 3 | 5 |
| 38° | 7893 | 7903 | 7913 | 7922 | 7932 | 7941 | 7951 | 7960 | 7970 | 7979 | 7989 | 51° | 2 | 3 | 5 |
| 39° | 7989 | 7998 | 8007 | 8017 | 8026 | 8035 | 8044 | 8053 | 8063 | 8072 | 1,8081 | 50° | 2 | 3 | 5 |
| 40° | 1,8081 | 8090 | 8099 | 8108 | 8117 | 8125 | 8134 | 8143 | 8152 | 8161 | 8169 | 49° | 1 | 3 | 4 |
| 41° | 8169 | 8178 | 8187 | 8195 | 8204 | 8213 | 8221 | 8230 | 8238 | 8247 | 8255 | 48° | 1 | 3 | 4 |
| 42° | 8255 | 8264 | 8272 | 8280 | 8289 | 8297 | 8305 | 8313 | 8322 | 8330 | 8338 | 47° | 1 | 3 | 4 |
| 43° | 8338 | 8346 | 8354 | 8362 | 8370 | 8378 | 8386 | 8394 | 8402 | 8410 | 8418 | 46° | 1 | 3 | 4 |
| 44° | 8418 | 8426 | 8433 | 8441 | 8449 | 8457 | 8464 | 8472 | 8480 | 8487 | 1,8495 | 45° | 1 | 3 | 4 |
| 45° | 1,8495 | 8502 | 8510 | 8517 | 8525 | 8532 | 8540 | 8547 | 8555 | 8562 | 8569 | 44° | 1 | 2 | 4 |
| 46° | 8569 | 8577 | 8584 | 8591 | 8598 | 8606 | 8613 | 8620 | 8627 | 8634 | 8641 | 43° | 1 | 2 | 4 |
| 47° | 8641 | 8648 | 8655 | 8662 | 8669 | 8676 | 8683 | 8690 | 8697 | 8704 | 8711 | 42° | 1 | 2 | 3 |
| 48° | 8711 | 8718 | 8724 | 8731 | 8738 | 8745 | 8751 | 8758 | 8765 | 8771 | 8778 | 41° | 1 | 2 | 3 |
| 49° | 8778 | 8784 | 8791 | 8797 | 8804 | 8810 | 8817 | 8823 | 8830 | 8836 | 1,8843 | 40° | 1 | 2 | 3 |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | А | 1′ | 2′ | 3′ | |
| ЛОГАРИФМЫ КОСИНУСОВ УГЛОВ |
| ЛОГАРИФМЫ СИНУСОВ УГЛОВ |
|||||||||||||||
| А | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 50° | 1,8843 | 8849 | 8855 | 8862 | 8868 | 8874 | 8880 | 8887 | 8893 | 8899 | 1,8905 | 39° | 1 | 2 | 3 |
| 51° | 8905 | 8911 | 8917 | 8923 | 8929 | 8935 | 8941 | 8947 | 8953 | 8959 | 8965 | 38° | 1 | 2 | 3 |
| 52° | 8965 | 8971 | 8977 | 8983 | 8989 | 8995 | 9000 | 9006 | 9012 | 9018 | 9023 | 37° | 1 | 2 | 3 |
| 53° | 9023 | 9029 | 9035 | 9041 | 9046 | 9052 | 9057 | 9063 | 9069 | 9074 | 9080 | 36° | 1 | 2 | 3 |
| 54° | 9080 | 9085 | 9091 | 9096 | 9101 | 9107 | 9112 | 9118 | 9123 | 9128 | 1,9134 | 35° | 1 | 2 | 3 |
| 55° | 1,9134 | 9139 | 9144 | 9149 | 9155 | 9160 | 9165 | 9170 | 9175 | 9181 | 9186 | 34° | 1 | 2 | 3 |
| 56° | 9186 | 9191 | 9196 | 9201 | 9206 | 9211 | 9216 | 9221 | 9226 | 9231 | 9236 | 33° | 1 | 2 | 3 |
| 57° | 9236 | 9241 | 9246 | 9251 | 9255 | 9260 | 9265 | 9270 | 9275 | 9279 | 9284 | 32° | 1 | 2 | 2 |
| 58° | 9284 | 9289 | 9294 | 9298 | 9303 | 9308 | 9312 | 9317 | 9322 | 9326 | 9331 | 31° | 1 | 2 | 2 |
| 59° | 9331 | 9335 | 9340 | 9344 | 9349 | 9353 | 9358 | 9362 | 9367 | 9371 | 1,9375 | 30° | 1 | 1 | 2 |
| 60° | 1,9375 | 9380 | 9384 | 9388 | 9393 | 9397 | 9401 | 9406 | 9410 | 9414 | 9418 | 29° | 1 | 1 | 2 |
| 61° | 9418 | 9422 | 9427 | 9431 | 9435 | 9439 | 9443 | 9447 | 9451 | 9455 | 9459 | 28° | 1 | 1 | 2 |
| 62° | 9459 | 9463 | 9467 | 9471 | 9475 | 9479 | 9483 | 9487 | 9491 | 9495 | 9499 | 27° | 1 | 1 | 2 |
| 63° | 9499 | 95рЗ | 9506 | 9510 | 9514 | 9518 | 9522 | 9525 | 9529 | 9533 | 9537 | 26° | 1 | 1 | 2 |
| 64° | 9537 | 9540 | 9544 | 9548 | 9551 | 9555 | 9558 | 9562 | 9566 | 9569 | 1,9573 | 25° | 1 | 1 | 2 |
| 65° | 1,9573 | 9576 | 9580 | 9583 | 9587 | 9590 | 9594 | 9597 | 9601 | 9604 | 9607 | 24° | 1 | 1 | 2 |
| 66° | 9607 | 9611 | 9614 | 9617 | 9621 | 9624 | 9627 | 9631 | 9634 | 9637 | 9640 | 23° | 1 | 1 | 2 |
| 67° | 9640 | 9643 | 9647 | 9650 | 9653 | 9656 | 9659 | 9662 | 9666 | 9669 | 9672 | 22° | 1 | 1 | 2 |
| 68° | 9672 | 9675 | 9678 | 9681 | 9684 | 9687 | 9690 | 9693 | 9696 | 9699 | 9702 | 21° | 0 | 1 | 1 |
| 69° | 9702 | 9704 | 9707 | 9710 | 9713 | 9716 | 9719 | 9722 | 9724 | 9727 | 1,9730 | 20° | 0 | 1 | 1 |
| 70° | 1,9730 | 9733 | 9735 | 9738 | 9741 | 9743 | 9746 | 9749 | 9751 | 9754 | 9757 | 19° | 0 | 1 | 1 |
| 71° | 9757 | 9759 | 9762 | 9764 | 9767 | 9770 | 9772 | 9775 | 9777 | 9780 | 9782 | 18° | 0 | 1 | 1 |
| 72° | 9782 | 9785 | 9787 | 9789 | 9792 | 9794 | 9797 | 9799 | 9801 | 9804 | 9806 | 17° | 0 | 1 | 1 |
| 73° | 9806 | 9808 | 9811 | 9813 | 9815 | 9817 | 9820 | 9822 | 9824 | 9826 | 9828 | 16° | 0 | 1 | 1 |
| 74° | 9828 | 9831 | 9833 | 9835 | 9837 | 9839 | 9841 | 9843 | 9845 | 9847 | 1,9849 | 15° | 0 | 1 | 1 |
| 75° | 1,9849 | 9851 | 9853 | 9855 | 9857 | 9859 | 9861 | 9863 | 9865 | 9867 | 9869 | 14° | 0 | 1 | 1 |
| 76° | 9869 | 9871 | 9873 | 9875 | 9876 | 9878 | 9880 | 9882 | 9884 | 9885 | 9887 | 13° | 0 | 1 | 1 |
| 77° | 9887 | 9889 | 9891 | 9892 | 9894 | 9896 | 9897 | 9899 | 9901 | 9902 | 9904 | 12° | 0 | 1 | 1 |
| 78° | 9904 | 9906 | 9907 | 9909 | 9910 | 9912 | 9913 | 9915 | 9916 | 9918 | 9919 | 11° | 0 | 1 | 1 |
| 79° | 9919 | 9921 | 9922 | 9924 | 9925. | 9927 | 9928 | 9929 | 9931 | 9932 | 1,9934 | 10° | 0 | 0 | 1 |
| 80° | 1,9934 | 9935 | 9936 | 9937 | 9939 | 9940 | 9941 | 9943 | 9944 | 9945 | 9946 | 9° | 0 | 0 | 1 |
| 81° | 9946 | 9947 | 9949 | 9950 | 9951 | 9952 | 9953 | 9954 | 9955 | 9956 | 9958 | 8° | 0 | 0 | 1 |
| 82° | 9958 | 9959 | 9960 | 9961 | 9962 | 9963 | 9964 | 9965 | 9966 | 9967 | 9968 | 7° | 0 | 0 | 1 |
| 83° | 9968 | 9968 | 9969 | 9970 | 9971 | 9972 | 9973 | 9974 | 9975 | 9975 | 9976 | 6° | 0 | 0 | 0 |
| 84° | 9976 | 9977 | 9978 | 9978 | 9979 | 9980 | 9981 | 9981 | 9982 | 9983 | 1,9983 | 5° | 0 | 0 | 0 |
| 85° | 1,9983 | 9984 | 9985 | 9985 | 9986 | 9987 | 9987 | 9988 | 9988 | 9989 | 9989 | 4° | 0 | 0 | 0 |
| 86° | 9989 | 9990 | 9990 | 9991 | 9991 | 9992 | 9992 | 9993 | 9993 | 9994 | 9994 | 3° | 0 | 0 | 0 |
| 87° | 9994 | 9994 | 9995 | 9995 | 9996 | 9996 | 9996 | 9996 | 9997 | 9997 | 9997 | 2° | 0 | 0 | 0 |
| 88° | 9997 | 9998 | 9998 | 9998 | 9998 | 9999 | 9999 | 9999 | 9999 | 9999 | 1,9999 | 1° | 0 | 0 | 0 |
| 89° | 9999 | 9999 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0,0000 | 0° | 0 | 0 | 0 |
| 90° | 0,0000 | ||||||||||||||
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | А | 1′ | 2′ | 3′ | |
| ЛОГАРИФМЫ КОСИНУСОВ УГЛОВ |
_______________
Источник информации: Брадис В.М. Четырехзначные математические таблицы: Для средней школы. / В.М. Брадис . — 57-е изд., — М.: Просвещение, 1990.
Логарифмы синусов малых углов и косинусов углов близких к 90° (Таблица Брадиса 15)
Логарифмы синусов любого угла, содержащего целое число градусов и минут, берется из таблица брадиса 15, если угол заключается между 0° и 14°, и из таблицы брадиса 16, если он заключается между 14° и’90°. В готовом виде таблицы брадиса 16 даёт только логарифмы синусов углов через 0,1° = 6′, для других нужна интерполяция, вводящая поправку на разность между данным углом и ближайшим табличным. Эта поправка берётся из соответствующего столбца справа (курсив). Она прибавляется к ближайшему меньшему табличному логарифму, если данный угол превосходит ближайший меньший табличный на 1, 2, 3 минуты, и отнимается от ближайшего большего в остальных случаях. Например, lg sin 20°38′ = 1,5470, так как 5463 + 7=5470, a lg sin 20°41′ =1,5481, так как 5484 – 3=5481.
Так же данная таблица брадиса служит для разыскания логарифмов косинусов, причём надо пользоваться нумерацией градусов справа, минут – снизу, и не забывать, что при возрастании острого угла его косинус убывает. Подыскание косинусов можно устранить, заменяя их синусами дополнительных углов.
| ЛОГАРИФМЫ СИНУСОВ УГЛОВ | ||||||||||||
| А | 0′ | 1′ | 2′ | 3′ | 4′ | 5′ | 6′ | 7′ | 8′ | 9′ | 10′ | |
| 0°00′ | 4,4637 | 7648 | 9408 | 0658 | 1627 | 2419 | 3088 | 3668 | 4180 | 3,4637 | 50′ | |
| 10′ | 3,4637 | 5051 | 5429 | 5777 | 6099 | 6398 | 6678 | 6942 | 7190 | 7245 | 7648 | 40′ |
| 20′ | 7648 | 7859 | 8061 | 8255 | 8439 | 8617 | 8787 | 8951 | 9109 | 9261 | 9408 | 30′ |
| 30′ | 9408 | 9551 | 9689 | 9822 | 9952 | 0078 | 0200 | 0319 | 0435 | 0548 | 2,0658 | 20′ |
| 40′ | 2,0658 | 0765 | 0870 | 0972 | 1072 | 1169 | 1265 | 1358 | 1450 | 1539 | 1627 | 10′ |
| 50′ | 1627 | 1713 | 1797 | 1880 | 1961 | 2041 | 2119 | 2196 | 2271 | 2346 | 2419 | 89°00′ |
| 1°00′ | 2,2419 | 2490 | 2561 | 2630 | 2699 | 2766 | 2832 | 2898 | 2962 | 3025 | 3088 | 50′ |
| 10′ | 3088 | 3150 | 3210 | 3270 | 3329 | 3388 | 3445 | 3502 | 3558 | 3613 | 3668 | 40′ |
| 20′ | 3668 | 3722 | 3775 | 3828 | 3880 | 3931 | 3982 | 4032 | 4082 | 4131 | 4179 | 30′ |
| 30′ | 4179 | 4227 | 4275 | 4322 | 4368 | 4414 | 4459 | 4504 | 4549 | 4593 | 4637 | 20′ |
| 40′ | 4637 | 4680 | 4723 | 4765 | 4807 | 4848 | 4890 | 4930 | 4971 | 5011 | 5050 | 10′ |
| 50′ | 5050 | 5090 | 5129 | 5167 | 5206 | 5243 | 5281 | 5318 | 5355 | 5392 | 2,5428 | 88°00′ |
| 2°00′ | 2,5428 | 5464 | 5500 | 5535 | 5571 | 5605 | 5640 | 5674 | 5708 | 5742 | 5776 | 50′ |
| 10′ | 5776 | 5809 | 5842 | 5875 | 5907 | 5939 | 5972 | 6003 | 6035 | 6066 | 6097 | 40′ |
| 20′ | 6097 | 6128 | 6159 | 6189 | 6220 | 6250 | 6279 | 6309 | 6339 | 6368 | 6397 | 30′ |
| 30′ | 6397 | 6426 | 6454 | 6483 | 6511 | 6539 | 6567 | 6595 | 6622 | 6650 | 6677 | 20′ |
| 40′ | 6677 | 6704 | 6731 | 6758 | 6784 | 6810 | 6837 | 6863 | 6889 | 6914 | 6940 | 10′ |
| 50′ | 6940 | 6965 | 6991 | 7016 | 7041 | 7066 | 7090 | 7115 | 7140 | 7164 | 2,7188 | 87°00′ |
| 3°00′ | 2,7188 | 7212 | 7236 | 7260 | 7283 | 7307 | 7330 | 7354 | 7377 | 7400 | 7423 | 50′ |
| 10′ | 7423 | 7445 | 7468 | 7491 | 7513 | 7535 | 7557 | 7580 | 7602 | 7623 | 7645 | 40′ |
| 20′ | 7645 | 7667 | 7688 | 7710 | 7731 | 7752 | 7773 | 7794 | 7815 | 7836 | 7857 | 30′ |
| 30′ | 7857 | 7877 | 7898 | 7918 | 7939 | 7959 | 7979 | 7999 | 8019 | 8039 | 8059 | 20′ |
| 40′ | 8059 | 8078 | 8098 | 8117 | 8137 | 8156 | 8175 | 8194 | 8213 | 8232 | 8251 | 10′ |
| 50′ | 8251 | 8270 | 8289 | 8307 | 8326 | 8345 | 8363 | 8381 | 8400 | 8418 | 2,8436 | 86°00′ |
| 4°00′ | 2,8436 | 8454 | 8472 | 8490 | 8508 | 8525 | 8543 | 8560 | 8578 | 8595 | 8613 | 50′ |
| 10′ | 8613 | 8630 | 8647 | 8665 | 8682 | 8699 | 8716 | 8733 | 8749 | 8766 | 8783 | 40′ |
| 20′ | 8783 | 8799 | 8816 | 8833 | 8849 | 8865 | 8882 | 8898 | 8914 | 8930 | 8946 | 30′ |
| 30′ | 8946 | 8962 | 8978 | 8994 | 9010 | 9026 | 9042 | 9057 | 9073 | 9089 | 9104 | 20′ |
| 40′ | 9104 | 9119 | 9135 | 9150 | 9166 | 9181 | 9196 | 9211 | 9226 | 9241 | 9256 | 10′ |
| 50′ | 9256 | 9271 | 9286 | 9301 | 9315 | 9330 | 9345 | 9359 | 9374 | 9388 | 2,9403 | 85°00′ |
| 5°00′ | 2,9403 | 9417 | 9432 | 9446 | 9460 | 9475 | 9489 | 9503 | 9517 | 9531 | 9545 | 50′ |
| 10′ | 9545 | 9559 | 9573 | 9587 | 9601 | 9614 | 9628 | 9642 | 9655 | 9669 | 9682 | 40′ |
| 20′ | 9682 | 9696 | 9709 | 9723 | 9736 | 9750 | 9763 | 9776 | 9789 | 9803 | 9816 | 30′ |
| 30′ | 9816 | 9829 | 9842 | 9855 | 9868 | 9881 | 9894 | 9907 | 9919 | 9932 | 2,9945 | 20′ |
| 40′ | 9945 | 9958 | 9970 | 9983 | 9996 | 0008 | 0021 | 0033 | 0046 | 0058 | 1,0070 | 10′ |
| 50′ | 1,0070 | 0083 | 0095 | 0107 | 0120 | 0132 | 0144 | 0156 | 0168 | 0180 | 0192 | 84°00′ |
| 6°00′ | 1,0192 | 0204 | 0216 | 0228 | 0240 | 0252 | 0264 | 0276 | 0287 | 0299 | 0311 | 50′ |
| 10′ | 0311 | 0323 | 0334 | 0346 | 0357 | 0369 | 0380 | 0392 | 0403 | 0415 | 0426 | 40′ |
| 20′ | 0426 | 0438 | 0449 | 0460 | 0472 | 0483 | 0494 | 0505 | 0516 | 0527 | 0539 | 30′ |
| 30′ | 0539 | 0550 | 0561 | 0572 | 0583 | 0594 | 0605 | 0616 | 0626 | 0637 | 0648 | 20′ |
| 40′ | 0648 | 0659 | 0670 | 0680 | 0691 | 0702 | 0712 | 0723 | 0734 | 0744 | 0755 | 10′ |
| 50′ | 0755 | 0765 | 0776 | 0786 | 0797 | 0807 | 0818 | 0828 | 0838 | 0849 | 1,0859 | 83°00′ |
| 10′ | 9′ | 8′ | 7′ | 6′ | 5′ | 4′ | 3′ | 2′ | 1′ | 0′ | A | |
| ЛОГАРИФМЫ КОСИНУСОВ УГЛОВ |
| ЛОГАРИФМЫ СИНУСОВ УГЛОВ |
||||||||||||
| А | 0′ | 1′ | 2′ | 3′ | 4′ | 5′ | 6′ | 7′ | 8′ | 9′ | 10′ | |
| 7°00′ | 1,0859 | 0869 | 0879 | 0890 | 0900 | 0910 | 0920 | 0930 | 0940 | 0951 | 1,0961 | 50′ |
| 10′ | 0961 | 0971 | 0981 | 0991 | 1001 | 1011 | 1020 | 1030 | 1040 | 1050 | 1060 | 40′ |
| 20′ | 1060 | 1070 | 1080 | 1089 | 1099 | 1109 | 1118 | 1128 | 1138 | 1147 | 1157 | 30′ |
| 30′ | 1157 | 1167 | 1176 | 1186 | 1195 | 1205 | 1214 | 1224 | 1233 | 1242 | 1252 | 20′ |
| 40′ | 1252 | 1261 | 1271 | 1280 | 1289 | 1299 | 1308 | 1317 | 1326 | 1336 | 1345 | 10′ |
| 50′ | 1345 | 1354 | 1363 | 1372 | 1381 | 1390 | 1399 | 1409 | 1418 | 1427 | 1,1436 | 82°00′ |
| 8°00′ | 1,1436 | 1445 | 1453 | 1462 | 1471 | 1480 | 1489 | 1498 | 1507 | 1516 | 1525 | 50′ |
| 10′ | 1525 | 1533 | 1542 | 1551 | 1560 | 1568 | 1577 | 1586 | 1594 | 1603 | 1612 | 40′ |
| 20′ | 1612 | 1620 | 1629 | 1637 | 1646 | 1655 | 1663 | 1672 | 1680 | 1689 | 1697 | 30′ |
| 30′ | 1697 | 1705 | 1714 | 1722 | 1731 | 1739 | 1747 | 1756 | 1764 | 1772 | 1781 | 20′ |
| 40′ | 1781 | 1789 | 1797 | 1806 | 1814 | 1822 | 1830 | 1838 | 1847 | 1855 | 1863 | 10′ |
| 50′ | 1863 | 1871 | 1879 | 1887 | 1895 | 1903 | 1911 | 1919 | 1927 | 1935 | 1,1943 | 81°00′ |
| 9°00′ | 1,1943 | 1951 | 1959 | 1967 | 1975 | 1983 | 1991 | 1999 | 2007 | 2015 | 2022 | 50′ |
| 10′ | 2022 | 2030 | 2038 | 2046 | 2054 | 2061 | 2069 | 2077 | 2085 | 2092 | 2100 | 40′ |
| 20′ | 2100 | 2108 | 2115 | 2123 | 2131 | 2138 | 2146 | 2153 | 2161 | 2169 | 2176 | 30′ |
| 30′ | 2176 | 2184 | 2191 | 2199 | 2206 | 2214 | 2221 | 2229 | 2236 | 2243 | 2251 | 20′ |
| 40′ | 2251 | 2258 | 2266 | 2273 | 2280 | 2288 | 2295 | 2303 | 2310 | 2317 | 2324 | 10′ |
| 50′ | 2324 | 2332 | 2339 | 2346 | 2353 | 2361 | 2368 | 2375 | 2382 | 2390 | 1,2397 | 80°00′ |
| 10°00′ | 1,2397 | 2404 | 2411 | 2418 | 2425 | 2432 | 2439 | 2447 | 2454 | 2461 | 2468 | 50′ |
| 10′ | 2468 | 2475 | 2482 | 2489 | 2496 | 2503 | 2510 | 2517 | 2524 | 2531 | 2538 | 40′ |
| 20′ | 2538 | 2545 | 2551 | 2558 | 2565 | 2572 | 2579 | 2586 | 2593 | 2600 | 2606 | 30′ |
| 30′ | 2606 | 2613 | 2620 | 2627 | 2634 | 2640 | 2647 | 2654 | 2661 | 2667 | 2674 | 20′ |
| 40′ | 2674 | 2681 | 2687 | 2694 | 2701 | 2707 | 2714 | 2721 | 2727 | 2734 | 2740 | 10′ |
| 50′ | 2740 | 2747 | 2754 | 2760 | 2767 | 2773 | 2780 | 2786 | 2793 | 2799 | 1,2806 | 79°00′ |
| 11°00′ | 1,2806 | 2812 | 2819 | 2825 | 2832 | 2838 | 2845 | 2851 | 2858 | 2864 | 2870 | 50′ |
| 10′ | 2870 | 2877 | 2883 | 2890 | 2896 | 2902 | 2909 | 2915 | 2921 | 2928 | 2934 | 40′ |
| 20′ | 2934 | 2940 | 2947 | 2953 | 2959 | 2965 | 2972 | 2978 | 2984 | 2990 | 2997 | 30′ |
| 30′ | 2997 | 3003 | 3009 | 3015 | 3021 | 3027 | 3034 | 3040 | 3046 | 3052 | 3058 | 20′ |
| 40′ | 3058 | 3064 | 3070 | 3077 | 3083 | 3089 | 3095 | 3101 | 3107 | 3113 | 3119 | 10′ |
| 50′ | 3119 | 3125 | 3131 | 3137 | 3143 | 3149 | 3155 | 3161 | 3167 | 3173 | 1,3179 | 78°00′ |
| 12°00′ | 1,3179 | 3185 | 3191 | 3197 | 3202 | 3208 | 3214 | 3220 | 3226 | 3232 | 3238 | 50′ |
| 10′ | 3238 | 3244 | 3250 | 3255 | 3261 | 3267 | 3273 | 3279 | 3284 | ,3290 | 3296 | 40′ |
| 20′ | 3296 | 3302 | 3308 | 3313 | 3319 | 3325 | 3331 | 3336 | 3342 | 3348 | 3353 | 30′ |
| 30′ | 3353 | 3359 | 3365 | 3370 | 3376 | 3382 | 3387 | 3393 | 3399 | 3404 | 3410 | 20′ |
| 40′ | 3410 | 3416 | 3421 | 3427 | 3432 | 3438 | 3444 | 3449 | 3455 | 3460 | 3466 | 10′ |
| 50′ | 3466 | 3471 | 3477 | 3482 | 3488 | 3493 | 3499 | 3504 | 3510 | 3515 | 1,3521 | 77°00′ |
| 13°00′ | 1,3521 | 3526 | 3532 | 3537 | 3543 | 3548 | 3554 | 3559 | 3564 | 3570 | 3575 | 50′ |
| 10′ | 3575 | 3581 | 3586 | 3591 | 3597 | 3602 | 3608 | 3613 | 3618 | 3624 | 3629 | 40′ |
| 20′ | 3629 | 3634 | 3640 | 3645 | 3650 | 3655 | 3661 | 3666 | 3671 | 3677 | 3682 | 30′ |
| 30′ | 3682 | 3687 | 3692 | 3698 | 3703 | 3708 | 3713 | 3719 | 3724 | 3729 | 3734 | 20′ |
| 40′ | 3734 | 3739 | 3745 | 3750 | 3755 | 3760 | 3765 | 3770 | 3775 | 3781 | 3786 | 10′ |
| 50′ | 3786 | 3791 | 3796 | 3801 | 3806 | 3811 | 3816 | 3822 | 3827 | 3832 | 1,3837 | 76°00′ |
| 10′ | 9′ | 8′ | 7′ | 6′ | 5′ | 4′ | 3′ | 2′ | 1′ | 0′ | А | |
| ЛОГАРИФМЫ КОСИНУСОВ УГЛОВ |
_______________
Источник информации: Брадис В.М. Четырехзначные математические таблицы: Для средней школы. / В.М. Брадис . – 57-е изд., – М.: Просвещение, 1990.
Поделитесь ссылкой с друзьями:
Похожие таблицы
Комментарии:
Так делают, например, в таблицах для логарифмов тригонометрических функций, меньших единицы. [c.78]
Полные сведения о таблицах натуральных значений (и логарифмов) тригонометрических функций и других математических таблицах, которые могут оказаться полезными вычислителю, содержатся в специальных справочных руководствах [21]-[23]. [c.34]
И. Десятичные логарифмы тригонометрических функции [c.70]
Десятичные логарифмы тригонометрических функций [c.71]
Таблица VII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ЛОГАРИФМЫ [c.41]
Величины я, десятичных и натуральных логарифмов, натуральных значений тригонометрических функций. Приближенные значения этих величин могут быть вычислены с любой, заданной, точностью. [c.6]
Макроструктура, понятие 29 Марганец 37, 70 Мартенсит 37 Математика длины дуг, хорд, стрел, площадь сегментов круга 8 , квадраты, кубы, корни, десятичные логарифмы чисел 6 краткие сведения 6 тригонометрические функции 11 функции углов 8 Машина, понятие 449 Медь 417 [c.491]
Если Л>0, то формулы (7), (8), (9), (16) содержат гиперболические функции и поэтому они неудобны для вычислений. Этого неудобства можно избежать путем такого преобразования этих формул, чтобы при вычислении приходилось сталкиваться лишь с таблицами вещественных тригонометрических функций и логарифмов. Для достижения этой цели достаточно лишь заменить эксцентрическую аномалию и другой вещественной независимой переменной и = и(ц), называемой обычно углом Ламберта и определяемой по формуле [c.244]
Логарифмы десятичные 48 Функции тригонометрические дополнительных углов — Зависимости 92 [c.565]
Логарифмы десятичные 1—48 Функции тригонометрические дополнительных углов—Зависимости 1—92 [c.491]
В иоследовате. и.ных приближениях изменяется лини, первый и третий из этих логарифмов. Логарифмы тригонометрических функций берутся из таблиц. Пусть табличная разность для логарифма sin и sin(( ,+ aip) равна Е,, где 5 f — некоторое подходяп1ее приращение к f , и пусть — соответствующая табличная разность для sin (а, 4- т). Эти величины выписываются из соответствующих столбцов таблиц, когда берутся логарифмы sin и sin( f,+ от). Тогда поправка A f дается уравнением [c.200]
Большие удобства при анализе создает применение электронных клавишных вычислительных машин-микрокалькуляторов. Микрокалькуляторы оперируют с восьмиразрядными десятичными числами и выполняют любое из четырех арифметических действий как простых, так и цепочечного типа, вычисляют обратные числа, проценты. Некоторые из них выполняют извлечение квадратного корня, вычисляют логарифмы, антилогарифмы, тригонометрические функции. Вводимые в машину числа и результаты считываются с восьмиразрядного цифрового светящегося индикатора. Скорость сложения восьмиразрядных чисел 50 мс, умножения или деления — 300 мс. Машины работают либо от четырех сменных элементов А-316 Квант непрерывно в течение шести часов, либо от сети переменного тока напряжением 220 В через блок питания БП2-1. [c.223]
Функции у = sin а у =– os а и т. д. называют круговыми, угловыми, гониометрическилш или тригонометрическими функциями. Числовые значения их и их логарифмы даны в таблицах для углов а от О до 90° (см. литературу). При малых углах а часто выгодно разложить круговую функцию в степенной ряд (см. раздел 131. 52). [c.61]
Математические таблицы даны, соответственно обычной практике технических справочников, в нижеследующем объёме степени, корни, натуральные логарифмы, длины окружностей, площади кругов и обратные величины (табл. I), мантиссы десятичных логарифмов (таблица 2), натуральные значения тригонометрических функций (табл. 3), характеристики дуг (табл. 4—6), специальные фужции (табл. 7 и 8), важнейщие постоянные (табл. 9) и сводка расчётных характеристик плоских фигур и тел (табл. 10 и 11). [c.9]
Мантиссы десятичных логарифмов (табл. 2) и натуральные значения тригонометрических функций (табл. 3) даны в расширенном объёме шестизначные мантиссы десятичных логарифмов для аргументов от 1 до 10000, шести-и семизначные таблицы тригонометрических функций через Г. Столь подробные таблицы исключают необходимость применения специальных математических справочников и позволяют осуществлять с необходимой точностью даже наиболее строгие вычисления по геодезии, механике, электротехнике и т. п. [c.9]
Общераспространенные таблицы логарифмов ц тригонометрических функций снабжены настолько малым табличныл интервалом, что интерполирование выполняется очень легко этот процесс известен как линейное интерполирование. Такая подробная табуляция не всегда осуществима даже для часто используемых таблиц, и поэтому необходимо иметь более общие методы интерполирования, чем линейный метод, применимые в тех случаях, когда линейное интерполирование привело бы к неточным результатам. Полезно также уметь дифференцировать и интегрировать функции, выраженные в табличной форме, особенна интегрировать такие функции, которые нельзя проинтегрировать аналитически или для которых аналитическое разложение пotpeбoвaлo бы много труда. Эти три операции —интерполирование, численное дифференцирование и численное интегрирование — составляют исчисление конечных разностей. [c.121]
При.менить тот же метод, что и для эллипса (п. 237) это введет логарифмы и показательные функции вместо функций тригонометрических и им обратных. [c.370]
Обратные тригонометрические и гиперболические функции определяются так же, как и для действительного переменного. Например, w = ar sin 2, если 2 = sin гг/. Эти функции выражаются через логарифмы [c.196]
c.4
,
c.48
]
Справочник машиностроителя Том 1 Изд.2 (1956) — [
c.4
,
c.48
]
Задача C1: логарифмы и тригонометрия в одном уравнении
19 февраля 2014
Сегодня у нас будет насыщенный урок, потому что уравнение, которое мы будем сегодня разбирать, содержит в себе и логарифмическую, и тригонометрическую функцию. Но все по порядку.
Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.
На первый взгляд, задача кажется весьма нестандартной: тут и логарифмы, и тригонометрия. Но если разобраться, то окажется, что уравнения такого типа вполне под силу большинству учеников.
Решение логарифмического уравнения
Итак, нужно решить уравнение:
log5 (cos x − sin 2 x + 25) = 2
Как видим, в первую очередь перед нами логарифмическое уравнение. Вспоминаем: как мы решаем логарифмическое уравнение? Очевидно, приводим его к каноническому виду, а именно:
log a f ( x ) = log a g ( x )
В нашем случае слева уже стоит логарифм по основанию 5. Следовательно, двойку тоже нужно представить в виде логарифма по тому же самому основанию 5. Вспоминаем, как это делается. С помощью нашей замечательной формулы:
Разумеется, мы можем подставить любое число b , удовлетворяющее требованиям, которые накладываются на основание логарифма:
Иначе наш логарифм просто не имеет смысла. Но какое именно b выбрать? Очевидно, что основание логарифма по нашей канонической записи должно быть равно основанию уже имеющегося логарифма, т. е. 5. Т.е. в нашем случае запишем:
Перепишем Все уравнение с учетом этого факта:
log5 (cos x − sin 2 x + 25) = log5 25
Перед нами каноническое логарифмическое уравнение. В нем мы можем смело убрать знаки логарифма (т.е. просто приравнять аргументы логарифмов). Получим:
cos x − sin 2 x + 25 = 25
Решение тригонометрического уравнения
Перед нами тригонометрическое уравнение. Переносим 25 влево и получаем:
cos x − sin 2 x = 0
Теперь нам нужно решить обычное тригонометрическое уравнение. Все тригонометрические уравнения должны быть сведены к простейшему уравнению одного из трех видов:
Подобно тому, как в логарифмах есть каноническая запись, точно так же и в тригонометрии есть каноническая запись уравнений. Давайте еще раз посмотрим на наше уравнение:
cos x − sin 2 x = 0
Что-то канонической записью тут не пахнет. Во-первых, аргументы у наших тригонометрических функций разные. И это первая проблема. Следовательно, надо каким-то образом избавится от аргумента 2 x и свести его к х. Или, наоборот: сделать так, чтобы вместо переменной x стояло 2 x .
Еще раз: когда мы видим тригонометрическое уравнение, первое, что нам нужно — это постараться сделать так, чтобы во всех тригонометрических функциях были одинаковые аргументы: везде либо х, либо 2х. Любыми правдами и неправдами, любыми преобразованиями функций мы должны добиться того, чтобы аргументы были равными.
При решении тригонометрических уравнений сводите все функции к одному и тому же аргументу.
Формула синуса двойного угла
В данном случае все очень легко. Вспоминаем формулу синуса двойного угла:
sin 2 x = 2sin x · cos x
Подставляем это выражение в наше уравнение:
cos x − 2sin x · cos x = 0
Мы видим, что и в первом, и во втором слагаемом есть cos x . Выносим его за скобку:
cos x (1- 2sin x · 1) = 0
Кто-то скажет, что 1 в скобках писать излишне. Да, я не спорю, можно сразу записать так:
cos x (1- 2sin x ) = 0
Однако если вы только разбираетесь в тригонометрических уравнениях, то лучше использовать эту избыточность и записать ту самую единицу. Почему? Да потому что если вы не запишете 1 в конце перед скобкой, то велика вероятность, что вы забудете про единицу и в начале. В итоге у вас получится неверное выражение и, соответственно, мы получим неверный ответ.
А вот так, с дополнительной единичкой, никаких проблем не возникнет. В общем, запомните правило: если из какого-то выражения выносим переменную или функцию, вместо этой нее мы везде пишем единицу. И лишь затем, после того, как мы запишем эту конструкцию в скобках, мы можем убрать лишние единицы, если это возможно.
Рекомендую оставлять единицы на месте <<всех>> общих множителей, которые выносятся за скобку. Так вы застрахуете себя от обидных ошибок.
Разложение уравнения на множители
В нашем случае все возможно. Получим:
cos x (1- 2sin x ) = 0
Произведение равно нулю, когда хотя бы один из множителей равен нулю: либо cos x = 0, либо 1 − 2sin x = 0
Перед нами совокупность из двух простейших тригонометрических уравнений:
cos x = 0; 1 = 2sin x = 0.
Однако cos x = 0 — это уже каноническая запись вида cos x = a — именно так, как нужно для решения задачи. А вот второе уравнение — 1− 2sin x — нужно преобразовать. Предлагаю выразить отсюда sin x :
-2sin x = -1;
sin x = 1/2.
Мы получили окончательную совокупность:
cos x = 0; sin x = 1/2.
Таким образом, перед нами два канонических уравнения, которые легко решаются. Вспоминаем, что cos x = 0 — это частный случай, поэтому x = π/2 + π n , n ∈ Z .
Особенности решения тригонометрических уравнений с синусом
С другой стороны, sin x = 1/2 — это не частный, а общий случай. Кроме того, всем своим ученикам я рекомендую расписывать решения уравнений вида sin x = a через совокупность двух множеств:
sin x = a ⇒
x = arcsin a + 2π n , n ∈ Z;
x = π − arcsin a + 2π n , n ∈ Z .
Обратите внимание: в обоих вариантах периодом будет именно величина 2π, т.е. полный оборот на тригонометрическом круге! В нашем случае получим:
Итого мы получили совокупность из трех наборов корней:
Область определения логарифмов — считать или не считать?
Внимательные ученики наверняка заметят: изначально мы решали логарифмическое уравнение и, следовательно, должны учесть область определения логарифма. Потому что если где-то в уравнении встречается выражение вида log a f ( x ) = log a g ( x ), мы обязаны проверить, что f ( x ) > 0.
Почему же при решении данного уравнения мы нигде это не записали? Это же ошибка! Спокойно: в данном случае никакой ошибки нет. Требование к логарифму, чтобы аргумент был больше нуля, выполняется автоматически на следующем шаге:
cos x − sin 2 x + 25 = 25
Получается, что выражение под знаком логарифма в нашем случае должно быть равно 25. А 25 заведомо больше нуля, т. е. область определения автоматически выполняется для всех корней, которые мы получим в процессе решения уравнения.
И вообще, запомните: когда в уравнении присутствует лишь один логарифм, в аргументе которого имеется функция переменного х, можно вообще не заморачиваться с проверкой области определения, потому что эта область определения будет автоматически выполняться в процессе решения уравнения. Но это работает только для уравнений и только в том случае, если логарифм с функцией присутствует лишь в одном экземпляре на все уравнение.
Требования к области определения выполняются автоматически, если функция стоит в аргументе логарифма, а сам логарифм встречается в уравнении лишь один раз.
В нашем случае это требование выполняется, потому что мы решаем именно уравнение, а не неравенство, и логарифм с функцией в аргументе встречается только один. Собственно, исходное уравнение вообще содержит только один логарифм, поэтому считать область определения в данном случае излишне. Следовательно, мы решили уравнение — получили ответ к первой части задачи.
Отбор корней на отрезке
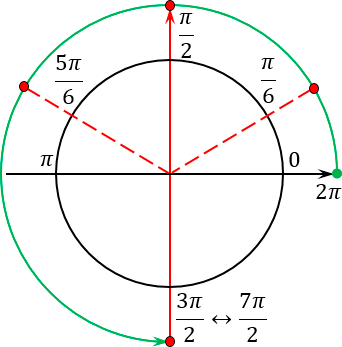
Переходим ко второй части задачи и находим корни, лежащие на заданном отрезке [2π; 7π/2]. Искать корни будем с помощью тригонометрического круга.
Первым делом обозначаем все три корня на тригонометрическом круге. Кроме того, отметим концы отрезка: 2π и 7π/2. Точка 2π совпадает с точкой началом отсчета, а в числе 7π/2 давайте выделим целую часть — по аналогии с обычными дробями:
Отметим полученное число на тригонометрическом круге. Теперь проведем лучи из начала координат в каждую точку. После этого ставим маркер в точку 2π и начинаем двигаться к точке 7π/2 против часовой стрелки. Получим:
- Самый первый корень: 2π + π/6;
- Затем — второй корень: 2π + π/2;
- Следующий корень: 2π + 5π/6;
- Наконец, последний корень совпадает с концом отрезка: 7π/2.
Особенности вычисления дробных корней
Ключевой момент в решении задачи таким методом состоит в том, каким образом мы отбираем корни. В первую очередь мы ставим маркер (ручку, карандаш или что там к вас) в самый левый конец отрезка — в нашем случае это 2π. Затем мы начинаем двигаться против часовой стрелки, т. е. в положительном направлении отсчета на тригонометрическом круге.
Первая точка, которую мы встречаем на своем пути, будет x = π/6. Чтобы записать корень, мы добавляем π/6 к началу отсчета 2π — это мы и записали. Идем дальше и прибавляем π/2. Потом, если идти еще дальше, мы попадаем точку 5π/6. И когда мы дойдем до конца, то обнаружим еще один корень — точку 7π/2.
Осталось посчитать те три корня из четырех, которые мы записали в виде выражения, потому что оставлять их в таком нерассчитанном виде нехорошо. Давайте посчитаем:
С последним корнем 7π/2 никаких дополнительных преобразований проводить не нужно — он уже рассчитан. Итого при отборе корней из всего бесконечного множества, разделенного на три набора, которые мы получили при решении нашего уравнения, остались лишь четыре конкретных корня:
Заключительные выкладки
Вот и все — задача решена. Как ни странно, решение получилось довольно простым, хотя изначально уравнение выглядело весьма угрожающе: в нем есть и логарифм, и тригонометрические функции. А получилось, что любой среднестатистический ученик вполне в состоянии справится с такими уравнениями.
И это правда. Достаточно помнить два простых факта:
- Логарифмические уравнения мы всегда стараемся привести к каноническому виду: log_a f(x) = log_a g(x) — основания должны быть одинаковыми.
- Тригонометрические уравнения тоже сводятся к каноническому виду. Точнее, к одной из трех моделей: sin x = a; cos x = a; tg x = a.
Однако нашем случае на пути к каноническому виду есть одна заминка. Дело в том, что в одной из функций, а именно sin 2 x , присутствует аргумент 2 x , в то время как в cos x есть только переменная х. Следовательно, придется вспомнить формулу двойного угла: sin 2 x = 2sin x · cos x — и уже на основании этой формулы наше исходное уравнение легко раскладывается на множители, откуда возникают канонические уравнения.
В общем, все, что требуется для решения уравнений подобного вида — это научиться работать с логарифмами, выучить несколько тригонометрических формул (особенно это касается формул синуса и косинуса двойного угла) и, конечно, не бояться преобразовать наше уравнение для того, чтобы получить красивые и легко решаемые конструкции.
Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем
-
Опубликовано 16.09.2020Подготовка к ЕГЭ
Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем
На сегодняшний день ЕГЭ по математике проходит в форме решения заданий, содержащихся в контрольно-измерительных материалах, при этом, ответы на задания выносят на отдельный бланк.
Уравнения могут быть следующих видов:
В данной статье рассмотрена профильная математика, а именно раздел по видам и системам рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений.
При решении уравнений нужно помнить основные термины:
— Корнем уравнения называют неизвестное число, которое нужно найти;
— Решение уравнения предполагает нахождение его корня;
— Уравнения, у которых совпадают решения называют равносильными;
— ОДЗ – область допустимых значений;
— Если возможно заменить переменные, то нужно это выполнить;
— После решения уравнения необходимо провести проверку на правильность нахождения корня.
Итак, рассмотрим каждый вид уравнений по отдельности, включая примеры решения.
- Рациональные уравнения – уравнения, у которых, как правило, слева расположено рациональное выражение, а справа – ноль.
Рациональным уравнением называют уравнение вида r(х)=0.
Если обе части уравнения являются рациональными выражениями, то рациональные уравнения называют целыми.
Дробно-рациональным называют уравнение, которое содержит дробное выражение.
Порядок действий при решении данного вида уравнения должен быть следующий:
— Все члены должны быть переведены в левую часть уравнения;
— Данную часть уравнения нужно представить в виде дроби p(x)/q(x);
— Для полученного решения нужно провести проверку, то есть.
При решение этого рационального уравнения понадобится формула (а-в)2=а2-2ав+в2.
Рассмотрим ещё один пример решения рационального уравнения:
На основе примеров показано, что рациональные уравнения могут быть с разным количеством переменных.
Иррациональными уравнениями считают уравнения с переменной под корнем. Для того, чтобы определить является ли уравнение иррациональным нужно просто посмотреть на корень переменной. Следует учитывать, что в некоторых учебниках по математике иррациональное уравнение определяют другим способом.
Способы решения таких уравнений:
— Возвести в степень обе части уравнения;
— Ввести новые переменные;
Пример решения уравнения по первому способу:
Пример решения по второму способу:
- Показательные уравнения
Показательные уравнения – уравнение, содержащее неизвестный показатель.
В учебниках по математике разных авторов определение показательного уравнения может отличаться. Обычно такие отличия касаются незначительных деталей.
Как правило, это уравнения вида af(x)=ag(x), где а не равно одному и число а больше нуля. Из этого следует, что f(x)=g(x).
— Уравнение с одним основанием;
— Уравнение с равными основаниями.
Существует следующие способы решения таких уравнений:
— Использовать метод логарифмов;
— Привести уравнение к квадратному виду;
— Вынести за скобку общий множитель;
— Ввести новую переменную.
Итак, как решить показательное уравнение? Любое по сложности уравнение нужно привести в простую форму.
Рассмотрим наиболее простой пример решения показательного уравнения:
Для решения данного уравнения следует 2 возвести во вторую степень.
Решение даже простейших показательных уравнений имеет большую значимость. Поэтому далее вам будет легче решать уравнения более сложного уровня.
Данная тема является одной из самых сложных, поэтому следует внимательно подойти к изучению данной темы. Известны три формулы тригонометрических уравнений, запомнить которые не составляет особой сложности.
Наиболее простое тригонометрическое уравнение имеет вид sin x=a, cos x=a, tg x=а, а – число действительное.
Способы решения таких уравнений:
— Решение с помощью форму и приведение к простейшему;
— Ввод других переменных;
— Разложить уравнение по множителям.
Пример решения тригонометрического уравнения:
Здесь нужно рисовать окружность, далее выделить точки с координатой ½, соответственно, это точки 5п/6 и п/6. Если пройти по окружности, исходя из данных точек, то х=п/6+2пk, x=5п/6+2пn. При этом синус и косинус принадлежат промежутку [-1;1]. Если при решении уравнения в его правой части стоит число не принадлежащее промежутку, считается, что уравнение не имеет решения.
Также рассмотрим пример решения уравнения, разложив его по множителям.
Нужно применить формулу sin2x = 2sinxcosx.
2sinxcosx – sinx = 0.
sinx (2cosx – 1) = 0.
Таким образом, если один из множителей равен нулю, то решение уравнения также равно нулю.
Далее, sinx=0, x=пk.
- Логарифмические уравнения
Особое значение имеет подготовка ЕГЭ по математике логарифмы, это обусловлено тем, что в КИМах чаще всего встречаются именно этого вида уравнения.
Логарифмическое уравнение – это уравнение с неизвестной величиной, находящейся внутри логарифма.
Примерами логарифмических уравнений являются уравнения следующего вида:
Способы решения уравнений данного вида:
— Применять способ уравнивания к единице;
— Применять способ умножать на единицу;
— Применять доступные правила логарифмов;
— Введение другого основания;
— Возвести в степень.
Самым простым логарифмическим уравнением принято считать уравнение вида log a x = b, при этом основание a>0,a≠1.
Пример решения уравнения:
Сначала следует найти значение области, то есть ОДЗ. При этом нужно помнить, что под логарифмом выражение всегда положительное. Воспользуемся логарифмическим определением, представим х степью основания 2 логарифма, степень будет равна 3.
Решение уравнения является ОДЗ, то есть корень уравнения найден.
Таким образом, подобное задание ЕГЭ по математике легко можно решить, зная логарифмы и способы их решения.
Оставить Комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Выбери тему
Самые популярные записи
Наука. Основные особенности научного мышления. Естественные и социально гуманитарные науки (3 293)
ЕГЭ по обществознанию: мышление и деятельность; потребности и интересы (2 238)
Строение растения. Стебель, лист и цветок. (2 196)
Свобода и необходимость в человеческой деятельности. Свобода и ответственность. (2 189)
StudyWay
Помощь
© 2021 StudyWay. Все права защищены.
Ты можешь попробовать 3 наших закрытых занятия из курса «Прорыв».
Записаться можно через Instagram
Для этого напиши в Direct (в личку) кодовое слово «Пробный«
Что за курс и что тебя там будет ждать?
12 мощнейших онлайн занятий по 2 часа в формате вебинаров.
Содержание вебинара: повторение предыдущей темы, теория, перерыв и практика.
Воркбук (рабочая тетрадь)абсолютно к каждому уроку со всей необходимой теорией к этой теме и практикой.
Личный куратор — это твой помощник во всех учебных вопросах.
Они занимаются проверкой твоих домашних заданий, поддерживают и мотивируют двигаться дальше, даже когда хочется сдаться.
На собственной онлайн платформе тебя ждут
Домашние задания, которые необходимо решать после каждого занятия.
Все задания построены на базе создателей ЕГЭ — Котова / Лискова.
К каждому тестовому вопросу будет подробный разбор от главного куратора.
А задания, где необходимо оценить ответ (вторая часть) — будет проверять твой личный куратор и писать подробный комментарий про ошибки
Общий чат единомышленников, поделенный на команды.
Название даете совместно (например «Воробушки»)
Ты будешь двигаться сообща с однокурсниками, поддерживая и мотивируя друг друга.
За лучшую командную успеваемость всей команде будут выделены призы в конце каждого месяца (скидка на обучение, стикерпаки и т.д).
Личный помощник — это твой верный друг и помощник, который поможет тебе со всеми техническими вопросами, ответит на вопросы про поступление, да и просто может обсудить какие-то личные вопросы, поделиться переживаниями.
Доступ к уникальной «Академии косатиков».
Там ты сможешь найти:
Банк теории, банк планов, банк аргументов, курсы по работе со всей второй частью, термины, курсы по саморазвитию, полезные лайфхаки и всю подробную информация о ЕГЭ.
Игровая система на нашей платформе StudyWay👇
За выполнение заданий получаешь баллы (XP).
При достижении нового уровня у тебя открываются новые персонажи из Marvel, DC Comics, Игра престолов и Star Wars, а также на каждом новом уровне тебя ждут призы от нашей школы.

Основная ценность курса
1. Изучение теории и практики с учетом изменений в ЕГЭ 2022
2. Заложение фундамента и основы предмета
3. Прохождение всей теории для первой части
4. Нарешивание всех возможных типов заданий
5. Повышение результата с 0 до 60 баллов
Отличия тарифа «Стандарт от «Профи».
Дополнительные домашние задания
необходимо выполнять. Это значительно повысит твою успеваемость и улучшит показатели.
Дополнительное объяснение
твой личный куратор объяснит тебе тему повторно, если останется что-то не понятным
Групповые зачеты
у тебя будут зачеты с твоим личным куратором в мини группах по 5 человек. Там спрашиваются пройденные темы, термины и так далее.
Карта памяти
будешь восполнять все пройденные в удобной интеллект карте и в конце учебы у тебя выйдет файл с полноценной теорией по всем темам и разделам.
Персональный звонок куратору
1 раз в месяц ты можешь позвонить своему куратору и обсудить все волнующие тебя вопросы в течении 20 минут.
Секретный квест
1 раз в месяц ты будешь созваниваться с другим учеником курса и проводить совместные зачеты, тем самым познакомишься с новыми ребятами из других городов, уберешь страхи знакомства, повторишь и закрепишь пройденные темы.
Задание №12. Уравнения — профильный ЕГЭ по математике
Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка . От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка От нее и отсчитываем.
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых 
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или . Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
[spoiler title=”источники:”]
http://thestudyway.com/education_ege/logarifmicheskie_trigonometricheskie_sistemy/
http://ege-study.ru/ru/ege/materialy/matematika/zadanie-12-profilnogo-ege-po-matematike-uravneniya/
[/spoiler]
19 февраля 2014
Сегодня у нас будет насыщенный урок, потому что уравнение, которое мы будем сегодня разбирать, содержит в себе и логарифмическую, и тригонометрическую функцию. Но все по порядку.
Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.

На первый взгляд, задача кажется весьма нестандартной: тут и логарифмы, и тригонометрия. Но если разобраться, то окажется, что уравнения такого типа вполне под силу большинству учеников.
Решение логарифмического уравнения
Итак, нужно решить уравнение:
log5 (cos x − sin 2x + 25) = 2
Как видим, в первую очередь перед нами логарифмическое уравнение. Вспоминаем: как мы решаем логарифмическое уравнение? Очевидно, приводим его к каноническому виду, а именно:
loga f (x) = loga g(x)
В нашем случае слева уже стоит логарифм по основанию 5. Следовательно, двойку тоже нужно представить в виде логарифма по тому же самому основанию 5. Вспоминаем, как это делается. С помощью нашей замечательной формулы:
a = logb ba
Разумеется, мы можем подставить любое число b, удовлетворяющее требованиям, которые накладываются на основание логарифма:
0 < b ≠ 1
Иначе наш логарифм просто не имеет смысла. Но какое именно b выбрать? Очевидно, что основание логарифма по нашей канонической записи должно быть равно основанию уже имеющегося логарифма, т. е. 5. Т.е. в нашем случае запишем:
2 = log5 52 = log5 25
Перепишем Все уравнение с учетом этого факта:
log5 (cos x − sin 2x + 25) = log5 25
Перед нами каноническое логарифмическое уравнение. В нем мы можем смело убрать знаки логарифма (т.е. просто приравнять аргументы логарифмов). Получим:
cos x − sin 2x + 25 = 25
Идем дальше.
Решение тригонометрического уравнения
Перед нами тригонометрическое уравнение. Переносим 25 влево и получаем:
cos x − sin 2x = 0
Теперь нам нужно решить обычное тригонометрическое уравнение. Все тригонометрические уравнения должны быть сведены к простейшему уравнению одного из трех видов:
- sin x = a;
- cos x = a;
- tg x = a.
Подобно тому, как в логарифмах есть каноническая запись, точно так же и в тригонометрии есть каноническая запись уравнений. Давайте еще раз посмотрим на наше уравнение:
cos x − sin 2x = 0
Что-то канонической записью тут не пахнет. Во-первых, аргументы у наших тригонометрических функций разные. И это первая проблема. Следовательно, надо каким-то образом избавится от аргумента 2x и свести его к х. Или, наоборот: сделать так, чтобы вместо переменной x стояло 2x.
Еще раз: когда мы видим тригонометрическое уравнение, первое, что нам нужно — это постараться сделать так, чтобы во всех тригонометрических функциях были одинаковые аргументы: везде либо х, либо 2х. Любыми правдами и неправдами, любыми преобразованиями функций мы должны добиться того, чтобы аргументы были равными.
При решении тригонометрических уравнений сводите все функции к одному и тому же аргументу.
Формула синуса двойного угла
В данном случае все очень легко. Вспоминаем формулу синуса двойного угла:
sin 2x = 2sin x · cos x
Подставляем это выражение в наше уравнение:
cos x − 2sin x · cos x = 0
Мы видим, что и в первом, и во втором слагаемом есть cos x. Выносим его за скобку:
cos x (1- 2sin x · 1) = 0
Кто-то скажет, что 1 в скобках писать излишне. Да, я не спорю, можно сразу записать так:
cos x (1- 2sin x) = 0
Однако если вы только разбираетесь в тригонометрических уравнениях, то лучше использовать эту избыточность и записать ту самую единицу. Почему? Да потому что если вы не запишете 1 в конце перед скобкой, то велика вероятность, что вы забудете про единицу и в начале. В итоге у вас получится неверное выражение и, соответственно, мы получим неверный ответ.
А вот так, с дополнительной единичкой, никаких проблем не возникнет. В общем, запомните правило: если из какого-то выражения выносим переменную или функцию, вместо этой нее мы везде пишем единицу. И лишь затем, после того, как мы запишем эту конструкцию в скобках, мы можем убрать лишние единицы, если это возможно.
Рекомендую оставлять единицы на месте {{всех}} общих множителей, которые выносятся за скобку. Так вы застрахуете себя от обидных ошибок.
Разложение уравнения на множители
В нашем случае все возможно. Получим:
cos x (1- 2sin x) = 0
Произведение равно нулю, когда хотя бы один из множителей равен нулю: либо cos x = 0, либо 1 − 2sin x = 0
Перед нами совокупность из двух простейших тригонометрических уравнений:
cos x = 0; 1 = 2sin x = 0.
Однако cos x = 0 — это уже каноническая запись вида cos x = a — именно так, как нужно для решения задачи. А вот второе уравнение — 1− 2sin x — нужно преобразовать. Предлагаю выразить отсюда sin x:
-2sin x = -1;
sin x = 1/2.
Мы получили окончательную совокупность:
cos x = 0; sin x = 1/2.
Таким образом, перед нами два канонических уравнения, которые легко решаются. Вспоминаем, что cos x = 0 — это частный случай, поэтому x = π/2 + πn, n ∈ Z.
Особенности решения тригонометрических уравнений с синусом
С другой стороны, sin x = 1/2 — это не частный, а общий случай. Кроме того, всем своим ученикам я рекомендую расписывать решения уравнений вида sin x = a через совокупность двух множеств:
sin x = a ⇒
x = arcsin a + 2πn, n ∈ Z;
x = π − arcsin a + 2πn, n ∈ Z.
Обратите внимание: в обоих вариантах периодом будет именно величина 2π, т.е. полный оборот на тригонометрическом круге! В нашем случае получим:
Итого мы получили совокупность из трех наборов корней:
Область определения логарифмов — считать или не считать?
Внимательные ученики наверняка заметят: изначально мы решали логарифмическое уравнение и, следовательно, должны учесть область определения логарифма. Потому что если где-то в уравнении встречается выражение вида loga f (x) = loga g(x), мы обязаны проверить, что f (x) > 0.
Почему же при решении данного уравнения мы нигде это не записали? Это же ошибка! Спокойно: в данном случае никакой ошибки нет. Требование к логарифму, чтобы аргумент был больше нуля, выполняется автоматически на следующем шаге:
cos x − sin 2x + 25 = 25
Получается, что выражение под знаком логарифма в нашем случае должно быть равно 25. А 25 заведомо больше нуля, т. е. область определения автоматически выполняется для всех корней, которые мы получим в процессе решения уравнения.
И вообще, запомните: когда в уравнении присутствует лишь один логарифм, в аргументе которого имеется функция переменного х, можно вообще не заморачиваться с проверкой области определения, потому что эта область определения будет автоматически выполняться в процессе решения уравнения. Но это работает только для уравнений и только в том случае, если логарифм с функцией присутствует лишь в одном экземпляре на все уравнение.
Требования к области определения выполняются автоматически, если функция стоит в аргументе логарифма, а сам логарифм встречается в уравнении лишь один раз.
В нашем случае это требование выполняется, потому что мы решаем именно уравнение, а не неравенство, и логарифм с функцией в аргументе встречается только один. Собственно, исходное уравнение вообще содержит только один логарифм, поэтому считать область определения в данном случае излишне. Следовательно, мы решили уравнение — получили ответ к первой части задачи.
Отбор корней на отрезке
Переходим ко второй части задачи и находим корни, лежащие на заданном отрезке [2π; 7π/2]. Искать корни будем с помощью тригонометрического круга.
Первым делом обозначаем все три корня на тригонометрическом круге. Кроме того, отметим концы отрезка: 2π и 7π/2. Точка 2π совпадает с точкой началом отсчета, а в числе 7π/2 давайте выделим целую часть — по аналогии с обычными дробями:
Отметим полученное число на тригонометрическом круге. Теперь проведем лучи из начала координат в каждую точку. После этого ставим маркер в точку 2π и начинаем двигаться к точке 7π/2 против часовой стрелки. Получим:
Выписываем корни:
- Самый первый корень: 2π + π/6;
- Затем — второй корень: 2π + π/2;
- Следующий корень: 2π + 5π/6;
- Наконец, последний корень совпадает с концом отрезка: 7π/2.
Особенности вычисления дробных корней
Ключевой момент в решении задачи таким методом состоит в том, каким образом мы отбираем корни. В первую очередь мы ставим маркер (ручку, карандаш или что там к вас) в самый левый конец отрезка — в нашем случае это 2π. Затем мы начинаем двигаться против часовой стрелки, т. е. в положительном направлении отсчета на тригонометрическом круге.
Первая точка, которую мы встречаем на своем пути, будет x = π/6. Чтобы записать корень, мы добавляем π/6 к началу отсчета 2π — это мы и записали. Идем дальше и прибавляем π/2. Потом, если идти еще дальше, мы попадаем точку 5π/6. И когда мы дойдем до конца, то обнаружим еще один корень — точку 7π/2.
Осталось посчитать те три корня из четырех, которые мы записали в виде выражения, потому что оставлять их в таком нерассчитанном виде нехорошо. Давайте посчитаем:
С последним корнем 7π/2 никаких дополнительных преобразований проводить не нужно — он уже рассчитан. Итого при отборе корней из всего бесконечного множества, разделенного на три набора, которые мы получили при решении нашего уравнения, остались лишь четыре конкретных корня:
Заключительные выкладки
Вот и все — задача решена. Как ни странно, решение получилось довольно простым, хотя изначально уравнение выглядело весьма угрожающе: в нем есть и логарифм, и тригонометрические функции. А получилось, что любой среднестатистический ученик вполне в состоянии справится с такими уравнениями.
И это правда. Достаточно помнить два простых факта:
- Логарифмические уравнения мы всегда стараемся привести к каноническому виду: log_a f(x) = log_a g(x) — основания должны быть одинаковыми.
- Тригонометрические уравнения тоже сводятся к каноническому виду. Точнее, к одной из трех моделей: sin x = a; cos x = a; tg x = a.
Однако нашем случае на пути к каноническому виду есть одна заминка. Дело в том, что в одной из функций, а именно sin 2x, присутствует аргумент 2x, в то время как в cos x есть только переменная х. Следовательно, придется вспомнить формулу двойного угла: sin 2x = 2sin x · cos x — и уже на основании этой формулы наше исходное уравнение легко раскладывается на множители, откуда возникают канонические уравнения.
В общем, все, что требуется для решения уравнений подобного вида — это научиться работать с логарифмами, выучить несколько тригонометрических формул (особенно это касается формул синуса и косинуса двойного угла) и, конечно, не бояться преобразовать наше уравнение для того, чтобы получить красивые и легко решаемые конструкции.
Смотрите также:
- Вебинар по заданию 13: тригонометрия
- Логарифмические уравнения в задаче C1
- Что такое числовая дробь
- Правила комбинаторики в задаче B6
- Сложные задачи на проценты
- Задача C1: тригонометрические уравнения и формула двойного угла