Алгебра высказываний
Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно. В алгебре простым высказываниям ставятся в соответствии логические переменные (А, В, С и т.д.)
Логическая переменная – это простое высказывание.
Логические переменные обозначаются прописными и строчными латинскими буквами (a-z, A-Z) и могут принимать всего два значения – 1, если высказывание истинно, или 0, если высказывание ложно.
Пример высказываний:
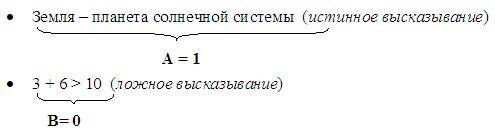
Логическая функция – это сложное высказывание, которое получается в результате проведения логических операций над простыми высказываниями.
Для образования сложных высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
Например,
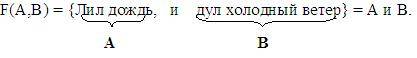
Многие люди не любят сырую погоду.
Пусть А = «Многие люди любят сырую погоду». Получаем логическую функцию F(A) = не А.
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
Логическая формула (логическое выражение) — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА (1) или ЛОЖЬ (0).
Значение логической функции зависит от значений входящих в нее логических переменных. Поэтому значение логической функции можно определить с помощью специальной таблицы (таблицы истинности), в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.
Основные (базовые) логические операции:
1. Логическое умножение (конъюнкция), от лат. konjunctio – связываю:
• Объединение двух (или нескольких) высказываний в одно с помощью союза И;
• в языках программирования — And.
• Принятые обозначения: / , •, и, and.
• В алгебре множеств конъюнкции соответствует операция пересечения множеств.
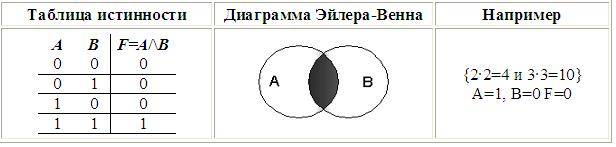
Конъюнкция истинна тогда и только тогда, все, входящие в нее высказывания истинны.
Пример:
Рассмотрим составное высказывание «2 • 2 = 4 и 3 • 3 = 10». Выделим простые высказывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «3 • 3 = 10» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A / B = 1 / 0 = 0 (в соответствии с таблицей истинности), то есть данное составное высказывание ложное.
2. Логическое сложение (дизъюнкция), от лат. disjunctio – различаю:
• Объединение двух (или нескольких) высказываний в одно с помощью союза ИЛИ;
• в языках программирования — Or.
• Обозначение: /, +, или, or.
• В алгебре множеств дизъюнкции соответствует операция объединения множеств.
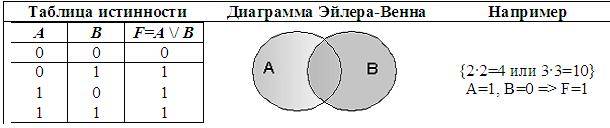
Дизъюнкция ложна тогда и только тогда, все, входящие в нее высказывания ложны.
Пример:
Рассмотрим составное высказывание «2 • 2 = 4 или 2 • 2 = 5». Выделим простые выска-зывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «2 • 2 = 5» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A / B = 1 / 0 = 1 (в соответствии с таблицей истинности), то есть данное составное высказывание истинно.
3. Отрицание (инверсия), от лат. InVersion – переворачиваю:
• Соответствует частице НЕ, словосочетаниям НЕВЕРНО, ЧТО или НЕ ЯВЛЯЕТСЯ ИСТИНОЙ, ЧТО;
• в языках программирования — Not;
• Обозначение: не А, ¬А, not
• В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества.
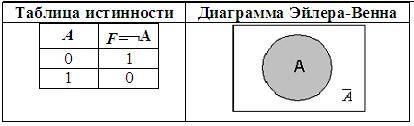
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
Пример:
А = {два умножить на два равно четырем} = 1.
¬A= {Неверно, что два умножить на два равно четырем}= 0.
Рассмотрим высказывание А : «Луна — спутник Земли«; тогда ¬А будет формулироваться так: «Луна — не спутник Земли«.
Рассмотрим высказывание: «Неверно, что 4 делится на 3». Обозначим через А простое высказывание «4 делится на 3». Тогда логическая форма отрицания этого высказывания имеет вид ¬А
Приоритет логических операций:
Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:
1. инверсия;
2. конъюнкция;
3. дизъюнкция;
Для изменения указанного порядка выполнения логических операций используются круглые скобки.
Составные логические выражения алгебры высказываний называют формулами.
Истинно или ложно значение формулы можно определить законами алгебры логики, не обращаясь к смыслу:
F = (0 / 1) / (¬0 / ¬1) = (0 / 1) / (1 / 0) =1 / 1=1 — истина
F = (¬0 / ¬1) / (¬1 / ¬1) = (1 / 0) / (0 / 0) = 0 / 0 = 0 — ложь
В зависимости от
характера логической связки все простые
высказывания могут быть либо
утвердительными, либо отрицательными.
Изменение логической связки с
утвердительной на отрицательную или
наоборот изменяет качество высказывания.
По местности
логического сказуемого все простые
высказывания можно разделить на
атрибутивные и реляционные.
Простые высказывания,
в которых логическое сказуемое выражает
свойство, называют атрибутивными. «Два
является простым числом»
Простые высказывания,
в которых логическое сказуемое выражает
отношение, называют реляционными. «Три
больше двух»
Условные обозначения
для логических и нелогических терминов
позволяют выявить логическую форму
атрибутивных высказываний.
Логические
термины:
-
Есть-символ
утвердительной логической связки -
Не
есть- символ отрицательной логической
связки -
Всякий-
символ квантора общности -
Некоторый-
символ квантора существования
Нелогические
термины:
-
a,
b,
c-
символы для логических подлежащих
единичных высказываний. -
S,
S1
и т.д.- символы для логических подлежащих. -
P,
P1
и т.д.- символы для логических сказуемых
множественных атрибутивных высказываний.
Правило выявления
логической формы- Термины, имеющие
однотипные значения, обозначаются
символами одного вида.
Логическая форма
множественных высказываний может быть
записана следующим образом:
Всякий S
есть P-
SaP; Некоторые
S
есть P-
SiP;
Всякий S
не есть P-
SeP;
Некоторые S
не есть P-
SoP.
Условие истинности
атрибутивного единичного высказывания
совпадает с условием ложности атрибутивного
единичного отрицательного высказывания,
а условие ложности атрибутивного
единичного утвердительного высказывания
совпадает с условием истинности
атрибутивного единичного отрицательного
высказывания.
Истинность
произвольного множественного высказывания
зависит от отношения между значениями
входящих в него терминов. В этом сходство
условий истинности единичных и
множественных высказываний.
Условия истинности
множественных высказываний могут быть
обобщены в таблице истинности.
8. Отношения между атрибутивными высказываниями
По своему содержанию
атрибутивные суждения могут находиться
в двух важнейших отношениях – сравнимости
и несравнимости.
Несравнимые
суждения. У
них разные субъекты или предикаты или
то и другое вместе. В подобных случаях
истинность или ложность одного из
суждений непосредственно не зависит
от истинности или ложности другого. Она
прямо определяется отношением к
действительности – соответствием или
несоответствием ей. Очевидна лишь их
относительная самостоятельность и
независимость с точки зрения истинности
или ложности.
Сравнимые суждения.
Они, наоборот, имеют одинаковые термины
– и субъект, и предикат, но могут
различаться по количеству и качеству.
Эти суждения сопоставимы по истинности
и ложности.
По своей логической
форме – прежде всего по количеству и
качеству – сравнимые суждения
подразделяются на совместимые и
несовместимые.
Совместимые
суждения
содержат одну и ту же мысль полностью
или частично. Между ними возникают
следующие логические отношения:
эквивалентности, подчинения, частичной
совместимости.
Эквивалентность
(равнозначность)
– это отношение между суждениями, у
которых субъект и предикат выражены
одни и теми же или равнозначными понятиями
“Все адвокаты юристы”
Последующие
отношения между простыми атрибутивными
суждениями – А, Е, I,
O
– для наглядности изображают графически
в виде логического квадрата.
Его вершины
символизируют простые категорические
суждения – A,
E,
I,
O;
стороны и диагонали отношения между
суждениями.
Подчинение
– это отношение между такими суждениями,
у которых количество различно, а качество
одно и то же. При подчинении действуют
следующие закономерности:
а) из истинности
подчиняющего (А или Е) следует истинность
подчиненного (соответственно I
или O),
но не наоборот;
б) из ложности
подчиненного (I
или O)
следует ложность подчиняющего
(соответственно А или Е), но не наоборот.
Примеры. Если
истинно А, что “Все адвокаты – юристы”,
то тем более истинно, что “По крайней
мере, некоторые адвокаты – юристы”. Но
если истинно, что “Некоторые свидетели
правдивы”, то отсюда еще не следует,
что истинно А: “Все свидетели правдивы”.
В данном случае это ложное суждение.
Частичная
совместимость–
это отношение между суждениями одинакового
количества, но разного качества: между
частноутвердительными (I)
и частноотрицательными (О) суждениями.
Для нее характерна следующая закономерность:
оба суждения могут быть одновременно
истинными, но не могут быть одновременно
ложными. Из ложности одного из них
следует истинность другого, но не
наоборот.
Несовместимые
суждения.
Они имеют следующие логические отношения:
противоположности и противоречия.
Противоположность
– это отношение между общеутвердительными
(А) и общеотрицательными (Е) суждениями.
Оба таких суждения не могут быть
одновременно истинными, но могут быть
одновременно ложными. Из истинности
одного непременно следует ложность
другого, но не наоборот.
Противоречие –
отношение между такими суждениями, как
общеутвердительное (А) и частноотрицательное
(О), общеотрицательное (Е) и частноутвердительное
(I).
Им присущи следующие закономерности:
они не могут быть одновременно истинными
и не могут быть одновременно ложными.
Из истинности одного непременно следует
ложность другого и наоборот.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 февраля 2022 года; проверки требует 1 правка.
У этого термина существуют и другие значения, см. Высказывание.
Выска́зывание в математической логике — предложение, выражающее суждение. Если суждение, составляющее содержание (смысл) некоторого высказывания, истинно, то и о данном высказывании говорят, что оно истинно. Сходным образом ложным называют такое высказывание, которое является выражением ложного суждения. Истинность и ложность называются логическими, или истинностными, значениями высказываний[1].
Высказывание должно быть повествовательным предложением, и противопоставляется повелительным, вопросительным и любым другим предложениям, оценка истинности или ложности которых невозможна[2].
Высказывание и суждение[править | править код]
Одно и то же суждение может быть выражено в разных языках и в разных знаковых формах в пределах одного языка. Когда суждение рассматривается в связи с какой-то конкретной формой его языкового выражения, оно называется высказыванием. Термин «суждение» употребляют, когда отвлекаются от того, какова именно его знаковая форма[3].
В современной математической логике ещё не установилось однозначное определение понятия “высказывание”, что позволяют некоторые логики иногда заменяя его термином “суждение”[что?]. Здесь высказывание нельзя отождествлять с суждением, которое, также обладает свойством выражать либо истину, либо ложь. Однако, в отличие от высказывания, которое в первом разделе математической логики – исчислении высказываний, рассматривается как нерасчленённое целое, суждение является абсолютным единством субъекта и объекта, которые связаны между собой по смыслу. Помимо истинностного значения суждение несёт в себе некоторое содержание, которое может быть выражено в утверждении или отрицании чего-либо относительно предметов и явлений, их свойств, связей и отношений. Различаются высказывания и суждения также символической записью их формул. Простое высказывание всегда обозначается простым знаком А или В и др. Простое категорическое суждение имеет выражение вида: «S есть (не есть) P».
Различаются и формулы сложных высказываний и сложных суждений. Так импликативное высказывание, в котором два простых высказывания, связанные союзом, «если…, то…», выражаются в логике высказываний формулой «А 
Виды высказываний[править | править код]
Логические высказывания принято подразделять на составные (или сложные) и элементарные. Составные логические высказывания — высказывания, содержащие логические постоянные. Составные высказывания строятся на основе других высказываний. Логическое значение сложного высказывания определяется логическим значением входящих в его состав высказываний и теми логическими постоянными, с помощью которых оно построено[1].
Элементарные логические высказывания — это высказывания, не относящиеся к составным. Примером элементарного высказывания может служить 


Логические постоянные[править | править код]
Логическая постоянная (логическая константа[4], логическая операция[2]) — название термина, сохраняющего одно и то же значение во всех высказываниях и не зависящего от конкретного содержания высказывания. Логические постоянные используются для соединения простых высказываний в сложные[5]. Логические постоянные делятся на кванторы и логические союзы (связки). Слова: не; неверно, что; и; или; если…, то; тогда и только тогда, когда; либо…, либо; несовместно; ни…, ни; не…, но; но и их ближайшие синонимы являются логическими связками, слова для всех…имеет место, что; для некоторых…имеет место, что и их ближайшие синонимы являются кванторами. Логические постоянные служат как для выражения мыслей в повседневных рассуждениях, так и в научных доказательствах[1].
В математической логике логические постоянные обозначаются следующими символами:[5]
— логические постоянные все, для всех…имеет место, что (квантор общности);
— логические постоянные существует такой, что…, для некоторых…имеет место, что (квантор существования);
,
— союз и (конъюнкция);
— союз или, когда он выступает в соединительно-разделительном значении (дизъюнкция);
,
— союз или, когда он выступает в строго-разделительном исключающем значении (строгая дизъюнкция);
,
— союз если…, то (импликация);
— слова не, неверно (отрицание).
Логические союзы являются частью языка логики высказываний, кванторы были дополнительно введены в язык логики предикатов, который является расширением языка логики высказываний[6].
Логическое подлежащее и логическое сказуемое[править | править код]
Логическое подлежащее — то, о чём говорится в предложении (высказывании)[7], то, к чему относятся содержащиеся в предложениях утверждения или отрицания[8]. Логическое сказуемое — содержащаяся в предложении (высказывании) информация о логическом подлежащем[9].
Роль логических подлежащих играют простые и сложные имена, роль логических сказуемых — предикаторы (или предикаты[10]). К последним относятся свойства и отношения[8]. Предикаторы выполняют роль предметно-истинностного отображения, давая предметам определённого класса оценку «истина» или «ложь». При этом свойства являются одноместными предикаторами, характеризуя один отдельный предмет, а отношения — многоместными, характеризуя пару, тройку и т. д. предметов[10][11]. Само высказывание в случае с многоместным предикатором содержит несколько логических подлежащих[12].
Формы высказываний[править | править код]
В логике предикатов высказывательной формой (формой высказывания, предикатом[8]) называется неполное логическое высказывание, в котором один из объектов заменён предметной переменной. При подстановке вместо такой переменной какого-либо значения высказывательная форма превращается в высказывание[1]. В качестве предметных переменных в естественном языке выступают общие имена, представляющие классы предметов и заменяемые в формализованных языках специальными символами. Форма сходна с высказыванием, однако она не истинна и не ложна (неопределенно-истинна), поскольку неизвестно, к чему относится утверждение или отрицание[8].
Форма высказывания требует дополнения, относится ли утверждение или отрицание в суждении ко всем или не ко всем предметам того класса, который представляет данное общее имя. Функцию таких указателей выполняют явно выраженные или подразумеваемые кванторы. Нельзя оценивать как истинное или ложное такую высказывательную форму, как Человек — справедлив. Приведённая фраза аналогична выражению y — справедлив. Из указанной формы можно получить высказывание, заменив общее имя единичным: Иванов — справедлив, или введя кванторы: Некоторые люди справедливы. Высказывания, использующие кванторы, выражают множественные — общие и частные — суждения[8].
См. также[править | править код]
- Суждение
- Логическая операция
- Квантор
- Логика высказываний
- Логика предикатов
- Алгебра логики
Примечания[править | править код]
- ↑ 1 2 3 4 5 Чупахин, Бродский, 1977, с. 200—203.
- ↑ 1 2 БСЭ, 1971.
- ↑ Войшвилло, Дегтярёв, 2001, с. 22.
- ↑ Кондаков, 1975, с. 301.
- ↑ 1 2 Кондаков, 1975, с. 307.
- ↑ Бродский, 1972, с. 56.
- ↑ Розенталь, 1976, статья «Логическое подлежащее».
- ↑ 1 2 3 4 5 Войшвилло, Дегтярёв, 2001, с. 58—66.
- ↑ Розенталь, 1976, статья «Логическое сказуемое».
- ↑ 1 2 Бродский, 1972, с. 54.
- ↑ НФЭ, 2010, статья «Логика предикатов».
- ↑ Войшвилло, Дегтярёв, 2001, с. 68.
Литература[править | править код]
- Бродский И. Н. Элементарное введение в символическую логику. — Издательство Ленинградского университета, 1972. — 63 с.
- Розенталь Д. Э., Теленкова М. А. Словарь-справочник лингвистических терминов. — 2-ое изд. — М.: Просвещение, 1976.
- Высказывание // Вешин — Газли. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
- Кондаков Н.И. Логический словарь. — 2-е изд. — М.: Наука, 1975. — 721 с.
- Чупахин И.Я.,Бродский И.Н. Формальная логика. — Ленинград: Издательство Ленинградского университета, 1977. — 357 с.
- Войшвилло Е. К., Дегтярев М. Г. Логика. — М.: ВЛАДОС-ПРЕСС, 2001. — 528 с. — ISBN 5-305-00001-7.
- Карпенко, А.С. Современные исследования в философской логике // Логические исследования. — М.: Наука, 2003. — Вып. 10. — С. 61—93. — ISBN 5-02-006257-X.
- Новая философская энциклопедия. — М., 2010. — Т. 2.
3.2. Логическая структура высказываний
Различие между высказываниями и предложениями проявляется в их структуре. Грамматическая структура повествовательных предложений состоит из подлежащего, сказуемого и второстепенных членов предложения. В логике суждения также расчленяют на субъект, играющий роль логического подлежащего, и предикат – логическое сказуемое. Если субъект обозначает предмет мысли, то предикат характеризует свойства, присущие предмету, или же отношения между предметами. Введение отношений на первый план выдвигает
предикат, ибо в этом случае нельзя выделить индивидуальный субъект, к которому бы относилось данное отношение. Например, когда мы говорим, что “Эльбрус выше Монблана.” или “5 больше 3.”, то отношение “выше” относится к обеим горным вершинам, а отношение “больше” – к двум числам. Напротив, в суждениях “Эльбрус – горная вершина.” или “5 – нечетное число.” их предикаты относятся к одному определенному субъекту. Часто поэтому при сравнении суждений и предложений под первыми подразумевают атрибутивные суждения традиционной логики. Атрибутивными (лат. atributum – предназначенное, наделенное, присовокупленное) они называются потому, что выражают принадлежность или непринадлежность свойства предмету. Так, в суждении “железо – металл” свойства металла признаются неотъемлемыми признаками железа, а в суждении “2 – четное число” – свойство четности для числа 2. Такие свойства называются атрибутивными именно потому, что они признаются атрибутами рассматриваемых предметов, т.е. необходимо присущими или неприсущими им.
Большинство суждений, с которыми мы встречаемся в науке и особенно в повседневной жизни, являются атрибутивными. В аристотелевской логике именно такие суждения только и анализировались. Их логическая структура может быть выражена схемой:
S есть Р,
где S обозначает субъект, т.е. предмет мысли, а Р – предикат, который обозначает свойство, которое присуще предмету мысли; термин “есть (или “суть”) – логическую связь между субъектом и предикатом, т.е. принадлежность свойства предмету.
Если такая связь отсутствует, то суждение будет отрицательным и выражается схемой:
S не есть Р или S есть не-Р.
В реляционных (лат. relatio – отнесение) суждениях, суждениях об отношениях, которые стали изучаться в середине прошлого века, речь идет об отношениях между различными предметами. Так, в суждении “Тверь находится между Санкт-Петербургом и Москвой” характеризуется отношение в пространстве, которое существует между указанными городами; в суждении “Эльбрус выше Монблана” – отношение по высоте между горными вершинами; в суждении “Михаил – брат Георгия” – отношение родства между братьями. Чаще всего суждения об отношениях встречаются в математике; с их исследования и началась разработка логики отношений.
В современной логике свойства и отношения обозначаются общим термином “предикат” (лат. praedicatum – сказуемое), в котором различают число мест. Так, свойство называют одноместным предикатом, а отношение “больше, чем” или “выше, чем”, “старше, чем” и т.д. – двухместным (бинарным) отношением. Более подробно речь об отношениях пойдет в следующей главе, здесь же мы продолжим рассмотрение суждений традиционной логики по качеству и количеству.
Термин “качество” употребляется в логике исключительно для характеристики принадлежности или непринадлежности свойств предмету.
По качеству суждения могут быть утвердительными или отрицательными. Как показывает само их название, утвердительными называются суждения, в которых говорится (“утверждается”) о принадлежности свойства предмету или присущности предиката субъекту, т.е. S есть Р. Например, “все металлы – проводники электричества”, “логика – наука”, “некоторые грибы ядовиты”.
Отрицательными называются суждения, в которых отрицается наличие свойства у предмета (неприсущность предиката субъекту), т.е. S не-есть Р или S есть не-Р. Например, “ничто человеческое мне не чуждо”, “кит – не рыба”, “астрология – не наука”. Формально отрицательные суждения могут быть преобразованы в утвердительные, в которых перед предикатом стоит отрицание:
S есть не-Р.
По количеству суждения делятся на общие, частные и единичные. Поскольку в суждении выражается наличие или отсутствие свойства (отношения) у предметов, мы можем выделить среди них такие, в которых интересующее нас свойство (отношение) принадлежат всем, нескольким и даже единичному предмету. Очевидно, что отношение требует наличия по меньшей мере двух предметов, тогда как принадлежность свойства предполагает существование всего одного предмета. Характеристика суждений по количеству описывает область их применения, т.е. их значение (денотат). Эта область может состоять из всех предметов класса, или некоторых, или даже одного предмета. Так, суждение “все металлы электропроводны” будет называться общим, суждение “некоторые рыбы – летающие” – частным, суждение “Москва – столица России” – единичным. Поскольку общие и частные суждения могут быть утвердительными и отрицательными, их можно классифицировать на четыре группы:
1) общеутвердительные, представляемые схемой: “все S есть Р”. В них свойство или предикат относится к каждому предмету, входящему в класс;
2) общеотрицательные представляются схемой: “ни одно S не есть Р”;
3) частноутвердительные: “некоторые S есть Р”;
4) частноотрицательные: “некоторые S не есть Р”.
Такая классификация пригодится нам при изучении силлогизмов в следующей главе.
Изучение логической структуры суждений позволяет выделить их логическую форму. В этих целях мы абстрагируемся, отвлекаемся от конкретного содержания и смысла предложений, с помощью которых они выражены в языке, и сосредоточиваем внимание только на том, как логически связаны элементы суждения друг с другом. Именно так подошел к анализу суждений основатель классической логики Аристотель, который использовал для обозначения логических терминов некоторые символы. Однако его формализация естественного языка была неполной и ограниченной. Для того чтобы выявить логическую форму высказывания или рассуждения, выраженного на естественном языке, необходимо отвлечься от дескриптивных (описательных) терминов языка и представить их как переменные – наподобие переменных величин математики. В результате мы получим скелет высказывания или рассуждения, в котором сохраняются лишь логические термины и отношения между ними.
Таким образом, для выявления логической формы необходимо располагать формализованным языком, т.е. построить символический, искусственный язык, который нередко отождествляют с исчислением.
Формализованный логический язык строится не столько для сокращения записей и удобства общения, сколько для обоснования правильности рассуждений, которые осуществляются на естественном языке. Еще в прошлом веке известный немецкий логик и математик Готлоб Фреге обращал внимание на то, что искусственные языки, в частности в математике и логике, строятся в ущерб легкости и краткости общения, в чем вы убедитесь после знакомства с символическими языками логики.
Знакомство с такими языками мы начнем с логики высказываний. Это простейший язык, в котором совершенно отвлекаются от внутренней логической структуры высказывания и рассматривают его как нечто целое: каждое высказывание характеризуется только с точки зрения его истинностного значения, т.е. как истинное или ложное. Сами высказывания мы будем обозначать переменными х, у, z,…, х1, у1, zi. Каждая переменная может принимать только два значения: “истину” и “ложь”, которые можно обозначить как 1 и 0. Элементарные (атомарные) высказывания могут объединяться в сложные (молекулярные) высказывания с помощью логических операторов, которые называют также связками, коннекторами или константами. Как мы увидим в дальнейшем, они приблизительно соответствуют некоторым грамматическим союзам. Зная истинностное значение элементарных высказываний и правил оперирования логическими связками, можно легко определить истинностное значение сложных высказываний, которые будут выступать как определенные логические функции. Подобно тому как в математике путем задания аргументов вычисляют значение математической функции, в логике высказываний определяют значение логической функции, образованной из элементарных (атомарных) высказываний. Аналогия с терминологией, заимствованной из химии, наглядно показывает, как сам процесс образования молекулярных высказываний из атомарных, так и в особенности тот факт, что высказывание, являющееся элементарным, считается далее неразложимым на части.
Нетрудно понять, что такое представление о высказывании крайне упрощает дело и является абстракцией, но оно дает возможность лучше понять структуру рассуждений на простейшем уровне. В дальнейшем можно вносить уточнения, дополнения в эту структуру, чтобы выразить реальную внутреннюю связь между элементами высказываний. Как мы покажем в гл. 5, именно для этого строится логика предикатов, где в рассуждениях учитывается внутренняя структура высказываний. Указанный способ анализа дает возможность понять, как происходит переход от простых логических систем к сложным, посредством увеличения истинностных значений и введения дополнительных логических операций. Это относится прежде всего к числу истинностных значений высказываний. Наряду с привычными двумя значениями истинности (истина и ложь) классической логики в современной неклассической логике рассматривают несколько значений истинности, например “истинно”, “ложно” и “неопределенно”. В вероятностной (индуктивной) логике оперируют даже бесконечным количеством значений истинности, поскольку вероятность имеет непрерывную шкалу значений в интервале 0 ?X?1.
Кроме того, высказывания можно анализировать не по их истинностному значению, а оценивать с точки зрения обоснованности содержащегося в нем знания или отношения к нему познающего субъекта посредством модальных категорий. О них мы подробнее скажем в конце этой главы. Классическая двузначная логика является простейшей логической системой, в которой легче всего понять, как образуются сложные высказывания из простых и как определяются сами логические операции над ними.
Читайте также
3 ГЛАВА. Логика высказываний
3 ГЛАВА. Логика высказываний
Под высказыванием (суждением) понимают форму мысли, которая выражает соответствие или несоответствие ее действительности. Так, еще великий античный философ Платон утверждал, что “тот, кто говорит о вещах в соответствии с тем, каковы они есть,
§ 3. Логическая структура понятия
§ 3. Логическая структура понятия
Логическую структуру понятия составляют его содержание и объем. Содержание понятия – это совокупность существенных признаков предмета или класса однородных предметов, отраженных в этом понятии. Например, содержание понятия «право»
§ 2. Логическая структура суждения
§ 2. Логическая структура суждения
Суждение, как и понятие, являясь структурой мышления, имеет свою внутреннюю структуру, однако более сложную, чем понятие. Элементами логической структуры суждения являются: субъект, предикат, связка и квантор.Субъект суждения – это
§ 1. Сущность и логическая структура вопроса
§ 1. Сущность и логическая структура вопроса
Вопрос – это логическая форма, включающая исходную информацию с одновременным указанием на ее недостаточность с целью получения новой информации в виде ответа.В естественном языке вопрос выступает чаще всего в виде
§ 1. Сущность и логическая структура гипотезы
§ 1. Сущность и логическая структура гипотезы
Познание любого явления действительности, как известно, начинают с собирания и накопления отдельных фактов, относящихся к этому явлению. Фактов, которыми располагают в начале познания, всегда недостаточно, чтобы полностью и
§ 2. Логическая структура доказательства
§ 2. Логическая структура доказательства
Доказательство как особый логический способ обоснования истины имеет свое строение. Всякое доказательство включает: тезис, аргументы, демонстрацию. Каждый из этих элементов в логической структуре доказательства выполняет свои
IV. ЛОГИЧЕСКАЯ СТРУКТУРА ДВУХ ОСНОВНЫХ ЗАКОНОВ МУЗЫКАЛbНОЙ ФОРМЫ
IV. ЛОГИЧЕСКАЯ СТРУКТУРА ДВУХ ОСНОВНЫХ ЗАКОНОВ МУЗЫКАЛbНОЙ ФОРМЫ
1Закон «золотого деления» как в искусстве вообще, так и в музыке может считаться вполне установленным и общепризнанным [160]. Не входя в конкретный анализ художественных произведений, построяемых по этому
Становление теоретического содержания и логическая структура «Манифеста Коммунистической партии»
Становление теоретического содержания и логическая структура «Манифеста Коммунистической партии»
[490] За последние годы марксоведы и историки марксизма получили много новых данных относительно предыстории и истории создания Манифеста (находки и новые публикации
3. Система экономических категорий в связи с системой логических категорий. Логическая структура «Капитала»
3. Система экономических категорий в связи с системой логических категорий.
Логическая структура «Капитала»
Каждая отдельная наука оперирует своими специфическими категориями. Специфичность категорий каждой данной науки двояка: во-первых, все они отличаются друг от
§ 4. ЯЗЫК ЛОГИКИ ВЫСКАЗЫВАНИЙ
§ 4. ЯЗЫК ЛОГИКИ ВЫСКАЗЫВАНИЙ
В современной логике разработано несколько специальных искусственных языков, применяемых для описания ее законов. Наиболее широко для этой цели используется язык логики высказываний, выражения которого точно определяются, что позволяет
§ 1. ВЫВОДЫ ЛОГИКИ ВЫСКАЗЫВАНИЙ
§ 1. ВЫВОДЫ ЛОГИКИ ВЫСКАЗЫВАНИЙ
Различают два вида дедуктивных умозаключений в зависимости от того, учитывается ли в них при осуществлении вывода внутренняя структура простых суждений, входящих в посылки и заключения, или нет. В этом параграфе описываются умозаключения,
4. ФОРМАЦИЯ МОДАЛЬНОСТЕЙ ВЫСКАЗЫВАНИЙ
4. ФОРМАЦИЯ МОДАЛЬНОСТЕЙ ВЫСКАЗЫВАНИЙ
Количественные описания, биографическое повествование, установление, интерпретация, выведение знаков, рассуждение по аналогии, экспериментальная верификация — и множество других форм высказываний — все это мы можем найти в
3. ОПИСАНИЕ ВЫСКАЗЫВАНИЙ
3. ОПИСАНИЕ ВЫСКАЗЫВАНИЙ
Направление анализа оказалось заметно смещено; я хотел дать определение высказыванию, которое изначально оставалось неопределенным. Все было сказано так, как будто высказывание — легко устанавливаемая общность, законы и возможности
28. Выражение высказываний
28. Выражение высказываний
Выражение высказываний происходит при помощи символов– переменных и знаков, обозначающих логические термины. Других символов для этой цели нет. Переменные высказывания выражаются в виде букв латинского алфавита (a, b, c, d и т. д.). Такие буквы
2. Выражение высказываний
2. Выражение высказываний
Выражение высказываний происходит при помощи символов — переменных и знаков, обозначающих логические термины. Других символов для этой цели нет. Переменные высказывания выражаются в виде букв латинского алфавита (a, b, c, d и т. д.). Такие буквы
Логика – одна из древнейших научных дисциплин. Ее название происходит из греческого языка и буквально переводится как «разум», «рассуждение», «мысль». Эта дисциплина понимается как наука о мышлении и способностях человека к рассуждениям, умению делать выводы.
Относится логика к нормативным философским наукам. В ее рамках изучаются методы, формы и закономерности процессов мышления людей. Одной из главных задач логики является определение пути от получения разумом информационной предпосылки до формирования вывода.
Чем является логическая форма? Определение
Как и для любой науки, для логики характерны собственные понятия и термины. Одним из таких понятий и является «логическая форма».
Что это такое? Под данным выражением понимается связь между отдельными составными частями, представляющими содержание мыслительного процесса. Понятие логической формы не является аналогом термина «содержание мысли». Форма не является чем-то неизменным, навсегда связанным с единственным вариантом содержания мысли.
Какими могут быть мыслительные процессы?
В общей структуре мышления выделяются следующие формы логического познания или же операции:
- анализ;
- сравнение;
- синтез;
- абстрагирование;
- обобщение.
Каждая из мыслительных операций имеет собственное значение и является необходимым компонентом деятельности разума.
Подробнее о мыслительных процессах
Под анализом понимается сложная мыслительная деятельность, в ходе которой поступившая извне информация расчленяется на составные элементы, которые подвергаются сравнению и обдумыванию.
Сравнения – это деятельность разума, в ходе которой выявляются моменты сходства и различия в рассматриваемых объектах. Именно в результате этого процесса возникает классификация, то есть первичная логическая форма теоретического познания чего-либо.

Синтез является мыслительной деятельностью, противоположной по своей сути анализу. То есть в течение данного процесса из отдельных, разрозненных частиц воссоздается целостное представление.
Под абстрагированием понимается умственная деятельность, в результате которой отделяются основные, существенные элементы от вторичных, не обладающих особым значением. Результатом данного процесса, как правило, становится формирование понятий о чем-либо.
Обобщениями же называют те процессы мышления, благодаря которым происходит объединение информации, предметов или объектов по определенным признакам.
Какими могут быть мыслительные формы?
Основные логические формы, характерные для мыслительных процессов, это:
- суждения;
- понятия;
- умозаключения.
Каждая из данных форм является гибкой, то есть не обладает постоянным содержимым.
Понятия и их критерии
Понятия – это особая логическая форма мыслительного процесса, которая может быть как абстрактной, так и конкретной.
Критериями понятий выступают:
- отношения рассматриваемых предметов или явлений;
- связи между ними и другими предпосылками;
- существенные характеризующие свойства.
Выражаться в речи понятия могут как одним или несколькими словами, так и длинными фразами.
Суждения, умозаключения и их критерии
Суждениями называют те формы, которым свойственно отражение связей в виде утверждений или же отрицаний. Оно наиболее близко по смыслу к выводу. Логическая форма суждения может быть как истинной, так и ложной. Также суждения являются неотъемлемым компонентом умозаключений.

Под умозаключением понимается мыслительная деятельность, в которой человек приходит к определенным выводам, основываясь на цепи суждений. Логические формы мышления, именуемые умозаключениями, характеризуются такими критериями:
- аналогия;
- дедукция;
- индукция.
Каждый из этих критериев, разумеется, обладает собственными характеристиками.
Аналогия – это логически обоснованные переходы от одного к другому, в основе которых лежит наличие очевидного сходства. Дедукцией называется та логическая форма, при которой умозаключения следуют по направлению от общего, целостного, к частному, конкретному элементу. Индукция – это обратный процесс, при котором мысль направляется от частиц, деталей к общему и целостному.
Что оказывает влияние на логическое мышление?
Процессы мышления подчиняются логическим закономерностям, однако они подвергаются влиянию со стороны испытываемых человеком эмоций.
Чувства и эмоции оказывают на разум чрезвычайно сильное действие. Они способны полностью изменить отношение к информации, ход суждений и умозаключений и, конечно же, выводы, к которым они приводят. Эмоциональная сторона человеческой натуры подчиняет себе разум, заставляя его находить именно те доводы и предпосылки, которые соответствуют испытываемым чувствам, приводят к изначально желаемым выводам. Это явление называется предвзятостью.

Однако действие эмоций на разум далеко не всегда становится негативным. Чувства не только мешают людям размышлять здраво, зачастую они, наоборот, стимулируют разум. Эмоциональная сторона человеческой натуры придает мыслительной деятельности целеустремленность, напряженность, пытливость, остроту и многие другие качества. К примеру, если речь идет о необходимости изобретения лекарственного препарата, то человек, испытывающий личную заинтересованность, добьется больших успехов, чем тот, чьи эмоции не оказывают влияния на разум.
Таким образом, эмоциональная составляющая столь же необходима для осуществления продуктивного мыслительного процесса, как и логическая.
Есть ли формы у высказываний?
Формы логических высказываний – это то, в каком виде озвучиваются мысли, суждения, умозаключения, выводы. Данный термин используется не только в философии, психологии и социальных науках, но и в математике и прочих.
Основная характеристика данных форм заключается в том, что их можно рассматривать в отрыве от непосредственного содержания мыслей, рассуждений или же выводов. Иными словами, любое высказывание, как простое, так и сложное, можно представить в виде формулы составляющих слагаемых.
Иными словами, любое высказанное вслух умозаключение, утверждение или рассуждение имеют уникальное содержание, но бывают облачены в одинаковую форму, не изменяющуюся в зависимости от сути мысли. Форма, которой пользуется человек для того, чтобы донести результаты своей мыслительной деятельности до других членов общества, существует отвлеченно от содержания произносимых или записываемых слов, символов.

В качестве наглядного примера можно привести аналогию с конфетами, завернутыми в фантики. В одну и ту же обертку можно поместить совершенно различные сладости – шоколад, карамель, леденцы, батончики, помадки и так далее. Однако свойства фантика не изменятся от того, какую именно конфету в него завернут.
О законах логики
Определенные закономерности свойственны каждой из существующих наук, и, разумеется, логика не является исключением.
К ее основным закономерностям относят следующие:
- тождество;
- отсутствие противоречия;
- исключение;
- достаточное основание.
Под законом тождества в философских дисциплинах понимаются сходство, логическая взаимосвязь. Постулат об отсутствии противоречий утверждает, что две и более различные по содержанию мысли не могут быть истинны одновременно. Иными словами, верным будет только одно рассуждение, остальные окажутся ложными.

Закон исключенного третьего логично продолжает правило, гласящее об отсутствии противоречий. Его суть заключается в том, что поскольку противоречащие рассуждения не могут быть одновременно верны, ложное нужно выявить и исключить. Закон достаточного основания гласит о том, что любая, доказанная, обоснованная и аргументированная мысль является истинной.
В чем значение логики?
Не существует ни одной бесполезной научной дисциплины. У каждой из них имеется собственное значение, все они занимают свою нишу. Конечно же, логика не является исключением.
Значение этой научной дисциплины напрямую зависит от того, в какой области она применяется в качестве инструмента. Логика задействуется в математических науках, социальных и психологических, в лингвистике и педагогике, во многих других областях. Попросту говоря, логика присутствует везде, где есть место для мыслительной деятельности.

Но применением в качестве инструмента, подспорья в различных научных дисциплинах, ее значение не ограничивается. Изучение логики как самостоятельного предмета способствует:
- развитию мыслительных способностей;
- умению точно и ясно излагать, доносить до других свои рассуждения;
- способности отличать истину от лжи;
- формированию привычки к самостоятельному анализу поступающей извне информации.
Логика необходима для ведения дискуссий или споров, осмысления происходящих событий, проработки научных теорий и многого другого.
