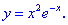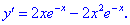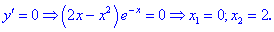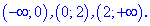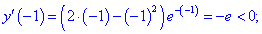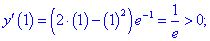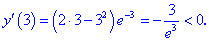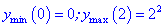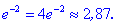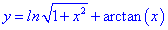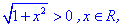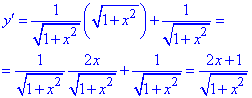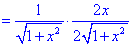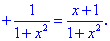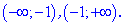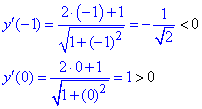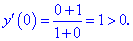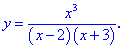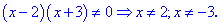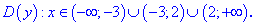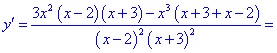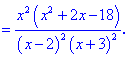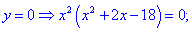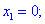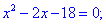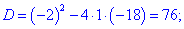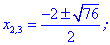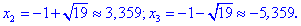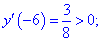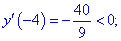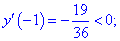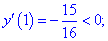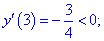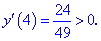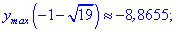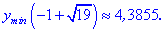Отыскание локальных максимумов и минимумов не обходится без дифференцирования и является необходимым при исследовании функции и построении ее графика.
Точка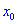 
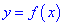
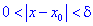
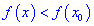
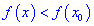
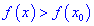
называется точкой локального максимума (или минимума) функции 
, сли существует такой окрестность 
этой точки, принадлежащий области определения функции, и для всех 
из этого окрестности выполняется неравенство (или 
).
Точки максимума и минимума называются точками экстремума функции, а значения функции в экстремальных точках – ее экстремальными значениями.
НЕОБХОДИМОЕ УСЛОВИЕ ЛОКАЛЬНОГО ЭКСТРЕМУМА:
Если функция имеет в точке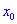 
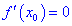
локальный экстремум, то либо производная равна нулю 
, либо не существует.
Точки которые удовлетворяют выписанным выше требованиям называют критическими точками.
Однако в каждой критической точке функция имеет экстремум. Ответ на вопрос: будет критическая точка точкой экстремума дает следующая теорема.
ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА ФУНКЦИИ
Теорема І. Пусть функция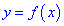 
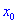
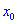
непрерывна в некотором интервале, содержащем критическую точку 
и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки 
).
Тогда для точки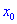 
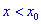
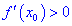
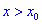
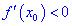
функция имеет максимум, если для аргументов 
выполняется условие, что производная больше нуля 
, а для 
условие – производная меньше нуля 
.
Если же для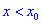 
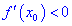
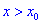
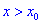
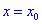
производная меньше нуля 
, а для 
больше нуля 
, то для точки 
функция имеет минимум.
Теорема ІІ. Пусть функция дважды дифференцируема в окрестности точки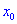 
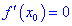
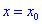
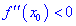
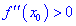
и производная равна нулю 
. Тогда в точке 
функция имеет локальный максимум, если вторая производная меньше нуля 
и локальный минимум, если наоборот 
.
Если же вторая производная равна нулю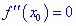 
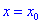
, то точка 
может и не быть точкой экстремума.
При исследовании функций на экстремумы используют обе теоремы. Первая на практике проще, поскольку не требует нахождения второй производной.
ПРАВИЛА НАХОЖДЕНИЯ ЕКСТРЕМУМОВ (МАКСИМУМОВ И МИНИМУМОВ) С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ
1) найти область определения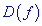 
;
2) найти первую производную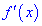 
;
3) найти критические точки;
4) исследовать знак производной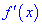 
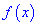
на интервалах, которые получили от разбиения критическими точками области определения 
.
При этом критическая точка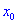 
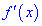
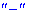
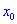
является точкой минимума, если при переходе через нее слева направо производная 
меняет знак с отрицательного 
на положительный 
, в противном случаэ 
является точкой максимума.
Вместо данного правила можно определять вторую производную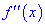 
и исследовать согласно второй теоремы.
5) вычислить значения функции в точках экстремума.
Рассмотрим теперь исследование функции на экстремумы на конкретных примерах.
———————————–
Примеры.
Сборник В.Ю. Клепко, В.Л. Голец “Высшая математика в примерах и задачах”
1. (4.53.7)
1) Областью определения будет множество действительных чисел
;
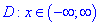
2) Находим производную
3) Вычисляем критические точки
Они разбивают область определения на следующие интервалы
4) Исследуем знак производной на найденных интервалах методом подстановки значений
Таким образом первая точка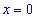 
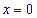
является точкой минимума, а вторая 
– точкой максимума.
5) Вычисляем значение функции
——————————
2. (4.53.9)
1) Областью определения будет множество действительных чисел 
, так корень всегда больше единицы
и функция арктангенс определена на всей действительной оси.
2) Находим производную
3) С условия равенства производной нулю находим критическую точку
Она разбивает область определения на два интервала
4) Определим знак производной в каждой из областей
Таким образом находим, что в критической точке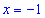 
функция принимает минимальное значение.
5) Вычислим экстремум функции
——————————
3. (4.53.13)
1) Функция определена когда знаменатель не превращается в ноль
Из этого следует, что область определения состоит из трех интервалов
2) Вычисляем производную
3) Приравниваем производную к нулю и находим критические точки.
4) Устанавливаем знак производной в каждой из областей, подстановкой соответствующих значений.
Таким образом точка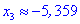 
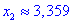
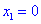
является точкой локального максимума, а 
локального минимума. В 
имеем перегиб функции, но о нем будет больше материала в следующих статьях.
5) Находим значение в критических точках
Несмотря на то, что значение функции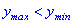 
, первая точка является точкой локального максимума, а дуга – минимума. Не бойтесь, если у Вас выйдут подобные результаты, при определении локальных экстремумов такие ситуации допустимы.
———————————————-
Посмотреть материалы:
- Исследования функции и построения графика
- Интервалы монотонности функции
- Наибольшее и наименьшее значение функции на отрезке
- Выпуклость и вогнутисть графика функции
- Асимптоты функции
- Область определения функции
Экстремумы, наибольшие и наименьшие значения функций
19. Локальный экстремум функции. Необходимое условие существования экстремума
Говорят, что функция
имеет вовнутреннейточке
областиD
локальный максимум(минимум),
если существует такая окрестность
точки
,
для каждой точки
которой выполняется неравенство
Если функция имеет в
точке
локальный максимум или локальный
минимум, то говорят, что она имеет в этой
точкелокальный экстремум (или
просто экстремум).
Теорема (необходимое
условие существования экстремума).
Если дифференцируемая функция
достигает экстремума в точке
,
то каждая частная производная первого
порядка от функции
в этой точке обращается в нуль.
Точки, в которых все
частные производные первого порядка
обращаются в нуль, называются стационарными
точками функции
.
Координаты этих точек можно найти,
решив систему из
уравнений
.
Необходимое условие
существования экстремума в случае
дифференцируемой функции коротко можно
сформулировать и так:
.
Встречаются случаи,
когда в отдельных точках некоторые
частные производные имеют бесконечные
значения или не существуют (в то время
как остальные равны нулю). Такие точки
называются критическими точками
функции.Эти точки тоже нужно
рассматривать в качестве «подозрительных»
на экстремум, как и стационарные.
В случае функции двух
переменных необходимое условие
экстремума, а именно равенство нулю
частных производных (дифференциала) в
точке экстремума, имеет геометрическую
интерпретацию: касательная плоскость
к поверхности
в точке экстремума должна быть параллельна
плоскости
.
20. Достаточные условия существования экстремума
Выполнение в некоторой
точке необходимого условия существования
экстремума вовсе не гарантирует наличия
там экстремума. В качестве примера можно
взять дифференцируемую всюду функцию
.
Обе ее частные производные и сама
функция обращаются в нуль в точке
.
Однако в любой окрестности этой точки
есть как положительные (большие
),
так и отрицательные (меньшие
)
значения этой функции. Следовательно,
в этой точке, по определению, экстремума
не наблюдается. Поэтому необходимо
знать достаточные условия, при которых
точка, подозрительная на экстремум,
является точкой экстремума исследуемой
функции.
Рассмотрим случай
функции двух переменных. Предположим,
что функция
определена, непрерывна и имеет непрерывные
частные производные до второго порядка
включительно в окрестности некоторой
точки
,
которая является стационарной точкой
функции
,
то есть удовлетворяет условиям
,
.
Введем обозначения:
Теорема(достаточные условия существования
экстремума). Пусть функция
удовлетворяет вышеприведенным условиям,
а именно: дифференцируема в некоторой
окрестности стационарной точки
и дважды дифференцируема в самой точке
.
Тогда, если
-
,
то в исследуемой точке функция имеет
локальный экстремум, -
то экстремума нет, -
то требуется дополнительное исследование.
,
то экстремума нет,
то требуется дополнительное исследование.В
случае если
то функция
в точке
достигает
локального максимумапри
и
локального минимумапри
.
В общем
случае, для функции
достаточным условием существования в
точке
локальногоминимума(максимума)
являетсяположительная (отрицательная)
определённость второго дифференциала.
Иными словами,
справедливо следующее утверждение.
Теорема. Если
в точке
для функции
для любых
не равных одновременно нулю
,
то в этой точке функция имеетминимум
(аналогичномаксимум, если
).
Пример
18.Найти точки локального экстремума
функции
Решение. Найдем
частные производные функции и приравниваем
их к нулю:
Решая эту систему,
находим две точки возможного экстремума:
Найдем частные
производные второго порядка для данной
функции:
В первой стационарной
точке
,
следовательно, и
Поэтому для этой точки требуется
дополнительное исследование. Значение
функции
в этой точке равно нулю:
Далее,
при
а
при
Следовательно, в любой
окрестности точки
функция
принимает значения как большие
,
так и меньшие
,
и, значит, в точке
функция
,
по определению, не имеет локального
экстремума.
Во второй стационарной
точке
следовательно,
Поэтому, так как
то в точке
функция имеет локальный максимум:
.
Экстремум функции двух переменных. Примеры исследования функций на экстремум.
Пусть функция $z=f(x,y)$ определена в некоторой окрестности точки $(x_0,y_0)$. Говорят, что $(x_0,y_0)$ – точка (локального) максимума, если для всех точек $(x,y)$ некоторой окрестности точки $(x_0,y_0)$ выполнено неравенство $f(x,y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)> f(x_0,y_0)$, то точку $(x_0,y_0)$ называют точкой (локального) минимума.
Точки максимума и минимума часто называют общим термином – точки экстремума.
Если $(x_0,y_0)$ – точка максимума, то значение функции $f(x_0,y_0)$ в этой точке называют максимумом функции $z=f(x,y)$. Соответственно, значение функции в точке минимума именуют минимумом функции $z=f(x,y)$. Минимумы и максимумы функции объединяют общим термином – экстремумы функции.
Алгоритм исследования функции $z=f(x,y)$ на экстремум
- Найти частные производные $frac{partial z}{partial x}$ и $frac{partial z}{partial y}$. Составить и решить систему уравнений $
left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$. Точки, координаты которых удовлетворяют указанной системе, называют стационарными. - Найти $frac{partial^2z}{partial x^2}$, $frac{partial^2z}{partial xpartial y}$, $frac{partial^2z}{partial y^2}$ и вычислить значение $Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2$ в каждой стационарной точке. После этого использовать следующую схему:
- Если $Delta > 0$ и $frac{partial^2z}{partial x^2} > 0$ (или $frac{partial^2z}{partial y^2} > 0$), то в исследуемая точка есть точкой минимума.
- Если $Delta > 0$ и $frac{partial^2z}{partial x^2} < 0$ (или $frac{partial^2z}{partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
- Если $Delta < 0$, то в расматриваемой стационарной точке экстремума нет.
- Если $Delta = 0$, то ничего определённого про наличие экстремума сказать нельзя; требуется дополнительное исследование.
Примечание (желательное для более полного понимания текста): показатьскрыть
Пример №1
Исследовать на экстремум функцию $z=4x^2-6xy-34x+5y^2+42y+7$.
Решение
Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=8x-6y-34; frac{partial z}{partial y}=-6x+10y+42.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 8x-6y-34=0;\
& -6x+10y+42=0.
end{aligned} right.
$$
Сократим каждое уравнение этой системы на $2$ и перенесём числа в правые части уравнений:
$$
left { begin{aligned}
& 4x-3y=17;\
& -3x+5y=-21.
end{aligned} right.
$$
Мы получили систему линейных алгебраических уравнений. Мне в этой ситуации кажется наиболее удобным применение метода Крамера для решения полученной системы.
$$ begin{aligned}
& Delta=left| begin{array} {cc} 4 & -3\ -3 & 5 end{array}right|=4cdot 5-(-3)cdot (-3)=20-9=11;\
& Delta_x=left| begin{array} {cc} 17 & -3\ -21 & 5 end{array}right|=17cdot 5-(-3)cdot (-21)=85-63=22;\
& Delta_y=left| begin{array} {cc} 4 & 17\ -3 & -21 end{array}right|=4cdot (-21)-17cdot (-3)=-84+51=-33.end{aligned} \
x=frac{Delta_{x}}{Delta}=frac{22}{11}=2; ; y=frac{Delta_{y}}{Delta}=frac{-33}{11}=-3.
$$
Значения $x=2$, $y=-3$ – это координаты стационарной точки $(2;-3)$. Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=8; frac{partial^2 z}{partial y^2}=10; frac{partial^2 z}{partial x partial y}=-6.
$$
Вычислим значение $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
8cdot 10-(-6)^2=80-36=44.
$$
Так как $Delta > 0$ и $frac{partial^2 z}{partial x^2} > 0$, то согласно алгоритму точка $(2;-3)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $(2;-3)$:
$$
z_{min}=z(2;-3)=4cdot 2^2-6cdot 2 cdot (-3)-34cdot 2+5cdot (-3)^2+42cdot (-3)+7=-90.
$$
Ответ: $(2;-3)$ – точка минимума; $z_{min}=-90$.
Пример №2
Исследовать на экстремум функцию $z=x^3+3xy^2-15x-12y+1$.
Решение
Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=3x^2+3y^2-15; frac{partial z}{partial y}=6xy-12.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 3x^2+3y^2-15=0;\
& 6xy-12=0.
end{aligned} right.
$$
Сократим первое уравнение на 3, а второе – на 6.
$$
left { begin{aligned}
& x^2+y^2-5=0;\
& xy-2=0.
end{aligned} right.
$$
Если $x=0$, то второе уравнение приведёт нас к противоречию: $0cdot y-2=0$, $-2=0$. Отсюда вывод: $xneq 0$. Тогда из второго уравнения имеем: $xy=2$, $y=frac{2}{x}$. Подставляя $y=frac{2}{x}$ в первое уравнение, будем иметь:
$$
x^2+left(frac{2}{x} right)^2-5=0;\
x^2+frac{4}{x^2}-5=0;\
x^4-5x^2+4=0.
$$
Получили биквадратное уравнение. Делаем замену $t=x^2$ (при этом имеем в виду, что $t > 0$):
$$
t^2-5t+4=0;\
begin{aligned}
& D=(-5)^2-4cdot 1 cdot 4=9;\
& t_1=frac{-(-5)-sqrt{9}}{2}=frac{5-3}{2}=1;\
& t_2=frac{-(-5)+sqrt{9}}{2}=frac{5+3}{2}=4.end{aligned}
$$
Если $t=1$, то $x^2=1$. Отсюда имеем два значения $x$: $x_1=1$, $x_2=-1$. Если $t=4$, то $x^2=4$, т.е. $x_3=2$, $x_4=-2$. Вспоминая, что $y=frac{2}{x}$, получим:
begin{aligned}
& y_1=frac{2}{x_1}=frac{2}{1}=2;\
& y_2=frac{2}{x_2}=frac{2}{-1}=-2;\
& y_3=frac{2}{x_3}=frac{2}{2}=1;\
& y_4=frac{2}{x_4}=frac{2}{-2}=-1.
end{aligned}
Итак, у нас есть четыре стационарные точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. На этом первый шаг алгоритма закончен.
Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=6x; frac{partial^2 z}{partial y^2}=6x; frac{partial^2 z}{partial x partial y}=6y.
$$
Найдём $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
6xcdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2).
$$
Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(1;2)$. В этой точке имеем:
$$Delta(M_1)=36(1^2-2^2)=-108.$$
Так как $Delta(M_1) < 0$, то согласно алгоритму в точке $M_1$ экстремума нет.
Исследуем точку $M_2(-1;-2)$. В этой точке имеем:
$$Delta(M_2)=36((-1)^2-(-2)^2)=-108.$$
Так как $Delta(M_2) < 0$, то согласно алгоритму в точке $M_2$ экстремума нет.
Исследуем точку $M_3(2;1)$. В этой точке получим:
$$
Delta(M_3)=36(2^2-1^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_3}=6cdot 2=12.
$$
Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(2;1)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:
$$
z_{min}=z(2;1)=2^3+3cdot 2cdot 1^2-15cdot 2-12cdot 1+1=-27.
$$
Осталось исследовать точку $M_4(-2;-1)$. В этой точке получим:
$$
Delta(M_4)=36((-2)^2-(-1)^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_4}=6cdot (-2)=-12.
$$
Так как $Delta(M_4) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_4} < 0$, то согласно алгоритму $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:
$$
z_{max}=z(-2;-1)=(-2)^3+3cdot (-2)cdot (-1)^2-15cdot (-2)-12cdot (-1)+1=29.
$$
Исследование на экстремум завершено. Осталось лишь записать ответ.
Ответ:
- $(2;1)$ – точка минимума, $z_{min}=-27$;
- $(-2;-1)$ – точка максимума, $z_{max}=29$.
Примечание
Вычислять значение $Delta$ в общем случае нет необходимости, потому что нас интересует лишь знак, а не конкретное значение данного параметра. Например, для рассмотренного выше примера №2 в точке $M_3(2;1)$ имеем $Delta=36cdot(2^2-1^2)$. Здесь очевидно, что $Delta > 0$ (так как оба сомножителя $36$ и $(2^2-1^2)$ положительны) и можно не находить конкретное значение $Delta$. Правда, для типовых расчётов это замечание бесполезно, – там требуют довести вычисления до числа 🙂
Пример №3
Исследовать на экстремум функцию $z=x^4+y^4-2x^2+4xy-2y^2+3$.
Решение
Будем следовать алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=4x^3-4x+4y; frac{partial z}{partial y}=4y^3+4x-4y.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 4x^3-4x+4y=0;\
& 4y^3+4x-4y=0.
end{aligned} right.
$$
Сократим оба уравнения на $4$:
$$
left { begin{aligned}
& x^3-x+y=0;\
& y^3+x-y=0.
end{aligned} right.
$$
Добавим к второму уравнению первое и выразим $y$ через $x$:
$$
y^3+x-y+(x^3-x+y)=0;\
y^3+x^3=0; y^3=-x^3; y=-x.
$$
Подставляя $y=-x$ в первое уравнение системы, будем иметь:
$$
x^3-x-x=0;\
x^3-2x=0;\
x(x^2-2)=0.
$$
Из полученного уравнения имеем: $x=0$ или $x^2-2=0$. Из уравнения $x^2-2=0$ следует, что $x=-sqrt{2}$ или $x=sqrt{2}$. Итак, найдены три значения $x$, а именно: $x_1=0$, $x_2=-sqrt{2}$, $x_3=sqrt{2}$. Так как $y=-x$, то $y_1=-x_1=0$, $y_2=-x_2=sqrt{2}$, $y_3=-x_3=-sqrt{2}$.
Первый шаг решения окончен. Мы получили три стационарные точки: $M_1(0;0)$, $M_2(-sqrt{2},sqrt{2})$, $M_3(sqrt{2},-sqrt{2})$.
Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=12x^2-4; frac{partial^2 z}{partial y^2}=12y^2-4; frac{partial^2 z}{partial x partial y}=4.
$$
Найдём $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
(12x^2-4)(12y^2-4)-4^2=\
=4(3x^2-1)cdot 4(3y^2-1)-16=16(3x^2-1)(3y^2-1)-16=16cdot((3x^2-1)(3y^2-1)-1).
$$
Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(0;0)$. В этой точке имеем:
$$Delta(M_1)=16cdot((3cdot 0^2-1)(3cdot 0^2-1)-1)=16cdot 0=0.$$
Так как $Delta(M_1) = 0$, то согласно алгоритму требуется дополнительное исследование, ибо ничего определённого про наличие экстремума в рассматриваемой точке сказать нельзя. Оставим покамест эту точку в покое и перейдём в иным точкам.
Исследуем точку $M_2(-sqrt{2},sqrt{2})$. В этой точке получим:
begin{aligned}
& Delta(M_2)=16cdot((3cdot (-sqrt{2})^2-1)(3cdot (sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_2}=12cdot (-sqrt{2})^2-4=24-4=20.
end{aligned}
Так как $Delta(M_2) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_2} > 0$, то согласно алгоритму $M_2(-sqrt{2},sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_2$:
$$
z_{min}=z(-sqrt{2},sqrt{2})=(-sqrt{2})^4+(sqrt{2})^4-2(-sqrt{2})^2+4cdot (-sqrt{2})sqrt{2}-2(sqrt{2})^2+3=-5.
$$
Аналогично предыдущему пункту исследуем точку $M_3(sqrt{2},-sqrt{2})$. В этой точке получим:
begin{aligned}
& Delta(M_3)=16cdot((3cdot (sqrt{2})^2-1)(3cdot (-sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_3}=12cdot (sqrt{2})^2-4=24-4=20.
end{aligned}
Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(sqrt{2},-sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:
$$
z_{min}=z(sqrt{2},-sqrt{2})=(sqrt{2})^4+(-sqrt{2})^4-2(sqrt{2})^2+4cdot sqrt{2}(-sqrt{2})-2(-sqrt{2})^2+3=-5.
$$
Настал черёд вернуться к точке $M_1(0;0)$, в которой $Delta(M_1) = 0$. Согласно алгоритму требуется дополнительное исследование. Под этой уклончивой фразой подразумевается “делайте, что хотите” :). Общего способа разрешения таких ситуаций нет, – и это понятно. Если бы такой способ был, то он давно бы вошёл во все учебники. А покамест приходится искать особый подход к каждой точке, в которой $Delta = 0$. Ну что же, поисследуем поведение функции в окрестности точки $M_1(0;0)$. Сразу отметим, что $z(M_1)=z(0;0)=3$. Предположим, что $M_1(0;0)$ – точка минимума. Тогда для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) > z(M_1) $, т.е. $z(M) > 3$. А вдруг любая окрестность содержит точки, в которых $z(M) < 3$? Тогда в точке $M_1$ уж точно не будет минимума.
Рассмотрим точки, у которых $y=0$, т.е. точки вида $(x,0)$. В этих точках функция $z$ будет принимать такие значения:
$$
z(x,0)=x^4+0^4-2x^2+4xcdot 0-2cdot 0^2+3=x^4-2x^2+3=x^2(x^2-2)+3.
$$
В всех достаточно малых окрестностях $M_1(0;0)$ имеем $x^2-2 < 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.
Но, может быть, точка $M_1(0;0)$ – точка максимума? Если это так, то для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) < z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) > 3$? Тогда в точке $M_1$ точно не будет максимума.
Рассмотрим точки, у которых $y=x$, т.е. точки вида $(x,x)$. В этих точках функция $z$ будет принимать такие значения:
$$
z(x,x)=x^4+x^4-2x^2+4xcdot x-2cdot x^2+3=2x^4+3.
$$
Так как в любой окрестности точки $M_1(0;0)$ имеем $2x^4 > 0$, то $2x^4+3 > 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z > 3$, посему точка $M_1(0;0)$ не может быть точкой максимума.
Точка $M_1(0;0)$ не является ни точкой максимума, ни точкой минимума. Вывод: $M_1$ вообще не является точкой экстремума.
Ответ: $(-sqrt{2},sqrt{2})$, $(sqrt{2},-sqrt{2})$ – точки минимума функции $z$. В обеих точках $z_{min}=-5$.
