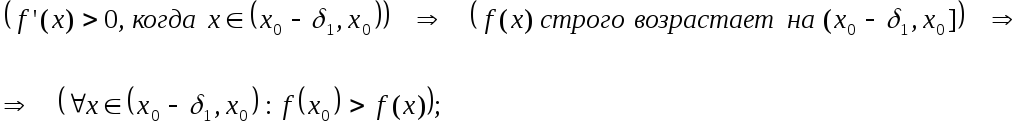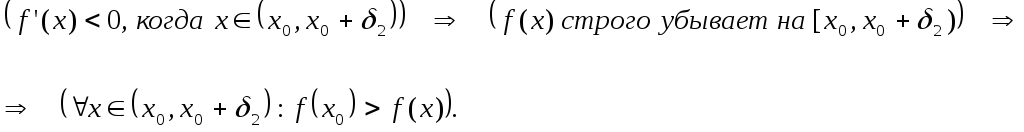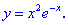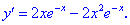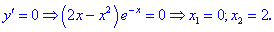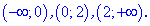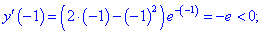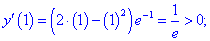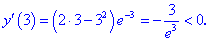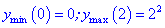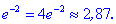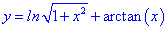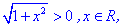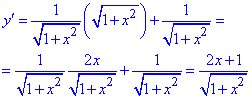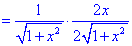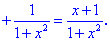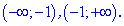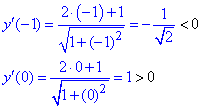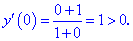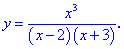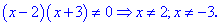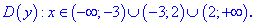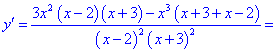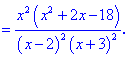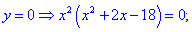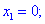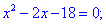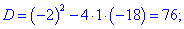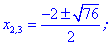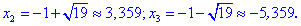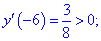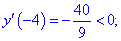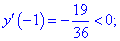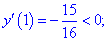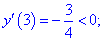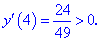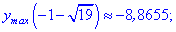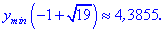Как найти локальный экстремум в точке

1. Стационарные точки функции.
   Необходимое условие локального
   экстремума функции

2. Первое достаточное условие локального
   экстремума

3. Второе и третье достаточные условия
   локального экстремума

4. Наименьшее и наибольшее
   значения функции на сегменте

5. Выпуклые функции и точки перегиба

1. Стационарные точки функции. Необходимое условие локального экстремума функции

_{Определение 1.}
Пусть функция
определена на _{.
Точка
называется стационарной точкой функции
,
если
дифференцирована в точке
и .}

Теорема 1 (необходимое
условие локального экстремума функции).
Пусть функция
определена на
_{и имеет в точке
локальный экстремум. Тогда выполняется
одно из условий:}

1. функция
   _{не имеет в точке
   производной;}

2. функция
   _{имеет в точке
   производную и .}

_{Таким образом, для того,
чтобы найти точки, которые являются
подозрительными на экстремум, надо
найти стационарные точки функции и
точки, в которых производная функции
не существует, но которые принадлежат
области определения функции.}

_{Пример.
Пусть .
Найти для нее точки, которые являются
подозрительными на экстремум. Для
решения поставленной задачи, в первую
очередь, найдем область определения
функции: .
Найдем теперь производную функции:}

_.

_{Точки, в которых производная
не существует: .
Стационарные точки функции:}

_.

_{Поскольку и ,
и
принадлежат области определения функции,
то они обе будут подозрительными на
экстремум. Но для того, чтобы сделать
вывод, будет ли там действительно
экстремум, надо применять достаточные
условия экстремума.}

2. Первое достаточное условие локального экстремума

Теорема 1 (первое достаточное
условие локального экстремума).
Пусть функция
определена на
_{и дифференцирована на этом интервале
везде за исключением, возможно, точки
,
но в этой точке
функция является
непрерывной. Если
существуют такие правая и левая
полуокрестности точки ,
в каждой из которых
сохраняет определенный знак, то}

_{1) функция
имеет локальный экстремум в точке ,
если
принимает значения разных знаков в
соответствующих полуокрестностях;}

<sub>2) функция
не имеет локальный экстремум в точке
,
если справа и слева от точки

имеет одинаковый знак.</sub>

_{Доказательство.
1) Предположим, что в полуокрестности
производная ,
а в
.}

_{Таким образом в точке
функция
имеет локальный экстремум, а именно –
локальный максимум, что и нужно было
доказать.}

_{2) Предположим, что слева
и справа от точки
производная сохраняет свой знак,
например, .
Тогда на
и
функция
строго монотонно возрастает, то есть:}

_,

_.

_{Таким образом экстремума
в точке
функция
не имеет, что и нужно было доказать.}

_{Замечание 1.
Если производная
при прохождении через точку
меняет знак с «+» на «-», то в точке
функция
имеет локальный максимум, а если знак
меняется с «-» на «+», то локальный
минимум.}

_{Замечание 2.
Важным является условие непрерывности
функции
в точке .
Если это условие не выполняется, то
теорема 1 может не иметь места.}

_{Пример.
Рассматривается функция (рис.1):}

Эта функция определена на
<sub>и непрерывна везде, кроме точки ,
где она имеет устранимый разрыв. При
прохождении через точку

меняет знак с «-» на «+», но локального
минимума в этой точке функция не имеет,
а имеет локальный максимум по определению.
Действительно, около точки
можно построить такую окрестность, что
для всех аргументов из этой окрестности
значения функции будут меньше, чем
значение .
Теорема 1 не сработала потому, что в
точке
функция имела разрыв.</sub>

_{Замечание 3.
Первое достаточное условие локального
экстремума не может быть использовано,
когда производная функции
меняет свой знак в каждой левой и каждой
правой полуокрестности точки .}

_{Пример.
Рассматривается функция:}

_{Поскольку ,
то ,
а потому ,
но .
Таким образом:}

_,

_{т.е. в точке
функция
имеет локальный минимум по определению.
Посмотрим, сработает ли здесь первое
достаточное условие локального
экстремума.}

_{Для :}

_.

Для первого слагаемого правой
части полученной формулы имеем:

_,

_{а потому в малой окрестности
точки
знак производной определяется знаком
второго слагаемого, то есть:}

_,

<sub>а это означает, что в любой
окрестности точки

будет принимать как положительные, так
и отрицательные значения. Действительно,
рассмотрим произвольную окрестность
точки :
.
Когда</sub>

_,

_то

_{(рис.2), а
меняет свой знак здесь бесконечно много
раз. Таким образом, нельзя использовать
в приведенном примере первое достаточное
условие локального экстремума.}

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Отыскание локальных максимумов и минимумов не обходится без дифференцирования и является необходимым при исследовании функции и построении ее графика.

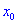
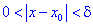
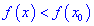
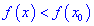
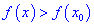
Точка называется точкой локального максимума (или минимума) функции , сли существует такой окрестность этой точки, принадлежащий области определения функции, и для всех из этого окрестности выполняется неравенство (или ).

Точки максимума и минимума называются точками экстремума функции, а значения функции в экстремальных точках – ее экстремальными значениями.

НЕОБХОДИМОЕ УСЛОВИЕ ЛОКАЛЬНОГО ЭКСТРЕМУМА:

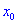
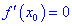
Если функция имеет в точке локальный экстремум, то либо производная равна нулю , либо не существует.

Точки которые удовлетворяют выписанным выше требованиям называют критическими точками.

Однако в каждой критической точке функция имеет экстремум. Ответ на вопрос: будет критическая точка точкой экстремума дает следующая теорема.

ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА ФУНКЦИИ

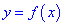
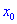
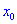
Теорема І. Пусть функция непрерывна в некотором интервале, содержащем критическую точку и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки ).

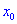
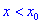
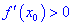
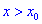
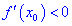
Тогда для точки функция имеет максимум, если для аргументов выполняется условие, что производная больше нуля , а для условие – производная меньше нуля .

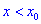
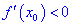
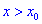
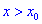
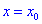
Если же для производная меньше нуля , а для больше нуля , то для точки функция имеет минимум.

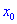
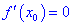
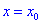
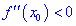
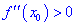
Теорема ІІ. Пусть функция дважды дифференцируема в окрестности точки и производная равна нулю . Тогда в точке функция имеет локальный максимум, если вторая производная меньше нуля и локальный минимум, если наоборот .

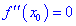
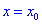
Если же вторая производная равна нулю , то точка может и не быть точкой экстремума.

При исследовании функций на экстремумы используют обе теоремы. Первая на практике проще, поскольку не требует нахождения второй производной.

ПРАВИЛА НАХОЖДЕНИЯ ЕКСТРЕМУМОВ (МАКСИМУМОВ И МИНИМУМОВ) С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ

1) найти область определения ;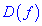

2) найти первую производную ;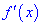

3) найти критические точки;

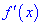
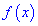
4) исследовать знак производной на интервалах, которые получили от разбиения критическими точками области определения .

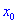
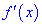
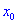
При этом критическая точка является точкой минимума, если при переходе через нее слева направо производная меняет знак с отрицательного на положительный , в противном случаэ является точкой максимума.

Вместо данного правила можно определять вторую производную 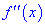и исследовать согласно второй теоремы.

5) вычислить значения функции в точках экстремума.

Рассмотрим теперь исследование функции на экстремумы на конкретных примерах.

———————————–

Примеры.

Сборник В.Ю. Клепко, В.Л. Голец “Высшая математика в примерах и задачах”

1. (4.53.7)

1) Областью определения будет множество действительных чисел

;

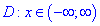
2) Находим производную

3) Вычисляем критические точки

Они разбивают область определения на следующие интервалы

4) Исследуем знак производной на найденных интервалах методом подстановки значений

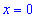
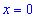
Таким образом первая точка является точкой минимума, а вторая – точкой максимума.

5) Вычисляем значение функции

——————————

2. (4.53.9)

1) Областью определения будет множество действительных чисел , так корень всегда больше единицы

и функция арктангенс определена на всей действительной оси.

2) Находим производную

3) С условия равенства производной нулю находим критическую точку

Она разбивает область определения на два интервала

4) Определим знак производной в каждой из областей

Таким образом находим, что в критической точке 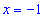функция принимает минимальное значение.

5) Вычислим экстремум функции

——————————

3. (4.53.13)

1) Функция определена когда знаменатель не превращается в ноль

Из этого следует, что область определения состоит из трех интервалов

2) Вычисляем производную

3) Приравниваем производную к нулю и находим критические точки.

4) Устанавливаем знак производной в каждой из областей, подстановкой соответствующих значений.

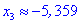
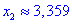
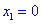
Таким образом точка является точкой локального максимума, а локального минимума. В имеем перегиб функции, но о нем будет больше материала в следующих статьях.

5) Находим значение в критических точках

Несмотря на то, что значение функции 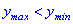, первая точка является точкой локального максимума, а дуга – минимума. Не бойтесь, если у Вас выйдут подобные результаты, при определении локальных экстремумов такие ситуации допустимы.

———————————————-

Посмотреть материалы:

• Исследования функции и построения графика
• Интервалы монотонности функции
• Наибольшее и наименьшее значение функции на отрезке
• Выпуклость и вогнутисть графика функции
• Асимптоты функции
• Область определения функции

Определение локального экстремума
было дано в начале § 4.12. Очевидно, ему можно придать и следующую форму.

Функция  достигает в точке  локального
максимума (минимума), если можно указать такое , что ее приращение  в точке  удовлетворяет неравенству

(соответственно  ).

По теореме Ферма (см. § 4.12),
если функция  достигает
в точке  локального
экстремума и в этой точке производная  существует, то она равна нулю:

.

По определению
точка  называется
стационарной для функции , если в ней производная от существует и равна
нулю .

Если задана на
некотором интервале  функция , и надо найти все ее точки локального
экстремума, то их, очевидно, надо искать среди, во-первых, стационарных точек, т.
е. таких, в которых производная  существует и равна нулю и, во-вторых,
среди точек, где  не
имеет производной, если таковые на самом деле имеются. Стационарные точки
находятся из уравнения

,                                
(1)

которое надо решить. Конечно, не
всякая стационарная точка функции  есть точка локального экстремума .

Условие (1) является необходимым
для того, чтобы дифференцируемая функция  имела в точке  локальный экстремум, но
недостаточным. Например,  есть стационарная точка функции , но в ней эта
функция возрастает.

Очевидно также, что не всякая
точка, где  не
имеет производной, есть точка локального экстремума .

Так или иначе, если нам уже
известно, что  есть
стационарная точка или точка, где производная от  не существует, нам нужны критерии
распознавания, будет ли действительно эта точка точкой локального экстремума, а
если будет, то какого – максимума или минимума.

Ниже мы приводим достаточные
критерии локального экстремума.

Т е о р е м а  
1. Пусть  –
стационарная точка функции  (т. е. ) и  имеет вторую
непрерывную производную в окрестности . Тогда:

если , то  есть точка локального
максимума ;

если же , то  есть точка локального
минимума .

Д о к а з а т е л ь с т в о.
Разложим   по
формуле Тейлора по степеням  при . Так как , то формула Тейлора функции  в
окрестности точки имеет вид

.                (2)

В этой формуле может быть .

Пусть . Так как
производная  по
условию непрерывна в окрестности , то найдется  такое, что

.

Но тогда остаточный член в
формуле (2)

,

что показывает, что

.

т. е.  имеет в  локальный максимум.

Аналогично,
если , то  в некоторой
окрестности  и
. Поэтому
остаточный член формулы (2) в окрестности  неотрицательный, а вместе с ним и , т. е.  имеет в  локальный минимум.

П р и м е р  
1.  –
стационарная точка;  для всех , следовательно, и в точке . Значит, в точке  – локальный
минимум.

З а м е ч а н и е   1. Если

,                                    
(3)

то функция  может иметь и не иметь
экстремум в .
Например, функции  и
 удовлетворяют
условиям (3) в точке , но первая из них не имеет экстремума
в этой точке, а вторая – имеет, а именно, минимум.

Т е о р е м а  
2. Пусть  и
, и
непрерывна в окрестности точки , тогда:

если  – четное и , то  имеет в  локальный
максимум;

если  – четное и , то  имеет в  локальный
минимум;

если  – нечетное и , то  заведомо не имеет в
 локального
экстремума.

Доказательство
этой теоремы снова основано на применении формулы Тейлора. Имеем

.        (4)

В случае, если  – четное,
рассуждаем в точности так же, как в случае формулы (2). Пусть теперь  – нечетное, и
пусть, как было предположено, . Вследствие непрерывности  в окрестности  существует интервал
, на
котором  сохраняет
знак .
Если  будет
возрастать в окрестности  слева направо, то  при переходе через  переменит знак, а  будет сохранять
один и тот же знак. Это показывает, что правая часть (4) и, следовательно,  при переходе  через  меняет знак и
экстремум в  невозможен.

Т е о р е м а  
3. Пусть функция  непрерывна на отрезке  и имеет производную
 отдельно
на интервалах  и
. При этом

,                         
(5)

.                         
(6)

Тогда  есть точка локального
максимума (минимума) функции .

Здесь не обязательно
предполагается, что  существует.

Д о к а з а т е л ь с т в о. Из
непрерывности  на
отрезке  и
свойства (5) следует (см. теорему 5 § 4.12), что  не убывает (не возрастает) на этом
отрезке и, следовательно,

.             (7)

А из непрерывности  на  и свойства (6)
следует (см. ту же теорему 5 § 4.12)

.             (8)

Но тогда из (7) и (8) следует:

,

и мы доказали теорему 3.

Теорема 3 утверждает,
что если первая производная функции  при переходе через точку  меняет знак, то  имеет в точке  минимум (рис. 52),
если знак меняется (при возрастании !) с  на , и максимум (рис. 53), если он
меняется с  на
. При этом
не обязательно, чтобы существовала. Но требуется, чтобы  была непрерывна в точке
 .

Рис.
52                                          Рис. 53

П р и м е р  
2.    Мы видим, что  при ,  при ,  и,  кроме того,  непрерывна в точке , поэтому по теореме
3 функция  имеет
локальный максимум в точке . Других локальных экстремумов функция
не имеет.

П р и м е р  
3. Функция ,
,
непрерывна в точке  и имеет локальный максимум: , . Однако нельзя
выделить окрестность точки  так, чтобы в ней  при  функция возрастала,
а при  убывала.

В самом деле,

,

.

При малых  слагаемое  как угодно мало,
поэтому знак производной  зависит от . При   принимает значения   сколько угодно раз.
Значит, во всякой окрестности точки  функция колеблющаяся.

Т е о р е м а   4. Пусть
функция  удовлетворяет
условиям  и
 . Тогда  в точке  имеет локальный
минимум (максимум).

Д о к а з а т е л ь с т в о. Так
как

,

то на основании теоремы 2 § 3.2  в достаточно малой
окрестности точки ,
т. е.  для
 и  для . По теореме 3
заключаем, что в точке  локальный минимум. Случай  исследуется аналогично.

З а м е ч а н и е   1. Теорема 4
содержит в себе теорему 1 как частный случай, потому что в ней не
предполагается, что  непрерывна в окрестности точки . Требуется лишь
существование .