Как найти лощадь сечения - Сайт, где вы сможете решить свои вопросы

Как вычислить площадь сечения

При решении задач по геометрии приходится вычислять площади и объемы фигур. Если сделать в любой фигуре сечение, обладая информацией о параметрах самой фигуры, можно найти и площадь этого сечения. Для этого необходимо знать специальные формулы и обладать пространственным мышлением.

Вам понадобится

Линейка, карандаш, ластик.

Инструкция

Шар является частным случаем простейшей объемной фигуры. Через него можно провести бесконечное количество сечений, и любое из них окажется кругом. Это произойдет независимо от того, насколько близко сечение расположено к центру шара. Вычислить площадь получившегося сечения проще всего в том случае, если оно проведено точно через центр шара, радиус которого известен. В таком случае площадь сечения равна:S=πR^2.

Другой фигурой, площадь сечения которой требуется найти в задачах по геометрии, является параллелепипед. Он имеет ребра и грани. Гранью называется одна из плоскостей параллелепипеда (куба), а ребром – сторона. Параллелепипед, у которого ребра и грани равны, называется кубом. Все сечения куба – квадраты. Зная это свойство, вычислите площадь сечения-квадрата:S=a^2, где a – ребро куба и сторона сечения.

Если в условиях задачи приведен обычный параллелепипед, у которого все грани являются разными, сечение может быть как квадратом, так и прямоугольником с различными сторонами. Сечение, проведенное параллельно двум квадратным граням, является квадратом, а сечение, проведенное параллельно двум прямоугольным – прямоугольником. Если сечение проходит через диагонали параллелепипеда, оно также является прямоугольником.

умножения диагонали нижнего основания на высоту параллелепипеда:S=d*h, где d – диагональ основания, h – высота основания.

Конус – одна из тех фигур вращения, сечения которой могут иметь различную форму. Если рассечь конус параллельно нижнему основанию, сечением будет круг, а если провести сечение параллельно пополам через вершину конуса, получится треугольник. В других случаях сечениями будут трапециевидные фигуры.Если сечением является круг, вычисляйте его площадь по следующей формуле:S=πR^2.Площадь сечения, представляющего собой треугольник, равно произведению половины основания на высоту:S=1/2f*h , где f – основание треугольника, h – высота треугольника.

Источники:

как найти площадь получившейся фигуры

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.

Объемные фигуры

Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.

Вам будет интересно:Что значит слыть: толкование, синонимы

Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.

Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).

Цилиндр

Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:

круглое;
прямоугольное;
эллиптическое.

Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.

Площадь круглого сечения рассчитывается по формуле:

S1 = pi*r2

Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:

S2 = 2*r*h

Сечения конуса

Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:

круглое;
эллиптическое;
параболическое;
гиперболическое;
треугольное.

Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.

Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:

S1 = pi*r2*z2/h2

Здесь z – это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z < h, то площадь изучаемого сечения будет всегда меньше ее значения для основания.

Треугольное получается, когда плоскость пересекает фигуру по ее оси вращения. Формой получившегося сечения будет равнобедренный треугольник, сторонами которого являются диаметр основания и две образующие конуса. Как находить площадь сечения треугольного? Ответом на этот вопрос будет следующая формула:

S2 = r*h

Это равенство получается, если применить формулу для площади произвольного треугольника через длину его основания и высоту.

Сечения призмы

Призма – это большой класс фигур, которые характеризуются наличием двух одинаковых параллельных друг другу многоугольных оснований, соединенных параллелограммами. Любое сечение призмы – это многоугольник. В виду разнообразия рассматриваемых фигур (наклонные, прямые, n-угольные, правильные, вогнутые призмы) велико и разнообразие их сечений. Далее рассмотрим лишь некоторые частные случаи.

Если секущая плоскость параллельна основанию, то площадь сечения призмы будет равна площади этого основания.

Если плоскость проходит через геометрические центры двух оснований, то есть является параллельной боковым ребрам фигуры, тогда в сечении образуется параллелограмм. В случае прямых и правильных призм рассматриваемый вид сечения будет представлять собой прямоугольник.

Пирамида

Пирамида – это еще один многогранник, который состоит из n-угольника и n треугольников. Пример треугольной пирамиды показан ниже.

Если сечение проводится параллельной n-угольному основанию плоскостью, то его форма будет в точности равна форме основания. Площадь такого сечения вычисляется по формуле:

S1 = So*(h-z)2/h2

Где z – расстояние от основания до плоскости сечения, So – площадь основания.

Если секущая плоскость содержит вершину пирамиды и пересекает ее основание, то мы получим треугольное сечение. Для вычисления его площади необходимо обратиться к использованию соответствующей формулы для треугольника.

Источник

Сечения трехмерных фигур — площади и периметр

Умеешь строить сечения трехмерных фигур – точно не пропадешь.

В этой статье я расскажу тебе об алгоритме построения сечений и разберу пример!

Поехали!

Алгоритм определения площади и периметра сечения объемных фигур

Нарисовать сечение.
Определить фигуру, которая получилась в этом сечении.
Вспомнить формулы площади/периметра этой фигуры.
Найти площадь/периметр фигуры.

Стандартное сечение имеет вид треугольника, круга или четырехугольника. Следовательно, нам необходимо искать площади именно этих фигур.

Площадь сечения

Площадь треугольника

Площадь круга

Площадь прямоугольника

Пример решения задачи

Диаметр основания конуса ( displaystyle left( AB right)) равен ( displaystyle 8) см.

Длина образующей ( displaystyle left( AC; BC right)) равна ( displaystyle 5) см (линия от вершины конуса до любой точки его основания).

Найдите площадь осевого сечения этого конуса.

Осевое сечение конуса – это равнобедренный треугольник ( displaystyle left( ABC right)), высота которого совпадает с высотой конуса ( displaystyle left( CO right)), а основание ( displaystyle left( AB right)) является диаметром основания конуса.

Значит, ( displaystyle S) осевого сечения конуса =( displaystyle S) треугольника ( displaystyle ABC).

Вспомним формулу площади треугольника:

( displaystyle S=frac{(COcdot AB)}{2} )

begin{matrix}
AB -длина стороны треугольника \
CO – высота, опущенная на сторону AB \
end{matrix}

Найдем высоту ( displaystyle Delta ABC):

Рассмотрим ( displaystyle Delta COA).

т.к. ( displaystyle OC) – высота ( displaystyle Delta ABC rightarrow angle COA=90{}^circ rightarrow Delta COA) – прямоугольный.

( displaystyle AO=frac{AB}{2}=frac{8}{2}=4) (т.к. ( displaystyle AO) – радиус окружности, ( displaystyle AB) – диаметр).

Найдем ( displaystyle AC):

По теореме Пифагора:

( displaystyle A{{C}^{2}}=C{{O}^{2}}+A{{O}^{2}}; C{{O}^{2}}=A{{C}^{2}}-A{{O}^{2}}={{5}^{2}}-{{4}^{2}}=9см; CO=sqrt{9}=3см)

Подставим получившиеся значения в формулу площади:

( displaystyle {{S}_{ABC}}=frac{left( COcdot AB right)}{2}=frac{3cdot 8}{2}=)( displaystyle 12см{{ }^{2}})

Площадь осевого сечения этого конуса равна ( displaystyle 12см{{ }^{2}}).

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

тысячи учеников, поступивших в лучшие ВУЗы страны
автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
закончил МФТИ, преподавал на малом физтехе;
репетиторский стаж — c 2003 года;
в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

Источник

Объемные фигуры

Цилиндр

Для этой фигуры существует три важных типа сечения:

круглое;
прямоугольное;
эллиптическое.

Площадь круглого сечения рассчитывается по формуле:

S₁ = pi*r²

Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:

S₂ = 2*r*h

Сечения конуса

Видов конических сечений существует несколько. Перечислим их:

круглое;
эллиптическое;
параболическое;
гиперболическое;
треугольное.

S₁ = pi*r²*z²/h²

Здесь z – это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S₁ будет равна нулю. Поскольку z < h, то площадь изучаемого сечения будет всегда меньше ее значения для основания.

S₂ = r*h

Сечения призмы

Изучение свойств пространственных фигур играет важную роль для решения практических задач. Наука,…

Пирамида

S₁ = S_o*(h-z)²/h²

Где z – расстояние от основания до плоскости сечения, S_o – площадь основания.

Источник

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

Скачиваний:

Добавлен:

15.05.2015

Размер:

406.75 Кб

Скачать

ПРИМЕНЕНИЕ ТЕОРЕМЫ О ПЛОЩАДИ ОРТОГОНАЛЬНОЙ ПРОЕКЦИИ МНОГОУГОЛЬНИКА ПРИ РЕШЕНИИ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ

Бардушкин В.В., Белов А.И., Ланцева И.А., Прокофьев А.А., Фадеичева Т.П.

Существует несколько методов решения стереометрических задач на вычисление площадей сечений, поверхностей многогранников и углов (между плоскостями, между прямой и плоскостью и т.д.). Эти методы достаточно подробно рассмотрены в школьных учебниках, изложены в различных пособиях по стереометрии. Так, например, при вычислении площадей широко применяется подход, основанный на разбиении многоугольника на части (на треугольники и четырёхугольники). Если в каждой из частей удаётся вычислить длины сторон (или диагоналей четырёхугольника) и какие-нибудь углы, то можно по известным формулам найти их площади, а значит, решить задачу. Довольно большое значение придаётся векторно-координатному методу решения подобных задач. Однако, на наш взгляд, многие из авторов-составителей не уделяют должного внимания методу вычисления площадей и углов, связанному с ортогональным проектированием многоугольника на некоторую плоскость. Накопленный нами опыт преподавания стереометрии, частично отражённый в настоящей статье, показывает, что изучение такой темы как «Площадь ортогональной проекции многоугольника» повышает у школьников интерес к предмету, стимулирует освоение ими других серьёзных тем по геометрии, что в итоге ведёт к интенсификации всего процесса обучения.

1. Теорема о площади ортогональной проекции плоской фигуры

Параллельное проектирование, при котором проектирующие прямые перпендикулярны к плоскости проекций, называется ортогональным.

Ортогональной проекцией фигуры на данную плоскость называют множество точек пересечений с этой плоскостью перпендикулярных к ней прямых, проходящих через все точки этой фигуры. В общем случае справедлива следующая теорема.

Если фигура Ф с площадью SФ лежит в плоскости , а фигура Ф с площадью SФ является ортогональной проекцией фигуры Ф на плоскость , то имеет место равенство

SФ SФ cos ,

где – угол между плоскостями и .

В школьном курсе стереометрии приведённая теорема формулируется и доказывается лишь для случая, когда проектируемая фигура – плоский многоугольник. В этом случае формулировка имеет вид:

Площадь Sпр ортогональной проекции многоугольника на плоскость равна произве-

дению его площади Sмн , умноженной на косинус угла между плоскостью много-

угольника и плоскостью проекции: Sпр Sмн cos .

2. Применение теоремы о площади ортогональной проекции многоугольника при нахождении площадей сечений

Эту теорему с успехом применяют, прежде всего, при вычислении площадей сечений многогранников. Данный подход используется в ситуациях, когда нахождение площади Sпр ортогональной проекции многоугольника, полученного в сечении, и угла между

секущей плоскостью и плоскостью проектирования сопряжено с меньшими трудностями, чем непосредственное вычисление площади сечения. В этом случае

Sсечения	S	пр	.	(1)
cos

В примерах 1 – 4 иллюстрируется это основное применение теоремы о площади ортогональной проекции многоугольника.


	B1		C1	Пример 1. В правильной четырёхугольной призме
				сторона основания равна 4 см. Через диагональ основа-
A1		D1		ния под углом 45	к плоскости основания проведена
		M	плоскость, пересекающая боковое ребро. Найти пло-

				щадь сечения.
				Решение. Согласно условию задачи, площадь ор-
	B			тогональной проекции сечения на плоскость основания
	45	C	призмы равна половине его площади (см. рис. 1), т.е.

	O			42	8 (см2). Тогда, используя формулу (1), полу-
A	D		Sпр
	2
				чаем: Sсечения	Sпр	2

	Рис. 1				8 2 (см ).

cos45

Ответ: 82 см2.

Пример 2. Стороны основания прямого параллелепипеда равны 4 и 5, угол между ними равен 30°. Найти площадь сечения параллелепипеда плоскостью, пересекающей все его боковые рёбра и образующей с плоскостью основания угол в 45°.

	Решение. Для нахождения площади сечения воспользуемся формулой (1). Поскольку
	B1				C1	секущая плоскость пересекает все боковые рёбра
				прямого параллелепипеда ABCDA BC D , то ортого-
A1		D1			1	1	1	1
		N	нальной проекцией сечения MQNP является паралле-
	Q				лограмм ABCD (см. рис. 2). Отметим, что MQNP так-
					же является параллелограммом, так как MQ\|\|PN и
		P
M				MP\|\|QN по свойству параллельных плоскостей (если
B				C	две параллельные плоскости пересечены третьей, то
A	30	D			линии пересечения параллельны).
			Найдем площадь параллелограмма ABCD. Пусть,
	Рис. 2					для определённости, AB 4, AD 5,	BAD 30 ,
					тогда SABCD AB AD sin BAD 10.
			SABCD
	Поскольку SMQNP		, где 45 – угол между плоскостью сечения и основани-

				cos

ем параллелепипеда (на рис. 2 этот угол не показан), то SMQNP 102 .

Ответ: 102 .

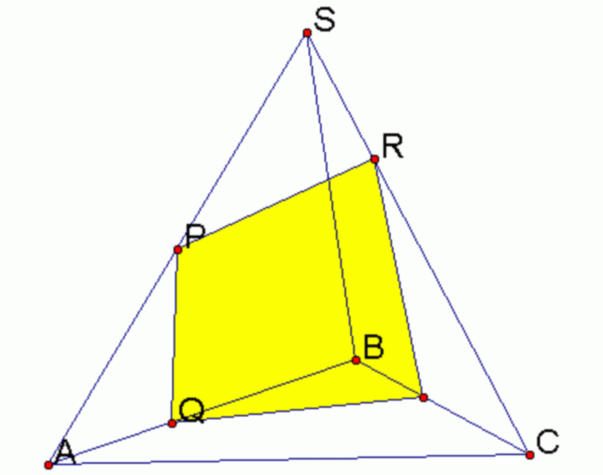
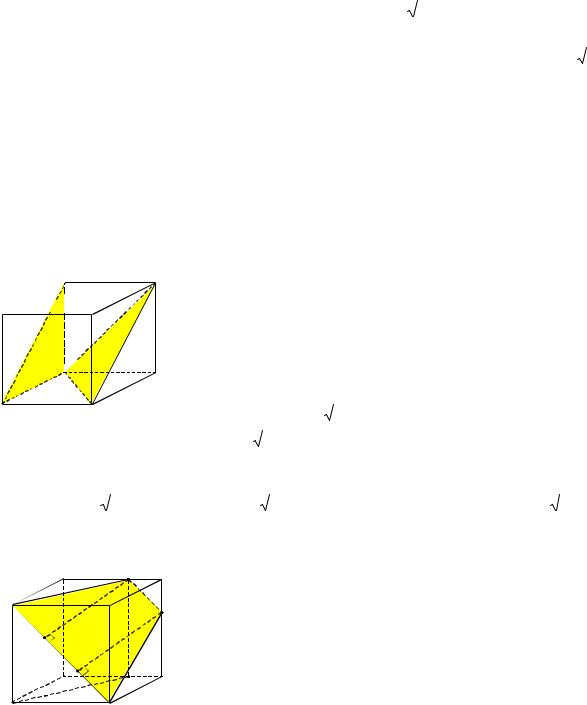
Пример 3. Дан куб ABCDA1B1C1D1 с ребром, равным a. На рёбрах основания AB и AD взяты соответственно точки M и N так, что AM :MB 2:1 и AN :ND 2:1. Найти площадь сечения куба плоскостью, проходящей через точки M, N и C1 .

Решение. Приведём два способа решения этой задачи. Первый способ основан на разбиении многоугольника, полученного в сечении, на части и вычислении по отдельности площадей этих частей, а второй – на использовании теоремы о площади ортогональной проекции многоугольника. Читатель сам сможет определить, какой из предложенных подходов предпочтительнее.

Прежде чем перейти к решению задачи этими двумя способами, используя метод следов, построим сечение куба плоскостью, проходящей через точки M, N и C1. Соединим вначале точки M и N, поскольку они лежат в одной плоскости ABC (см. рис. 3а). Прямая MN лежит в плоскости ABC и пересекает прямые BC и DC в точках P и L соответственно.

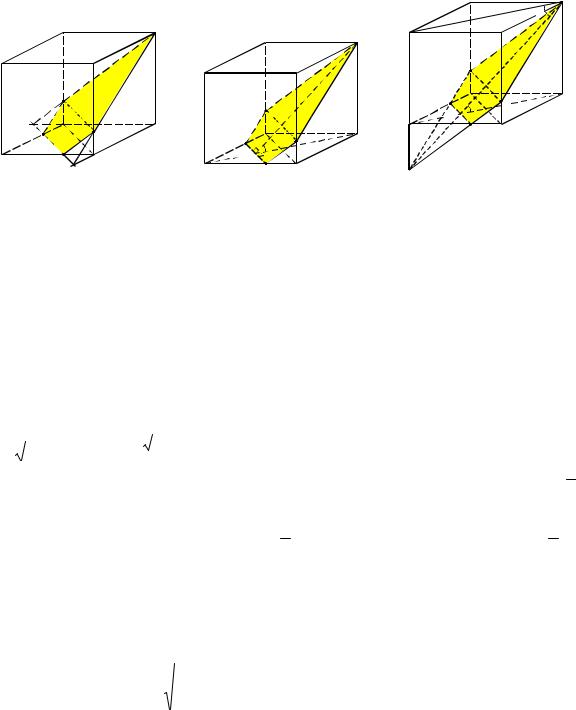
Точка P принадлежит не только плоскости нижнего основания куба, но и плоскости грани BB1C1 (как и точка C1), поэтому, соединив P и C1, получим на ребре BB1 принадлежащую сечению точку F. Далее, точка L принадлежит не только плоскости нижнего основания куба, но и плоскости грани DD1C1 (как и точка C1), поэтому, соединив L и C1, получим на ребре DD1 принадлежащую сечению точку T. В завершение построения соединим в грани

AA1B1 точки M и F, а в грани AA1D1 точки T и N. Таким образом, сечением куба

ABCDA1B1C1D1 является пятиугольник MFC1TN .

							B1		C1
	B1					A1		D1
		C1	B1
				C1

A1	D1
A1		D1		F

	F					M	B		C
P			F			T
B
		B		O		D
M	T		C	T	A	N
			M		C
A	N	D	A	O	D	A2
	L		N
	а				б		в
				Рис. 3

Первый способ решения. Проведём в пятиугольнике MFC1TN диагональ FT. Она ра-

зобьёт сечение на треугольник FC1T и четырёхугольник MFTN. Вычислим их площади по отдельности.

Найдем вначале площадь четырёхугольника MFTN. Поскольку MN || BD и BD лежит в плоскости BB1D1 , то MN || BB1D1 (по признаку параллельности прямой и плоскости). Так как секущая плоскость проходит через MN и пересекает плоскость BB1D1 по прямой TF, то TF ||MN (по теореме о линии пересечения). Далее, поскольку BD||MN и TF ||MN , то TF || BD. Следовательно, четырёхугольник MFTN – трапеция.

Из	прямоугольного треугольника AMN по теореме Пифагора находим
			2a	. Поскольку BF \|\| DT , как отрезки, расположенные на боко-
		2
MN	AM2 AN2

		3

вых рёбрах куба, то четырёхугольник BFTD – параллелограмм, а значит, TF BD a2 . Покажем, что трапеция MFTN – равнобедренная. Для этого рассмотрим вначале пря-

моугольный треугольник LDN. В нём ND a , LND 45 , следовательно, LD a . Да-

									3	3
лее, треугольники LDT и	LCC		подобны	с коэффициентом k	LD	1	. Поэтому

						1				LC 4
	CC1
DT		a	. Так как четырёхугольник BFTD – параллелограмм, то BF DT	a	, а зна-


4	4							4
чит, прямоугольные треугольники NDT и MBF равны по двум катетам. Поэтому, по тео-
реме Пифагора, NT MF	a	2		a	2	5a
							.
		12
					3		4

Далее находим длину h1 высоты этой равнобедренной трапеции MFTN. Опуская очевидные выкладки (читателю предлагается проделать их самостоятельно), получим


h			a 17		. Отсюда S	MFTN	TF MN	h	a 2 2a 2 3	a 17	5a2 34	.
	12		2	2			12		72
1					1
		Решим теперь задачу вычисления площади треугольника FC1T . Найдём в нём длины
сторон FC1 и TC1 . Для этого рассмотрим прямоугольные треугольники FB1C1	и TD1C1.

Они равны по двум катетам, поэтому по теореме Пифагора FC1 TC1 a	2	3a	2		5a
							,
			4
													4

т.е. треугольник FC1T – равнобедренный. Найдем длину h2 высоты этого треугольника. Опуская очевидные выкладки (читателю предлагается проделать их самостоятельно), по-


		a 17									TF h			1				a	17			a2 34

лучим h				. Отсюда S	FC T			2				a	2							.

2		4							2				2					4			8
						1

Наконец, площадь всего сечения:
						5a2					a2				7a2								7a2
SMFC TN SMFTN	S FC T		34				34			34		.				Ответ:	34	.

1			1			72					8						36							36

Второй способ решения. Для нахождения площади сечения воспользуемся формулой (1). Ортогональной проекцией пятиугольника MFC1TN на плоскость ABC служит многоугольник MBCDN (см. рис. 3б). Найдём площадь MFC1TN . Очевидно, что SMBCDN SABCD S AMN . Треугольник AMN – прямоугольный. Длины его катетов AM и

AN, согласно условию задачи, равны

. Поэтому SMBCDN a

7a2

2 3

Далее, проведём в квадрате ABCD диагонали BD и AC. Равнобедренные прямоуголь-

ные

треугольники

AMN

ABD

подобны

с коэффициентом

. Тогда

OC AC AO

. Кроме того, поскольку MN || BD и BD AC ,

то MN OC.

Соединим точки O и C1. Тогда OC1

– наклонная к плоскости ABC, OC – проекция на-

клонной

OC1

и MN OC.

Следовательно, по

теореме

трёх

перпендикулярах,

MN OC1 . Значит,

COC1

– линейный угол двугранного угла CMNC1 .

Вычислим теперь косинус угла между плоскостью сечения и нижним основанием куба. Для этого рассмотрим прямоугольный треугольник CC1O . По теореме Пифагора

			a 17	. Откуда cos	OC	2	2	.
OC	OC2 CC2

1	1	3		OC1	17

Поскольку, согласно теореме о площади ортогональной проекции многоугольника,


SMFC TN	S	MBCDN	, то окончательно получим: SMFC TN	7a	2		17			7a2 34
									.
	cos
1		1	9			2 2		36

Замечание. При решении задачи вторым способом для нахождения cos можно до-

строить секущую плоскость до её пересечения с продолжением ребра AA1 за точку A (см.

рис. 3в). Тогда cos	SA BC D
	1 1 1 1	.

	SA MFC TN
2	1

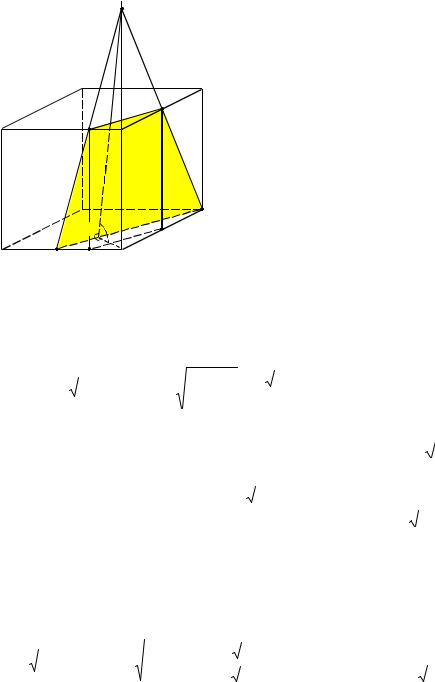
Пример 4. Дан куб ABCDA1B1C1D1 с ребром, равным a. Точка M – середина ребра AD,

точка N – середина ребра C1D1 . Найти площадь сечения куба плоскостью, проходящей через точки M, N и C.

Решение. Построим сечение куба плоскостью, проходящей через точки M, N и C. Соединим вначале точки M и C, поскольку они лежат в одной плоскости ABC. Затем соединим точки C и N, так как они лежат в одной плоскости DD1C1 (см. рис. 4). Прямые СN и

DD1 лежат в плоскости DD1C1	и не параллельны. Значит, они пересекаются в точке Q.
Точка Q принадлежит не только плоскости DD1C1, но и плоскости грани AA1D1 (как и
точка M),	поэтому,	соединив M и Q, получим на ребре A1D1 принадлежащую сечению
точку P. В завершение построения соединим в верхней грани куба точки P и N.
			Q	Отметим, что плоскости оснований куба парал-
			лельны друг другу. Значит, по свойству параллель-
				ных плоскостей (если две параллельные плоскости
				пересечены третьей, то линии пересечения парал-
		B1	C1	лельны) MC\|\| PN . Далее, поскольку прямые MP и
		CN пересекаются в точке Q, то стороны MP и CN че-
A1		P	N	тырёхугольника MPNC не параллельны. Таким обра-
	D1	зом, сечением куба ABCDA1B1C1D1 является трапеция

			MPNC.

				Для нахождения площади сечения воспользуемся
				формулой (1). Построим вначале линейный угол дву-
		BO	C	гранного угла DMCQ. Для этого в прямоугольном
		треугольнике MCD опустим перпендикуляр DO к ги-
			N1	потенузе MC. Соединим точки O и Q. Тогда QO – на-
A	M	P1 D	клонная к плоскости ABC, DO – проекция наклонной
				QO и MC DO.	Следовательно, по теореме о трёх
		Рис. 4		перпендикулярах,	MC QO. Значит, QOD –
				линейный угол двугранного угла DMCQ.

Вычислим теперь косинус угла между плоскостью сечения и нижним основанием куба. Для этого рассмотрим вначале прямоугольный треугольник MCD. По теореме Пифа-

a 5

. Для нахождения высоты DO выразим пло-

гора MC

MD2 DC2

щадь S MCD

двумя способами:

MD DC

MC DO

S MCD

, S MCD

DO.

DO. Отсюда DO

Тогда, приравняв их, получим

Далее, рассмотрим прямоугольные треугольники CDQ и ND1Q. У этих треугольников острый угол при вершине Q – общий. Значит, они подобны. Поскольку, согласно условию

задачи, точка N –

середина ребра C1D1, то коэффициент подобия треугольников CDQ и

ND1Q равен 2. Отсюда, очевидно, что DQ 2a.

Рассмотрим,

наконец,

прямоугольный треугольник QOD. По теореме Пифагора

QO DQ

. Откуда cos

Построим теперь четырёхугольник MP1N1C, являющийся ортогональной проекцией трапеции MPNC на плоскость ABC. Так как PN лежит в плоскости, построенной на парал-

лельных прямых PP1 и NN1,

и параллельна плоскости ABC,

то линия пересечения

P1N1

плоскостей ABC и PNN1

параллельна PN (по теореме о линии пересечения). Поскольку

P1N1 || PN и MC|| PN , то P1N1 ||MC, а значит, четырёхугольник MP1N1C – трапеция.

Найдём площадь трапеции MP1N1C. Очевидно, что SMPN C S

MCD

S PN D . Прямо-

угольные треугольники MCD и P1N1D подобны, так как P1N1D MCD (как соответст-

венные). Точка

N1 – середина ребра CD, значит,

коэффициент подобия треугольников

MCD и PN

D равен 2. Поэтому S

MPN C

MCD

3a2

1 1

Согласно

теореме

площади

ортогональной

проекции

многоугольника,

SMP1N1C

3a2

SMPNC

, откуда окончательно получим: SMPNC

cos

3a2

Ответ:

3. Применение теоремы о площади ортогональной проекции многоугольника при вычислении угла между плоскостями

Кроме рассмотренного основного применения теоремы о площади ортогональной проекции многоугольника её можно также использовать при вычислении угла между плоскостью сечения и плоскостью какой-либо грани многогранника (обычно в качестве такой грани выступает основание пирамиды или призмы). Так поступают в случаях, когда нахождение Sпр и Sсечения является более простой задачей, чем непосредственное вычисление двугранного угла , сопряжённое с построением на чертеже его линейного угла.

A1 D1

A D

Рис. 5

Из формулы о

Пример 5. В кубе

ABCDA1B1C1D1 найти угол между

плоскостью грани AA1B1B и плоскостью BC1D.

Решение. Пусть ребро куба равно a. Ортогональной

проекцией треугольника BC1D является треугольник AB1B

(см. рис. 5), площадь

которого равна

Поскольку

BD BC1

C1A a

(как диагонали

граней

куба), то

a2 .

S BC D

площади ортогональной проекции многоугольника получим:

S AB B

. Отсюда arccos

Ответ: arccos

S BC D

Пример 6. В кубе

ABCDA1B1C1D1 через его вершины

A , D и точку M, расположенную на ребре CC

так, что

CM :MC1 2:1, проведено сечение. Найти угол наклона

секущей плоскости к плоскости основания ABCD.

Решение. Построим сечение куба плоскостью, прохо-

дящей через точки A1, D и M. Соединим вначале точки A1

и D, поскольку они лежат в одной плоскости DD A . Затем

Dсоединим точки D и M, так как они лежат в одной плоскости DD1C1 (см. рис. 6). Противоположные боковые грани

Рис. 6	DD1A1	и CC1B1 в кубе параллельны. Поэтому секущая

плоскость, согласно свойству параллельных плоскостей (если две параллельные плоскости пересечены третьей, то линии пересечения параллельны) будет пересекать грань CC1B1 по прямой MP так, что MP|| A1D . Наконец, соединим точки A1 и P, так как они лежат в одной плоскости A1B1C1. Поскольку A1P и DM не параллельны, то четырёхуголь-

ник A1PMD, являющийся сечением куба, – трапеция.

Ортогональной проекцией трапеции A1PMD плоскости основания ABCD является прямоугольная трапеция ALCD. Для определения угла наклона секущей плоскости к

плоскости основания ABCD воспользуемся формулой cos SALCD . Для этого найдем

SA1PMD

площади указанных трапеций.

Пусть ребро куба равно a. Тогда, согласно условию задачи, MC a . Кроме того,
1	3

очевидно, что A1D a2. Поскольку MP|| A1D и DD1 ||MC1, то A1DD1 PMC1 (как углы с соответственно сонаправленными сторонами). Поэтому прямоугольные треуголь-

ники A DD и PMC подобны с коэффициентом k	1	. Следовательно, MP	A1D		a 2

1	1							1																						3						3	3
	A1D1			a
и PC		.

1	3	3
																										2a
Далее,	так как	A B DC a, B P CM		,				то		прямоугольные	треугольники

										1	1												1				3
A1B1P			DCM
и		равны				по			двум		катетам.		Поэтому			по		теореме		Пифагора

		4a2				a						.
A P DM a2			13

1								9							3

Следовательно, трапеция A1PMD равнобедренная. Найдём её высоту. Для этого опус-
тим из	точек P	и				M		перпендикуляры		PQ и					MK		на			основание A1D. Тогда
	A1D MP			a			. Отсюда по теореме Пифагора из прямоугольного треуголь-
AQ DK		2

1		2							3

																																				13a2		2a2		a	.
																																						11
ника A PQ высота трапеции A PMD равна:	PQ					A P2		AQ2

1																				1												1		1	9	9			3

																											A D MP				2a2	22
Таким образом, площадь сечения: SAPMD		1							PQ									.
			2								9
																						1
																																				a
В прямоугольной трапеции ALCD основания равны AD a	и LC PC	,		а высота
3
																								AD LC				2a2					1
DC a . Тогда её площадь:		SALCD	DC	.
		2					3

Подставляя полученные значения площадей в формулу, находим
																					S					2a	2	2a2	3
														cos		ALCD	:	22	22		.
															SAPMD	3	9							22

																						1
	3																								Ответ: arccos	3		.
Следовательно, arccos	22		.																					22

															22																					22

Пример 7. Плоскость пересекает прямоугольный параллелепипед с квадратным основанием по ромбу с острым углом . Под каким углом эта плоскость пересекает боковые рёбра параллелепипеда?

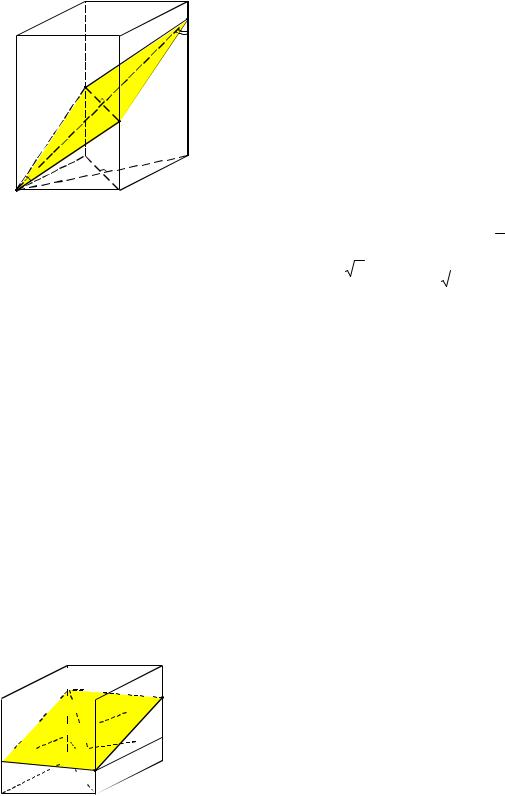
Решение. Без ограничения общности рассуждений будем считать, что секущая плоскость проходит через вершину A нижнего основания параллелепипеда, пересекая его бо-

ковые рёбра BB1, CC1	и DD1	в точках M, N и P соответственно (см. рис. 7).
	B1		C1	Рассмотрим прямоугольные треугольники AMB и
		D1		N	APD. В них AM AP , т.к., согласно условию, AMNP –
A1			ромб. Кроме того, AB AD как стороны основания
		x		параллелепипеда ABCD, являющегося квадратом. Сле-

			x		довательно, AMB APD по гипотенузе и катету, а
	M			значит, MB PD.
		O			Рассмотрим теперь четырёхугольник BMPD. В нём
x		P			противоположные стороны MB и PD параллельны и
	x B	a			равны, значит, BMPD – параллелограмм (отметим до-
		C	полнительно, что BMPD – прямоугольник). Отсюда
	a		a	MP\|\| BD и MP BD.
A	a	D			Пусть сторона ромба AMNP равна x, а ребро осно-
	Рис. 7			вания параллелепипеда равно a. Тогда SAMNP x2 sin ,

SABCD a2 . Поскольку MP BD a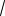2, то из прямо-

угольного треугольника AOP имеем: sin

a 2

, или a x

sin

Вычислим косинус угла между секущей плоскостью и основанием:

SABCD

2x2 sin2

cos

SAMNP

x2 sin

Обозначим через угол,

x2 sin

под которым секущая плоскость пересекает боковые рёбра

параллелепипеда. Поскольку

, то

cos cos

sin . Значит,

sin tg

Отсюда arcsin tg


						Ответ: arcsin tg	.

								2
	Пример 8. В кубе ABCDA1B1C1D1 с ребром, равным a, через точки M, P и N на рёбрах
BB , CC и DD соответственно, такие, что BM	3a	, CP	2a	и DN	a	, проведена се-
1	1	1	4	3	4

кущая плоскость. Найти угол между плоскостью сечения и плоскостью основания куба.

Решение. Построим сечение куба плоскостью, проходящей через точки M, P и N. Соединим вначале точки M и P, поскольку они лежат в одной плоскости BB1C1 . Затем соединим точки P и N, т.к. они лежат в одной плоскости

DD1C1 (см. рис. 8).

Противоположные боковые грани AA1D1 и BB1C1 в кубе параллельны. Поэтому секущая плоскость, согласно свойству параллельных плоскостей (если две параллельные плоскости пересечены третьей, то линии пересечения параллельны) будет пересекать грань AA1D1 по прямой NQ так, что

NQ|| MP.

Соединим точки M и Q, т.к. они лежат в одной плоскости AA1B1. Тогда MQ|| NP по

тому же свойству параллельных плоскостей AA1B1

CC1D1 . Таким образом,

сечение

представляет собой параллелограмм MPNQ.

Вычислим площадь MPNQ и, поскольку квадрат ABCD – ортогональная проекция

MPNQ, определим косинус угла между плоскостью сечения и плоскостью ABC.

Найдём стороны треугольника MNP. Используя теорему Пифагора, получим:

из прямоугольного треугольника MLP (ML CC1 )

145

MP (LC PC)2 MC2

144

из прямоугольного треугольника NPS (NS CC1)

25a2

13a

(PC SC)2 NS2

из прямоугольного треугольника MNK (KN BB1)

144

2a2

(BM BK)2 KN2

Полупериметр треугольника MNP равен p

31)

. Используя формулу Герона,

145

найдём его площадь:

SMNP

170

. Следовательно,

SMPNQ 2SMNP

170

. Из фор-

SABCD

мулы для

площади

ортогональной

проекции получим: cos

. Отсюда

SMPNQ

170

arccos

170

Ответ: arccos

170

4. Применениетеоремы о площади ортогональной проекции многоугольника при вычислении площади боковой поверхности пирамиды

Ещё одной известной задачей, при решении которой применяется теорема о площади ортогональной проекции многоугольника, является задача вычисления площади Sбок бо-

ковой поверхности пирамиды, у которой все боковые грани одинаково наклонены к плоскости её основания (под углом ), или вершина пирамиды лежит на перпендикуляре, восставленном из центра вписанной в её основание окружности. Тогда

Sбок	Sосн	.	(2)

	cos

Пример 9. Стороны основания треугольной пирамиды равны 6 см, 10 см и 14 см. Каждый двугранный угол при её основании равен 30°. Найти площадь боковой поверхности пирамиды.

Решение. Для нахождения площади сечения воспользуемся формулой (2). Найдём вначале площадь основания треугольной пирамиды, воспользовавшись формулой Герона. Поскольку полупериметр треугольника в основании равен 15 см, то

Sосн 15 (15 6) (15 10) (15 14) 153 (см2).

Тогда Sбок		Sосн	3	2
	15 3:	30
		(см ).
cos30	2

Ответ: 30 см2.

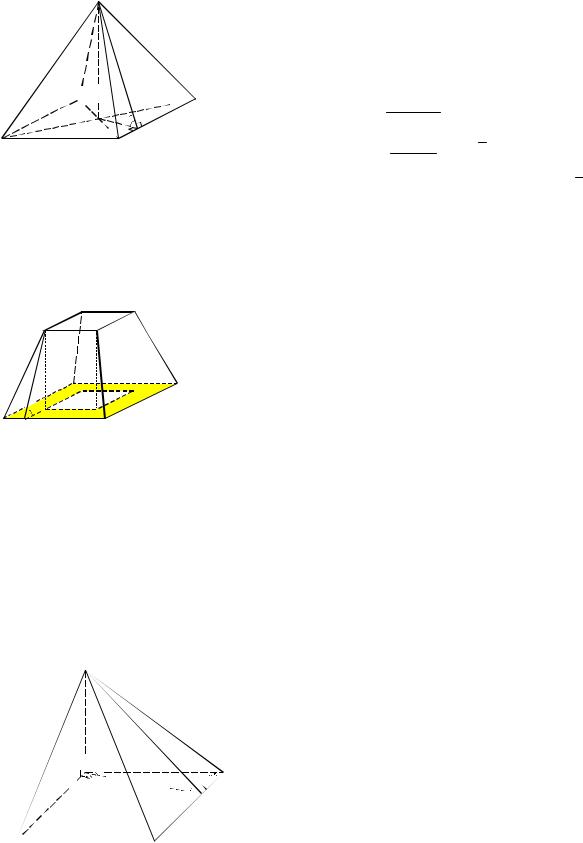
Пример 10. Боковые грани пирамиды, в основании которой лежит ромб, наклонены к плоскости основания под углом 30°. Диагонали ромба равны 10 см и 24 см. Найти площадь боковой поверхности пирамиды.

Решение. Для нахождения площади сечения воспользуемся формулой (2). Поскольку боковые грани пирамиды SABCD наклонены к основанию ABCD под одинаковым углом, то её вершина S проектируется в центр вписанной в ромб окружности, т. е. в точку O пересечения его диагоналей (см. рис. 9). Тогда

SABCD AC BD 120 (см2). 2

Следовательно, Sбок SABCD 803 (см2). cos30

Ответ: 803 см2.

Пример 11. В правильной усечённой четырёхугольной пирамиде стороны нижнего и верхнего оснований равны соответственно a и b (a b). Найти площадь полной поверхности усечённой пирамиды, если её боковые грани наклонены к плоскости основания под углом .

Решение. Поскольку основаниями правильной усе-

чённой четырёхугольной пирамиды являются квадраты со

сторонами a и b, то сумма их площадей равна

a2 b2 .

Очевидно, что ортогональная проекция боковой поверхно-

сти усечённой пирамиды на плоскость нижнего основания

представляет собой квадрат со стороной a, из которого

«вырезан» квадрат со стороной b. При этом стороны «вы-

Рис. 10

резанного» квадрата параллельны сторонам нижнего осно-

вания пирамиды (см. рис. 10). Так как боковые грани усе-

чённой пирамиды наклонены к плоскости основания под

одинаковым углом , то площадь её боковой поверхности равна: Sбок

Sпр

cos

Таким образом, S

полн a

a2 b2

Ответ: a

a2 b2

cos

Пример 12. Основанием пирамиды является ромб. Две боковые грани перпендикулярны к плоскости основания и образуют двугранный угол в 120°, а две другие боковые грани наклонены к плоскости основания под углом 30°. Найти площадь поверхности пирамиды, если её высота равна 12.

Решение. Площадь полной поверхности пирамиды равна сумме площадей боковых граней и основания, т. е.

Sполн SASB SBSC SASD SDSC SABCD .

Положим, что сторона ромба ABCD равна a. C Пусть боковые грани ASB и BSC пирамиды

SABCD перпендикулярны к плоскости основания ABCD (см. рис. 11). Тогда боковое ребро SB пирамиды перпендикулярно к плоскости ромба и равно высоте, а боковые грани ASB и BSC пирамиды являются равными прямоугольными треугольниками

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Как вычислить площадь сечения

Объемные фигуры

Цилиндр

Сечения конуса

Сечения призмы

Пирамида

Сечения трехмерных фигур — площади и периметр

Алгоритм определения площади и периметра сечения объемных фигур

Площадь сечения

Площадь треугольника

Площадь круга

Площадь прямоугольника

Пример решения задачи

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Объемные фигуры

Цилиндр

Сечения конуса

Сечения призмы

Пирамида

Вам также может понравиться

Как нашли титаник под водой фильм

Как составить акт при отсутствии отопления

Как составить акт дарения дома

Добавить комментарий Отменить ответ