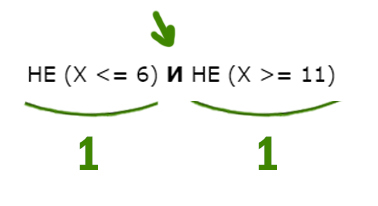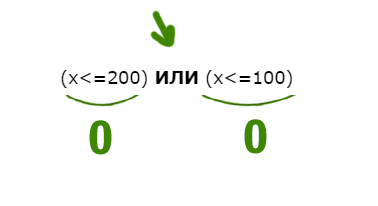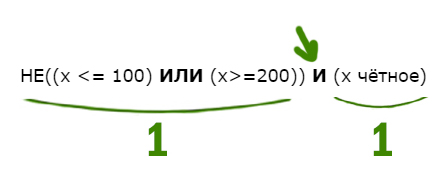На уроке рассмотрен материал для подготовки к огэ по информатике, решение задания 3
3-е задание: «Значение логического выражения»
Уровень сложности — базовый,
Максимальный балл — 1,
Примерное время выполнения — 3 минуты.
* до 2020 г — это задание № 2 ОГЭ
Содержание:
- Объяснение 3 задания ОГЭ по информатике
- ОГЭ информатика разбор задания 3
- Актуальное
- Тренировочные
- Для подготовки к решению 3 задания ОГЭ по информатике следует вспомнить знаки сравнения. В логических выражениях используются следующие знаки сравнения:
- В логических выражениях участвуют всего два значения выражений: ИСТИНА и ЛОЖЬ.
- Рассмотрим результат выполнения логических выражений для двух высказываний — А и Б:
- Если отрицание НЕ стоит перед скобкой с выражением, то НЕ ставится перед каждой частью выражения в скобках и при этом операция внутри скобок меняется:
|
> |
больше |
|
< |
меньше |
|
= |
равно |
|
≥ |
больше или равно |
|
≤ |
меньше или равно |
| 1 | А ИЛИ Б = ИСТИНА → | если А=истина И Б=истина |
| 2 | если А=истина И Б=ложь | |
| 3 | если А=ложь И Б=истина | |
| 4 | А ИЛИ Б = ЛОЖЬ → | если А=ложь И Б=ложь |
Вывод: логическое выражение с операцией ИЛИ легче проверить «на ложь»:
с операцией ИЛИ результатом будет ЛОЖЬ только в одном единственном случае, — когда оба выражения — А и Б — ложны
| 1 | А И Б = ИСТИНА → | если А=истина И Б=истина |
| 2 | А И Б = ЛОЖЬ → | если А=истина И Б=ложь |
| 3 | если А=ложь И Б=истина | |
| 4 | если А=ложь И Б=ложь |
Вывод: логическое выражение с операцией И легче проверить «на истинность»:
с операцией И результатом будет ИСТИНА только в одном единственном случае, — когда оба выражения — А и Б — истинны
| Исходные значения | Результат | |
|---|---|---|
| 1 | НЕ А если А=истина |
А = ЛОЖЬ |
| НЕ(5 > 0) | 5 ≤ 0 | |
| 2 | НЕ А если А=ложь |
А = ИСТИНА |
| НЕ(-2 > 0) | -2 ≤ 0 | |
| 3 | НЕ (НЕ А) | = А |
| 1 | НЕ |
| 2 | выражение в скобках |
| 3 | И |
| 4 | ИЛИ |
| 1 | НЕ (А ИЛИ Б) | НЕ А И НЕ Б |
| 2 | НЕ (А И Б) | НЕ А ИЛИ НЕ Б |
ОГЭ информатика разбор задания 3
Подробный видеоразбор по ОГЭ 3 задания:
📹 Видеорешение на RuTube здесь
Актуальное
Значение логического выражения
Разбор задания 3.7. Демонстрационный вариант ОГЭ 2022 г ФИПИ:
Напишите наименьшее число x, для которого истинно высказывание:
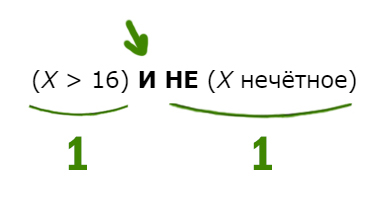
(x > 16) И НЕ (x нечётное)
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (x нечётное) результат: x чётное
(x > 16) И (x чётное)
(x > 16) И (x чётное) = ИСТИНА истина истина
Ответ: 18
Разбор задания 3.12:
Напишите наименьшее число x, для которого ложно высказывание:
(x ≤ 15) ИЛИ НЕ (x нечётное)
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (x нечётное) результат: x чётное
(x ≤ 15) ИЛИ (x чётное) = 0 (ложь)
(x ≤ 15) ИЛИ (x чётное) = ЛОЖЬ ложь ложь
Ответ: 17
Тренировочные
Разбор задания 3.1:
Для какого из приведённых значений числа X ложно высказывание:
НЕ (X < 6) ИЛИ (X < 5) ?
1) 7
2) 6
3) 5
4) 4
Подобные задания для тренировки
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (X < 6) (X < 6) - ложь, значит результат: X ≥ 6
(X ≥ 6) ИЛИ (X < 5)
(X ≥ 6) ИЛИ (X < 5) = ЛОЖЬ ложь ложь
1. (X ≥ 6) = ЛОЖЬ => X < 6 2. (X < 5) = ЛОЖЬ => X ≥ 5
5 < 6 и 5 ≥ 5
Ответ: 3
Разбор задания 3.2:
Для какого из приведённых значений числа X истинно высказывание:
(X < 8) И НЕ (X < 7) ?
1) 9
2) 8
3) 7
4) 6
Подобные задания для тренировки
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (X < 7) (X < 7) - ложь, значит результат: X ≥ 7
(X < 8) И (X ≥ 7)
(X < 8) И (X ≥ 7) = ИСТИНА истина истина
1. (X < 8) = ИСТИНА => X < 8 2. (X ≥ 7) = ИСТИНА => X ≥ 7
7 < 8 и 7 ≥ 7
Ответ: 3
Разбор задания 3.3:
Для какого из приведённых имён ЛОЖНО высказывание:
НЕ ((Третья буква согласная) И (Последняя буква гласная)) ?
1) Анна
2) Елена
3) Павел
4) Егор
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ, по таблице 6 для НЕ перед скобкой с выражением имеем:
НЕ ((Третья буква согласная) И (Последняя буква гласная)) = = (НЕ(Третья буква согласная) ИЛИ НЕ(Последняя буква гласная))
1. НЕ(Третья буква согласная) => Третья буква НЕ согласная 2. НЕ(Последняя буква гласная) => Последняя буква НЕ гласная
(Третья буква не согласная) ИЛИ (Последняя буква не гласная)
(Третья буква не согласная) ИЛИ (Последняя буква не гласная) = ЛОЖЬ
ложь ложь
1. (Третья буква не согласная) = ЛОЖЬ => Третья буква согласная 2. (Последняя буква не гласная) = ЛОЖЬ => Последняя буква гласная
Третья буква "н" согласная и Последняя буква "а" гласная
Ответ: 1
Разбор задания 3.4:
Для какого из приведённых имён ИСТИННО высказывание:
НЕ ((число > 50) ИЛИ НЕ(число четное)) ?
1) 43
2) 50
3) 61
4) 72
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ в малых скобках:
НЕ(число четное) => число нечетное
НЕ ((число > 50) ИЛИ (число нечетное)) = = (НЕ(число > 50) И НЕ(число нечетное))
1. НЕ(число > 50) => число <= 50 2. НЕ(число нечетное) => число четное
(число <= 50) И (число четное)
(число <= 50) И (число нечетное) = ИСТИНА
истина истина
Ответ: 2
Разбор задания 3.5.:
Для какого из приведённых слов ЛОЖНО высказывание:
(последняя буква согласная) ИЛИ НЕ ((первая буква согласная) И (вторая буква гласная)) ?
1) Тигр
2) Выдра
3) Енот
4) Краб
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ, по таблице 6 для НЕ перед скобкой с выражением имеем:
НЕ ((первая буква согласная) И (вторая буква гласная)) = = (НЕ(первая буква гласная) ИЛИ НЕ(вторая буква гласная))
1. НЕ(первая буква согласная) => первая буква гласная 2. НЕ(вторая буква гласная) => вторая буква согласная
(первая буква гласная) ИЛИ (вторая буква согласная)
(последняя буква согласная) ИЛИ (первая буква гласная) ИЛИ (вторая буква согласная)
(последняя буква согласная) ИЛИ (первая буква согласная) ИЛИ
ложь ложь
(вторая буква согласная) = ЛОЖЬ
ложь
1. (последняя буква согласная) = ЛОЖЬ => последняя буква гласная 2. (первая буква гласная) = ЛОЖЬ => первая буква согласная 3. (вторая буква согласная) = ЛОЖЬ => вторая буква гласная
Ответ: 2
Разбор задания 3.6:
Для какого из приведённых слов верно высказывание:
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная)) ?
1) АИДА
2) СЕРГЕЙ
3) СТЕПАН
4) АРТЕМ
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении находятся большие скобки, с которых необходимо начать решение.
- Внешняя операция, т.е. последняя по приоритету — это операция И. Рассмотрим ее подробней, разделив общее высказывание на две части относительно этой операции:
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная))
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная)) истина истина
((последняя буква согласная) ИЛИ (вторая буква согласная))
истина ИЛИ истина
(первая буква гласная) И (или первая или вторая буква в слове согласная) истина истина
Ответ: 4
Осуществление поиска в готовой базе данных по сформулированному условию
* до 2020 г – это задание № 12 ОГЭ
Разбор задания 3.8:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Рига | скорый | 15:45 | Рижский |
| Ростов | фирменный | 17:36 | Казанский |
| Самара | фирменный | 14:20 | Казанский |
| Самара | скорый | 17:40 | Казанский |
| Самара | скорый | 15:56 | Казанский |
| Самара | скорый | 15:56 | Павелецкий |
| Самара | фирменный | 23:14 | Курский |
| Санкт-Петербург | скорый | 8:00 | Ленинградский |
| Санкт-Петербург | скорый | 4:00 | Ленинградский |
| Саратов | скорый | 14:57 | Павелецкий |
| Саратов | пассажирский | 15:58 | Павелецкий |
| Саратов | скорый | 15:30 | Павелецкий |
Сколько записей в данном фрагменте удовлетворяют условию:
(Категория поезда = «скорый») ИЛИ (Вокзал = «Павелецкий»)?
✍ Решение:
- В условии находится логическая операция ИЛИ, которая истинна тогда, кода хоть одно из логических выражений истинно. Для нашего случая это говорит о том, что нужно посчитать те строки, в которых:
1. Категория поезда = «скорый» и Вокзал = любой 2. Категория поезда = «скорый» и Вокзал = «Павелецкий» 3. Категория поезда = любой и Вокзал = «Павелецкий»
Ответ: 9
Разбор задания 3.9:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Балаково | скорый | 20:22 | Павелецкий |
| Бийск | скорый | 61:11 | Казанский |
| Бишкек | скорый | 121:20 | Казанский |
| Благовещенск | пассажирский | 142:06 | Ярославский |
| Брест | скорый | 14:19 | Белорусский |
| Валуйки | фирменный | 14:57 | Курский |
| Варна | скорый | 47:54 | Киевский |
| Волгоград | скорый | 18:50 | Павелецкий |
| Волгоград | скорый | 24:50 | Курский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Гродно | скорый | 16:34 | Белорусский |
Сколько записей в данном фрагменте удовлетворяют условию:
(Категория поезда = «скорый») И (Время в пути > 40:00)?
✍ Решение:
- В условии находится логическая операция И, которая истинна только тогда, кода оба (все) выражения истинны. Для нашего случая это говорит о том, что нужно посчитать те строки, в которых:
Категория поезда = «скорый» и Время в пути > 40:00 одновременно
Ответ: 3
Разбор задания 3.10:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Балаково | скорый | 20:22 | Павелецкий |
| Бийск | скорый | 61:11 | Казанский |
| Бишкек | скорый | 121:20 | Казанский |
| Благовещенск | пассажирский | 142:06 | Ярославский |
| Брест | скорый | 14:19 | Белорусский |
| Валуйки | фирменный | 14:57 | Курский |
| Варна | скорый | 47:54 | Киевский |
| Волгоград | скорый | 18:50 | Павелецкий |
| Волгоград | скорый | 24:50 | Курский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Гродно | скорый | 16:34 | Белорусский |
Сколько записей в данном фрагменте удовлетворяют условию:
(Пункт назначения = «Волгоград») ИЛИ (Категория поезда = «пассажирский») И (Время в пути < 50:00)?
В ответе укажите одно число — искомое количество записей.
✍ Решение:
- В условии находятся две логических операции: И и ИЛИ. Первой всегда выполняется операция И, затем добавляются записи для операции ИЛИ.
- Операция И истинна только тогда, кода оба (все) выражения истинны.
(Категория поезда = «пассажирский») И (Время в пути < 50:00) одновременно
(Пункт назначения = «Волгоград») добавить к предыдущему результату
Ответ: 4
Разбор задания 3.11:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Махачкала | скорый | 39.25 | Павелецкий |
| Махачкала | скорый | 53.53 | Курский |
| Мурманск | скорый | 35.32 | Ленинградский |
| Мурманск | скорый | 32.50 | Ленинградский |
| Мурманск | пассажирский | 37.52 | Ленинградский |
| Мурманск | пассажирский | 37.16 | Ленинградский |
| Назрань | пассажирский | 40.23 | Павелецкий |
| Нальчик | скорый | 34.55 | Казанский |
| Нерюигри | скорый | 125.41 | Казанский |
| Новосибирск | скорый | 47.30 | Ярославский |
| Нижневартовск | скорый | 52.33 | Казанский |
| Нижний Тагил | фирменный | 31.36 | Ярославский |
Сколько записей в данном фрагменте удовлетворяют условию:
НЕ (Вокзал = «Ленинградский») И (Время в пути > 50.00)?
✍ Решение:
- В условии находятся две логических операции: НЕ и И.
- Первой всегда выполняется операция НЕ, затем добавляются записи для операции И.
- Операция НЕ обозначает обратное высказывание:
НЕ(Вокзал = «Ленинградский»)
то же самое, что
(Вокзал ≠ «Ленинградский»)
(Вокзал ≠ «Ленинградский») И (Время в пути > 50.00) одновременно
Ответ: 3
Привет! Продолжаем разбирать ОГЭ по информатике 2023. Сегодня посмотрим 3 задание.
Третье задание из ОГЭ по информатике проверяет умение работать с логическим выражением.
В логическом выражении могут использоваться союз И и союз ИЛИ.
Пусть 0 – это ложь, 1 – Истина. Тогда напишем таблицу истинности для союза И и для союза ИЛИ.
Таблица истинности для союза И
| Выражение | Результат |
| 0 И 0 | 0 |
| 0 И 1 | 0 |
| 1 И 0 | 0 |
| 1 И 1 | 1 |
Союз И похож на умножение в математике. Если в логическом выражении присутствует 0 (ложь), то в итоге тоже получается 0 (ложь). Лишь две единицы дают тоже единицу.
Таблица истинности для союза ИЛИ
| Выражение | Результат |
| 0 ИЛИ 0 | 0 |
| 0 ИЛИ 1 | 1 |
| 1 ИЛИ 0 | 1 |
| 1 ИЛИ 1 | 1 |
Эта операция похоже на суммирование в математике. Лишь 1 или 1 даёт не 2, как в математике, а 1.
Перейдём к решению примерных задач из ОГЭ по информатике 2023.
Задача (Классическая)
Напишите наименьшее число X, для которого истинно высказывание:
(X > 16) И НЕ (X нечётное)
Решение:
Нужно, чтобы высказывание было истинным. Посмотрим, когда единица (истина) получается для союза И. Такое происходит только когда слева и справа стоят 1 (единицы).
Получается наш X должен быть больше 16, и число должно быть не нечётное, т.е. чётное! Наименьшее чётное число большее 16 будет 18.
Ответ: 18
Задача (Закрепление)
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X <= 6) И НЕ (X >= 11)
Решение:
Опять высказывание должно быть истинным.
С одной стороны X должен быть НЕ меньше или равно 6, т.е значит, X нужно взять больше 6 (X > 6). Причём само число 6 не входит в этот диапазон.
С другой стороны X НЕ больше или равно 11, т.е. X должен быть меньше 11 (X < 11).
Наибольшее целое число будет 10.
Ответ: 10
Задача (Союз И)
Напишите наименьшее натуральное двузначное число, для которого истинно высказывание:
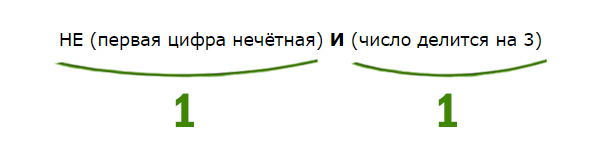
НЕ (первая цифра нечётная) И (число делится на 3)
Решение:
Высказывание должно быть истинным.
Первая цифра должна быть НЕ нечётная. Значит, она должна быть чётная. Число должно делится на 3. Найдём наименьшее двухзначное число, у которого первая цифра чётная, и оно делится на 3. Это будет 21.
Ответ: 21
Задача (Союз ИЛИ)
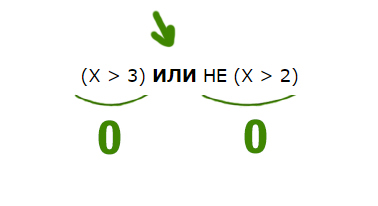
Для какого целого числа X ЛОЖНО высказывание:
(X > 3) ИЛИ НЕ (X > 2)
Решение:
В этой задаче используется союз ИЛИ. Нужно, чтобы высказывание было ложным. Ложь при союзе ИЛИ получается только в одном случае, когда слева и справа стоят нули.
Утверждение, что X > 3 должно быть ложно, значит, если его перевернуть, получится X <= 3. Второе утверждение НЕ (X > 2) тоже должно быть ложно. Значит, если перевернём это утверждение, частицу НЕ нужно убрать. Получается просто X > 2.
Получается, что только одно целое число входит в допустимый диапазон. Это тройка.
Ответ: 3
Задача (Частица НЕ над всем выражением)
Напишите наименьшее натуральное число x, для которого истинно высказывание:
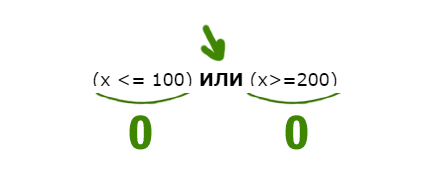
НЕ((x<=200) ИЛИ (x<=100))
Решение:
Нам нужно сделать выражение истинным. Но всё выражение находится под влиянием частицы НЕ. Можно эту частицу полностью убрать, но воспринимать, как будто нужно сделать выражение ложным. А дальше всё как обычно.
Ложь у союза ИЛИ получается в одном случае.
Первое выражение выдаёт ноль, когда x>200 (равно 200 не входит). Второе выражение выдаёт ноль, когда x>100. Объединив эти два условия получаем:
x > 200
Наименьшее число получается 201.
Ответ: 201
Задача (Крепкий орешек)
Напишите наименьшее натуральное число x, для которого истинно высказывание:
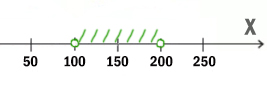
НЕ((x <= 100) ИЛИ (x>=200)) И (x чётное)
Решение:
В этой примерной задаче из ОГЭ по информатике применим все приёмы, которые мы разбирали до этого.
Когда союз И выдаёт единицу ?
Посмотрим, когда левое выражение выдаёт 1. Уберём частицу НЕ, но тогда будем смотреть, когда левое выражение выдаёт 0.
Перевернём оба выражения, которые находятся по обе стороны от союза ИЛИ. С одной стороны X>100, с другой X<200.
Учтём правое от союза И выражение. Наименьшее чётное число получается 102.
Ответ: 102
Здравствуйте, сейчас я вам покажу и расскажу как решать информатику.
1. Информационные объекты.
Есть несколько типов:
- 1 тип:
1) Мы смотрим, сколькими битами кодируется символ (Первое предложение); видим, что 16 битами . Переводим биты в байты, деля на 8.
16/8=2 (Если у вас в задание уже выражено в байтах, ничего делать не надо!).
2)Находим, насколько изменился размер. У нас в задание на 16 байт меньше, делим это число на полученное в прошлом действие, 16/2=8 (Столько символов убрали).
3)Мы вычитаем 2, потому что убрали так же пробел и запятую. 8-2=6.
4)Ищем слово из 6 символов ( букв ).
Ответ: Тюлень
- 2 тип:
Для его решения повторяем 1,2 действия из прошлого типа.
3)Мы вычитаем теперь 1, потому что убирается только пробел 8-1=7
Ответ: Скользя
- 3 тип:
1) Перемножаем всё.
20 (страницы)*40(строки)*48(символы)*2(байты)=76800 байт
2)Читаем во что нам надо перевести. У нас написало в Кбайты.
Используем таблицу:
получаем, что нужно разделить 76800/1024 =75 Кбайт.
Ответ: 75
- 4 тип:
1)Переводим биты в байты (Биты указаны в 1 предложении). 16/8 = 2 байта.
2)Считаем символы в предложении (Пробелы, запятые, точки УЧИТЫВАЕТСЯ!!). Получаем что у нас 42 символа.
3)Полученное кол-во байт в первом действии, умножаем на ответ во втором действии. 42*2=84
Ответ: 84
2. Кодировка и декодирование информации.
Тут нету какого-то плана решения. Просто методом подбора ищите, где есть только 1 декодирование. Это долгое задание. Могу дать важные советы:
1)Читайте, что от вас просят занести в ответ: максимальное кол-во символов или что получилось.
2)Не обязательно должно получиться слово из русского языка, может быть так же ответ: АБВААС.
3.Значение логического выражения.
План решения:
1)Отмечаем, что от нас хотят в первом предложении: наименьшее число, наибольшее число.
2)Смотрим дальше предложение, какое нужно: Целое ( 1, -124), натуральное (1, 6 ,924 “>0”).
3)Читаем дальше и смотрим, выражение чему должно быть равно: ЛОЖНОЕ, ИСТИННОЕ.
4)Смотрим на союз между двумя утверждениями: и ( то и то должно соблюдаться), или (либо это, либо то).
5)Если перед выражением стоит НЕ, то полностью меняется условие. – –Больше меняется на меньше или равно (> <=).
-Меньше меняется на больше или равно ( < >=).
-Больше или равно на меньше (>= <).
(Строгий знает на не строгий и на оборот).
(Чётное меняется на нечётное).
4. Табличка с путями.
Тут перед вами появляется табличка с буквами и цифрами, вам нужно определить самый короткий путь.
1)Рисуем пути по табличке, идя как на фото:
Пример пути к этому заданию:
2)Читаем предложение после таблички и смотрим, из какого города в какой нужен путь. У нас из (A в E). Читаем внимательно, может быть, что будет проходить через три города!
Просто считаем возможные пути:
A-C-D-E=12
A-B-C-D-E=10
и т.д.
Находим самый короткий. У нас это будет: A-B-C-D-E=10
Ответ: 10
5. Линейный алгоритм.
Тут вы встретимся с программой, который нужно решить. Есть 2 вида этого задания:
- 1 тип:
К первому типу я отнёс: умножить на b и разделить на b.
Решим с умножить:
1)Читаем предпоследние предложение и смотрим, какое число в какое мы делаем (у нас число 9 в число 77). Потом смотрим на программу ( У нас 12111)
Записываем так: Пишем первое число – программа- Второе число.
Пример: 9-12111-77
2)Записываем в виде выражение. Смотрим за что отвечает 1 и 2 в задание. (Пишите с первого числа!), второе число мы пишем после равно.
(9+4)b+4+4+4=77
переносим через равно
13b = 65
b = 5
Деление:
Делаем точно так же, только в конце там будет по примеру из прошлого:
65/b = 13 ( решаем через пропорцию).
- 2 тип:
Написать программу из 5 действий.
Нам так же дано первое число и второе число. Тут я дам вам совет:
1)Пытайтесь в первую очередь возводить в квадраты или делить.
Например как у нас: 3-xxxxx-81
По совету, возводим в квадрат: 3*3=9. Опять возводим, пока не приблизимся. 9*9=81. Если мы ещё раз возведем, то мы уйдем далеко от нужного числа, поэтому прибавляем 1, 81+1=82. 82+1=83. 83+1=84.
Ответ: 22111
6.Программа с оператором.
Тут нам даны языки программирования, и мы должны решить задание. Тут есть 2 типа задания. Сначала разберём знаки и предлоги. Буду разбирать знаки на примере языка Алгоритмический, потому что он самый лёгкий и большинство сдающих информатику взяли её, потому что маленький проходной балл:
>, >=, <, <=, или (либо то, либо то), и (то и то), div(деление без остатка) например: 7/2=3,5; Целая часть 3.
Первое число S, второе T; (s , t).
- 1 тип:
Найти, сколько раз программа скажет NO/YES.
В нашем случает “YES”
1)Смотрим условие в коде (После Если); Первое число < 9 ИЛИ второе число < 9.
Примечание: 9<9 (NO); 9<=9(Yes)
И смотрим:
Ответ: 7
- 2 тип:
Коэффициент A. Смысл этого задание, определить какое это число и при скольких запусках выдаст YES/NO “n” кол-во раз (n)- число из текста
1)Смотрим сколько раз должно выдать NO (У нас 8)
2)Смотрим условие: или
3)Ищем из приведённого снизу 9 пар чисел, которые 100% дают YES (У нас это (1,13) ; потому что, 13>12).
4)Просто подбираем числа, при которых первое число будет ‘NO‘ 8 раз
(Решается просто подбором, прибавляя по 1 к число)
Ответ: 13
7.Адрес или IP.
Легкое задание, так же делиться на 3 типа:
- 1 тип:
Адрес. Решается по алгоритму “Протокол://Сервер/Файл”
По алгоритму пишем: ЖГБЕВДА
- 2 тип
IP. IP-адрес представляет собой четыре разделённых точками числа, каждое из которых не больше 255.
1)Идём от конца. Ищем такое число, к которому если сзади приписать число, то оно выйдет за рамки 255.
У нас это будет .44 потому что, Если приписать ещё 1 цифру, она выйдет за 255, то есть буква “Б”- последняя.
2) Ищем число, которое будет выглядеть таким образом: x.xxx , Оно будет идти перед пред последним.
У нас такое 4.144 , потому что после этого должна идти точка, чтобы не превысить лимит в 255. Получаем, что предпоследняя буква B
3)Просто смотрим на два последних и соединяем их в голове или на листочке:
-Если АГ, то получим 179.13
-Если ГА, то 9.1317 (1317 превышает лимит в 255, значит начинаться ip будет с А)
Ответ: АГВБ
- 3 тип:
Почтовый ящик.
1)Сначала указывается имя почтового ящика, потом «@», потом сервер.
Ответ: 513462
8. Поисковые запросы:
Простое задание. Имеет два типа.
- 1 тип:
Лёгкий, состоящий максимум из двух запросов в одной ячейке.
Решается по формуле:
Na = Na&b + Na|b – Nb
Na – слово без символов
Nb –слово без символов
Na&b – Два слова с символом &
Na|b – Два слова с символом |
Наш пример:
За Na и Nb можно указать в нашем случае как и Рыба, так и Рыбак
Na = 780+ 50 -260
Ответ: 570
- 2 тип
Усложнённый первый тип, состоящий максимум из трёх запросов в одной ячейке.
Он решается вычёркиванием одинаковые запроса с одинаковым символом.
Например: Хлам| и Хлам& (Это разные)
Тут одинаковый запрос Вега&, зачёркиваем:
И решаем так же по формуле как и в первом типе.
Na = 467 + 119 – 260
Ответ: 326
9. Кол-во путей.
1)Мы читаем условие (последние предложение).
Из Точка X в точку Y, не проходящая(проходящую) через точку Z.
2)Зачеркиваем пути, противоречащие условию.
3)Считаем пути от вершин, А-1; Б-1; B=A+Б-2 (Две направленные в неё стрелки)
Ответ: 10
10. Перевод из одной системы счисления в другую.
Примечание: 5A= 51 (Английские алфавит, какая буква по порядку в алфавите, такую цифру она за собой держит).
- 1 тип:
1)Смотрим, что нас просят найди (наименьшее или наибольшее число) и в какую переводить.
2)Переводим:
2.1) Нумеруем число справа налево и записываем: число, умножить на его систему (16, 10, 8 ,2) в степени указанной при нумерации.
Ответ: 35
- 2 тип:
1) Последовательно делить заданное число и получаемые целые части на 2 до тех пор, пока целая часть не станет меньше 2-х.
2)Полученные остатки от деления, представленные цифрами из нового счисления, записать в виде числа, начиная с последней целой части.
Пример (Вы не выдержите моего почерка;D):
3)Считаем кол-во единиц (Просят по заданию)
Ответ: 3
11. Поисковая операция.
1)Скачиваете файл и извлекаете на рабочий стол.
2)Открывает папку и смотрим в задание на ключевое слово и что нужно найти. (На фото показано, что такое ключевое слово и что найти)
3)В папке вводим сюда ключевое слово. (В нашем случае Гнилотёрка или речка). Когда вы нашли, открываем любую. (!Если у вас ничего не нашлось. Измените род, число, склонение, падеж слова, если и так не нашли, прогрузите каждую папку. Если и так не нашло, заходите в каждое произведение и проверяйте как в пункте 4!)
4)Используя быстрый поиск (Почти везде это F3, кроме word)
В окошке пишем ключевое и ищем, что нужно найти в тексте.
Ответ: Овсяников
12. Найти ко-во файлов расширения.
1)Скачиваете файл и извлекаете на рабочий стол.
2)Вводим в поиск “*.расширение”, например: *.txt ; *.pdf
*–любое название файла.
3)Смотрим снизу слева на кол-во элементов. (!Если у вас ничего нет или вам кажется, что слишком мало. Подождите или прогрузите каждую папку и опять подождите, скорость обработки зависит от компьютера. Для проверки можете подсчитать вручную!)
4)Прочитайте внимательно задание, что нужно найти. В некоторых заданиях надо найти с размером файлов.
Ответ: 33
Алгебра логики в информатике начинает с 8 класса с изучения отдельных элементов алгебры логики.
По определению алгеброй логики является раздел математики, однако, элементами алгебры логики в информатике могут быть и высказывания.
Высказывание
Высказывание — это предложение, содержание которого можно однозначно определить как ложное иди истинное. И не важно на каком языке это ваысказывание.
Какое же предложение в русском языке является высказыванием?
По факту мы можем выделить повествовательные предложения, побудительные и вопросительные. Но это не говорит нам о том, является предложение высказыванием или не является.
Однозначно можно сказать, что вопросительные и побудительные предложения не могут являться высказыванием.
«Что вы изучаете?» или «Как найти школу № 75?» — эти предложения не являются высказыванием, как и «Сдайте на проверку домашнее задание.» или «Сходите на субботник.»
Повествовательные предложения тоже не все можно назвать высказыванием. главное условие высказывания — это условие при котором можно точно определить истинность или ложность этого высказывания.
«Это предложение является ложным» — повествовательное предложение, которое не является высказыванием. Причина: относительно данного предложения нельзя наверняка сказать ложно оно или истинно.
Если предположить, что предложение истинно, то возникнет между сказанным предложением и его содержанием противоречие.
Если принять, что предложение ложно, то надо признать, что оно истинно.
Построение высказываний
Высказывания могут строиться не только простыми предложениями, но и с использованием различных знаков формальных языков. Например, формальным языком является математика, химия, физика и т.д.
Высказываниями являются следующие предложения:
- Битва при Ватерло́о является последним крупным сражением французского императора Наполеона I.
- Fe (Ферум) — металл и элемент таблицы Менделеева.
- Ра́диус — это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка.
Числовые выражения не являются высказыванием. Однако, используя числовые выражения можно составить высказывание. При этом надо две части этого выражения соединить знаком либо равенства, либо неравенства.
В случае, если в математическом выражении есть переменные, то такое выражение нельзя включить в высказывание до тех пор, пока переменная не будет заменена числом.
Рассмотрим пример.
«5+8 = 15-2»
Это высказывание истинно.
«5+8 > 5 +10»
Это высказывание ложно
«Х>8» не является высказыванием.
Однако, если Х заменить на число из множества (9;+∞), то будет высказывание, истинное высказывание.
В целом, истинность или ложность высказывания можно рассматривать лишь с точки зрения той науки к сфере которой эти выражения относятся. А алгебра логики отвлекается от специфики выражения, от его содержательной части, поэтому все высказывания обозначаются буквами, которые называют логическими переменными.
Алгебра логики определяет правила записи, упрощение и преобразования высказываний и вычислений их значений.
Логические переменные могут быть только 0 или 1.
Оперируя только логическими переменными, алгебра логики сводит все операции к операциями с двоичными данными.
Алгебра логики является основой компьютерных устройств хранения и обработки данных, основой алгоритмизации и программирования.
Далее рассмотрим простые и сложные высказывания.
Практические задания
Приведите примеры как истинных, так и ложных высказываний по следующим изучаемым предметам: истории, математике, литературе.
В демо-версии присутствует типовое задание 3 без выбора вариантов ответов, так что скорее всего и на реальном ОГЭ это задание будет не тестовым, а нужно будет посчитать и написать в ответе свое число.
Как решать. Если есть НЕ, в первую очередь избавимся от него, поменяв знак сравнения на противоположный. Если это >, меняем на ≤; если <, меняем на ≥. Четное меняется на нечетное, все остальное меняется на противоположное. То же самое, когда истинное переделываем в ложное и наоборот.
Далее, в истинном высказывании И означает, что выполняются ОБА условия одновременно; ИЛИ – выполняется хоть то, хоть другое, хоть оба сразу.
I закон де Моргана: Отрицание дизъюнкции двух простых высказываний равносильно конъюнкции отрицаний этих высказываний.
II закон де Моргана: Отрицание конъюнкции двух простых высказываний равносильно дизъюнкции отрицаний этих высказываний.
Пояснение ГДЗответ ру: Конъюнкция И, дизъюнкция ИЛИ.
Логическое ИЛИ ложно только тогда, когда ложны оба высказывания. Значит, когда переделываем ложное в истинное, меняем не только знаки и четность, но ИЛИ на И, а И на ИЛИ (по законам де Моргана)! Если есть НЕ перед скобкой с несколькими условиями, то при избавлении от отрицания внутри этой скобки так же помимо изменения условий И меняется на ИЛИ и наоборот.
В ложных высказываниях можно сразу применять законы де Моргана, не избавляясь предварительно от НЕ, но мы в ответах будем делать пошагово и избавляться от отрицания для наглядности.
В заключение заметим, что в логических выражениях, представленных в заданиях, могут быть также не числа, а слова. Подобные задания выполняются аналогично заданиям с числами.
Варианты задания 3 ОГЭ по информатике с ФИПИ
Напишите натуральное число x, для которого ложно высказывание:
НЕ (x < 8) ИЛИ (x < 7).
Решение:
Сначала избавимся от НЕ и запишем выражение в виде
(х >= 8) ИЛИ (х < 7). Оно ложно.
Логическое «ИЛИ» ложно только тогда, когда ложны оба высказывания.
То есть нам надо найти натуральное число не больше и не равное 8 (значит < 8) И не меньше 7 (значит >= 7).
Переделаем ложное высказывание в истинное, применяя закон де Моргана:
(х < 8) И (х >= 7) – истинно
7 8
__.____.__
Это 7
Проверяем:
7 >= 8 ? НЕТ, ложно
7 < 7 ? НЕТ, ложно. Оба высказывания ложны, значит мы нашли верный ответ.Ответ: 7
1A3B0C
Напишите натуральное число x, для которого ложно высказывание:
НЕ (x < 6) ИЛИ (x < 5).
Решение:
Сначала избавимся от НЕ и запишем выражение в виде
(х >= 6) ИЛИ (х < 5). Оно ложно.
Логическое «ИЛИ» ложно только тогда, когда ложны оба высказывания.
То есть нам надо найти натуральное число не больше и не равное 6 (значит < 6) И не меньше 5 (значит >= 5).
Переделаем ложное высказывание в истинное, применяя закон де Моргана:
(х < 6) И (х >= 5) – истинно
5 6
___.____.___
Это 5Ответ: 5
C2590F
Напишите наибольшее трёхзначное число x, для которого истинно высказывание:
НЕ (Первая цифра нечётная) И (x делится на 3).
Решение:
Избавимся от НЕ.
(Первая цифра чётная) И (x делится на 3) – истинное, значит должны выполняться ОБА условия.
Первая цифра – четная, максимум – 8.
Число делится на 3, если сумма его цифр делится на 3.
Проверяем 899. 8 + 9 +9 = 26 = 8, не делится на 3.
Проверяем 898. 25 = 7, не делится на 3.
Проверяем 897. 8 + 9 + 7 = 24 = 6, делится на 3.Ответ: 897
24647F
Напишите наибольшее трёхзначное число x, для которого истинно высказывание:
НЕ (Первая цифра чётная) И (x делится на 3).
Решение:
Избавимся от НЕ
(Первая цифра нечётная) И (x делится на 3) – истинно
Наибольшая нечетная цифра – 9
Наибольшее трехзначное число, начинающееся с девятки 999 – делится на 3.
Ответ: 999
AB2DCD
Напишите натуральное число x, для которого ложно высказывание:
(x < 4) ИЛИ НЕ (x < 5).
Решение:
Избавимся от НЕ:
(x < 4) ИЛИ (x ≥ 5) – ложно
Тогда по законам де Моргана
(x ≥ 4) И (x < 5) истинно
4 5
_______._____._______
Это 4
Ответ: 4
BA3498
Напишите наибольшее трёхзначное число x, для которого истинно высказывание:
(Первая цифра нечётная) И НЕ (x делится на 3).
Решение:
Избавимся от НЕ:
(Первая цифра нечётная) И (x не делится на 3) – истинно
Наибольшая нечетная цифра 9, наибольшее трехзначное число на девятку – 999, но оно делится на 3. Проверим 998 – не делится нацело на 3, значит второе условие выполняется.
Ответ: 998
668CE8
Напишите натуральное число x, для которого ложно высказывание:
(X < 8) ИЛИ НЕ (X < 9).
Решение:
Избавимся от НЕ:
(X < 8) ИЛИ (X ≥ 9) – ложно
Тогда по законам де Моргана
(X ≥ 8) И (X < 9) истинно
8 9
_______._____._______
Это 8
Ответ: 8
820268
Напишите наибольшее трёхзначное число x, для которого истинно высказывание:
НЕ (Первая цифра нечётная) И НЕ (x делится на 3).
Решение:
Избавимся от НЕ:
(Первая цифра чётная) И (x не делится на 3)
Наибольшая четная цифра 8,
наибольшее трехзначное число на восьмерку 899, оно не делится на 3.
Ответ: 899
997D3D
Определите наименьшее трёхзначное число x, для которого истинно логическое выражение:
(x оканчивается на 3) И НЕ (x < 230).
Решение:
Избавимся от НЕ:
(x оканчивается на 3) И (x ≥ 230)
По первому условию последний разряд числа 3.
По второму условию это число больше или равно 230.
Наименьшее число, удовлетворяющее обоим условиям 233
Ответ: 233
0A6843
Определите наименьшее натуральное число x, для которого логическое выражение истинно:
(НЕ (x ≥ 15) И НЕ (x < 8)) И (x нечётное).
Решение:
Избавимся от НЕ:
((x < 15) И (x ≥ 8)) И (x нечётное) истинно,
значит нужно найти наименьшее нечетное натуральное число от 8 (включая 8) до 15 (не включая 15).
Это 9
Ответ: 9
5F2747
Определите количество натуральных двузначных чисел x, для которых ложно логическое выражение:
НЕ (x чётное) И НЕ (x > 39).
Решение:
Зададим вопрос: «Если среди N некоторых чисел, некоторому условию удовлетворяют M из них, то сколько чисел не удовлетворяют этому условию?». — Конечно, N – M чисел.
Учитывая это, определим сначала количество натуральных двузначных чисел х, для которых заданное выражение истинно.
Запишем его без операций отрицания:
(x нечётное) И (x <= 39)
Далее рассуждения такие. Двузначные натуральные числа, меньшие или равные 39 и являющиеся нечетными:
11, 13, 15, …, 39.
Всего их (39 – 11) : 2 + 1 = 15.
Но это количество чисел, для которых полученное логическое выражение истинно, а в задании требуется количество чисел, для которых оно ложно. В искомое количество входят все остальные двузначные числа. Это количество равно 90 – 15 = 75 (напомним, что общее количество натуральных двузначных чисел равно 90).Ответ: 75.
Можно также поступить по-другому.
Вопрос: «Если для некоторых чисел результат проверки заданного логического выражения является ложным, то для какого выражения эти же числа дадут истинный результат?» — Для противоположного логического выражения.
Пример: для положительных чисел логическое выражение (число <= 0) является ложным — для них истинным является противоположное логическое выражение (число > 0).
Как известно, для определения логического выражения, противоположного выражению с операциями конъюнкции и дизъюнкции (с логическими связками И и ИЛИ), можно применить так называемые «законы де Моргана».
Применим соответствующий закон к заданному в условии выражению
(НЕ (x чётное) И НЕ (x > 39)) — получим логическое выражение для определения количества чисел, требуемого по условию:
(x чётное) ИЛИ (x > 39)
С учетом того, что должны учитываться только двузначные числа, полученному выражению будут соответствовать числа:
10, 12, 14, … 38, 40, 41, 42, 43, …, 99.
Их общее число ((38 – 10) : 2 + 1) + (99 – 40 + 1) = 75.Ответ: 75.
Примечание. В данном случае первый способ решения лучше.
7C8BF1
! Определите наименьшее натуральное число x, для которого логическое выражение ложно:
НЕ ((x < 8) И (x < 21)) ИЛИ (x нечётное).
Решение:
НЕ ((x < 8) И (x < 21)) ИЛИ (x нечётное) – ложно
Из (x < 8) И (x < 21) можем оставить только (x < 8), потому что любое число менее 8-ми одновременно меньше 21-го, получится
НЕ (x < 8) ИЛИ (x нечётное) – ложно
Тогда по законам де Моргана
(x < 8) И (x чётное) истинно, то есть нужно найти наименьшее натуральное четное число меньше 8.
Ответ: 2Другой вариант решения
Можно было применить закон де Моргана ко всему начальному выражению.
НЕ ((x < 8) И (x < 21)) ИЛИ (x нечётное) ложно по условию
Избавимся от НЕ. НЕ отрицает все условия из скобки, значит И оно тоже отрицает, меняем его на ИЛИ:
((x ≥ 8) ИЛИ (x ≥ 21) ИЛИ (x нечётное) – ложное
По закону де Моргана
((x < 8) И (x < 21)) И (x чётное) истинноеОтвет: 2
5986FB
Определите наименьшее натуральное число x, для которого истинно логическое выражение:
НЕ ((x ≥ 15) ИЛИ (x < 7)).
Решение:
Избавимся от НЕ:
(x < 15) И (x ≥ 7) истинно
7 15
_______._____._______
Это 7
Ответ: 7
75C77D
! Определите количество натуральных чисел x, для которых логическое выражение ложно:
НЕ ((x < 8) И (x < 21)) ИЛИ (x нечётное).
Решение:
Прежде всего, ясно, что вместо составного высказывания (x < 8) И (x < 21) можно записать только (x < 8), то есть все заданное выражение примет вид:
НЕ (x < 8) ИЛИ (x нечётное)
Отказ от отрицания: (x >= 8) ИЛИ (x нечётное) не позволит сразу найти искомое значение.
Тогда применим закон де Моргана к краткому варианту (НЕ (x < 8) ИЛИ (x нечётное)) — получим логическое выражение для определения количества чисел, требуемого по условию:
(x < 8) И (x чётное)
Итак, искомое количество равно количеству четных натуральных чисел, меньших 8, то есть трём (это числа 2,4,6).
Можно было также применить закон де Моргана ко всему выражению в условии:
(x < 8) И (x < 21) И (x чётное)
В этом случае искомое количество чисел также равно трём.
Ответ: 3.
1ED874
! Определите наибольшее натуральное число x, для которого логическое выражение ложно:
НЕ ((x < 8) И (x < 21)) ИЛИ (x нечётное).
Решение:
По законам де Моргана
((x < 8) И (x < 21)) И (x чётное) истинно,
то есть нужно найти наибольшее натуральное четное число меньше 8-ми.
Ответ: 6
568E7E
! Определите количество натуральных двузначных чисел x, для которых истинно логическое выражение:
НЕ (x чётное) И НЕ (x кратно 5).
Решение:
Отказавшись, от операций отрицания, можно получить другое логическое выражение:
(x нечётное) И (x не кратно 5)
Как определить искомое количество? Можно рассуждать так.
Общее количество натуральных двузначных чисел равно 90 (99 – 10 + 1). Из них нечетных — 45. В числе этих 45 не следует учитывать числа, кратные 5. Их 9 (15, 25, …, 95).
Следовательно, количество нечетных натуральных двузначных чисел, не кратных 5, равно 45 – 9 = 36.Ответ: 36.
578573
! Определите количество натуральных двузначных чисел x, для которых истинно логическое выражение:
НЕ (x нечётное) И НЕ (x > 51).
Решение:
Избавимся от НЕ:
(x чётное) И (x <= 51) истинно,
то есть нужно найти количество натуральных двузначных четных чисел < либо = 51, это 12, 14, 16, … 48, 50.
Интервал от 10 до 51, но только четные.
Тогда 51-10=41 и прибавляем еще 1, так как подсчет не учитывает включительно крайнее число. Получаем 42. Делим пополам, так как нужны только четные.
42/2 =21
Ответ: 21
A9E611
Определите количество натуральных чисел x, для которых логическое выражение истинно:
(НЕ (x ≥ 15) И НЕ (x < 8)) И (x нечётное).
Решение:
Отказ от операций отрицания позволяет получить другое логическое выражение:
((x < 15) И (x >= 8)) И (x нечётное)
Числа, удовлетворяющие указанным границам: 8, 9, 10, 11, 12, 13, 14. Из них нечетными являются три числа.Ответ: 3
7AEE27
! Определите наибольшее натуральное число x, для которого логическое выражение истинно:
(НЕ (x ≥ 15) И НЕ (x < 8)) И (x нечётное).
Решение:
Избавимся от НЕ:
((x < 15) И (x ≥ 8)) И (x нечётное) истинно
то есть нужно найти наибольшее натуральное нечетное число от 8 (включительно) до 15 (не включая 15). Это 13
Ответ: 13
C4D725
! Определите количество натуральных чисел x, для которых истинно логическое выражение:
НЕ ((x ≥ 33) ИЛИ (x < 19)) И (x чётное).
Решение:
Здесь в заданном логическом выражении отрицание применено к двум простым высказываниям, соединенных дизъюнкцией (логической связкой ИЛИ). Вспомнив соответствующий закон де Моргана, можем заменить отрицание:
((x < 33) И (x >= 19)) И (x чётное)
то есть это натуральные четные числа от 19-ти (включая 19) и до 33 (не включая 33).
Соответствующие четные числа: 20, 22, 24, 26, 28, 30, 32.
32-19=13 и учитываем крайнее показание не включенного числа 23+1 = 14
14/2=7
Их общее число равно 7.
Ответ: 7.
C63DD8
! Определите количество натуральных двузначных чисел x, для которых истинно логическое выражение:
НЕ (x чётное) И НЕ (x > 67).
Решение:
Избавимся от НЕ:
(x нечётное) И (x <= 67) истинно
то есть, нужно найти количество натуральных двузначных нечетных чисел меньше или равное 67.
Интервал от 10 до 67.
67-10=57 чисел, к результату прибавляем 1, чтобы включить крайнее число, то есть 57+1=58. Так как числа нечетные, это половина от общего количества.
58/2=29
Ответ: 29
40FF5E
Определите наибольшее трёхзначное число x, для которого истинно логическое выражение:
НЕ (x оканчивается на 3) И НЕ (x > 115).
Решение:
Избавимся от НЕ:
(x не оканчивается на 3) И (x ≤ 115)
По первому условию число не оканчивается на 3.
По второму условию число меньше или равно 115.
Наибольшее трёхзначное ≤ 115, не оканчивающееся на 3 – это 115
Ответ: 115
CAA4AD
Напишите наименьшее натуральное число x, для которого истинно высказывание:
((x > 3) И НЕ (x < 4)) ИЛИ (x < 1).
Решение:
Избавимся от НЕ:
((x > 3) И (x ≥ 4)) ИЛИ (x < 1)
Первое условие: 4 и больше.
Второе: меньше 1.
Но так как меньше 1 – это уже не натуральное, то наименьшее натуральное будет в диапазоне от 4 до бесконечности. Наименьшее из них 4.
Ответ: 4
09B748
! Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x > 2) И ((x < 4) ИЛИ (x > 4)).
Решение:
(x > 2) И ((x < 4) ИЛИ (x > 4)) истинно
Первое условие: значения больше 2-х.
Второй диапазон: все, кроме числа 4.
Между ними И, значит оба условия выполняются одновременно.
2 4
_______._____._______…..
Наименьшее натуральное 3
Ответ: 3Будьте внимательны, смотрите, где стоят круглые скобки, какие именно условия они обобщают.
5C6C4C
Напишите наибольшее натуральное число x, для которого истинно высказывание:
НЕ (x < 5) И (x < 6).
Решение:
Избавимся от НЕ:
(x ≥ 5) И (x < 6) истинно
5 6
_______._____._______
Это 5
Ответ: 5
83F641
Напишите наибольшее натуральное число x, для которого истинно высказывание:
(x < 7) И НЕ (x < 6).
Решение:
Избавимся от НЕ:
(x < 7) И (x ≥ 6)
6 7
_______._____._______
Это 6
Ответ: 6
742DF5
Напишите наименьшее натуральное число x, для которого ложно высказывание:
(x > 3) ИЛИ НЕ (x > 2).
Решение:
По законам де Моргана
(x ≤ 3) И (x > 2)
2 3
_______._____._______
Это 3
Ответ: 3
1259F7
! Напишите наибольшее натуральное число x, для которого ложно высказывание:
НЕ (x < 6) ИЛИ ((x < 5) И (x ≥ 4)).
Решение:
По законам де Моргана
(x < 6) И ((x ≥ 5) ИЛИ (x < 4)) – истинное высказывание
4 5 6
…___.___.___.___
То есть число меньше 6-ти и ≥ 5; либо меньше 6-ти и меньше 4-х.
Наибольшее натуральное, соответствующее условиям, число 5
Ответ: 5
5FC8F4
Напишите количество натуральных двузначных чисел, для которых истинно высказывание:
НЕ (Число < 88) И НЕ (Число нечётное).
Решение:
Избавимся от отрицания:
(Число ≥ 88) И (Число чётное) так же истинно
Подходят четные числа больше или равные 88. По условию они двузначные, значит интервал от 88 до 99.
99-88=11 чисел, при этом учитываем включительно крайнее число, которое не включено при подсчете.
11+1=12
Так как четных чисел в два раза меньше, то
12/2=6
Ответ: 6
A4BCFA
Напишите наименьшее натуральное число x, для которого ложно высказывание:
(x ≥ 3) ИЛИ НЕ (x ≥ 2).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x < 3) И (x ≥ 2) истинно
2 3
__.____.______
Наименьшее натуральное из этого интервала – число 2
Ответ: 2
2AD501
Дано четыре числа: 638, 442, 357, 123. Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И НЕ (Сумма цифр чётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра нечётная) И (Сумма цифр нечётная) – тоже истинное высказывание
Рассмотрим 357 и 123.
3+5+7=15 и 1+2+3=6.
Подходит 357
Ответ: 357
D1CC0C
Напишите наименьшее трёхзначное число, большее 121, для которого ложно высказывание:
НЕ (Число > 50) ИЛИ (Число чётное).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив один из законов де Моргана:
(число > 50) И (число нечётное) – истинное высказывание.
Наименьшее трёхзначное число, большее 121, удовлетворяющее условию – это 123.Ответ: 123
908105
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x > 4) И НЕ (x > 5).
Решение:
Избавимся от отрицания:
(x > 4) И (x ≤ 5) – тоже истинно
4 5
__.____.____
Ответ: 5
E9780D
Напишите наибольшее натуральное двузначное число, для которого истинно высказывание:
НЕ (Число нечётное) И (Число кратно 11).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число кратно 11) – тоже истинно
Наибольшее четное, кратное 11-ти – это 88
Ответ: 88
7FBEB2
Напишите наименьшее натуральное число x, для которого ложно высказывание:
НЕ (x > 2) ИЛИ ((x < 4) И (x > 1)).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x > 2) И ((x ≥ 4) ИЛИ (x ≤ 1)) истинно
х не может быть больше 2-х и ≤ 1 одновременно, так что условие (x ≤ 1) можно вычеркнуть. Остается:
(x > 2) И (x ≥ 4) истинно
1 2 4
_.____.______._______…..
Наименьшее 4
Ответ: 4
4F2C17
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число нечётное) И НЕ (Число > 18).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число ≤ 18) – тоже истинно
То есть ищем количество четных натуральных чисел до 18-ти включительно.
18 натуральных чисел, из которых каждое второе четное (половина лишь четных).
18/2=9
Ответ: 9
481611
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x > 1) И (x > 2) И (x ≠ 3).
Решение:
1 2 3
___.___.___.____…
Наименьшее из натуральных в подходящем диапазоне – число 4.
Ответ: 4
4C6A11
Дано четыре числа: 648, 452, 357, 123. Для какого из приведённых чисел истинно высказывание:
(Первая цифра чётная) И НЕ (Сумма цифр чётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра чётная) И (Сумма цифр нечётная) – тоже истинно
По первому условию 648 или 452.
По второму 6+4+8=18 – не подходит
4+5+2=11 – подходит
Ответ: 452
9E2E1E
Напишите наименьшее натуральное трехзначное число, для которого истинно высказывание:
НЕ (Число нечётное) И (Число кратно 3).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число кратно 3) – тоже истинно
Получается, это число 102, так как оно четное и делится на 3, при этом минимальное трехзначное (больше 100).
Ответ: 102
E5BC1A
Напишите наименьшее натуральное число x, для которого ложно высказывание:
(НЕ (x ≥ 6) И НЕ (x = 5)) ИЛИ (x ≤ 7).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив один из законов де Моргана:
((x ≥ 6) ИЛИ (x = 5)) И (x > 7) истинно
5 6 7
___.___.___._________
Наименьшее натуральное, соответствующее условиям, число 8
Ответ: 8
1EAF20
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x ≤ 2) И НЕ (x ≤ 1).
Решение:
Избавимся от отрицания:
(x ≤ 2) И (x > 1) – тоже истинно
1 2
___.___.___
Ответ: 2
D1C824
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x < 3) И НЕ (x < 2).
Решение:
Избавимся от отрицания:
(x < 3) И (x ≥ 2) – тоже истинно
2 3
___.___.__
Ответ: 2
DCCB2A
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число нечётное) И НЕ (Число > 14).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число ≤ 14) – тоже истинно
Надо узнать количество четных от 1 до 14, где четное каждое второе.
14/2=7 четных чисел.
Ответ: 7
A0DD26
Напишите наибольшее натуральное число x, для которого истинно высказывание:
(x < 5) И НЕ (x < 4).
Решение:
Избавимся от отрицания:
(x < 5) И (x ≥ 4) – тоже истинно
4 5
___.____.___
Ответ: 4
C93020
Напишите наибольшее натуральное число x, для которого истинно высказывание:
(x < 8) И НЕ (x < 7).
Решение:
Избавимся от отрицания:
(x < 8) И (x ≥ 7) – тоже истинно
7 8
__.___.__
Ответ: 7
97E220
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число > 19) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Число ≤ 19) И (Число нечётное) – тоже истинно
То есть, надо найти количество нечетных натуральных от 1 по 19 включительно. Их 10.
Ответ: 10
9FCC22
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ (x > 5) И (x > 4).
Решение:
Избавимся от отрицания:
(x ≤ 5) И (x > 4) – тоже истинно
4 5
__.___.___
Ответ: 5
603E2F
! Напишите наибольшее двузначное число, меньшее 55, для которого истинно высказывание:
(Число < 75) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Число < 75) И (Число нечётное) – тоже истинно
То есть под условия подходят все нечетные менее 75-ти. Но нам сказано найти наибольшее двузначное, меньшее 55. Из нечетных это число 53
Ответ: 53
67AF2A
Дано четыре числа: 6843, 4562, 3561, 1234. Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И (Последняя цифра нечётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра нечётная) И (Последняя цифра нечётная) – тоже истинно
Ответ: 3561
31FE21
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x > 2) И НЕ (x > 3).
Решение:
Избавимся от отрицания:
(x > 2) И (x ≤ 3) – тоже истинно
2 3
__.___.__
Ответ: 3
8A9928
Дано четыре числа: 6843, 4562, 3561, 1234. Для какого из приведённых чисел истинно высказывание:
(Первая цифра чётная) И НЕ (Последняя цифра нечётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра чётная) И (Последняя цифра чётная) – тоже истинно
Первая и последняя четная.
Ответ: 4562
592550
Напишите наибольшее натуральное число x, для которого истинно высказывание:
НЕ (x < 10) И (x < 11) И (x > 8).
Решение:
Избавимся от отрицания:
(x ≥ 10) И (x < 11) И (x > 8) – тоже истинно
8 10 11
___._____.___.____
Ответ: 10
5E6651
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ (x < 6) И (x < 7).
Решение:
Избавимся от отрицания:
(x ≥ 6) И (x < 7) – тоже истинно
6 7
__.___.___
Ответ: 6
CF5FA5
Напишите наименьшее натуральное трёхзначное число, для которого истинно высказывание:
НЕ (Число нечётное) И (Число кратно 11).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число кратно 11) – тоже истинно
Первое условие – четное.
Второе: делится на 11 без остатка.
Еще и наименьшее трехзначное при этом.
110 : 11 = 10, подходит.
Ответ: 110
F10CCC
! Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x < 3) И ((x < 2) ИЛИ (x > 2)).
Решение:
(x < 3) И ((x < 2) ИЛИ (x > 2)) – тоже истинно
То есть, х меньше 3-х, кроме числа 2.
Наименьшее натуральное число 1
Ответ: 1
291BC6
Дано четыре числа: 35, 4598, 54321, 24. Для какого из приведённых чисел истинно высказывание:
(Число > 100) И НЕ (Число нечётное)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Число > 100) И (Число чётное) – тоже истинно
То есть, четное больше сотни.
Подходит 4598.
Ответ: 4598
DC5FC8
! Напишите наибольшее натуральное число x, для которого истинно высказывание:
(x < 5) ИЛИ НЕ (x > 3).
Решение:
Избавимся от отрицания:
(x < 5) ИЛИ (x ≤ 3) – тоже истинно
3 5
…___.___.__
Ответ: 4
93C0C4
Напишите наибольшее натуральное число x, для которого ложно высказывание:
НЕ (x < 7) ИЛИ (x < 6).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x < 7) И (x ≥ 6) истинно,
в соответствии с этим высказыванием можем построить числовой луч и отметить нужный интервал:
6 7
__.___.____
Ответ: 6
3E8BCD
Напишите наибольшее натуральное двузначное число, для которого истинно высказывание:
НЕ (Число нечётное) И (Число кратно 3).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число кратно 3) – тоже истинно
Ищем наибольшее натуральное двузначное четное, кратное 3-м.
Ответ: 96
4A4395
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x > 4) И (x < 7) И (x < 6).
Решение:
4 6 7
__._____.___._
Ответ: 5
BED497
Напишите наименьшее натуральное число x, для которого ложно высказывание:
(x > 2) ИЛИ НЕ (x > 1).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x ≤ 2) И (x > 1) истинно
1 2
__.____.__
Ответ: 2
C8BAED
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число нечётное) И НЕ (Число > 12).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число ≤ 12) – тоже истинно
То есть, нужны четные с 1 по 12 включительно.
Так как четные числа идут через одно, то берем половину от общего количества чисел.
12/2=6
Ответ: 6
3B55E9
Напишите наибольшее натуральное число x, для которого истинно высказывание:
НЕ (x < 3) И (x < 4).
Решение:
Избавимся от отрицания:
(x ≥ 3) И (x < 4) – тоже истинно
3 4
_.___.___
Ответ: 3
B9AD6A
Дано четыре числа: 638, 442, 357, 123. Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И (Сумма цифр чётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра не чётная) И (Сумма цифр чётная) – тоже истинно
Первая нечетная у 357, 123.
3+5+7=15 – нечетное 1+2+3=6 – четное.
Ответ: 123
D47460
Напишите наибольшее трехзначное число, меньшее 124, для которого истинно высказывание:
(Сумма цифр кратна 5) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Сумма цифр кратна 5) И (Число нечётное) – тоже истинно
Подбираем, перебирая нечетные числа меньше 124-х.
113 – нечетное, меньше 124, 1+1+3=5 делится на 5
Ответ: 113
AB9560
Напишите наименьшее двузначное число, большее 54, для которого ложно высказывание:
(Число < 40) ИЛИ НЕ (Число чётное).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(Число ≥ 40) И (Число чётное) истинно
Наименьшее четное ≥ 40 больше 54 – это число 56
Ответ: 56
6D4D61
Напишите наименьшее натуральное число x, для которого ложно высказывание:
(x = 2) ИЛИ НЕ (x < 3).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x ≠ 2) И (x < 3) – истинное выражение
2 3
…__.___.___
Ответ: 1
3BC762
Напишите количество натуральных двузначных чисел, для которых истинно высказывание:
НЕ (Число < 83) И (Число нечётное).
Решение:
Избавимся от отрицания:
(Число ≥ 83) И (Число нечётное) – тоже истинно
У нас условие, что это 83 и больше и нечетные числа.
100-83=17 чисел с 83 до 100. И прибавляем 1, дабы включить крайнее неучтенное число. 17+1=18.
Нечетных – половина из них: 18/2=9
Ответ: 9
44FE34
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число > 15) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Число ≤ 15) И (Число нечётное) – тоже истинно
Нечетные до 15 включительно.
(15+1):2=8
Ответ: 8
4A2239
Дано четыре числа: 6843, 4562, 3561, 1234. Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И НЕ (Последняя цифра нечётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра нечётная) И (Последняя цифра чётная) – тоже истинно
Ответ: 1234
013A31
Напишите наибольшее двузначное число большее 50, для которого истинно высказывание:
НЕ (Число > 75) И (Число чётное).
Решение:
Избавимся от отрицания:
(Число ≤ 75) И (Число чётное) – тоже истинно
Ищем наибольшее четное двузначное большее 50, но ≤ 75
Ответ: 74
204E3B
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ ((x > 3) ИЛИ (x < 2)) И (x > 2).
Решение:
НЕ ((x > 3) ИЛИ (x < 2)) И (x > 2)
Избавимся от отрицания:
((x ≤ 3) И (x ≥ 2)) И (x > 2) – тоже истинно
По первым двум условиям получается интервал
2 3
___.___._____
По второму условию x > 2, значит это 3
Ответ: 3
20BF36
Напишите наибольшее натуральное число x, для которого ложно высказывание:
НЕ (x < 6) ИЛИ (x < 5).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x < 6) И (x ≥ 5) – истинное выражение
5 6
__.__.__
Ответ: 5
54C33D
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число > 13) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Число ≤ 13) И (Число нечётное) – тоже истинно
Нечетные до 13-ти включительно.
Числа можно разбить на пары чет/нечет, нечетных среди них будет половина. 13-ти до пары не хватает 1.
(13+1):2=7
Ответ: 7
97A63B
Напишите наибольшее двузначное число, меньшее 75, для которого истинно высказывание:
(Сумма цифр нечетная) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Сумма цифр нечетная) И (Число нечётное) – тоже истинно
Подберем нечетное число с нечетной суммой цифр, меньшее 75. Оно должно начинаться на четное число, иначе сумма будет четной. Проверяем седьмой десяток: 69 подходит.
Ответ: 69
836839
Дано четыре числа: 54321, 45980, 125, 24. Для какого из приведённых чисел истинно высказывание:
НЕ (Число > 10000) И (Число нечётное)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Число ≤ 10000) И (Число нечётное) – тоже истинно
10000 и меньше и нечетное. Это 125
Ответ: 125
B5AB8F
! Напишите наименьшее натуральное число x, для которого ложно высказывание:
(x > 3) ИЛИ НЕ ((x < 4) И (x > 2)).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x ≤ 3) И ((x < 4) И (x > 2)) – истинное выражение
2 3 4
__.___.__.___
Ответ: 3
B16C83
! Напишите наименьшее натуральное число x, для которого ложно высказывание:
НЕ (x > 2) ИЛИ (x = 4).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x > 2) И (x ≠ 4) – истинное выражение
2 4
__.___.__…
Ответ: 3
1A868B
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x < 4) И (x > 1) И (x ≠ 2).
Решение:
1 2 4
__.___._____._
Наименьшее, да и единственное натуральное число из этого интервала – число 3
Ответ: 3
293C81
Дано четыре числа: 54324, 4597, 46, 25. Для какого из приведённых чисел истинно высказывание:
НЕ (Число < 100) И НЕ (Число чётное)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Число ≥ 100) И (Число нечётное) – тоже истинно
Больше или равно 100 и одновременно нечетное.
Ответ: 4597
8D4389
! Определите количество натуральных трёхзначных чисел x, для которых истинно логическое выражение:
(x оканчивается на 7) И НЕ (x > 119).
Решение:
Избавимся от отрицания:
(x оканчивается на 7) И (x ≤ 119) – тоже истинно
Берем все числа, оканчивающиеся на 7 до 119. И мы знаем, что в каждом десятке только одно число может иметь вариацию числа, где оно оканчивается на 7. И нам надо трехзначное число, то есть берем десятки со 100 до 110. Это один десяток. И получаем 1 неполный десяток, где также можно встретить число 7 в конце, в числе 117. Итого 1+1 =2.
Ответ: 2
83D5CA
Определите наименьшее натуральное двузначное число x, для которого ложно логическое выражение:
НЕ (x нечётное) И НЕ (x > 88).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x нечётное) ИЛИ (x > 88) – истинное выражение
То есть выбор из всех двузначных нечетных, потому что среди них значения меньше, чем после 88.
Ответ: 11
5F31E5
Определите количество натуральных чисел x, для которых истинно логическое выражение:
НЕ ((x ≥ 53) ИЛИ (x < 29)).
Решение:
Избавимся от отрицания:
(x < 53) И (x ≥ 29) тоже истинно
29 53
__._____.____
То есть, если брать только натуральные числа, это интервал от 29 по 52 включительно.
52-29+1=24
Ответ: 24Обратите внимание, что оба условия отрицаются в одних скобках, значит ИЛИ меняем на И.
3FE867
! Определите наибольшее натуральное двузначное число x, для которого ложно логическое выражение:
(x чётное) ИЛИ НЕ (x > 92).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x нечётное) И (x > 92) – истинное выражение
Наибольшее из нечетных больше чем 92 – это 99.
Ответ: 99
674B8F
!! Определите количество натуральных двузначных чисел x, для которых ложно логическое выражение:
НЕ (x чётное) И НЕ (x кратно 13).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x чётное) ИЛИ (x кратно 13) – истинное выражение
То есть это все натуральные четные двузначные числа + нечетные двузначные числа, которые делятся нацело на 13.
Двузначных четных 45 штук. (Интервал от 10 до 99; 99-10=89, 89+1 (крайнее число, которое не учтено)=90, 90/2=45)
Делятся на 13 следующие: 13, 26, 39, 52, 65, 78, 91. Но все четные мы уже учли в первом условии, так что берем только нечетные, их 4.
45 + 4 = 49
Ответ: 49
367282
Определите наибольшее натуральное число x, для которого истинно логическое выражение:
НЕ ((x ≥ 23) ИЛИ (x < 18)).
Решение:
Избавимся от отрицания:
(x < 23) И (x ≥ 18) – тоже истинно
18 23
__.___.__
Наибольшее натуральное в этом интервале 22.
Ответ: 22
88B087