Математика
5 класс
Урок №21
Прямая, луч, отрезок
Перечень рассматриваемых вопросов:
– понятия «прямая», «луч», «отрезок»;
– отличия прямой, луча, отрезка;
– прямая, луч, отрезок на чертежах, рисунках и моделях.
Тезаурус
Отрезок – часть прямой, ограниченный двумя точками.
Концы отрезка – точки, ограничивающие отрезок.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.
Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).
Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.
Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.
Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.

Через любые две точки можно провести только одну прямую.
Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.

Провести через точки А и В другую прямую, отличную от прямой b, нельзя.
Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.
Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.

Каждую из этих частей называют лучом, исходящим из точки А.
Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.
Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.

Переставлять буквы в названии луча нельзя.
Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.
Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.
В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.
Заметим, что два отрезка называются равными, если они совмещаются при наложении.
Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.
Это интересно
Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.
- Космические лучи – это элементарные частицы и ядра атомов, движущиеся с высокими энергиями в космическом пространстве.
- Противосумеречные лучи (англ. anticrepuscular rays) – расходящиеся веером лучи, наблюдающиеся на закате дня со стороны, противоположной Солнцу (то есть, на востоке).
- Белохохлый солнечный луч (лат. Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae).
- Луч света в темном царстве – крылатое выражение, вошедшее в речь после публикации в 1860 году статьи публициста-демократа Николая Александровича Добролюбова, посвящённой драме А. Н. Островского «Гроза».
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: добавление подписей к изображениям.
Разместите нужные подписи к изображениям.

Для выполнения задания обратитесь к теоретическому материалу урока.
Правильные ответы:
1) а – это прямая.
2) АВ – это отрезок.
3) А – это луч.
№ 2. Тип задания: подстановка элементов в пропуски в тексте.
Вставьте в текст нужные слова.
Через__________ две____________ можно провести только одну _________.
Слова: любые; точки; прямую; ломаную.
Правильный ответ: через любые две точки можно провести только одну прямую.

- Точка
- Линия
- Прямая линия
- Луч
- Отрезок
- Ломанная линия
- Многоугольник
- Как научить складывать и вычитать числа
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A
B
C
точка 1, точка 2, точка 3
1
2
3
Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А". Но как понять через какие? A A A
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a
b
c
Линия может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
a
прямая линия AB
B
A
Прямые могут быть
- пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча
A
A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
a
луч AB
B
A
Лучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C
B
A
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B
A
прямая линия AB
B
A
От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.
✂
B
A
✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
B
A
Задача: где прямая, луч, отрезок, кривая?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A
B
C
D
E
64
62
127
52
Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: “пойти на все четыре стороны”, “бежать в сторону дома”, “с какой стороны стола сядешь?”) — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A
B
C
D
E
F
120
60
58
122
98
141
Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.д.
треугольники
четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция
пятиугольники
На этой странице вы узнаете
- Что общего у солнечного луча и геометрического?
- Можно ли кого-то наказать углом?
- Одинаковы ли прямые?
Геометрические понятия
В жизни мы часто встречаемся с такими выражениями как “точка на карте”, “идти по прямой” или “угол комнаты”. Но знали ли вы, что в этих фразах упоминаются термины из геометрии?
Для начала давайте разберемся именно с геометрическими терминами.
Что такое точка, прямая, луч, отрезок и угол?
Точка – это математический объект, точного определения для которого не существует.
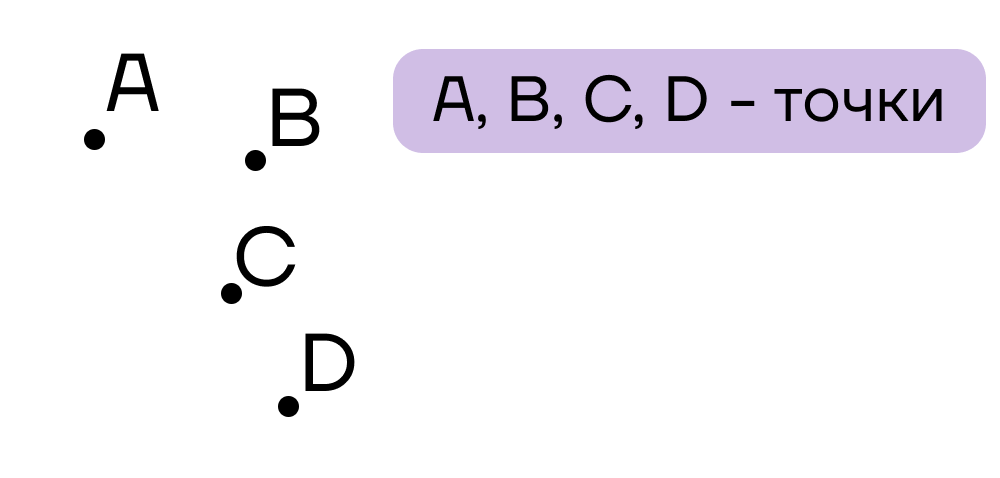
Прямая – это бесконечная линия.

Луч – это прямая, ограниченная точкой с одной стороны. У луча есть начало, но нет конца.
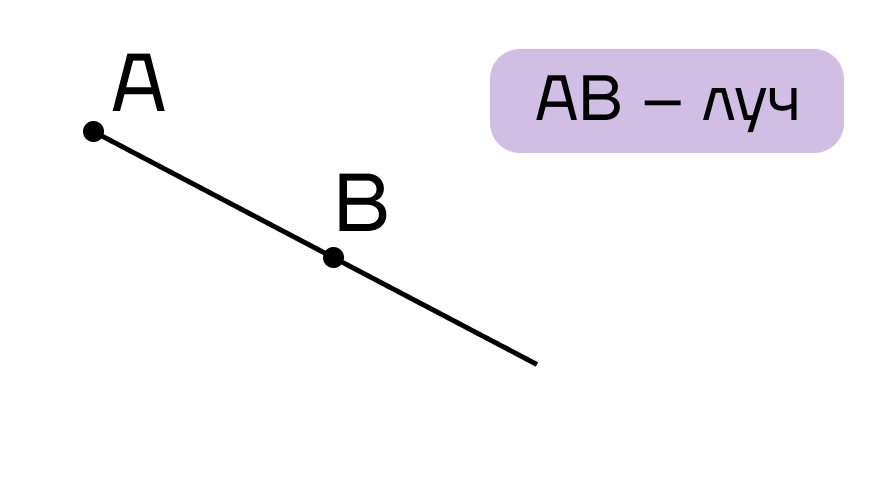
Солнечный луч и геометрический луч отличаются друг от друга почти во всем. Но и тот, и другой имеет начало и не имеет конца.

Отрезок – это прямая, ограниченная точками с обеих сторон. Отрезок состоит из бесконечного множества точек, лежащих на линии между концами отрезка.

Чем отличается луч от отрезка?
Луч ограничен только с одной стороны, а отрезок ограничен с двух.
Угол – это фигура, образованная двумя лучами, исходящими из одной точки.

Провинившегося ребенка могут поставить в угол. Возможно ли поставить кого-то в геометрический угол?
Да. Для такого наказания можно использовать не только прямой угол, но и тупой, и даже некоторые острые углы. Только, пожалуй, не очень узкие острые углы, иначе человек туда просто не поместится.
Углы и прямые
Давайте детально рассмотрим углы
Элементы угла

Виды углов и их градусная мера
Существует четыре вида углов.

Смежные и вертикальные углы
Смежные углы – это два угла, у которых одна общая сторона, а две другие лежат на одной прямой. Такие углы в сумме дают 1800.

Вертикальные углы – это углы, вершиной которых является одна и та же точка, стороны одного такого угла являются продолжениями сторон другого такого угла. Вертикальные углы всегда равны.

Теперь давайте перейдём к прямым и их расположению на плоскости.
Пересекающиеся и параллельные прямые
Пересекающиеся прямые – это прямые, у которых есть одна общая точка.

Перпендикулярные прямые – это прямые, пересекающиеся под прямым углом. Такие прямые образуют четыре прямых угла при пересечении.

А что такое параллельные прямые?
Параллельные прямые – это прямые, не имеющие ни одной общей точки.
Параллельные и перпендикулярные прямые можно встретить не только в планиметрии, но и в повседневной жизни, например, рельсы и шпалы.

Какие могут быть прямые на плоскости?
Аксиома параллельных прямых
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Следствия из аксиомы параллельных прямых:
- Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую параллельную прямую.
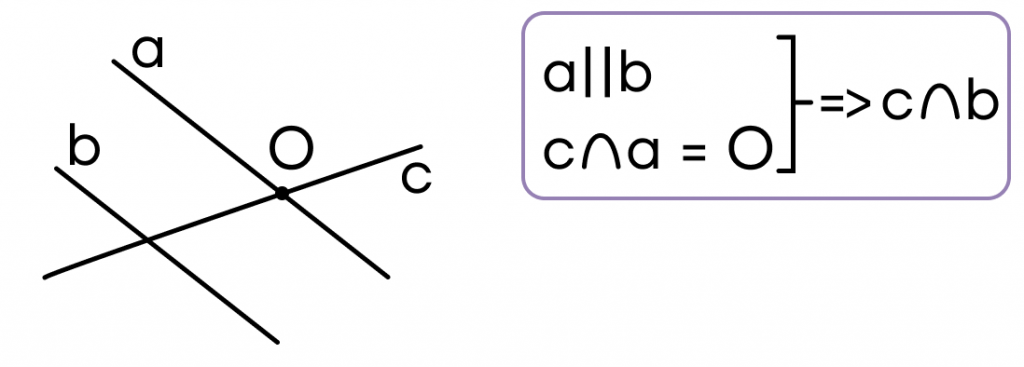
- Если одна из двух параллельных прямых параллельна третьей прямой, то все эти прямые параллельны друг другу.

Чтобы доказать, что прямые являются параллельными, используются признаки параллельности прямых.
Прежде чем перейти к признакам параллельности прямых, рассмотрим углы при пересечении двух прямых секущей.
Секущая – это прямая, пересекающая несколько других прямых.

При таком расположении прямых можно выделить три вида углов:
- накрест лежащие углы,
- односторонние углы,
- соответственные углы.
Рассмотрим данные углы на примере

Накрест лежащие: 4 и 6, 3 и 5.
Односторонние: 4 и 5, 3 и 6.
Соответственные: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
А теперь вернёмся к признакам
Признаки параллельности прямых:
Теорема 1:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Теорема 2:
Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Теорема 3:
Если при пересечении двух прямых секущей сумма односторонних углов равна 1800,то прямые параллельны.

Также существуют свойства параллельности прямых. Что мы назовем свойствами параллельности прямых?
Удивительно, но это те же самые признаки, только ставшие перевертышами. Свойства действуют в обратную сторону. Посмотрим, какие свойства параллельных прямых бывают:
- Если прямые параллельны, то при пересечении этих прямых секущей накрест лежащие углы равны.
- Если прямые параллельны, то при пересечении этих прямых секущей соответственные углы равны.
- Если прямые параллельны, то при пересечении этих прямых секущей сумма односторонних углов равна 1800.
Фактчек
- Основными геометрическими элементами являются точка, прямая, луч, отрезок, угол.
- Углы бывают смежные и вертикальные.
- Прямые бывают пересекающиеся и параллельные. К пересекающимся прямым относятся и перпендикулярные прямые.
- Углы при пересечении двух прямых секущей: накрест лежащие, односторонние и соответственные.
- Для определения параллельных прямых существует три признака. Также существуют и свойства параллельных прямых, которыми являются обратные признакам утверждения.
Термины
Аксиома – это утверждение, не требующее доказательства.
Проверь себя

Задание 1.
Какими углами являются углы 1 и 2?
- Вертикальными
- Накрест лежащими
- Смежными
- Односторонними
Задание 2.
Какими углами являются углы 4 и 8?
- Вертикальными
- Соответственными
- Смежными
- Односторонними
Задание 3.
Угол 4 равен 600. Чему равен угол 5?
- 1200
- 600
- 300
- 200
Задание 4.
Угол 4 равен 600. Чему равен угол 7?
- 1200
- 600
- 300
- 200
Задание 5.
Угол 5 равен 500. Чему равен угол 8?
- 1500
- 650
- 1300
- 500
Ответы: 1. – 3; 2. – 2; 3. – 2; 4. – 1; 5. – 4
Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Познакомимся с основными геометрическими понятиями, изучаемыми в начальной школе.
Точка
Запомните!
![]()
Точка — это основная и самая простая геометрическая фигура.
В геометрии точка обозначается заглавной латинской буквой или цифрой.
Многие латинские буквы по написанию похожи на английские буквы.
В тексте точку обозначают следующим символом: «(·) A» — точка «А».
Прямая
Запомните!
![]()
Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
- Через две точки можно провести единственную прямую.
- Две прямые могут пересекаться только в одной точке.
- Через одну точку можно провести бесконечное множество прямых.
Способы обозначения прямых
- Строчной латинской буквой:
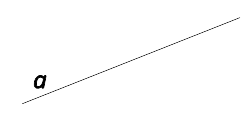
Прямая «a».
- Двумя заглавными латинскими буквами в том случае, если этими буквами обозначены
точки, расположенные на прямой.

Прямая «АB».
Луч
Запомните!
![]()
Луч — это часть прямой линии, которая расположена по одну сторону от какой-либо точки.
У луча есть начало, но нет конца.
Способы обозначения лучей
- Строчной латинской буквой:
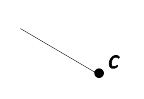
Луч «c».
- Двумя заглавными латинскими буквами в том случае, когда первая точка — начало луча, а
вторая точка лежит на луче.
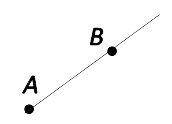
Луч «AB».
Отрезок
Запомните!
![]()
Отрезок — это часть прямой линии, которая ограничена двумя точками (концами отрезка).
У отрезка есть и начало, и конец.
Основное свойство отрезка — это его длина.
Длина отрезка — это расстояние между его концами.
В математике отрезок обозначается заглавными латинскими буквами.
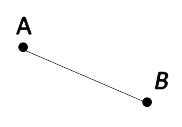
Отрезок «AB».
Ломаная
Запомните!
![]()
Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.
Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.
Звенья ломаной — это отрезки ломаной.
В математике ломаная обозначается заглавными латинскими
буквами.
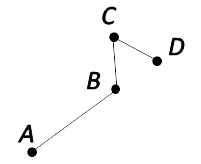
Ломаная «ABCD».
Вершины ломаной — A, B, C, D.
Звенья ломаной — AB, BC, CD.
Запомните!
![]()
Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из
которых она состоит.
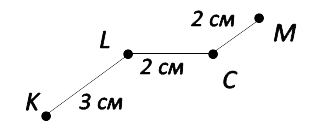
KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см
Вот мы и познакомились с основами геометрии. Теперь мы готовы рассмотреть не менее важную
геометрическую фигуру — угол.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
25 февраля 2017 в 9:40
Ильназ Хуснутдинов

Профиль
Благодарили: 0
Сообщений: 2

Ильназ Хуснутдинов
Профиль
Благодарили: 0
Сообщений: 2
6. (4 балла) Дан отрезок MP длиной 39 см. На нем отмечены точки G и H таким образом, что длины отрезков GP = 26 см, MH = 23 см. Найти длину отрезка GH в дециметрах.
0
Спасибо
Ответить
25 февраля 2017 в 9:37
Ильназ Хуснутдинов

Профиль
Благодарили: 0
Сообщений: 2

Ильназ Хуснутдинов
Профиль
Благодарили: 0
Сообщений: 2
Дан отрезок MP длиной 39 см. На нем отмечены точки G и H таким образом, что длины отрезков GP = 26 см, MH = 23 см. Найти длину отрезка GH в дециметрах.
0
Спасибо
Ответить
13 сентября 2016 в 8:06
Serega Pavlichenko

Профиль
Благодарили: 0
Сообщений: 1

Serega Pavlichenko
Профиль
Благодарили: 0
Сообщений: 1
найдите длину единичного отрезка координатного луча.Отметьте на координатном луче точки Е(2) и Д(5)
0
Спасибо
Ответить
19 сентября 2016 в 14:44
Ответ для Serega Pavlichenko
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Единичный отрезок- это отрезок равный 1делению. Точка E — на расстоянии 2 деления от начала луча, а точка Д — на расстоянии 5 делений от начала луча.
0
Спасибо
Ответить
10 июня 2016 в 9:50
Дарья Бондарь

Профиль
Благодарили: 0
Сообщений: 4

Дарья Бондарь
Профиль
Благодарили: 0
Сообщений: 4
Объясните, какой отрезок называется перпендикуляром, проведенным из данной точки к данной прямой.
0
Спасибо
Ответить
24 июня 2016 в 12:39
Ответ для Дарья Бондарь
Павел Асафов

Профиль
Благодарили: 0
Сообщений: 2

Павел Асафов
Профиль
Благодарили: 0
Сообщений: 2
отрезок, образующий с данной прямой угол 90 градусов
0
Спасибо
Ответить
9 июня 2016 в 10:28
Дарья Бондарь

Профиль
Благодарили: 0
Сообщений: 4

Дарья Бондарь
Профиль
Благодарили: 0
Сообщений: 4
Какими инструментами пользуются для измерения расстояний?
0
Спасибо
Ответить
9 июня 2016 в 10:53
Ответ для Дарья Бондарь
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Линейка, рулетка. Расстояние можно измерить по карте, зная масштаб и имея линейку.
0
Спасибо
Ответить
19 марта 2016 в 17:01
Настюшка Петрухова

Профиль
Благодарили: 0
Сообщений: 1

Настюшка Петрухова
Профиль
Благодарили: 0
Сообщений: 1
Дается отрезок, единичный отрезок равен 10 клеточкам. Как на нем указать 0,75 и 2,15???
0
Спасибо
Ответить
25 марта 2016 в 19:21
Ответ для Настюшка Петрухова
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Если я правильно понимаю задание, то необходимо нарисовать соответствующие отрезки. Если единичный отрезок равен 10 клеточек, то 0,75 от него =10*0,75=7,5 клеток. А 2,15 = 2,15*10=21,5 клетка.
0
Спасибо
Ответить
3 октября 2015 в 11:37
Ольга Сырая

Профиль
Благодарили: 0
Сообщений: 1

Ольга Сырая
Профиль
Благодарили: 0
Сообщений: 1
На прямой поставили 3 точки. Сколько получилось отрезков? Мы решили, что 2. Но это олимпиадная задача и ответ пришел -3. Неужели АС это тоже отрезок?
0
Спасибо
Ответить
6 октября 2015 в 17:56
Ответ для Ольга Сырая
Альбина Серб

Профиль
Благодарили: 0
Сообщений: 2

Альбина Серб
Профиль
Благодарили: 0
Сообщений: 2
да
0
Спасибо
Ответить
25 сентября 2015 в 19:16
Снежана Бабюк

Профиль
Благодарили: 0
Сообщений: 1

Снежана Бабюк
Профиль
Благодарили: 0
Сообщений: 1
выберите геометрические фигуры понятие которых не определяется:
прямая, квадрат, плоскость, треугольник, окружность, точка, полупрямая, отрезок.
![]()
0
Спасибо
Ответить
12 сентября 2016 в 11:39
Ответ для Снежана Бабюк
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Прямая, плоскость и точка.
0
Спасибо
Ответить
15 сентября 2015 в 13:19
Марьям Туманова

Профиль
Благодарили: 0
Сообщений: 1

Марьям Туманова
Профиль
Благодарили: 0
Сообщений: 1
начерти отрезок мн длиной 4 см.начерти отрезок, каторий длиннееотрезкамн: а)на 3см; б)в3раза.какой длиныполулся каждый отрезок?
0
Спасибо
Ответить
17 сентября 2015 в 21:23
Ответ для Марьям Туманова
Ега Превосходный

Профиль
Благодарили: 0
Сообщений: 2

Ега Превосходный
Профиль
Благодарили: 0
Сообщений: 2
1 отрезок 4 см., второй 7 см., третий в трираза больше когого? если первого то полусится12см если вророго то получится 21см записать так( 4+3)* 3=21 см
0
Спасибо
Ответить
Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.
Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.
Запомните
Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.
Плоскость нельзя измерять, потому что она бесконечная.
Плоскость нельзя согнуть, в каком бы положении она ни находилась.
Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.
Прямая линия
Запомните
Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.
Даже когда мы рисуем на листе бумаги небольшой кусок прямой линии, то мы предполагаем, что этот лист бумаги – это бесконечная плоскость, и мы можем мысленно раздвинуть видимые границы бумаги и продлить прямую бесконечно долго.
Обозначение прямой
В основном прямую, как и любую другую линию, обозначают при помощи строчной (маленькой) буквы латинского алфавита.
Иногда обозначение прямой линии происходит при помощи двух точек, которые принадлежат (часто говорят просто – лежат на) этой прямой. В этом случае ее обозначают названием этих двух точек.
Например, на рисунке 1 обозначены такие прямые:
- c
- KL

Рис. 1 Обозначение прямой линии
Если на одной прямой лежат три и более известных нам точек, то обозначить эту линию можно любой из комбинаций имен любых двух точек.

Рис. 2 Обозначение прямой с несколькими точками
На рисунке 2 видно, что на одной прямой b лежат четыре точки: D, G, H, O. Поэтому данную прямую мы можем назвать любым из этих семи имен: b, DG, DH, DO, GH, GO или HO.
Некоторые свойства прямой
Две точки, лежащие на одной прямой, создают отрезок этой прямой.
Через две любые точки на плоскости можно провести единственную прямую.

Рис. 3 Отрезок на прямой
Две разные прямые могут пересекаться или не пересекаться.
Две прямые пересекаются в том случае, если у них есть общая точка.
И наоборот, если у двух разных прямых нет общей точки, тогда эти прямые не пересекаются.

Рис. 5 Пересечение прямых
На рисунке 5 можно видеть, что прямые l и q пересекаются в точке O, а прямые q и g не пересекаются.
Обозначение пересечения письменно записывается при помощи символа ∩: l ∩ q — прямая l пересекается с прямой q.
Как вам уже известно из этого урока, на рисунках мы можем отображать только часть прямых (поскольку они бесконечные), и что их можно мысленно увеличивать, делать более протяженными. Поэтому, если мысленно продлить прямые l и g, то станет понятно, что они тоже пересекаются.
Взаимное расположение точек и прямой, а также их обозначение, точно такое же, как и у всех линий вообще.
Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.
Луч
Определение
Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.

Рис. 6 Деление прямой линии точкой
На рисунке 1 точка O делит прямую a на две части, то есть, на два луча. Один из них, как вы видите, длится бесконечно вправо, а другой – бесконечно влево. Оба они начинаются в одной и той же точке O, которую называют началом луча.
У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.
Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.
Обозначение луча
Луч, как и прямую, обозначают двумя способами.

Рис. 7 Обозначение луча
На рисунке 2 приведены примеры обозначения луча:
- a – строчной (маленькая) буква латинского алфавита;
- OF – точками, расположенными на луче. При этом на первом месте всегда пишут точку начала луча, а на втором – любую точку, которая принадлежит лучу.
Луч имеет второе название – полупрямая.
Два луча, которые лежат на одной прямой, начинаются в одной точке и направлены в разные стороны, называются дополнительными друг другу лучами, поскольку в соединенном виде они формируют одну прямую линию в точке их начала.
Если лучи лежат на одной прямой, начинаются в одной точке и направлены в одну сторону, их называют совпадающие, или говорят, что эти лучи совпадают.
![]()
Рис. 8 Дополнительные друг другу и совпадающие лучи
На рисунке 8 видно, что:
- CB и CH – дополнительные друг другу лучи,
- BC и BH – совпадающие лучи,
- HC и HB – совпадающие лучи.
