Как найти лямбду вектора

Автор	Сообщение
	Заголовок сообщения: Найти все значения λ Добавлено: 07 ноя 2017, 20:01
Продвинутый Зарегистрирован: 06 окт 2017, 15:28 Сообщений: 76 Cпасибо сказано: 9 Спасибо получено: 0 раз в 0 сообщении Очков репутации: 1	Найти все значения λ, при которых вектор x линейно выражается через векторы l1 и l2. l1 = (4;4;3) l2 = (2;-1;3) x = (5;9;λ)
Вернуться к началу

mkolmi	Заголовок сообщения: Re: Найти все значения λ Добавлено: 07 ноя 2017, 21:00
	Как получить уравнение относительно λ ?
Вернуться к началу

Andy	Заголовок сообщения: Re: Найти все значения λ Добавлено: 07 ноя 2017, 21:06
	mkolmi писал(а): Как получить уравнение относительно λ ? Расписать определитель, составленный из координат векторов [math]vec{l_1},~vec{l_2},~vec{x},[/math] приравняв его к нулю.
Вернуться к началу

mkolmi	Заголовок сообщения: Re: Найти все значения λ Добавлено: 08 ноя 2017, 15:44
	Andy писал(а): Расписать определитель, составленный из координат векторов l1→, l2→, x⃗ , l1→, l2→, x→, приравняв его к нулю. То есть, если посчитать, то ответы будет равен 1,75?
Вернуться к началу

Andy	Заголовок сообщения: Re: Найти все значения λ Добавлено: 08 ноя 2017, 15:52
	mkolmi mkolmi писал(а): То есть, если посчитать, то ответы будет равен 1,75? Я проверил, вычислив определитель при [math]lambda=1,75.[/math] Получил ноль. Значит, ответ правильный.
Вернуться к началу
	За это сообщение пользователю Andy “Спасибо” сказали: mkolmi, scharafetdinov

scharafetdinov	Заголовок сообщения: Re: Найти все значения λ Добавлено: 11 окт 2020, 16:41
	Andy,а если мне нужно найти для 3-х векторов значения h ,при которых вектор б будет линейно выражаться через векторы а1,а2,а3
Вернуться к началу

scharafetdinov	Заголовок сообщения: Re: Найти все значения λ Добавлено: 11 окт 2020, 16:43
Вернуться к началу

Andy	Заголовок сообщения: Re: Найти все значения λ Добавлено: 11 окт 2020, 16:50
	scharafetdinov scharafetdinov писал(а): Andy,а если мне нужно найти для 3-х векторов значения h ,при которых вектор б будет линейно выражаться через векторы а1,а2,а3 Если у Вас возник вопрос с решением какой-то другой задачи, то создайте, пожалуйста, новую тему.
Вернуться к началу

Векторы

1. Векторы на
плоскости и в пространстве

Обобщим некоторые
сведения о векторах, известные в основном
из школьного курса геометрии.

Вектором
называется
направленный отрезок

с начальной
точкой
А
и
конечной точкой В
(который
можно перемещать параллельно
самому себе.

Векторы
могут обозначаться как двумя
прописными буквами, так и одной строчной
с чертой или стрелкой,
например:
.

Длиной
(или
модулем)

вектора


называется
число, равное
длине отрезка АВ,
изображающего
вектор.

Векторы,
лежащие на одной прямой или на параллельных
прямых,
называются коллинеарными
(параллельными).

Если
начало
и конец вектора совпадают, например,
,
то
такой
вектор называют нулевым
и
обозначают
.

Длина
нулевого
вектора равна нулю. Так как направление
нулевого вектора
произвольно, то считают, что он коллинеарен
(параллелен) любому вектору.

Произведением
вектора


на
число

(лямбда)
называется
вектор
,
имеющий длину
,
направление
которого совпадает
с направлением вектора
,
если

,
и противоположно
ему, если
.

Противоположным
вектором

называется
произведение вектора

на
число (-1).

Суммой
двух
векторов

и

называется вектор
,
начало
которого совпадает
с началом вектора
,
а конец – с концом вектора

при условии, что начало вектора

совпадает
с концом вектора

(правило
треугольников).

Аналогично
определяется сумма
нескольких векторов.
Так,
например,
сумма четырех векторов (рис. а)
есть
вектор

,
начало
которого совпадает с началом вектора

,
а
конец – с концом вектора

(правило многоугольника)
(рис.
б).

Разностью
двух
векторов

и

называется сумма вектора

и
вектора
,
противоположного

.

Легко
убедиться в том,
что в параллелограмме,
построенном
на векторах

и
,
одна диагональ
– вектор

–
представляет
сумму векторов

и
,
а
другая диагональ
— вектор
–
их разность.

Перенесем
вектор

параллельно
самому себе так, чтобы его начало
совпало с началом координат.

Координатами
вектора


называются
координаты его конечной
точки.

Так,
координатами вектора

на
плоскости
Оxy
являются

два
числа x
и
y:

,

а
в
пространстве
Oxyz
– три
числа x,
y
и z:

.

Для
векторов

и

,
заданных координатами,

сумма
определяется по формуле

разность
– по формуле

произведение
вектора

на число
λ – по формуле

.

Длина вектора
равна корню квадратному из суммы
квадратов его координат:

.

Если
A(a₁,
a₂,
a₃)
– начало вектора, B(b₁,
b₂,
b₃)
– его конец, то

Скалярное
произведение.
Скалярным произведением векторов
называется произведение их модулей на
косинус угла между векторами (не больше
пи)

.

Из
данного выражения можно найти косинус:
.

Если
векторы выражены через координаты в
декартовой системе координат
,

,
то скалярное произведение определяется
как сумма попарных произведений
соответствующих координат

.

Условием
перпендикулярности векторов является
равенство нулю их скалярного произведения

.

Скалярное
произведение обладает следующими
свойствами:

1. ;

2. .

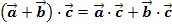Модуль
вектора можно представить в виде
.

Соседние файлы в папке Matematika

• #
• #
• #
• #
• #
• #
• #

Обновлено: 20.05.2023

Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.

Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…

λ-исчисление: основные понятия

Синтаксис

В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.

Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.

Термы:

переменная:	x
лямбда-абстракция (анонимная функция):	λx.t , где x — аргумент функции, t — её тело.
применение функции (аппликация):	f x , где f — функция, x — подставляемое в неё значение аргумента

• Применение функции левоассоциативно. Т.е. s t u — это тоже самое, что (s t) u
• Аппликация (применение или вызов функции по отношению к заданному значению) забирает себе всё, до чего дотянется. Т.е. λx. λy. x y x означает то же самое, что λx. (λy. ((x y) x))
• Скобки явно указывают группировку действий.

Процесс вычисления

Рассмотрим следующий терм-применение:

Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:

который для простоты можно переписать как

(напомним, что id — это функция тождества вида λx.x )

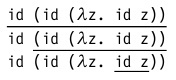
В этом терме содержится три редекса:

Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение

(λx.λy. x) z ((λx.x x)(λx.x x))

Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y . Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y , а z — первоначальный терм имел бы вид (λx.λz.x)y и после редукции выглядел бы как λz.y . Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.

Так же бывает, что у нас есть абстракция λx.t x , причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t . Такое преобразование называется η-конверсией.

На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Как уже говорилось ранее, в чистом бестиповом лямбда-исчислении отсутствует всё, кроме функций. Так что даже такие элементарные вещи, как числа или булевы значения необходимо реализовывать самим. Точнее, надо создать некие активные сущности, которые будут вести себя подобно необходимым нам объектам. И, естественно, процесс кодирования будет заключаться в написании соответствующих функций.

Начнём мы с самого простого: True и False . Два терма, воплощающие поведение этих констант, выглядят следующим образом:

tru = λt.λf.t	Двухаргументная функция, всегда возвращающая первый аргумент
fls = λt.λf.f	Двухаргументная функция, всегда возвращающая второй аргумент

Оператор if под такие булевы константы будет имеет вид:
if = λb. λx. λy.b x y
Здесь b — tru или fls , x — ветка then , y — ветка else .

Посмотрим, как это будет работать:
if fls t e

Поскольку условие if ложно ( fls ), то должно возвращаться выражение из ветки else ( e в нашем случае).

(λb. λx. λy. b x y) fls t e	по определению if
(λx. λy. fls x y) t e	редукция подчёркнутого выражения из предыдущей строки
(λy. fls t y) e	редукция подчёркнутого выражения из предыдущей строки
fls t e	редукция подчёркнутого выражения из предыдущей строки
(λt.λf. f) t e	по определению fls
(λf. f) e	редукция подчёркнутого выражения из предыдущей строки
e	редукция подчёркнутого выражения из предыдущей строки

or = λx.λy. x tru y

not = λx. x fls tru

Числа Чёрча

Мы с вами будем кодировать только натуральные числа, для чего вспомним аксиомы Пеано, определяющие их множество. В основе реализации по-прежнему будут лежать функции, ведущие себя в заданном контексте подобно единице, двойке и т.д. Собственно, это одна из особенностей лямбда-исчисления: сущности, записанные в его терминах, не обладают самодостаточностью, поскольку воплощают поведение того или иного объекта.

Итак, нам нужна функция, принимающая два аргумента: фиксированное начальное значение и функцию для определения следующего элемента (функцию следования). Число будет закодировано в количестве применений функции следования к начальному значению:

0 ≡ λs.λz. z	функция s применяется к начальному значению z нуль раз
1 ≡ λs.λz. s z	функция s применяется к начальному значению z один раз
2 ≡ λs.λz. s (s z)	функция s применяется к начальному значению z два раза
.	и так далее

Легко заметить, что нуль кодируется так же, как и логическое False. Тем не менее, не стоит делать из этого какие-либо далеко идущие выводы: это всего лишь совпадение.

Задача функции следования состоит в том, чтобы прибавить к заданному числу единицу. Т.е. в качестве аргумента она будет принимать значение, которое требуется увеличить, и которое тоже является функцией двух аргументов. Таким образом, суммарно функция (+1) имеет три аргумента: предшествующее число Чёрча n , функцию, которую надо будет применить n+1 раз к начальному значению, и само начальное значение. Выглядит это так:
scc = λn. λs. λz. s (n s z)
Здесь n s z — n раз применённая к z функция s . Но нам нужно применить её n+1 раз, откуда и берётся явное s (n s z) .

Арифметические операции

Сложение

Функция, осуществляющая сложение двух чисел Чёрча, будет принимать два слагаемых: x и y , которые в свою очередь тоже имеют по два аргумента — s (функцию следования) и z (начальное значение). Сложение будет состоять в том, чтобы сначала применить s к z x раз, а потом ещё y раз.

plus = λx. λy. λs. λz. x s (y s z)

В качестве примера сложим one = λs.λz. s z и two = λs.λz. s (s z) . Ответ должен будет выглядеть так: three = λs.λz. s (s (s z)) .

plus one two s’ z’	s’ и z’ — чтобы не путать подставляемые значения с именами переменных
(λx. λy. λs. λz. x s (y s z)) one two s’ z’	по определению plus
one s’ (two s’ z’)	после проведения редукции
(λs.λz. s z) s’ (two s’ z’)	по определению one
s’ (two s’ z’)	после проведения редукции
s’ (( λs.λz. s (s z) s’ z’)	по определению two
s’ (s’ (s’ z’))	после проведения редукции
three s’ z’	по определению three

Умножение

Функцию для умножения можно определить через функцию сложения. В конце-концов, умножить x на y означает сложить x копий y .

times = λx. λy. x (plus y) z

Есть ещё один способ определения умножения на числах Чёрча, без использования plus . Его идея заключается в том, что для получения произведения x и y нужно x раз взять y раз применённую к начальному значению функцию s :

times’ = λx.λy.λs.λz. x (y s) z

Для примера умножим two = λs.λz. s (s z) на three = λs.λz. s (s (s z)) . Результат должен будет иметь вид: six = λs.λz. s (s (s (s (s (s z))))) .

times’ two three s’ z’	s’ и z’ — чтобы не путать подставляемые значения с именами переменных
(λx.λy.λs.λz. x (y s) z) two three s’ z’	по определению times’
two (three s’) z’	после проведения редукции
(λs.λz. s (s z)) (three s’) z’	по определению two
three s’ ((three s’) z’)	после проведения редукции
(λs.λz. s (s (s z))) s’ ((three s’) z’)	по определению three
s’ (s’ (s’ ((three s’) z’)))	после проведения редукции
s’ (s’ (s’ (((λs.λz. s (s (s z))) s’) z’)))	по определению three
s’ (s’ (s’ (( (λz. s’ (s’ (s’ z))) z’ )))	после проведения редукции
s’ (s’ (s’ (s’ (s’ (s’ z’)))))	редукция подчёркнутого выражения
six s’ z’	по определению six

Определите терм для возведения числа в степень

Для x в степени y :

power = λx.λy.λs.λz . y x s z

Заключение

Как видим, технически ничего сложного в лямбда-исчислении нет: всё сводится к элементарным подстановкам и редукциям. Но столь малого набора инструментов вполне хватает, чтобы при желании реализовать активные сущности, ведущие себя подобно парам, спискам, рекурсивным функциям и т.п. Они будут достаточно громоздкими, но, как уже говорилось, λ-исчисление предназначено не для написания программ, а для исследования и спецификации языков программирования и систем типов. С чем, собственно, и прекрасно справляется.

В очередном опусе Итана Сигеля резанула фраза

Пронаблюдав за удалёнными сверхновыми и измерив, как Вселенная расширялась миллиарды лет, астрономы обнаружили нечто удивительное, загадочное и неожиданное.

By observing distant supernovae and measuring how the Universe had expanded over billions of years, astronomers discovered something remarkable, puzzling and entirely unexpected

О чём вообще весь сыр-бор?

Первую версию Общей Теории Относительности (ОТО) Альберт Эйнштейн представил публике 25 ноября 1915 года. В оригинале уравнения ОТО Эйнштейна выглядели вот так:

или, в современной записи, вот так:

Для неумеющего в тензоры читателя понятнее уравнение (1) в оригинальной записи Эйнштейна. Там написано, что энергия-импульс материи G равен кривизне пространства R плюс тензор Риччи S. (Этот самый тензор Риччи тоже есть кривизна, только в более другой форме).
Сейчас, решая уравнение ОТО, энергию-импульс обычно считают известным, а ищут как раз кривизну. Поэтому в современной записи стороны уравнения поменяли местами. Заодно поменяли буковки: G → T, S → R_μν.

Откуда есть пошла лямбда

Но физика — это вам не математика. Здесь нельзя взять формулу и напихать в неё добавочных слагаемых просто так. Нужно иметь очень веские основания, и теоретические, и экспериментальные.

Хотя ниже вы увидите, насколько мало Эйнштейн знал о Вселенной в те годы, но тогда, в 1916, такие основания у него были. Альберт Германович точно знал, что звёзды не попадали друг на друга и совершенно не собираются этого делать в обозримом будущем. Однако, в ОТО-1915 было только притяжение, которое нужно было чем-то сбалансировать.

Первое физическое толкование смысла лямбды

В такой трактовке ненулевое значение Λ означает, что наша Вселенная искривлена сама по себе, в том числе и при отсутствии какой-либо гравитации. Ну, вот такой нам достался мир. Однако, большинство физиков в это не верят, и считают, что у наблюдаемого искривления должна быть какая-то внутренняя причина. Какая-то неведомая доселе фигня, которую можно открыть.

На сегодняшний день измеренная кривизна пространства Вселенной таки равна нулю, но с очень паршивой точностью, порядка 0.4%. И не очень-то видно способов эту точность улучшить.
С измерениями кривизны есть две концептуальные проблемы.

Первая в том, что мы не можем измерить совсем пустое пространство, потому что просто ничего там не видим. А если там есть что-то, что мы таки видим, то пространство уже не пустое и, значит, уже дополнительно искривлено гравитацией.

Допустим, у нас есть как-то измеренные координаты объектов, плюс пачка фотографий этих объектов в разных ракурсах (снятых из разных точек). Тогда мы можем вычислить кривизну пространства. Например, гравитация Солнца отклоняет пролетающий мимо свет далёких звёзд. Во время солнечных затмений это отклонение можно измерить экспериментально и сравнить с предсказаниями ОТО.

Теперь наоборот: допустим, мы знаем кривизну пространства, и у нас есть пачка фотографий. Тогда, если кривизна достаточно хорошая, без чёрных дыр и т.п. — мы можем вычислить координаты объектов на фото. Именно так работают наши глаза, точнее мозги, когда вычисляют расстояние до объектов по двум фоткам с разных точек.

Поэтому измерить кривизну наблюдаемой Вселенной в целом мы можем только из очень окольных соображений.

Вселенная Фридмана

Meanwhile in Russia, не смотря на войны и революции, над теорией ОТО бился прапорщик (и по совместительству профессор) Александр Александрович Фридман. Он рассмотрел все варианты лямбд и выяснил следующее:

При Λ < 0 имеют место лишь силы притяжения, как гравитационные, так и вызванные кривизной впуклоговогнутого пространства. Рано или поздно звёзды и галактики в таком мире таки попадают друг на друга. Причём конец будет неожиданно быстрым и очень горячим.

Но самое интересное происходит при Λ = 0. Здесь всё зависит от начальных условий — т.е. координат и скоростей конкретных галактик. Возможны три варианта: большое сжатие, большой разлёт и стационарный вариант, когда галактики разлетаются, но с относительно небольшими скоростями и без ускорения.

Сегодня вышеописанные ситуации называются космологическими решениями Фридмана.

Статьи Фридмана 1922 и 1924 годов отменяли необходимость в лямбда-члене, из-за чего поначалу были приняты Эйнштейном в штыки.

За свою работу Фридман вполне мог претендовать на Нобелевку.

Летом 1925 он женился, поехал в свадебное путешествие в Крым, съел там немытую грушу, заразился тифом и в сентябре — умер.

И да, статья Итана про примерно такой график (конкретно на этом учтены данные на 2010 год):

Здесь по горизонтали отложено z — это красное смещение, по вертикали наблюдаемая яркость сверхновых особого типа Ia, которые всегда выделяют одно и то же количество энергии. Вообще, это два способа измерения одного и того же расстояния, но, так сказать, в разные моменты времени.

Серые палки — наблюдавшиеся события с их погрешностью измерений. Синим пунктиром отложено предсказание при Λ = 0, красной линией — аппроксимация фактически наблюдаемых значений. Отклонение красной линии от прямой означает, что Вселенная расширяется ускоренно. Но Эйнштейн об этом так и не узнал.

Вселенная Каптейна

Перейдём к экспериментальной части.

Голландский астроном Якобус Корнелиус Каптейн открыл звезду Каптейна в 1897, после чего приступил к opus magnum всей своей жизни. Объединяя огромное количество наблюдений разных обсерваторий, он попытался создать первую карту Вселенной. По его карте выходило, что вселенная имеет форму вращающегося (sic!) диска крышесносящего по тем временам размера 40000 световых лет, причём Солнце находится отнюдь не в центре, а вполне себе на задворках. Закончена и опубликована эта работа была только в 1922.

Для понимания уровня тогдашних знаний: то, что Каптейн считал невероятно огромной Вселенной, сегодня считается совершенно рядовой, ничем не примечательной среди миллиардов таких же… галактикой Млечный Путь. Тем не менее, заслуга Каптейна в том, что он открыл её вращение и приблизительно вычислил её центр.

Наблюдения Хаббла (астронома, а не телескопа)

Статью со своими открытиями, из которой следовало, что Вселенная значительно больше, чем наш Млечный путь, Хаббл представил американскому астрономическому обществу первого января 1925. За что и был освистан страдающими от похмелья коллегами, едва свыкшимися с расстояниями Каптейна.

Хаббл не унимался и прикрутил к телескопу ещё и спектрометр. Анализируя красное смещение галактик, он выяснил, что галактики разбегаются, а Вселенная, соответственно, расширяется. Заодно он открыл закон имени себя с константой имени себя (впрочем, закон был предсказан Леметром), и описал всё это в статьях к концу 20-ых годов. Согласно его наблюдениям, оказалась верна модель Фридмана для Λ = 0.

Это выбило из-под лямбды теперь уже и экспериментальные основания её существования.

Здесь ещё нужно упомянуть, что первоначальные оценки Хаббла были очень уж неточными и показывали возраст Вселенной порядка 2 миллиардов лет. Позднее это войдёт в противоречие с данными геофизиков, которые при помощи радиоизотопного анализа оценят возраст Земли в несколько миллиардов лет, и десятилетиями будет сильнейшей головной болью для физиков-космологов.

Стационарная Вселенная Хойла

С начала 30-ых годов вопрос с лямбдой считался решённым, и из мейнстримных физиков ей никто толком не занимался. Одним из редких исключений, рискнувших попереть супротив самого Эйнштейна, стал британец Фред Хойл.

Речь пойдёт о гелии. Этот элемент феноменально инертен и не хочет ни с чем реагировать. Причём не только химически, но и физически тоже, если мы говорим про гелий-4. Его ядро — альфа частица — имеет пиковую энергию связи на нуклон в своей области. см. рис из какого-то реферата:

Это значит, что альфа-частица не может присоединить дополнительные протоны или другую альфа-частицу иначе как случайно: это просто-напросто энергетически невыгодно. А в ядрах звёзд ничего кроме протонов и альфа-частиц и нет.

Возникал резонный вопрос: а откуда, собственно, взялись химические элементы тяжелее гелия?

Ближайшее ядро, в которое может превращаться гелий-4, это углерод-12. Но для этого нужно объединить три альфа-частицы.

Проблема в том, что вероятность столкновения трёх альфа-частиц одновременно слишком мала. А двухшаговый процесс (сначала сталкиваются две частицы, потом очень быстро, пока они не разлетелись обратно на две альфа-частицы, в них врезается ещё одна), в принципе, возможен, но расчёты Эдвина Солпитера показывали, что такой процесс идёт слишком вяло, чтобы производить существенные количества углерода.

Однако, по расчётам Хойла выходило, что при наличии такого уровня в три-альфа процессе наступает резонанс, и звёзды — красные гиганты производят достаточно много углерода для нашего существования.

Удивительно, но американцы решили провести небольшой эксперимент на своём ускорителе. И да — триумфально нашли нужный энергетический уровень на 7.65 МэВ, который физики-ядерщики всего мира почему-то проглядели во всех предыдущих экспериментах.

Сегодня такое возбуждённое состояние углерода-12, когда три альфа-частицы фактически выстраиваются по линии, называется хойловским. Соответствующая статья Хойла, Фаулера и супругов-астрономов Джефри и Маргерит Бёрбиджей является краеугольным камнем современных теорий звёздного нуклеосинтеза и настолько часто цитируется, что обозначается просто B²FH, без ссылок и расшифровок.

И — да, на сегодня это чуть ли не единственное известное успешное предсказание на основе антропного принципа.

Однако, из квантовых флуктуаций постоянно рождается новое вещество, причём так, что средняя плотность материи остаётся одинаковой. Расчёты показывают, что в одном кубическом километре пространства должен рождаться всего-навсего один протон раз в 300000 лет (а так же один электрон или что-то типа того для сохранения электрического заряда). Прекрасное число, чтобы исключить любую возможность какой-либо экспериментальной проверки!

Теория стационарной Вселенной серьёзно рассматривалась как альтернатива теории Большого Взрыва в 50-х и начале 60-х. Но экспериментальное открытие в 1964 году предсказанного ТББ реликтового излучения поставило на ней крест.

За статью B²FH дали Нобелевку. Но только Фаулеру, который распорядился провести десятидневный эксперимент. Ни супругам Бёрбиджам, проводившим длительные астрономические наблюдения и собственно написавшим статью, ни автору идеи Хойлу нобелевку не дали — за упорствование в космологической ереси.

Квантовая лямбда

Вернёмся к уравнению ОТО.

Слева (в современной записи) стоит кривизна пространства, сиречь гравитация по ОТО. Справа — тензор энергии-импульса. Под этим тензором стоит жутко сложный матан, но суть в следующем: там учтена вся-вся-вся материя Вселенной во всех видах и состояниях. И обычное вещество, и всякие хитрые частицы, и все виды излучений (кроме гравитации, которая слева).

Теперь мысленно перенесём лямбду вправо. В такой записи это будет не дополнительная кривизна, а какая-то неучтённая энергия (замечу, отрицательная, раз уж мы считаем лямбду положительной). И здесь просматриваются две возможности.

Первая гипотеза состоит в том, что лямбда — это энергия собственно вакуума. Звучит диковато, но на самом деле вполне согласуется с квантовой механикой. Возьмём кусок пространства и уберём из него всё, что хотя бы в принципе можно убрать. Уберём всё вещество, все частицы и все волны, независимо от их природы. Останутся только физические поля в невозмущённом состоянии. Полный штиль.

Так вот, у некоторых полей (например, Хиггсовских) в пустоте ненулевое значение. И теоретически у них есть некоторая энергия. Кроме того, в силу принципа неопределённости у любых полей есть квантовые флуктуации — и они тоже имеют некоторую энергию.

Вместо заключения

Лямбда-исчисление — это формальная система в математической логике для выражения подсчетов на основе абстракции и применения функций с использованием привязки и подстановки переменных. Это универсальная модель, которую можно применять для проектирования любой машины Тьюринга. Впервые введена лямбда-исчисления Черчем, известным математиком, в 1930-х годах.

Система состоит из построения лямбда-членов и выполнения над ними операций сокращения.

Пояснения и приложения

Греческая буква lambda (λ) используется в лямбда-выражениях и лямбда-терминах для обозначения связывания переменной в функции.

Лямбда-исчисление может быть нетипизировано или типизировано. В первом варианте функции могут быть применены только в том случае, если они способны принимать данные этого типа. Типизированные лямбда-исчисления слабее, могут выражать меньшее значение. Но, с другой стороны, они позволяют доказывать больше вещей.

Одной из причин того, что существует много разных типов — это желание ученых сделать больше, не отказываясь от возможности доказывать сильные теоремы лямбда-исчислений.

Система находит применение во многих различных областях математики, философии, лингвистики, и компьютерных наук. В первую очередь, лямбда-исчисления — это расчет, который сыграл важную роль в развитии теории языков программирования. Именно стили функционального создания реализуют системы. Они также являются актуальной темой исследований в теории этих категорий.

Для чайников

Лямбда-исчисление была введена математиком Алонзо Черчем в 1930-х годах в рамках исследования основ науки. Первоначальная система была показана как логически несовместимая в 1935 году, когда Стивен Клин и Дж. Б. Россер разработали парадокс Клини-Россера.

В последствии, в 1936 году Черч выделил и опубликовал только ту часть, которая имеет отношение к расчетам, то, что сейчас называется нетипизированным лямбда-исчислением. В 1940 он также представил более слабую, но логически непротиворечивую теорию, известную как система простого типа. В свое работе он объясняет всю теорию простым языком, поэтому, можно сказать, что Черч опубликовал лямбду исчисления для чайников.

До 1960-х годов, когда выяснилось его отношение к языкам программирования, λ стала лишь формализмом. Благодаря применениям Ричарда Монтегю и других лингвистов в семантике естественного языка, исчисление стало занимать почетное место как в лингвистике, так и в информатике.

Происхождение символа

Введение в лямбда исчисление

Система состоит из языка терминов, которые выбираются определенным формальным синтаксисом, и набора правил преобразования, которые позволяют манипулировать ими. Последний пункт можно рассматривать как эквациональную теорию или как операционное определение.

Все функции в лямбда-исчислении являются анонимными, то есть не имеющими имен. Они принимают только одну входную переменную, при этом каррирование используется для реализации графиков с несколькими непостоянными.

Лямбда-термины

Следующие три правила дают индуктивное определение, которое можно применять для построения всех синтаксически допустимых понятий:

Переменная x сама по себе является действительным лямбда-термином:

• если T это ЛТ, и x непостоянная, то (lambda xt) называется абстракцией.
• если T, а также s понятия, то (TS) называется приложением.

Ничто другое не является лямбда-термином. Таким образом, понятие действительно тогда и только тогда, когда оно может быть получено повторным применением этих трех правил. Тем не менее некоторые скобки могут быть опущены в соответствии с другими критериями.

Определение

Лямбда-выражения состоят из:

• переменных v 1, v 2. v n.
• символов абстракции ‘λ’ и точки ‘.’
• скобок ().

Множество Λ, может быть определено индуктивно:

• Если x переменная, то x ∈ Λ;
• x непостоянная и M ∈ Λ, то (λx.M) ∈ Λ;
• M, N ∈ Λ, то (MN) ∈ Λ.

Обозначение

Чтобы сохранить нотацию лямбда-выражений в незагроможденном виде, обычно применяются следующие соглашения:

• Внешние скобки опущены: MN вместо (MN).
• Предполагается, что приложения остаются ассоциативными: взамен ((MN) P) можно написать MNP.
• Тело абстракции простирается дальше вправо: λx.MN означает λx. (MN), а не (λx.M) N.
• Сокращается последовательность абстракций: λx.λy.λz.N можно λxyz.N.

Свободные и связанные переменные

Оператор λ соединяет свою непостоянную, где бы он ни находился в теле абстракции. Переменные, попадающие в область, называются связанными. В выражении λ x. М, часть λ х часто называют связующим. Как бы намекая, что переменные становятся группой с добавлением Х х к М. Все остальные неустойчивые называются свободными.

Множество свободных переменных M обозначается как FV (M) и определяется рекурсией по структуре терминов следующим образом:

• FV (x) = , где x – переменная.
• FV (λx.M) = FV (M) .
• FV (MN) = FV (M) ∪ FV (N).

Формула, которая не содержит свободных переменных, называется закрытой. Замкнутые лямбда-выражения также известны как комбинаторы и эквивалентны терминам в комбинаторной логике.

Сокращение

Значение лямбда-выражений определяется тем, как они могут быть сокращены.

Существует три вида урезания:

• α-преобразование: изменение связанных переменных (альфа).
• β-редукция: применение функций к своим аргументам (бета).
• η-преобразование: охватывает понятие экстенсиональности.

Здесь речь также идет о полученных эквивалентностях: два выражения являются β-эквивалентными, если они могут быть β-преобразованы в одно и то же составляющее, а α / η-эквивалентность определяется аналогично.

Термин redex, сокращение от приводимого оборота, относится к подтемам, которые могут быть сокращены одним из правил. Лямбда исчисление для чайников, примеры:

(λ x.M) N является бета-редексом в выражении замены N на x в M. Составляющее, к которому сводится редекс, называется его редуктом. Редукция (λ x.M) N есть M [x: = N].

Если x не является свободной в M, λ х. М х также ет-REDEX с регулятором М.

α-преобразование

Альфа-переименования позволяют изменять имена связанных переменных. Например, λ x. х может дать λ у. у. Термины, которые отличаются только альфа-преобразованием, называются α-эквивалентными. Часто при использовании лямбда-исчисления α-эквивалентные считаются взаимными.

Точные правила для альфа-преобразования не совсем тривиальны. Во-первых, при данной абстракции переименовываются только те переменные, которые связаны с одной и той же системой. Например, альфа-преобразование λ x.λ x. x может привести к λ y.λ x. х, но это может не ввергнуть к λy.λx.y Последний имеет иной смысл, чем оригинал. Это аналогично понятию программирования затенения переменных.

Во-вторых, альфа-преобразование невозможно, если оно приведет к захвату непостоянной другой абстракцией. Например, если заменить x на y в λ x.λ y. x, то можно получить λ y.λ y. у, что совсем не то же самое.

В языках программирования со статической областью видимости альфа-преобразование можно использовать для упрощения разрешения имен. При этом следя за тем, чтобы понятие переменной не маскировало обозначение в содержащей области.

В нотации индекса Де Брюйна любые два альфа-эквивалентных термина синтаксически идентичны.

Замена

Изменения, написанные Е [V: = R], представляют собой процесс замещения всех свободных вхождений переменной V в выражении Е с оборотом R. Подстановка в терминах λ определяется лямбдой исчисления рекурсии по структуре понятий следующим образом (примечание: x и y – только переменные, а M и N – любое λ-выражение).

y [x: = N] ≡ y, если x ≠ y

(M 1 M 2) [x: = N] ≡ (M 1 [x: = N]) (M 2 [x: = N])

(λ x.M) [x: = N] ≡ λ x.M

(λ y.M) [x: = N] y λ y. (M [x: = N]), если x ≠ y, при условии, что y ∉ FV (N).

Для подстановки в лямбда-абстракцию иногда необходимо α-преобразовать выражение. Например, неверно, чтобы (λ x. Y) [y: = x] приводило к (λ x. X), потому что замещенный x должен был быть свободным, но в итоге был связанным. Правильная замена в этом случае (λ z. X) с точностью до α-эквивалентности. Стоит обратить внимание, что замещение определяется однозначно с верностью до лямбды.

β-редукция

Бета-редукция отражает идею применения функции. Бета-восстановительный определяется в терминах замещения: ((X V. E) Е ‘) является Е [V: = Е’].

Например, предполагая некоторое кодирование 2, 7, ×, имеется следующее β-уменьшение: ((λ n. N × 2) 7) → 7 × 2.

Бета-редукция может рассматриваться как то же самое, что и концепция локальной сводимости при естественной дедукции через изоморфизм Карри – Ховарда.

η-преобразование

Эта-конверсия выражает идею экстенсиональности, которая в этом контексте заключается в том, что две функции равны тогда, когда они дают одинаковый результат для всех аргументов. Эта конвертация обменивает между λ x. (F x) и f всякий раз, когда x не кажется свободным в f.

Данное действие может рассматриваться как то же самое, что и концепция локальной полноты в естественной дедукции через изоморфизм Карри – Ховарда.

Нормальные формы и слияние

Для нетипизированного лямбда-исчисления β-редукция как правило переписывания не является ни сильно нормализующей, ни слабо.

Тем не менее можно показать, что β-редукция сливается при работе до α-преобразования (т. е. можно считать две нормальные формы равными, если возможно α-преобразование одной в другую).

Поэтому и сильно нормализующие члены, и слабо налаживающие понятия имеют единственную нормальную форму. Для первых терминов любая стратегия сокращения гарантированно приведет к типичной конфигурации. Тогда как для слабо нормализующих условий некоторые стратегии сокращения могут не найти ее.

Дополнительные методы программирования

Существует большое количество идиом создания для лямбда-исчисления. Многие из них были первоначально разработаны в контексте использования систем в качестве основы для семантики языка программирования, эффективно применяя их в качестве создания низкого уровня. Поскольку некоторые стили включают лямбда-исчисление (или что-то очень похожее) в качестве фрагмента, эти методы также находят применение в практическом создании, но затем могут восприниматься как неясные или чужие.

Именованные константы

В лямбда-исчислении библиотека принимает форму набора ранее определенных функций, в которой термины являются просто конкретными константами. Чистое исчисление не имеет понятия именованных неизменных, поскольку все атомные лямбда-термины являются переменными. Но их также можно имитировать, выделив непостоянную в качестве имени константы, используя лямбда-абстракцию для связывания этой изменчивой в основной части, и применить эту абстракцию к намеченному определению. Таким образом, если использовать f для обозначения M в N, можно сказать,

Авторы часто вводят синтаксическое понятие, такое как let, чтобы разрешить писать все в более интуитивном порядке.

Заметным ограничением этого let является то, что имя f не определено в M, поскольку M находится вне области привязки лямбда-абстракции f. Это означает, что атрибут рекурсивной функции не может использоваться как M с let. Более продвинутая синтаксическая конструкция letrec, которая позволяет писать рекурсивные определения функций в этом стиле, вместо этого дополнительно использует комбинаторы с фиксированной точкой.

Печатные аналоги

Данный тип является типизированным формализмом, который использует символ для обозначения анонимной функции абстракция. В этом контексте типы обычно являются объектами синтаксической природы, которые присваиваются лямбда-терминам. Точная натура зависит от рассматриваемого исчисления. С определенной точки зрения, типизированные ЛИ можно рассматривать как уточнения нетипизированного ЛИ. Но с другой стороны, их также можно считать более фундаментальной теорией, а нетипизированное лямбда-исчисление — особым случаем только с одним типом.

Типизированные ЛИ являются основополагающими языками программирования и основой функциональных, таких как ML и Haskell. И, более косвенно, императивных стилей создания. Типизированные лямбда-исчисления играют важную роль в разработке систем типов для языков программирования. Здесь типизируемость обычно захватывает желательные свойства программы, например, она не вызовет нарушения доступа к памяти.

Типизированные лямбда-исчисления тесно связаны с математической логикой и теорией доказательств через изоморфизм Карри – Говарда, и их можно рассматривать как внутренний язык классов категорий, например, который просто является стилем декартовых замкнутых.

Обобщим некоторые сведения о векторах, известные в основном из школьного курса геометрии.

Вектором называется направленный отрезок с начальной точкой А и конечной точкой В (который можно перемещать параллельно самому себе.

Векторы могут обозначаться как двумя прописными буквами, так и одной строчной с чертой или стрелкой, например: .

Длиной (или модулем) вектора называется число, равное длине отрезка АВ, изображающего вектор.

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными (параллельными).

Если начало и конец вектора совпадают, например, , то такой вектор называют нулевым и обозначают .

Длина нулевого вектора равна нулю. Так как направление нулевого вектора произвольно, то считают, что он коллинеарен (параллелен) любому вектору.

Произведением вектора на число (лямбда) называется вектор , имеющий длину , направление которого совпадает с направлением вектора , если , и противоположно ему, если .

Противоположным вектором называется произведение вектора на число (-1).

Суммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец – с концом вектора при условии, что начало вектора совпадает с концом вектора (правило треугольников).

Аналогично определяется сумма нескольких векторов. Так, например, сумма четырех векторов (рис. а) есть вектор , начало которого совпадает с началом вектора , а конец – с концом вектора (правило многоугольника) (рис. б).

Разностью двух векторов и называется сумма вектора и вектора , противоположного .

Легко убедиться в том, что в параллелограмме, построенном на векторах и , одна диагональ – вектор – представляет сумму векторов и , а другая диагональ — вектор – их разность.

Перенесем вектор параллельно самому себе так, чтобы его начало совпало с началом координат.

Координатами вектора называются координаты его конечной точки.

Так, координатами вектора на плоскости Оxy являются

два числа x и y: ,

а в пространстве Oxyz – три числа x, y и z: .

Для векторов и , заданных координатами,

сумма определяется по формуле

разность – по формуле

произведение вектора на число λ – по формуле

.

Длина вектора равна корню квадратному из суммы квадратов его координат:

.

Если A(a₁, a₂, a₃) – начало вектора, B(b₁, b₂, b₃) – его конец, то

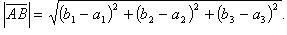
Скалярное произведение. Скалярным произведением векторов называется произведение их модулей на косинус угла между векторами (не больше пи)

.

Из данного выражения можно найти косинус: .

Если векторы выражены через координаты в декартовой системе координат , , то скалярное произведение определяется как сумма попарных произведений соответствующих координат

.

Условием перпендикулярности векторов является равенство нулю их скалярного произведения .

Скалярное произведение обладает следующими свойствами:

;

.

Модуль вектора можно представить в виде .

Читайте также:

  

• Какие кондиционеры ставят на гранту

  

• 4 дроссельный впуск на ваз как установить

  

• Как отличить бош от киржача ваз 2110

  

• Парктроник рено каптур не работает

  

• Какие подушки двигателя лучше поставить на ваз 2114

Линейно зависимые и линейно независимые вектора.

Навигация по странице:

• Определение линейной комбинации векторов
• Определение линейно независимой комбинации векторов
• Определение линейно зависимой комбинации векторов
• Свойства линейно зависимых векторов
• Примеры задач на линейную зависимость и линейную независимость векторов

Определение. Линейной комбинацией векторов a₁, …, a_n с коэффициентами x₁, …, x_n называется вектор

x₁a₁ + … + x_na_n.

Определение. Линейная комбинация x₁a₁ + … + x_na_n называется тривиальной, если все коэффициенты x₁, …, x_n равны нулю.

Определение. Линейная комбинация x₁a₁ + … + x_na_n называется нетривиальной, если хотя быбы один из коэффициентов x₁, …, x_n не равен нулю.

Определение. Вектора a₁, …, a_n называются линейно независимыми, если не существует нетривиальной комбинации этих векторов равной нулевому вектору.

То есть вектора a₁, …, a_n линейно независимы если x₁a₁ + … + x_na_n = 0 тогда и только тогда, когда x₁ = 0, …, x_n = 0.

Определение. Вектора a₁, …, a_n называются линейно зависимыми, если существует нетривиальная комбинация этих векторов равная нулевому вектору.

Свойства линейно зависимых векторов:

• Для 2-х и 3-х мерных векторов.

  Два линейно зависимые вектора – коллинеарные. (Коллинеарные вектора – линейно зависимы.)
  .

• Для 3-х мерных векторов.

  Три линейно зависимые вектора – компланарные. (Три компланарные вектора – линейно зависимы.)

• Для n -мерных векторов.

  n + 1 вектор всегда линейно зависимы.

Примеры задач на линейную зависимость и линейную независимость векторов:

Пример 1. Проверить будут ли вектора a = {3; 4; 5}, b = {-3; 0; 5}, c = {4; 4; 4}, d = {3; 4; 0} линейно независимыми.

Решение:

Вектора будут линейно зависимыми, так как размерность векторов меньше количества векторов.

Пример 2. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1} линейно независимыми.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

x₁a + x₂b + x₃c₁ = 0

Это векторное уравнение можно записать в виде системы линейных уравнений

	x1 + x2 = 0
x1 + 2x2 – x3 = 0
x1 + x3 = 0

Решим эту систему используя метод Гаусса

1100
12-10
1010

~

из второй строки вычтем первую; из третей строки вычтем первую:

1100
1 – 12 – 1-1 – 00 – 0
1 – 10 – 11 – 00 – 0

~

1100
01-10
0-110

~

из первой строки вычтем вторую; к третей строке добавим вторую:

1 – 01 – 10 – (-1)0 – 0
01-10
0 + 0-1 + 11 + (-1)0 + 0

~

1010
01-10
0000

Данное решение показывает, что система имеет множество решений, то есть существует не нулевая комбинация значений чисел x₁, x₂, x₃ таких, что линейная комбинация векторов a, b, c равна нулевому вектору, например:

–a + b + c = 0

а это значит вектора a, b, c линейно зависимы.

Ответ: вектора a, b, c линейно зависимы.

Пример 3. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 2} линейно независимыми.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

x₁a + x₂b + x₃c₁ = 0

Это векторное уравнение можно записать в виде системы линейных уравнений

	x1 + x2 = 0
x1 + 2x2 – x3 = 0
x1 + 2x3 = 0

Решим эту систему используя метод Гаусса

1100
12-10
1020

~

из второй строки вычтем первую; из третей строки вычтем первую:

1100
1 – 12 – 1-1 – 00 – 0
1 – 10 – 12 – 00 – 0

~

1100
01-10
0-120

~

из первой строки вычтем вторую; к третей строке добавим вторую:

1 – 01 – 10 – (-1)0 – 0
01-10
0 + 0-1 + 12 + (-1)0 + 0

~

1010
01-10
0010

~

из первой строки вычтем третью; к второй строке добавим третью:

1 – 00 – 01 – 10 – 0
0 + 01 + 0-1 + 10 + 0
0010

~

1010
0100
0010

Данное решение показывает, что система имеет единственное решение x₁ = 0, x₂ = 0, x₃ = 0, а это значит вектора a, b, c линейно независимые.

Ответ: вектора a, b, c линейно независимые.