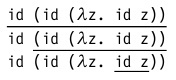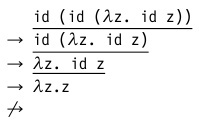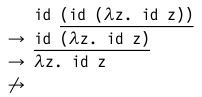Как найти лямбду все формулы

Ля́мбда-исчисле́ние (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем для формализации и анализа понятия вычислимости.

Чистое λ-исчисление[править | править код]

Чистое λ-исчисление, термы которого, называемые также объектами («обами»), или λ-термами, построены исключительно из переменных применением аппликации и абстракции. Изначально наличие каких-либо констант не предполагается.

Аппликация и абстракция[править | править код]

В основу λ-исчисления положены две фундаментальные операции:

• Абстракция или λ-абстракция (лат. abstractio — отвлечение, отделение), в свою очередь, строит функции по заданным выражениям. Именно, если  — выражение, свободно^[en] содержащее , тогда запись означает: λ функция от аргумента , которая имеет вид , и обозначает функцию . Здесь скобки не обязательны и использованы для ясности, так как точка является частью нотации и отделяет имя связанной переменной от тела функции. Таким образом, с помощью абстракции можно конструировать новые функции. Требование, чтобы свободно входило в , не обязательно — в этом случае обозначает функцию , т.е. такую, которая игнорирует свой аргумент.

α-эквивалентность[править | править код]

Основная форма эквивалентности, определяемая в лямбда-термах, это альфа-эквивалентность. Например, и это альфа-эквивалентные лямбда-термы которые оба представляют одну и ту же функцию – а именно, функцию тождества . Термы и не являются альфа-эквивалентными, так как являются свободными переменными.

Вообще говоря, -преобразование это переименование связанных переменных, не меняющее “смысла” терма. Структурно, два λ-терма -эквивалентны если это один и тот же терм, либо если какие-либо их составляющие термы соответстветственно -эквивалентны.

Для абстракций, терм -эквивалентен , если это в котором все свободные появления заменены на , при условии, что 1.) не входит свободно в , и 2.) не входит свободно ни в одну абстракцию внутри (если такие есть).

Требование, чтобы не была свободной переменной в – существенно, т.к. иначе она окажется “захваченной” абстракцией после -преобразования, и из свободной переменной в превратится в связанную переменную в .

Второе требование необходимо чтобы предотвратить случаи подобные тому, когда, например, является частью . Тогда необходимо произвести -преобразование такой абстракции, например, в данном случае, в .

β-редукция[править | править код]

Применение некой фунции к некоему аргументу выражается в -исчислении как аппликация -терма, выражающего эту функцию, и -терма аргумента. Например, применение функции к числу 3 выражается аппликацией

в которой на первом месте находится соответствующая абстракция. Поскольку эта функция ставит в соответствие каждому значение , для вычисления результата необходимо заменить каждое свободное появление переменной в терме на терм 3.

В результате получается . Это соображение в общем виде записывается как

и носит название β-редукция. Выражение вида , то есть применение абстракции к некоему терму, называется редексом (redex). Несмотря на то, что β-редукция по сути является единственной «существенной» аксиомой λ-исчисления, она приводит к весьма содержательной и сложной теории. Вместе с ней λ-исчисление обладает свойством полноты по Тьюрингу и, следовательно, представляет собой простейший язык программирования.

η-преобразование[править | править код]

-преобразование выражает ту идею, что две функции являются идентичными тогда и только тогда, когда, будучи применёнными к любому аргументу, дают одинаковые результаты.

-преобразование переводит друг в друга формулы и , но только если не появляется свободно в . Иначе, свободная переменная в после преобразования стала бы связанной внешней абстракцией , и наоборот; и тогда применение этих двух выражений сводилось бы -редукцией к разным результатам.

Перевод в называют -редукцией, а перевод в – -экспансией.

Каррирование (карринг)[править | править код]

Функция двух переменных и может быть рассмотрена как функция одной переменной , возвращающая функцию одной переменной , то есть как выражение . Такой приём работает точно так же для функций любой арности. Это показывает, что функции многих переменных могут быть выражены в λ-исчислении и являются «синтаксическим сахаром». Описанный процесс превращения функций многих переменных в функцию одной переменной называется карринг (также: каррирование), в честь американского математика Хаскелла Карри, хотя первым его предложил Моисей Шейнфинкель (1924).

Соответственно, аппликация n-арных функций это на самом деле аппликация вложенных унарных функций, одна за другой. Например, для бинарных функций:

  (λxy.    ...x...y... )  a  b   =
  (λx.λy.  ...x...y... )  a  b   =
  (λx.(λy. ...x...y... )) a  b   =
(((λx.(λy. ...x...y... )) a) b)  =
      (λy. ...a...y... )     b   =
           ...a...b...

Семантика бестипового λ-исчисления[править | править код]

Тот факт, что термы λ-исчисления действуют как функции, применяемые к термам λ-исчисления (то есть, возможно, к самим себе), приводит к сложностям построения адекватной семантики λ-исчисления. Чтобы придать λ-исчислению какой-либо смысл, необходимо получить множество , в которое вкладывалось бы его пространство функций . В общем случае такого не существует по соображениям ограничений на мощности этих двух множеств, и функций из в : второе имеет бо́льшую мощность, чем первое.

Эту трудность в начале 1970-х годов преодолел Дана Скотт, построив понятие области (изначально на полных решётках^[1], в дальнейшем обобщив до полного частично упорядоченного множества со специальной топологией) и урезав до непрерывных в этой топологии функций^[2]. На основе этих построений была создана денотационная семантика^[en] языков программирования, в частности, благодаря тому, что с помощью них можно придать точный смысл таким двум важным конструкциям языков программирования, как рекурсия и типы данных.

Связь с рекурсивными функциями[править | править код]

Рекурсия — это определение функции через саму себя; на первый взгляд, лямбда-исчисление не позволяет этого, но это впечатление обманчиво. Например, рассмотрим рекурсивную функцию , вычисляющую факториал:

f(n) = 1, if n = 0; else n × f(n – 1).

Эта функция не может быть выражена λ-термом (λn.(1, if n = 0; else n × (f (n-1)))), так как в нём f является свободной переменной. Функция ссылается на саму себя посредством ссылки на своё имя, но в лямбда-исчислении у λ-термов имен нет.

Тем не менее, λ-термы могут быть переданы как аргумент, в том числе и самим себе. Терм-функция может получить сам себя как аргумент, который окажется связанным с его параметром. Как правило, этот параметр стоит на первом месте. Когда он связан с самой функцией, получается новый λ-терм, выражающий уже саму рекурсивную функцию. Для этого параметр, ссылающийся на себя (здесь обозначен как ), обязательно должен быть передан явным образом как аргумент при рекурсивном вызове (как ):

U := λh. h h

F := U (λh. λn. (1, if n = 0; else n × (h h (n-1))))

где – это комбинатор само-аппликации, .

Этот приём позволяет решить каждую конкретную проблему, как вычисление факториала здесь, создавая рекурсивную функцию через изменение λ-терма, для его явной передачи самому себе как добавочного аргумента. Но решение в общем виде также возможно. Несколькими несложными преобразованиями получается (подразумевая каррирование):

     U (λh.      λn. (1, if n = 0; else n × (h h (n-1))))
     U (λh. (λr. λn. (1, if n = 0; else n × (r   (n-1)))) (h h))
(λg. U (λh. g (h h))) (λr. λn. (1, if n = 0; else n × (r (n-1))))

Это эквивалентое выражение состоит из аппликации двух независимых λ-термов, где второй – это просто лямбда-выражение рекурсивной функции без изменений, но с абстрагированным рекурсивным вызовом . А первый это некий комбинатор, называемый :

G :=                  (λr. λn. (1, if n = 0; else n × (r (n-1))))
Y := λg. U (λh. g (h h)) 
   = λg. (λh. g (h h)) (λh. g (h h))

Этот комбинатор создает рекурсивную функцию из аргумента, являющегося закрытым (т.е. в котором нет свободных переменных) λ-термом исходного выражения функции (т.е. без удвоения параметра). Таким образом,

Y g = (λh. g (h h)) (λh. g (h h))
    = g ((λh. g (h h)) (λh. g (h h)))
    = g (Y g)

т.е. – это комбинатор неподвижной точки: он вычисляет неподвижную точку своего аргумента. Для закрытого λ-терма с соотвествующей арностью, его неподвижная точка выражает рекурсивную функцию, так как , т.е. аргумент который здесь создаётся для вызова внутри – это та же самая функция .

F = Y (λr. λn. (1, if n = 0; else n × (r (n-1))))
  = Y G
  = G (Y G)
  = (λr. λn. (1, if n = 0; else n × (r (n-1)))) (Y G)
  = (    λn. (1, if n = 0; else n × (Y G (n-1)))) 
  = (    λn. (1, if n = 0; else n × (F   (n-1)))) 
  = G F

Итак, – это закрытый функционал, т.е. λ-терм, вызывающий свой аргумент в качестве функции; его неподвижная точка – это функция (здесь, ), которая передаётся ему в качестве аргумента; а вызов той же самой функции и есть рекурсивный вызов.

Существует несколько определений комбинаторов неподвижной точки. Вышеуказанное – самое простое:

Y := λg. (λh. g (h h)) (λh. g (h h))

Используя стандартные комбинаторы и ,

Y g = U (λh. g (U h)) = U (λh. B g U h)
    = U (B g U) = U (C B U g) 
    = B U (C B U) g

Indeed,

U (B g U) = B g U (B g U)
    = g (U (B g U))
    = g (Y g)

Итак, чтобы определить факториал как рекурсивную функцию, мы можем просто написать , где  — число, для которого вычисляется факториал. Пусть , получаем:

Y G 4
Y (λrn.(1, if n = 0; else n×(r (n-1)))) 4
(λrn.(1, if n = 0; else n×(r (n-1)))) (Y G) 4
(λn.(1, if n = 0; else n×(Y G (n-1)))) 4
1, if 4 = 0; else 4×(Y G (4-1))
4×(Y G 3)
4×(G (Y G) 3)
4×((λrn.(1, if n = 0; else n×(r (n-1)))) (Y G) 3)
4×(1, if 3 = 0; else 3×(Y G (3-1)))
4×(3×(G (Y G) 2))
4×(3×(1, if 2 = 0; else 2×(Y G (2-1))))
4×(3×(2×(G (Y G) 1)))
4×(3×(2×(1, if 1 = 0; else 1×(Y G (1-1)))))
4×(3×(2×(1×(G (Y G) 0))))
4×(3×(2×(1×(1, if 0 = 0; else 0×(Y G (0-1))))))
4×(3×(2×(1×(1))))
24

Итак, каждое определение рекурсивной функции может быть представлено как неподвижная точка соответствующего закрытого функционала описывающего “один вычислительный шаг” рекурсивной функции. Следовательно, используя , каждое рекурсивное определение может быть выражено как лямбда-выражение (λ-терм). В частности, мы можем определить вычитание, умножение, сравнение натуральных чисел рекурсивно, и выразить их как λ-термы.

В языках программирования[править | править код]

В языках программирования под «λ-исчислением» зачастую понимается механизм «анонимных функций» — callback-функций, которые можно определить прямо в том месте, где они используются, и которые имеют доступ к локальным переменным текущей функции (замыкание).

См. также[править | править код]

• Аппликативные вычислительные системы
• Типизированное λ-исчисление
• Комбинаторная логика
• Функциональное программирование
• Теорема Чёрча — Россера
• Анонимная функция

Примечания[править | править код]

Литература[править | править код]

• Барендрегт X. Ламбда-исчисление. Его синтаксис и семантика: Пер. с англ. — М.: Мир, 1985. — 606 с.

λ-исчисление. Часть первая: история и теория

Идею, короткий план и ссылки на основные источники для этой статьи мне подал хабраюзер z6Dabrata, за что ему огромнейшее спасибо.

UPD: в текст внесены некоторые изменения с целью сделать его более понятным. Смысловая составляющая осталась прежней.

Вступление

Возможно, у этой системы найдутся приложения не только
в роли логического исчисления. (Алонзо Чёрч, 1932)

Вообще говоря, лямбда-исчисление не относится к предметам, которые «должен знать каждый уважающий себя программист». Это такая теоретическая штука, изучение которой необходимо, когда вы собираетесь заняться исследованием систем типов или хотите создать свой функциональный язык программирования. Тем не менее, если у вас есть желание разобраться в том, что лежит в основе Haskell, ML и им подобных, «сдвинуть точку сборки» на написание кода или просто расширить свой кругозор, то прошу под кат.

Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.

Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…

λ-исчисление: основные понятия

Синтаксис

В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции,

только хардкор

. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.

Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.

Термы:

переменная:	x
лямбда-абстракция (анонимная функция):	λx.t, где x — аргумент функции, t — её тело.
применение функции (аппликация):	f x, где f — функция, x — подставляемое в неё значение аргумента

Соглашения о приоритете операций:

Может показаться, будто нам нужны какие-то специальные механизмы для функций с несколькими аргументами, но на самом деле это не так. Действительно, в мире чистого лямбда-исчисления возвращаемое функцией значение тоже может быть функцией. Следовательно, мы можем применить первоначальную функцию только к одному её аргументу, «заморозив» прочие. В результате получим новую функцию от «хвоста» аргументов, к которой применим предыдущее рассуждение. Такая операция называется каррированием (в честь того самого Хаскелла Карри). Выглядеть это будет примерно так:

f = λx.λy.t	Функция с двумя аргументами x и y и телом t
f v w	Подставляем в f значения v и w
(f v) w	Эта запись аналогична предыдущей, но скобки явно указывают на последовательность подстановки
((λy.[x → v]t) w)	Подставили v вместо x. [x → v]t означает «тело t, в котором все вхождения x заменены на v»
[y → w][x → v]t	Подставили w вместо y. Преобразование закончено.

И напоследок несколько слов об области видимости. Переменная x называется связанной, если она находится в теле t λ-абстракции λx.t. Если же x не связана какой-либо вышележащей абстракцией, то её называют свободной. Например, вхождения x в x y и λy.x y свободны, а вхождения x в λx.x и λz.λx.λy.x(y z) связаны. В (λx.x)x первое вхождение x связано, а второе свободно. Если все переменные в терме связаны, то его называют замкнутым, или комбинатором. Мы с вами будем использовать следующий простейший комбинатор (функцию тождества): id = λx.x. Она не выполняет никаких действий, а просто возвращает без изменений свой аргумент.

Процесс вычисления

Рассмотрим следующий терм-применение:

(λx.t) y

Его левая часть — (λx.t) — это функция с одним аргументом x и телом t. Каждый шаг вычисления будет заключаться в замене всех вхождений переменной x внутри t на y. Терм-применение такого вида носит имя редекса (от reducible expression, redex — «сокращаемое выражение»), а операция переписывания редекса в соответствии с указанным правилом называется бета-редукцией.

Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:

(λx.x) ((λx.x) (λz. (λx.x) z)),

который для простоты можно переписать как

id (id (λz. id z))

(напомним, что id — это функция тождества вида λx.x)

В этом терме содержится три редекса:

1. Полная β-редукция. В этом случае каждый раз редекс внутри вычисляемого терма выбирается произвольным образом. Т.е. наш пример может быть вычислен от внутреннего редекса к внешнему:
   
2. Нормальный порядок вычислений. Первым всегда сокращается самый левый, самый внешний редекс.
   
3. Вызов по имени. Порядок вычислений в этой стратегии аналогичен предыдущей, но к нему добавляется запрет на проведение сокращений внутри абстракции. Т.е. в нашем примере мы останавливаемся на предпоследнем шаге:
   
   Оптимизированная версия такой стратегии (вызов по необходимости) используется Haskell. Это так называемые «ленивые» вычисления.
4. Вызов по значению. Здесь сокращение начинается с самого левого (внешнего) редекса, у которого в правой части стоит значение — замкнутый терм, который нельзя вычислить далее.
   
   Для чистого лямбда-исчисления таким термом будет λ-абстракция (функция), а в более богатых исчислениях это могут быть константы, строки, списки и т.п. Данная стратегия используется в большинстве языков программирования, когда сначала вычисляются все аргументы, а затем все вместе подставляются в функцию.

Если в терме больше нет редексов, то говорят, что он вычислен, или находится в нормальной форме. Не каждый терм имеет нормальную форму, например (λx.xx)(λx.xx) на каждом шаге вычисления будет порождать самоё себя (здесь первая скобка — анонимная функция, вторая — подставляемое в неё на место x значение).

Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение

(λx.λy. x) z ((λx.x x)(λx.x x))

Этот терм имеет нормальную форму z несмотря на то, что его второй аргумент такой формой не обладает. На её-то вычислении и зависнет стратегия вызова по значению, в то время как стратегия вызова по имени начнёт с самого внешнего терма и там определит, что второй аргумент не нужен в принципе. Вывод: если у редекса есть нормальная форма, то «ленивая» стратегия её обязательно найдёт.

Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y. Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y, а z — первоначальный терм имел бы вид(λx.λz.x)y и после редукции выглядел бы как λz.y. Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.

Так же бывает, что у нас есть абстракция λx.t x, причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t. Такое преобразование называется η-конверсией.

На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Список источников

1. «What is Lambda Calculus and should you care?», Erkki Lindpere
2. «Types and Programming Languages», Benjamin Pierce
3. Вики-конспект «Лямбда-исчисление»
4. «Учебник по Haskell», Антон Холомьёв
5. Лекции по функциональному программированию

Лямбда-исчисление

А сегодня немного теории. Я не считаю, что лямбда-исчисление является необходимым знанием для любого программиста. Однако, если вам нравится докапываться до истоков, чтобы понять на чем основаны многие языки программирования, вы любознательны и стремитесь познать все в этом мире или просто хотите сдать экзамен по функциональном программированию (как, например, я), то этот пост для вас.

Что это такое

Лямбда-исчисление – это формальная система, то есть набор объектов, формул, аксиом и правил вывода. Благодаря таким системам с помощью абстракций моделируется теория, которую можно использовать в реальном мире, и при этом выводить в ней новые математически доказуемые утверждения. Например, язык запросов SQL основан на реляционном исчислении. Благодаря математической базе, на которой он существует, оптимизаторы запросов могут анализировать алгебраические свойства операций и влиять на скорость работы.

Но речь сегодня не о SQL, а о функциональных языках. Именно для них лямбда-исчисление является основой. Функциональные языки далеко не столь популярны, как, например, объектно-ориентированные, но тем не менее прочно занимают свою нишу. Кроме того, многие идеи из функционального программирования и лямда-исчисления постепенно прокрадываются в другие языки, под видом новых фич.

Если вы изучали формальные языки, то знаете о таком понятии как Машина Тьюринга. Эта вычислительная абстракция определяет класс вычислимых функций. Этот класс столь важен, так как по тезису Черча он эквивалентен понятию алгоритма. Другими словами, любую программу, которую можно запрограммировать на вычислительном устройстве, можно воспроизвести и на машине Тьюринга. А для нас главное то, что лямбда-исчисление по мощности эквивалентно машине Тьюринга и определяет этот же класс функций. Причем создателем лямбда-исчисления является тот самый Алонзо Черч!

Основные понятия

В нотации лямбда-исчисления есть всего три типа выражений:

1. Переменные: ` x, y, z `
2. Абстракция – декларация функции: ` lambda x.E ` . Определяем функцию с параметром ` x ` и телом ` E `.
3. Аппликация – применение функции ` E_1 ` к аргументу ` E_2 ` : ` E_1 E_2`

Сразу пара примеров:

• Тождественная функция: ` lambda x. x `
• Функция, вычисляющая тождественную функцию: ` lambda x.(lambda y . y) `

Соглашения

Несколько соглашений для понимания, в каком порядке правильно читать выражения:

1. Аппликация лево-ассоциативна. То есть выражение ` x y z ` читается как ` (x y) z `.
2. В абстракции группируем скобки вправо. Другими словами, читая абстракцию необходимо распространять ее максимально вправо насколько возможно. Пример: выражение ` lambda x. x lambda y . x y z ` эквивалентно ` lambda x. (x (lambda y . ((x y) z))) ` , так как абстракция функции с аргументом ` x ` включила в себя все выражение. Следом было проведено включение абстракцией с аргументом ` y ` и ,наконец, в теле этой функции были расставлены скобки для аппликации.

Области видимости переменных

Определим контекст переменной, в котором она может быть использована.
Абстракция ` lambda x.E ` связывает переменную ` x `. В результате мы получаем следующие понятия:

1. ` x ` – связанная переменная в выражении .
2. ` E ` – область видимости переменной ` x `.
3. Переменная свободна в ` E ` , если она не связана в ` E ` . Пример: ` lambda x. x (lambda y. x y z) ` . Cвободная переменная – ` z ` .

Взглянем на следующий пример: ` lambda x. x (lambda x. x) x ` .

Понимание лямбда-выражений существенно усложняется, когда переменные с разными значениями и контекстами используют идентичные имена. Поэтому впредь мы будем пользоваться следующим соглашением: связанные переменные необходимо переименовывать для того, чтобы они имели уникальные имена в выражении. Это возможно благодаря концептуально важному утверждению: выражения, которые могут быть получены друг из друга путем переименования связанных переменных, считаются идентичными. Важность этого утверждения в том, что функции в исчислении определяются лишь своим поведением, и имена функций не несут никакого смысла. То есть, функции ` lambda x. x ` , ` lambda y. y ` , ` lambda z. z ` на самом деле одна тождественная функция.

Вычисление лямбда-выражений

Вычисление выражений заключается в последовательном применении подстановок. Подстановкой ` E’ ` вместо ` x ` в ` E ` (запись: ` [E’//x]E ` ) называется выполнение двух шагов:

1. Альфа-преобразование. Переименование связанных переменных в ` E ` и ` E’ ` , чтобы имена стали уникальными.
2. Бета-редукция. По сути единственная значимая аксиома исчисления. Подразумевает замену ` x ` на ` E’ ` в ` E ` .
   Рассмотрим несколько примеров подстановок:

• Преобразование к тождественной функции. ` (lambda f. f (lambda x. x)) (lambda x. x) -> ` (пишем подстановку) ` -> [lambda x. x // f] f ( lambda x. x)) = ` (делаем альфа-преобазование) ` = [(lambda x. x) // f] f (lambda y. y)) = ` (производим бета-редукцию) ` = (lambda x. x) (lambda y. y) -> ` (еще одна подстановка) ` -> [lambda y. y // x] x = lambda y. y `
• Бесконечные вычисления. ` (lambda x. x x)(lambda x. x x) -> [lambda x. x x // x]x x = [lambda y. y y // x] x x = ` ` = (lambda y. y y)(lambda y. y y) -> … `
• Также небольшой пример, почему нельзя пренебрегать альфа-преобразованием. Рассмотрим выражение ` (lambda x. lambda y. x) y ` . Если не выполнить первый шаг, результатом будет тождественная функция ` lambda y. y ` . Однако, после правильного выполнения подстановки с заменой ` y ` на ` z ` мы получим совсем другой результат ` lambda z. y ` , то есть константную функцию.

Функции нескольких переменных

Для того чтобы использовать функции нескольких переменных добавим в исчисление новую операцию ` add ` : она применяется к двум аргументам и является синтаксическим сахаром для следующих вычислений: ` (lambda x. lambda y. add x y) E_1 E_2 -> ([E_1 // x] lambda y. add x y) E_2 = ` ` (lambda y. add E_1 y) E_2 -> ` ` [E_2 // y] add E_1 y = add E_1 E_2 `

Как результат мы получили функцию от одного аргумента, которая возвращает еще одну функцию от одного аргумента. Такое преобразование называется каррирование (в честь Хаскелла Карри назвали и язык программирования, и эту операцию), а функция, возвращающая другую, называется функцией высшего порядка.

Порядок вычислений

Бывают ситуации, когда произвести вычисление можно несколькими способами. Например, в выражении ` (lambda y. (lambda x. x) y) E ` сначала можно подставлять ` y ` вместо ` x ` во внутреннее выражение, либо ` E ` вместо ` y ` во внешнее. Теорема Черча-Рассера говорит о том, что в не зависимости от последовательности операций, если вычисление завершится, результат будет одинаков. Тем не менее, эти два подхода принципиально отличаются. Рассмотрим их подробнее:

1. Вызов по имени. В вычислении всегда в первую очередь применяются самые внешние подстановки. Другими словами, нужно вычислять аргумент уже после подстановки в функцию. Кроме того нельзя использовать редукцию внутри абстракции. Пример: ` (lambda y. (lambda x. x) y) ((lambda u. u) (lambda v. v)) -> ` (применяем редукцию к внешней функции) ` -> (lambda x. x) ((lambda u. u) (lambda v. v)) -> ` (вновь подставляем, не меняя аргумент) ` -> (lambda u. u) (lambda v. v) = lambda v. v `
2. Вызов по значению. В этом способе вычисление проходит ровно наоборот, то есть сначала вычисляется аргумент функции. При этом редукция внутри абстракции также не применяется. Пример: ` (lambda y. (lambda x. x) y) ((lambda u. u) (lambda v. v)) -> ` (вычисляем аргумент функции) ` -> (lambda y. (lambda x. x) y) (lambda v. v) -> (lambda x. x) (lambda v. v) -> lambda v. v `

Из практических отличий этих двух подходов отметим, то что вычисление по значению более сложно в реализации и редко используется для всех вычислений в неисследовательских языках. Однако, второй подход может не привести к завершению вычисления. Пример: ` (lambda x. lambda z.z) ((lambda y. y y) (lambda u. u u)) ` . При вычислении аргумента мы попадаем в бесконечный цикл, в то время как, проводя вычисления по имени функции, мы сразу получим тождественную функцию.

Кодирование типов

В чистом лямбда-исчислении есть только функции. Однако, программирование трудно представить без различных типов данных. Идея заключается в том, чтобы закодировать поведение конкретных типов в виде функций.

1. Булевые значения. Поведение типа можно описать как функцию, выбирающую одно из двух. Тогда значения выглядят так: ` true = lambda x. lambda y. x ` и ` false = lambda x. lambda y. y `
2. Натуральные числа. Каждое натуральное число может быть описано как функция, проитерированная заданное число раз. Выпишем несколько первых чисел ( ` f ` – функция, которую итерируем, а ` s ` – начальное значение):
   • ` 0 = lambda f. lambda s. s `
   • ` 1 = lambda f. lambda s. f s `
   • ` 2 = lambda f. lambda s. f (f s) `
3. Операции с натуральными числами.
   • Следующее число. ` succ n = lambda f. lambda s. f (n f s) ` . Аргумент функции – число ` n ` , которое, будучи так же функцией, принимает еще два аргумента: начальное значение и итерируемую функцию. Для числа ` n ` один раз применяем функцию ` f ` и получаем следующее число.
   • Сложение. ` add n_1 n_2 = n_1 succ n_2 ` . Для сложения чисел ` n_1 ` и ` n_2 ` нужно одному из слагаемых передать в параметры функцию ` succ `, как итерруемую функцию, и другое слагаемое, как начальное значение. В результате мы увеличим заданное число на единицу необходимое число раз.
   • Умножение. ` mult n_1 n_2 = n_1 (add n_2) 0 ` . В роли итерируемой функции для множителя ` n_1 ` выступает функция ` succ ` с аргументом ` n_2 ` , а в роли начального значения уже определенное число ` 0 ` . То есть мы определяем умножение как прибавление ` n_2 ` к нулю ` n_1` раз.

Аналогично, с помощью лямбда-исчисления можно выразить любые конструкции языков программирования, такие как циклы, ветвления, списки и тд.

Заключение

Лямбда-исчисление – очень мощная система, которая позволяет писать любые программы. Однако, непосредственно программирование на лямбда-исчислении получается черезчур громоздким и неудобным. Тем не менее, чистое лямбда-исчисление предназначено вовсе не для программирования на нем, а для изучения существующих и создания новых языков программирования. А следующим шагом на пути к типовым функциональным языкам является типизированное лямбда-исчисление – расширение чистого исчисления типовыми метками.

По материалу лекций Салищева С. И.

Written on

October
21st
,
2017
by

Alexey Kalina

Feel free to share!

Лямбда-исчисление (англ. lambda calculus) — формальная система, придуманная в 1930-х годах
Алонзо Чёрчем. Лямбда-функция является, по сути, анонимной функцией.
Эта концепция показала себя удобной и сейчас активно используется во многих
языках программирования.

Лямбда-исчисление

Определение:

Лямбда-выражением (англ. -term) называется выражение, удовлетворяющее следующей грамматике: где — множество всех строк над фиксированным алфавитом .

Пробел во втором правиле является терминалом грамматики. Иногда его обозначают как @, чтобы он не сливался с другими символами в выражении.

В первом случае функция является просто переменной.
Во втором происходит аппликация (применение) одной функции к другой.
Это аналогично вычислению функции-левого операнда на аргументе-правом операнде.
В третьем — абстракция по переменной. В данном случае происходит
создание функции одного аргумента с заданными именем аргумента и телом функции.

Рассмотрим, например, -терм . Эта функция принимает аргумент и
возвращает его неизменённым. Например,
. Аналогично, .

Еще примеры:

Иногда -термы пишут по другому. Для краткости подряд идущие лямбды заменяют на одну. Например:

Приоритет операций

• Аппликация:
• Абстракция забирает себе всё, до чего дотянется:
• Скобки играют привычную роль группировки действий

Свободные и связанные переменные

Связанными переменными называются все переменные, по которым выше в
дереве разбора были абстракции. Все остальные переменные называются свободными.

Например, в , и связана, а — свободна. А в
в своём первом вхождении переменная свободна, а во втором — связана.

Связанные переменные — это аргументы функции. То есть для функции они являются локальными.

Рассмотрим функции и . В первой из них при взгляде на
понятно, что она имеет отношение к переменной, по которой производилась
абстракция. Если по одной и той же
переменной абстракция производилась более одного раза, то переменная связана
с самым поздним (самым нижним в дереве разбора) абстрагированием. Например, в
, переменная связана с самой правой абстракцией
по .

α-эквивалентность

Определение:

-эквивалентностью (англ. -equivalence) — называется наименьшее соотношение эквивалентности на такое что: для любого если и замкнуто относительно следующих правил:

Функции и являются -эквивалентными,
а и — нет.

β-редукция

Определение:

-редукция (англ. -reduction) — это наименьшее соотношение на такое что и замкнуто относительно следующих правил

Определение:

Через обозначают сведение к с помощью одной -редукции. А через — за ноль или более.

В -редукции вполне возможна функция вида . Во время подстановки вместо внутренняя переменная не заменяется – действует принцип локальной переменной. Но принято считать, что таких ситуаций не возникает и все переменные называются разными именами.

Каррирование

Определение:

Каррирование (англ. carrying) — преобразование функции от многих переменных в функцию, берущую свои аргументы по одному. Для функции типа оператор каррирования выполняет преобразование . Таким образом берет аргумент типа и возвращает функцию типа . С интуитивной точки зрения, каррирование функции позволяет фиксировать ее некоторый аргумент, возвращая функцию от остальных аргументов. Таким образом, представляет собой функцию типа .

Нотация Де Брауна

Существует также альтернативное эквивалентное определение -исчисления.
В оригинальном определении для обозначения переменных использовались имена,
и была проблема с тем, что не были запрещены одинаковые имена в разных
абстракциях.

От этой проблемы можно избавиться следующим образом. Вместо имени переменной
будет храниться натуральное число — количество абстракций в дереве разбора,
на которое нужно подняться, чтобы найти ту лямбду, с которой данная переменная
связана. В данной нотации получаются несколько более простые определения
свободных переменных и -редукции.

Грамматику нотации можно задать как:

Примеры выражений в этой нотации:

Standart	de Bruijn
$lambda x.x$	$lambda .0$
$lambda z.z$	$lambda .0$
$lambda x. lambda y.x$	$lambda . lambda .1$
$lambda x. lambda y. lambda s. lambda z.x s (y s z)$	$lambda . lambda . lambda . lambda .3 1(2 1 0)$
$(lambda x.x x)(lambda x.x x)$	$(lambda .0 0)(lambda .0 0)$
$(lambda x. lambda x.x)(lambda y.y)$	$(lambda .lambda .0)(lambda .0)$

Переменная называется свободной, если ей соответствует число, которое больше
количества абстракций на пути до неё в дереве разбора.

При -редукции же нужно будет ко всем свободным переменным заменяющего
дерева при каждой замене прибавить число, равное разницы уровней раньше и сейчас.
Это будет соответствовать тому, что эта переменная продолжит «держаться» за
ту же лямбду, что и раньше.

Нумералы Чёрча и программирование на -исчислении

Определение

Введём на основе лямбда-исчисления аналог натуральных чисел, основанный на идее,
что натуральное число — это или ноль, или увеличенное на единицу натуральное
число.

Каждое число будет функцией двух аргументов: какой-то функции и начального значения.
Число будет раз применять функцию к начальному значению и возвращать
результат. Если такому “числу” дать на вход функцию и в качестве
начального значения, то на выходе как раз будет ожидаемое от функции число:
.

+1

Функция, прибавляющая к числу, должна принимать первым аргументом число.
Но число — функция двух аргументов. Значит, эта функция должна принимать три
аргумента: “число” , которое хочется увеличить, функция, которую надо будет
раз применить, и начальное значение.

Здесь — раз применённая к функция . Но нужно применить
раз. Отсюда .

Сложение

Сложение двух чисел похоже на прибавление единицы. Но только надо прибавить не единицу, а второе число.

раз применить к применённому раз к

Умножение

Умножение похоже на сложение, но прибавлять надо не единицу, а второе число.
Или, в терминах нумералов Чёрча, в качестве применяемой несколько раз
функции должна быть не , а функция, применяющая раз .

Здесь — функция, которая раз применит к тому, что дадут ей на
вход. С помощью -редукции можно немного сократить эту формулу

Возведение в степень

It’s a kind of magic

Логические значения

Функции двух аргументов, возвращающие первый и второй, соответственное, аргументы.
Забавный факт: . Эти функции сделаны такими для того,
чтобы красиво написать функцию :

Если ей в качестве первого аргумента дадут , то вернётся , иначе — .

Стандартные функции булевой логики:

Ещё одной важной функцией является функция проверки, является ли число нулём:

Функция выглядит несколько странно. – функция, которая независимо
от того, что ей дали на вход, возвращает . Тогда, если в качестве
будет дан ноль, то функция, по определению нуля, не выполнится ни разу, и будет
возвращено значение по умолчанию . Иначе же функция будет запущено, и
вернётся .

Пара

Функция принимает два значения и запаковывает их в пару так, чтобы к ним можно было обращаться по и . В и вместо в будет подставлено или , возвращающие, соответственно, первый и второй аргументы, то есть или , соответственно.

Вычитание

В отличие от всех предыдущих функций, вычитание для натуральных чисел определено только в случае, если уменьшаемое больше вычитаемого. Положим в противном случае результат равным нулю. Пусть уже есть функция, которая вычитает из числа единицу. Тогда на её основе легко сделать, собственно, вычитание.

Это то же самое, что раз вычесть единицу из .

Осталось, собственно, функция для вычитания единицы. Однако, это не так просто, как может показаться на первый взгляд. Проблема в том, что, имея функцию, которую нужно применить для того, чтобы продвинуться вперёд, продвинуться назад будет проблематично. Если попробовать воспользоваться идеей о том, чтобы, начав от нуля, идти вперёд, и пройти на один шаг меньше, то будет не очень понятно, как же остановиться ровно за один шаг до конца. Для реализации вычитания единицы сделаем следующее. раз выполним следующее: имея пару построим пару . Тогда после шагов во втором элементе пары будет записано число , которое и хочется получить.

Если вы ничего не поняли, не огорчайтесь. Вычитание придумал Клини, когда ему вырывали зуб мудрости. А сейчас наркоз уже не тот.

Сравнение

Так как вычитание определено таким способом, чтобы для случая, в котором уменьшаемое больше, чем вычитаемое, возвращать ноль, можно определить сравнение на больше-меньше через него. Равными же числа и считаются, если .

Комбинатор неподвижной точки

Попробуем выразить в лямбда-исчислении какую-нибудь функцию, использующую рекурсию. Например, факториал.

Мы столкнулись с проблемой. В определении функции используется функция . При формальной замене, получим бесконечную функцию. Можно попытаться решить эту проблему следующим образом

Определение:

Неподвижной точкой лямбда-функции назовём такую функцию , что .

Лямбда исчисление обладаем замечательным свойством: у каждой функции есть неподвижная точка!

Рассмотрим следующую функцию.

Заметим, что .
Или, что то же самое,

Рассмотрим функцию

Как было показано выше, , то есть, , где — искомая функция, считающая факториал.

Это даст функцию, которая посчитает факториал числа. Но делать она это будет мееедленно-меееедленно. Для того, чтобы посчитать потребовалось сделать 66066 -редукций.

Наиболее известным комбинатором неподвижной точки является -комбинатор, введенный известным американским ученым Хаскеллом Карри как

Деление

Воспользовавшись идеей о том, что можно делать рекурсивные функции, сделаем функцию, которая будет искать частное двух чисел.

И остатка от деления

Проверка на простоту

— принимает число, которое требуется проверить на простоту и то, на что его надо опытаться поделить, перебирая это от до . Если на что-нибудь разделилось, то число — составное, иначе — простое.

Следующее простое число. — следующее, больше либо равное заданного, — следующее, большее заданного.

пропрыгает простых чисел вперёд. принимает число и пропрыгивает столько простых чисел вперёд, начиная с двойки.

…и всего через 314007 -редукций вы узнаете, что третье простое число — семь!

Списки

Для работы со списками чисел нам понадобятся следующие функции:

• — возвращает пустой список
• — принимает первый элемент и оставшийся список, склеивает их
• — вернуть голову списка
• — вернуть хвост списка

Список будем хранить в следующем виде: . При этом, голова списка будет храниться как показатель степени при .

Выводы

На основе этого всего уже можно реализовать эмулятор машины тьюринга: с помощью пар, списков чисел можно хранить состояния. С помощью рекурсии можно обрабатывать переходы. Входная строка будет даваться, например, закодированной аналогично списку: пара из длины и числа, характеризующего список степенями простых. Я бы продолжил это писать, но уже на операции я не дождался окончания выполнения. Скорость лямбда-исчисления как вычислителя печальна.

Примеры (слабонервным не смотреть)

fact

head

tail

См. также

• Неразрешимость задачи вывода типов в языке с зависимыми типами

Источники информации

• Lectures on the Curry Howard – Isomorphism
• Д. Штукенберг. Лекции
• Английская Википедия
• Русская Википедия
• Игра про крокодилов

Ля́мбда-исчисле́ние (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем для формализации и анализа понятия вычислимости.

Чистое λ-исчисление

Чистое λ-исчисление, термы которого, называемые также объектами («обами»), или λ-термами, построены исключительно из переменных применением аппликации и абстракции. Изначально наличие каких-либо констант не предполагается.

Аппликация и абстракция

В основу λ-исчисления положены две фундаментальные операции:

• Аппликация (лат. applicatio — прикладывание, присоединение) означает применение или вызов функции по отношению к заданному значению. Её обычно обозначают [math]displaystyle{ f a }[/math], где [math]displaystyle{ f }[/math] — функция, а [math]displaystyle{ a }[/math] — аргумент. Это соответствует общепринятой в математике записи [math]displaystyle{ f(a) }[/math], которая тоже иногда используется, однако для λ-исчисления важно то, что [math]displaystyle{ f }[/math] трактуется как алгоритм, вычисляющий результат по заданному входному значению. В этом смысле аппликация [math]displaystyle{ f }[/math] к [math]displaystyle{ a }[/math] может рассматриваться двояко: как результат применения [math]displaystyle{ f }[/math] к [math]displaystyle{ a }[/math], или же как процесс вычисления [math]displaystyle{ f a }[/math]. Последняя интерпретация аппликации связана с понятием β-редукции.

• Абстракция или λ-абстракция (лат. abstractio — отвлечение, отделение) в свою очередь строит функции по заданным выражениям. Именно, если [math]displaystyle{ tequiv t[x] }[/math] — выражение, свободно^[en] содержащее [math]displaystyle{ x }[/math], тогда запись [math]displaystyle{ lambda x.t[x] }[/math] означает: λ функция от аргумента [math]displaystyle{ x }[/math], которая имеет вид [math]displaystyle{ t[x] }[/math], обозначает функцию [math]displaystyle{ xmapsto t[x] }[/math]. Таким образом, с помощью абстракции можно конструировать новые функции. Требование, чтобы [math]displaystyle{ x }[/math] свободно входило в [math]displaystyle{ t }[/math], не очень существенно — достаточно предположить, что [math]displaystyle{ lambda x.tequiv t }[/math], если это не так.

α-эквивалентность

Основная форма эквивалентности, определяемая в лямбда-термах, это альфа-эквивалентность. Например, [math]displaystyle{ lambda x.x }[/math] и [math]displaystyle{ lambda y.y }[/math]: альфа-эквивалентные лямбда-термы и оба представляют одну и ту же функцию (функцию тождества). Термы [math]displaystyle{ x }[/math] и [math]displaystyle{ y }[/math] не альфа-эквивалентны, так как они не находятся в лямбда-абстракции.

β-редукция

Поскольку выражение [math]displaystyle{ lambda x. 2cdot x + 1 }[/math] обозначает функцию, ставящую в соответствие каждому [math]displaystyle{ x }[/math] значение [math]displaystyle{ 2cdot x + 1 }[/math], то для вычисления выражения

[math]displaystyle{ (lambda x. 2cdot x + 1) 3, }[/math]

в которое входят и аппликация и абстракция, необходимо выполнить подстановку числа 3 в терм [math]displaystyle{ 2cdot x + 1 }[/math] вместо переменной [math]displaystyle{ x }[/math]. В результате получается [math]displaystyle{ 2cdot 3+1=7 }[/math]. Это соображение в общем виде записывается как

[math]displaystyle{ (lambda x.t) a = t[x:=a] }[/math]

и носит название β-редукция. Выражение вида [math]displaystyle{ (lambda x.t) a }[/math], то есть применение абстракции к некому терму, называется редексом (redex). Несмотря на то, что β-редукция по сути является единственной «существенной» аксиомой λ-исчисления, она приводит к весьма содержательной и сложной теории. Вместе с ней λ-исчисление обладает свойством полноты по Тьюрингу и, следовательно, представляет собой простейший язык программирования.

η-преобразование

[math]displaystyle{ eta }[/math]-преобразование выражает ту идею, что две функции являются идентичными тогда и только тогда, когда, будучи применёнными к любому аргументу, дают одинаковые результаты. [math]displaystyle{ eta }[/math]-преобразование переводит друг в друга формулы [math]displaystyle{ lambda x.f x }[/math] и [math]displaystyle{ f }[/math] (только если [math]displaystyle{ x }[/math] не имеет свободных вхождений в [math]displaystyle{ f }[/math]: иначе свободная переменная [math]displaystyle{ x }[/math] после преобразования станет связанной внешней абстракцией или наоборот).

Каррирование (карринг)

Функция двух переменных [math]displaystyle{ x }[/math] и [math]displaystyle{ y }[/math] [math]displaystyle{ f(x,y) = x + y }[/math] может быть рассмотрена как функция одной переменной [math]displaystyle{ x }[/math], возвращающая функцию одной переменной [math]displaystyle{ y }[/math], то есть как выражение [math]displaystyle{ lambda x.lambda y.x+y }[/math]. Такой приём работает точно так же для функций любой арности. Это показывает, что функции многих переменных могут быть выражены в λ-исчислении и являются «синтаксическим сахаром». Описанный процесс превращения функций многих переменных в функцию одной переменной называется карринг (также: каррирование), в честь американского математика Хаскелла Карри, хотя первым его предложил Моисей Шейнфинкель (1924).

Семантика бестипового λ-исчисления

Тот факт, что термы λ-исчисления действуют как функции, применяемые к термам λ-исчисления (то есть, возможно, к самим себе), приводит к сложностям построения адекватной семантики λ-исчисления. Чтобы придать λ-исчислению какой-либо смысл, необходимо получить множество [math]displaystyle{ D }[/math], в которое вкладывалось бы его пространство функций [math]displaystyle{ D to D }[/math]. В общем случае такого [math]displaystyle{ D }[/math] не существует по соображениям ограничений на мощности этих двух множеств, [math]displaystyle{ D }[/math] и функций из [math]displaystyle{ D }[/math] в [math]displaystyle{ D }[/math]: второе имеет бо́льшую мощность, чем первое.

Эту трудность в начале 1970-х годов преодолел Дана Скотт, построив понятие области [math]displaystyle{ D }[/math] (изначально на полных решётках^[1], в дальнейшем обобщив до полного частично упорядоченного множества со специальной топологией) и урезав [math]displaystyle{ D to D }[/math] до непрерывных в этой топологии функций^[2]. На основе этих построений была создана денотационная семантика^[en] языков программирования, в частности, благодаря тому, что с помощью них можно придать точный смысл таким двум важным конструкциям языков программирования, как рекурсия и типы данных.

Связь с рекурсивными функциями

Рекурсия — это определение функции через себя; на первый взгляд, лямбда-исчисление не позволяет этого, но это впечатление обманчиво. Например, рассмотрим рекурсивную функцию, вычисляющую факториал:

f(n) = 1, if n = 0; else n × f(n – 1).

В лямбда-исчислении функция не может непосредственно ссылаться на себя. Тем не менее, функции может быть передан параметр, связанный с ней. Как правило, этот аргумент стоит на первом месте. Связав его с функцией, мы получаем новую, уже рекурсивную функцию. Для этого аргумент, ссылающийся на себя (здесь обозначен как [math]displaystyle{ r }[/math]), обязательно должен быть передан в тело функции.

g := λr. λn.(1, if n = 0; else n × (r r (n-1)))

f := g g

Это решает специфичную проблему вычисления факториала, но решение в общем виде также возможно. Получив лямбда-терм, представляющий тело рекурсивной функции или цикл, передав себя в качестве первого аргумента, комбинатор неподвижной точки возвратит необходимую рекурсивную функцию или цикл. Функции не нуждаются в явной передаче себя каждый раз.

Существует несколько определений комбинаторов неподвижной точки. Самый простой из них:

Y = λg.(λx.g (x x)) (λx.g (x x))

В лямбда-исчислении, [math]displaystyle{ operatorname{Y g} }[/math] — неподвижная точка [math]displaystyle{ operatorname{g} }[/math]; продемонстрируем это:

Y g

(λh.(λx.h (x x)) (λx.h (x x))) g

(λx.g (x x)) (λx.g (x x))

g ((λx.g (x x)) (λx.g (x x)))

g (Y g)

Теперь, чтобы определить факториал, как рекурсивную функцию, мы можем просто написать [math]displaystyle{ operatorname{g (Y g)} n }[/math], где [math]displaystyle{ n }[/math] — число, для которого вычисляется факториал. Пусть [math]displaystyle{ n = 4 }[/math], получаем:

g (Y g) 4
   (λfn.(1, if n = 0; and n·(f(n-1)), if n>0)) (Y g) 4
   (λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0)) 4
   1, if 4 = 0; and 4·(g(Y g) (4-1)), if 4>0
   4·(g(Y g) 3)
   4·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 3)
   4·(1, if 3 = 0; and 3·(g(Y g) (3-1)), if 3>0)
   4·(3·(g(Y g) 2))
   4·(3·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 2))
   4·(3·(1, if 2 = 0; and 2·(g(Y g) (2-1)), if 2>0))
   4·(3·(2·(g(Y g) 1)))
   4·(3·(2·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 1)))
   4·(3·(2·(1, if 1 = 0; and 1·((Y g) (1-1)), if 1>0)))
   4·(3·(2·(1·((Y g) 0))))
   4·(3·(2·(1·((λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 0))))
   4·(3·(2·(1·(1, if 0 = 0; and 0·((Y g) (0-1)), if 0>0))))
   4·(3·(2·(1·(1))))
   24

Каждое определение рекурсивной функции может быть представлено как неподвижная точка соответствующей функции, следовательно, используя [math]displaystyle{ operatorname{Y} }[/math], каждое рекурсивное определение может быть выражено как лямбда-выражение. В частности, мы можем определить вычитание, умножение, сравнение натуральных чисел рекурсивно.

В языках программирования

В языках программирования под «λ-исчислением» зачастую понимается механизм «анонимных функций» — callback-функций, которые можно определить прямо в том месте, где они используются, и которые имеют доступ к локальным переменным текущей функции (замыкание).

См. также

• Аппликативные вычислительные системы
• Типизированное λ-исчисление
• Комбинаторная логика
• Функциональное программирование
• Теорема Чёрча — Россера
• Анонимная функция

Примечания

Литература

• Барендрегт X. Ламбда-исчисление. Его синтаксис и семантика: Пер. с англ. — М.: Мир, 1985. — 606 с.